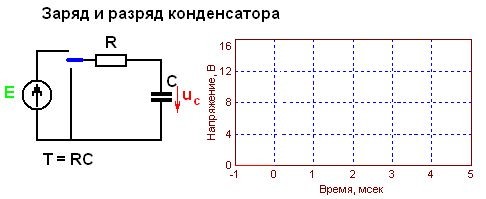
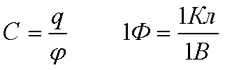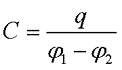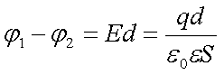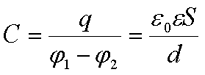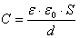Всем доброго времени суток. В прошлой статье я рассказывал о методах расчёта электрических цепей, в которых основным элементом является резистор. Резистор представляет собой один из элементов с сосредоточенными параметрами, в данном случае таким параметром является сопротивление. Однако кроме сопротивления ещё одними из основных параметров элементов цепи являются ёмкость и индуктивность, которые представлены элементами конденсатор и индуктивными элементами (различные дросселя, катушки, трансформаторы и т.д.). В данной статье я рассмотрю такой элемент с сосредоточенными параметрами, как конденсатор.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Проводник в электрическом поле
Помещая проводник в электрическое поле, носители заряда внутри проводника начинают перемещаться. Причем данное перемещение подчиняется двум правилам:
-
Напряжённость электрического поля внутри проводника должно равняться нулю
Это означает, что потенциал внутри проводника остается постоянным (φ = const).
- Напряжённость поля на поверхности проводника направлена перпендикулярно к самой поверхности данного проводника. Или другими словами поверхность проводника становится эквипотенциальной, то есть все точки данной поверхности имеют одинаковый потенциал.
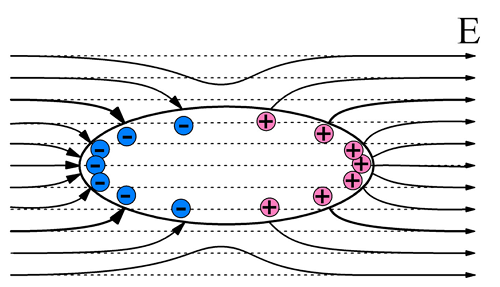
Из этих двух правил следует, что когда проводник вносится в электрическое поле его носители заряда (в металлах это электроны, а в жидкостях – ионы) приходят в движение, причем положительные по направлению напряжённости электрического поля, а отрицательные в противоположную сторону. Результатом движения зарядов в проводнике является возникновение зарядов противоположного знака на концах проводника, такие заряды называют индуцированными. Перераспределение заряда в проводнике показано на рисунке ниже
Распределение носителей зарядов проводника в электрическом поле.
Таким образом, нейтральный проводник, помещённый в электрическое поле, как бы разрывает часть линий электрического поля, а индуцированные заряды распределяются по поверхности проводника.
Практический интерес представляет следующая ситуация, когда внутри проводника имеется некоторая полость. Так как индуцирование зарядов происходит на поверхности проводника, то внутри этого проводника, а значит и во внутренней полости электрическое поле обращается в нуль. На данном явлении основана электростатическая защита, когда необходимо защитить какой-нибудь прибор от воздействия электрического поля, то его помещают внутрь экрана из проводника. Индуцированные заряды на поверхности экрана скомпенсируют электростатическое поле. Вместо сплошного экрана часто используют экран из электропроводящей сетки, что тоже позволяет создать защиту от электростатического поля.
Электроемкость
Если на проводник переместить некоторый заряд q, то он как мы уже знаем, распределится по всей поверхности проводника, так чтобы напряженность электрического поля внутри него была равна нулю. Однако относительно любой точки пространства данный проводник будет обладать некоторым потенциалом φ. Если на данный заряженный проводник переместить ещё один заряд, то опять же он равномерно распределится по всей поверхности проводника, а величина потенциала вырастит на некоторую величину.
Таким образом, между величиной заряда проводника и его потенциалом существует связь, которая определяется следующим выражением
где q – величина заряда, сообщенная проводнику,
φ – потенциал проводника относительно любой точки пространства,
С – коэффициент пропорциональности, называемый электроемкостью проводника, или просто емкостью.
Исходя из этого, электроемкость проводника может быть вычислена из следующего выражения
Таким образом, электроемкость численно равна заряду, передача которого проводнику повышает его потенциал на единицу. Единица измерения электроемкости называется Фарада (обозначается Ф).
Однако емкость уединенного проводника невелика, так емкостью в 1 Ф обладает шар радиусом 9*109 м, что почти в 1500 раз больше радиуса Земли. Поэтому на практике используют специальные устройства для накопления зарядов и обладающие большой емкостью при минимальных размерах. Такие устройства называются конденсаторами.
Конденсаторы
Принцип действия конденсатора основывается на явлении индуцирования зарядов на проводнике в электрическом поле или на свойстве диэлектрика поляризоваться под воздействием электрического поля, а также возрастания электроемкости проводника при приближении к нему других тел. Рассмотрим подробнее.
Как известно из предыдущего параграфа, что если к заряженному телу, вокруг которого существует электрическое поле поднести проводник, то на поднесенном проводнике начнут индуцироваться заряды, в результате чего потенциал заряженного проводника будет уменьшаться, а, следовательно, электроемкость возрастать. Поэтому конденсаторы делают в виде двух близкорасположенных проводников, называемых обкладками конденсатора.
Чтобы ограничить влияние посторонних предметов на электрическое поле конденсатора, а следовательно и его емкость, обкладки изготавливают такими, чтобы электрическое поле создаваемое ими было полностью сосредоточенно внутри конденсатора. Такому условию соответствуют плоские, цилиндрические и сферические конденсаторы.
Так как обкладки расположены очень близко, то практически весь заряд обкладок будет сосредоточен на их внутренних поверхностях, то есть обращённых друг к другу, поэтому емкость конденсатора будет определяться следующим выражением
где q – заряд одной из обкладок конденсатора,
φ1 и φ2 – потенциалы обкладок конденсатора.
Самым простым является плоский конденсатор, его мы и рассмотрим в качестве примера.
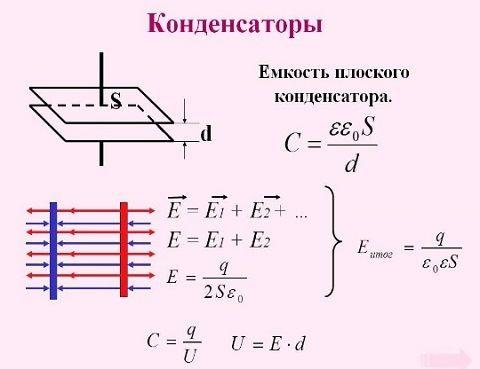
Плоский конденсатор
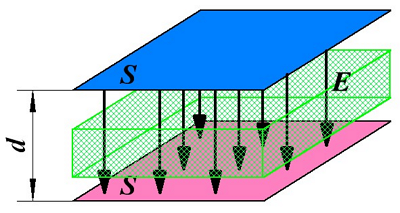
Плоский конденсатор представляет собой две одинаковые пластины площадью S, расположенные параллельно, расстояние между пластинами d очень незначительно по отношению к размерам самих пластин, поэтому практически всё электрическое поле сосредоточенно между пластинами-обкладками. Кроме этого между пластинами расположен диэлектрик, который имеет диэлектрическую проницаемость ε, зависящую от свойств диэлектрика.
Плоский конденсатор.
Тогда разность потенциалов между обкладками конденсатора будет определяться следующим выражением
где S – площадь обкладки конденсатора,
d – расстояние между обкладками,
ε0 – электрическая постоянная, ε0 = 8,85 * 10-12 Кл2/(Н*м2),
ε – относительная диэлектрическая проницаемость диэлектрика, зависящая от его свойств.
Тогда емкость плоского конденсатора будет определяться по следующей формуле
На этом с физикой, пожалуй, закончим и приступим к электронике.
Реальный конденсатор
В прошлой статье я рассказал об идеальных элементах электрических схем (я рассматривал сопротивление, как идеальный резистор). Идеальный элемент конденсатор отличается от реального конденсатора наличием паразитных характеристик, для определения этих характеристик рассмотрим эквивалентную схему реального конденсатора изображённую ниже
Эквивалентная схема замещения конденсатора.
Кроме непосредственно емкости конденсатора можно выделить следующие параметры, которые являются паразитными и в некоторых схемах не позволяют использовать конденсаторы некоторых типов. Таким параметрами являются сопротивление утечки Rут, эквивалентное последовательное сопротивление RЭПС (или ESR) и эквивалентная последовательная индуктивность LЭПИ (или ESL). Разберём каждый параметр в отдельности.
Сопротивление утечки Rут конденсатора определяется как отношение постоянного напряжения, до которого заряжен конденсатор Uc к току утечки Iут
эквивалентную схему реального конденсатора изображённую ниже
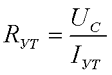
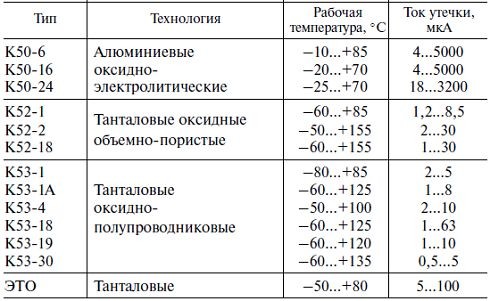
Ток утечки существует в любом случае, так как сопротивление изоляции и диэлектрика не может быть бесконечным. Вследствие этого заряженный конденсатор с течением времени теряет некоторый заряд. Поэтому часто в документации на конденсаторы вводится параметр постоянная времени саморазряда конденсатора Т = RутС0.
Современные высококачественные конденсаторы имеют постоянную времени саморазряда несколько сотен тысяч часов.
Эквивалентное последовательное сопротивление RЭПС или ESR довольно важный параметр в некоторых схемах, в частности, в схемах выпрямления импульсных блоков питания и стабилизаторах напряжения. Связан с непосредственным сопротивлением обкладок конденсатора и его выводов, а также с потерями в диэлектрике. Довольно часто служит показателем исправности конденсатора и для его измерения используют приборы ESR-метры.
Эквивалентная последовательная индуктивность LЭПИ или ESL, данный параметр обусловлен, прежде всего, индуктивностью обкладок конденсатора и его выводов. Данный паразитный параметр вместе с емкостью конденсатора образует последовательный колебательный контур с собственной частотой резонанса. Поэтому для конденсаторов нормируется максимальная частота работы.
Тангенс угла потерь конденсатора tgδ характеризует работу конденсатора при переменном напряжении. В идеальном конденсаторе, в котором отсутствуют паразитные параметры tgδ = 90°. Но в реальных конденсаторах часть энергии рассеивается на сопротивлении обкладок и в диэлектрике, то есть на RЭПС вследствие чего tgδ отличается от 90° в меньшую сторону. Тангенс угла потерь вычисляется по следующему выражению
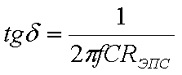
В следующих статьях я расскажу о работе конденсаторов при переменном напряжении, где проявляются основные свойства данного электронного компонента.
|
Гл. 6. Постоянный электрический ток |
181 |
|
§6.2. Основные типы задач (классификация)
6.1.Определение сопротивления, электрических полей, напряжений и тока утечки в сплошной среде.
6.2.Определение теплоты, выделяющейся в проводнике (среде), при протекании тока.
6.3.Расчет цепей квазилинейных проводников.
6.4.Расчет разветвленных цепей, сводимых к неразветвленным благодаря элементам симметрии.
§6.3. Методы решения и примеры решения задач
Задачи типа 6.1
Определение сопротивления, электрических полей, напряжений и тока утечки в сплошной проводящей среде
Метод решения. При рассмотрении токов в проводящих средах и нахождении сопротивления среды между электродами целесообразно придерживаться следующей схемы решения задачи (электрод – эквипотенциальный проводник, электропроводность которого много больше электропроводности среды).
Для расчета сопротивления по закону Ома нужно найти отношение напряжения на электродах U и полного тока I через систему.
В качестве исходного параметра удобнее всего взять полный ток I, поскольку величины зарядов на электродах заранее могут быть не очевидны.
а) Начать решение целесообразно с нахождения плотности тока j(r), поскольку при протекании постоянного тока для j(r) всегда соблюдается соотношение (6.2) div j = 0, независимо от особенностей диэлектрических и проводящих свойств среды. С другой стороны, j(r) легко связать с полным током через электрод соотношением (6.4). В задачах с симметрией условие (6.2) обычно позволяет сразу определить характер зависимости плотности тока j от координат.
б) Далее, пользуясь дифференциальным законом Ома (6.3), перейти к напряженности электрического поля E(r) = ρ(r) j(r).
в) Зная Е(r), интегрированием можно найти разность потенциалов (напряжение) между электродами 1 и 2:

182 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
(2)
U = − ∫E(r)dr .
(1)
Используя закон Ома (6.5), определить сопротивление среды между электродами
R = U .
I
Таким образом, задача решается в следующей последовательности:
Если проводящая среда однородна, то поле полностью определяется зарядами и потенциалами электродов, и можно исходным параметром взять напряжение на электродах и решать в обратной последовательности:
или же исходить из свободного заряда на электродах ±q и решать по схеме:
Однако в случае неоднородной проводимости среды простой переход U → E или q → E невозможен. Поле Е будет определяться при этом не только геометрическими факторами и напряжением U или зарядом электродов q, но и характером зависимости ρ(r) из-за появления в проводящей среде ненулевой плотности свободных зарядов.
Задача 6.3.1. На плоский конденсатор ёмкостью С подано постоянное напряжение U. Найти ток утечки через конденсатор, если удельное сопротивление однородного вещества, которым заполнен зазор между обкладками конденсатора, равно ρ, а диэлектрическая
проницаемость равна ε.
Решение
Так как напряжение на обкладках конденсатора постоянно, а среда, заполняющая пространство между его обкладками, однородна, то для нахождения тока утечки, текущего через конденсатор можно воспользоваться схемой (6.17).

|
Гл. 6. Постоянный электрический ток |
183 |
|
Электростатическое поле конденсатора однородно и напряжен-
ность его равна E = U , где d – расстояние между обкладками. d
U
Согласно закону Ома в дифференциальной форме (6.3) j = ρd . Сила тока, текущего между обкладками равна
|
I = jS = |
US |
= |
UC |
, |
||
|
ρd |
ρεε0 |
|||||
|
где учтено, что |
емкость плоского |
конденсатора C = εε0S d (см. |
||||
|
(3.7), глава 3). |
||||||
|
Ответ: I = |
UC |
. |
||||
|
ρεε0 |
Замечание. Возможен также более короткий способ решения данной задачи, основанный на использовании соотношении (6.7) теоретического материала. Так как среда, заполняющая пространство между обкладками конденсатора однородна, то согласно (6.7) её сопротивление равно R = ρεε0 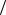
Задача 6.3.2 (базовая задача). Пространство между обкладками плоского конденсатора заполнено последовательно двумя диэлектрическими слоями толщиной d1 и d2, диэлектрические проницаемости и удельные сопротивления которых соответственно равны ε1, ε2, ρ1 и ρ2, площадь каждой из пластин равна S (рис. 6.4). Опре-
делить:
1) общее сопротивление конденсато-
ра;
2) заряд пластин конденсатора, если он подключен к источнику постоянного напряжения U.
Решение
1) Виду неоднородности проводимости среды вдоль линий тока, воспользуемся схемой решения (6.16).
Так как ток однороден и постоянен, то
+q1 –q2
q12
Рис. 6.4. Конденсатор с утечкой, заполненный двумя
разными материалами (задача 6.3.2)

184 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
j1 = j2= j = I .
S
Из закона Ома в дифференциальной форме (6.3) получаем напряженности полей в слоях 1 и 2:
E1 = ρ1 j, E2 = ρ2 j.
Ввиду однородности полей для напряжения между обкладками конденсатора получим
U = ϕ1 − ϕ2 = E1d1 + E2d2 = j(ρ1d1 +ρ2d2),
откуда находим плотность тока и полную силу тока через конденсатор
|
j = |
U |
, |
I = jS = |
U |
S . |
|||||||||
|
ρ d + ρ |
d |
2 |
ρ d |
1 |
+ ρ |
2 |
d |
2 |
||||||
|
1 |
1 |
2 |
1 |
Используя закон Ома (6.5), найдем сопротивление данного слоистого конденсатора
R = U = ρ1d1 + ρ2d2 .
IS
2)Для нахождения заряда пластин можно воспользоваться граничным условием для нормальной компоненты вектора электрического смещения
D2n – D1n = σ,
где σ – поверхностная плотность свободных зарядов, n – вектор нормали в направлении сред 1 → 2. Учитывая, что вне конденсатора D = 0, для левой пластины получим
σ1 = D1 = ε0ε1E1,
для правой пластины
σ2 = –D2 = –ε0ε2E2.
Напряженности полей E1 и E2 легко найти из найденной плотности тока:
|
E1 = jρ1 = |
Uρ1 |
; |
E2 = jρ2 = |
Uρ2 |
. |
||||||||
|
ρ d + ρ |
d |
2 |
ρ d + ρ |
d |
2 |
||||||||
|
1 |
1 |
2 |
1 |
1 |
2 |
Далее можно определить полный заряд каждой из пластин:
|
q1 = σ1S = ε0 |
ε1 ρ1 |
SU и |
q2 = σ2S = −ε0 |
ε2 ρ2 |
SU . |
||||||||
|
ρ d + ρ |
d |
2 |
ρ d + ρ |
2 |
d |
2 |
|||||||
|
1 |
1 |
2 |
1 |
1 |

|
Гл. 6. Постоянный электрический ток |
185 |
|
|
Ответ: 1) R = ρ1d1 + ρ2d2 |
; |
||||||||||||||
|
S |
|||||||||||||||
|
2) |
q1 = ε0 |
ε1 ρ1 |
SU ; |
q2 = −ε0 |
ε2 ρ2 |
SU . |
|||||||||
|
ρ d + ρ |
2 |
d |
2 |
ρ d |
1 |
+ ρ |
d |
2 |
|||||||
|
1 |
1 |
1 |
2 |
Замечание.В отличие от случая конденсатора с непроводящей средой или средой проводящей, но имеющей однородную проводимость, здесь заряды обкладок не равны друг другу: |q1| ≠ |q2|. Такая система эквивалентна двум последовательно включённым конденсаторам с утечкой. Причина в том, что при заряде такого конденсатора на границе раздела сред также накапливаются свободные заряды, поверхностная плотность которых равна
|
σ = D |
− D |
= ε |
ε2ρ2 − ε1ρ1 |
U , |
||||||
|
12 |
2n |
1n |
0 ρ d |
1 |
+ ρ |
d |
2 |
|||
|
1 |
2 |
а полный заряд на этой границе будет
|
q = σ S = ε |
ε2ρ2 − ε1ρ1 |
SU . |
|||||||
|
12 |
12 |
0 ρ d |
1 |
+ ρ |
2 |
d |
2 |
||
|
1 |
Знак этого заряда определяется знаком выражения ε2ρ2 – ε1ρ1, т.е. зависит от параметров сред. Очевидно, что |q12| =| |q1| – |q2| |.
Полный заряд q, получаемый конденсатором при зарядке, равен большему по модулю из зарядов пластин q = max (|q1|, |q2|). Заряд противоположного знака той же суммарной величины будет находиться на противоположной пластине и внутри конденсатора на поверхности раздела сред.
Задача 6.3.3. Между двумя концентрическими сферами (1) и (2) из идеального проводника, находится вещество с удельным сопротивлением ρ и диэлектрической проницаемостью ε = 1. Определить сопротивление R такого слоя, если его внешний радиус в два раза больше внутреннего, равного а (рис. 6.5).
Решение
(1)
(2)
Рис. 6.5. Сферический проводящий слой (за-
|
Так как среда однородна (ρ = const), объ- |
дача 6.3.3) |
|
ёмная плотность заряда внутри вещества рав- |
на нулю. Считая внутреннюю и внешнюю сферы идеальными про-

186 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
водниками, их можно рассматривать как электроды с равными по модулю зарядами +q и –q и решать задачу согласно схеме 6.18.
Согласно теореме Гаусса ((1.10), глава 1) напряженность электрического поля в пространстве между сферами (a < r < 2a) равна
|
E = |
q |
. |
|||||||||||||||
|
4πε |
r2 |
||||||||||||||||
|
0 |
|||||||||||||||||
|
Напряжение между сферами можно найти как |
|||||||||||||||||
|
r2 |
2a |
q |
2a |
q |
1 |
1 |
q |
||||||||||
|
− |
= |
− |
= |
. |
|||||||||||||
|
U = ϕ1 − ϕ2 = ∫Edr = ∫Edr = |
4πε0 |
8πε0a |
|||||||||||||||
|
r1 |
a |
4πε0r |
a |
a |
2a |
||||||||||||
Определим силу тока, текущего в такой системе. Так как заряды на электродах постоянны, то через любую поверхность (концентрическую сферу радиуса a ≤ r ≤ 2a) сила тока одинакова и равна
|
I = λES = |
1 q |
4πr2 = |
q |
. |
|||||
|
ρ 4πε |
r2 |
||||||||
|
ρε |
0 |
||||||||
|
0 |
|||||||||
|
Согласно закону Ома (6.5) R = |
U |
= |
ρ |
. |
|||||
|
I |
8πa |
ρ
Ответ: R = 8πa .
Замечание 1. Сопротивление безграничной среды с удельным сопротивлением ρ, окружающей уединенную проводящую сферу
ρ
радиуса а, равно R∞ = 4πa , так как в этом случае r2→∞.
Замечание 2. Используя связь между сопротивлением однородной среды и её ёмкостью данную задачу можно решить короче. Так как ёмкость сферического конденсатора равна (см. (3.9) главы 3)
|
C = |
4πε0 R1R2 |
= 8πε |
a , |
то воспользовавшись соотношением (6.7) |
||
|
0 |
||||||
|
R2 − R1 |
||||||
|
будем иметь R = |
ρε0 |
= |
ρ |
. |
||
|
C |
8πa |
Задача 6.3.4. Доказать справедливость соотношения (6.7), то есть показать, что сопротивление однородной проводящей среды, заполняющей всё пространство, между двумя идеально проводя-

|
Гл. 6. Постоянный электрический ток |
187 |
|
щими телами произвольной формы, равно R = εε0 . Здесь С – ём-
λC
кость системы, λ – удельная электропроводность вещества, ε – его диэлектрическая проницаемость.
Решение
Ввиду однородности среды будем следовать схеме (6.18). Пусть проводники (электроды) заряжены одинаковыми по величине, но разными по знаку зарядами ± q , а напряжение между ними
U = q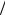
Вектор электрической индукции вблизи поверхности каждого проводника перпендикулярен поверхности и равен D = σ (где σ – поверхностная плотность свободного заряда на проводнике). Напряженность электростатического поля вблизи поверхности
E = D = σ . εε0 εε0
Согласно закону Ома в дифференциальной форме (6.3) вектор плотности тока параллелен вектору напряженности поля и поэтому вблизи поверхности проводников перпендикулярен поверхности и
λσ
по модулю равен j = jn = λE = εε0 .
Силу тока через электрод можно найти интегрированием плотности тока по поверхности электрода
|
I = ∫ jdS = |
λ |
∫σdS = |
λq |
= λ |
CU |
. |
|||||
|
εε |
|||||||||||
|
S |
εε |
0 S |
0 |
εε |
0 |
||||||
|
Используя закон Ома (6.5), окончательно получаем |
|||||||||||
|
R = |
U |
= εε0 . |
|||||||||
|
I |
λC |
Замечание. Поместим в однородную проводящую среду, заполняющую всё пространство, локализованный заряд объёмной плотности ρ0. Электрическое поле, создаваемое этим зарядом, вызовет ток плотности j = λE, который будет уменьшать объёмную плот-
|
ность заряда. Из соотношений (4.6) D = εε0E и (4.8) |
divD = ρ тео- |
||
|
ретического материала главы 4 следует, что divE = |
ρ |
. Подставив |
|
|
εε0 |

188 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
|
полученное |
выражение в |
уравнение |
непрерывности (6.1) |
|||||||
|
∂ρ + div j = 0, имеем: |
||||||||||
|
∂t |
||||||||||
|
∂ρ + div(λE)= ∂ρ + |
λρ |
= 0 . |
||||||||
|
εε0 |
||||||||||
|
∂t |
∂t |
|||||||||
|
Или |
dρ |
= − |
λ |
dt . |
||||||
|
ρ |
εε0 |
|||||||||
|
Учитывая начальное условие, ρ |
t=0 = ρ0 |
получаем, что с тече- |
||||||||
нием времени плотность заряда будет уменьшаться по закону:
|
t |
|||||
|
ρ = ρ0 exp |
− |
, |
|||
|
τ |
|||||
|
где τ = |
εε0 |
= RC – время релаксации. |
|||
|
λ |
|||||
Задача 6.3.5. Определить сопротивление единицы длины провода круглого сечения радиусом b, сделанного из материала, удельная электропроводность которого зависит от расстояния r до оси
провода по закону λ = αr2 , где α – постоянная величина. Считать, что длина проводника много больше его диаметра.
Решение
Рис. 6.6. К определению сопротивления единицы длины провода круглого сечения (задача 6.3.5)
Выберем цилиндрическую систему координат, ось Z которой совпадает с осью провода (см. рис. 6.6).
Данный проводник можно представить как совокупность тонких цилиндрических слоев, сопротивление каждого из которых (в расчете на единицу длины) одинаково по всей длине проводника. В пределах такого слоя плотность тока j также постоянна.
Пусть напряжение между точками на оси проводника, находящимися на расстоянии l друг от друга равно U. Используя закон Ома в дифференциальной форме, получим

|
Гл. 6. Постоянный электрический ток |
189 |
|
j = λE = λ U . l
Таким образом, плотность тока в слое толщины dr, находящемся на расстоянии r от оси Z, будет равна
j = λ U = αUr2 . l l
Согласно (6.4) найдем полную силу тока
|
b |
U r2 |
πb4 |
||||||||||
|
I = ∫ jdS = ∫ |
α |
2πr dr = αU |
. |
|||||||||
|
l |
||||||||||||
|
S |
0 |
2l |
||||||||||
|
Тогда по закону Ома для участка цепи (6.5) сопротивление уча- |
||||||||||||
|
стка провода длиной l = 1 м равно |
||||||||||||
|
R = |
U |
= |
2 |
. |
||||||||
|
απb4 |
||||||||||||
|
l |
I |
|||||||||||
|
Ответ: R = |
2 |
. |
||||||||||
|
απb4 |
||||||||||||
|
l |
Задача 6.3.6 (базовая задача). Зазор между обкладками плоского конденсатора заполнен веществом с диэлектрической проницаемостью ε и с удельной проводимостью, меняющейся в направлении, перпендикулярном к обкладкам, по линейному закону от λ1 до λ2. Площадь пластин S, ширина зазора d. На конденсатор подано напряжение U.
Найти: 1) ток I через конденсатор; 2) заряды пластин q1 и q2; 3) заряд конденсатора q; 4) плотность свободных зарядов ρсвоб(x) внутри зазора; 5) плотность связанных (поляризационных) зарядов ρ′(x) в среде; 6) полный свободный заряд в среде qсвоб.
Решение
Ввиду неоднородности среды в направлении протекания тока воспользуемся схемой (6.16).
Запишем линейный закон изменения удельной проводимости λ (x) = λ1 + αx. Для нахождения α подставим граничное условие:
λ(d) = λ1 + αd = λ2 . Отсюда получаем, что α = λ2 − λ1 , и d

190 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
λ(x) = λ1 + λ2 − λ1 x . d
В плоском конденсаторе плотность тока везде однородна и постоянна j = I / S = const. Однако напряженность электрического поля
|
j |
|||||||||||||||||
|
уже будет зависеть от х: |
E(x) = |
. |
|||||||||||||||
|
λ(x) |
|||||||||||||||||
|
Для напряжения между пластинами получаем |
|||||||||||||||||
|
U = ϕ − ϕ |
= d |
E(x)dx = jd |
dx |
= |
j |
ln |
λ2 |
, |
|||||||||
|
2 |
|||||||||||||||||
|
1 |
∫ |
∫λ |
+ αx |
α λ |
|||||||||||||
|
1 |
|||||||||||||||||
|
0 |
0 |
1 |
|||||||||||||||
|
Таким образом, j = |
αU |
и |
|||||||||||||||
|
ln(λ2 /λ1) |
|||||||||||||||||
|
I = jS = |
αSU |
= |
λ2 − λ1 |
SU . |
|||||||||||||
|
ln(λ2 /λ1) |
d ln(λ2 /λ1) |
Согласно закону Ома (6.5) сопротивление конденсатора равно
|
R = |
U |
= |
d |
ln(λ2 /λ1) |
. |
||
|
I S λ |
2 |
− λ |
|||||
|
1 |
Заряды пластин определим аналогично задаче 6.3.2 из граничных условий для вектора электрического смещения, величина которого в среде
|
D(x) = ε0ε·E(x) = ε0ε |
j |
. |
|||
|
λ(x) |
|||||
|
На левой пластине (х = 0): |
|||||
|
q = Sσ = SD(0) = εε0 jS |
= εε0I |
= |
(λ2 − λ1)SU |
, |
|
|
1 |
1 |
λ1 |
λ1 |
λ1d ln(λ2 /λ1) |
|
на правой пластине (x = d):
|
q |
= Sσ |
= −SD(d) = − εε0 jS |
= − εε0I = − |
(λ2 − λ1)SU |
. |
||
|
2 |
2 |
||||||
|
λ2 |
λ2 |
λ2d ln(λ2 /λ1) |
|||||
Полный заряд q, получаемый конденсатором при зарядке, равен большему по модулю из зарядов пластин: q = max (|q1|, |q2|).
Объемную плотность свободных зарядов в среде можно найти
как
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.
В чем измеряется емкость конденсатора
Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.
Для измерения емкости применяется единица – фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме.
Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q – заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.
Для расчетов емкости плоского конденсатора используется формула:
в которой ε = 8,854187817 х 10-12 ф/м представляет собой постоянную величину. Прочие величины: ε – является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S – означает площадь обкладки, а d – зазор между обкладками.
Формула энергии конденсатора
С емкостью самым тесным образом связана другая величина, известная как энергия заряженного конденсатора. После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.
В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.
Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.
Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed. Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде: W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: Wэл = CU2/2.
Формула заряда конденсатора
Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: Uc = E.
Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.
В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).
Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома Iзар = Е/Ri, поскольку к сопротивлению Ri приложена вся ЭДС генератора.
Формула тока утечки конденсатора
Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.
Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора – способность получать и сохранять заряд электрического тока.
Основная формула для расчета выглядит следующим образом: Iут = U/Rd, где Iут, – это ток утечки, U – напряжение, прилагаемое к конденсатору, а Rd – сопротивление изоляции.
Сопротивление – утечка – конденсатор
Cтраница 1
Сопротивление утечки конденсатора должно значительно превышать сопротивление нагрузки RH.
[1]
Сопротивление утечки конденсаторов зависит от их типа. У металлобумажных конденсаторов, наиболее распространенных в схемах с УЗ, сопротивление утечки составляет примерно 600 – 1000 МОм / мкФ при температуре 20 С, но падает до 40 – 60 МОм / мкФ при температуре 60 С.
[2]
Сопротивление утечки конденсатора некоторой емкости можно определить по данным табл. 3 – 4 как отношение удельного сопротивления к величине емкости.
[3]
Сопротивления утечки конденсаторов С и С2 пренебрежимо малы.
[5]
Определяют сопротивление утечки конденсатора Сь включая его в цепь вместо сопротивления.
[6]
Величина сопротивления утечки конденсатора у обратно пропорциональна его емкости С.
[8]
Следует отметить, что величина сопротивления утечки конденсаторов г, а следовательно, и величина т ] ( табл. 3 – 2 и 3 – 3) зависят от температуры окружающей среды. Сопротивление утечки при увеличении температуры уменьшается. При соизмеримости сопротивлений утечек конденсаторов с сопротивлениями С-цепей окружающая температура оказывает влияние на основные параметры рассмотренных элементов.
[9]
Это ограничение связано с соизмеримостью сопротивления утечки конденсатора и входного сопротивления усилителей с сопротивлением, определяющим постоянную интегрирования, а также с ограниченностью значений коэффициентов усиления усилителей.
[10]
Увеличение емкости Cg связано с уменьшением сопротивления утечки Rym конденсатора), что может привести, как показано ниже, к нежелательным последствиям.
[11]
Необходимо учитывать как емкость, так и сопротивление утечки конденсатора С. Эти конденсаторы позволяют расширить диапазон токов для заряда С, что позволяет изменять длительность времени заряда. Температурная зависимость для тефлоно-вых конденсаторов имеет отрицательный коэффициент – 10 – 4 1 / С и они сохраняют работоспособность до 125 С. Емкость не зависит от температуры до 65 С, а затем быстро увеличивается с ростом температуры.
[12]
Для таких цепей необходимо при расчетах учитывать сопротивления утечек конденсаторов и входные сопротивления усилителей.
[13]
На сетку лампы Л4 ( Л5) через сопротивление утечки Конденсатора попадает постоянное напряжение.
[14]
Страницы:
1
2
3
4
Как найти ток утечки через конденсатор?
|
Между обкладками плоского конденсатора находится диэлектрик, удельное сопротивление которого изменяется по линейному закону от r1=110^11 Омм до r2=110^10 Омм. Найти ток утечки через конденсатор, если разность потенциалов между обкладками U=200 В. Площадь обкладок S=200 см^2 и расстояние между ними d=3 мм.
задан niden 100% принятых |
1 ответ
Из условия задачи не совсем понятно, от чего зависит удельное сопротивление диэлектрика (известно только, что зависимость линейная). Предположив, что это зависимость от координаты в направлении, перпендикулярном пластинам, получаем:
$$R=ρS/d=(ρ1+ρ2)S/2d$$
$$I = U/R$$
Здравствуйте
Физика – это совместно редактируемый форум вопросов и ответов по естественным наукам для физиков, химиков, астрономов и биологов.
Присоединяйтесь!
отмечен:
ток
×18
задан
3 Апр ’14 23:48
показан
2983 раза
обновлен
4 Апр ’14 19:21
Связанные вопросы
Отслеживать вопрос
по почте:
Зарегистрировавшись, вы сможете подписаться на любые обновления
по RSS:
Ответы
Ответы и Комментарии