Схемы замещения и сопротивления элементов сети



При расчетах токов КЗ необходимо определить сопротивления элементов и ЭДС, входящих в расчетную схему сети. Для этого необходимо элемент представить его схемой замещения и определить параметры этой схемы.
Схема замещения – это электрическая схема, в которой все магнитные связи заменяются электрическими, источники питания представляются ЭДС и сопротивлениями, а элементы СЭС, связывающие источники питания с точкой КЗ – сопротивлениями.
Сопротивления одного провода воздушной или одной жилы кабельной линии электропередачи:
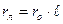 ; (2)
; (2)
индуктивное сопротивление прямой последовательности
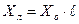 , (3)
, (3)
где 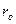 – погонное активное сопротивление проводов ВЛ или жил кабеля КЛ при расчетной температуре,
– погонное активное сопротивление проводов ВЛ или жил кабеля КЛ при расчетной температуре,  , т.е. сопротивление
, т.е. сопротивление 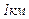 провода ВЛ или жилы кабеля КЛ; принимается по каталожным данным, исходя из материала и сечения провода (жилы) и конструкции кабеля (приложения Б, В);
провода ВЛ или жилы кабеля КЛ; принимается по каталожным данным, исходя из материала и сечения провода (жилы) и конструкции кабеля (приложения Б, В);
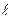 – длина линии,
– длина линии, 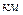 ;
;
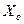 – погонное индуктивное сопротивление прямой последовательности проводов ВЛ или жил КЛ; принимается по справочным таблицам для КЛ, исходя из сечения жил, конструкции и напряжения кабеля (приложение В), для ВЛ – марки (материала) и сечения провода, напряжения и среднего геометрического расстояние между проводами разных фаз (приложения А, Б); среднее геометрическое расстояние между проводами фаз ВЛ равно
– погонное индуктивное сопротивление прямой последовательности проводов ВЛ или жил КЛ; принимается по справочным таблицам для КЛ, исходя из сечения жил, конструкции и напряжения кабеля (приложение В), для ВЛ – марки (материала) и сечения провода, напряжения и среднего геометрического расстояние между проводами разных фаз (приложения А, Б); среднее геометрическое расстояние между проводами фаз ВЛ равно
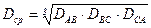 . (4)
. (4)
Если отсутствуют данные о сечениях проводов и жил, допустимо принимать для ВЛ напряжением до 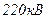
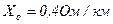 [1], для КЛ напряжением
[1], для КЛ напряжением 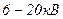
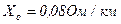 [3].
[3].
Схемы замещения выше рассмотренных элементов представляют цепочки из последовательно соединенных активного и индуктивного сопротивлений, рассчитываемых соответственно по формулам 2 и 3.
Для трехфазного двухобмоточного трансформатора необходимо определить активное и индуктивное сопротивления одной фазы трансформатора.
Условное графическое обозначение в расчетной схеме и упрощенная (без учета цепи намагничивания) схема замещения одной фазы этого трансформатора показаны на рисунке 4.
а) 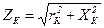 б)
б)
Рисунок 4 – Условное графическое обозначение в расчетной схеме и схема замещения одной фазы двухобмоточного трансформатора
а) условное графическое обозначение;
Активное сопротивление одной фазы
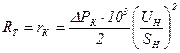 , (5)
, (5)
где 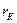 – активное сопротивление короткого замыкания;
– активное сопротивление короткого замыкания;
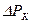 – потери короткого замыкания,
– потери короткого замыкания,  , (из приложений Г и Д);
, (из приложений Г и Д);
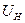 – номинальное напряжение трансформатора на стороне КЗ,
– номинальное напряжение трансформатора на стороне КЗ, 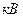 ;
;
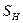 – номинальная мощность трансформатора,
– номинальная мощность трансформатора, 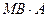 .
.
Индуктивное сопротивление одной фазы
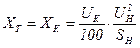 , (6)
, (6)
где 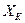 – индуктивное сопротивление короткого замыкания;
– индуктивное сопротивление короткого замыкания;
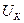 – номинальное напряжение короткого замыкания трансформатора,
– номинальное напряжение короткого замыкания трансформатора, 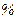 , (из приложений Г и Д).
, (из приложений Г и Д).
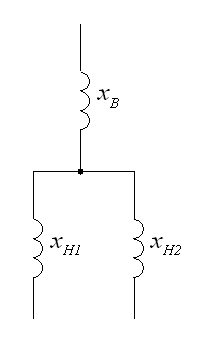
Для трехфазного двухобмоточного трансформатора с обмоткой низшего напряжения, расщепленной на две ветви, определяют индуктивные сопротивления ветвей схемы замещения одной фазы трансформатора.
Условное графическое обозначение в расчетной схеме и схема замещения показаны на рисунке 5.
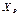
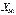
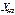



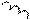
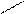


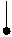
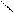
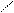 а) б)
а) б)
Рисунок 5 – Условное графическое обозначение в расчетной схеме и схема замещения одной фазы трансформатора с расщепленной обмоткой НН
а) условное графическое обозначение;
Как видно из рисунка 5б, схема замещения представляет трехлучевую звезду, индуктивные сопротивления лучей которой
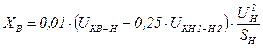 ;
;
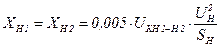 , (7)
, (7)
где 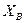 – индуктивное сопротивление фазной обмотки ВН;
– индуктивное сопротивление фазной обмотки ВН;
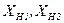 – индуктивные сопротивления ветвей фазной обмотки НН;
– индуктивные сопротивления ветвей фазной обмотки НН;
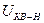 – номинальное напряжение короткого замыкания между обмоткой ВН и параллельно соединенными ветвями обмотки НН,
– номинальное напряжение короткого замыкания между обмоткой ВН и параллельно соединенными ветвями обмотки НН, 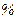 , (из приложений Г, Д);
, (из приложений Г, Д);
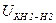 – номинальное напряжение короткого замыкания между ветвями обмотки НН при разомкнутой обмотке ВН,
– номинальное напряжение короткого замыкания между ветвями обмотки НН при разомкнутой обмотке ВН, 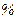 , (из приложений Г, Д).
, (из приложений Г, Д).
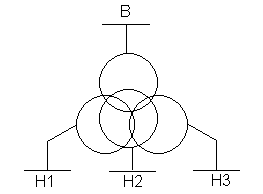
Для трехфазного трехобмоточного трансформатора определяют активное и индуктивное сопротивления обмоток одной фазы трансформатора.
Условное графическое обозначение в расчетной схеме и схема замещения одной фазы этого трансформатора приведены на рисунке 6.
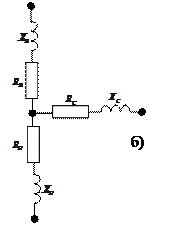

Рисунок 6 – Условное графическое обозначение в расчетной схеме и схема замещения одной фазы трехобмоточного трансформатора
а) условное графическое обозначение;
Схема замещения представляет трехлучевую звезду, сопротивления ветвей которой равны сопротивлениям фазных обмоток ВН, СН и НН.
Активные сопротивления ветвей схемы замещения (фазных обмоток)
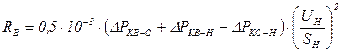 ;
;
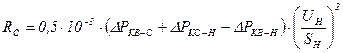 ; (8)
; (8)
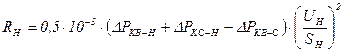 ,
,
где 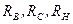 – активные сопротивления соответственно фазных обмоток ВН, СН и НН;
– активные сопротивления соответственно фазных обмоток ВН, СН и НН;
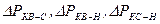 – потери короткого замыкания соответствующих пар обмоток,
– потери короткого замыкания соответствующих пар обмоток,  , (из приложений Г, Д).
, (из приложений Г, Д).
Индуктивные сопротивления лучей схемы замещения (фазных обмоток)
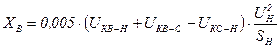 ;
;
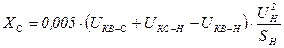 ; (9)
; (9)
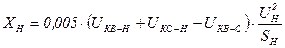 ,
,
где 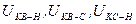 – номинальные напряжения короткого замыкания соответствующих пар обмоток,
– номинальные напряжения короткого замыкания соответствующих пар обмоток, 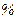 , (из приложений Г, Д).
, (из приложений Г, Д).
Если для трехобмоточного трансформатора приведено в справочных данных только значение 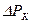 для любой пары обмоток, то допустимо определить активное сопротивление короткого замыкания этой пары обмоток по формуле двухобмоточного трансформатора, найти отношение
для любой пары обмоток, то допустимо определить активное сопротивление короткого замыкания этой пары обмоток по формуле двухобмоточного трансформатора, найти отношение 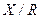 этих обмоток и принять его одинаковым для всех обмоток [1].
этих обмоток и принять его одинаковым для всех обмоток [1].
Одинарный токоограничивающий реактор имеет условное графическое обозначение и схему замещения, изображенные на рисунке 7.






Рисунок 7 – Условное графическое обозначение в расчетной схеме и схема замещения одинарного реактора
а) условное графическое обозначение;
Активное сопротивление одинарного реактора
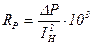 , (10)
, (10)
где 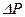 – номинальные потери мощности в реакторе,
– номинальные потери мощности в реакторе,  ;
;
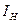 – номинальный ток реактора,
– номинальный ток реактора, 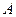 .
.
Индуктивное сопротивление одинарного реактора
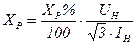 , (11)
, (11)
где 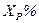 – относительное индуктивное сопротивление реактора,
– относительное индуктивное сопротивление реактора, 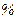 ;
;
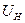 – номинальное напряжение реактора,
– номинальное напряжение реактора, 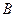 .
.
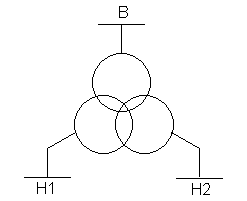
Для сдвоенного токоограничивающего реактора определяют индуктивные сопротивления лучей схемы его замещения, которая представляет собой трехлучевую звезду.
Условное графическое обозначение в расчетной схеме и схема замещения сдвоенного реактора изображены на рисунке 8.
Рисунок 8 – Условное графическое обозначение в расчетной схеме и схема замещения сдвоенного реактора
а) условное графическое обозначение;
Индуктивное сопротивление луча со стороны среднего зажима – зажима, обращенного в сторону источника питания
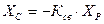 , (12)
, (12)
где 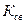 – коэффициент связи между ветвями реактора;
– коэффициент связи между ветвями реактора;
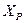 – номинальное индуктивное сопротивление реактора – сопротивление одной ветви реактора при отсутствии тока в другой.
– номинальное индуктивное сопротивление реактора – сопротивление одной ветви реактора при отсутствии тока в другой.
Индуктивные сопротивления двух других лучей схемы замещения
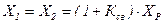 . (13)
. (13)
Условное графическое обозначение и схема замещения синхронного двигателя (СD) приведены на рисунке 9.
Рисунок 9 – Условное графическое обозначение в расчетной схеме и схема замещения синхронного двигателя
а) условное графическое обозначение;
Индуктивное сопротивление фазной обмотки статора СД
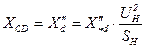 , (14)
, (14)
где 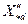 – сверхпереходное относительное индуктивное сопротивление по продольной оси; при отсутствии справочных данных можно принимать [3]
– сверхпереходное относительное индуктивное сопротивление по продольной оси; при отсутствии справочных данных можно принимать [3] 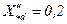 .
.
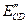 – сверхпереходная ЭДС синхронного двигателя
– сверхпереходная ЭДС синхронного двигателя
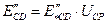 , (15)
, (15)
где 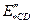 – сверхпереходная относительная ЭДС синхронного двигателя;
– сверхпереходная относительная ЭДС синхронного двигателя;
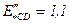 для перевозбужденных,
для перевозбужденных, 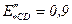 для недовозбужденных СД;
для недовозбужденных СД;
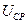 – среднее напряжение сети в месте подключения СД.
– среднее напряжение сети в месте подключения СД.
Активное сопротивление фазной обмотки СД 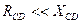 и обычно при расчетах токов КЗ не учитывается.
и обычно при расчетах токов КЗ не учитывается.
Условное графическое обозначение и схема замещения асинхронного двигателя (AD) показаны на рисунке 10.
Рисунок 10 – Условное графическое обозначение в расчетной схеме и схема замещения асинхронного двигателя
а) условное графическое обозначение;
Индуктивное сопротивление фазной обмотки статора AД
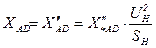 , (16)
, (16)
где 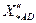 – сверхпереходное относительное индуктивное сопротивление асинхронного двигателя; можно принять [3]
– сверхпереходное относительное индуктивное сопротивление асинхронного двигателя; можно принять [3] 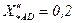 .
.
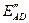 – сверхпереходная ЭДС асинхронного двигателя
– сверхпереходная ЭДС асинхронного двигателя
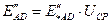 ,
,
где 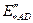 – относительное значение сверхпереходной ЭДС асинхронного двигателя;
– относительное значение сверхпереходной ЭДС асинхронного двигателя; 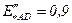 .
.
Активное сопротивление фазной обмотки статора АД 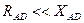 и в расчетах токов КЗ не учитывается.
и в расчетах токов КЗ не учитывается.
Как показывает практика расчетов токов КЗ в сетях напряжением выше 1000В, необходимо обязательно учитывать индуктивные сопротивления электродвигателей, генераторов, трансформаторов, реакторов, воздушных и кабельных ЛЭП, токопроводов и активные сопротивления проводов ВЛ и жил кабелей КЛ.
Источник
Формулы
определения сопротивлений приведены
в относительных единицах при приближенном
приведении к базисным условиям.
Генераторы.
У генераторов
практически никогда не учитывается
активное сопротивление, так как оно
пренебрежительно мало по сравнению с
индуктивным. Номинальное сопротивление
генератора в относительных единицах
![]()
может
быть определено из паспортных данных:
−
![]()
,
![]()
−
синхронные
сопротивления по продольной и поперечной
оси, которые характеризуют установившийся
режим.
−
![]()
и
![]()
,
![]()
и
![]()
− переходные и
сверхпереходные сопротивления в момент
времени t
= 0.
−
![]()
,![]()
− сопротивления
обратной и нулевой последовательностей.
Номинальное
сопротивление генератора в относительных
единицах при базисных
условиях определяется формулой:

.
Двигатели.
Параметры
синхронных электродвигателей определяются
аналогично
генераторам.
Реакторы.
Токоограничивающие
реакторы могут иметь различное устройство
и конструктивное исполнение, а также
технические и технико-экономические
характеристики и параметры.
Линейные
реакторы,
включаемые последовательно в
соответствующую линию, ограничивают
ток КЗ и поддерживают относительно
высокий уровень остаточного напряжения.
Сопротивление линейного реактора можно
определить по формуле:

,
где
![]()
лежит в пределах 0,1…0,4 Ом.
Сдвоенный
реактор
обладает лучшими характеристиками.
Между ветвями реактора существует
магнитная связь, которая в сквозном
режиме позволяет уменьшить потери
напряжения в реакторе. Коэффициент
магнитной связи идентичных ветвей
обмотки реактора равен:
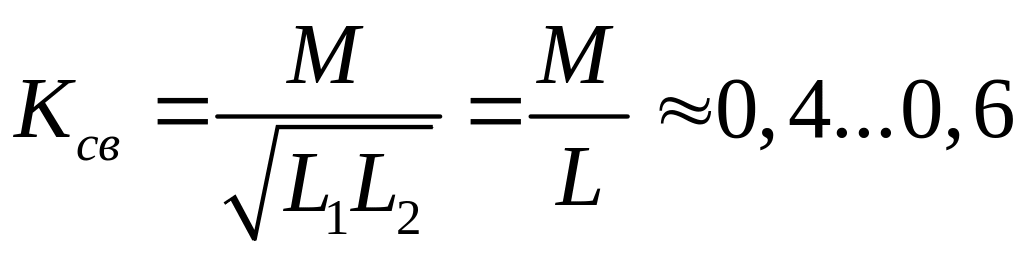
.
Сдвоенный
реактор имеет 3 режима работы (рис. 4.11)
Одноцепный
режим (рис.
4.11а). В
одноцепном режиме общее сопротивление
реактора определятся как сопротивление
одной его ветви:
![]()
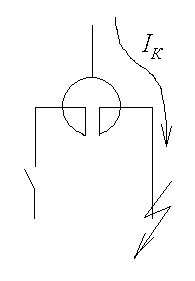
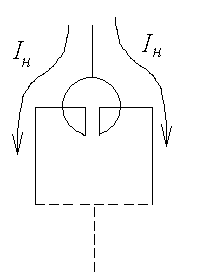
а)
б) в)
Рис.
4.11. Режимы работы сдвоенного реактора
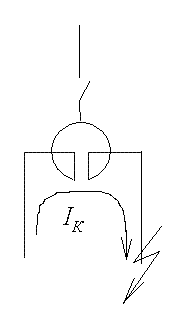
Двухцепный
(сквозной) режим (рис.
4.11б). Двухцепный режим – это нормальный
режим работы реактора. В таком режиме
магнитные потоки
ветвей
направлены
встречно, что вызывает уменьшение
индуктивного сопротивления одной ветви.
Индуктивное
сопротивление одной ветви:
![]()
.
Общее
индуктивное сопротивление:

.
Продольный
режим (рис.
4.11в). В
продольном режиме магнитные потоки
ветвей
направлены
согласно и индуктивность ветви
увеличивается.
![]()
.
Каждый
режим работы реактора может быть
представлен своей схемой замещения.
Активное сопротивление обычно не
учитывается, но оно может быть найдено
по потерям активной мощности в реакторе.
На рисунке 3 приведена общая схема
замещения сдвоенного реактора.
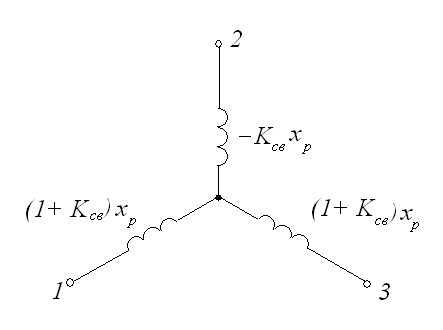
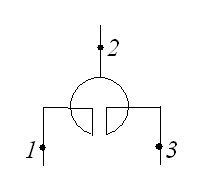
Рис. 4.12. Обозначение
сдвоенного реактора и его схема замещения
Рассмотрим
пример. Используя схему замещения (рис.
4.12), определим сопротивление реактора
в одноцепном, сквозном и продольном
режимах. Коэффициент связи равен
![]()
0,5.
В
режиме КЗ (одноцепном):
![]()
.
В нормальном
(сквозном) режиме:

.
В
продольном режиме:
![]()
.
Трансформаторы
Д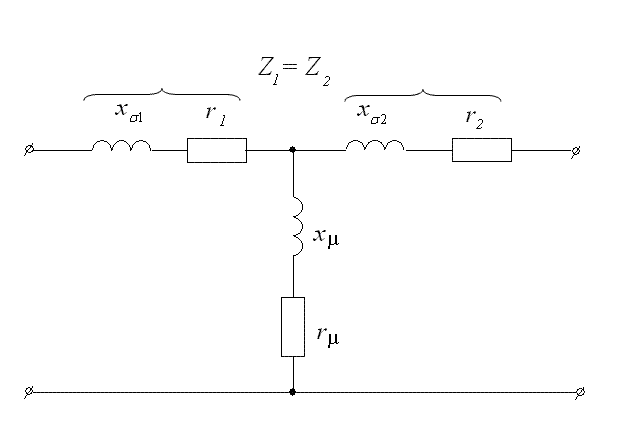
вухобмоточный
трансформатор. Схема
замещения двухобмоточного трансформатора
приведена на рисунке 4.13.
Рис. 4.13. Условное
обозначение и схема замещения
двухобмоточного трансформатора
Параметры
схемы замещения производятся по данным
опытов холостого хода и короткого
замыкания.
О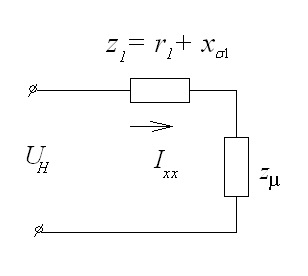
пыт
холостого хода (рис.
4.14) позволяет определить ток холостого
хода
![]()
,
потери в ветви намагничивания
![]()
и
сопротивление холостого хода.
Потери холостого
хода:
![]()
Сопротивление
холостого хода:

;
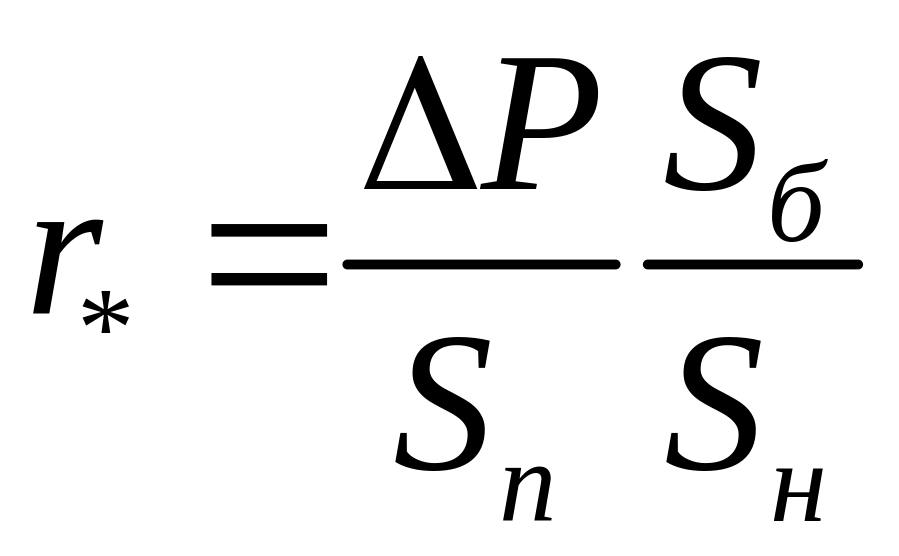
.
Рис. 4.14. Опыт
холостого хода
Опыт
короткого замыкания (рис.
4.15) позволяет определить напряжение
короткого замыкания и потери короткого
замыкания:

,
следовательно, индуктивное сопротивление
рассеивания определяется как
![]()
.
Напряжение
короткого замыкания
![]()
.
Рис. 4.15. Опыт
короткого замыкания
![]()
Потери
короткого замыкания:
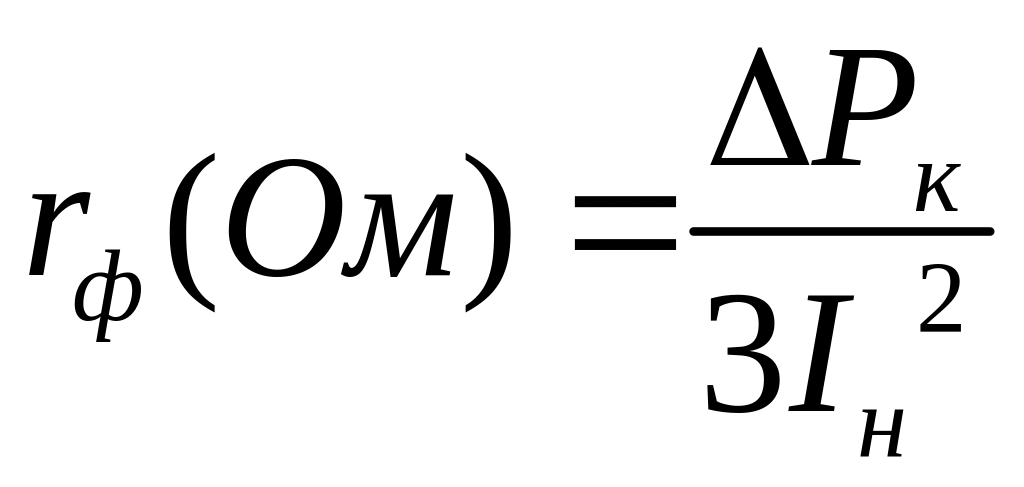
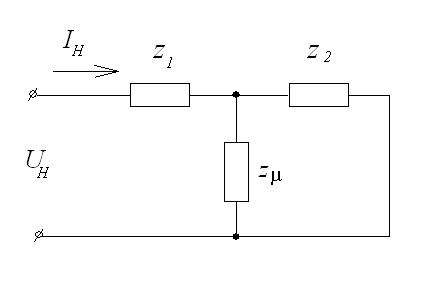
Активное
сопротивление трансформатора:
Пренебрегая
ветвью намагничивания
![]()
,
получим упрощенную
схему замещения (рис. 4.16):
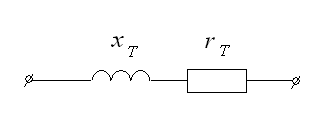
![]()
Рис. 4.16. Схема
замещения
Активное
сопротивление трансформатора в
относительных единицах, приведенное к
базисным условиям:

,
где
![]()
− номинальное
активное сопротивление в относительных
единицах.
Т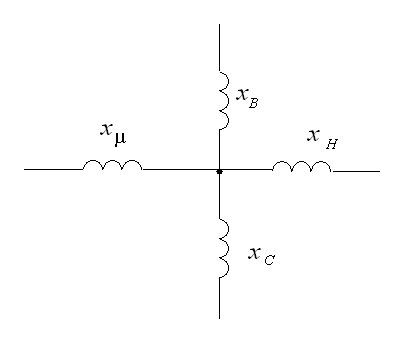
рехобмоточный
трансформатор
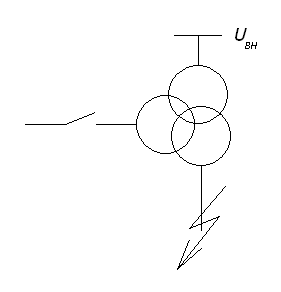
Рис. 4.17. Условное
обозначение и схема замещения
трёхобмоточного трансформатора
В
относительных единицах напряжения
короткого замыкания обмоток будут
равняться их сопротивлениям рассеивания
и их значения для обмоток высшего,
среднего и низшего напряжений
трехобмоточного трансформатора могут
быть определены по формулам:

,где
![]()
;

Данные
формулы справедливы и для автотрансформатора,![]()
![]()
обычно в расчеты не вводится.
Трансформатор
с расщепленной обмоткой. На
электростанциях и подстанциях применяются
силовые трансформаторы и автотрансформаторы
с расщепленной обмоткой низшего
напряжения, так как это позволяет
существенно снизить ток КЗ в сетях
низшего напряжения. Повышающие
трансформаторы и автотрансформаторы
с расщепленной обмоткой используются
для формирования укрупненных блоков
электростанций, особенно на ГЭС.
а)
б)
Рис. 4.18 Условное
обозначение трансформатора с расщепленной
обмоткой:
а) обмотка низшего
напряжения расщеплена на 2 части;
б) обмотки низшего
напряжения расщеплена на 3 части
Сопротивление
трансформатора с расщепленной обмоткой
характеризуется следующими параметрами:
− сопротивление
расщепления
![]()
,
равное сопротивлению
между выводами двух произвольных частей
расщепленной обмотки;
− сквозное
сопротивление
![]()
,
равное сопротивлению
между выводами обмотки высшего напряжения
и объединенными выводами частей
расщепленной обмотки низшего напряжения;
− коэффициент
расщепления
![]()
,
равный отношению
сопротивления расщепления к сквозному
сопротивлению:

П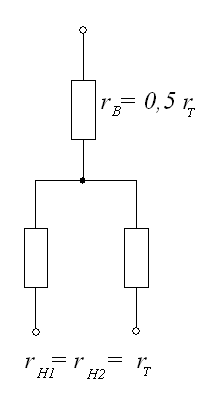
ри
расщеплении обмотки на две части
![]()
(рис. 4.18а), а при
расщеплении на три части
![]()
(рис. 4.18б).
Коэффициент
расщепления также зависит от исполнения
трансформатора, например, для трансформатора
броневого исполнения (рис. 4.18а) при
отсутствии других данных следует
принимать
![]()
.
Для группы однофазных
трансформаторов
![]()
.
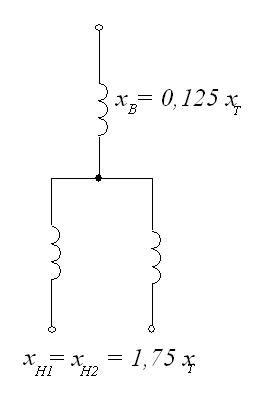
а)
б) в)
г)
Рис. 4.19 Схемы
замещения трансформатора с расщепленной
обмоткой
Сопротивление
рассеивания обмоток трансформатора:

При
расщеплении низшей обмотки на 2
части (рис.
4.19а) сопротивление обмоток низшего
напряжения:
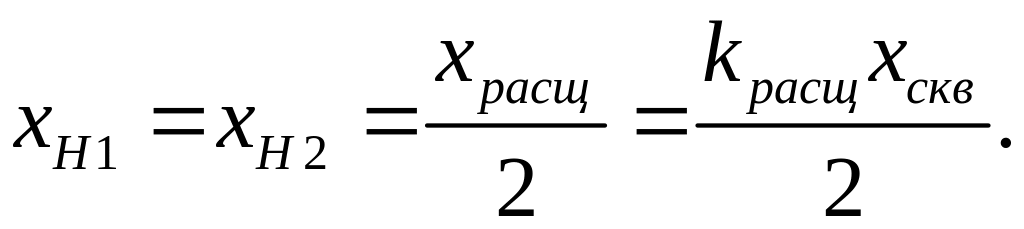
Сопротивление
обмотки высшего напряжения:
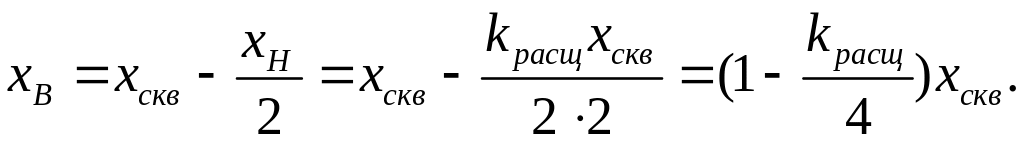
Для
трансформатора стрежневого типа и
схемы замещения
для активных и индуктивных сопротивлений
приведены на рис. 4.19б, в.
При
расщеплении низшей обмотки на 3
части (рис.
4.19г) сопротивление обмотки высшего
напряжения:

.
Сопротивление
обмоток низшего напряжения:
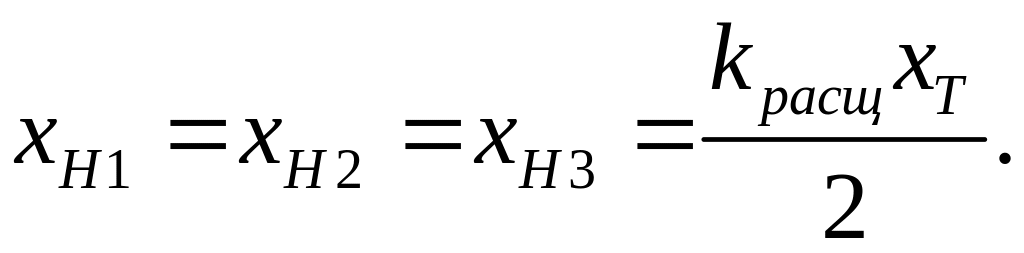
Пример.
Автотрансформатор с расщепленной
обмоткой низшего напряжения на 2 части
(рис. 4.20).
Сопротивление
расщепленных обмоток низшего напряжения:
![]()
Сопротивления
обмоток высшего, среднего и низшего
напряжений:
![]()
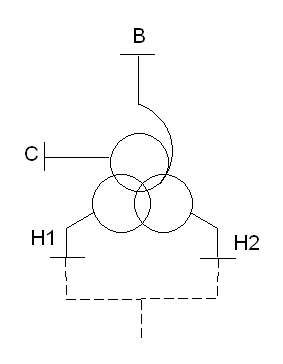
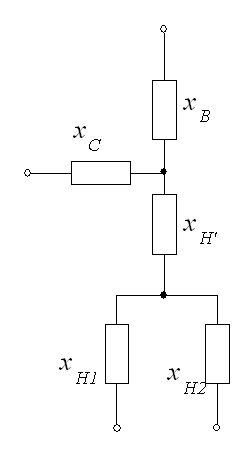
Рис. 4.20.
Автотрансформатор с расщепленной
обмоткой и его схема замещения
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- 1. Определение сопротивлений питающей энергосистемы
- 2. Определение сопротивлений трансформаторов
- 3. Определение сопротивлений кабелей
- 4. Определение сопротивлений шин и шинопроводов
- 5. Определение сопротивлений воздушных линии
- 6. Определение сопротивлений реакторов
- 7. Определение сопротивлений трансформаторов тока
- 8. Определение сопротивлений автоматических выключателей, рубильников, разъединителей
- 9. Определение сопротивлений контактных соединений кабелей и шинопроводов
- 10. Список литературы
Для того чтобы рассчитать токи КЗ в сети до 1000 В, следует первоначально составить схему замещения, которая состоит из всех сопротивлений цепи КЗ. Активные и индуктивные сопротивления всех элементов схемы замещения выражают в миллиомах (мОм).
Как определять сопротивления отдельных элементов схемы замещения, об этом вы и узнаете в этой статье.
1. Определение сопротивлений питающей энергосистемы
Активные и индуктивные сопротивления питающей энергосистемы рассчитывают на стороне ВН понижающего трансформатора и приводят к стороне НН по формуле 2-6 [Л3. с. 28].

На практике можно не учитывать активное сопротивление энергосистемы, а значение индуктивного сопротивления приравнивать как к полному сопротивлению энергосистемы (на точность расчетов это никак не скажется). В этом случае значение (в Омах) индуктивное (полное) сопротивление энергосистемы определяется по формуле 2-7 [Л3. с. 28].

После того как определили индуктивное сопротивление системы по формуле 2-7 [Л3. с. 28], данное сопротивление нужно привести к стороне НН по формуле 2-6 [Л3. с. 28].
Индуктивное сопротивление системы, также можно определить по формулам представленных в ГОСТ 28249-93:

Как мы видим формула 1 из ГОСТ 28249-93 соответствует формулам 2-6, 2-7 из [Л3. с. 28].
Пример
Определить сопротивление энергосистемы, учитывая, что ток КЗ со стороны энергосистемы на зажимах ВН трансформатора 6/0,4 кВ составляет в максимальном режиме – 19 кА, в минимальном – 13 кА.
Решение
Определяем индуктивное сопротивление энергосистемы по формулам 2-6, 2-7.
Сопротивление энергосистемы в максимальном режиме, приведенное к напряжению 0,4 кВ:
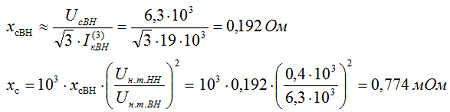
Сопротивление энергосистемы в минимальном режиме, приведенное к напряжению 0,4 кВ:
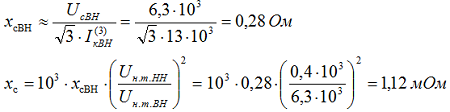
2. Определение сопротивлений трансформаторов
Значения (в мОм) полного (zт), активного (rт) и индуктивного (хт) сопротивления понижающего трансформатора приведенных к стороне НН определяются по формулам: 2-8, 2-9, 2-10 [Л3. с. 28].

На большинстве трансформаторов 10(6)/0,4 кВ имеется возможность регулирования напряжения путем переключения без возбуждения (ПБВ) при отключенном от сети трансформаторе как со стороны высшего так и низшего напряжения. Напряжение регулируется со стороны высшего напряжения на величину ±2х2,5% от номинального значения.

Для трансформаторов с пределом регулирования ПБВ ±2х2,5%, полное сопротивление будет изменятся в пределах:

Значения индуктивного и активного сопротивления трансформатора по ГОСТ 28249-93 определяются по формулам:

Как видно, формулы из ГОСТ 28249-93 совпадают с формулами приведенными в [Л3. с. 28].
Для упрощения расчета активного и индуктивного сопротивления тр-ра, можно использовать таблицу 2-4 [Л3. с. 29] для схем соединения обмоток трансформатора Y/Yo и ∆/Yo. Причем для схем соединения обмоток трансформатора ∆/Yo, значения активного (r0) и индуктивного (х0) сопротивления нулевой последовательности равны значениям активного и индуктивного сопротивления прямой последовательности: r0 = rт и х0 = хт.
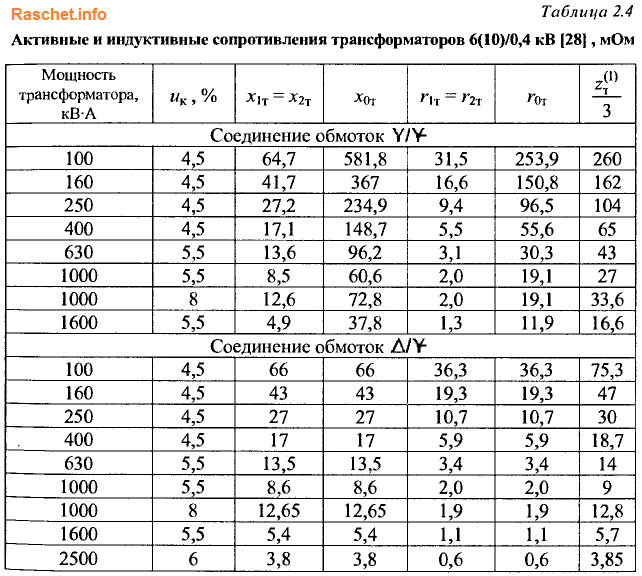
Пример
Определить сопротивление трансформатора ТМ 50/6 со схемой соединения обмоток ∆/Yо.
Решение
По справочным данным определяем технические данные трансформатора: Sном. = 50 кВА, Uном.ВН = 6,3 кВ, Uном.НН = 0,4 кВ, Uкз = 4%, ∆Ркз=1,1 кВт.
Определяем полное сопротивление трансформатора для стороны 0,4 кВ по формуле 2-8:
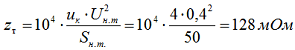
Определяем активное сопротивление трансформатора для стороны 0,4 кВ по формуле 2-9:
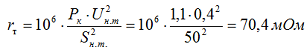
Определяем индуктивное сопротивление трансформатора для стороны 0,4 кВ по формуле 2-10:

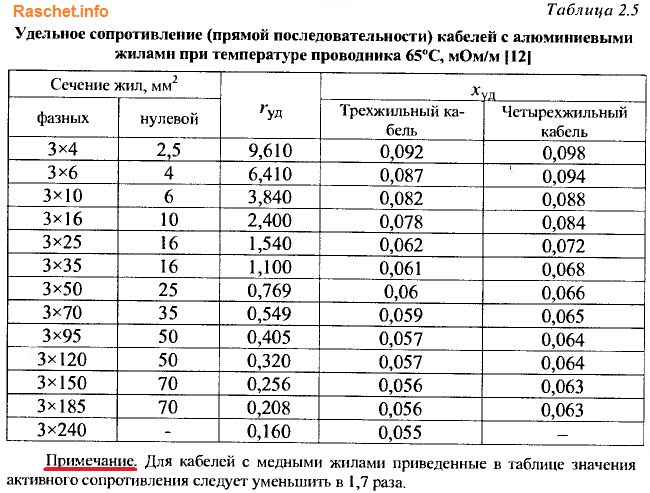
3. Определение сопротивлений кабелей
Значения активного и индуктивного сопротивления кабелей определяются по формуле 2-11 [Л3. с. 29].

4. Определение сопротивлений шин и шинопроводов
Сопротивление шин и шинопроводов длиной 5м и меньше, можно не рассчитывать, так как они не влияют на значение токов КЗ.
Значения активного и индуктивного сопротивления шин и шинопроводов определяется аналогично кабелям.

Зная расстояние между прямоугольными шинами, можно приближенно определить индуктивное сопротивление (мОм/м) по формуле 2-12 [Л3. с. 29].
Пример
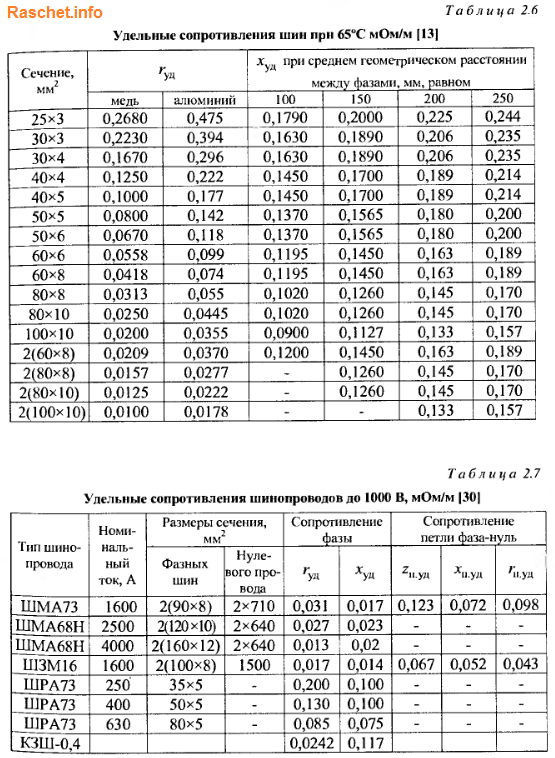
Определить активное и индуктивное сопротивление алюминиевых шин сечением 60х8 мм2 от трансформатора ТМ-630/6 до распределительного щита 0,4 кВ, общая длина проложенных от трансформатора до РП-0,4 кВ составляет 10 м. В данном примере определим сопротивление шин, когда шины находятся как в горизонтальном положении, так и в вертикальном.
Решение
4.1 Определим активное и индуктивное сопротивление шин при горизонтальном расположении.
По таблице 2.6 определяем погонное активное сопротивление rуд. = 0,074 мОм/м, индуктивное сопротивление определяем по формуле 2-12 [Л3. с. 29].
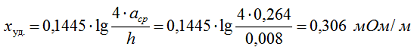
где: расстояние между шинами первой и второй фазы а12 = 200 мм, между второй и третью а23 = 200 мм, между первой и третью а13 = 200 + 60 + 200 = 460 мм, а среднегеометрическое расстояние:
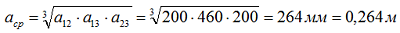
Сопротивление шин от тр-ра до РП-0,4 кВ:

4.2 Определим активное и индуктивное сопротивление шин при вертикальном расположении
При вертикальном расположении шин, активное сопротивление не изменяется, а индуктивное сопротивление составляет:
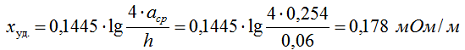
где: расстояние между шинами первой и второй фазы а12 = 200 мм, между второй и третью а23 = 200 мм, между первой и третью а13 = 200 + 8 + 200 = 408 мм, а среднегеометрическое расстояние:
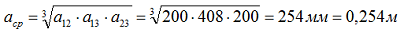
Сопротивление шин от тр-ра до РП-0,4 кВ:
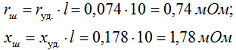
5. Определение сопротивлений воздушных линии
Активное и индуктивное сопротивления линий определяется по той же формуле 2-11 [Л3. с. 29], что и кабели.
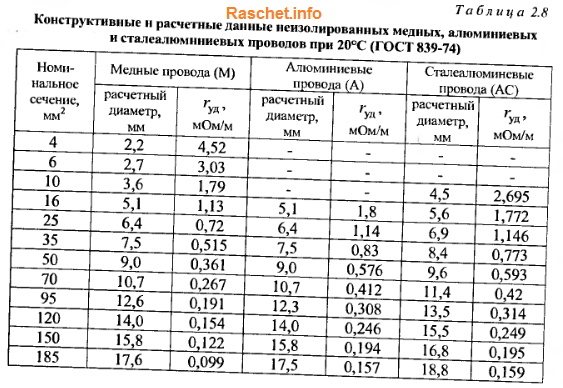
Значение индуктивного сопротивления для проводов из цветных металлов можно приближенно принимать равным 0,3 мОм/м, активного по табл. 2.8.
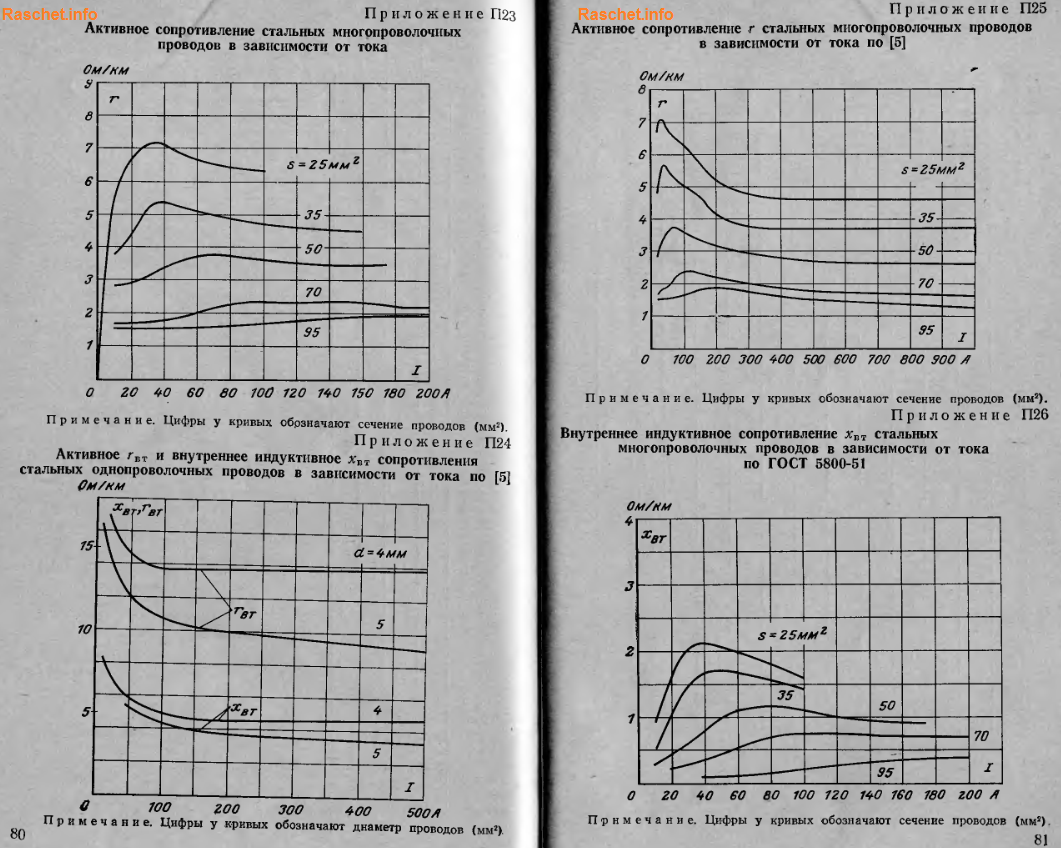
Для стальных проводов активное и индуктивное сопротивление определяется исходя из конструкции провода и значения протекающего по нему тока. Зависимость эта сложная и математическому расчету не поддается, из-за большого количества переменных (сечение провода, температура окружающего воздуха, которая постоянно меняется в течении года, времени суток; нагревом провода током КЗ), которые влияют на значение сопротивление стальных проводов.
Поэтому учесть все эти зависимости практически не возможно и на практике активное сопротивление условно принимают при температуре 20°С и определяют по кривым зависимости стальных проводов от проходящего по ним токам, представленных в приложениях П23-П27 [Л4. с. 80-82].

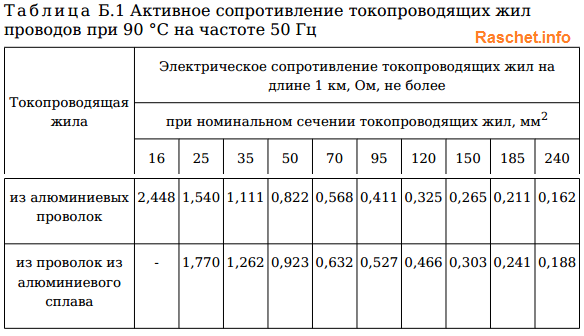
Активное и индуктивное сопротивление для проводов самонесущих изолированных (СИП) определяют по таблицам Б.1, Б.2 [Л5. с. 23-26].
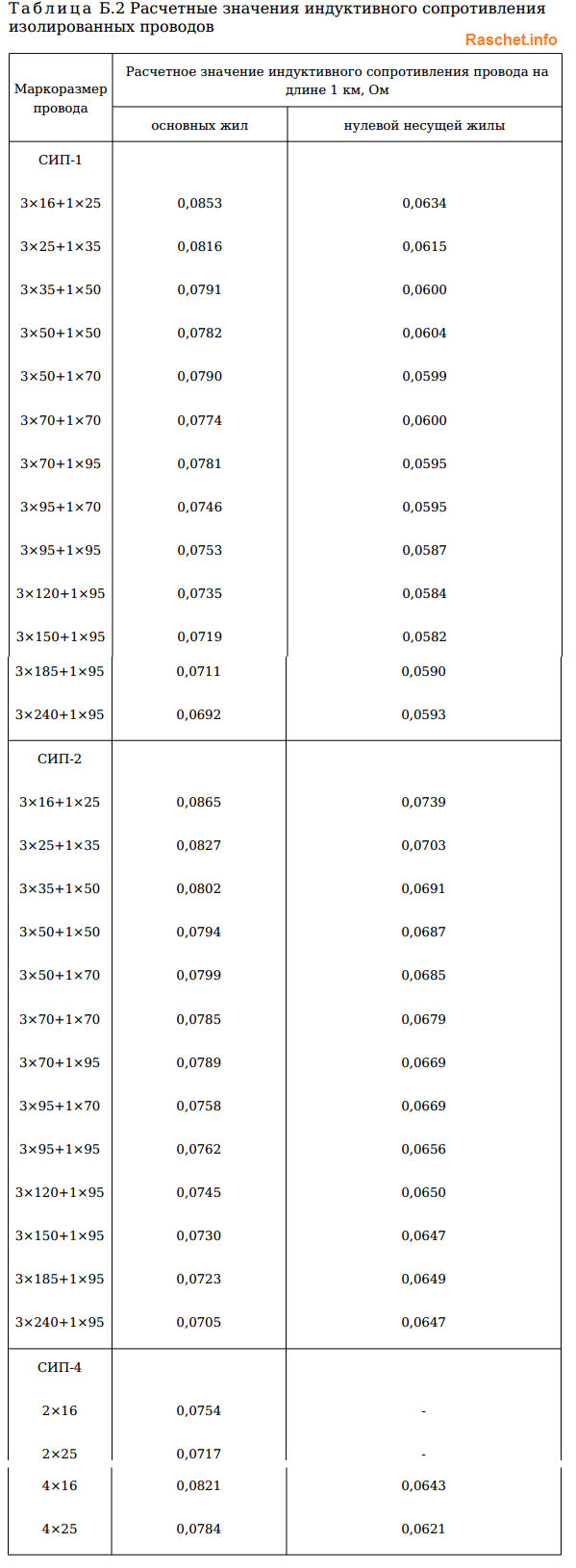
6. Определение сопротивлений реакторов
Номинальные параметры реактора уже заданы в обозначении самого реактора типа РТТ и РТСТ. Например у реактора типа РТТ-0,38-100-0,15:
- 0,38 – номинальное напряжение 380 В;
- 100 – номинальный ток 100 А;
- 0,15 – индуктивное сопротивление при частоте 50 Гц равно 150 мОм.
Активное сопротивление для исполнения У3 (алюминиевая обмотка) — 17 мОм, для исполнения Т3 (медная обмотка) – 16 мОм.
7. Определение сопротивлений трансформаторов тока
Значения активных и индуктивных сопротивлений трансформаторов тока принимаются по приложению 5 таблица 20 ГОСТ 28249-93. Активным и индуктивным сопротивлением одновитковых трансформаторов (на токи более 500 А) при расчетах токов КЗ можно пренебречь.
Согласно [Л3. с. 32] для упрощения расчетов, сопротивления трансформаторов тока не учитывают ввиду почти незаметного влияния на токи КЗ.

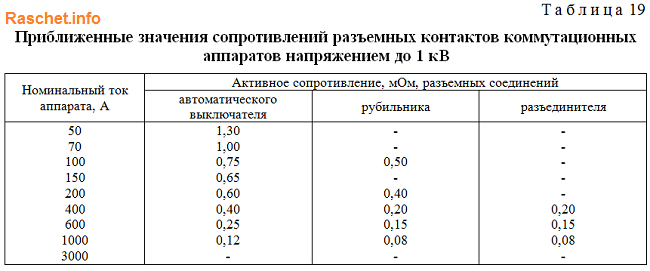
8. Определение сопротивлений автоматических выключателей, рубильников, разъединителей
Приближенные значения сопротивлений разъемных контактов коммутационных аппаратов напряжением до 1 кВ определяются по приложению 4 таблица 19 ГОСТ 28249-93. При приближенном учете сопротивление коммутационных аппаратов принимают — 1 мОм.
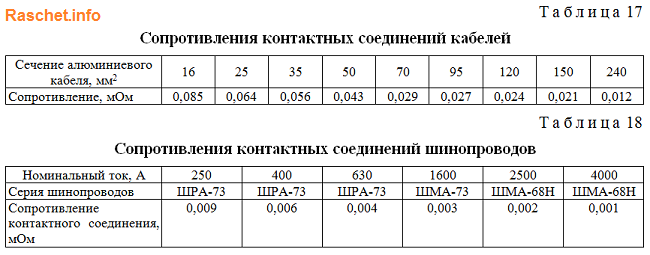
9. Определение сопротивлений контактных соединений кабелей и шинопроводов
Значения сопротивления контактных соединений кабелей и шинопроводов определяют по приложению 4 таблицы 17,18 ГОСТ 28249-93. Для упрощения расчетов, данными сопротивлениями можно пренебречь. При приближенном учете сопротивлений контактов принимают:
• rк = 0,1 мОм — для контактных соединений кабелей;
• rк = 0,01 мОм — для шинопроводов.
10. Список литературы
1. Рекомендации по расчету сопротивления цепи «фаза-нуль». Главэлектромонтаж. 1986 г.
2. ГОСТ 28249-93 – Методы расчета в электроустановках переменного тока напряжением до 1 кВ.
3. Беляев А.В. Выбор аппаратуры, защит и кабелей в сети 0,4 кВ. Учебное пособие. 2008 г.
4. Голубев М.Л. Расчет токов короткого замыкания в электросетях 0,4 — 35 кВ. 2-e изд. 1980 г.
5. ТУ 16-705.500-2006. Провода самонесущие изолированные и защищенные для воздушных линий электропередач.
Всего наилучшего! До новых встреч на сайте Raschet.info.
Схема замещения трансформатора, как и других элементов электрической сети, зависит от целей выполняемых расчётов. В настоящей статье представлены схемы замещения различных типов трансорфматоров используемых для расчётов: установившихся режимов, токов короткого замыкания и электромеханических переходных процессов.
Содержание
- 1 Двухобмоточный трансформатор
- 1.1 Полные формулы
- 1.2 Приближённые формулы
- 1.3 Двухобмоточный трансформатор с расщепленной обмоткой
- 2 Особенности учёта обмоток Т и АТ с множественным расщеплением
- 2.1 Двухобмоточный трансформатор с расщепленной обмоткой на n ветвей
- 2.2 Автотрансформатор с расщепленной обмоткой на 2 ветви
- 2.3 Автотрансформатор с расщепленной обмоткой на n ветвей
- 3 Трёхобмоточный трансформатор
- 4 См. также
- 5 Использованные источники
Двухобмоточный трансформатор
Для представления двухобмоточных трансформаторов используется Г-образная схема замещения.
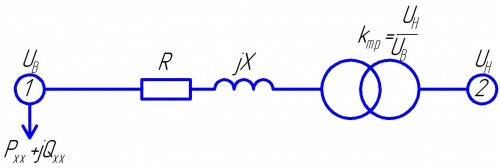
Схема замещения двухобмоточного трансформатора, потери в стали представлены постоянной мощностью.
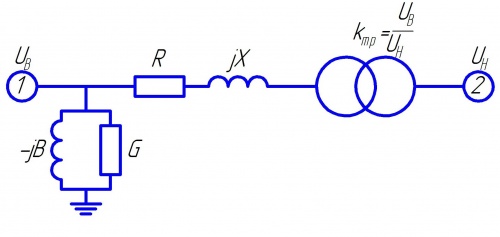
Схема замещения двухобмоточного трансформатора, потери в стали представлены шунтами.
Полные формулы
В каталоге двухобмоточного трансформатора указываются: [math]displaystyle S_{text{ном} } [/math] — номинальная мощность трансформатора, кВА; [math]displaystyle U_{ text{В} }[/math] и [math]displaystyle U_{ text{Н} } [/math] – номинальные напряжения обмоток, кВ; [math]displaystyle u_{text{к}}[/math],% — напряжение короткого замыкания в процентах от номинального высшего напряжения; [math]displaystyle Delta P_{text{кз}} [/math] — потери (потери в меди) короткого замыкания, кВт; [math]displaystyle i_{text{хх}} [/math], % — ток холостого хода в процентах от номинального тока обмотки высшего напряжения; [math]displaystyle Delta P_{ text{хх} } [/math] — потери (потери в стали) холостого хода, кВт.
Активное и индуктивное сопротивления трансформатора обусловлены соответственно нагревом обмоток и наличием поля рассеяния и определяются для одной фазы из опыта короткого замыкания. При проведении опыта короткого замыкания вторичная обмотка замыкается накоротко, а к первичной подводится такое напряжение, чтобы по ней протекал номинальный ток [math]displaystyle I_{ text{ном} }[/math]. При этом замеряются потери активной мощности в трёх фазах трансформатора [math]displaystyle Delta P_{ text{кз} } [/math] и напряжение [math]displaystyle u_{ text{к} }[/math], подводимое к первичной обмотке.
Параметры Г-образной схемы замещения определяются по следующим формулам:
- [math]displaystyle Z = frac{ u_{text{к}} }{ 100 } frac{ U^2_{ text{ном} } }{S_{ text{ном} }} [/math];
- [math]displaystyle R = Delta P_{text{кз}} frac{ U^2_{ text{ном} } }{ S^2_{ text{ном} } } [/math];
- [math]displaystyle X = sqrt{ Z^2 – R^2 } [/math];
- [math]displaystyle G = frac{ Delta P_{text{хх}} }{ U^2_{ text{ном} } } [/math];
- [math]displaystyle Y = frac{ i_{text{хх}} }{ 100 } frac{ S_{ text{ном} } }{ U^2_{ text{ном} } } [/math];
- [math]displaystyle B = sqrt{ Y^2 – G^2 } [/math];
- [math]displaystyle k_{text{Т}} = frac{ U_{ text{Н} } }{ U_{ text{В} } } [/math],
где [math]displaystyle U_{ text{ном} } [/math] – номинальное междуфазное напряжение стороны трансформатора, к которой приводится сопротивление трансформатора (как правило, это сторона высокого напряжения [math]displaystyle U_{ text{В} }[/math]); [math]displaystyle S_{text{ном} } [/math] — номинальная мощность трехфазного трансформатора или трёхфазной группы однофазных трансформаторов, МВА; [math]displaystyle k_{text{Т}} [/math] — коэффициент трансформации идеального трансформаторного двухполюсника.
Приближённые формулы
Напряжение короткого замыкания [math]displaystyle u_{text{к}}[/math], кВ, складывается из падения напряжения на активном и реактивном сопротивлениях при протекании номинального тока:
[math]displaystyle u_{text{к}} = Delta U_R + Delta U_X = sqrt{3} I_{ text{ном} } R_Т + sqrt{3} I_{ text{ном} } X_Т [/math],
где [math]displaystyle Delta U_R[/math] и [math]displaystyle Delta U_X[/math] – падение напряжения (линейное) на соответствующих продольных элементах схемы замещения двухобмоточного трансформатора.
Упрощено можно считать, что у современных крупных трансформаторов ( [math]displaystyle S_{text{ном} }gt 1[/math] МВА) активное сопротивление существенно меньше реактивного:
[math]displaystyle R_Т ll X_Т [/math].
поэтому можно считать, что [math]u_{text{к}} = Delta U_X = sqrt{3} I_{ text{ном} } X_Т [/math], тогда
[math]displaystyle X_Т = frac{ u_{text{к}} }{ sqrt{3} I_{ text{ном} } } [/math],
и по каталожным данным, [Ом]:
- [math]displaystyle X_Т = frac{ u_{text{к}}% }{ 100 } frac{ U^2_{ text{ном} } }{ S_{text{ном} } } [/math].
Активная и индуктивная проводимости трансформатора обусловлены соответственно нагревом стали за счет вихревых токов и потерями на намагничивание и определяются из опыта холостого хода. При проведении опыта холостого хода вторичная обмотка разомкнута, а к первичной подводится номинальное напряжение, замеряются ток холостого хода [math]displaystyle i_{text{хх}} [/math] в первичной обмотке и потери активной мощности [math]displaystyle Delta P_{ text{хх} } [/math].
Потери активной мощности холостого хода можно выразить через активную проводимость:
[math]displaystyle Delta P_{ text{хх} } = 3 i^2_{text{хх}} frac{1}{G_Т} = U^2_{text{в}} G_Т[/math],
отсюда
[math]displaystyle G_Т = frac{ Delta P_{ text{хх} } }{U^2_{text{в}}} [/math].
Ток холостого хода состоит из тока в проводимостях [math]G_Т[/math] и [math]B_Т[/math]:
[math]displaystyle i_{text{хх}}= frac{ U_{text{в}} cdot B_Т }{ sqrt{3}} [/math];
[math]displaystyle B_Т = frac{ sqrt{3} i_{text{хх}}}{ U_{text{в}} } [/math]
или через каталожные данные
[math]displaystyle B_Т = frac{ i_{text{хх}} }{ 100 } frac{ S_{text{ном} } }{ U^2_{text{в}} } [/math]
Зачастую при расчётах пренебрегают изменением напряжения на шинах трансформатора и используют схему замещения с постоянными потерями в шунте трансформатора, эти потери принимаются равными потерям холостого хода. Тогда в схеме замещения шунт заменяется постоянным значением активной и реактивной мощности потерь холостого хода [math]displaystyle Delta P_{ text{хх} } + j cdot Delta Q_{ text{хх} }[/math].
Для того чтобы при использовании формул при расчётах параметров электрических систем не возникало путаницы в единицах измерения, рекомендуется выражать электрические величины в следую-щих единицах:
- мощности, потери мощности — МВА, МВт, Мвар;
- напряжения, потери напряжения — кВ;
- токи — кА;
- сопротивления — Ом.
Тогда ни в одной из формул не возникает необходимости использовать пере-водные коэффициенты.
Так как результаты опытов КЗ и х.х. однофазных трансформаторов относятся к одной фазе, то эквивалентные сопротивления и проводимости трехфазных групп подсчитываются на основе номинальных и паспортных данных однофазных трансформаторов по следующим формулам:
[math]displaystyle R_Т = frac{ Delta P_{text{кз}} cdot U^2_{text{ном}} }{ 3 cdot S^2_{text{ном ф}} }[/math];
[math]displaystyle X_Т = frac{ u_{text{к}}% }{ 100 } frac{ U^2_{ text{ном} } }{3 cdot S_{text{ном} } } [/math];
[math]displaystyle G_Т = frac{ 3 Delta P_{ text{хх} } }{ U^2_{ text{ном} } } [/math];
[math]displaystyle B_Т = frac{ i_{text{хх}} }{ 100 } frac{3 cdot S_{text{ном} } }{ U^2_{text{в}} } [/math].
Двухобмоточный трансформатор с расщепленной обмоткой
Разновидностью двухобмоточного трансформатора является трансформатор с расщепленной обмоткой, обмотка низшего напряжения которого расщепляется на две ( или более). В типе трансформатора расщепление обмоток обозначается буквой “Р”. . Расщепление обмотки позволяет решить целый ряд задач:
- обеспечивается возможность подключения нескольких электроприемников, секций подстанций или генераторов через один трансформатор;
- ограничиваются уровни токов короткого замыкания, в силу увеличения сопротивления каждой из ветвей трансформатора нескольким менее, чем в два раза.
Существенной проблемой в данной связи является ограниченность данных о параметрах расщепленных обмоток: в наиболее распространенной постановке, когда обмотка трансформатора расщепляется на две обмотки одного напряжения, трансформатор фактически становится трехобмоточным и параметры его схемы следует также расчитывать, используя напряжения короткого замыкания для каждой пары обмоток соответственно: [math]displaystyle U_{text{ВН-СН}}[/math], [math]displaystyle U_{text{СН-НН}}[/math], [math]displaystyle U_{text{ВН-НН}}[/math], но при этом такие данные зачастую отсутствуют и для таких трансформаторов параметры задаются как для классических двухобмоточных элементов.
Очевидно, что при наличии указанных выше паспортных или экспериментальных характеристик оборудования, расчет параметров схемы замещения следует осуществлять аналогично оному для трехобмоточных трансформаторов.
В противном случае можно использовать, например, подход описанный в [1], где для расчета параметров модели трансформатора используется коэффицент расщепления [math]displaystyle K_{text{p}}[/math], который определяется взаимным расположением расщепленных обмоток. Данный коэффициент рассчитывается по следующему выражению:
[math]displaystyle K_{text{p}} = frac{ U_{text{НН1-НН2}} }{ U_{text{ВН-НН}} } [/math],
где [math]displaystyle U_{text{НН1-НН2}}[/math] – напряжение короткого замыкания между расщепленными обмотками НН1 и НН2, кВ; [math]displaystyle U_{text{ВН-НН}}[/math] – напряжение короткого замыкания между обмотками ВН и НН при параллельном соединении расщепленных обмоток, кВ.
Важно заметить, что данный коэффициент для случая расщепления на две обмотки принадлежит диапазону от 0 до 4, и при отсутствии фактических данных допустимо:
- применять коэффициент [math]displaystyle K_{text{p}} = 3.5 [/math] для случая расположения расщепленных обмоток трансформатора “одна над другой”;
- применять коэффициент [math]displaystyle K_{text{p}} = 4.0 [/math] для упрощенных расчетов и в случаях, когда нагрузки на расщепленных обмотках примерно равны.
Используя указанный выше коэффицент, можно произвести расчет активного и реактивного сопротивлений обмоток по следующим выражениям:
[math]displaystyle R_{ text{ВН}} = Delta P_{text{кз}} frac{ U^2_{ text{ном} } }{ 2 cdot S^2_{ text{ном} } } [/math];
[math]displaystyle R_{ text{НН1}} = R_{ text{НН2}} = 2 cdot R_{ text{ВН}}; [/math]
[math]displaystyle X_{ text{ВН}} = frac{ u_{text{к}}% }{ 100 } frac{ U^2_{ text{ном} } }{S_{text{ном} } } cdot Big(1 – frac{ K_{text{p}} }{ 4 }Big) [/math];
[math]displaystyle X_{ text{НН1}} = X_{ text{НН2}} = frac{ u_{text{к}}% }{ 100 } frac{ U^2_{ text{ном} } }{S_{text{ном} } } cdot frac{ K_{text{p}} }{ 2 } [/math].
Параметры шунта, описывающего потери на вихревые токи и намагничивание, при отсутствии полных данных определяются в соответствии с методикой для двухобмоточных трансформаторов.
Особенности учёта обмоток Т и АТ с множественным расщеплением
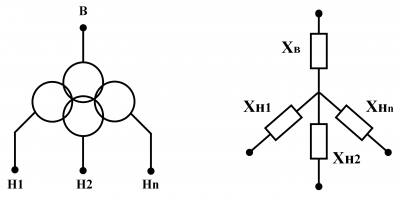
Схема замещения 2х обмоточного трансформатора с обмоткой низшего напряжения, расщепленной на n ветвей.
Двухобмоточный трансформатор с расщепленной обмоткой на n ветвей
Расчет реактивных сопротивлений схемы замещения двухобмоточных трансформаторов с обмоткой низшего напряжения, расщепленной на n ветвей производится по следующим формулам:
[math]displaystyle X_{ text{В} } = 0,01 cdot Big( u_{text{к В-Н}} – frac{u_{text{к Н1-Нn}}}{text{2n}} Big) [/math];
[math]displaystyle X_{ text{Н1} } = X_{ text{Н2} } = … = X_{ text{Нn} } = 0,005 cdot u_{text{к Н1-Нn}}[/math].
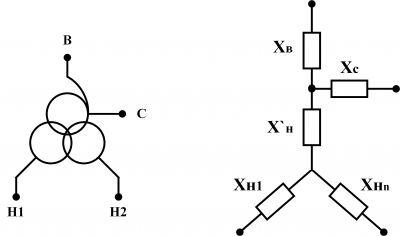
Схема замещения автотрансформатора с обмоткой низшего напряжения, расщепленной на 2 ветви.
Автотрансформатор с расщепленной обмоткой на 2 ветви
Расчет реактивных сопротивлений схемы замещения автотрансформаторов с обмоткой низшего напряжения, расщепленной на 2 ветви производится по следующим формулам:
[math]displaystyle X_{ text{В} } = 0,005 cdot Big( u_{text{к В-Н}} + u_{text{к В-С}} – u_{text{к С-Н}} Big)[/math];
[math]displaystyle X_{ text{С} } = 0,005 cdot Big( u_{text{к В-С}} + u_{text{к С-Н}} – u_{text{к В-Н}} Big)[/math];
[math]displaystyle X_{ text{Н} } = 0,005 cdot Big( u_{text{к В-Н}} + u_{text{к С-Н}} – u_{text{к В-С}} Big)[/math];
[math]displaystyle X_{ text{Н1} } = X_{ text{Н2} } = 0,005 cdot u_{text{к Н1-Н2}}[/math];
[math]displaystyle X’_{ text{Н1} } = X_{ text{Н} } – 0,0025 cdot u_{text{к Н1-Н2}}[/math];

Схема замещения автотрансформатора с обмоткой низшего напряжения, расщепленной на n ветвей.
Автотрансформатор с расщепленной обмоткой на n ветвей
Расчет реактивных сопротивлений схемы замещения автотрансформаторов с обмоткой низшего напряжения, расщепленной на n ветвей производится по следующим формулам:
[math]displaystyle X_{ text{В} } = 0,005 cdot Big( u_{text{к В-Н}} + u_{text{к В-С}} – u_{text{к С-Н}} Big)[/math];
[math]displaystyle X_{ text{С} } = 0,005 cdot Big( u_{text{к В-С}} + u_{text{к С-Н}} – u_{text{к В-Н}} Big)[/math];
[math]displaystyle X_{ text{Н} } = 0,005 cdot Big( u_{text{к В-Н}} + u_{text{к С-Н}} – u_{text{к В-С}} Big)[/math];
[math]displaystyle X_{ text{Н1} } = X_{ text{Н2} } = … = X_{ text{Нn} } = 0,005 cdot u_{text{к Н1-Нn}}[/math];
[math]displaystyle X’_{ text{Н1} } = X_{ text{Н} } – 0,01 cdot frac{u_{text{к Н1-Нn}}}{text{2n}}[/math];
Трёхобмоточный трансформатор
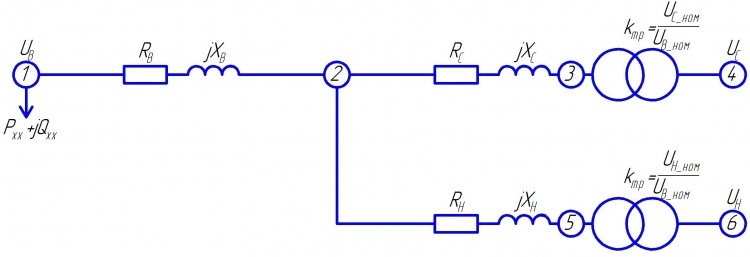
Схема замещения трёхбмоточного трансформатора, потери в стали представлены постоянной мощностью.
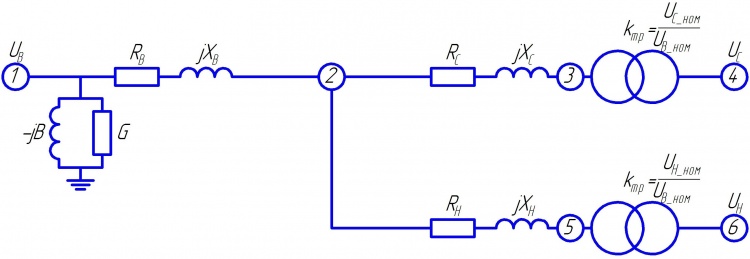
Схема замещения трёхобмоточного трансформатора, потери в стали представлены шунтами.
Схема замещения трехобмоточного трансформатора приведена на рисунке.
В каталоге трехобмоточного трансформатора указываются: [math]displaystyle S_{text{ном} } [/math] — номинальная мощность трансформатора, кВА; [math]displaystyle U_{ text{В} }[/math], [math]displaystyle U_{ text{С} } [/math], [math]displaystyle U_{ text{Н} } [/math] – номинальные напряжения обмоток, кВ; [math]displaystyle i_{text{хх}} [/math], % — ток холостого хода в процентах от номинального тока обмотки высшего напряжения; [math]displaystyle Delta P_{ text{хх} } [/math] — потери (потери в стали) холостого хода, кВт; [math]displaystyle u_{text{к ВС}}[/math], [math]displaystyle u_{text{к ВН}}[/math], [math]displaystyle u_{text{к СН}}[/math],% — три напряжение короткого замыкания по парам обмоток в процентах от номинального высшего напряжения; [math]displaystyle Delta P_{text{кз ВН}} [/math],[math]displaystyle Delta P_{text{кз ВС}} [/math], [math]displaystyle Delta P_{text{кз СН}} [/math] — три значения потерь короткого замыкания по парам обмоток, кВт.
Каждое из каталожных значений [math]displaystyle Delta P_{text{кз}} [/math] и [math]displaystyle u_{text{к}}[/math],% относится к одному из трех возможных опытов короткого замыкания: высшая – средняя обмотки, высшая-низшая, средняя-низшая.
Например, значения [math]displaystyle Delta P_{text{кз ВН}} [/math] и [math]displaystyle u_{text{к ВН}}[/math] определяются при замыкании накоротко обмотки низшего напряжения при разомкнутой обмотке среднего напряжения и подведении к обмотке высшего напряжения такого напряжения [math]displaystyle u_{text{к ВН}}[/math], чтобы ток в обмотке низшего напряжения трансформатора был равен номинальному.
Как и в двухобмоточном трансформаторе, будем считать сопротивления средней и низшей обмоток приведёнными к высшей стороне напряжения.
Из опыта короткого замыкания определяются сопротивления обмоток:
- [math]displaystyle R_{text{В}} = frac{Delta P_{text{кз В}} cdot U^2_{ text{В} } }{ S^2_{ text{ном} } } [/math];
- [math]displaystyle R_{text{С}} = frac{Delta P_{text{кз С}} cdot U^2_{ text{В} } }{ S^2_{ text{ном} } } [/math];
- [math]displaystyle R_{text{Н}} = frac{Delta P_{text{кз Н}} cdot U^2_{ text{В} } }{ S^2_{ text{ном} } } [/math].
Величины [math]displaystyle Delta P_{text{кз В}} [/math],[math]displaystyle Delta P_{text{кз С}} [/math], [math]displaystyle Delta P_{text{кз Н}} [/math],найдём из каталожных данных по формулам:
- [math]displaystyle Delta P_{text{кз В}} = frac{displaystyle Delta P_{text{кз ВН}} + displaystyle Delta P_{text{кз ВС}} – displaystyle Delta P_{text{кз СН}} }{ 2 }[/math];
- [math]displaystyle Delta P_{text{кз C}} = frac{displaystyle Delta P_{text{кз CН}} + displaystyle Delta P_{text{кз ВС}} – displaystyle Delta P_{text{кз ВН}} }{ 2 }[/math];
- [math]displaystyle Delta P_{text{кз Н}} = frac{displaystyle Delta P_{text{кз ВН}} + displaystyle Delta P_{text{кз СН}} – displaystyle Delta P_{text{кз ВС}} }{ 2 }[/math].
Аналогично этому по каталожным значениям напряжений КЗ для пар обмоток [math]displaystyle u_{text{к В}}[/math], [math]displaystyle u_{text{к C}}[/math], [math]displaystyle u_{text{к Н}}[/math] % определяются напряжения КЗ для лучей схемы замещения:
- [math]displaystyle u_{text{к В}} = frac{displaystyle u_{text{к ВН}} + displaystyle u_{text{к ВС}} – displaystyle u_{text{к СН}} }{ 2 }[/math];
- [math]displaystyle u_{text{к С}} = frac{displaystyle u_{text{к СН}} + displaystyle u_{text{к ВС}} – displaystyle u_{text{к ВН}} }{ 2 }[/math];
- [math]displaystyle u_{text{к Н}} = frac{displaystyle u_{text{к ВН}} + displaystyle u_{text{к СН}} – displaystyle u_{text{к ВС}} }{ 2 }[/math].
По найденным значения [math]displaystyle u_{text{к В}}[/math], [math]displaystyle u_{text{к C}}[/math], [math]displaystyle u_{text{к Н}}[/math] % определяются реактивные сопротивления обмоток:
- [math]displaystyle X_{text{В}} = frac{u_{text{к В}} cdot U^2_{ text{В} } }{100 cdot S_{ text{ном} } } [/math];
- [math]displaystyle X_{text{С}} = frac{u_{text{к C}} cdot U^2_{ text{В} } }{100 cdot S_{ text{ном} } } [/math];
- [math]displaystyle X_{text{Н}} = frac{u_{text{к Н}} cdot U^2_{ text{В} } }{100 cdot S_{ text{ном} } } [/math].
Активное и индуктивное сопротивления шунта трехобмоточного трансформатора рассчитываются идентично двухобмоточному.
- [math]displaystyle G = frac{ Delta P_{text{хх}} }{ U^2_{ text{В} } } [/math];
- [math]displaystyle В = frac{i_{text{хх}} cdot S_{ text{ном} } }{100 cdot U^2_{ text{В} } } [/math].
Для расчёта потерь мощности на шуте, без расчёта сопротивлений, потребуются следующие формулы:
- [math]displaystyle P_{text{хх}} = Delta P_{text{хх}} [/math];
- [math]displaystyle Q_{text{хх}} = frac{i_{text{хх}} cdot S_{ text{ном} } }{100} [/math].
См. также
- Трансформатор
- Справочные данные параметров трансформаторов до 35 кВ
- Справочные данные параметров трансформаторов от 35 кВ
- Пример расчёта параметров схемы замещения трансформатора
Использованные источники
- ↑ Мартиросян А.А., Бушуева О.А. Параметры схем замещения силовых трансформаторов и автотрансформаторов: методические указания – Иваново:ИГЭУ, 2011. http://xn--b1ajwv.xn--p1ai/files/mu_ess.pdf
Схемы замещения выполняют в однолинейном изображении; при этом удобно сопротивления и э. д. с. отмечать порядковыми номерами и указывать их численные значения.
При расчете в именованных единицах сопротивления всех элементов приводят к одной ступени напряжения.
Для каждой ступени напряжения приняты следующие значения средних номинальных междуфазных напряжений Uсp (кВ): 515; 340; 230; 154; 115; 37; 24; 20; 18; 15,75; 13,8; 10,5; 6,3; 3,15.
В практических расчетах возможно приближенное приведение сопротивлений по средним коэффициентам трансформации, равным отношению средних номинальных напряжений Uсp соответствующих ступеней.
Сопротивление всех элементов схемы замещения можно выражать в относительных единицах при выбранных базисных условиях или в омах. При расчете в относительных единицах базисная мощность ![]() может быть взята произвольной (например, 100 или 1 000 MBА). Базисное напряжение
может быть взята произвольной (например, 100 или 1 000 MBА). Базисное напряжение ![]() для каждой ступени напряжения обычно принимается равным Uсp. Базисный ток и базисное сопротивление определяют по выражениям
для каждой ступени напряжения обычно принимается равным Uсp. Базисный ток и базисное сопротивление определяют по выражениям

Сопротивления в относительных единицах при базисных условиях ![]() определяют следующим образом.
определяют следующим образом.
Если сопротивление, включенное на ступени Uсp, задано:
а) в относительных единицах ![]() при Sн и
при Sн и ![]() (генераторы, трансформаторы), то
(генераторы, трансформаторы), то
![]()
б) в процентах ![]() при
при ![]() и
и ![]() (реакторы), то
(реакторы), то
![]()
в) в омах х (воздушные линии, кабели) на единицу длины, то при длине l

Примечания:
1. В указанных формулах следует принимать Ucp и ![]() той ступени, на которой находится данный элемент.
той ступени, на которой находится данный элемент.
2. Сопротивления элементов, выраженные в относительных единицах при базисных условиях, дают схему замещения, приведенную по средним коэффициентам трансформации к одной (и притом любой из указанных в расчетной схеме) ступени напряжения.
Электродвижущая сила источников питания в относительных единицах выражается через![]()
где Е — междуфазная э. д. с. источника, кВ; ![]() — фазная э. д. с. источника, кВ; Uсp — среднее междуфазное номинальное напряжение той ступени, где находится данный источник, кВ;
— фазная э. д. с. источника, кВ; Uсp — среднее междуфазное номинальное напряжение той ступени, где находится данный источник, кВ; ![]() — то же, но фазное напряжение, кВ.
— то же, но фазное напряжение, кВ.
При расчете в именованных единицах сопротивления всех элементов выражаются в омах и должны быть приведены к какой-либо одной ступени напряжения (например, к ![]() ) по формуле
) по формуле
где ![]() — сопротивление в омах, приведенное к ступени
— сопротивление в омах, приведенное к ступени ![]() ;
; ![]() — сопротивление в омах, заданное на ступени
— сопротивление в омах, заданное на ступени ![]() .
.
Соответственно приведение э. д. с, известных на других ступенях напряжения, выполняется по формуле

где ![]() — фазная э. д. с. в киловольтах, приведенная к ступени
— фазная э. д. с. в киловольтах, приведенная к ступени ![]() ; En — междуфазная э. д. с. в киловольтах, заданная на ступени
; En — междуфазная э. д. с. в киловольтах, заданная на ступени ![]() .
.
Дополнительные условия для составления схемы замещения определяются видом к. з.
Составленную схему замещения путем соответствующих преобразований приводят к простейшему виду для определения результирующей э. д. с. ![]() и результирующего сопротивления
и результирующего сопротивления ![]() относительно точки к. з.
относительно точки к. з.
Основные формулы преобразования схем и нахождения токораспределения приведены в табл. 38-1.
Для приведения к простейшему виду схемы замещения с несколькими источниками производят замену отдельных генерирующих ветвей результируюс э. д. с. ![]() и сопротивлениями
и сопротивлениями ![]() (рис. 38-10, а) одной эквивалентной генерирующей ветвью (рис. 38-10,6), э. д. с. и сопротивление которой определяются следующими выражениями:
(рис. 38-10, а) одной эквивалентной генерирующей ветвью (рис. 38-10,6), э. д. с. и сопротивление которой определяются следующими выражениями:

где ![]() — проводимости ветвей.
— проводимости ветвей.
При двух генерирующих ветвях в узле

По найденным результирующей э. д. с. ![]() и результирующему сопротивлению
и результирующему сопротивлению ![]() определяют периодическую слагающую тока в месте к. з.
определяют периодическую слагающую тока в месте к. з.
После этого, постепенно развертывая схему, можно найти токи и напряжения в отдельных ветвях и точках исходной схемы.
Рис. 38-10. Замена нескольких генерирующих ветвей одной эквивалентной.

Таблица 38-1




