Как найти сопротивление ветви

Загрузить PDF

Элементы электрической цепи можно соединить двумя способами. Последовательное соединение подразумевает подключение элементов друг к другу, а при параллельном соединении элементы являются частью параллельных ветвей. Способ соединения резисторов определяет метод вычисления общего сопротивления цепи.

1

Определите, является ли цепь последовательной. Последовательное соединение представляет собой единую цепь без каких-либо разветвлений. Резисторы или другие элементы расположены друг за другом.
2
Сложите сопротивления отдельных элементов. Сопротивление последовательной цепи равно сумме сопротивлений всех элементов, входящих в эту цепь.^[1] Сила тока в любых частях последовательной цепи одна и та же, поэтому сопротивления просто складываются.
- Например, последовательная цепь состоит из трех резисторов с сопротивлениями 2 Ом, 5 Ом и 7 Ом. Общее сопротивление цепи: 2 + 5 + 7 = 14 Ом.
3
Вычислите сопротивление по известной силе тока и напряжению. Если сопротивление каждого элемента цепи не известно, воспользуйтесь законом Ома: V = IR, где V – напряжение, I – сила тока, R – сопротивление. Сначала найдите силу тока и общее напряжение.
- Сила тока в любых частях последовательной цепи одна и та же.^[2] Поэтому можно использовать известное значение силы тока на любом участке последовательной цепи.
- Общее напряжение равно напряжению источника тока. Оно не равно напряжению на каком-либо элементе цепи.^[3]
4
Подставьте известные значения в формулу, описывающую закон Ома. Перепишите формулу V = IR так, чтобы обособить сопротивление: R = V/I. Подставьте известные значения в эту формулу, чтобы вычислить общее сопротивление.
- Например, напряжение источника тока равно 12 В, а сила тока равна 8 А. Общее сопротивление последовательной цепи: R_O = 12 В / 8 А = 1,5 Ом.
Реклама

1
Определите, является ли цепь параллельной. Параллельная цепь на некотором участке разветвляется на несколько ветвей, которые затем снова соединяются. Ток течет по каждой ветви цепи.
- Если цепь включает элементы, расположенные до или после разветвления, или если на одной ветви два и более элементов, перейдите к третьему разделу этой статьи (такая цепь является комбинированной).
2

Вычислите общее сопротивление на основе сопротивления каждой ветви. Каждый резистор уменьшает силу тока, проходящего через одну ветвь, поэтому она оказывает небольшое влияние на общее сопротивление цепи. Формула для вычисления общего сопротивления: ${frac {1}{R_{O}}}={frac {1}{R_{1}}}+{frac {1}{R_{2}}}+{frac {1}{R_{3}}}+...{frac {1}{R_{n}}}$ , где R₁ – сопротивление первой ветви, R₂ – сопротивление второй ветви и так далее до последней ветви R_n.
3
Вычислите сопротивление по известной силе тока и напряжению. Сделайте это, если сопротивление каждого элемента цепи не известно.
- В параллельной цепи напряжение на одной ветви равно общему напряжению в цепи.^[4] Поэтому достаточно знать значение напряжение на любой ветви цепи. Общее напряжение также равно напряжению источника тока.
- В параллельной цепи сила тока на каждой ветви разная. Поэтому необходимо знать значение общей силы тока, чтобы найти общее сопротивление.
4
Подставьте известные значения в формулу закона Ома. Если известны значения общей силы тока и напряжения в цепи, общее сопротивление вычисляется по закону Ома: R = V/I.
- Например, напряжение в параллельной цепи равно 9 В, а общая сила тока равна 3 А. Общее сопротивление: R_O = 9 В / 3 А = 3 Ом.
5
Поищите ветви с нулевым сопротивлением. Если у ветви параллельной цепи вообще нет сопротивления, то весь ток будет течь через такую ветвь. В этом случае общее сопротивление цепи равно 0 Ом.
- В реальной жизни это означает, что резистор неисправен или шунтирован (замкнут); в этом случае большая сила тока может повредить другие элементы цепи.^[5]
Реклама

1
Разбейте комбинированную цепь на последовательную и параллельную. Комбинированная цепь включает элементы, которые соединены как последовательно, так и параллельно. Посмотрите на схему цепи и подумайте, как разбить ее на участки с последовательным и параллельным соединением элементов. Обведите каждый участок, чтобы упростить задачу по вычислению общего сопротивления.
- Например, цепь включает резистор, сопротивление которого равно 1 Ом, и резистор, сопротивление которого равно 1,5 Ом. За вторым резистором схема разветвляется на две параллельные ветви – одна ветвь включает резистор с сопротивлением 5 Ом, а вторая – с сопротивлением 3 Ом. Обведите две параллельные ветви, чтобы выделить их на схеме цепи.
2

Найдите сопротивление параллельной цепи. Для этого воспользуйтесь формулой для вычисления общего сопротивления параллельной цепи: ${frac {1}{R_{O}}}={frac {1}{R_{1}}}+{frac {1}{R_{2}}}+{frac {1}{R_{3}}}+...{frac {1}{R_{n}}}$ .
3
Упростите цепь. После того как вы нашли общее сопротивление параллельной цепи, ее можно заменить одним элементом, сопротивление которого равно вычисленному значению.
- В нашем примере избавьтесь от двух параллельных ветвей и замените их одним резистором с сопротивлением 1,875 Ом.
4
Сложите сопротивления резисторов, соединенных последовательно. Заменив параллельную цепь одним элементом, вы получили последовательную цепь. Общее сопротивление последовательной цепи равно сумме сопротивлений всех элементов, которые включены в эту цепь.
- После упрощения цепи она состоит из трех резисторов со следующими сопротивлениями: 1 Ом, 1,5 Ом и 1,875 Ом. Все три резистора соединены последовательно: $R_{O}=1+1,5+1,875=4,375$ Ом.
5

Воспользуйтесь законом Ома, чтобы найти неизвестные величины. Если сопротивление каждого элемента цепи не известно, попытайтесь вычислить его. Вычислить сопротивление по известной силе тока и напряжению можно по закону Ома: R = V/I.

Реклама

1
Запомните формулы, включающие мощность. Электрическая мощность – это величина, которая характеризует скорость преобразования электроэнергии и скорость ее передачи (например, к лампочке).^[6] Общая мощность цепи равна произведению общего напряжения на общую силу тока. Формула: P = VI.^[7]
- Запомните: чтобы вычислить общее сопротивления, нужно знать общую мощность. Значение мощности на одном элементе цепи для этих целей не подходит.
2
Вычислите сопротивление по известным значениям мощности и силы тока. В этом случае можно объединить две формулы, чтобы найти сопротивление.
- P = VI (мощность = напряжение х сила тока)
- Закон Ома: V = IR.
- В первую формулу вместо V подставьте произведение IR: P = (IR)I = I²R.
- Обособьте переменную R: R = P / I².
- Сила тока в любых частях последовательной цепи одна и та же. Это не так в параллельной цепи.
3
Вычислите сопротивление по известным значениям мощности и напряжения. В этом случае можно объединить две формулы, чтобы найти сопротивление. Учитывайте общее напряжение в цепи, которое равно напряжению источника тока.
- P = VI
- Перепишите закон Ома так: I = V/R
- В первой формуле замените I на V/R: P = V(V/R) = V²/R.
- Обособьте переменную R: R = V²/P.
- В параллельной цепи напряжение на одной ветви равно общему напряжению в цепи. Это не так в последовательной цепи, где общее напряжение не равно напряжению на одном элементе цепи.
Реклама

Советы

Мощность измеряется в ваттах (Вт).
Напряжение измеряется в вольтах (В).
Сила тока измеряется в амперах (А) или в миллиамперах (мА). 1 мА = $1*10^{{-3}}$ A = 0,001 А.
В приведенных формулах переменная Р – это мгновенная мощность, то есть мощность в определенный момент времени. Если цепь подключена к источнику переменного тока, мощность постоянно меняется. Поэтому для цепей с источником переменного тока специалисты вычисляют среднюю мощность; для этого используется формула: P_СР = VIcosθ, где cosθ – это коэффициент мощности цепи.^[8]

Об этой статье

Эту страницу просматривали 407 314 раз.

Была ли эта статья полезной?

Источник

Download Article

There are two ways to hook together electrical components. Series circuits use components connected one after the other, while parallel circuits connect components along parallel branches. The way resistors are hooked up determines how they contribute to the total resistance of the circuit.

1

Identify a series circuit. A series circuit is a single loop, with no branching paths. All the resistors or other components are arranged in a line.
2
Add all resistances together. In a series circuit, the total resistance is equal to the sum of all resistances.^[1] The same current passes through each resistor, so each resistor does its job as you would expect.
- For example, a series circuit has a 2 Ω (ohm) resistor, a 5 Ω resistor, and a 7 Ω resistor. The total resistance of the circuit is 2 + 5 + 7 = 14 Ω.
Advertisement
3
Start with current and voltage instead. If you don’t know the individual resistance values, you can rely on Ohm’s Law instead: V = IR, or voltage = current x resistance. The first step is to find the circuit’s current and total voltage:
- The current of a series circuit is the same at all points on the circuit.^[2] If you know the current at any point, you can use that value in this equation.
- The total voltage is equal to the voltage of the supply (the battery). It is not equal to the voltage across one component.^[3]
4
Insert these values into Ohm’s Law. Rearrange V = IR to solve for resistance: R = V / I (resistance = voltage / current). Plug the values you found into this formula to solve for total resistance.
- For example, a series circuit is powered by a 12 volt battery, and the current is measured at 8 amps. The total resistance across the circuit must be R_T = 12 volts / 8 amps = 1.5 ohms.

1
Understand parallel circuits. A parallel circuit branches into multiple paths, which then join back together. Current flows through each branch of the circuit.
- If your circuit has resistors on the main path (before or after the branched area), or if there are two or more resistors on a single branch, Skip down to the combination circuit instructions instead.
2

Calculate the total resistance from the resistance of each branch. Since each resistor only slows current passing through one branch, it only has a small effect on the total resistance of the circuit. The formula for total resistance R_T is ${frac {1}{R_{T}}}={frac {1}{R_{1}}}+{frac {1}{R_{2}}}+{frac {1}{R_{3}}}+...{frac {1}{R_{n}}}$ , where R₁ is the resistance of the first branch, R₂ is the resistance of the second branch, and so on up to the last branch R_n.
3
Begin with total current and voltage instead. If you don’t know the individual resistances, you’ll need the current and voltage instead:
- In a parallel circuit, the voltage across one branch is the same as the total voltage across the circuit.^[4] As long as you know the voltage across one branch, you’re good to go. The total voltage is also equal to the voltage of the circuit’s power source, such as a battery.
- In a parallel circuit, the current may be different along each branch. You need to know the total current, or you won’t be able to solve for total resistance.
4
Use these values in Ohm’s Law. If you know the total current and the voltage across the whole circuit, you can find the total resistance using Ohm’s Law: R = V / I.
- For example, a parallel circuit has a voltage of 9 volts and total current of 3 amps. The total resistance R_T = 9 volts / 3 amps = 3 Ω.
5
Watch out for branches with zero resistance. If a branch on the parallel circuit has no resistance, all of the current will flow through that branch. The resistance of the circuit is zero ohms.
- In practical applications, this usually means a resistor has failed or been bypassed (short-circuited), and the high current could damage other parts of the circuit.^[5]

1
Break down your circuit into series sections and parallel sections. A combination circuit has some components linked together in series (one after the other), and others in parallel (on different branches). Look for areas of your diagram that simplify to a single series or parallel section.^[6] Circle each one to help you keep track of them.
- For example, a circuit has a 1 Ω resistor and a 1.5 Ω resistor connected in series. After the second resistor, the circuit splits into two parallel branches, one with a 5 Ω resistor and the other with a 3 Ω resistor.
  Circle the two parallel branches to separate them from the rest of the circuit.
2

Find the resistance of each parallel section. Use the parallel resistance formula ${frac {1}{R_{T}}}={frac {1}{R_{1}}}+{frac {1}{R_{2}}}+{frac {1}{R_{3}}}+...{frac {1}{R_{n}}}$ to find the total resistance of a single parallel section of the circuit.^[7]
3
Simplify your diagram. Once you’ve found the total resistance of a parallel section, you can cross out that whole section on your diagram. Treat that area as a single wire with resistance equal to the value you found.
- In the example above, you can ignore the two branches and treat them as one resistor with resistance 1.875Ω.
4
Add up resistances in series. Once you’ve replaced each parallel section with a single resistance, your diagram should be a single loop: a series circuit. The total resistance of a series circuit is equal to the sum of all individual resistances, so just add them up to get your answer.
- The simplified diagram has a 1 Ω resistor, 1.5 Ω resistor, and the section with 1.875 Ω you just calculated. These are all connected in series, so $R_{T}=1+1.5+1.875=4.375$ Ω.
5

Use Ohm’s Law to find unknown values. If you do not know the resistance in one component of your circuit, look for ways to calculate it. If you know the voltage V and current I across that component, find its resistance using Ohm’s Law: R = V / I.

1
Learn the formula for power. Power is the rate that the circuit consumes energy, and the rate it delivers energy to whatever the circuit is powering (such as a light bulb).^[8] The total power of a circuit is equal to the product of the total voltage and the total current. Or in equation form: P = VI.^[9]
- Remember, when solving for total resistance, you need to know the total power of the circuit. It’s not enough to know the power flowing through one component.
2
Solve for resistance using power and current. If you know these two values, you can combine two formulas to solve for resistance:
- P = VI (power = voltage x current)
- Ohm’s Law tells us that V = IR.
- Substitute IR for V in the first formula: P = (IR)I = I²R.
- Rearrange to solve for resistance: R = P / I².
- In a series circuit, the current across one component is the same as the total current. This is not true for a parallel circuit.
3
Find resistance from power and voltage. If you only know the power and voltage, you can use a similar approach to find resistance. Remember to use the total voltage across the circuit, or the voltage of the battery powering the circuit:
- P = VI
- Rearrange Ohm’s Law in terms of I: I = V / R.
- Substitute V / R for I in the power formula: P = V(V/R) = V²/R.
- Rearrange to solve for resistance: R = V²/P.
- In a parallel circuit, the voltage across one branch is the same as the total voltage. This is not true for a series circuit: the voltage across one component is not the same as the total voltage.
- Alternatively, you can isolate the circuit and physically test resistance using a multimeter. ^[10]

Calculator, Practice Problems, and Answers

Add New Question

Question

How do I calculate the resistance of 2 resistors when I know the sum of the resistors?

Assuming you mean total resistance, you first need to determine if they are in series or parallel. In series the total resistance simply equals the sum of the resistors. In parallel, the inverse of the total resistance equals the sum of the inverse of each individual resistor. Therefore, you will not be able to calculate total resistance in a parallel circuit if you only know the sum.
Question

If V = IR, how do I calculate if one cell = 2V and the resistor is 4 ohm?

I = V/R . This is derived from the equation V =I R. In the question the value of potential difference (v) is mentioned as 2V, i.e, 2 volts. The value of resistance of the resistor is given as 4 ohms. Substitute these values in the first equation; i.e, l = V/R, so, I = 2/4. Therefore, I = 0.5 amps.
Question

Can I use frequency to calculate resistance?

Resistance does not change with frequency. However, AC circuits do have a similar quality called reactance which does change with frequency. Learn more here.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

The power value P used in these formulas refers to instantaneous power, or power at a specific moment in time. If the circuit uses AC power, the power is changing constantly. Electricians calculate the average power for AC circuits using the formula P_average = VIcosθ, where cosθ is the power factor of the circuit.^[11]
Power is measured in watts (W).
Voltage is measured in volts (V).

Show More Tips

About This Article

Article SummaryX

To calculate total resistance in series circuits, look for a single loop with no branching paths. Add all of the resistances across the circuit together to calculate the total resistance. If you don’t know the individual values, use the Ohm’s Law equation, where resistance = voltage divided by current. Plug in the values for voltage and current and solve for R to get the total resistance in a circuit. Keep reading the article if you want to learn how to calculate the resistance on a parallel or combination circuit!

Did this summary help you?

Thanks to all authors for creating a page that has been read 1,787,504 times.

Did this article help you?

Источник

Что такое полное сопротивление цепи и как его правильно найти

Содержание

1 Виды электрических сопротивлений
2 Определение эквивалентного сопротивления
3 Как определяется ПС при последовательном соединении емкостей и индуктивностей
4 Определение ПС при использовании параллельного соединения элементов
5 Видео по теме

Для начала нужно понять, что такое электрическое сопротивление. Это физическая величина, которая отражает противодействие движению электротока по схеме или же внутри проводника. Данная величина взаимосвязана с электронапряжением и силой электротока, что отражено в законе Ома, названном так по имени немецкого физика.

Формулировка закона Ома

Виды электрических сопротивлений

Известно о двух видах электронапряжения — постоянном и переменном. В электроцепи постоянного тока присутствует исключительно активное электросопротивление. Таким является любое электросопротивление, поглощающее энергию. В этом случае найти полное сопротивление поможет формулировка закона Ома.

В электроцепях с переменным напряжением есть реактивное электросопротивление, то есть такое, которое энергию не поглощает. Оно делится на емкостное и индуктивное. В реальности не существует электроцепей только с каким-либо одним видом электросопротивления. Наряду с резисторами в них используются емкости и катушки индуктивности. Поэтому в электротехнике вводится такое понятие, как полное сопротивление цепи, представляющееся в виде векторной суммы всех электросопротивлений, присутствующих в данной цепи.

Классификация электроцепей переменного электротока

Величина реактивного электросопротивления зависит от частоты параметров используемой электросети. Формула, с помощью которой можно определить емкостное электросопротивление, выглядит так:

Определение емкостного сопротивления

Здесь ω — угловая частота. Она связана с частотой электросети f и определяется по формуле:

Значение угловой частоты

Индуктивное электросопротивление находим с помощью такого выражения:

Определение индуктивного электросопротивления

В формулах для определения емкостного и индуктивного электросопротивления используются определенные физические величины. Их обозначение и единицы измерения приводятся в таблице ниже. Само электросопротивление измеряется в омах.

Таблица физических величин

Чтобы вычислить полное сопротивление цепи Z, учитывающее все имеющиеся активные и реактивные составляющие, следует воспользоваться формулой:

Вычисление импеданса

Определение эквивалентного сопротивления

В электросхеме может быть использовано несколько нагрузок одного вида, соединенных между собой последовательно или параллельно. В первом случае их электросопротивления складываются. Поэтому эквивалентное сопротивление будет тем больше, чем больше элементов соединено последовательно.

Электроцепь с последовательно соединенными активными проводниками

Если используется параллельное соединение проводников, расчет полного сопротивления цепи выполняется несколько иначе:

Определение эквивалентного электросопротивления при параллельном соединении

В данном случае эквивалентное сопротивление с увеличением количества используемых нагрузок будет уменьшаться. Такое явление можно наблюдать в повседневной жизни: чем больше к электросети подключено потребителей, тем меньшим будет значение эквивалентного электросопротивления и большим электроток нагрузки.

Как определяется ПС при последовательном соединении емкостей и индуктивностей

При наличии реактивной нагрузки в электроцепи будет наблюдаться опережение или отставание электротока от электронапряжения. При подключении индуктивной нагрузки электроток отстает от электронапряжения, а емкостной, наоборот, опережает. То есть, при подключении конденсатора к источнику переменного электротока он будет постоянно перезаряжаться с частотой, соответствующей частоте электросети. Электроток при этом будет увеличиваться раньше, чем электронапряжение. При подключении индуктивного контура наблюдается обратный результат.

Графическое изображение электрических величин при последовательно соединенных элементах электроцепи

Рассмотрим схему с использованием последовательно соединенных резистора и индуктивности.

Электросхема с использованием резистора и индуктивности соединенных последовательно

Для этого участка цепи результирующее электронапряжение в точках А и В можно определить достаточно простым способом — геометрическим сложением векторов U_L и U_R. Как видно из рисунка, результирующий вектор U_АВ — это гипотенуза треугольника. Следовательно, чтобы рассчитать ее, можно применить теорему Пифагора:

Определение результирующего электронапряжения

Если исходить из формулировки закона Ома, то электронапряжение — это произведение электросопротивления и силы электротока. Поскольку последний параметр во всех точках электроцепи имеет одинаковое значение, то квадрат ПС — это сумма квадратов электросопротивлений, называемых активными и реактивным:

Сумма квадратов электросопротивлений

Следовательно, полное сопротивление приведенной цепи Z определяется выражением:

Определение ПС

Кроме расчетов для определения ПС в цепи можно использовать еще и геометрический способ, являющийся построением треугольника, представленного на рисунке 11д. Его катеты — это активное и реактивное электросопротивление для участка цепи. Понятно, что стороны треугольника следует откладывать в одном масштабе.

Полное сопротивление цепи в рассматриваемом случае не будет исключительно активным или реактивным. В него входят обе составляющие. По этой причине угол сдвига по фазе между электротоком и электронапряжением может меняться от 0 до 90 градусов. К какому из этих предельных значений будет приближена величина φ, зависит от вида преобладающего электросопротивления. Если индуктивная составляющая превышает активную, φ стремится к 90 градусам, а преобладающая активная составляющая уменьшает его до нуля.

Теперь рассмотрим электроцепь с присутствующими в ней резистором и конденсатором, соединенными последовательно. Полное сопротивление цепи и в данном случае можно определить, используя построение треугольника.

Электросхема с последовательно соединенными резистором и конденсатором

Как можно увидеть из рисунка, треугольник сопротивлений, построенный для активно-емкостного участка цепи, развернут в другую сторону. Это связано с тем, что электроток в емкости опережает электронапряжение (в активно-индуктивной ветви электроток отстает от электронапряжения). Полное электрическое сопротивление цепи Z в данном случае будет равно:

Определение импеданса при использовании резистора и конденсатора в электроцепи

Если же в электроцепи присутствуют все виды электросопротивлений, то сначала следует найти реактивную составляющую, а потом уже и значение ПС или импеданса.

Электросхема с использованием разных видов электросопротивлений

Общее реактивное электросопротивление для данного участка цепи — это разница между индуктивной и емкостной составляющими, поскольку они по своему характеру являются противоположными друг другу.

Расчет общего реактивного электросопротивления

Полное сопротивление электрической цепи при наличии индуктивной и емкостной составляющей определяется по формуле:

Определение ПС при наличии индуктивности и емкости в электроцепи

Треугольник электросопротивлений при наличии индуктивной и емкостной составляющей показан на рисунке.

Немаловажно понимать, что если одно из электросопротивлений (емкостное или индуктивное) больше другого более, чем в десять раз, то составляющую с наименьшим значением можно оставить без внимания.

Определение ПС при использовании параллельного соединения элементов

На рисунке ниже изображены графики электронапряжений и электротоков, присутствующих на нагрузках при параллельном соединении.

Графики электронапряжений и электротоков при параллельном соединении элементов электроцепи

Чтобы определить полное электрическое сопротивление цепи, включающей резистор и индуктивность или резистор и емкость, соединенные параллельно, необходимо в первую очередь найти проводимость каждой параллельной линии, затем общую проводимость этой цепи между точками А и В. На последнем этапе вычисляется ПС между А и В.

Пример электросхемы с параллельно соединенными элементами

Вычисляемое значение проводимости активного участка цепи равняется 1/R, индуктивного — 1/ ωL. Формула для определения полной проводимости выглядит так:

Полная проводимость участка электроцепи

Приводя к общему знаменателю выражение под знаком корня, получаем следующее выражение:

Формула после преобразования

Отсюда находим формулу для определения ПС для участка цепи с параллельно соединенными резистором и индуктивностью:

Определение ПС при параллельно соединенных элементах

Формула для вычисления ПС при использовании параллельного соединения резистора и емкости имеет такой вид:

Определение ПС при параллельном соединении резистора и емкости

В радиотехнике чаще всего используется параллельное соединение конденсатора и катушки индуктивности, например, в колебательном контуре. Поскольку катушка имеет и индуктивное, и активное сопротивление, то в индуктивную ветвь включается еще резистор.

Схема колебательного контура

Для определения ПС следует воспользоваться формулой:

Определение ПС колебательного контура

Учитывая то, что активное электросопротивление катушки значительно меньше индуктивного, формулу можно представить так:

Формула для расчета ПС колебательного контура

Значение индуктивности и емкости для колебательного контура принято выбирать так, чтобы соблюдалось условие:

Условие для колебательного контура

В данном случае для определения ПС колебательного контура получаем очень простую формулу:

Упрощенная формула для расчета ПС колебательного контура

С целью облегчения расчетов импеданса используют комплексные числа. Действительную часть такого числа представляет активное электросопротивление, а мнимую — реактивное.

Для последовательно соединенных радиоэлементов ПС в комплексном виде можно представить так:

Определение комплексного ПС

В тригонометрической интерпретации модулем комплексного числа является ПС, а аргументом — угол φ.

Треугольник сопротивлений

Следовательно, активную и реактивную составляющие ПС можно найти по формулам:

Определение составляющих ПС

При вычислении ПС или импеданса для параллельно соединенных элементов используют сумму проводимостей — величин, обратных электросопротивлениям.

Треугольник проводимостей

Комплексная проводимость является величиной, обратной комплексному электросопротивлению. Алгебраически она выражается так:

Определение комплексной проводимости

Вычисление импеданса является достаточно сложной задачей, поскольку используется большое количество формул, тригонометрических функций. Поэтому с целью облегчения расчетов можно воспользоваться онлайн калькулятором. Чтобы получить результат, понадобится лишь ввести значение частоты электротока, емкость конденсатора, индуктивность катушки, сопротивление резистора.

Видео по теме

Источник

Комплексное
сопротивление ветви для первой третьей
гармоник

где
– активное сопротивлениеi–ой
ветви;

–
реактивное сопротивление i–ой
ветви

–
модуль сопротивления i–ой
ветви

–
аргумент сопротивления i–ой
ветви

Рис.
4.3. Зависимости

При
определении сопротивлении для третьей
гармоники необходимо учесть, что
индуктивное сопротивление в 3 раза
больше, чем на первой
,
а емкостное в 3 раза меньше.

Для
определения сопротивлений для нулевой
гармоники воспользуемся расчетной
схемой рис. 4.2.

Результаты
расчетов сведены в табл. 4.5.

	Обозначение	Значения гармоник	Ед. изм.
		нулевой	первой	третьей
Число		1.571	1.571	1.571
Активное сопротивление 1 ветви		15.00	15.00	15.00	Ом
Реактивное сопротивление 1 ветви		0.00	15.00	45.00	Ом
Полное сопротивление 1 ветви		15.00	21.21	47.43	Ом
Аргумент сопротивления 1 ветви		0.00	0.79	1.25	рад
Активное сопротивление 2 ветви		20.00	20.00	20.00	Ом
Реактивное сопротивление 2 ветви		нет цепи	-30.00	16.67	Ом
Полное сопротивление 2 ветви		нет цепи	36.06	26.03	Ом
Аргумент сопротивления 2 ветви		0.00	-0.98	0.69	рад
Активное сопротивление 3 ветви		25.00	25.00	25.00	Ом
Реактивное сопротивление 3 ветви		0.00	25.00	75.00	Ом
Полное сопротивление 3 ветви		25.00	35.36	79.06	Ом
Аргумент сопротивления 3 ветви		0.00	0.79	1.25	рад

5. Расчет комплексных сопротивлений параллельного участка и входного сопротивления

Комплексное
сопротивление параллельного участка
dh
для 1 и 3 гармоник

где
– модуль знаменателя

–
аргумент знаменателя

–
модуль сопротивления параллельного
участка

–
аргумент сопротивления параллельного
участка

Активная часть
сопротивления параллельного участка

Реактивная часть
сопротивления параллельного участка

Для
нулевой гармоники вторая ветвь разомкнута
(рис. 4.2), поэтому
.

Результаты расчетов
сводим в табл. 4.6.

Таблица
4.6

	Обозначение	Значения гармоник	Ед. изм.
		нулевой	первой	третьей
Модуль числителя		25.00	1274.75	2058.18	Ом
Аргумент числителя		0.00	-0.20	1.94	рад
Модуль знаменателя		25.00	45.00	45.00	Ом
Аргумент знаменателя		0.00	-5.00	91.67	Ом
Модуль сопротивления параллельного участка		25.00	45.28	102.12	Ом
Аргумент сопротивления параллельного участка		0.00	-0.11	1.11	рад
Активное сопротивление параллельного участка		25.00	28.15	20.16	Ом
Реактивное сопротивление параллельного участка		0.00	-0.09	0.83	Ом

Соседние файлы в папке Кон раб_3

#
11.02.2015140.8 Кб55Exsel_3_2.xls
#
11.02.2015254.46 Кб51Exsel_3_3.xls
#
11.02.201588.06 Кб45Exsel_3_4.xls
#
#
#

Источник

Расчет сопротивления цепи

Расчет сопротивления цепи необходим при решении различных задач по электротехнике. Суть заключается в приведении сложной разветвленной электрической цепи к цепи с единственным эквивалентным сопротивлением, которую называют простой электрической цепью.

Пример 1

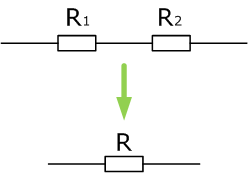
Цепь в данном примере состоит из двух последовательно соединенных сопротивлений, следовательно, их общее сопротивление будет равно сумме их сопротивлений. Подробнее о видах соединений тут.

Допустим, что R₁=10 Ом R₂=20 Ом, тогда

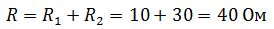
Пример 2

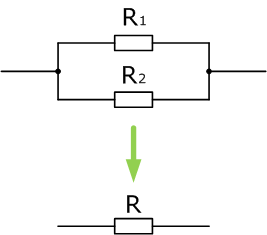
Два сопротивления соединены параллельно, значит при сворачивании схемы, общее сопротивление будет равно (значения R₁,R₂ такие же как и в примере 1)

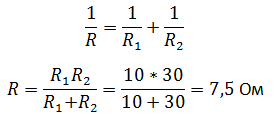
Можно заметить, что при параллельном соединении общее сопротивление меньше, чем при последовательном в несколько раз.

Пример 3

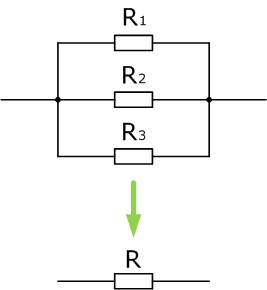
В данном примере ситуация аналогична примеру 2, за тем лишь исключением, что сопротивлений три. Тогда общее сопротивление будет равно (R₁,R₂ прежние, R₃=105 Ом)

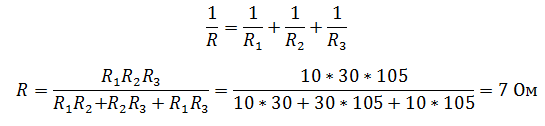
Пример 4

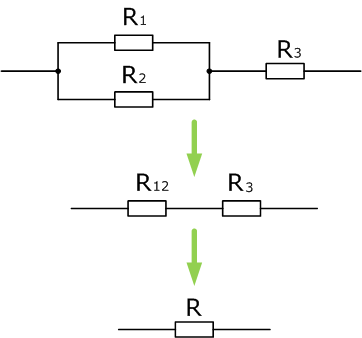
Чтобы рассчитать общее сопротивление смешанного соединения проводников, необходимо для начала найти общее сопротивление резисторов R₁ и R₂ соединенных параллельно, а затем общее сопротивление, как сумму R₁₂ и R₃ соединенных последовательно.

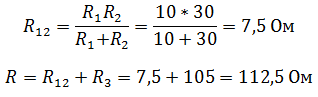
Пример 5

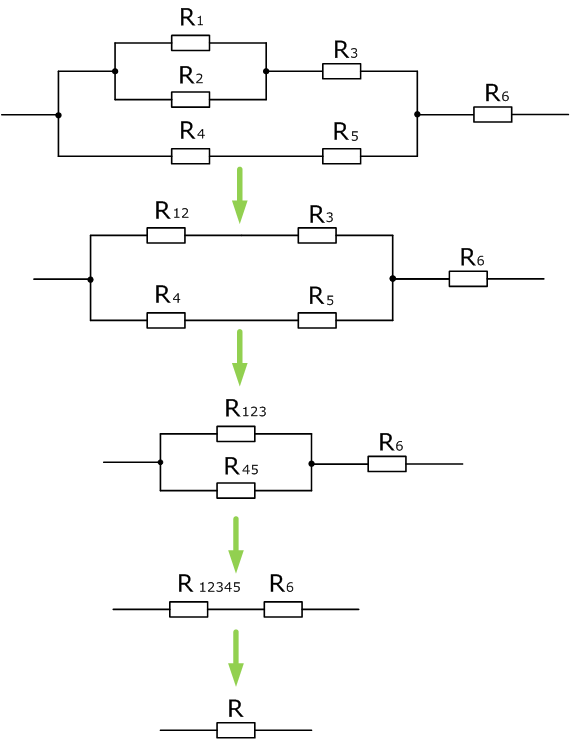
Данная электрическая цепь сложнее, чем предыдущие, но как можно увидеть, она также состоит из последовательно или параллельно соединенных сопротивлений, которые можно постепенно сворачивать, приводя цепь к единственному эквивалентному сопротивлению R.

R₄=20 Ом, R₅=40 Ом, R₆=15 Ом

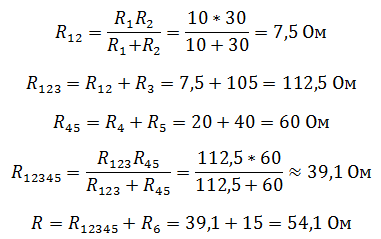
Путем сворачивания цепи с помощью преобразований последовательно и параллельно соединенных проводников, можно максимально упростить для дальнейшего расчета сколь угодно сложную схему. Исключением служат цепи содержащие сопротивления, соединенные по схеме звезда и треугольник.

Источник

Советы

Похожие статьи

Об этой статье

Была ли эта статья полезной?

Calculator, Practice Problems, and Answers

About This Article

Did this article help you?

Что такое полное сопротивление цепи и как его правильно найти

Виды электрических сопротивлений

Определение эквивалентного сопротивления

Как определяется ПС при последовательном соединении емкостей и индуктивностей

Определение ПС при использовании параллельного соединения элементов

Видео по теме

5. Расчет комплексных сопротивлений параллельного участка и входного сопротивления

Расчет сопротивления цепи

Пример 1

Пример 2

Пример 3

Пример 4

Пример 5

Добавить комментарий Отменить ответ

Советы

Похожие статьи

Об этой статье

Была ли эта статья полезной?

Calculator, Practice Problems, and Answers

About This Article

Did this article help you?

Что такое полное сопротивление цепи и как его правильно найти

Виды электрических сопротивлений

Определение эквивалентного сопротивления

Как определяется ПС при последовательном соединении емкостей и индуктивностей

Определение ПС при использовании параллельного соединения элементов

Видео по теме

5. Расчет комплексных сопротивлений параллельного участка и входного сопротивления

Расчет сопротивления цепи

Пример 1

Пример 2

Пример 3

Пример 4

Пример 5

Вам также может понравиться

Have to модальный глагол как составить вопрос

0x800f0805 как исправить ошибку windows 10

Как найти порт в усть луге

Добавить комментарий Отменить ответ