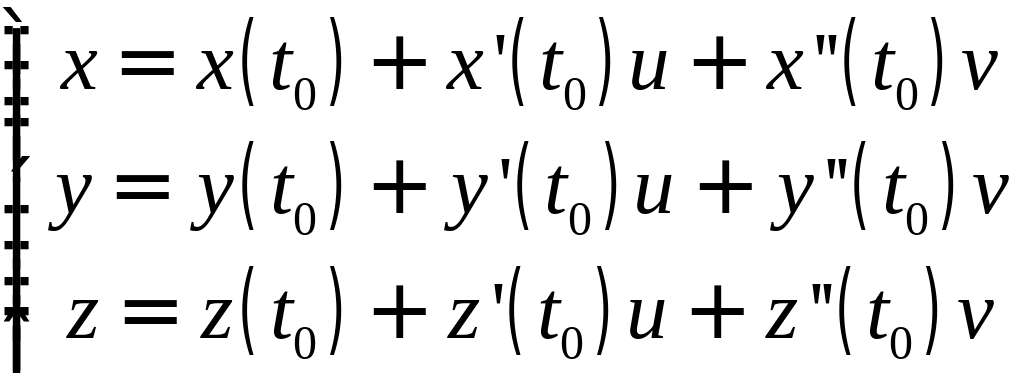Рассмотрим
гладкую кривую
в пространстве
.
Пусть
– любая точка кривой. Найдем плоскость,
проходящую через
и «ближе всего подходящую» к кривой
в окрестности точки
.
Заметим, что если кривая
– плоская (то есть лежащая в некоторой
плоскости
),
то искомой плоскостью будет плоскость
.
Определение
3.1. Соприкасающейся
плоскостью к
кривой
в точке
называется предел секущей плоскости,
проходящей через точки
кривой
при
стремлении
Более
строго, плоскость
,
проходящая через точку
кривой
,
является соприкасающейся к кривой
в точке
,
если
.
Теорема
3.1.
-гладкая
кривая
имеет в каждой точке
соприкасающуюся плоскость.
Дадим
необходимые разъяснения для кривой
более высокого порядка гладкости.
Пусть
в
пространстве
задана прямоугольная система координат
Оxyz.
Пусть
r
(t)
– одна из гладких параметризаций кривой
:
и
Рассмотрим
произвольную точку
,
близкую к точке
.
Разложим
в ряд Тейлора вектор смещения
:
Пусть
– неколлинеарные векторы.
Тогда
искомая плоскость единственна и проходит
через точку
параллельно векторам
.
Замечание
3.1.
Неколлинеарность векторов
не
зависит от способа параметризации
кривой.
В частности, для любой допустимой замены
параметра
,
где
,
векторы
также будут неколлинеарны.
Пусть
– коллинеарные векторы.
Тогда
соприкасающаяся плоскость не единственна.
В качестве одной из соприкасающихся
плоскостей можно взять любую из
плоскостей, проходящих через касательную
к кривой в точке
.
Определение
3.2. Спрямляющей
плоскостью к
кривой
в точке
называется плоскость, проходящая через
точку
кривой
перпендикулярно
спрямляющей и нормальной плоскостям в
этой точке.
Определение
3.3. Главной
нормалью к
кривой
в точке
называется прямая пересечения
соприкасающейся и нормальной плоскостей,
проведенных в точке
.
Главная
нормаль перпендикулярна спрямляющей
плоскости
.
Определение
3.4. Бинормалью
к
кривой
в точке
называется прямая пересечения спрямляющей
и нормальной плоскостей, проведенных
в точке
.
Бинормаль
перпендикулярна соприкасающейся
плоскости в точке
.
Определение
3.5. Сопровождающим
трехгранником (или
репером
Френе)
кривой
в точке
называется совокупность трех прямых
– касательной, главной нормали и
бинормали, и трех плоскостей – нормальной
спрямляющей и соприкасающейся, проведенных
в точке
.
Рисунок 12.
Пусть
r
(t)
– одна из гладких параметризаций кривой
:
,
и
– любая точка кривой.
Напишем
уравнения всех прямых и всех плоскостей
сопровождающего трехгранника кривой.
Уравнения
касательной прямой и нормальной плоскости
мы уже выписывали в §2.
Если
соприкасающаяся плоскость к кривой
в точке
единственна, то она может быть задана
параметрическими уравнениями
,
где
.
В
качестве направляющего вектора бинормали
возьмем вектор
.
Уравнение бинормали в параметрическом
виде
,
где
.
В
качестве направляющего вектора главной
нормали возьмем вектор
.
Уравнение главной нормали в параметрическом
виде
,
где
.
Уравнение спрямляющей
плоскости в параметрическом виде
,
где
.
Уравнение
соприкасающейся плоскости можно также
написать в общем виде как уравнение
плоскости, проходящей через точку
перпендикулярно вектору
:
.
Аналогично,
так как спрямляющая плоскость проходит
через точку
перпендикулярно вектору
,
то ее общее уравнение имеет вид:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пусть (Gamma) — дважды дифференцируемая кривая без особых точек, для которой выполняются условие, описанное здесь ((displaystylefrac{dtau}{ds}neq 0)). Тогда выполняются это и это равенства, где (boldsymboltau) — единичный вектор касательной, (nu) — единичный вектор нормали к кривой (Gamma) в данной ее точке.
Рассмотрим вектор
$$
boldsymbolbeta=[boldsymboltau,boldsymbolnu].label{ref47}
$$
Тогда (boldsymbolbeta) — единичный вектор, ортогональный векторам (boldsymboltau) и (boldsymbolnu):
$$
boldsymboltau=[boldsymbolnu,boldsymbolbeta],qquad boldsymbolnu=[boldsymbolbeta,boldsymboltau].label{ref48}
$$
Прямую, проходящую через точку кривой параллельно вектору (boldsymbolbeta), называют бинормалью. Тетраэдр с вершиной в точке кривой, ребра которого имеют длину, равную единице, и параллельны векторам (boldsymbol{tau, nu, beta}), называют сопровождающим трехгранником Френе (рис. 22.12).
Утверждение 1.
Если (Gamma) — трижды непрерывно дифференцируемая кривая, удовлетворяющая данному условию, то справедливы формулы Френе
$$
frac{dboldsymboltau}{ds}=kboldsymboleta,nonumber
$$
$$
frac{dboldsymbolnu}{ds}=-kboldsymboltau+varkappaboldsymbolbeta,label{ref49}
$$
$$
frac{dboldsymbolbeta}{ds}=-varkappaboldsymbolnu.label{ref50}
$$
Доказательство.
(circ) Первая из формул Френе получена здесь. Докажем формулу eqref{ref50}. Дифференцируя равенство eqref{ref47} с учетом первой формулы Френе и равенства ([boldsymbolnu,boldsymbolnu]=0), получаем
$$
frac{dboldsymbolbeta}{ds}=left[frac{dboldsymboltau}{ds},boldsymbolnuright]+left[boldsymboltau,frac{dboldsymbolnu}{ds}right]=left[boldsymboltau,frac{dboldsymbolnu}{ds}right].nonumber
$$
Так как (boldsymbolnu) — единичный вектор, то он ортогонален вектору (displaystyle frac{dboldsymbolnu}{ds}). Кроме того, вектор (boldsymbolnu) ортогонален вектору (boldsymboltau). Поэтому вектор (left[tau,displaystyle frac{dboldsymbolnu}{ds}right]) параллелен вектору (boldsymbolnu) и справедливо равенство eqref{ref50}. Коэффициент (varkappa) в формуле eqref{ref50} называют кручением кривой в данной ее точке.
Пользуясь первой формулой Френе, формулами eqref{ref47}, eqref{ref48} и eqref{ref50}, получаем
$$
frac{dboldsymbolnu}{ds}=left[frac{dboldsymbolbeta}{ds},boldsymboltauright]+left[boldsymbolbeta,frac{dboldsymboltau}{ds}right]=-varkappa[boldsymbolnu,boldsymboltau]+k[boldsymbolbeta,boldsymbolnu]=-kboldsymboltau+varkappaboldsymbolbeta,nonumber
$$
то есть справедлива формула eqref{ref49}. (bullet)
Докажем, наконец, следующее: если кривая, заданная натуральным уравнением, трижды дифференцируема, а ее кривизна (k=k(s)) отлична от нуля, то кручение кривой (varkappa=x(s)) выражается формулой
$$
varkappa=frac{left(frac{dtextbf{r}}{ds},frac{d^{2}textbf{r}}{ds^{2}},frac{d^{3}textbf{r}}{ds^{3}}right)}{k^{2}}.label{ref51}
$$
(circ) Используя первую формулу Френе и eqref{ref49}, находим
$$
frac{d^{2}textbf{r}}{ds^{2}}=k(s)boldsymbolnu,quad frac{d^{3}textbf{r}}{ds^{3}}=k'(s)boldsymbolnu+k(s)frac{dboldsymbolnu}{ds}=k'(s)boldsymbolnu-k^{2}(s)boldsymboltau+k(s)varkappa(s)boldsymbolbeta.nonumber
$$
Вычислим смешанное произведение векторов, указанных в формуле eqref{ref51}, пользуясь тем, что ((boldsymboltau,boldsymbolnu,boldsymbolnu)=(boldsymboltau,boldsymbolnu,boldsymboltau)=0) и ((boldsymboltau,boldsymbolnu,boldsymbolbeta)=1). Тогда из равенства
$$
left(frac{dtextbf{r}}{ds},frac{d^{2}textbf{r}}{ds^{2}},frac{d^{3}textbf{r}}{ds^{3}}right)=(boldsymboltau,k(s)boldsymbolnu,k'(s)boldsymbolnu-k^{2}(s)boldsymboltau+k(s)varkappa(s)boldsymbolbeta)=\=k^{2}(s)varkappa(s)(boldsymboltau,boldsymbolnu,boldsymbolbeta)=k^{2}(s)varkappa(s)nonumber
$$
следует формула eqref{ref51}. (bullet)
Замечание 1.
Из формулы eqref{ref50} следует, что (left|displaystyle frac{dboldsymbolbeta}{ds}right|=|varkappa|), так как (|nu|=1). Повторяя рассуждения, связанные с выяснением физического смысла кривизны кривой, отсюда получим, что
$$
|varkappa|=lim_{Delta srightarrow 0}left|frac{Deltaalpha}{Delta s}right|,label{ref52}
$$
где (Deltaalpha) — угол поворота бинормали к кривой (Gamma) при изменении ее параметра от (s) до (s+Delta s). Выражение в правой части eqref{ref52} назовем скоростью вращения вектора бинормали. Эта скорость равна скорости вращения соприкасающейся плоскости кривой, так как вектор (boldsymbolbeta) перпендикулярен этой плоскости. Таким образом, модуль кручения кривой равен скорости вращения соприкасающейся плоскости.
Пример 1.
Вычислим кривизну (k) и кручение (varkappa) винтовой линии:
$$
x=acos t,quad y=asin t,quad z=bt,quad 0leq tleq T,nonumber
$$
где (a > 0, b > 0)
Решение.
(triangle) В примере получено натуральное уравнение винтовой линии
$$
textbf{r}=textbf{r}(s)=(acoslambda s,asinlambda s,blambda s),nonumber
$$
где
$$
lambda=frac{1}{sqrt{a^{2}+b^{2}}}.nonumber
$$
Поэтому
$$
tau=frac{dtextbf{r}}{ds}=(-alambdasinlambda s,alambdacoslambda s,blambda),nonumber
$$
$$
frac{dtau}{ds}=(-alambda^2coslambda s,-alambda^{2}sinlambda s,0),nonumber
$$
откуда по формуле отсюда находим
$$
k=left|frac{dtau}{ds}right|=alambda^{2}=frac{a}{a^{2}+b^{2}}.nonumber
$$
используя первую формулу Френе, отсюда получаем
$$
nu=(-coslambda s,-sin lambda s,0).nonumber
$$
Для нахождения (varkappa) воспользуемся формулой eqref{ref50}, а вектор (boldsymbolbeta) найдем по формуле eqref{ref47}. Имеем
$$
boldsymbolbeta=(blambdasinlambda s,-blambdacoslambda s,alambda),nonumber
$$
откуда
$$
frac{dboldsymbolbeta}{ds}=(blambda^{2}cos lambda s,blambda^{2}sinlambda s,0)=-blambda^{2}(-coslambda s,-sinlambda s,0),nonumber
$$
то есть
$$
frac{dboldsymbolbeta}{ds}=-blambda^{2}boldsymbolnu,nonumber
$$
отсюда по формуле eqref{ref50} находим
$$
varkappa=blambda^2=frac{b}{a^{2}+b^{2}}.nonumber
$$
Таким образом, кривизна кривой и кручение для винтовой линии постоянные. (blacktriangle)
1. Сопровождающим трехгранником, связанным с текущей точкой 
пространственной кривой, называется трехгранник, ребрами которого являются касательная, главная нормаль и бинормаль.
Рис. 102.
Грани этого трехгранника носят следующие названия (рис. 102).
Грань, проходящая через касательную и главную нормаль, называется соприкасающейся плоскостью.
Грань, проходящая через главную нормаль и бинормаль, называется нормальной плоскостью.
Грань, проходящая через касательную и бинормаль, называется спрямляющей плоскостью.
Замечание. Небольшой кусочек кривой в окрестности данной точки можно считать приближенно расположенным в соприкасающейся плоскости. Эта плоскость перпендикулярна спрямляющей плоскости. Поэтому проекция указанного кусочка кривой на спрямляющую плос кость будет в первом приближении прямая линия.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 марта 2021 года; проверки требуют 2 правки.
Репер или трёхгранник Френе
или Френе — Серре
известный также, как
естественный,
сопровождающий,
сопутствующий — ортонормированный репер в трёхмерном пространстве, возникающий при изучении бирегулярных кривых, то есть таких, что первая и вторая производная линейно независимы в любой точке.
Определение[править | править код]
Пусть 
— произвольная натурально параметризованная бирегулярная кривая в евклидовом пространстве. Под репером Френе понимают тройку векторов 
, 
, 
, сопоставленную каждой точке бирегулярной кривой , где
Свойства[править | править код]
- называемыми формулами Френе. Величины
- называют, соответственно, кривизной и кручением кривой в данной точке.
Скорость и ускорение в осях естественного трёхгранника[править | править код]
Трёхгранник Френе играет важную роль в кинематике точки при описании её движения в «сопутствующих осях». Пусть материальная точка движется по произвольной бирегулярной кривой. Тогда, очевидно, скорость точки направлена по касательному вектору 
. Дифференцируя по времени находим выражение для ускорения: 
. Компоненту при векторе 
называют тангенциальным ускорением, она характеризует изменение модуля скорости точки. Компоненту при векторе 
называют нормальным ускорением.
Она показывает, как меняется направление движения точки.
Вариации и обобщения[править | править код]
При описании плоских кривых часто вводят понятие так называемой ориентированной кривизны.
Пусть 
— произвольная натурально параметризованная плоская регулярная кривая. Рассмотрим семейство единичных нормалей 
, таких что двойка 
образуют правый базис в каждой точке 
. Ориентированной кривизной кривой 
в точке 
называют число 
. В сделанных предположениях имеет место следующая система уравнений, называемая формулами Френе для ориентированной кривизны
.
По аналогии с трёхмерным случаем, уравнения вида 
называются натуральными уравнениями плоской регулярной кривой и полностью её определяют.
См. также[править | править код]
- Трёхгранник Дарбу — аналогичная конструкция для кривой на поверхности.
Литература[править | править код]
- Топоногов, В. А. Дифференциальная геометрия кривых и поверхностей. — Физматкнига, 2012. — ISBN 978-5-89155-213-5.
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
