Как найти сопряженное комплексное число в маткаде

Как найти сопряженное комплексное число в маткаде

Специальные операции над комплексными числами

В
Mathcad есть следующие специальные функции
и операторы для работы с комплексными
числами:

Re(z)

Вещественная
часть z.

Im(z)

Мнимая
часть z.

arg(z)

Угол
в комплексной плоскости между
вещественной осью и z.
Возвращает результат между - 
и

радиан.

Модуль
z.
Чтобы записать модуль от выражения,
заключите его в выделяющую рамку и
нажмите клавишу с вертикальной полосой
| .

Число,
комплексно сопряженное к z.
Чтобы применить к выражению оператор
сопряжения, выделите выражение, затем
нажмите двойную кавычку (“). Число,
сопряжённое к a
+ bi
есть a
– bi
.

Рисунок
2 показывает некоторые примеры
использования комплексных чисел в
Mathcad.

Рисунок
2: Комплексные числа в Mathcad.

Многозначные функции

При
использовании в комплексной области
многие функции, о которых мы привыкли
думать как о возвращающих одно значение,
становятся многозначными.

Общее
правило состоит в том, что для многозначной
функции Mathcad всегда возвращает значение,
составляющее на комплексной плоскости
самый маленький положительный угол с
положительным направлением действительной
оси. Оно называется главным значением.

Например,
если требуется вычислить (-1)1/3
, Mathcad вернёт .5 + .866i
, хотя мы обычно считаем -1 кубическим
корнем из 1. Дело в том, что .5 + .866i
  составляет с положительным
направлением вещественной оси угол
только в 60 градусов, в то время как -1
составляет 180 градусов.

Единственное
исключение из этого правила — оператор
n-ого
корня, описанный в главе Список
операторов.
Этот оператор возвращает вещественный
корень всякий раз, когда это возможно.
Рисунок 3 показывает эту особенность.

Рисунок
3: Нахождение вещественных корней n–ой
степени из отрицательного
числа.

Разделы

  • Создание
    вектора или матрицы

Как
создавать или редактировать векторы
и матрицы

  • Вычисления
    с массивами

Определение
переменных как массивов и использование
их в выражениях

  • Нижние
    индексы и верхние индексы

Обращение
к отдельным столбцам и элементам
массива.

  • Отображение
    векторов и матриц

Как
Mathcad отображает матрицы и векторы.

  • Ограничения
    размеров массивов

Ограничения
размеров массивов, которые нужно
вводить, сохранять или отображать.

  • Векторные
    и матричные операторы

Операторы,
предназначенные для использования
с векторами и матрицами.

  • Векторные
    и матричные функции

Встроенные
функции, предназначенные для
использования с векторами и матрицами.

  • Выполнение
    параллельных вычислений

Использование
в Mathcad оператора векторизации для
ускорения  вычислений.

  • Одновременные
     определения

Использование
векторов для одновременного определения
нескольких переменных.

  • Функции,
    определяемые пользователем, и массивы

Использование
массивов как аргументов к функциям,
определяемым  пользователем.

  • Составные
    массивы

Массивы,
элементы которых сами являются
массивами.

прямоугольная
таблица чисел — матрицей. Общий термин
для вектора или матрицы — массив.

Имеются
три способа создать массив:

  • Заполняя
    массив пустых полей, как обсуждается
    в этом разделе. Эта методика подходит
    для не слишком больших массивов.

  • Используя
    дискретный аргумент, чтобы определить
    элементы с его помощью, как обсуждено
    в следующей главе. Эта методика подходит,
     когда  имеется  некоторая явная
     формула  для вычисления  элементов
    через их индексы.

  • Считывая
    их из файлов данных.

Можно
различать имена матриц, векторов и
скаляров, используя различный шрифт
для их написания. Например, во многих
математических и инженерных книгах
имена векторов пишутся жирным, а имена
скалярных переменных — курсивом.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Уравнение с комплексными числами маткад

Как описано в предшествующем разделе, Mathcad воспринимает комплексные числа в форме a + bi, где a и b — обычные числа. Можно использовать букву j вместо i, если это удобнее.

Комплексные числа могут также возникать в результате вычислений, даже если все исходные значения вещественны. Например, если вычислить , Mathcad вернёт i.

Хотя можно вводить мнимые числа, сопровождая их i или j, Mathcad обычно отображает их сопровождаемыми i. Чтобы Mathcad показывал мнимые числа с j, выберите Формат числа из меню Математика, нажмите на кнопку “Глобальный” и переключите “Мн. ед”. на j.

При вводе комплексных чисел не забудьте, что нельзя использовать i или j сами по себе для ввода комплексной единицы. Нужно всегда печатать 1i или 1j, в противном случае Mathcad истолкует i или j как переменную. Когда курсор покидает выражение, содержащее 1i или 1j, Mathcad скрывает избыточную 1.

Специальные операции над комплексными числами

В Mathcad есть следующие специальные функции и операторы для работы с комплексными числами:

Re(z) Вещественная часть z.
Im(z) Мнимая часть z.
arg(z) Угол в комплексной плоскости между вещественной осью и z. Возвращает результат между – p и p радиан.
Модуль z. Чтобы записать модуль от выражения, заключите его в выделяющую рамку и нажмите клавишу с вертикальной полосой | .
Число, комплексно сопряженное к z. Чтобы применить к выражению оператор сопряжения, выделите выражение, затем нажмите двойную кавычку (“). Число, сопряжённое к a + bi есть a – bi .

Рисунок 2 показывает некоторые примеры использования комплексных чисел в Mathcad.

Рисунок 2: Комплексные числа в Mathcad.

При использовании в комплексной области многие функции, о которых мы привыкли думать как о возвращающих одно значение, становятся многозначными.

Общее правило состоит в том, что для многозначной функции Mathcad всегда возвращает значение, составляющее на комплексной плоскости самый маленький положительный угол с положительным направлением действительной оси. Оно называется главным значением.

Например, если требуется вычислить (-1) 1/3 , Mathcad вернёт .5 + .866i , хотя мы обычно считаем -1 кубическим корнем из 1. Дело в том, что .5 + .866i составляет с положительным направлением вещественной оси угол только в 60 градусов, в то время как -1 составляет 180 градусов.

Единственное исключение из этого правила — оператор n-ого корня, описанный в главе Список операторов. Этот оператор возвращает вещественный корень всякий раз, когда это возможно. Рисунок 3 показывает эту особенность.

Рисунок 3: Нахождение вещественных корней n-ой степени из отрицательного числа.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Уравнение с комплексными числами маткад

Глава 3. Работа с векторами и матрицами

3 . 12 Работа с комплексными числами

MathCAD с одинаковым успехом вычисляет выражения с действительными и комплексными числами.

Комплексные числа можно записывать в любой принятой в математике форме:

– обычной (в виде суммы действительной и мнимой частей числа) – с=а+ b · i ;

– в тригонометрической форме – c = A ·( sin ( φ )+ i · cos (φ));

– в экспоненциальной форме – c = A · e i ·φ .

Для ввода мнимой единицы надо набрать с клавиатуры 1 i или 1 j и ввести число. При выведении курсора из области числа символ 1 исчезает, остается комплексное число в привычном виде (рис. 3.23 ).

расчет токов в цепи по уравнениям Кирхгофа ORIGIN:=1

Рис. 3. 23 Ввод комплексных чисел

В качестве примера рассмотрим расчет токов и напряжений в цепи переменного тока по законам Кирхгофа. В этом случае ЭДС в цепи Е, напряжение U , токи J , сопротивление Z – комплексные числа. ЭДС Е задана в экспоненциальной форме, но при нажатии клавиши=выводится в обычном виде. После ввода констант в комплексной форме все формулы записываются также, как и для действительных чисел. При расчете вектора напряжений на различных участках цепи по закону Ома использован оператор векторизации для расчета попарных произведений (рис. 3.24 ).

Расчет напряжений по закону Ома

без оператора векторизации выведено скалярное произведение векторов

это не аргумент функции–без вывод комплексно-сопряженных чисел

оператора векторизации не обойтись

Рис. 3. 24 Расчеты с векторами комплексных чисел

В MathCAD есть оператор преобразования комплексного числа в комплексно – сопряженное. Он не представлен на математической панели, а вызывается с помощью символа “ .

Модуль комплексного числа вычисляется оператором || вводимым с панелей Calculator (Калькулятор) или Matrix (Матрица). Тот же оператор позволяет вычислить модуль вектора или определитель матрицы.

Аргумент комплексного числа вычисляется по формуле встроенной функцией arg ( A ), которая выдает угол поворота вектора в системе координат Re – Im (рис. 3.25 ).

модуль комплексного числа. необходим оператор векторизации

аргумент комплексного числа

угол в радианах угол в градусах

Рис. 3. 25 Вычисление модуля и аргумента комплексных чисел

MathCAD — это просто! Часть 19. Немного о работе с комплексными числами

Комплексные числа — одна из важнейших математических абстракций, очень часто используемая в реальных расчетах инженерами, физиками, электронщиками и другими специалистами. Само собой, настолько важная часть математики, как работа с комплексными числами, не могла остаться вне поля зрения разработчиков MathCAD’а. Сегодня мы с вами как раз и поговорим о том, как можно работать в MathCAD’е с ними — вы сможете самостоятельно убедиться в том, что это, в общем-то, не представляет каких-либо особых сложностей для пользователя этого мощнейшего математического пакета.

Суть теории комплексных чисел заключается, по существу, в том, что множество действительных чисел можно расширить до другого, нового, множества (оно как раз таки и имеет название множества комплексных чисел), в котором каждое число представимо в виде z = a + b*i, где i — мнимая единица (корень из числа -1, или, вернее, один из корней). При этом a называется действительной частью комплексного числа (обозначается как Re(z)), а b, соответственно, принято называть его мнимой частью. Обозначается же мнимая часть комплексного числа как Im(z). Стоит отметить тот факт, что нередко даже образованные люди теряются, когда им нужно произнести вслух термин “комплексное число”. На какую букву ставить ударение в слове “комплексный” — на “о” или “е”? Честно говоря, правильного ответа на этот вопрос я не знаю. Даже в математических словарях и справочниках нет единодушия: в некоторых ударение ставят на одну букву, в некоторых — на другую. Традиционно используют, впрочем, ударение на букву “е” (есть даже шутка такая: “комплексными бывают обеды, а числа — только комплексные”). Но если вы где-то скажете “комплексные числа”, то в тюрьму вас за это, конечно же, никто не посадит. Фактически же комплексное число является упорядоченной парой действительных чисел, и часто даже вместо a + b*i записывают комплексные числа в виде (a; b). В ряде практических вычислений нужно оперировать именно такими упорядоченными парами чисел — например, в той же радиоэлектронике такой парой могут служить амплитуда и частота сигнала. Чем же в таком случае комплексное исчисление так принципиально отличается от векторного? В первую очередь, своим математическим аппаратом, позволяющим осуществлять с довольно большой степенью удобства некоторые преобразования над ними.

Существуют различные формы представления комплексного числа, каждая из которых удобна в своем виде операций над этими числами. Та форма, с которой мы с вами уже успели познакомиться, называется алгебраической формой, или алгебраическим представлением комплексного числа. Она удобна для того, чтобы такие числа суммировать (ну, и вычитать, конечно же, тоже). Действительная часть складывается с действительной, мнимая с мнимой, и все получается хорошо. Но вот умножать или возводить в степень комплексные числа в алгебраической форме уже, мягко говоря, не так удобно. Для этого используют тригонометрическую или экспоненциальную формы записи комплексных чисел. В общем-то, эти две формы фактически представляют собой одну и ту же форму записи, которую чаще все же называют тригонометрической. Получается она из алгебраической формы довольно-таки просто. Для начала нужно получить два параметра, с помощью которых комплексное число представляется в тригонометрической форме. Первый параметр называется модулем числа и вычисляется как корень из суммы квадратов a и b. Второй параметр принято называть аргументом комплексного числа z, и вычисляется он как арктангенс выражения b/a. Для любого из комплексных чисел переход от алгебраической формы к тригонометрической не представляет никакой сложности, поскольку формулы, по которым вычисляются и модуль, и аргумент, очень просты и для понимания, и для запоминания, и для применения. Само же комплексное число z записывается в тригонометрической форме следующим образом: z = r (cos? + i*sin?). Здесь r — это модуль комплексного числа z, а ? — соответственно, как вы уже навреняка успели догадаться, его же аргумент. Экспоненциальная форма записи комплексного числа — это, как я уже говорил, по сути, та же тригонометрическая, поскольку на множестве комплексных чисел экспонента ведет себя совсем не так, как на множестве чисел действительных. Фактически та формула для тригонометрической записи числа, которую я только что показал вам, с помощью экспоненты может быть записана гораздо короче: z = r*ei*?. Как видите, с использованием экспоненциального представления становится особенно просто умножать комплексные числа друг на друга, а также возводить их в степень. Для того, чтобы возводить в степень числа в тригонометрическом их представлении, можно воспользоваться формулой Муавра, которая безо всяких сложностей отыщется в любом справочнике по высшей математике.

Комплексные числа в MathCAD: основы

Весь тот небольшой экскурс в работу с комплексными числами, который я привел выше, нужен только для того, чтобы напомнить (или, если кто-то не знал этого, то разъяснить), что же такое комплексные числа, и как именно с ними нужно работать. При работе в MathCAD’е, само собой, вам не понадобится собственноручно вычислять модуль и аргумент комплексного числа, не надо будет самостоятельно высчитывать степень экспоненты при перемножении комплексных чисел и даже не понадобится самому складывать действительную часть с действительной, а мнимую — с мнимой. Все за вас сделает этот мощный математический пакет. То есть, конечно, не все, а только черновую, вычислительную работу — постановка задачи и интерпретация результатов вычислений все равно останется за вами. Хорошая новость состоит в том, что для работы с комплексными числами не нужно как-то по- особенному настраивать среду MathCAD или применять какие-то новые арифметические операторы. Среда точно так же работает с комплексными числами, как и с действительными. Простой пример — сложение комплексных чисел. Попробуйте сложить два комплексных числа — например, 1+2i и 7-15i. Здесь, правда, стоит отдельно сказать пару слов относительно ввода в MathCAD’е мнимой единицы. Дело в том, что, если вы просто напишете ее как i, нажав на клавиатуре соответствующую клавишу, то система MathCAD посчитает, что вы ввели имя какой-либо переменной. Поэтому можно либо воспользоваться панелью инструментов Calculator (см. иллюстрацию, на которой нужная кнопка обведена кружком), либо вводить с клавиатуры комбинацию 1i.

После того, как вы попробуете складывать комплексные числа, можно попробовать их перемножать, чтобы убедиться в том, что MathCAD умеет делать и это. Можете попробовать возводить комплексные числа в какую-либо степень, а также любым другим образом поиздеваться над ними. Как и следовало ожидать, MathCAD с легкостью справляется с подобными заданиями. Поэтому вы можете работать с комплексными числами фактически точно так же, как и с действительными.

Комплексные числа в MathCAD: подробности и тонкости

Впрочем, конечно же, есть и некоторые тонкие моменты, связанные с отличиями в работе с комплексными и действительными числами. Самое главное из подобного рода отличий состоит, собственно говоря, в том, что операция извлечения корня с ними работает не совсем так, как надо — как, впрочем, и операция возведения в дробную степень, хотя для действительных чисел данные операции и абсолютно корректны. Дело в том, что на множестве комплексных чисел мы рассматриваем корень p n-й степени из числа z как множество решений уравнения pn = z. Если вы попробуете решить это уравнение с помощью оператора solve (хоть о нем мы говорили уже достаточно давно — думаю, вы еще не до конца забыли, как им пользоваться), то увидите, что для n-й степени это уравнение, согласно основной теореме алгебры, будет иметь ровно n решений. Если же для вычисления корня комплексного числа вы воспользуетесь операторами извлечения корня или возведения комплексного числа в дробную степень, то увидите, что подобные вычисления дадут вам только один корень из всех возможных, что не вполне корректно. Впрочем, в ряде практических задач вам будет нужен только один корень, но все равно его лучше получать с помощью solve, а затем уже выбирать среди результатов.

Ну, и напоследок такой вопрос: а как лучше обозначать мнимую единицу? Дело в том, что в литературе встречается два варианта ее обозначения: i и j. Первый более характерен для советских и постсоветских источников, второй — для зарубежных. Вполне может случиться так, что вам потребуется в вашем проекте использовать второе, а не первое, которое используется в MathCAD по умолчанию. Конечно же, эта мощная математическая среда позволяет нам изменить обозначение мнимой единицы на то, которое будет для нас наиболее удобным. Для того, чтобы поменять обозначение, нужно в меню Format выбрать пункт Result, а в появившемся окне на вкладке Display Options заменить параметр Imaginary Value. Вариантов этого параметра, конечно, не много — собственно, их всего два: либо i, либо j. Но больше вариантов, собственно говоря, и нету.

Итак, мы с вами познакомились с комплексными числами, а также с тем, как именно работать с ними в MathCAD’е. Вы смогли сами убедиться, что это совсем несложно, хотя, конечно, некоторые вычисления и имеют свои тонкости. Но тонкости есть везде, и главное — быть заранее готовым к тому, что есть немалый шанс с ними столкнуться. Поэтому, если вы внимательно читаете статьи серии “MathCAD — это просто”, то будете хорошо подготовлены к встречам с различными неожиданностями в среде MathCAD. Успехов вам в работе с этим мощным математическим пакетом и интересных вычислений!

Компьютерная газета. Статья была опубликована в номере 33 за 2008 год в рубрике soft

[spoiler title=”источники:”]

http://www.math.mrsu.ru/text/courses/mcad/3.12.htm

http://nestor.minsk.by/kg/2008/33/kg83303.html

[/spoiler]

Источник

Вычисления с комплексными числами в MathCAD

В MathCAD определена мнимая единица j: , и, следовательно, определены комплексные числа и операции с ними. Для того, чтобы ввести в MathCAD мнимую единицу, следует набрать на клавиатуре <1><j> (в рабочем документе будет отображен символ i, который MathCAD при таком способе ввода воспринимает как мнимую единицу).

Комплексные числа записывают в MathCAD в общепринятой математической нотации. Это означает, что выражение z = a + bj, где а и b – действительные числа, воспринимается как комплексное число, действительная часть которого равна а, а мнимая – b.

В MathCAD можно определять комплексные числа в алгебраической, тригонометрической и показательной форме; однако при символьных вычислениях (с помощью знака символьных преобразований ® или ключевого слова complex) комплексное число все равно отображается в алгебраической форме.

Для вычислений с комплексными числами в MathCAD определены все арифметические операции, а также специфические для комплексной арифметики операции:

u Re(z) – действительная часть комплексного числа z;

u Im(z) – мнимая часть комплексного числа z;

u аrg(z) – главное значение аргумента комплексного числа z;

u – модуль комплексного числа Z;

u = a — jb – число, комплексно сопряженное к числу z.

В MathCAD можно вычислять значения элементарных функций, как действительного, так и комплексного аргумента. Однако при вычислении значений многозначных функций вычисляются только главные значения. Для того, чтобы вычислить все значения многозначных функций, пользователь должен определить их в рабочем документе соответствующими выражениями.

Если уравнение имеет комплексные корни, то MathCAD вычисляет не только действительные, но и комплексные корни.

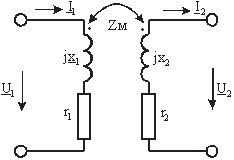
Расчет электрических цепей с трансформаторами

Уравнения двухобмоточного трансформатора

могут быть представлены в виде уравнений четырехполюсника в Z-форме:

(3.26)

При выбранном направлении токов и напряжений

.

Цепь с каскадным соединением трансформаторов

Если известно сопротивление вторичной цепи 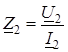, можно из второго уравнения (3.26) выразить I2 через I1 и таким образом пересчитать сопротивление вторичной цепи в первичную:

. (3.27)

Пересчет сопротивления Z2 из вторичной цепи в первичную дает возможность при известном напряжении на входе трансформатора определить ток первичной цепи. Для определения тока и напряжения вторичной цепи можно воспользоваться уравнением четырехполюсника в В-форме:

, (3.28)

Литература

1. Теоретические основы электротехники: В 3 т. Учебник для вузов. Том 1, 2. – 4-е изд. / К.С. Демирчян, Л.Р. Нейман, Н.В. Коровкин, В.Л. Чечурин. – СПБ Питер, 2004. – 463, 576 с.

2. Основы теории цепей: Учебник для вузов. Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. – 5-е изд., перераб. – М.: Энергоатомиздат, 1989. – 528 с.

3. К.С. Демирчян, П.А. Бутырин. «Моделирование и машинный расчет электрических цепей». – М.: ВШ., 1988. – 335 с.

4. И. Влах, К. Сингхал. Машинные методы анализа и проектирование электронных схем. – М.: Радиосвязь, 1988. – 560 с.

5. Данилов Л.В. и др. Теория нелинейных электрических цепей (Л.В. Данилов, П.Н. Матханов, Е.С. Филиппов). – Л.: Энергоатомиздат, Ленинград. отд-ие, 1999. – 256 с.

6. Леон О. Чуа и Пен-Мин Лиин. Машинный анализ электронных схем (алгоритмы и вычислительные методы). – М.: Энергия, 1980. – 640 с.

7. Плис А.И., Сливина Н.А. MathCAD. Математический практикум для инженеров и экономистов: учеб. Пособие – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2003. – 656 с.

8. Шабалин В.Д. Машинное моделирование электрических цепей. – Кострома: Изд. Костромской ГСХА, 200. – 80 с.

9. Шабалин В.Д. Пересчет сопротивления нагрузки трехфазной цепи, содержащей трансформатор. / Актуальные проблемы науки в агропромышленном комплексе: материалы 58-й международной научно-практической конференции: в 3 т. Т. 3. – Кострома: КГСХА, 2007. с. 184–185.

Как в маткаде считать комплексные числа

В этой главе рассматриваются типы данных, применяемых в документах Mathcad, и принципы их ввода-вывода в наиболее простой числовой форме. Обычные типы данных (действительные и комплексные числа, константы и строковые данные) перечисляются в начале главы (см. разд. 4.1), параллельно с объяснением принципов их ввода в документы. Наряду с обычными числами, в Mathcad имеется мощный аппарат работы с массивами. Массивы реализованы в виде векторов и матриц, что максимально приближает стиль вычислений к общепринятой математической форме (см. разд. 4.3). Описана возможность форматирования результатов численных расчетов (см. разд. 4.4).

Отличительной чертой среды Mathcad является возможность обращения с размерными переменными, снабженными физическими единицами измерений (см. разд. 4.2). Эти средства существенно облегчают инженерные и научные расчеты.

В некоторых случаях удобно осуществлять ввод данных при помощи элементов управления (см. разд. 4.5). Другие формы ввода-вывода (графики, анимация, ввод-вывод в файлы) разобраны в последней части книги (см. гл. 16).

Наиболее простой и распространенный ввод-вывод данных в Mathcad реализован присваиванием и выводом (либо численным, либо символьным) непосредственно в документе. Переменные и функции, посредством которых осуществляется ввод-вывод, могут иметь значения различных типов (числовые, строковые и т. д.). Перечислим основные типы данных, которые обрабатываются процессорами системы Mathcad:

  • числа (в том числе, действительные, комплексные, а также встроенные константы) — Mathcad хранит все числа в формате двойной точности с плавающей точкой (не разделяя их на целые, булевы и т. д.);
  • строки — любой текст, заключенный в кавычки;
  • массивы (в том числе ранжированные переменные, векторы и матрицы) — упорядоченные последовательности чисел или строк.

Рассмотрим более подробно типы данных и то, как осуществляется их непосредственный ввод в документ с помощью присваивания значения переменным.

4.1.1. Действительные числа

Любое выражение, начинающееся с цифры, Mathcad интерпретирует как число. Поэтому для ввода числа просто начните его набирать на клавиатуре. Несмотря на то, что Mathcad хранит все числа в одинаковом формате, вводить их можно в наиболее подходящем представлении (notation), исходя из контекста документа:

  • как целое число;
  • как десятичное число (decimal notation) с любым количеством десятичных цифр после точки;
  • в представлении с порядком (exponential notation) — в так называемом научном формате или представлении (scientific notation), для чего после ввода числа напечатайте символ умножения и введите ю в нужной степени;
  • как число в другой системе счисления.

Три первых представления иллюстрируются содержанием соответствующей строки листинга 4.1.

При вводе целых чисел, больших или равных 1000, все цифры пишутся слитно (как показано в первой строке листинга 4.1) и ни в коем случае не разделяются на порядки запятыми. Например, ввод числа 1000 как 1,000 или 1.000 недопустим.

Листинг 4.1. Ввод действительных чисел

Если вы продолжите листинг 4.1 последовательным выводом всех переменных, то с удивлением обнаружите, что некоторые из чисел выглядят по-иному (например, число d=0). Объяснение этому будет дано в разд. 4.2.

Для ввода числа в других системах счисления: двоичной (binary), восьмеричной (octal) или шестнадцатеричной (hexadecimal) сделайте следующее:

  • Введите его представление в соответствующей системе, применяя лишь корректные символы (для двоичной системы допустимы только цифры 0 и 1; для восьмеричной — цифры от 0 до 7, для шестнадцатеричной — цифры от 0 до 9 и буквы от а до f)- Например, число 34 в двоичной системе представлено такой последовательностью: 100010.
  • После ввода последнего символа числа введите b (для двоичного числа), 0 (для восьмеричного числа) или h (для шестнадцатеричного).

Использование чисел в других системах счисления иллюстрируется листингом 4.2. Обратите внимание, что вывод осуществляется все равно в десятичной системе.

Листинг 4.2. Ввод чисел в других системах исчисления

В логических функциях используются битовые числа (ложь или истина). Они в Mathcad обозначаются обычными действительными числами 0 и 1.

4.1.2. Комплексные числа

Большинство операций в среде Mathcad по умолчанию осуществляются над комплексными числами. Комплексное число является суммой действительного и мнимого числа, получающегося путем умножения любого действительного числа на мнимую единицу (imaginary unit) i. По определению, i 2 =-1.

Чтобы ввести мнимое число, например 3i:

  • Введите действительный сомножитель (3).
  • Введите символ “i” или “j” непосредственно после него.

Для ввода мнимой единицы надо нажать клавиши <1>, <i.>. Если просто ввести символ “i”, то Mathcad интерпретирует его как переменную i. Кроме того, мнимая единица имеет вид 1i, только когда соответствующая формула выделена. В противном случае мнимая единица отображается просто как i (рис. 4.1).

Рис. 4.1. Ввод мнимой единицы

Комплексное число можно ввести в виде обычной суммы действительной и мнимой частей или в виде любого выражения, содержащего мнимое число. Примеры ввода и вывода комплексных чисел иллюстрируются листингом 4.3.

Листинг 4.3. Комплексные числа

Для работы с комплексными числами имеются несколько простых функций и операторов (см. разд. “Функции работы с комплексными числами” гл. 10), действие которых показано в листинге 4.4.

Листинг 4.4. Функций работы с комплексными числами

Можно выводить мнимую единицу в результатах вычислений не как i, а как j. Для смены представления выберите нужное в списке Imaginary Value (Мнимое значение) диалогового окна Result Format (Формат результата), доступного по команде Format / Result / Display Options (Формат / Результат / Опции отображения).

4.1.3. Встроенные константы

Некоторые имена в Mathcad зарезервированы под системные переменные, которые называются встроенными константами (built-in constants). Встроенные константы делятся на два типа: математические, хранящие значения некоторых общеупотребительных специальных математических символов, и системные, определяющие работу большинства численных алгоритмов, реализованных в Mathcad.

Математические константы (math constants)

  • символ бесконечности (вводится клавишами <Ctrl>+<Shift>+<z>);
  • е — основание натурального логарифма (клавиша <е>);
  • число “пи” (вводится клавишами <Ctrl>+<Shift>+<p>);
  • i, j — мнимая единица (вводится клавишами <1>, <i> или <1>, <j>);
  • % — символ процента, <%>, эквивалентный 0.01.

Математические константы по-разному интерпретируются при численных и символьных вычислениях. Вычислительный процессор просто воспринимает их как некоторые числа (листинг 4.5), а символьный распознает каждое из них, исходя из математического контекста, и способен выдавать математические константы в качестве результата.

Листинг 4.5. Значения математических констант

При желании можно изменить значение любой из перечисленных констант или использовать их в качестве переменных в расчетах (см. листинг 4.1, в котором переопределена константа е). Разумеется, если присвоить константе новое значение, прежнее станет недоступным.

Системные переменные (system variables)

  • TOL — точность численных методов;
  • CTOL — точность выполнения выражений, используемая в некоторых численных методах;
  • ORIGIN — номер начального индекса в массивах (см. разд. 4.3.1);
  • PRNPRECISION — установка формата данных при выводе в файл;
  • PRNCOLWIDTH — установка формата столбца при выводе в файл;
  • CWD — строковое представление пути к текущей рабочей папке.

Предустановленные значения системных переменных перечислены в листинге 4.6. Их можно поменять в любой части документа, присвоив соответствующей переменной новое значение. Кроме того, переопределение значения переменной для всего документа производится при помощи команды Tools / Worksheet Options / Built-in Variables (Сервис / Опции документа / Встроенные переменные) в диалоговом окне Worksheet Options (Опции документа ), приведенном на рис. 4.2. Чтобы в любой момент вернуть значения по умолчанию, нажмите кнопку Restore Defaults (Восстановить установки по умолчанию).

Листинг 4.6. Предустановленные значения системных переменных

Рис. 4.2. Вкладка Built-in Variables диалога Worksheet Options

4.1.4. Строковые выражения

Значением переменной или функции может быть не только число, но и строка, состоящая из любой последовательности символов, заключенной в кавычки (листинг 4.7). Для работы со строками в Mathcad имеется несколько встроенных функций (см. разд. “Строковые функции” гл. 10).

Листинг 4.7. Ввод и вывод строк

Совершенно аналогичным образом можно определять пользовательские функции строкового типа.

4.2. Размерные переменные

В Mathcad числовые переменные и функции могут обладать размерностью. Сделано это для упрощения инженерных и физических расчетов. В Mathcad встроено большое количество единиц измерения, с помощью которых и создаются размерные переменные.

4.2.1. Создание размерной переменной

Чтобы создать размерную переменную, определяющую, например, силу тока в 10 А:

  • Введите выражение, присваивающее переменной i значение ю: i:=io.
  • Сразу после ввода ю введите символ умножения “*”.
  • Находясь в области местозаполнителя, выберите команду Insert / Unit (Вставка / Единицы) либо нажмите кнопку с изображением мерного стакана на стандартной панели инструментов, либо клавиши <Ctrl>+<U> (рис. 4.3).
  • В списке Unit (Единица измерения) диалогового окна Insert Unit (Вставк-единицы измерений) выберите нужную единицу измерения Ampere (A).
  • Нажмите кнопку ОК.

Если Вы затрудняетесь с выбором конкретной единицы измерения, нэ знаете, какова размерность переменной (в нашем случае это электрический ток), то попробуйте выбрать ее в списке Dimension (Размерность) диалогового окна Insert Unit (Вставка единицы измерений) (рис. 4.4). Тогда в списке Unit (Единица измерения) появятся допустимые для этой величины единицы измерений, из которых выбрать нужную будет легче (рис. 4.5).

Просмотреть вставку единиц измерения можно и без выхода из диалогового окна Insert Unit, нажимая вместо кнопки ОК кнопку Insert (Вставить).

В этом случае Вы увидите, что единица измерений появилась в нужном месте документа, и можете поменять ее, оставаясь в диалоге Insert Unit.

Рис. 4.3. Вставка единиц измерения размерной величины

Рис. 4.4. Диалоговое окно Insert Unit

Рис. 4.5. Выбор размерности

4.2.2. Работа с размерными переменными

Работая с размерными переменными, приготовьтесь к тому, что Mathcad будет постоянно контролировать корректность расчетов. Например, нельзя складывать переменные разной размерности, в противном случае (рис. 4.6) будет получено сообщение об ошибке “The units in this expression do not match” (Размерности в этом выражении не совпадают). Тем не менее, позволяется складывать, например, амперы с килоамперами (см. рис. 4.9).

Рис. 4.6. Нельзя складывать переменные разной размерности

Рис. 4.7. Изменение единиц измерения в ответе

Над размерными переменными можно производить любые корректные с физической точки зрения расчеты. Пример расчета сопротивления через отношение напряжения к току приведен в листинге 4.8.

Листинг 4.8. Расчеты с размерными переменными

Обратите внимание, что результат в листинге 4.8 выдан не в омах. Тем не менее, легко перевести его в омы, как и в другие единицы. Для этого достаточно дважды щелкнуть на местозаполнителе, присутствующем после вычисленного значения формулы в момент, когда она выделена (рис. 4.7, внизу). В результате появляется то же самое диалоговое окно Insert Unit (Вставка единицы измерений), в котором можно поменять единицу измерений вычисленного ответа. В результате ответ будет пересчитан в соответствии с вновь введенной единицей измерения (как сделано для верхней формулы на рис. 4.7).

Можно включить автоматический перевод единиц измерения в более простые единицы. Для этого перейдите в диалоговое окно Result Format (Формат результата) на вкладку, посвященную размерностям, с помощью команды Format/ Result/ Unit Display (Формат/ Результат/ Отображение размерности). Установите в ней флажок Simplify units when possible (Упрощать единицы, когда это возможно).

Процесс смены единиц в момент их выбора в диалоге Insert Unit (Вставка единицы измерений) показан на рис. 4.8. В результате приведенного выбора выведенное в амперах значение силы тока будет изменено на значение в килоамперах: 1.01 кА.

Рис. 4.8. Сложение переменных одной размерности, выраженных в разных единицах

4.2.3. Выбор системы единиц

Как легко заметить, во всех примерах этого раздела вставлялись единицы системы измерения SI. Об этом можно было судить как по перечню самих единиц, так и по недоступному списку System (Система) в диалоге Insert Unit (Вставка единицы измерений) с выбранным пунктом SI. Сменить систему единиц во всем документе можно, выполнив команду Tools / Document Options (Сервис / Опции документа) и переходя на вкладку Unit System (Система единиц). В ней следует выбрать один из переключателей, соответствующий желаемой системе.

4.2.4. Определение новой размерности

Чтобы определить новую (пользовательскую) единицу измерения, достаточно присвоить ее выражение через используемые размерности переменной с соответствующим именем. Пример создания новой единицы измерения “наноампер” приведен в листинге 4.9.

Листинг 4.9. Определение новой единицы измерения

Созданные пользователем единицы измерения недоступны в диалоговом окне Insert Unit (Вставка единицы измерений), поэтому их приходится вводить вручную с клавиатуры (как это сделано для новой единицы ПА во второй строке листинга 4.9).

Массивами (arrays) называют упорядоченные последовательности чисел или элементов массива. Доступ к любому элементу массива возможен по его индексу, т. е. номеру в последовательности чисел (в листинге 4.10 а — это массив, ах — его элемент). Применение массивов чрезвычайно эффективно в математических расчетах.

Листинг 4.10. Одномерный массив (вектор)

В Mathcad условно выделяются два типа массивов:

  • векторы (одноиндексные массивы, листинг 4.10), матрицы (двухиндекс-ные, листинг 4.11) и тензоры (многоиндексные);
  • ранжированные переменные (range variables) — векторы, элементы которых определенным образом зависят от их индекса.

Листинг 4.11. Двумерный массив (матрица)

4.3.1. Доступ к элементам массива

Доступ ко всему массиву осуществляется по имени векторной переменной. Например, последовательность символов “а”, “=” в листингах 4.10 и 4.11 приведет к выводу соответствующего вектора или матрицы. В Mathcad имеются и операторы, и встроенные функции, которые действуют на векторы и матрицы целиком (они рассматриваются в гл. 9), например, транспонирование, матричное умножение и т. д.

Над элементами массива можно совершать действия как над обычными числами. Нужно только правильно задать соответствующий индекс или сочетание индексов массива. Например, чтобы получить доступ к нулевому элементу вектора а из листинга 4.10:

  • Введите имя переменной массива (а).
  • Нажмите кнопку Subscript (Нижний индекс) со значком хn на панели Matrix (Матрица) либо введите [.
  • В появившийся справа снизу от имени массива местозаполнитель введите желаемый индекс (0).

Если после этого ввести знак численного вывода, то справа от него появится значение нулевого элемента вектора, как показано во второй строке листинга 4.10.

Чтобы получить доступ к элементу многоиндексного массива (например элементу а1,0 матрицы а из листинга 4.11):

  • Введите имя переменной массива (а).
  • Перейдите к вводу нижнего индекса, введя [.
  • Введите в местозаполнитель индекса первый индекс (1), запятую “,” и в появившийся после запятой местозаполнитель введите второй индекс (0).

В результате будет получен доступ к элементу, как показано в предпоследней строке листинга 4.11.

В рассмотренных листингах нумерация индексов массивов начинается с нуля, иными словами, первый элемент массива имеет индекс о. Стартовый индекс массива задается системной переменной ORIGIN, которая по умолчанию равна нулю. Если Вы привыкли нумеровать элементы векторов и матриц с единицы, присвойте этой переменной значение 1 (листинг 4.12). Обратите внимание, что в этом случае попытка выяснить значение нулевого элемента вектора приводит к ошибке, поскольку его значение не определено.

Помимо доступа к отдельным элементам массива, имеется возможность совершать действия над его подмассивами (например векторами-столбцами, образующими матрицу). Делается это с помощью оператора со значком х на панели Matrix (Матрица) (см. гл. 9).

Листинг 4.12. Изменение нумерации индексов массивов

4.3.2. Ранжированные переменные

Ранжированные переменные в Mathcad являются разновидностью векторов и предназначены, главным образом, для создания циклов или итерационных вычислений. Простейший пример ранжированной переменной — это массив с числами, лежащими в некотором диапазоне с некоторым шагом.

Например, для создания ранжированной переменной s с элементами 0,1,2,3,4,5:

  • Поместите курсор ввода в нужное место документа.
  • Введите имя переменной (s) и оператор присваивания “:”.
  • Нажмите кнопку Range Variable (Ранжированная переменная) на панели Matrix (Матрица), показанную на рис. 4.9, либо введите символ точки с запятой с клавиатуры.
  • В появившиеся местозаполнители (рис. 4.9) введите левую и правую границы диапазона изменения ранжированной переменной 0 и 5.

Рис. 4.9. Создание ранжированной переменной

Результат создания ранжированной переменной показан на рис. 4.10.

Чтобы создать ранжированную переменную с шагом, не равным 1, например, 0,2,4,6,8:

  • Создайте ранжированную переменную в диапазоне от о до 8 (см. рис. 4.9).
  • Поместите линии ввода на значение начала диапазона (о).
  • Введите запятую.
  • В появившийся местозаполнитель (рис. 4.11) введите значение шага изменения ранжированной переменной (2).

Созданная ранжированная переменная будет иметь значения от о до 8 включительно, с шагом, равным 2.

Рис. 4.10. Вывод ранжированной переменной

Рис. 4.11. Создание ранжированной переменной с шагом, не равным 1

Чаще всего ранжированные переменные используются:

  • при параллельных вычислениях (листинги 4.13 и 4.14);
  • для присвоения значений элементам других массивов (листинги 4.14 и 4.15).

Обратите внимание на типичный пример использования ранжированной переменной из листингов 4.13 и 4.14. Большинство математических действий, реализованных в Mathcad, совершаются над ранжированными переменными точно так же, как над обычными числами. В этом случае одно и то же действие осуществляется параллельно над всеми элементами ранжированной переменной.

Листинг 4.13. Ранжированная переменная при параллельных вычислениях

Параллельные вычисления производятся точно так же и над произвольными векторами, не обязательно являющимися ранжированными переменными. Например, можно определить в листинге 4.14 вектор i, подобно вектору из листинга 4.10, и провести те же параллельные вычисления над его элементами.

Листинг 4.14. Ранжированная переменная при параллельных вычислениях

Листинг 4.15. Использование ранжированной переменной для определения матрицы

Определяя массив с помощью ранжированных переменных (листинги 4.14 и 4.15), позаботьтесь о том, чтобы их значения пробегали все необходимые индексы массива. Например, если задать шаг изменения ранжированной переменной, равный 2, то половина элементов вектора будет не определена.

Помните о том, что ранжированные переменные — просто разновидности векторов с упрощенной формой задания элементов. Часто необходимо провести одни и те же вычисления циклически, большое количество раз, например, вычисление некоторой функции f (х) в некотором диапазоне х для построения подробного графика. Задание вручную всех значений аргумента (наподобие вектора из листинга 4.10) очень трудоемко, а с помощью задания ранжированной переменной х это делается в одну строку.

4.3.3. Создание массивов

Существует несколько способов создания массива:

  • ввод всех элементов вручную с помощью команды Insert Matrix;
  • определение отдельных элементов массива;
  • создание таблицы данных и ввод в нее чисел;
  • применение встроенных функций создания массива (см. гл. 9);
  • создание связи с другим приложением, например Excel или MATLAB;
  • чтение из внешнего файла данных;
  • импорт из внешнего файла данных.

Рассмотрим основные способы создания массива, учитывая, что две последних возможности будут разобраны в последней части книги Применяйте способ, который оптимален в смысле простоты и читаемости конкретного документа, либо ставший наиболее для Вас привычным.

Создание матрицы командой Insert Matrix

Самый простой и наглядный способ создания вектора или матрицы заключается в следующем:

  • Нажмите кнопку Matrix or Vector (Матрица или вектор) на панели Matrix (Матрица) (рис. 4.12) либо клавиши <Ctrl>+<M>, либо выберите пункт меню Insert / Matrix (Вставка / Матрица).
  • В диалоговом окне Insert Matrix (Вставка матрицы) задайте целое число столбцов и строк матрицы, которую хотите создать. Например, для создания вектора 3×1 введите показанные на рис. 4.12 значения.
  • Нажмите кнопку ОК или Insert (Вставить) — в результате в документ будет вставлена заготовка матрицы с определенным числом строк и столбцов (рис. 4.13).
  • Введите значения в местозаполнители элементов матрицы. Переходить от одного элемента матрицы к другому можно с помощью указателя мыши либо клавиш со стрелками.

Добавление в уже созданную матрицу строк или столбцов производится точно так же:

  • Выделите линиями ввода элемент матрицы, правее и ниже которого будет осуществлена всгавка столбцов и (или) строк.
  • Вставьте в него матрицу, как было описано выше. При этом допускается задание числа столбцов или строк равным нулю (рис. 4.14).
  • Заполните местозаполнители недостающих элементов матрицы.

Рис. 4.12. Вставка матрицы

Рис. 4.13. Заполнение матрицы элементами

На рис. 4.14 и 4.15 показаны результаты последовательной вставки в матрицу столбца и строки после определения соответствующего числа столбцов и строк в диалоге Insert Matrix и нажатия в нем кнопки Insert (Вставить).

Рис. 4.14. Добавление одного столбца к матрице

Рис. 4.15. Добавление одной строки к матрице

В местозаполнители элементов матрицы можно вставлять не только числа (действительные или комплексные), но и любые математические выражения, состоящие из переменных, операторов, встроенных и пользовательских функций (листинг 4.16, вторая строка).

Листинг 4.16. Использование переменных и функций при определении матрицы

Создание массива определением его отдельных элементов

Массив можно определить следующим образом:

  • присваивая значения непосредственно отдельным элементам массива;
  • применяя ранжированные переменные (см. листинг 4.15).

Любой из этих способов позволяет присвоить нужное значение как всем элементам массива (см. листинг 4.15), так и части из них, либо даже одно-му-единственному элементу. В последнем случае создается массив, размерность которого задается индексами введенного элемента (листинг 4.17), а неопределенным элементам по умолчанию присваиваются нулевые значения.

Листинг 4.17. Создание матрицы определением одного ее элемента.

В любом месте документа допускается как переопределение любого из элементов массива (листинг 4.18, первая строка), так и изменение его размерности. Чтобы поменять размерность всего массива, просто присвойте любое значение новому элементу, индексы которого выходят за границы прежней размерности (вторая строка листинга 4.18).

В местозаполнители элементов матрицы допускается вставка любых функций, подобно применению обычного оператора присваивания,

Листинг 4.18. Изменение матрицы (продолжение листинге 4.17)

Определение отдельных элементов — удобный способ создания тензоров (многоиндексных массивов). В Mathcad имеется непосредственная возможность работы только с векторами и матрицами. Тем не менее, можно создать тензор путем определения вложенного массива (nested array). Для этого необходимо присвоить каждому элементу матрицы значение в виде другого вектора или матрицы (листинг 4.19). Пользователь должен лишь позаботиться о корректности задания индексов тензора и не запутаться в индексировании вложенных матриц (последняя строка листинга).

Листинг 4.19. Создание тензора и доступ к его элементам

Процесс создания тензора автоматизирует применение ранжированных переменных.

Обратите внимание, что Mathcad по умолчанию не отображает трехмерную структуру тензора (предпоследняя строка листинга 4.19), а вместо этого показывает информацию о размерах каждого элемента матрицы s. Развернуть вложенные массивы можно с помощью команды Format / Result / Display Options (Формат / Результат / Опции отображения), устанавливая флажок Expand Nested Arrays (Разворачивать вложенные массивы) на вкладке Display Options (Опции отображения).

4.3.4. Отображение вывода векторов и матриц

Вы, вероятно, обратили внимание, что матрицы, векторы и ранжированные переменные отображались в различных примерах по-разному. Это связано с автоматическими установками отображения матриц, принятыми в Mathcad по умолчанию. Существуют два стиля отображения массива: в форме матрицы и в форме таблицы (рис. 4.16).

Рис. 4.16. Отображение массивов в форме матрицы (слева) и таблицы (справа)

Изменение стиля отображения какого-либо массива выполняется командой Format/ Result (Формат/ Результат), вызывающей диалог Result Format (Формат результата). В этом диалоге следует перейти на вкладку Display Options (Опции отображения) (рис. 4.17) и в списке Matrix display style (Стиль отображения матриц) выбрать один из стилей:

  • Automatic (Авто) — стиль выбирается Mathcad;
  • Matrix (Матрица);
  • Table (Таблица).

Рис. 4.17. Изменение стиля отображения массива

Стиль отображения в виде таблицы допускает различное выравнивание матрицы относительно выражения слева от оператора вывода (рис. 4.18). Для изменения выравнивания вызовите контекстное меню из области таблицы, наведите в нем указатель мыши на пункт Alignment (Выравнивание) и в подменю выберите тип выравнивания.

Рис. 4.18. Различные стили выравнивания матриц

В диалоговом окне Result Format (Формат результата), помимо стиля отображения матрицы, можно задать стиль отображения тензоров (вложенных массивов). Для того чтобы отображать тензоры в стиле, показанном на рис. 4.19, установите флажок Expand nested arrays (Разворачивать вложенные массивы). Чтобы отображать их в свернутой форме (см. листинг 4.19), снимите этот флажок.

Рис. 4.19. Разворачивание вложенных массивов

Особенно наглядной формой отображения вектора является построение его в виде графика).

4.4. Формат вывода числовых данных

Несмотря на то, что невозможно влиять на результат, который отображается справа от оператора вывода значений переменных, функций и выражений, допускается изменять формат его отображения. Напомним, что как ввод, так и вывод данных может осуществляться в двух основных представлениях (см. разд. 4.1.1):

  • десятичное (decimal), например 13478.74559321;
  • с порядком (exponential notation), например 1.348×10 4 .

Выбор формата вывода числовых данных осуществляется при помощи диалогового окна Result Format (Формат результата). Оно вызывается командой Format / Result (Формат / Результат).

4.4.1. Формат результата

Управление представлением числа в десятичном представлении или представлении с порядком осуществляется при помощи следующих параметров:

  • количество отображаемых десятичных знаков (decimal places) после точки. Например, число 122,5587 с четырьмя десятичными знаками при отображении с двумя знаками будет выглядеть как 122,56;
  • отображение или скрытие незначащих нулей (trailing zeros) — опция, позволяющая показывать или скрывать незначащие нули в десятичном представлении числа, т. е. выводить, к примеру, “1,5” вместо “1,500” (даже если установлено количество десятичных знаков, равное 3);
  • порядковый порог (exponential threshold), при превышении степени 10 которого число будет показываться с порядком. Например, при пороге 3 число 122,56 будет отображаться как десятичное, а при пороге 2 — уже как”1,23хЮ2″;

Количество десятичных знаков левого сомножителя числа с порядком контролируется в некоторых форматах первым из трех перечисленных параметров.

  • кроме того, число с порядком может представляться в эквивалентных видах: “1,23х10 2 ” или с порядком в инженерном формате (engineering format): “1.23E+002”.

В Mathcad имеется несколько типов форматов, в каждом из которых разрешается изменение различных параметров представления числа. Формат выбирается на вкладке Number Format (Формат числа) диалогового окна Result Format (Формат результата) (рис. 4.20).

Рис. 4.20. Выбор формата вывода числа

Основной (general) формат

Этот формат принят при выводе чисел по умолчанию. Можно управлять и количеством отображаемых десятичных знаков (поле Number of decimal places), и порядковым порогом (поле Exponential threshold). При превышении порога число отображается с порядком (как показано на рис. 4.20). Несколько примеров вывода одного и того же числа в общем формате показано в листинге 4.21. В левой колонке приведены числа с порядковым порогом, равным 3, и количеством десятичных знаков (сверху вниз) 3, 4, 5, соответственно. Для нижнего числа установлен флажок отображения незначащих нулей. В правой колонке сгруппированы числа с порядковым порогом от 1 до 4 (сверху вниз).

Листинг 4.21. Основной формат результата

Десятичный (decimal) формат

Числа отображаются только в десятичном представлении и никогда — в представлении с порядком.

Научный (scientific) формат

Числа отображаются только с порядком, причем количество десятичных знаков левого сомножителя, как и отображение незначащих нулей, определяется пользователем.

Инженерный (engineering) формат

Числа отображаются только с порядком, причем обязательно кратным 3; как и в научном формате, пользователю разрешается изменять количество десятичных знаков.

Дробный (fraction) формат

Этот формат сильно отличается от предыдущих, представляя число в виде дроби (рис. 4.21). Причем можно управлять как точностью представления числа с помощью поля level of accuracy (Уровень точности), так и задать модификацию этого формата — отображение числа в виде целой и дробной части (как показано на рис. 4.21 внизу слева) посредством установки флажка Use mixed numbers (Смешанные числа).

Вид одного и того же числа в различных форматах приведен в листинге 4.22. В первой строке показан десятичный формат, во второй строке — научный с тремя десятичными знаками, в третьей — инженерный также с тремя десятичными знаками. В последних двух строках представлен дробный формат: в предпоследней с уровнем точности 5, в последней — 10. К тому же, для выражения последней строки установлен флажок Use mixed numbers (Смешанные числа).

Рис. 4.21. Дробный формат

Листинг 4.22. Другие форматы результаа вычислений

4.4.2. Округление малых чисел до нуля

Mathcad автоматически округляет малые числа до нуля (листинг 4.23). Допускается установка порогового значения округления (в степенях 10), отдельно для действительной и мнимой части числа. При этом числа, по модулю меньшие порога, отображаются в виде нуля.

Помните, что это касается только отображения чисел. В памяти компьютера они хранятся корректно.

Листинг 4.23. Представление близких к нулю чисел

Чтобы изменить пороговые значения:

  • Щелкните на любом пустом месте документа.
  • Войдите в диалоговое окно Result Format (Формат результата): Format / Result (Формат / Результат).
  • Перейдите на вкладку Tolerance (Точность).
  • Установите пороговые значения для действительного нуля в поле Zero threshold (Порог нуля) и мнимого нуля в поле Complex threshold (Комплексный порог нуля).
  • Нажмите кнопку ОК.

Рис. 4.22. Задание порога мнимого нуля

Рис. 4.23. Просмотр точного значения числа в строке состояния

Изменение порога мнимого нуля возможно и в режиме редактирования формулы (рис. 4.22), но изменение действительного порога нуля при этом недоступно.

Просмотреть число в точном представлении можно, нажав клавиши <Ctrl>+<Shift>+<N>. В этом случае на строке состояния (в самой нижней части окна Mathcad, слева) будет на короткое время выведен результат с максимальной точностью (рис. 4.23).

4.4.3. Вывод чисел в других системах счисления

Аналогично вводу чисел в других системах, счисления (см. разд. 4.1.1), вывести результат также возможно в виде десятичного, двоичного, восьмеричного или шестнадцатеричного числа (листинг 4.24, сверху вниз).

Листинг 4.24. Вывод чисел в других системах счисления

Чтобы задать систему счисления, выберите команду Format / Result / Display Options (Формат / Результат / Опции отображения), а затем желаемый элемент списка Radix (Система счисления) (рис. 4.24). При отображении чисел в других системах счисления также доступно форматирование их представления на вкладке Number Format (Формат числа) того же диалога Result Format (Формат результата). В листинге 4.25 приведено несколько примеров форматирования чисел в двоичном представлении.

Рис. 4.24. Задание вывода результата в других системах счисления

Листинг 4.25. Форматирование вывода чисел в других системах счисления

Мы рассмотрели в этой главе основные принципы наиболее простого численного ввода и вывода данных. О более впечатляющих формах ввода-вывода (графики, анимация, ввод-вывод в файлы) рассказывается в последней части книги.

4.5. Элементы управления (controls)

Одна из редко используемых возможностей Mathcad — ввод данных при помощи общеупотребительных элементов управления (такие, как поле ввода, ползунковый регулятор и т. п.). Очевидно, что такой способ ввода удобен, если Вы занимаетесь разработкой расчетов, которые предназначены для непрофессиональных пользователей Mathcad.

В Mathcad 11 имеются следующие элементы управления (рис. 4.25):

  • Check Box (флажок проверки);
  • Radio Button (переключатель);
  • Push Button (кнопка);
  • Slider (ползунковый регулятор);
  • Text Box (поле текстового ввода);
  • List Box (список).

Рис. 4.25. Элементы управления MathSoft и панель Controls

Как видно из рис. 4.25, элементы управления в Mathcad используются для присваивания переменным значений, которые определяются действиями пользователя над элементами управления. К примеру, на рис. 4.26 два флажка проверки определяют переменные х0 и x1. Если флажок проверки выставлен, переменная принимает значение 1, а если снят — 0.

Рис. 4.26. Пример использования флажка проверки

Для того чтобы вставить элемент управления в документ, можно использовать либо команду меню Insert / Controls (Вставка / Элемент управления), либо панель инструментов Controls (Элементы управления), которую можно вызвать при помощи пункта Toolbars / Controls (Панели инструментов / Элементы управления) меню View (Вид). После нажатия кнопки с пиктограммой нужного элемента управления новый элемент управления появляется в документе вместе с местозаполнителем, который следует заменить именем переменной.

Чтобы отредактировать свойства самого элемента управления, следует вызвать на нем контекстное меню и выбрать в меню пункт Properties (Свойства). Большинство свойств имеет интуитивный смысл, и Вам будет несложно управлять характеристиками ввода данных посредством регулировки параметров самих элементов управления. Дополнительную информацию об использовании элементов управления Вы сможете найти в специальном справочном пособии, доступном по команде Help / Developer’s Reference (Справка / Руководство разработчика).

Как в маткаде считать комплексные числа

  • Главная Страница
  • Поиск По Сайту
  • Контакты Обратная связь

Построение графиков функций в среде MathCad

  • Печать
  • E-mail

Лабораторная работа: Построение графиков функций в среде MathCad. Работа с комплексными числами.

Теоретическая часть.

1. Построение графиков функций. В среде MathCad имеется мощная поддержка построения графиков (в том числе и трехмерных) и диаграмм. Предварительно построению графика функции следует определить векторную переменную или массив, в который будут занесены значения функции на заданном интервале. Для работы с графиками используется меню Graphics в главном меню или на панели инструментов (рис.1)

График функции и панель инструментов для его построения.

Рис. 1. График функции и панель инструментов для его построения.

Для определения параметров графика следует выделить необходимый элемент на графике (аналогично мастеру диаграмм в Excel) и дважды нажать на левую кнопку мыши. В открывшемся окне необходимо определить необходимые параметры (рис.2).

Определение параметров области построения графика

Рис.2 Определение параметров области построения графика, изображенного на рис.1.

2. Построение двумерных графиков в Декартовых и Полярных координатах.

2.1 Определите размерность вектора, в который Вы будете помещать значения функции

2.2 Определите значение аргумента функции для каждого элемента вектора

2.3 Определите значение функции через значение аргумента (рис.1).

2.4 Для построения графика в Декартовых координатах выберите пункт «Create X-Y Plot» меню Graphics или нажмите на клавишу @. Определите переменные, соответствующие осям координат. Двойным нажатием на левую клавишу мыши внутри графика определите формат области построения.

2.5 Для построения графика в полярных координатах выберите пункт «Create Polar Plot» меню Graphics или воспользуйтесь комбинацией клавиш ctrl+7.

3. Построение трехмерных графиков.

2.1 Определите размерность векторов аргументов функции.

2.2 Определите значение каждого аргумента функции для соответствующего ему элемента вектора

2.3 Определите значение функции через значение аргумента (рис.3).

2.4 Для построения графика в выберите пункты «Create Surface Plot» меню Graphics или нажмите комбинацию клавиш ctrl+2. Определите переменную, соответствующие оси z. Двойным нажатием на левую клавишу мыши внутри графика определите формат области построения.

Построение трехмерного графика

Рис. 3. Построение трехмерного графика

4. Работа с комплексными числами в среде MathCad

Для задания комплексного числа следует определить . Затем при задании комплексной части числа этот аргумент используется так же, как и в математических выражениях. Для получения комплексной части числа y используется функция Re(y), а для вычисления его действительной части — Im(y).

Задание к лабораторной работе:

1) Постройте графики Re(y(x)), Im(y(x)), Im(y(Re(x))) на интервале -1£x£1 c шагом 0.01 заданных в варианте задания (табл.1) комплексных функций в Декартовых и Полярных координатах.

2) Постройте трехмерные графики двух аргументов согласно варианту задания (табл.2). -5£x£5, Dx=0.2; -3£x£3, Dx=0.1

Источник

Добавить комментарий