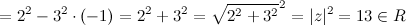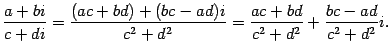Как найти сопряженные числа для комплексных чисел

Как найти сопряженные числа для комплексных чисел

Комплексно сопряженные числа

ОПРЕДЕЛЕНИЕ

Сопряженное (или комплексно сопряженное) число с комплексным числом (
z=x+i y
) является числом (
overline{z}=x-i y
)

ПРИМЕР

  • Задачей

    поиска для комплексного числа (
    z=-34-i
    ) является его сопряженное число.

  • Решение.

    Комплексное сопряженное число является числом вида (
    overline{z}=x-i y
    ) . Вещественной частью комплексного числа (
    z=-34-i
    ) является число (
    x=operatorname{Re}
    ), (
    z=-34
    ), мнимая часть равна (
    y=operatorname{lm}
    ), (
    z=-1
    ).

    Следовательно, сопряженное число имеет вид: (
    overline{z}=-34+i
    )

  • Ответ

    (
    overline{z}=-34+i
    )

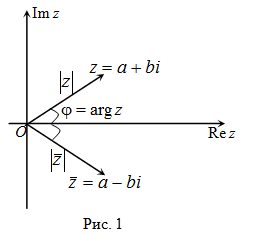
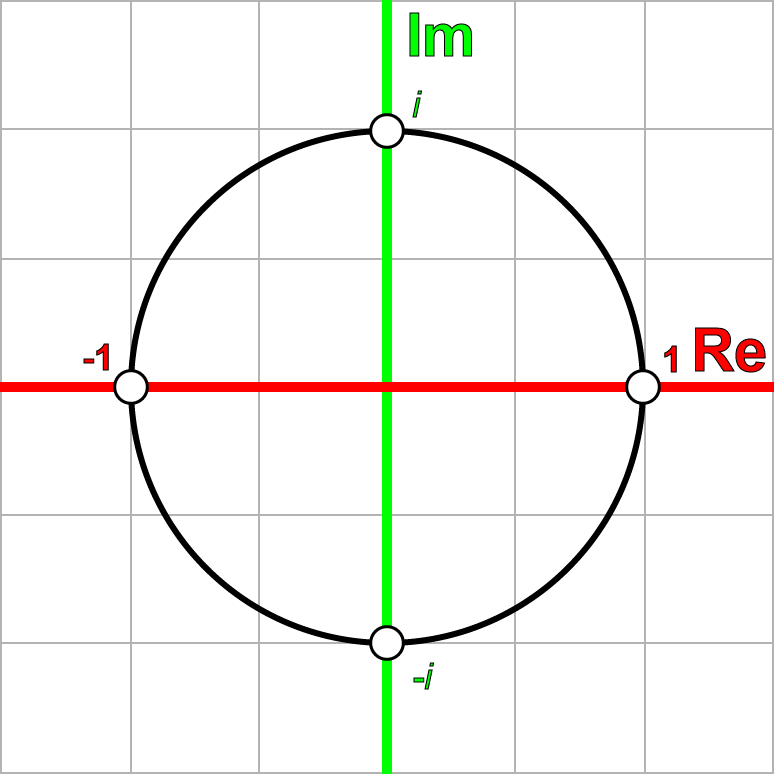
    На комплексной плоскости сопряженные числа зеркалируются относительно оси действительных чисел.

    Свойства комплексно-сопряженных чисел

    1. (
    |z|=|z|
    ), т. е. модули сопряженных чисел равны.

    Например.

    Модуль комплексного числа (
    z=-4+i
    ) равен (
    r=sqrt{(-4)^{2}+1^{2}}=sqrt{17}
    ). Присоединенным к комплексному числу является число (
    z=-4-i
    ), модуль (
    r=sqrt{(-4)^{2}+(-1)^{2}}=sqrt{17}
    ) которого равен модулю исходного числа.

    2. (
    arg z=-arg overline{z}
    ) т. е. Аргументы сопряженных чисел различаются по знаку.

    3. (
    overline{overline{z}}=z
    ) т. е. Комплексное сопряженное сопряженное число является исходным комплексным числом.

    4. (
    z cdot overline{z}=|z|^{2}
    ) т. е. В результате произведения сопряженных чисел получается вещественное число.

    5.(
    z+overline{z}=2 operatorname{Re} z
    ) т. е. Сумма сопряженных чисел также является вещественным числом.

    6.(
    overline{z_{1} cdot z_{2}}=overline{z_{1}} cdot overline{z_{2}}
    ) т. е. Сопряженное произведение двух комплексных чисел является произведением их сопряженных чисел.

    7.(
    overline{z_{1} div z_{2}}=overline{z_{1}} div overline{z_{2}}
    ) т. е. Сопряженное к ним частное число есть фактор сопряженного.

    Примеры решения проблем

    ПРИМЕР 1

  • Задача

    Чтобы умножить комплексное число (
    z=4-7 i
    ) на его сопряженное.

  • Решение.

    Сопряженное с номером (
    z=4-7 i
    ) – это число (
    z=4+7 i
    ). Найдите произведение двух чисел:

    (
    z cdot overline{z}=(4-7 i) cdot(4+7 i)=4 cdot 4+(-7) cdot 7 cdot i^{2}+i(4 cdot 7-7 cdot 4)=65
    )

  • Ответ

    (
    z cdot overline{z}=65
    )

    ПРИМЕР 2

  • Задача

    Чтобы найти сопряженное к частному два комплексных числа: (
    z 1=1-3 i
    ), (
    z 2=2+5 i
    ).

  • Решение

    Фактор комплексных чисел определяется путем умножения числителя и знаменателя на сопряженное число:

    (
    z_{1} div z_{2}=frac{1-3 i}{2+5 i}=frac{(1-3 i)(2-5 i)}{(2+5 i)(2-5 i)}=frac{1 cdot 2-3 cdot 5}{2^{2}+5^{2}}+i frac{-5 cdot 1-3 cdot 2}{2^{2}+5^{2}}=-frac{13}{29}-i frac{11}{29}
    )

    Сопряженным числом для конкретного будет число (
    -frac{13}{29}+i frac{11}{29}
    )

    Мы получим тот же результат, если найдем фактор сопряженных чисел (
    z rceil=1-3 i
    ), (
    z 2=2+5 i
    ):

    (
    overline{z_{1}} div overline{z_{2}}=frac{1+3 i}{2-5 i}=frac{(1+3 i)(2+5 i)}{(2-5 i)(2+5 i)}=frac{1 cdot 2-3 cdot 5}{2^{2}+5^{2}}+i frac{5 cdot 1+3 cdot 2}{2^{2}+5^{2}}=-frac{13}{29}+i frac{11}{29}
    )

  • Ответ

    (
    overline{z_{1} div z_{2}}=-frac{13}{29}+i frac{11}{29}
    )

    • Источник

    Геометрическое представление z и его сопряжённого {displaystyle {bar {z}}} на комплексной плоскости

    Сопряжённые числа (комплексно-сопряжённые числа) — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине, но противоположными по знаку, мнимыми частями[1]. Например, сопряжёнными являются числа {displaystyle 3+4i} и {displaystyle 3-4i}. Число, сопряжённое к числу z, обозначается overline{z}. В общем случае, сопряжённым к числу {displaystyle z=a+ib} (где a и b — действительные числа) является {displaystyle {overline {z}}=a-ib}.

    Например:

    {displaystyle {overline {(3-2i)}}=3+2i}
    {displaystyle {overline {7}}=7}
    {displaystyle {overline {i}}=-i.}

    На комплексной плоскости сопряжённые числа представлены точками, симметричными относительно действительной оси. В полярной системе координат сопряжённые числа имеют вид {displaystyle re^{iphi }} и {displaystyle re^{-iphi }}, что непосредственно следует из формулы Эйлера.

    Сопряжёнными числами являются корни квадратного уравнения с действительными коэффициентами и отрицательным дискриминантом.

    Свойства[править | править код]

    Для произвольных комплексных чисел z и w:

    Если phi является голоморфной функцией, сужение которой на множество действительных чисел является действительной функцией, и определены {displaystyle phi (z)}, то:

    {displaystyle phi ({overline {z}})={overline {phi (z)}}}.

    В частности:

    Определение координат числа и сопряжения[править | править код]

    Прямоугольные и полярные координаты комплексного числа могут быть определены с помощью формул:

    Примечания[править | править код]

    1. ↑ Weisstein, Eric W. Complex Conjugates (англ.) на сайте Wolfram MathWorld.

    Литература[править | править код]

    • Шабат Б. В. Введение в комплексный анализ. — М.: Наука, 1969. — 577 с.
    Источник

    Содержание:

    • Определение
    • Свойства комплексно-сопряженных чисел

    Определение

    Если $z=a+b i$, то число
    $overline{z}=a-b i$ называется
    комплексным сопряженным к числу $z$ .

    То есть у комплексно сопряженных чисел действительные части равны, а мнимые отличаются знаком.

    Например. Комплексно сопряженным к числу
    $z=2-i$ есть число
    $overline{z}=2+i$ .

    На комплексной плоскости комплексно сопряжённые числа получаются зеркальным отражением друг друга относительно действительной оси.

    Свойства комплексно сопряженных чисел

    1) Если $z=overline{z}$, то можно сделать вывод,
    что рассматриваемое число $z$ является действительным.

    Например. $z=2 in R Rightarrow overline{z}=2$ и
    $z=overline{z}$

    2) Для любого комплексного числа
    $z$ сумма
    $z+overline{z}=2 operatorname{Re} z$ –
    действительное число.

    Например. Пусть
    $z=2-3 i$, тогда
    $overline{z}=2+3 i$, а тогда

    $z+overline{z}=2-3 i+(2+3 i)=2-3 i+2+3 i=2+2=4 in R$

    3) Для произвольного комплексного числа
    $z=a+b i$ произведение
    $z cdot overline{z}=|z|^{2} in R$ .

    Например. Пусть
    $z=2-3 i$, комплексно сопряженное к нему число
    $overline{z}=2+3 i$, тогда произведение

    $z cdot overline{z}=(2-3 i)(2+3 i)=2^{2}-(3 i)^{2}=2^{2}-3^{2} cdot i^{2}=$

    4) Модули комплексно сопряженных чисел равны:
    $|z|=|overline{z}|$, а аргументы отличаются знаком (рис. 1).

    5)  $overline{z_{1} pm z_{2}}=overline{z}_{1} pm overline{z}_{2}$

    6)  $overline{z_{1} cdot z_{2}}=overline{z_{1}} cdot overline{z}_{2}$

    7)  $frac{overline{z_{1}}}{z_{2}}=frac{overline{z}_{1}}{overline{z}_{2}}$

    8)  $overline{(overline{z})}=z$

    9) Если $z=a+b i$ и
    $overline{z}=a-b i$ – комплексно сопряженные числа, то

    $a=operatorname{Re} z=frac{z+overline{z}}{2}, b=operatorname{Im} z=frac{z-overline{z}}{2 i}$

    Читать дальше: формы записи комплексного числа.

    236

    проверенных автора готовы помочь в написании работы любой сложности

    Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

    Источник

    Сопряжённые числа

    Геометрическое
    представление сопряжённых чисел

    Если
    комплексное число 
    ,
    то число 
     называется сопряжённым (или
    комплексно сопряжённым) к 
     (обозначается
    также 
    ).
    На комплексной плоскости сопряжённые
    числа получаются зеркальным отражением
    друг друга относительно вещественной
    оси. Модуль сопряжённого числа такой
    же, как у исходного, а их аргументы
    отличаются знаком.

    Переход
    к сопряжённому числу можно рассматривать
    как одноместную
    операцию    ;
    перечислим её свойства.


    •  (сопряжённое
      к сопряжённому есть исходное).

    Обобщение: 
    ,
    где 
     —
    произвольный многочлен с вещественными
    коэффициентами.

    Значимость
    сопряжения объясняется тем, что оно
    является образующей группы
    Галуа     
    .

    Представление комплексных чисел Алгебраическая форма

    Запись
    комплексного числа 
     в
    виде 
    , 
    ,
    называется алгебраической
    формой     комплексного
    числа.

    Сумма
    и произведение комплексных чисел могут
    быть вычислены непосредственным
    суммированием и перемножением таких
    выражений, как обычно раскрывая скобки
    и приводя подобные, чтобы представить
    результат тоже в стандартной форме (при
    этом надо учесть, что 
    ):

    Тригонометрическая и показательная формы

    Если
    вещественную 
     и
    мнимую 
     части
    комплексного числа выразить через
    модуль 
     и
    аргумент 
     (
    , 
    ),
    то всякое комплексное число 
    ,
    кроме нуля, можно записать в тригонометрической
    форме

    Также
    может быть полезна показательная форма
    записи комплексных чисел, тесно связанная
    с тригонометрической через формулу
    Эйлера    :

    где 
     —
    расширение экспоненты для
    случая комплексного показателя степени.

    Отсюда
    вытекают следующие широко используемые
    равенства:

    Формула Муавра и извлечение корней из комплексных чисел

    Основная
    статья:     Формула
    Муавра

    Корни
    пятой степени из единицы    (вершины
    пятиугольника)

    Эта
    формула позволяет возводить в целую
    степень ненулевое комплексное число,
    представленное в тригонометрической
    форме. Формула Муавра имеет вид:

    где 
     —
    модуль, а 
     —
    аргумент комплексного числа. В современной
    символике она опубликована Эйлером в 1722
    году    .
    Приведенная формуле справедлива при
    любом целом n,
    не обязательно положительном.

    Аналогичная
    формула применима также и при вычислении
    корней 
    -ой
    степени из ненулевого комплексного
    числа:

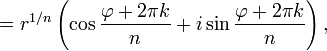
    Отметим,
    что корни 
    -й
    степени из ненулевого комплексного
    числа всегда существуют, и их количество
    равно 
    .
    На комплексной плоскости, как видно из
    формулы, все эти корни являются вершинами
    правильного 
    -угольника,
    вписанного в окружность радиуса 
     с
    центром в начале координат (см. рисунок).

    История

    Впервые,
    по-видимому, мнимые величины появились
    в известном труде «Великое искусство,
    или об алгебраических правилах» Кардано (1545),
    который счёл их непригодными к
    употреблению. Пользу мнимых величин, в
    частности, при решении кубического
    уравнения, в так называемом неприводимом
    случае (когда вещественные корни
    многочлена выражаются через кубические
    корни из мнимых величин), впервые
    оценил Бомбелли (1572).
    Он же дал некоторые простейшие правила
    действий с комплексными числами.

    Выражения
    вида 
    ,
    появляющиеся при решении квадратных и
    кубических уравнений, стали называть
    «мнимыми» в XVI—XVII
    веках    ,
    однако даже для многих крупных ученых XVII
    века     алгебраическая
    и геометрическая сущность мнимых величин
    представлялась неясной. Лейбниц,
    например, писал: «Дух божий нашёл
    тончайшую отдушину в этом чуде анализа,
    уроде из мира идей, двойственной сущности,
    находящейся между бытием и небытием,
    которую мы называем мнимым корнем из
    отрицательной единицы».[5]

    Долгое
    время было неясно, все ли операции над
    комплексными числами приводят к
    комплексным результатам, или, например,
    извлечение корня может привести к
    открытию какого-то нового типа чисел.
    Задача о выражении корней степени 
     из
    данного числа была решена в
    работах Муавра (1707)
    и Котса (1722).

    Символ 
     предложил Эйлер (1777,
    опубл. 1794),
    взявший для этого первую букву
    слова лат. imaginarius.
    Он же распространил все стандартные
    функции, включая логарифм,
    на комплексную область. Эйлер также
    высказал в 1751
    году     мысль
    об алгебраической замкнутости поля
    комплексных чисел. К такому же выводу
    пришел д’Аламбер (1747),
    но первое строгое доказательство этого
    факта     принадлежит Гауссу (1799).
    Гаусс и ввёл в широкое употребление
    термин «комплексное число» в 1831
    году    ,
    хотя этот термин ранее использовал в
    том же смысле французский математик Лазар
    Карно     в 1803
    году    .

    Геометрическое
    истолкование комплексных чисел и
    действий над ними появилось впервые в
    работе Весселя (1799).
    Первые шаги в этом направлении были
    сделаны Валлисом(Англия)
    в 1685
    году    .
    Современное геометрическое представление,
    иногда называемое «диаграммой Аргана»,
    вошло в обиход после опубликования
    в 1806-м
    и 1814-м
    годах работыЖ. Р. Аргана,
    повторявшей независимо выводы Весселя.
    Термины «модуль», «аргумент» и «сопряжённое
    число» ввёл Коши.

    Арифметическая
    модель комплексных чисел как пар
    вещественных чисел была
    построена Гамильтоном (1837);
    это доказало непротиворечивость их
    свойств. Гамильтон предложил и обобщение
    комплексных чисел — кватернионы,
    алгебра которых некоммутативна.


      Построение
    поля комплексных чисел

    Из
    курса школьной математики известно,
    что любое уравнение 
     имет
    решение при 
     .
    С другой стороны, квадратное уравнение
    не всегда имеет решение. Например,
    решения не имеет уравнение 
     .
    Возникает вопрос, нельзя ли сделать
    так, чтобы любое квадратное уравнение
    имело решение?

    Предположим,
    что уравнение 
     имет
    решение. Число (абстрактный элемент, не
    принадлежащий полю вещественных чисел),
    которое является решением, обозначим
    буквой 
     ,
    то есть 
     .
    Мы должны иметь возможность умножать
    это число на любое вещественное число.
    Значит, должны появиться числа вида 
     ,
    где 
      —
    вещественное число. Для них должна быть
    возможность сложения с любым вещественным
    числом. Поэтому должны появиться числа
    вида 
     .

            Определение 17.1  
    Числа вида 
     ,
    где 
     и 
      —
    вещественные числа, называются комплексными
    числами    .
            

    Посмотрим,
    какие действия арифметики можно
    производить с комплексными числами.
    Сложение чисел должно удовлетворять
    обычным правилам, поэтому:

    (17.1)

    При
    вычислении произведения скобки раскроем
    привычным способом:

    Так
    как 
     ,
    то получим

    (17.2)

    Итак,
    результаты сложения и умножения
    комплексных чисел снова оказались
    комплексными числами. Операцию вычитания
    определить не сложно:

    (17.3)

    Рассмотрим
    операцию деления. Учтем, что при умножении
    числителя и знаменателя дроби на одно
    и то же число дробь не меняется:

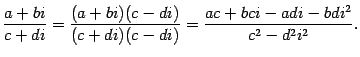
    Так
    как 
     ,
    то

    (17.4)

    Результат
    деления двух комплексных чисел оказывается
    снова комплексным числом. Как видно из
    полученной формулы, деление нельзя
    выполнить лишь в том случае, когда 
     ,
    но в этом случае делитель 
     тоже
    равен нулю. Следовательно, невозможно
    лишь деление на нуль, что соответствует
    обычным правилам действий с числами.

    Итак,
    мы вроде бы расширили множество
    вещественных чисел. Но есть в этом
    построении один существенный пробел.
    Мы предположили, что есть такое число 
     ,
    что 
     .
    А, может быть, его на самом деле нет?2 Чтобы
    исправить это упущение, используем для
    построения комплексных чисел уже
    существующее множество.

    Пусть 
      —
    множество пар вещественных чисел: 
     .
    На этом множестве определим операции

    1. сложения:

    1. вычитания:

    1. умножения:

    1. деления:

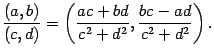
    Очевидно,
    что комплексное число, как оно было
    определено раньше, — просто другая
    форма записи пары вещественных чисел 
     ,
    где вместо запятой стоит “+”, а
    второй элемент пары выделяется умножением
    на букву 
     .
    В новой форме записи вещественные
    числа — это пары 
     ,
    числу 
     соответствует
    пара 
     ,
    сложение, вычитание, умножение и деление
    пар чисел и комплексных чисел происходят
    по одинаковым правилам. Таким образом,
    комплексные числа стали реально
    существующим множеством.

    Однако
    в математике, в силу традиции, используется
    запись комплексного числа 
     ,
    введенная в начале раздела3.
    Причем принято считать, что

    Можно
    проверить, что комплексные числа образуют
    поле. В нем обратным элементом к
    комплексному числу 
     служит
    результат деления 1 на 
     :

    Это
    поле называется полем
    комплексных чисел     и
    обозначается 
     .

    Число 
     называется мнимой
    единицей    ,
    числа 
      — мнимыми
    числами    .
    Если 
     ,
    то число 
     называется вещественной
    частью     комплексного
    числа и обозначается 
     ,
    число 
    называется мнимой
    частью     и
    обозначается 
     .
    Число 
     называется сопряженным числу 
     и
    обозначается 
     ,
    то есть 
     .

            Замечание 17.1  
    В электротехнике, где буква 
     обозначает
    ток, мнимую единицу обозначают буквой 
     .
            

    Если
    операции сложения, вычитания и умножения
    комплексных чисел соответствуют обычным
    правилам раскрытия скобок, то для
    выполнения деления нужно или запомнить
    формулу (17.4),
    или, что проще, каждый раз при выполнении
    деления умножать числитель и знаменатель
    дроби на число, сопряженное знаменателю.

            Пример 17.1  
    Пусть 
     , 
     .
    Тогда:

    Вычислим
    еще 
     :

    Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

    • #
    • #
    • #
    • #
    • #
    • #
    • #
    • #
    • #
    • #
    • #
    Источник

    Доступно о кватернионах и их преимуществах

    Время на прочтение
    13 мин

    Количество просмотров 178K

    От переводчика: ровно 175 лет и 3 дня назад были изобретены кватернионы. В честь этой круглой даты я решил подобрать материал, объясняющий эту концепцию понятным языком.

    Концепция кватернионов была придумана ирландским математиком сэром Уильямом Роуэном Гамильтоном в понедельник 16 октября 1843 года в Дублине, Ирландия. Гамильтон со своей женой шёл в Ирландскую королевскую академию, и переходя через Королевский канал по мосту Брум Бридж, он сделал потрясающее открытие, которое сразу же нацарапал на камне моста.

    $i^2=j^2=k^2=ijk=-1$

    Памятная табличка на мосту Брум Бридж через Королевский канал в честь открытия фундаментальной формулы умножения кватернионов.

    В этой статье я постараюсь объяснить концепцию кватернионов простым для понимания образом. Я объясню, как можно визуализировать кватернион, а также расскажу о разных операциях, которые можно выполнять с кватернионами. Кроме того, я сравню использование матриц, углов Эйлера и кватернионов, а затем попытаюсь объяснить, когда стоит использовать кватернионы вместо углов Эйлера или матриц, а когда этого делать не нужно.

    Содержание

    • 1. Введение
    • 2. Комплексные числа
      • 2.1. Сложение и вычитание комплексных чисел
      • 2.2. Умножение комплексного числа на скалярное значение
      • 2.3. Произведение комплексных чисел
      • 2.4. Квадрат комплексных чисел
      • 2.5. Сопряжённые комплексные числа
      • 2.6. Абсолютное значение комплексного числа
      • 2.7. Частное двух комплексных чисел
    • 3. Степени $i$
    • 4. Комплексная плоскость
      • 4.1. Роторы
    • 5. Кватернионы
      • 5.1. Кватернионы как упорядоченная пара
      • 5.2. Сложение и вычитание кватернионов
      • 5.3. Произведение кватернионов
      • 5.4. Вещественный кватернион
      • 5.5. Умножение кватерниона на скалярную величину
      • 5.6. Чистые кватернионы
      • 5.7. Аддитивная форма кватерниона
      • 5.8. Единичный кватернион
      • 5.9. Бинарная форма кватерниона
      • 5.10. Сопряжённые кватернионы
      • 5.11. Норма кватерниона
      • 5.12. Нормализация кватерниона
      • 5.13. Обратный кватернион
      • 5.14. Скалярное произведение кватернионов
    • 6. Повороты
    • 7. Интерполяция кватернионов
      • 7.1. SLERP
        • 7.1.1. Разность кватернионов
        • 7.1.2. Возведение кватерниона в степень
        • 7.1.3. Дробная разность кватернионов
        • 7.1.4. Факторы, которые нужно учитывать
      • 7.2. SQUAD
    • 8. Заключение
    • 9. Загрузка демо
    • 10. Справочные материалы

    Невозможно полностью понять кватернионы за 45 минут.

    В этой статье чрезвычайно много математики, так что она не для слабаков.

    Введение

    В компьютерной графике для описания позиции в пространстве (перемещения), а также ориентации в пространстве (поворота) используются матрицы. Также можно также использовать одну матрицу преобразований для описания масштаба объекта. Эту матрицу можно считать «пространством базиса». Если умножить вектор или точку (или даже другую матрицу) на матрицу преобразований, то мы «преобразуем» этот вектор, точку или матрицу в пространство, представленное этой матрицей.

    В этой статье я не буду в подробностях рассказывать о матрицах преобразований. Подробно о матрицах преобразований можно прочитать в моей статье Matrices.

    В данной статье я хочу рассказать об альтернативном способе описания ориентации объекта (поворота) в пространстве при помощи кватернионов.

    Комплексные числа

    Для того, чтобы полностью понять кватернионы, нам сначала нужно понять, откуда они взялись. Принцип кватернионов основан на концепции системы комплексных чисел.

    Наряду с хорошо известными множествами чисел (натуральным, целым, вещественным и рациональным), система комплексных чисел добавляет новое множество чисел, называемых мнимыми числами. Мнимые числа были придуманы для решения определённых уравнений, не имевших решений, например:

    $x^2+1=0$

    Чтобы решить это выражение, нам нужно заявить, что

    $x^2=-1$, а это, как известно, невозможно, потому что квадрат любого числа (положительного или отрицательного) всегда положителен.

    Математики не могли смириться с тем, что выражение не имеет решения, поэтому было изобретено новое понятие — мнимое число, которое можно использовать для решения таких уравнений.

    Мнимое число имеет следующий вид:

    $i^2=-1$

    Не пытайтесь понять это допущение, потому что логичных причин его существования нет. Нам просто нужно принять, что

    $i$ — это просто некая величина, квадрат которой равен

    $-1$.

    Множество мнимых чисел можно обозначить как

    $mathbb{I}$.

    Множество комплексных чисел (обозначаемое символом

    $mathbb{C}$ — это сумма вещественного и мнимого числа в следующей форме:

    $z=a+bi~~a,binmathbb{R},~~i^2=-1$

    Можно также заявить, что все вещественные числа являются комплексными с

    $b=0$, а все мнимые числа являются комплексными с

    $a=0$.

    Сложение и вычитание комплексных чисел

    Комплексные числа можно складывать и вычитать сложением и вычитанием вещественной и мнимой частей.

    Сложение:

    $(a_1+b_1i)+(a_2+b_2i)=(a_1+a_2)+(b_1+b_2)i$

    Вычитание:

    $(a_1+b_1i)-(a_2+b_2i)=(a_1-a_2)+(b_1-b_2)i$

    Умножение комплексного числа на скалярное значение

    Комплексное число умножается на скаляр умножением каждого члена комплексного числа на скаляр:

    $lambda(a+bi)=lambda{a}+lambda{b}i$

    Произведение комплексных чисел

    Кроме того, комплексные числа можно также перемножать, используя обычные алгебраические правила.

    $begin{array}{rcl}z_1 & = & (a_1+b_1i) \ z_2 & = & (a_2+b_2i) \ z_1z_2 & = & (a_1+b_1i)(a_2+b_2i) \ & = & a_1a_2+a_1b_2i+b_1a_2i+b_1b_2i^2 \ & = & (a_1a_2-b_1b_2)+(a_1b_2+b_1a_2)iend{array}$

    Квадрат комплексных чисел

    Также комплексное число можно возвести в квадрат, умножив на само себя:

    $begin{array}{rcl}z & = & (a+bi) \ z^2 & = & (a+bi)(a+bi) \ & = & (a^2-b^2)+2abiend{array}$

    Сопряжённые комплексные числа

    Сопряжённой величиной комплексного числа является комплексное число с изменённым знаком мнимой части, обозначаемой как

    $bar{z}$ или как

    $z^*$.

    $begin{array}{rcl}z & = & (a+bi) \ z^* & = & (a-bi)end{array}$

    Перемножение комплексного числа с его сопряжённой величиной даёт интересный результат.

    $begin{array}{rcl}z & = & (a+bi) \ z^* & = & (a-bi) \ zz^* & = & (a+bi)(a-bi) \ & = & a^2-abi+abi+b^2 \ & = & a^2+b^2end{array}$

    Абсолютное значение комплексного числа

    Мы можем использовать сопряжённое число комплексного числа, чтобы вычислить абсолютное значение (или норму, или величину) комплексного числа. Абсолютное значение комплексного числа — это квадратный корень из комплексного числа, умноженного на его сопряжённое число. Оно обозначается как

    $|z|$:

    $begin{array}{rcl}z & = & (a+bi) \ |z| & = & sqrt{zz^*} \ & = & sqrt{(a+bi)(a-bi)} \ & = & sqrt{a^2+b^2}end{array}$

    Частное двух комплексных чисел

    Чтобы вычислить частное двух комплексных чисел, мы умножаем числитель и знаменатель на сопряжённое число знаменателя.

    $begin{array}{rcl}z_1 & = & (a_1+b_1i) \ z_2 & = & (a_2+b_2i) \ cfrac{z_1}{z_2} & = & cfrac{a_1+b_1i}{a_2+b_2i} \ & = & cfrac{(a_1+b_1i)(a_2-b_2i)}{(a_2+b_2i)(a_2-b_2i)} \ & = & cfrac{a_1a_2-a_1b_2i+b_1a_2i-b_1b_2i^2}{a_2^2+b_2^2} \ & = & cfrac{a_1a_2+b_1b_2}{a_2^2+b_2^2}+cfrac{b_1a_2-a_1b_2}{a_2^2+b_2^2}i end{array}$

    Степени $i$

    Если мы утверждаем, что

    $i^2=-1$, то должна существовать возможность возводить

    $i$ и в другие степени.

    $begin{array}{rrrrrrr}i^0 & = & & & & & 1 \ i^1 & = & & & & & i \ i^2 & = & & & & & -1 \ i^3 & = & ii^2 & = & & & -i \ i^4 & = & i^{2}i^{2} & = & & & 1 \ i^5 & = & ii^4 & = & & & i \ i^6 & = & ii^5 & = & i^2 & = & -1end{array}$

    Если мы продолжим записывать этот ряд, то заметим закономерность

    $(1,i,-1,-i,1,dots)$.

    Похожая закономерность возникает при увеличении отрицательных степеней.

    $begin{array}{rcr}i^0 & = & 1 \ i^{-1} & = & -i \ i^{-2} & = & -1 \ i^{-3} & = & i \ i^{-4} & = & 1 \ i^{-5} & = & -i \ i^{-6} & = & -1end{array}$

    Возможно, вы уже видели такую закономерность в математике, но в виде

    $(x,y,-x,-y,x,dots)$, который получается поворотом точки на 90° против часовой стрелки на двухмерной декартовой плоскости; ряд

    $(x,-y,-x,y,x,dots)$ создаётся поворотом точки на 90° градусов на двухмерной декартовой плоскости.

    Декартова плоскость

    Комплексная плоскость

    Мы можем аналогичным образом нанести комплексные числа на двухмерную сетку, называемую комплексной плоскостью, привязав вещественную часть к горизонтальной оси, а мнимую — к вертикальной.

    Комплексная плоскость

    Как видно из предыдущего ряда, мы можем сказать, что если умножим комплексное число на

    $i$, то сможем поворачивать комплексное число на комплексной плоскости с шагом в 90°.

    Давайте проверим, верно ли это. Мы возьмём на комплексной плоскости произвольную точку

    $p$:

    $p=2+i$

    и умножим её на

    $i$, получив

    $q$:

    $begin{array}{rcl}p & = & 2+i \ q & = & pi \ & = & (2+i)i \ & = & 2i+i^2 \ & = & -1+2iend{array}$

    Умножив

    $q$ на

    $i$, получим

    $r$:

    $begin{array}{rcl}q & = & -1+2i \ r & = & qi \ & = & (-1+2i)i \ & = & -i+2i^2 \ & = & -2-iend{array}$

    А умножив

    $r$ на

    $i$, получим

    $s$:

    $begin{array}{rcl}r & = & -2-i \ s & = & ri \ & = & (-2-i)i \ & = & -2i-i^2 \ & = & 1-2iend{array}$

    А умножив

    $s$ на

    $i$, получим

    $t$:

    $begin{array}{rcl}s & = & 1-2i \ t & = & si \ & = & (1-2i)i \ & = & i-2i^2 \ & = & 2+iend{array}$

    И мы получили ровно то, с чего начинали (

    $p$). Если нанести эти комплексные числа на комплексную плоскость, то получим следующий результат.

    Комплексные числа на комплексной плоскости

    Теперь мы можем выполнять поворот на комплексной плоскости и по часовой стрелке, умножая комплексное число на

    $-i$.

    Роторы

    Также мы можем выполнять на комплексной плоскости произвольные повороты, задав комплексное число в следующем виде:

    $q=costheta+isintheta$

    При умножении любого комплексного числа на ротор

    $q$ получаем общую формулу:

    $begin{array}{rcl} p & = & a + bi \ q & = & costheta+isintheta \ pq & = & (a+bi)(costheta+isintheta) \ a^{prime}+b^{prime}i & = & acostheta-bsintheta+(asintheta+bcostheta)i end{array}$

    Что также можно записать в матричном виде:

    $begin{bmatrix} a^{prime} & -b^{prime} \ b^{prime} & a^{prime} end{bmatrix}=begin{bmatrix} costheta & -sintheta \ sintheta & costheta end{bmatrix}begin{bmatrix}a & -b \b & a end{bmatrix}$

    Что является способом поворота против часовой стрелки произвольной точки на комплексной плоскости относительно точки начала координат.

    Кватернионы

    Узнав о системе комплексных чисел и комплексной плоскости, мы можем вывести их в трёхмерное пространство, добавив к системе чисел наряду с

    $i$ ещё два мнимых числа.

    Кватернионы имеют следующий обобщённый вид

    $q=s+xi+yj+zk~~s,x,y,zinmathbb{R}$

    Где в соответствии со знаменитым выражением Гамильтона:

    $i^2=j^2=k^2=ijk=-1$

    $begin{array}{ccc}ij=k & jk=i & ki=j \ ji=-k & kj=-i & ik=-jend{array}$

    Можно заметить, что отношения между

    $i$,

    $j$ и

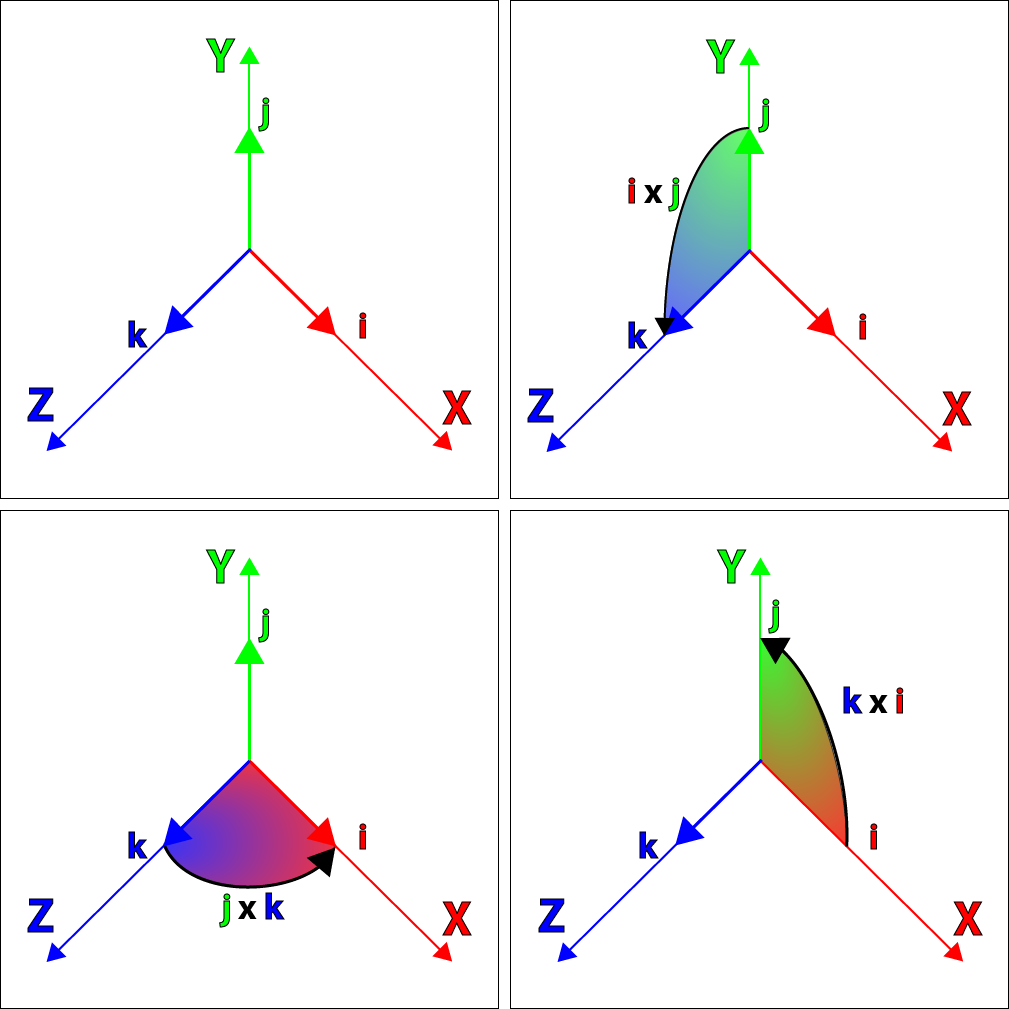
    $k$ очень похожи на правила векторного умножения единичных декартовых векторов:

    $begin{array}{ccc}mathbf{x}times mathbf{y}=mathbf{z} & mathbf{y}times mathbf{z}=mathbf{x} & mathbf{z}times mathbf{x}=mathbf{y} \ mathbf{y}times mathbf{x}=-mathbf{z} & mathbf{z}times mathbf{y}=-mathbf{x} & mathbf{x}times mathbf{z}=-mathbf{y}end{array}$

    Гамильтон также заметил, что мнимые числа

    $i$,

    $j$ и

    $k$ можно использовать для представления трёх декартовых единичных векторов

    $mathbf{i}$,

    $mathbf{j}$ и

    $mathbf{k}$ с теми же свойствами мнимых чисел, так что

    $mathbf{i}^2=mathbf{j}^2=mathbf{k}^2=-1$.

    Графическое представление свойств $mathbf{ij}$, $mathbf{jk}$, $mathbf{ki}$

    На представленном выше изображении графически представлены взаимосвязи между декартовыми единичными векторами в виде

    $mathbf{i}$,

    $mathbf{j}$ и

    $mathbf{k}$.

    Кватернионы как упорядоченная пара

    Также мы можем представить кватернионы в виде упорядоченной пары:

    $q=[s,mathbf{v}]~~sinmathbb{R}, mathbf{v}inmathbb{R}^3$

    Где

    $mathbf{v}$ можно также представить как его отдельные компоненты:

    $q=[s,xmathbf{i}+ymathbf{j}+zmathbf{k}]~~s,x,y,zinmathbb{R}$

    С помощью этой записи мы можем проще представить общие черты кватернионов и комплексных чисел.

    Сложение и вычитание кватернионов

    Кватернионы можно складывать и вычитать аналогично комплексным числам:

    $begin{array}{rcl}q_a & = & [s_a,mathbf{a}] \ q_b & = & [s_b,mathbf{b}] \ q_a+q_b & = & [s_a+s_b,mathbf{a}+mathbf{b}] \ q_a-q_b & = & [s_a-s_b,mathbf{a}-mathbf{b}]end{array}$

    Произведения кватернионов

    Также мы можем выразить произведение двух кватернионов:

    $begin{array}{rcl}q_a & = & [s_a,mathbf{a}] \ q_b & = & [s_b,mathbf{b}] \ q_{a}q_{b} & = & [s_{a},mathbf{a}][s_{b},mathbf{b}] \ & = & (s_{a}+x_{a}i+y_{a}j+z_{a}k)(s_{b}+x_{b}i+y_{b}j+z_{b}k) \ & = & (s_{a}s_{b}-x_{a}x_{b}-y_{a}y_{b}-z_{a}z_{b}) \ & & +(s_{a}x_{b}+s_{b}x{a}+y_{a}z_{b}-y_{b}z_{a})i \ & & +(s_{a}y_{b}+s_{b}y_{a}+z_{a}x_{b}-z_{b}x_{a})j \ & & +(s_{a}z_{b}+s_{b}z_{a}+x_{a}y_{b}-x_{b}y_{a})kend{array}$

    Что даёт нам ещё один кватернион. Если мы заменим в предыдущем выражении мнимые числа

    $i$,

    $j$ и

    $k$ упорядоченными парами (также известными как кватернионные единицы), то получим

    $i=[0,mathbf{i}]~j=[0,mathbf{j}]~k=[0,mathbf{k}]$

    А подставив обратно в исходное выражение с

    $[1,mathbf{0}]=1$, получим:

    $begin{array}{rcl}[s_{a},mathbf{a}][s_{b},mathbf{b}] & = & (s_{a}s_{b}-x_{a}x_{b}-y_{a}y_{b}-z_{a}z_{b})[1,mathbf{0}] \ & & +(s_{a}x_{b}+s_{b}x{a}+y_{a}z_{b}-y_{b}z_{a})[0,mathbf{i}] \ & & +(s_{a}y_{b}+s_{b}y_{a}+z_{a}x_{b}-z_{b}x_{a})[0,mathbf{j}] \ & & +(s_{a}z_{b}+s_{b}z_{a}+x_{a}y_{b}-x_{b}y_{a})[0,mathbf{k}]end{array}$

    Развернув это выражение в сумму упорядоченных пар, получим:

    $begin{array}{rcl}[s_{a},mathbf{a}][s_{b},mathbf{b}] & = & [s_{a}s_{b}-x_{a}x_{b}-y_{a}y_{b}-z_{a}z_{b},mathbf{0}] \ & & +[0,(s_{a}x_{b}+s_{b}x{a}+y_{a}z_{b}-y_{b}z_{a})mathbf{i}] \ & & +[0,(s_{a}y_{b}+s_{b}y_{a}+z_{a}x_{b}-z_{b}x_{a})mathbf{j}] \ & & +[0,(s_{a}z_{b}+s_{b}z_{a}+x_{a}y_{b}-x_{b}y_{a})mathbf{k}]end{array}$

    Если умножить на кватернионную единицу и извлечь общие векторые компоненты, то можно переписать это уравнение следующим образом:

    $begin{array}{rcl}[s_{a},mathbf{a}][s_{b},mathbf{b}] & = & [s_{a}s_{b}-x_{a}x_{b}-y_{a}y_{b}-z_{a}z_{b},mathbf{0}] \ & & +[0,s_{a}(x_{b}mathbf{i}+y_{b}mathbf{j}+z_{b}mathbf{k})+s_{b}(x_{a}mathbf{i}+y_{a}mathbf{j}+z_{a}mathbf{k}) \ & & +(y_{a}z_{b}-y_{b}z_{a})mathbf{i}+(z_{a}x_{b}-z_{b}x_{a})mathbf{j}+(x_{a}y_{b}-x_{b}y_{a})mathbf{k}]end{array}$

    Это уравнение даёт нам сумму двух упорядоченных пар. Первая упорядоченная пара — это вещественный кватернион, а вторая — чистый кватернион. Две этих упорядоченных пары можно соединить в одну упорядоченную пару:

    $begin{array}{rcl}[s_{a},mathbf{a}][s_{b},mathbf{b}] & = & [s_{a}s_{b}-x_{a}x_{b}-y_{a}y_{b}-z_{a}z_{b}, \ & & s_{a}(x_{b}mathbf{i}+y_{b}mathbf{j}+z_{b}mathbf{k})+s_{b}(x_{a}mathbf{i}+y_{a}mathbf{j}+z_{a}mathbf{k}) \ & & +(y_{a}z_{b}-y_{b}z_{a})mathbf{i}+(z_{a}x_{b}-z_{b}x_{a})mathbf{j}+(x_{a}y_{b}-x_{b}y_{a})mathbf{k}]end{array}$

    Если подставить, то мы получим

    $begin{array}{rcl}mathbf{a} & = & x_{a}mathbf{i}+y_{a}mathbf{j}+z_{a}mathbf{k} \ mathbf{b} & = & x_{b}mathbf{i}+y_{b}mathbf{j}+z_{b}mathbf{k} \ mathbf{a}cdotmathbf{b} & = & x_{a}x_{b}+y_{a}y_{b}+z_{a}z_{b} \ mathbf{a}timesmathbf{b} & = & (y_{a}z_{b}-y_{b}z_{a})mathbf{i}+(z_{a}x_{b}-z_{b}x_{a})mathbf{j}+(x_{a}y_{b}-x_{b}y_{a})mathbf{k}end{array}$

    Получаем:

    $[s_{a},mathbf{a}][s_{b},mathbf{b}]=[s_{a}s_{b}-mathbf{a}cdotmathbf{b},s_{a}mathbf{b}+s_{b}mathbf{a}+mathbf{a}timesmathbf{b}]$

    Это и есть общее уравнение произведения кватернионов.

    Вещественный кватернион

    Вещественный кватернион — это кватернион, в который входит вектор

    $mathbf{0}$:

    $q=[s,mathbf{0}]$

    А произведением двух вещественных кватернионов является ещё один вещественный кватернион:

    $begin{array}{rcl}q_a & = & [s_a,mathbf{0}] \ q_b & = & [s_b,mathbf{0}] \ q_{a}q_{b} & = & [s_a,mathbf{0}][s_b,mathbf{0}] \ & = & [s_{a}s_{b},mathbf{0}]end{array}$

    Что аналогично произведению двух комплексных чисел, содержащих нулевой мнимый член.

    $begin{array}{rcl}z_1 & = & a_1+0i \ z_2 & = & a_2+0i \ z_{1}z_{2} & = & (a_1+0i)(a_2+0i) \ & = & a_{1}a_{2}end{array}$

    Умножение кватерниона на скалярную величину

    Также мы можем умножать кватернион на скаляр, при этом придерживаясь следующего правила:

    $begin{array}{rcl}q & = & [s,mathbf{v}] \ lambda{q} & = & lambda[s,mathbf{v}] \ & = & [lambda{s},lambdamathbf{v}]end{array}$

    Мы можем убедиться в этом с помощью показанного выше произведения вещественных кватернионов, умножив кватернион на скаляр как вещественный кватернион:

    $begin{array}{rcl}q & = & [s,mathbf{v}] \ lambda & = & [lambda,mathbf{0}] \ lambda{q} & = & [lambda,mathbf{0}][s,mathbf{v}] \ & = & [lambda{s},lambdamathbf{v}]end{array}$

    Чистые кватернионы

    Кроме вещественных кватернионов, Гамильтон также определил чистый кватернион как кватернион с нулевым скалярным членом:

    $q=[0,mathbf{v}]$

    Или если записать по компонентам:

    $q=xi+yj+zk$

    И мы снова можем взять произведение двух чистых кватернионов:

    $begin{array}{rcl}q_a & = & [0,mathbf{a}] \ q_b & = & [0,mathbf{b}] \ q_{a}q_{b} & = & [0,mathbf{a}][0,mathbf{b}] \ & = & [-mathbf{a}cdotmathbf{b},mathbf{a}timesmathbf{b}]end{array}$

    в соответствии с представленным выше правилом произведения кватернионов.

    Аддитивная форма кватерниона

    Кроме того, мы можем выразить кватернионы как сумму вещественной и чистой частей кватерниона:

    $begin{array}{rcl}q & = & [s,mathbf{v}] \ & = & [s,mathbf{0}]+[0,mathbf{v}]end{array}$

    Единичный кватернион

    Взяв произвольный вектор

    $mathbf{v}$, можно выразить этот вектор и через его скалярную величину, и через его направление следующим образом:

    $mathbf{v}=vmathbf{hat{v}}~text{где}~v=|mathbf{v}|~text{и}~|mathbf{hat{v}}|=1$

    Объединив это определение с определением чистого кватерниона, получим:

    $begin{array}{rcl}q & = & [0,mathbf{v}] \ & = & [0,vmathbf{hat{v}}] \ & = & v[0,mathbf{hat{v}}]end{array}$

    Также мы можем описать единичный кватернион, имеющий нулевой скаляр и единичный вектор:

    $hat{q}=[0,mathbf{hat{v}}]$

    Бинарная форма кватерниона

    Теперь мы можем объединить определения единичного кватерниона и аддитивную форму кватерниона, получив форму кватернионов, схожую с записью, используемой при описании комплексных чисел:

    $begin{array}{rcl}q & = & [s,mathbf{v}] \ & = & [s,mathbf{0}]+[0,mathbf{v}] \ & = & [s,mathbf{0}]+v[0,mathbf{hat{v}}] \ & = & s+vhat{q}end{array}$

    Что даёт нам способ представить кватернион в форме, очень похожей на комплексные числа:

    $begin{array}{rcl}z & = & a+bi \ q & = & s + vhat{q}end{array}$

    Сопряжённое число кватерниона

    Сопряжённое число кватерниона можно вычислить, взяв противоположную по знаку векторную часть кватерниона:

    $begin{array}{rcl}q & = & [s,mathbf{v}] \ q^* & = & [s,-mathbf{v}]end{array}$

    Произведение кватерниона и его сопряжённого числа даёт нам следующее:

    $begin{array}{rcl}qq^* & = & [s,mathbf{v}][s,-mathbf{v}] \ & = & [s^2-mathbf{v}cdot-mathbf{v},-smathbf{v}+smathbf{v}+mathbf{v}times-mathbf{v}] \ & = & [s^2+mathbf{v}cdotmathbf{v},mathbf{0}] \ & = & [s^2+v^2,mathbf{0}]end{array}$

    Норма кватерниона

    Вспомним определение нормы комплексного числа:

    $begin{array}{rcl}|z| & = & sqrt{a^2+b^2} \ zz^* & = & |z|^2end{array}$

    Аналогично, норма (или величина) кватерниона определяется как:

    $begin{array}{rcl}q & = & [s,mathbf{v}] \ |q| & = & sqrt{s^2+v^2}end{array}$

    Что позволяет нам выразить норму кватерниона следующим образом:

    $qq^*=|q|^2$

    Нормализация кватерниона

    Имея определение нормы кватерниона, мы можем использовать её для нормализации кватерниона. Кватернион нормализуется делением на

    $|q|$:

    $q^{prime}=frac{q}{sqrt{s^2+v^2}}$

    Например, давайте нормализуем кватернион:

    $q=[1,4mathbf{i}+4mathbf{j}-4mathbf{k}]$

    Сначала нам нужно вычислить норму кватерниона:

    $begin{array}{rcl}|q| & = & sqrt{1^2+4^2+4^2+(-4)^2} \ & = & sqrt{49} \ & = & 7end{array}$

    Затем мы должны разделить кватернион на норму кватерниона, чтобы вычислить нормализованный кватернион:

    $begin{array}{rcl}q^{prime} & = & cfrac{q}{|q|} \[1.0em] & = & cfrac{(1+4mathbf{i}+4mathbf{j}-4mathbf{k})}{7} \[1.0em] & = & cfrac{1}{7}+cfrac{4}{7}mathbf{i}+cfrac{4}{7}mathbf{j}-cfrac{4}{7}mathbf{k}end{array}$

    Обратный кватернион

    Обратный кватернион обозначается как

    $q^{-1}$. Для вычисления обратного кватерниона мы берём сопряжённое число кватерниона и делим его на квадрат нормы:

    $q^{-1}=frac{q^*}{|q|^2}$

    Чтобы показать это, мы можем воспользоваться определением обратной величины:

    $qq^{-1}=[1,mathbf{0}]=1$

    И умножить обе стороны на сопряжённое число кватерниона, что даст нам:

    $q^{*}qq^{-1}=q^{*}$

    Подстановкой мы получаем:

    $begin{array}{rcl}|q|^{2}q^{-1} & = & q^{*} \ q^{-1} & = & cfrac{q^{*}}{|q|^{2}}end{array}$

    Для единичных кватернионов-норм, норма которых равна 1, мы можем записать:

    $q^{-1}=q^{*}$

    Скалярное произведение кватернионов

    Аналогично скалярному произведению векторов мы можем вычислить скалярное произведение двух кватернионов, перемножив соответствующие скалярные части и просуммировав результаты:

    $begin{array}{rcl}q_1 & = & [s_1,x_1mathbf{i}+y_1mathbf{j}+z_1mathbf{k}] \ q_2 & = & [s_2,x_2mathbf{i}+y_2mathbf{j}+z_2mathbf{k}] \ q_1{cdot}q_2 & = & s_{1}s_{2}+x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{2}end{array}$

    Также мы можем использовать скалярное произведение кватернионов для вычисления угловой разности между кватернионами:

    $costheta=frac{s_{1}s_{2}+x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{2}}{|q_{1}||q_{2}|}$

    Для единичных кватернионов-норм мы можем упростить уравнение:

    $costheta=s_{1}s_{2}+x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{2}$

    Повороты

    Напомню, что мы определили особую форму комплексного числа под названием ротор, которую можно использовать для поворота точки на двухмерной плоскости следующим образом:

    $q=costheta+isintheta$

    Благодаря схожести комплексных чисел с кватернионами должна существовать возможность выразить кватернион, который можно использовать для поворота точки в трёхмерном пространстве:

    $q=[costheta,sinthetamathbf{v}]$

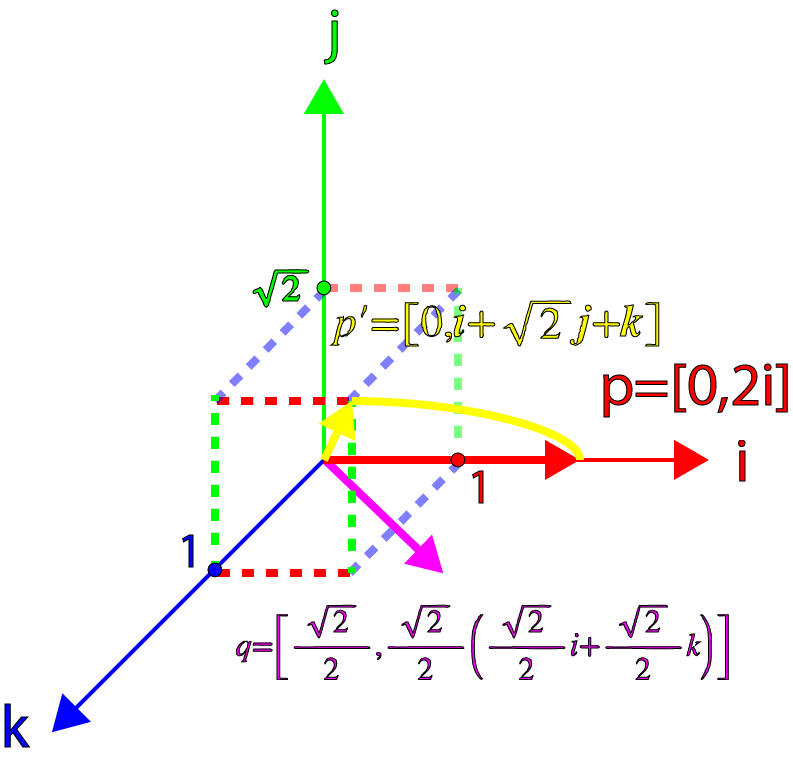
    Давайте проверим, верна ли эта теория, вычислив произведение кватерниона

    $q$ и вектора

    $mathbf{p}$. Во-первых, мы можем выразить

    $mathbf{p}$ как чистый кватернион в следующем виде:

    $p=[0,mathbf{p}]$

    А

    $q$ — это единичный кватернион-норма в виде:

    $q=[s,lambdamathbf{hat{v}}]$

    Тогда

    $begin{array}{rcl}p^{prime} & = & qp \ & = & [s,lambdamathbf{hat{v}}][0,mathbf{p}] \ & = & [-lambdamathbf{hat{v}}cdotmathbf{p},smathbf{p}+lambdamathbf{hat{v}}timesmathbf{p}]end{array}$

    Мы видим, что результатом является общий кватернион со скалярной и векторной частями.

    Давайте сначала рассмотрим «особый» случай, при котором

    $mathbf{p}$ перпендикулярен

    $mathbf{hat{v}}$. В таком случае член скалярного произведения

    $-lambdamathbf{hat{v}}cdotmathbf{p}=0$ и результат становится чистым кватернионом:

    $p^{prime}=[0,smathbf{p}+lambdamathbf{hat{v}}timesmathbf{p}]$

    В таком случае для поворота

    $mathbf{p}$ относительно

    $mathbf{hat{v}}$ мы просто подставляем

    $s=costheta$ и

    $lambda=sintheta$.

    $p^{prime}=[0,costhetamathbf{p}+sinthetamathbf{hat{v}}timesmathbf{p}]$

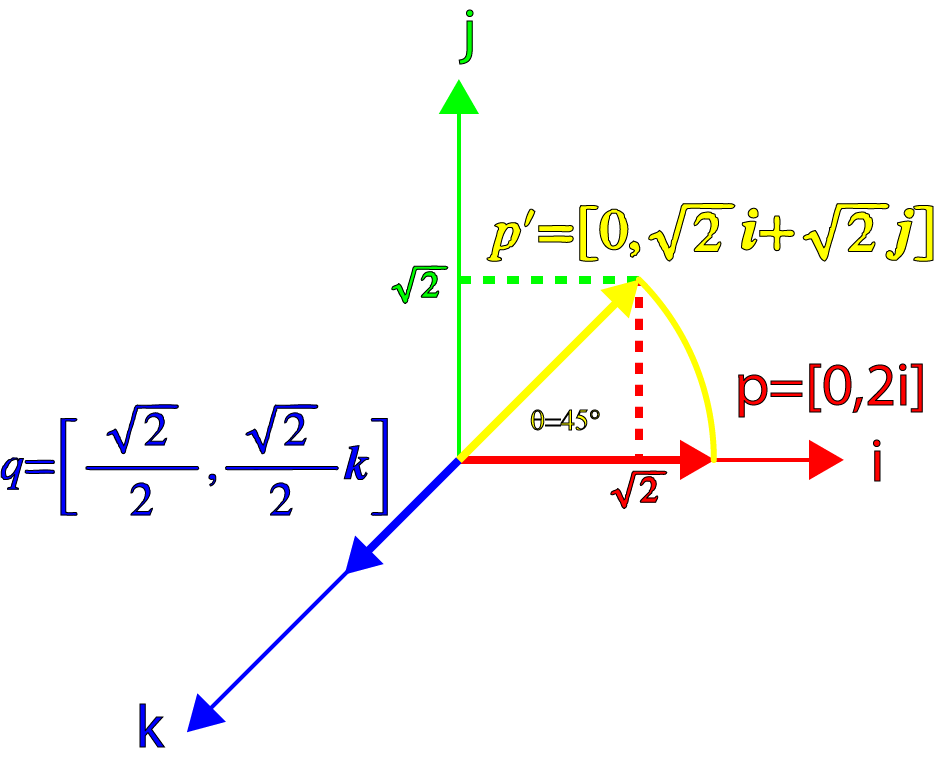
    Например, давайте повернём вектор

    $mathbf{p}$ на 45° относительно оси Z; тогда наш кватернион

    $q$ будет равен:

    $begin{array}{rcl}q & = & [costheta,sinthetamathbf{k}] \ & = & left[frac{sqrt{2}}{2},frac{sqrt{2}}{2}mathbf{k}right]end{array}$

    И давайте возьмём вектор

    $mathbf{p}$, который относится к особому случаю, где

    $mathbf{p}$ перпендикулярен

    $mathbf{k}$:

    $p=[0,2mathbf{i}]$

    Теперь давайте найдём произведение

    $qp$

    :

    $begin{array}{rcl}p^{prime} & = & qp \ & = & left[frac{sqrt{2}}{2},frac{sqrt{2}}{2}mathbf{k}right][0,2mathbf{i}] \ & = & left[0,2frac{sqrt{2}}{2}mathbf{i}+2frac{sqrt{2}}{2}mathbf{k}timesmathbf{i}right] \ & = & [0, sqrt{2}mathbf{i}+sqrt{2}mathbf{j}]end{array}$

    Что даёт нам чистый кватернион, повёрнутый на 45° относительно оси

    $mathbf{k}$. Мы можем также убедиться, что величина конечного вектора сохранилась:

    $begin{array}{rcl}|mathbf{p}^{prime}| & = & sqrt{sqrt{2}^{2}+sqrt{2}^{2}} \ & = & 2end{array}$

    В точности то, чего мы и ожидали!

    Мы можем показать это графически следующим изображением:

    Поворот кватерниона (1)

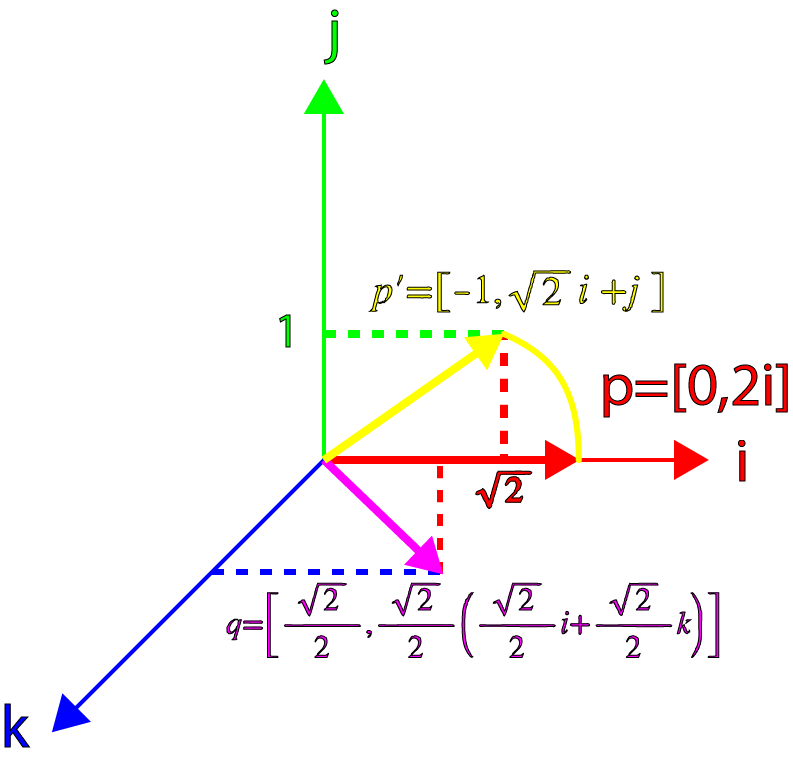
    Теперь давайте рассмотрим кватернион, не ортогональный к

    $mathbf{p}$. Если мы примем для векторной части кватерниона смещение в 45° от

    $mathbf{p}$, то получим:

    $begin{array}{rcl}mathbf{hat{v}} & = & frac{sqrt{2}}{2}mathbf{i}+frac{sqrt{2}}{2}mathbf{k} \ mathbf{p} & = & 2mathbf{i} \ q & = & [costheta,sinthetamathbf{hat{v}}] \ p & = & [0,mathbf{p}]end{array}$

    А умножив наш вектор

    $mathbf{p}$ на

    $q$, получим:

    $begin{array}{rcl}p^{prime} & = & qp \ & = & [costheta,sinthetamathbf{hat{v}}][0,mathbf{p}] \ & = & [-sinthetamathbf{hat{v}}cdotmathbf{p},costhetamathbf{p}+sinthetamathbf{hat{v}}timesmathbf{p}]end{array}$

    После подстановки

    $mathbf{hat{v}}$,

    $mathbf{p}$ и

    $theta=45^{circ}$ получаем:

    $begin{array}{rcl}p^{prime} & = & left[-frac{sqrt{2}}{2}left(frac{sqrt{2}}{2}mathbf{i}+frac{sqrt{2}}{2}mathbf{k}right)cdot(2mathbf{i}),frac{sqrt{2}}{2}2mathbf{i}+frac{sqrt{2}}{2}left(frac{sqrt{2}}{2}mathbf{i}+frac{sqrt{2}}{2}mathbf{k}right)times2mathbf{i}right] \ & = & [-1,sqrt{2}mathbf{i}+mathbf{j}]end{array}$

    То есть это больше не чистый кватернион, он не повёрнут на 45° а норма вектора больше не равна 2 (она уменьшилась до

    $sqrt{3}$).

    Этот результат можно показать графически.

    Поворот кватерниона (2)

    Строго говоря, некорректно представлять кватернион $p^{prime}$ в трёхмерном пространстве, потому что на самом деле это четырёхмерный вектор! Ради упрощения я покажу только векторный компонент кватернионов.

    Однако не всё потеряно. Гамильтон выяснил (но не опубликовал этого), что если мы затем умножим результат

    $qp$ на значение, обратное

    $q$, то результатом будет чистый кватернион, а норма векторного компонента сохранится. Давайте посмотрим, можно ли применить это в нашем примере.

    Для начала давайте вычислим

    $q^{-1}$:

    $begin{array}{rcl}q & = & left[costheta,sinthetaleft(frac{sqrt{2}}{2}mathbf{i}+frac{sqrt{2}}{2}mathbf{k}right)right] \ q^{-1} & = & left[costheta,-sinthetaleft(frac{sqrt{2}}{2}mathbf{i}+frac{sqrt{2}}{2}mathbf{k}right)right]end{array}$

    При

    $theta=45^{circ}$ получаем:

    $begin{array}{rcl}q^{-1} & = & left[frac{sqrt{2}}{2},-frac{sqrt{2}}{2}left(frac{sqrt{2}}{2}mathbf{i}+frac{sqrt{2}}{2}mathbf{k}right)right] \ & = & frac{1}{2}left[sqrt{2},-mathbf{i}-mathbf{k}right]end{array}$

    Объединив предыдущее значение

    $qp$ и

    $q^{-1}$, получим:

    $begin{array}{rcl}qp & = & left[-1,sqrt{2}mathbf{i}+mathbf{j}right] \ qpq^{-1} & = & left[-1,sqrt{2}mathbf{i}+mathbf{j}right]frac{1}{2}left[sqrt{2},-mathbf{i}-mathbf{k}right] \ & = & frac{1}{2}left[-sqrt{2}-left(sqrt{2}mathbf{i}+mathbf{j}right)cdot(-mathbf{i}-mathbf{k}),mathbf{i}+mathbf{k}+sqrt{2}left(sqrt{2}mathbf{i}+mathbf{j}right)-mathbf{i}+sqrt{2}mathbf{j}+mathbf{k}right] \ & = & frac{1}{2}left[-sqrt{2}+sqrt{2},mathbf{i}+mathbf{k}+2mathbf{i}+sqrt{2}mathbf{j}-mathbf{i}+sqrt{2}mathbf{j}+mathbf{k}right] \ & = & left[0,mathbf{i}+sqrt{2}mathbf{j}+mathbf{k}right]end{array}$

    Что является чистым кватернионом, а норма результата равна:

    $begin{array}{rcl}|p^{prime}| & = & sqrt{1^2+sqrt{2}^2+1^2} \ & = & sqrt{4} \ & = & 2end{array}$

    что равно

    $mathbf{p}$, то есть норма вектора сохранилась.

    На изображении ниже показан результат поворота.

    Поворот кватерниона (3)

    Мы видим, что результат является чистым кватернионом, а норма исходного вектора сохранилась, но вектор повернулся на 90°, а не на 45°, что вдвое больше необходимого! Поэтому для корректного поворота вектора

    $mathbf{p}$ на угол

    $theta$ относительно произвольной оси

    $mathbf{hat{v}}$ нам нужно взять половинный угол и создать следующий кватернион:

    $q=left[cosfrac{1}{2}theta,sinfrac{1}{2}thetamathbf{hat{v}}right]$

    Что является общим видом кватерниона поворота!

    Интерполяция кватерниона

    Одна из самых важных причин использования кватернионов в компьютерной графике заключается в том, что кватернионы очень хорошо описывают повороты в пространстве. Кватернионы избавляют от проблем, отягощающих другие способы поворота точек в 3D-пространстве, такие как складывание рамок, в котором проблема заключается в представлении поворота в углах Эйлера.

    С помощью кватернионов мы можем определить несколько методов, представляющих интерполяцию поворота в 3D-пространстве. Первый рассматриваемый мной метод называется SLERP. Он используется для плавной интерполяции точки между двумя ориентациями. Второй метод является развитием SLERP и называется SQUAD. Он используется для интерполяции по ряду ориентаций, задающих путь.

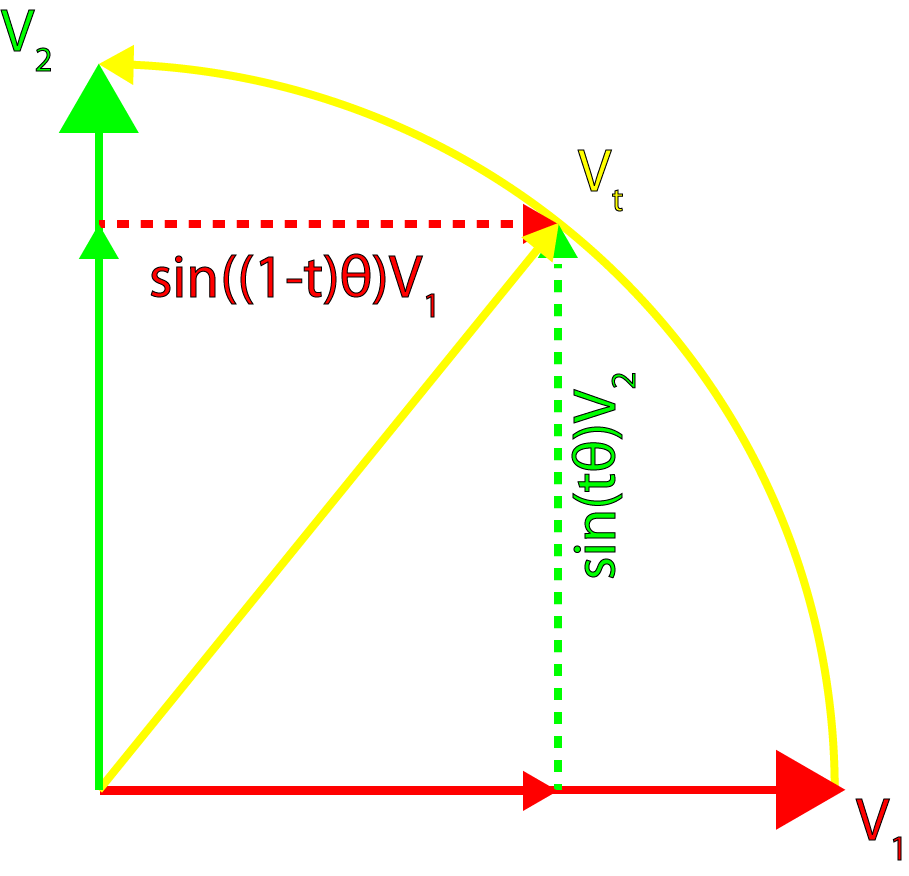
    SLERP

    SLERP расшифровывается как Spherical Linear Interpolation (сферическая линейная интерполяция). SLERP предоставляет возможность плавной интерполяции точки между двумя ориентациями.

    Я обозначу первую ориентацию как

    $q_1$, а вторую как

    $q_2$. Интерполируемую точку обозначим как

    $mathbf{p}$, интерполированную точку обозначим как

    $mathbf{p}^{prime}$. Параметр интерполяции

    $t$ будет интерполировать

    $mathbf{p}$ от

    $q_1$ при

    $t=0$ до

    $q_2$ при

    $t=1$.

    Стандартная формула линейной интерполяции имеет вид:

    $mathbf{p}^{prime}=mathbf{p_1}+t(mathbf{p_2}-mathbf{p_1})$

    Вот основные шаги для применения этого уравнения:

    Мы можем использовать тот же основной принцип, чтобы выполнить интерполяцию между двумя ориентациями кватернионов.

    Разность кватернионов

    Первый шаг означает, что нам нужно вычислить разность между

    $q_1$ и

    $q_2$. В контексте кватернионов это аналогично вычислению угловой разности между двумя кватернионами.

    $Delta{q}=q_1^{-1}q_2$

    Возведение кватерниона в степень

    На следующем шаге нужно взять дробную часть этой разности. Мы можем вычислить дробную часть кватерниона, возведя его в степень, значение которой находится в интервале

    $[0…1]$.

    Общая формула возведения кватерниона в степень имеет следующий вид:

    $q^t=exp(tlog{q})$

    Где экпоненциальная функция для кватернионов выглядит так:

    $begin{array}{rcl}exp(q) & = & expleft([0,thetamathbf{hat{v}}]right) \ & = & [costheta,sinthetamathbf{hat{v}}] end{array}$

    А логарифм кватерниона имеет вид:

    $begin{array}{rcl}log{q} & = & log(costheta{+}sinthetamathbf{hat{v}}) \ & = & logleft(exp(thetamathbf{hat{v}})right) \ & = & thetamathbf{hat{v}} \ & = & [0,thetamathbf{hat{v}}] end{array}$

    При

    $t=0$ мы имеем следующее:

    $begin{array}{rcl}q^0 & = & exp(0log{q}) \ & = & exp([cos(0),sin(0)mathbf{hat{v}}]) \ & = & exp([1,mathbf{0}]) \ & = & [1,mathbf{0}]end{array}$

    А при

    $t=1$ мы имеем

    $begin{array}{rcl}q^1 & = & exp(log{q}) \ & = & qend{array}$

    Дробная разность кватернионов

    Чтобы вычислить интерполированный угловой поворот, мы изменяем исходную ориентацию

    $q_1$ на дробную часть разности между

    $q_1$ и

    $q_2$.

    $q^{prime}=q_1left(q_1^{-1}q_2right)^t$

    Что является общим видом сферической линейной интерполяции для кватернионов. Однако это не тот вид уравнения SLERP, который обычно используется на практике.

    Мы можем применить похожую формулу для выполнения сферической интерполяции векторов в кватернионы. Общий вид сферической интерполяции для векторов задаётся так:

    $mathbf{v}_t=frac{sin(1-t)theta}{sintheta}mathbf{v}_1+frac{sin{ttheta}}{sintheta}mathbf{v}_2$

    Графически это можно показать следующим изображением.

    Интерполяция кватернионов

    Эту формулу можно без изменений применить к кватернионам:

    $q_t=frac{sin(1-t)theta}{sintheta}q_1+frac{sin{ttheta}}{sintheta}q_2$

    И мы можем получить угол

    $theta$, вычислив скалярное произведение

    $q_1$ и

    $q_2$.

    $begin{array}{rcl}costheta & = & cfrac{q_1{cdot} q_2}{|q_1||q_2|} \ & = & cfrac{s_{1}s_{2}+x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{2}}{|q_1||q_2|} \ theta & = & cos^{-1}left(cfrac{s_{1}s_{2}+x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{2}}{|q_1||q_2|}right)end{array}$

    Факторы, которые нужно учитывать

    У этой реализации есть две проблемы, которые нужно учитывать при использовании.

    Во-первых, если скалярное произведение кватернионов оказывается отрицательным значением, то интерполяция пойдёт по «долгому пути» на четырёхмерной сфере, а это не всегда желательно. Чтобы решить эту проблему, мы можем проверить результат скалярного произведения и если он отрицательный, то можно взять значение, противоположное одной из ориентаций. Инвертирование скалярной и векторной части кватерниона не меняет представляемую им ориентацию, но сделав это, мы гарантируем, что поворот будет происходить по «кратчайшему» пути.

    Ещё одна проблема возникает, если угловая разность между

    $q_1$ и

    $q_2$ очень мала, при этом

    $sintheta$ становится 0. Если это происходит, то при делении на

    $sintheta$ мы можем получить неопределённый результат. В таком случае можно вернуться к использованию линейной интерполяции между

    $q_1$ и

    $q_2$.

    SQUAD

    Так же, как SLERP можно использовать для интерполяции между двумя кватернионами, SQUAD (Spherical and Quadrangle — сферическая и четырёхугольная) можно использовать для плавной интерполяции по пути поворотов.

    Если у нас есть ряд кватернионов:

    $q_1,q_2,q_3,cdots,q_{n-2},q_{n-1},q_{n}$

    И мы определили «вспомогательный» кватернион (

    $s_i$), который мы можем считать промежуточной контрольной точкой:

    $s_i=expleft(-frac{logleft(q_{i+1}q_i^{-1}right)+logleft(q_{i-1}q_i^{-1}right)}{4}right)q_i$

    Ориентация вдоль части кривой определяется как:

    $q_{i-1},q_i,q_{i+1},q_{i+2}$

    при времени t это даёт нам:

    $mathrm{squad}(q_i,q_{i+1},s_i,s_{i+1},t)=mathrm{slerp}(mathrm{slerp}(q_i,q_{i+1},t),mathrm{slerp}(s_i,s_{i+1},t),2t(1-t))$

    Заключение

    Несмотря на сложность для понимания, при работе с поворотами кватернионы обеспечивают несколько очевидных преимуществ по сравнению с матрицами и углами Эйлера.

    • Интерполяция кватернионов с помощью SLERP и SQUAD предоставляет способ плавной интерполяции между ориентациями в пространстве.
    • Конкатенация поворотов с помощью кватернионов выполняется быстрее, чем объединение поворотов, выраженных в матричном виде.
    • Для единичных кватернионов-норм обратная величина поворота берётся вычитанием векторной части кватерниона. Вычисление обратной величины матрицы поворота значительно медленнее, если матрица не ортонормирована (если она ортонормирована, то это всего лишь транспонирование матрицы).
    • Преобразование кватернионов в матрицы немного быстрее, чем для углов Эйлера.
    • Для описания поворота кватернионам требуется всего 4 числа (3, если они нормализованы. Вещественную часть можно вычислять во время выполнения программы), в то время как матрицам необходимо не менее 9 значений.

    Однако наряду со всеми преимуществами использования кватернионов существует также несколько недостатков.

    • Кватернионы могут становиться недействительными из-за ошибки округления чисел с плавающей запятой; однако эту «вкравшуюся ошибку» можно устранить ренормализацией кватерниона.
    • Вероятно, самое значительное препятствие для применения кватернионов — высокая сложность их понимания. Надеюсь, эту проблему вы решите, прочитав мою статью.

    Есть множество математических библиотек, реализующих кватернионы, и только некоторые из них реализуют кватернионы правильно. По моему собственному опыту хорошей математической библиотекой с качественной реализацией кватернионов является GLM (OpenGL Math Library). Если вы хотите использовать кватернионы в собственных приложениях, то рекомендую эту библиотеку.

    Загрузка демо

    Я создал небольшое демо, демонстрирующее использование кватерниона для поворота объекта в пространстве. Демо было создано в Unity 3.5.2, можете скачать бесплатно скачать этот движок и просмотреть исходный код демо. В файле zip также содержится двоичный исполняемый файл Windows, но в Unity вы можете собрать приложение и для Mac.

    Understanding Quaternions.zip

    Справочные материалы

    Quaternions for Computer Graphics

    Vince, J (2011). Quaternions for Computer Graphics. 1st. ed. London: Springer.

    Dunn, F. and Parberry, I. (2002). 3D Math Primer for Graphics and Game Development. 1st. ed. Plano, Texas: Wordware Publishing, Inc.
    Источник

    Добавить комментарий