Как найти центр трапеции
Трапецией называется четырехугольник, у которого только одна пара противолежащих сторон параллельна. Найти центр трапеции очень просто. Следуйте пошаговой инструкции ниже.

Вам понадобится
- Карандаш, линейка
Инструкция
Возьмите линейку. С ее помощью найдите середину одного основания трапеции. Основание трапеции – это одна из параллельных сторон. Измерьте длину основания, разделите ее на два. Отмерьте от начала основания по ее длине найденную величину и поставьте точку.Так же измерьте и длину второго основания трапеции. В результате на двух параллельных сторонах у вас будут отметки точно на их серединах.
Соедините найденные в предыдущем шаге середины оснований прямой линией. Сделайте это с помощью карандаша и линейки.Теперь точки, обозначающие середины трапеции, соединены прямой.
Найдите середину прямой линии, которую вы провели в предыдущем шаге.Для этого с помощью линейки измерьте длину линии и разделите ее на два.От любого из оснований трапеции отмерьте по этой линии половину ее длины и поставьте точку.Эта точка является центром трапеции.
Видео по теме
Полезный совет
Чтобы проверить правильность расчетов, вырежьте трапецию из бумаги, проведите все вышеописанные действия, чтобы найти ее центр, и поместите трапецию на кончик карандаша или на зубочистку. Острие карандаша/зубочистки должно приходиться точно на центр трапеции.
Если центр трапеции найден верно, бумажная фигура не будет падать с кончика карандаша или с зубочистки.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
1. Формула средней линии равнобедренной трапеции через основания
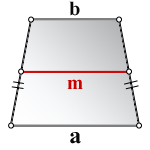
a – нижнее основание
b – верхнее основание
m – средняя линия
Формула средней линии, (m ):
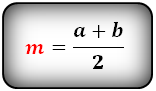
2. Формулы средней линии через основание, высоту и углы при нижнем основании
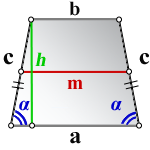
a – нижнее основание
b – верхнее основание
c – боковая сторона
α – угол при нижнем осровании
h – высота трапеции
m – средняя линия
Формулы средней линии трапеции, (m ):
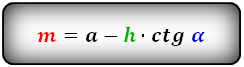
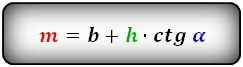
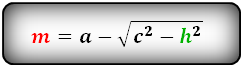
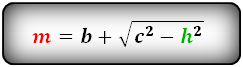
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
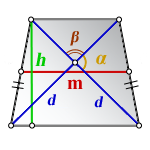
d – диагонали трапеции
α , β – углы между диагоналями
h – высота трапеции
m – средняя линия
Формула средней линии трапеции, (m ):
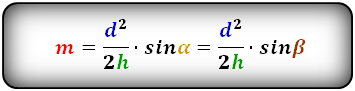
4. Формула средней линии трапеции через площадь и высоту
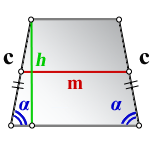
S – площадь трапеции
h – высота трапеции
α – угол при нижнем осровании
m – средняя линия
Формула средней линии трапеции, (m ):

Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 12 октября 2013
-
Обновлено: 13 августа 2021
Сообщения без ответов | Активные темы
Найти косинус угла в трапеции – помогите, не получается
Модераторы: Prokop, mad_math
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Toma |
|
|||
|
Если в трапеции [math]ABCD[/math] ([math]AB||DC[/math] ) [math]AB=6,~BC=3,~CD=4,~DA=2[/math], найти косинуса угла [math]C[/math]. Заранее пребольшое спасибо!
|
|||
| Вернуться к началу |
|
|||
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Найти косинус угла между векторами
в форуме Аналитическая геометрия и Векторная алгебра |
Ilia213 |
2 |
186 |
19 дек 2022, 20:35 |
|
Найти косинус третьего угла треугольника
в форуме Геометрия |
Onex |
6 |
985 |
19 сен 2013, 15:49 |
|
Как найти косинус угла у вершины треугольника С ?
в форуме Аналитическая геометрия и Векторная алгебра |
Leonor19 |
2 |
429 |
01 окт 2016, 13:56 |
|
Найти косинус, синус и тангенс угла
в форуме Аналитическая геометрия и Векторная алгебра |
Cris_21 |
2 |
457 |
01 мар 2017, 02:15 |
|
Найти синус, косинус и котангенс угла
в форуме Тригонометрия |
nikpasternak |
3 |
413 |
20 мар 2018, 23:58 |
|
Косинус угла AOB
в форуме Алгебра |
belinum |
1 |
346 |
25 окт 2013, 19:15 |
|
Косинус половинного угла
в форуме Тригонометрия |
III_X |
12 |
1065 |
30 ноя 2013, 14:48 |
|
Косинус угла между сторонами
в форуме Аналитическая геометрия и Векторная алгебра |
Ket |
1 |
762 |
05 фев 2014, 06:19 |
|
Косинус угла между векторами p q
в форуме Векторный анализ и Теория поля |
proclown3 |
2 |
125 |
18 окт 2022, 21:35 |
|
Найдите косинус угла между векторами
в форуме Аналитическая геометрия и Векторная алгебра |
ivan kumaev |
1 |
82 |
20 дек 2022, 19:56 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 6 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB
Средняя линия трапеции
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Мы снова затронем тему трапеций (что это?).
И расскажем о том, что такое средняя линия этой геометрической фигуры.
Средняя линия – это…
Вообще, этот термин в геометрии весьма распространен.
Средняя линия – это отрезок, проходящий через противоположные стороны, и который делит их ровно на две одинаковых части.
Средняя линия есть практически у каждой геометрической фигуры. Например, у четырехугольников она выглядит вот так:
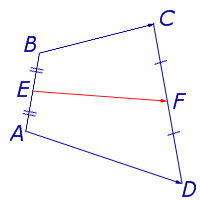
А вот так у треугольников:
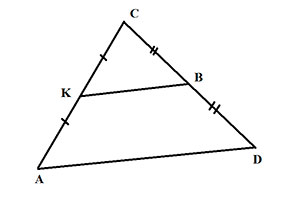
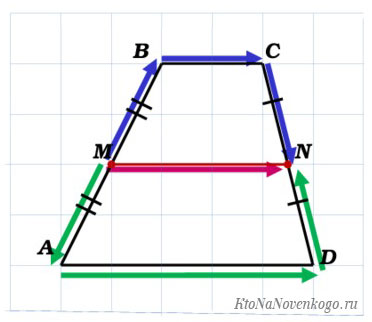
И наконец, в случае трапеции изображение средней линии будет вот таким:
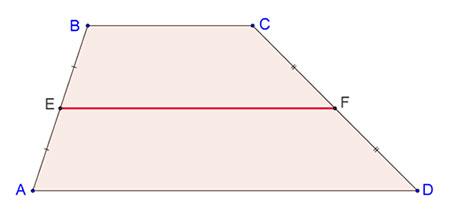
На данном рисунке показана трапеция ABCD. Если кто забыл, то у такой фигуры две противоположные грани расположены на параллельных прямых.
Они называются основаниями. А оставшиеся стороны, которые соответственно не параллельны друг другу, это боковые.
Так вот в нашем случае мы имеем среднюю линию EF, которая делит боковые стороны АВ и СD на две половинки. То есть:
AE = EB и СF = FD
Как найти среднюю линию трапеции (формула)
Есть одна главная формула, позволяющая рассчитать значение нашего отрезка.
Так, длина средней линии будет равна сумме оснований фигуры, поделенной на два. Или, другими словами, половине суммы оснований.
Возьмем для примера трапецию:
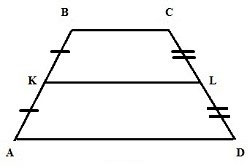
И тогда формула расчета будет выглядеть так:
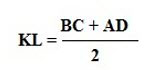
Если есть желание доказать правдивость этой формулы, нужно несколько дорисовать нашу изначальную фигуру. А именно провести линию через В и L, а также продлить сторону АD. И сделать так, чтобы эти две линии пересеклись.
В итоге получится вот что:
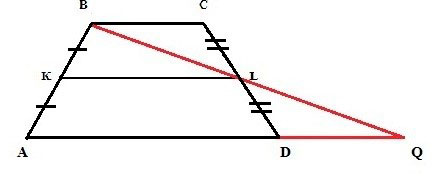
Далее нас будут интересовать оба треугольника, которые получились. Это BLC и DLQ. Необходимо доказать, что они имеют равные размеры.
И это просто, так как у них одинаковы углы:
- BLC и QLD – как вертикальные;
- BCL и QDL – как лежащие накрест при имеющихся параллельных прямых и секущей.
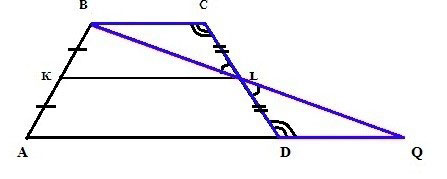
Соответственно, если равны в треугольниках углы и стороны между ними, то и сами фигуры одинаковы.
DLQ = BLC
А уже из этого следует, что ВL и LQ равны. А значит, КL является не только средней линией трапеции, но также и аналогичной линией для треугольника ABQ.
А дальше уже совсем просто, так как есть специальная формула для расчета средней линии треугольника. Она равна одной второй (половине) длины параллельной стороны:
KL = 1/2AQ
Длина стороны AQ у нас равна AD + DQ (или ВС). И таким образом мы и получаем ту самую формулу расчета средней линии трапеции:
KL = ½ AQ = ½ (AD + DQ) = ½ (AD + ВС)
Как принято говорить в таких случаях – что и требовалось доказать.
Свойства средней линии трапеции
У средней линии трапеции есть три главных свойства:
- Она параллельна основаниям трапеции;
- Она равна полусумме оснований (та самая формула, о которой мы только что рассказывали);
- Она разбивает исходную трапецию на две более маленькие по площади. Причем их площади имеют вполне конкретное соотношение друг к другу. А именно:
S1/S2 = (3BC + AD) / (BC + 3AD)
Эту формулу мы не будем доказывать. Просто поверьте, что так и есть на самом деле.
Вторая средняя линия
Внимательный читатель мог бы заметить, что мы рассказывали до этого только про одну среднюю линию. Ту, что лежит параллельно основаниям. Но ведь у этой геометрической фигуры, как и любого четырехугольника, таких отрезков должно быть два.
И действительно, у трапеции имеется вторая такая линия. И она уже делит на две равные части оба основания:
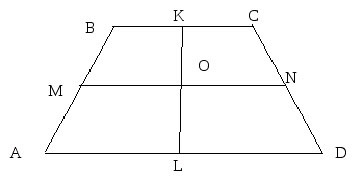
В нашем случае, это отрезок KL.
Интересно, что эту среднюю линию крайне мало изучают во время школьного обучения. И на экзаменах нет задач, с ней связанных. Хотя у нее есть несколько интересных свойств:
- Диагонали трапеции и эта средняя линия пересекаются в одной точке;
- Та прямая, частью которой эта линия является, пересекается в единой точке с теми прямыми, которые совпадают с боковыми сторонами;
- В равнобокой трапеции (у которой боковые стороны идут под одним углом) средняя линия пересекает основания под углом в 90 градусов;
- В точке, в которой пересекаются две средние линии, они делятся пополам…
Вот и все, что мы хотели рассказать о средних линиях в трапеции.
Трапеция — это выпуклый четырехугольник с двумя параллельными основами и двумя непараллельными
боковыми сторонами.
Иногда фигура определяется как четырёхугольник, у которого пара противолежащих сторон параллельна,
поэтому параллелограмм и прямоугольник являются частными случаями трапеции. Также это
четырехугольник, у которого одна пара противоположных сторон параллельна, а остальные стороны не
равны между собой.
Параллельные стороны называются основами, а остальные боковыми.
Вычисление стороны необходимо для нахождения периметра, площади трапеции, ее диагоналей и других
значимых параметров.
- Длина основания через среднию линию и другое известное
основание - Нижнее основание через верхнее основание, высоту и углы при
нижнем основании - Верхнее основание через нижнее основание, высоту и углы при
нижнем основании - Нижнее основание через боковые стороны, верхнее основание и
углы при нижнем основании - Верхнее основание через боковые стороны, нижнее основание и
углы при нижнем основании - Боковую сторону через высоту и угол при нижнем
основании
Длина основания через среднюю линию и известное основание
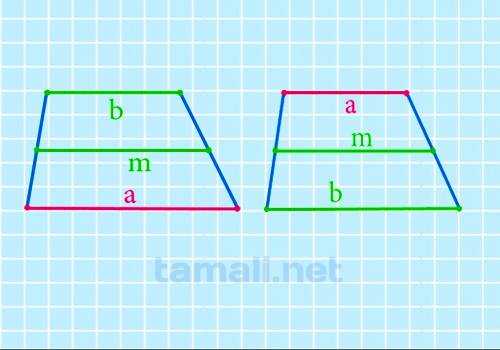
Средняя линия — отрезок, соединяющий середины боковых сторон фигуры. Через её значение
вычисляется одна из основ. Нужно умножить ее на два и вычесть известную:
a = 2m – b
Цифр после
запятой:
Результат в:
Например, средняя линия MN равна 6, а основание а – 9. Соответственно, значения, подставленные в
формулу, показывают, что b = 2*6 – 9 = 3.
Нижнее основание через верхнее основание, высоту и углы при нижнем основании
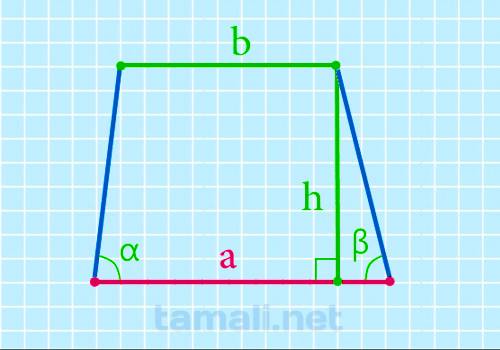
Высота h или BK – перпендикуляр, проведенный от одной основы к другой. Высота проводится в любой их
точке, но удобнее всего это делать из вершины углов при меньшей основе. Чтобы найти нижнее
основание, надо к верхнему прибавить произведение высоты на сумму котангенсов углов при нижнем:
a = b + h*(ctga + ctgb)
Цифр после
запятой:
Результат в:
Дано верхнее основание 10, высота 6 и углы 30 и 45. По формуле а = 10 + 6*(3+1) = 10 + 63 + 6 = 16+63.
Для равнобедренного четырёхугольника выведены две формулы. В первой (a = 2S/h – b) основа выражена с
помощью формулы площади. Пример: Площадь равнобедренной трапеции ABCD = 18, высота = 6, а AD = 5.
Найти BC. BC = 2*18/6 – 5 = 6 – 5 = 1
Второе выражение сформулировано следующим образом: (a = b + 2h*ctga). Высота АН в трапеции ADEF =
10, DE = 4, а DAF = 45 градусам. Найти AF: AF = 4 + 10*2*1 = 24
Верхнее основание через нижнее основание, высоту и углы при нижнем основании
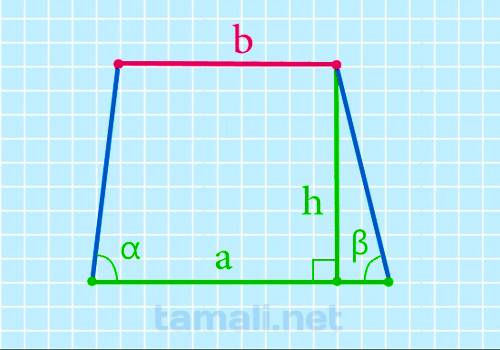
Чтобы найти верхнюю основу, надо из нижней вычесть произведение высоты на сумму котангенсов углов при
ней:
b = a – h*(ctg α + ctg β)
Цифр после
запятой:
Результат в:
Дана трапеция с нижним основанием 15, высотой 8 и углами в 45 градусов. По формуле а = 15 + 8*(1+1) =
15 + 16 = 31
Формулы для равнобедренного четырёхугольника: b = 2S/h – a и b = a – 2h*ctga.
- Площадь трапеции KLMN = 44, KL=MN, высота равна 8, KN = 5. Найти LM: LM = 44*2/8 – 5 = 6
- Высота трапеции DEFG = 15, DG= 5, а EDG = 45 градусам. Найти EF: EF = 5 + 15*2*1 = 35
Нижнее основание через боковые стороны, верхнее основание и углы при нижнем основании
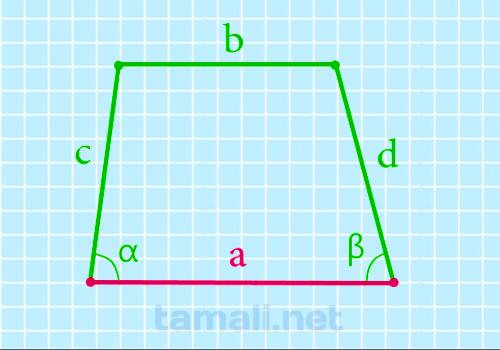
Для нахождения основы а нужно к основе b прибавить произведение одной и другой стороны и косинусов
углов при них
a = b + c * cos α + d * cos β
Цифр после
запятой:
Результат в:
Дана равнобокая трапеция с верхним основанием 6, боковыми сторонами 5 и 11 и углами в 45 градусов.
Найти нижнее основание: а = 6 + 5*2/2 + 11*2/2 = 6 + 162/2 = 6 + 82
Отдельно для подобного типа фигур было выведено два выражения: a = (d1^2 – c^2)/b и a = b +
2c*cosa.
- трапеции ABCD AB = CD = 8, диагональ AC = 12, а BC = 4. Вычислить AD: AD = (12*12 – 8*8)/4
= (144 – 64)/4 = 20 - В трапеции KLMN KL = MN = 4, LM = 7, а LKN равен 30 градусам. Вычислить KN: KN = 7 +
4*2*3/2 = 7 + 43
Верхнее основание через боковые стороны, нижнее основание и углы при нем
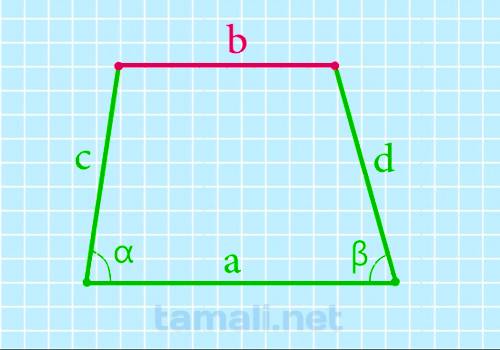
Для нахождения основы b нужно из основы а вычесть произведение одной и другой боковой стороны и углов
при них
b = a – c * cos α – d * cos β
Цифр после
запятой:
Результат в:
Дана трапеция с нижним основанием 27, боковыми сторонами 20 и 14 и углами в 30 и 60 градусов. Найти
верхнее основание: b = 27 — 20*3/2 — 14*1/2 = 27 — 103 — 7 = 20 —
103. Формулы для равнобедренного типа: b = (d1^2 — c^2)/a и b = a — 2c*cosa.
- В трапеции DEFG DE и FG = 11, диагональ АС = 13, а EF = 12. Вычислить DG: DG = (13*13 –
11*11)/12= (169 – 121)/12 = 4 - Боковые стороны трапеции BCDE BC и DE = 25, BE = 10, а CBE равен 60 градусам. Вычислить CD:
CD = 25 – 10*2*1/2 = 15
Боковая сторона через высоту и угол при нижнем основании
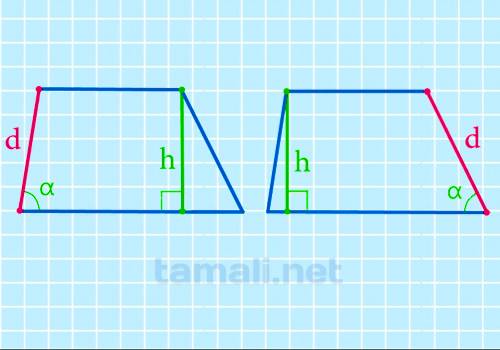
Чтобы найти боковую сторону, надо разделить высоту на синус угла при ней
d = h / sin α
Цифр после
запятой:
Результат в:
Дана трапеция с высотой 12 и углами в 30 и 60 градусов. Найти боковые стороны: c = 12/0,5 =
24, d = 12/3/2 = 243
Для прямоугольного типа формулы несколько отличаются. Самая простая из них связывает высоту и меньшую
боковую сторону: c = h.
Для нее существует еще несколько формул: с = d*sina; c = (a – b)*tga; c
= (d^2 – (a – b)^2)
- В прямоугольной трапеции CDEF сторона EF равна 22, а прилежащий угол = 45. Найти CD. CD =
22*2/2 = 112 - Прямоугольная трапеция MNOP имеет основания MP и NO, равные 32 и 19 соответственно. NMP равен 60
градусам. Найти MP: MP = (32 – 19)*3 = 133 - В прямоугольной трапеции ABCD AD и BC равны 35 и 15 соответственно. Диагональ АС = 26. Найти AB.
AB = (26^2 – (35 – 15)^2) = 676 – 400 = 276 = 269
Первая вытекает из прямоугольного треугольника и свидетельствует о том, что отношение катета к
гипотенузе равно синусу противолежащего угла. В этом треугольнике второй катет равен разности двух
оснований. Отсюда возникает утверждение, приравнивающее тангенс угла к отношению катетов. Третья
формула выведена на основании теоремы Пифагора.
Для второй боковой стороны выведено и записано три выражения: d = (a — b)/cosa; d = c/sina; d =
(c^2 — (a — b)^2). Первое и второе получаются из соотношения сторон в прямоугольном
треугольнике, а третье выводится из теоремы Пифагора.
- В прямоугольной трапеции KLMN KN = 28, LM = 13 а прилежащий угол = 30. Найти KL: KL = (28 –
13)/3/2 = 103 - В прямоугольной трапеции EFGH EF равна 45. FEH равен 30 градусам. Найти GH: GH = 45/0,5 =
90 - В прямоугольной трапеции NOPQ NQ и OP =.36 и 17. Диагональ равна 29. Найти NO: NO = (29^2 –
(36 – 17)^2) = 841 – 361= 480 = 430
Для равнобокой трапеции существуют формулы c = d1^2 – ab; c = (a – b)/2cosa; c = S/m*sina; c =
2S/(a+b)*sina.
- В трапеции LMNO LM = NO. LO = 16, MN = 6, диагональ равна 10. Найти LM: LM = 10^2 – 16*6 =
100 – 96 = 4 - Трапеция ABCD – равнобокая, AB = CD. AD = 18, BC = 4, а прилежащий угол равен 45 градусам. Найти
AB: AB = (18 – 4)/2/2 = 14/2/2 = 14/2 - В трапеции BCDE BC=DE. Площадь фигуры равна 48, BE = 17, CD = 7, а CBE равен 30 градусам.
Вычислить BC: m = (17 – 7)/2 = 5, BC = 48/5*1/2 = 96/5 = 19,2 - Площадь равнобедренной трапеции KLMN = 90, основания KN и LM = 32 и 18 соответственно, а LKN =
60 градусов. Вычислить KL: KL = 2*90/(32 + 18)*3/2 = 360/503 = 129600/7500 = 17,28
Виды трапеций
Существуют следующие виды трапеций:
- Равнобедренная трапеция — фигура, у которой боковые стороны и углы при основании равны.
Диагонали также равны. Треугольники, образованные диагоналями и основой, являются
равнобедренными. Если диагонали взаимно перпендикулярны, то площадь равна квадрату высоты. Если
разделить обе основы пополам и повести через эти точки линию, то она будет осью геометрической
фигуры. Отрезки, последовательно соединяющие середины смежных сторон, образуют ромб. - Прямоугольная трапеция — фигура, у которой одна из боковых сторон перпендикулярна основам
и равна высоте. Два угла будут равны 90 градусам, и они всегда принадлежат смежным вершинам, а
другие всегда острый и тупой, их сумма всегда будет равна 180 градусам. Каждая диагональ
образует с ее меньшей боковой стороной прямоугольный треугольник. А высота, которая проведена из
вершины с тупым углом, делит фигуру на две. Одна из них прямоугольник, другая прямоугольный
треугольник. - Разносторонняя трапеция — фигура, боковые стороны которой не равны и углы при основании не
являются прямыми. Ее диагонали делят фигуру на четыре треугольника, два из которых подобны, а
остальные — равновелики, то есть имеют одинаковые площади. Сумма углов при боковой стороне 180
градусов.
Свойства трапеции
- Средняя линия параллельна основаниям и равна их полусумме.
- Любая биссектриса, выведенная из угла четырёхугольника, отсекает на основании (продолжении)
отрезок с длиной боковой стороны. - Треугольники AOD и COD, образованные отрезками диагоналей и основами, подобны.
Коэффициент
подобия – k = AD/BC.
Отношение площадей треугольников — k^2. - Треугольники ABO и DCO, образованные отрезками диагоналей и боковыми сторонами, имеют одинаковую
площадь. - В трапецию можно вписать окружность, если сумма оснований равняется сумме её боковых сторон.
- Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений
боковых сторон лежат на одной прямой. - Отрезок, соединяющий середины диагоналей, равняется половине разности основ и лежит на средней
линии.




