Пришла пора рассмотреть первые алгоритмы на графах. К классические алгоритмам относятся обходы графов. Под обходом графа обычно понимают процесс систематического просмотра всех вершин или рёбер графа, чтобы найти некоторые вершины, удовлетворяющие определённым условиям. Мы рассмотрим обход в ширину и обход в глубину.
Обход в глубину заключается в систематическом просмотре вершин графа и прохождении его ветвями. Иными словами, идея поиска в глубину — когда возможные пути по рёбрам, выходящим из вершин, разветвляются, нужно сначала полностью исследовать одну ветку и только потом переходить к другим веткам (если они останутся нерассмотренными).
Опишем алгоритм поиска в глубину:
- Шаг 1. Все вершины графа отмечаем, как не посещенные. Выбирается первая вершина и помечается как посещённая.
- Шаг 2. Для последней помеченной как посещённой вершины выбирается смежная вершина, которая первая помеченная как не посещенная, и ей присваивается значение посещённой. Если таких вершин нет, то берётся предыдущая помеченная вершина.
- Шаг 3. Повторяем шаг 2 до тех пор, пока все вершины не будут помечены как посещённые.
Пример реализации приведён ниже.
DFS(graph, v, used):
used[v] = 1
for (var u : graph[v])
if (!used[v])
DFS(graph, u, used)
✒️ Упражнение:
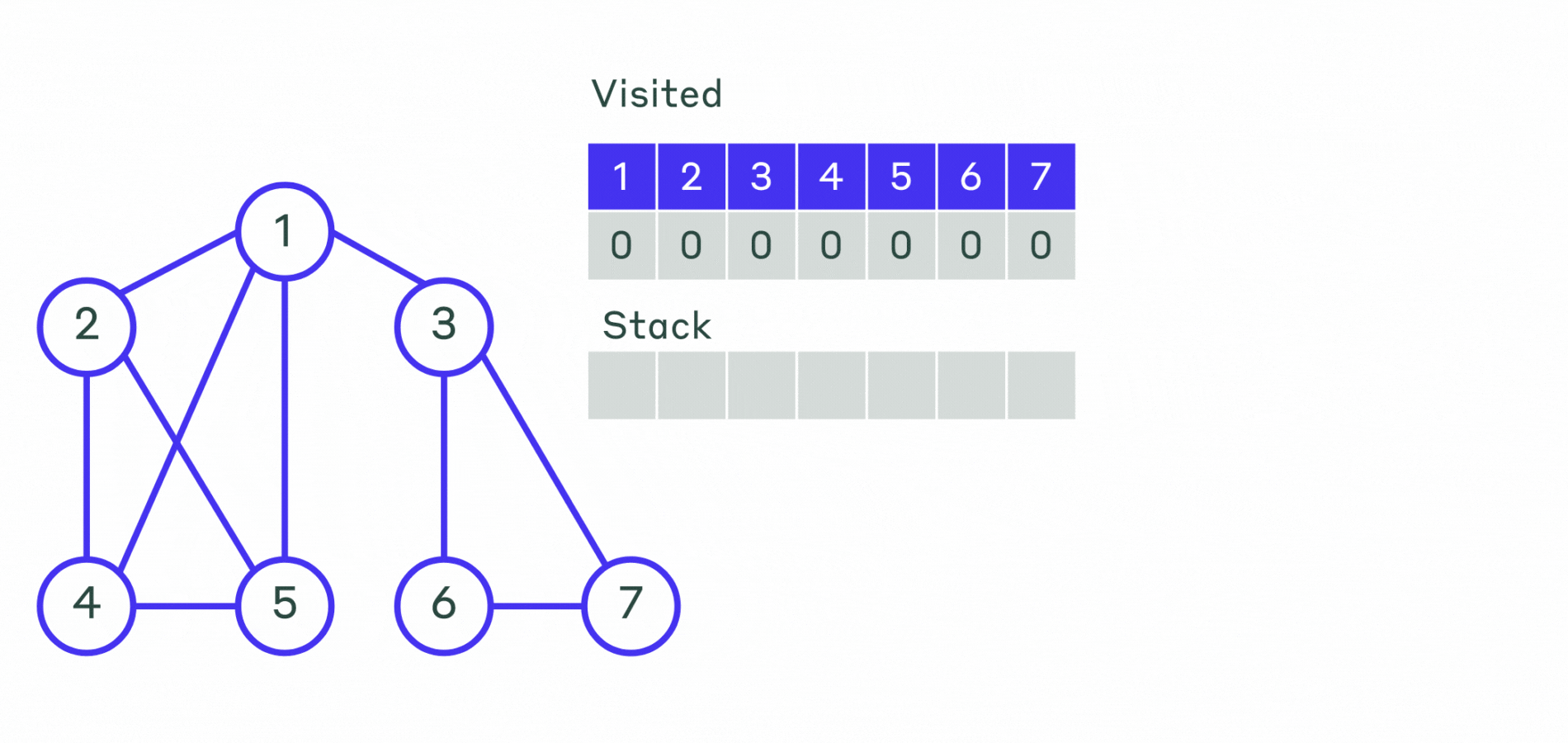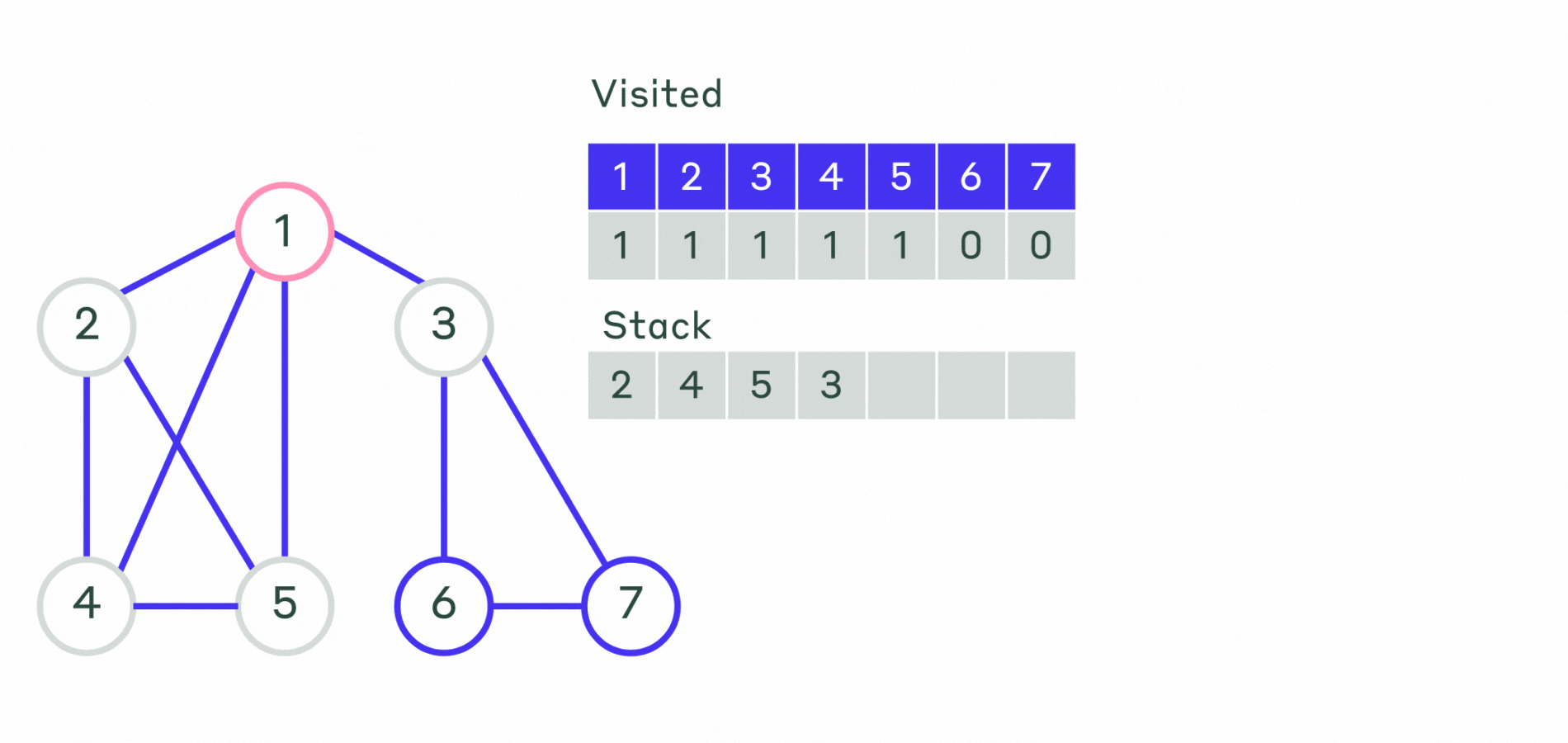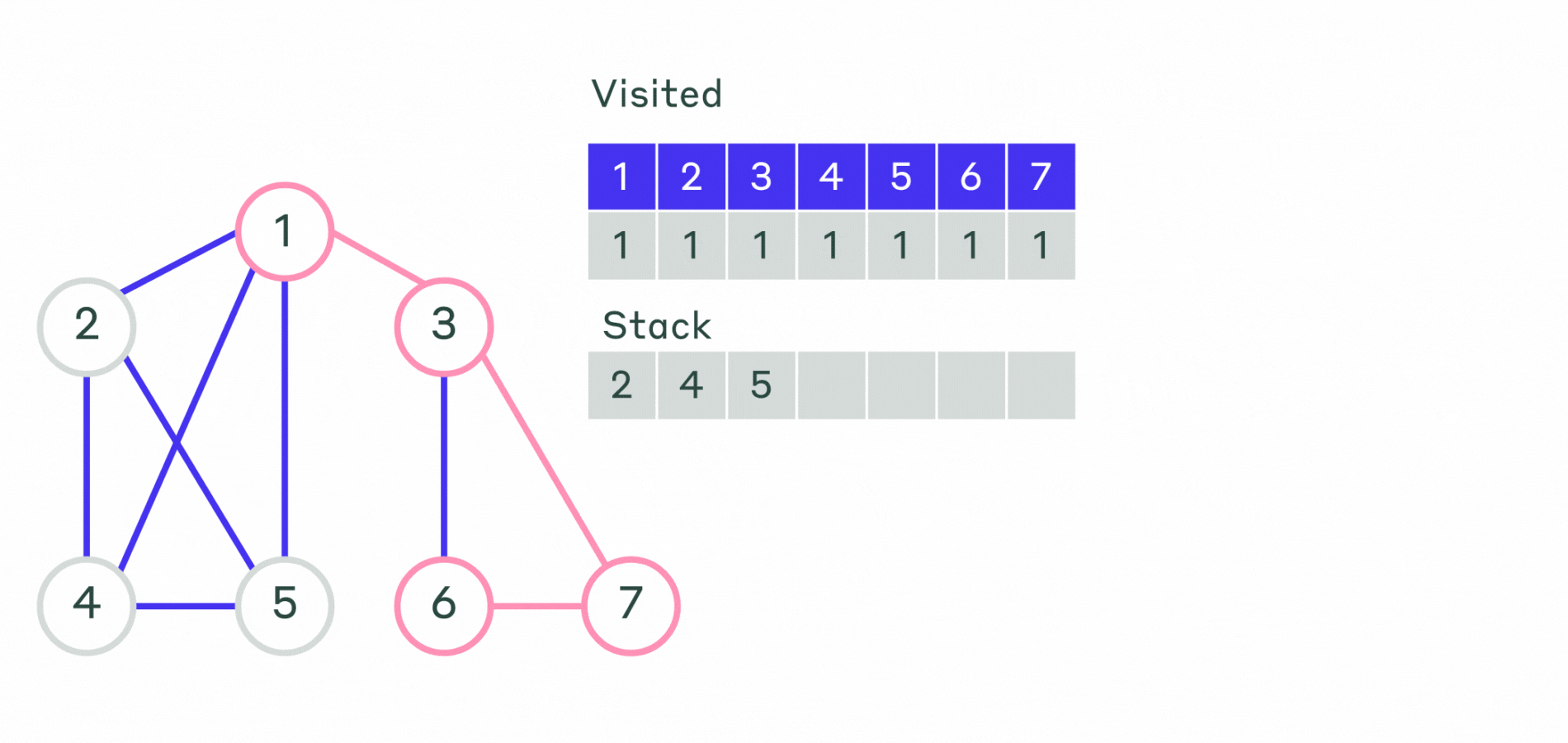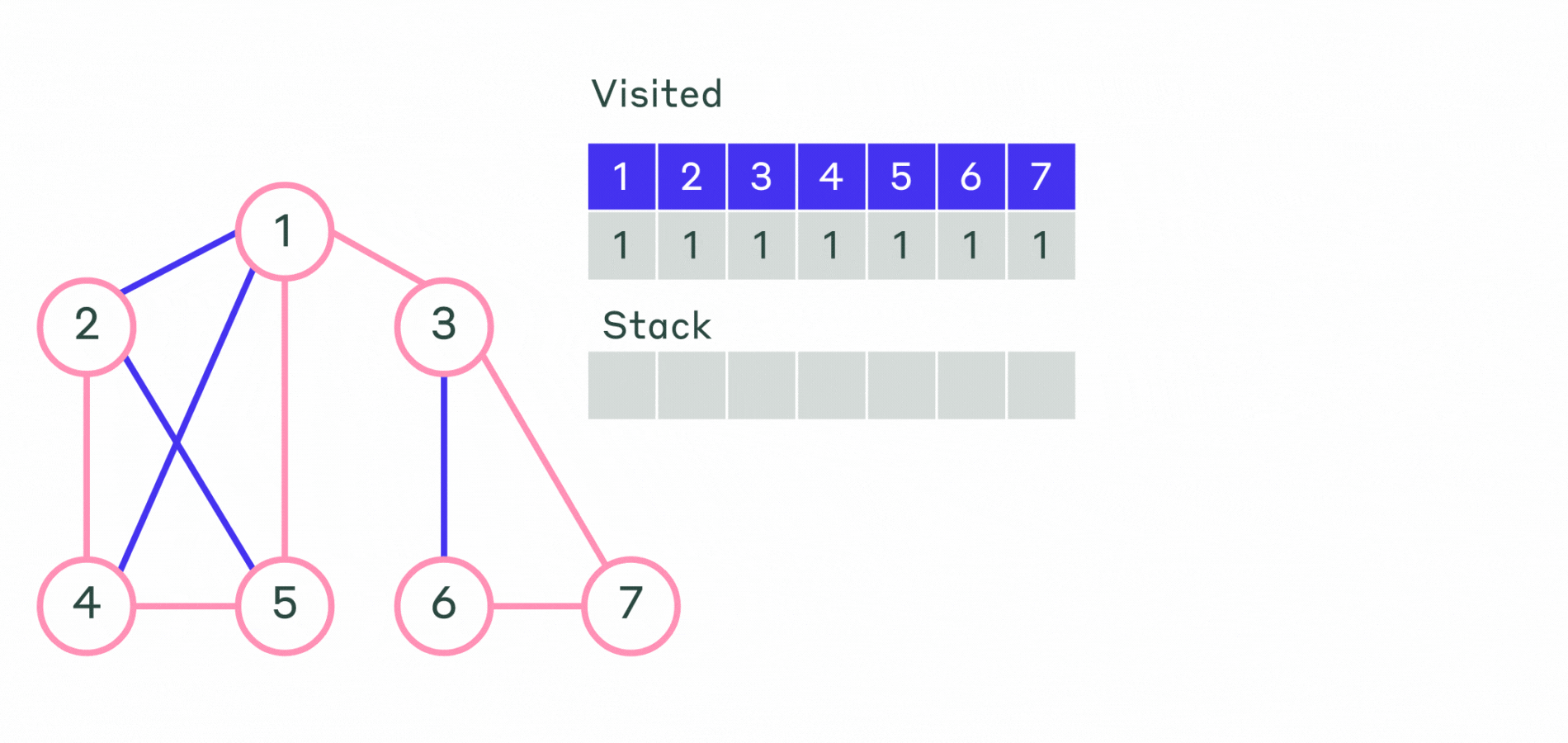
Попробуйте выполнить алгоритм поиска в глубину пошагово для графа.
Обратите внимание, сейчас мы посмотрели на рекурсивную реализацию. Конечно, преимущество использования рекурсивного подхода заключается в простоте его написания, однако, рекурсивный подход имеет свои ограничения.
Можно переписать алгоритм поиска в глубину с использованием особых структур данных. Например, стека.
Опишем алгоритм поиска в глубину в нерекурсивной форме:
- Шаг 1. Все вершины графа отмечаем, как не посещённые. Выбирается первая вершина и помечается как посещённая. Эту вершину кладем в контейнер — стек.
- Шаг 2. Пока стек не пустой:
- Извлекаем последнюю добавленную вершину.
- Просматриваем все смежные с ней не посещённые вершины и помещаем их в стек. Порядок выхода вершин из стека и будет порядком обхода вершин графа.
Пример работы не рекурсивного алгоритма можно посмотреть на анимации.
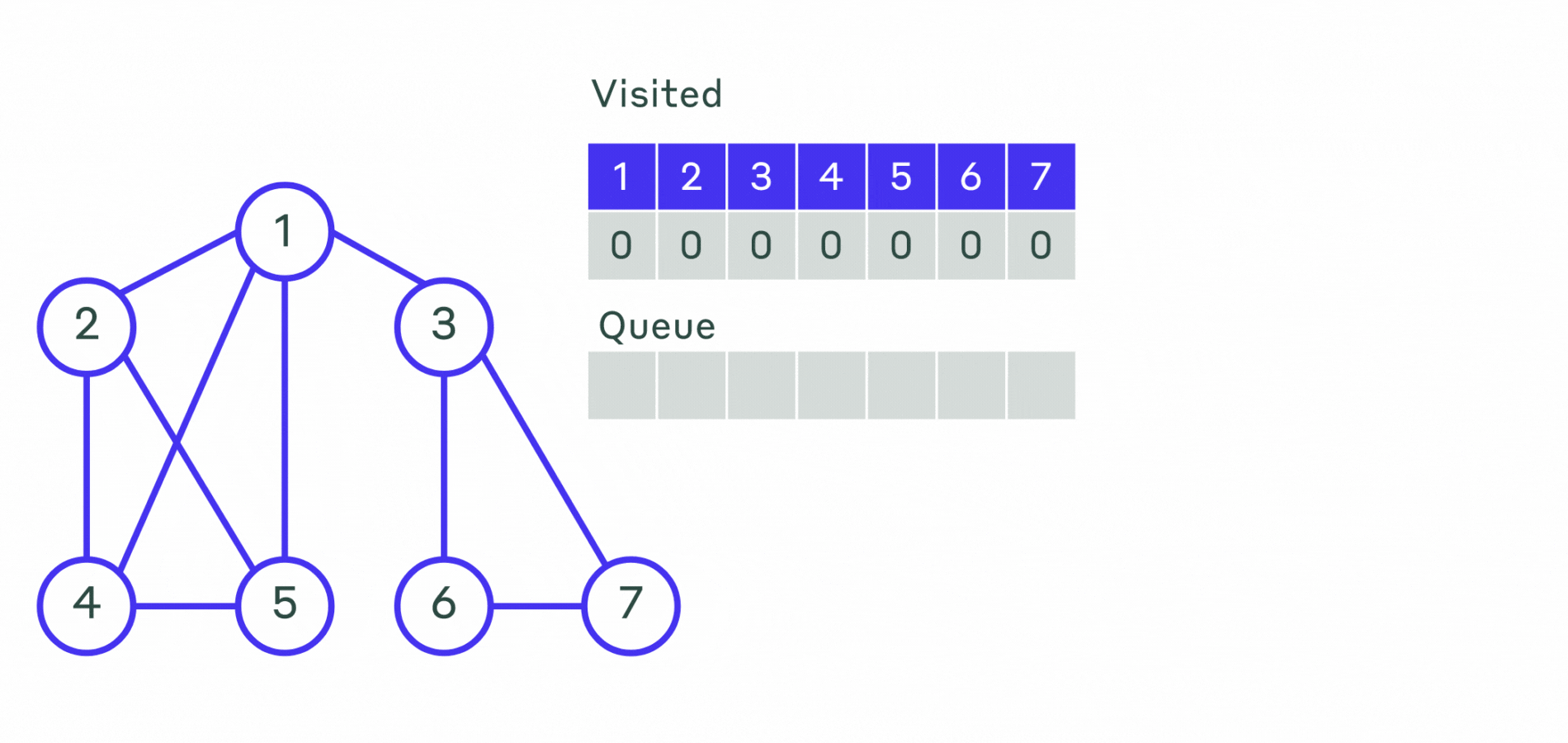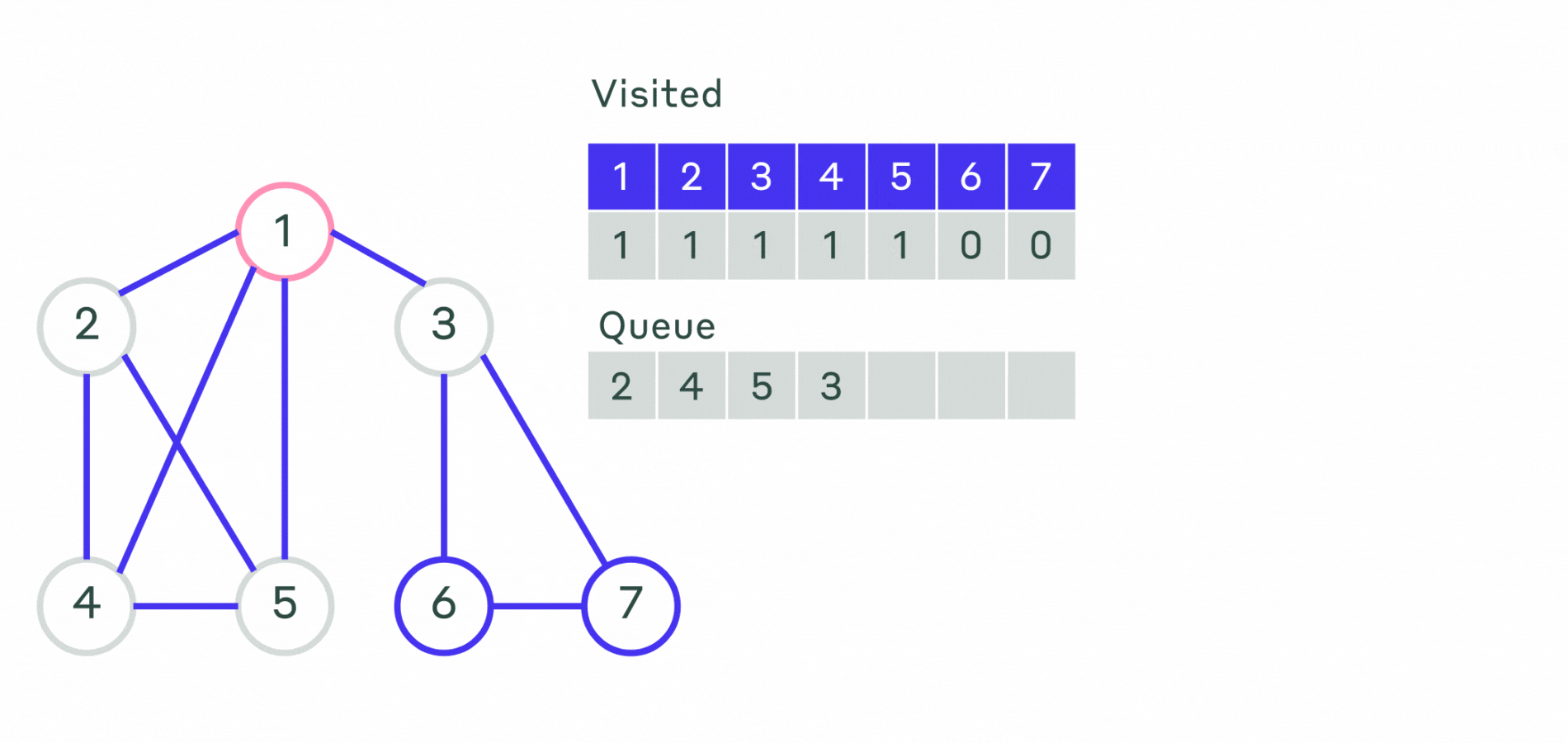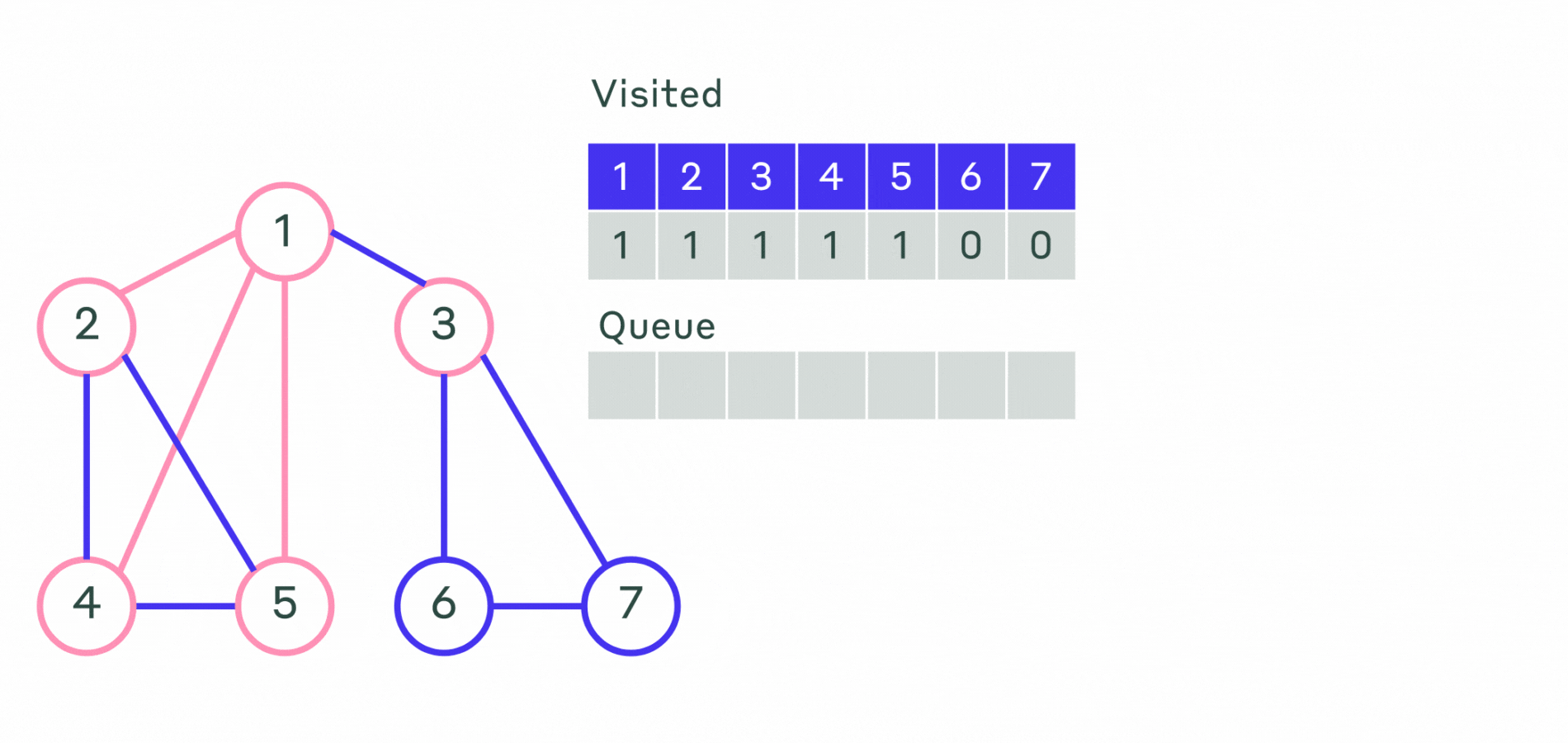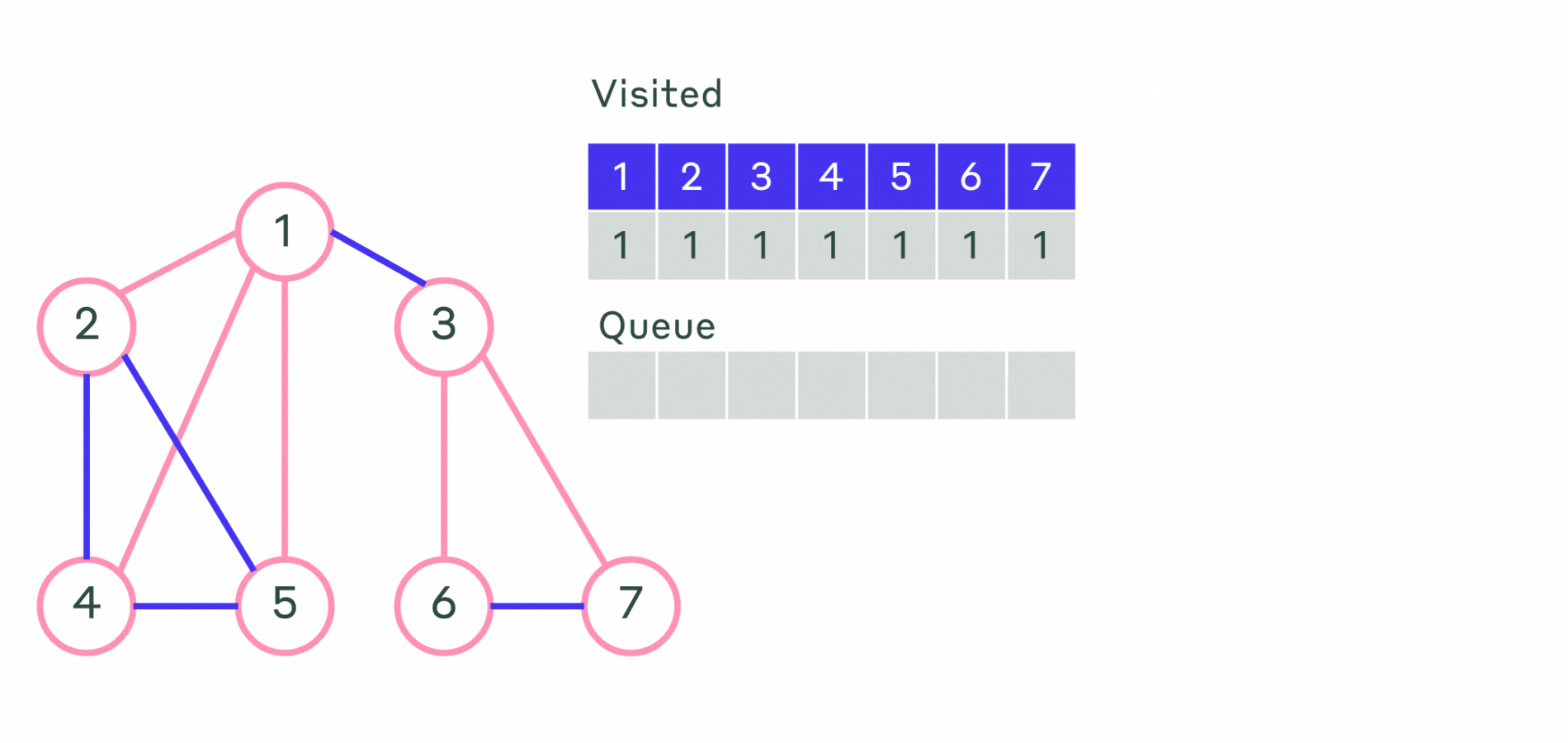
Пример реализации приведён ниже.
DFS(graph, v, used):
stack q
q.push(v)
used[v] = 1
while(!q.empty())
v = q.front()
q.pop()
for (var to : graph[v]):
if (!used[to]):
used[to] = true
q.push(to)
Ещё один способ обхода графа — обход в ширину. Основное его отличие в том, что сначала исследуются смежные вершины, а уже потом вершины на следующем уровне. Иначе говоря, сначала исследуются все вершины, смежные с начальной вершиной (вершина с которой начинается обход). Эти вершины находятся на расстоянии 1 от начальной. Затем исследуются все вершины на расстоянии 2 от начальной, затем все на расстоянии 3 и так далее. Обратим внимание, что при этом для каждой вершины сразу находятся длина кратчайшего маршрута от начальной вершины.
Опишем алгоритм поиска в ширину:
- Шаг 1. Всем вершинам графа присваивается значение не посещённой. Выбирается первая вершина и помечается как посещённая и заносится в очередь.
- Шаг 2. Посещается первая вершина из очереди (если она не помечена как посещённая). Все её соседние вершины заносятся в очередь. После этого она удаляется из очереди.
- Шаг 3. Повторяется шаг 2 до тех пор, пока очередь не станет пустой.
Пример реализации приведён ниже.
BFS(graph, v, used):
queue q
q.push(v)
used[v] = 1
while(!q.empty())
v = q.front()
q.pop()
for (var to : graph[v]):
if (!used[to]):
used[to] = true
q.push(to)
✒️ Упражнение:
Подумайте, какое отличие алгоритма поиска в ширину от алгоритма поиска в глубину?
Асимптотическая сложность алгоритма поиска в глубину и ширину — $O(V+E)$, где $V$ — число вершин, а $E$ — число рёбер и дуг. Обходы графов могут применяться для решения задач, связанных с теорией графов:
- Волновой алгоритм поиска пути в лабиринте.
- Волновая трассировка печатных плат.
- Поиск компонент связности в графе.
- Поиск кратчайшего пути между двумя узлами невзвешенного графа.
- Поиск в пространстве состояний: нахождение решения задачи с наименьшим числом ходов, если каждое состояние системы можно представить вершиной графа, а переходы из одного состояния в другое — рёбрами графа.
- Нахождение кратчайшего цикла в ориентированном невзвешенном графе.
- Нахождение всех вершин и рёбер, лежащих на каком-либо кратчайшем пути между двумя вершинами.
- Поиск увеличивающего пути в алгоритме Форда-Фалкерсона (алгоритм Эдмондса-Карпа).
Вес (длина) ребра – это число или несколько чисел, которые интерпретируются по отношению к ребру как длина, пропускная способность.
Вес вершины – это число (действительное, целое или рациональное), поставленное в соответствие данной вершине.
Взвешенный граф – это граф, каждому ребру которого поставлен в соответствие его вес.
Вершины (узлы) графа – это множество точек, составляющих граф.
Замкнутый маршрут – это маршрут в графе, у которого начальная и конечная вершины совпадают.
Кратные ребра – это ребра, соединяющие одну и ту же пару вершин.
Маршрут в графе – это конечная чередующаяся последовательность смежных вершин и ребер, соединяющих эти вершины.
Матрица инцидентности – это двумерный массив, в котором указываются связи между инцидентными элементами графа (ребро и вершина).
Матрица смежности – это двумерный массив, значения элементов которого характеризуются смежностью вершин графа
Мультиграф – это граф, у которого любые две вершины соединены более чем одним ребром.
Неориентированный граф (неорграф) – это граф, у которого все ребра не ориентированы, то есть ребрам которого не задано направление.
Обход графа (поиск на графе) – это процесс систематического просмотра всех ребер или вершин графа с целью отыскания ребер или вершин, удовлетворяющих некоторому условию.
Ориентированный граф (орграф) – это граф, у которого все ребра ориентированы, то есть ребрам которого присвоено направление.
Открытый маршрут – это маршрут в графе, у которого начальная и конечная вершины различны.
Петля – это ребро, соединяющее вершину саму с собой.
Поиск в глубину – это обход графа по возможным путям, когда нужно сначала полностью исследовать одну ветку и только потом переходить к другим веткам (если они останутся нерассмотренными).
Поиск в ширину – это обход графа по возможным путям, когда после посещения вершины, посещаются все соседние с ней вершины.
Простой граф – это граф, в котором нет ни петель, ни кратных ребер.
Путь – это открытая цепь, у которой все вершины различны.
Ребра (дуги) графа – это множество линий, соединяющих вершины графа.
Связный граф – это граф, у которого для любой пары вершин существует соединяющий их путь.
Смежные вершины – это вершины, соединенные общим ребром.
Смешанный граф – это граф, содержащий как ориентированные, так и неориентированные ребра.
Список ребер – это множество, образованное парами смежных вершин
Тупик – это вершина графа, для которой все смежные с ней вершины уже посещены
Цепь – это маршрут в графе, у которого все ребра различны.
Цикл – это замкнутая цепь, у которой различны все ее вершины, за исключением концевых.
I need to find a fast way to solve the following graph problem.
I have a graph with two types of vertices in it (illustrated by circles and squares in the picture).
I wish to find all edges between two squares, which have the following property:
Both of the two square vertices making up this edge needs to share a connection to at least two circle vertices. Meaning that the two squares needs to have two circular neighbors in common.
I have added two illustrations to showcase what my graphs might look like. The first illustration is a graph where there are no connections fulfilling the criteria I’m looking for, while in the second illustration the connection between the two right-most squares fulfill the criteria.


Does anyone have a good idea about how I might solve such a problem? I am currently using python igraph, but any help would be appreciated, or even just a pointer in the direction of graph theory concepts you think might be useful for me in order to solve this problem.
(While I have a background in mathematics, I never did take graph theory, which I regret now)
Edit:
The problem I’m trying to solve is to calculate the potential moves for a piece in a boardgame called hive.
The pieces live on a hexagonal grid, and this particular piece can move adjacent to any other piece, provided it can fit through. A boardgame state is shown in the picture below and the particular piece I’m trying to calculate the movement for is selected. The green hexagons highlight potential movement places, note how the 3 hexagons at the top hole are not highlighted, this is because the piece cannot fit through the hole going into that place. Finding those choke points where the piece cannot enter is exactly the problem I’m trying to solve.
I already have a recursive function that goes through each position and checks all neighbors for potentially valid moves (this method uses an axial grid). This method works, but it is slow, so I’m hoping for a faster option using graph theory. (My current recursive option is responsible for roughly 40% of the total computational time in a recent profiling of my code).
I want to train a neural network to play this game, requiring thousands of iterations hence I need to make this as fast as possible.

Время на прочтение
5 мин
Количество просмотров 156K
Доброго времени суток.
Представляю вашему вниманию перевод статьи «Algorithms on Graphs: Let’s talk Depth-First Search (DFS) and Breadth-First Search (BFS)» автора Try Khov.
Что такое обход графа?
Простыми словами, обход графа — это переход от одной его вершины к другой в поисках свойств связей этих вершин. Связи (линии, соединяющие вершины) называются направлениями, путями, гранями или ребрами графа. Вершины графа также именуются узлами.
Двумя основными алгоритмами обхода графа являются поиск в глубину (Depth-First Search, DFS) и поиск в ширину (Breadth-First Search, BFS).
Несмотря на то, что оба алгоритма используются для обхода графа, они имеют некоторые отличия. Начнем с DFS.
Поиск в глубину
DFS следует концепции «погружайся глубже, головой вперед» («go deep, head first»). Идея заключается в том, что мы двигаемся от начальной вершины (точки, места) в определенном направлении (по определенному пути) до тех пор, пока не достигнем конца пути или пункта назначения (искомой вершины). Если мы достигли конца пути, но он не является пунктом назначения, то мы возвращаемся назад (к точке разветвления или расхождения путей) и идем по другому маршруту.
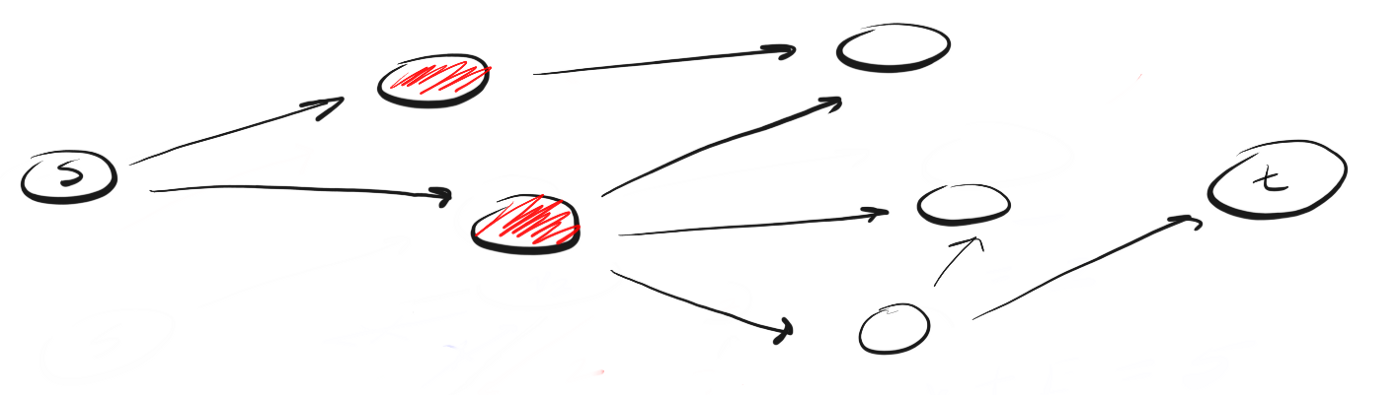
Давайте рассмотрим пример. Предположим, что у нас есть ориентированный граф, который выглядит так:

Мы находимся в точке «s» и нам нужно найти вершину «t». Применяя DFS, мы исследуем один из возможных путей, двигаемся по нему до конца и, если не обнаружили t, возвращаемся и исследуем другой путь. Вот как выглядит процесс:

Здесь мы двигаемся по пути (p1) к ближайшей вершине и видим, что это не конец пути. Поэтому мы переходим к следующей вершине.

Мы достигли конца p1, но не нашли t, поэтому возвращаемся в s и двигаемся по второму пути.

Достигнув ближайшей к точке «s» вершины пути «p2» мы видим три возможных направления для дальнейшего движения. Поскольку вершину, венчающую первое направление, мы уже посещали, то двигаемся по второму.

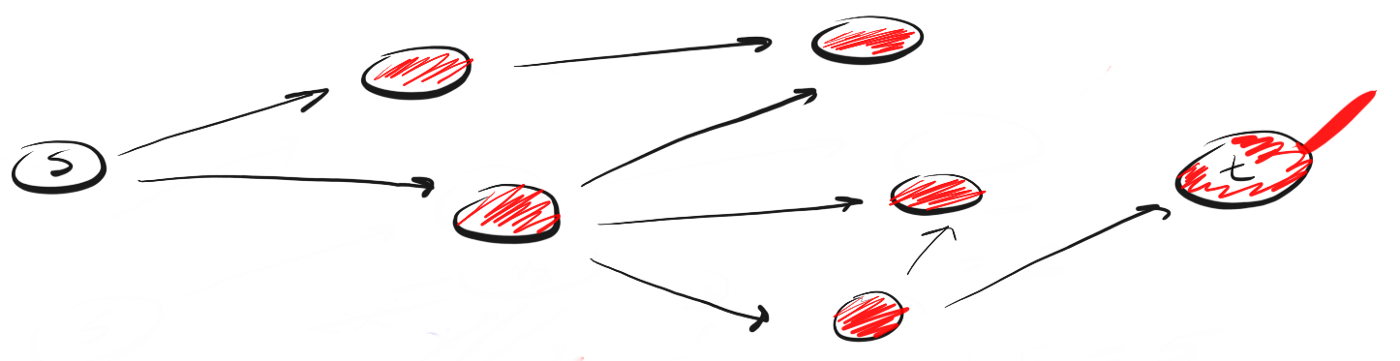
Мы вновь достигли конца пути, но не нашли t, поэтому возвращаемся назад. Следуем по третьему пути и, наконец, достигаем искомой вершины «t».

Так работает DFS. Двигаемся по определенному пути до конца. Если конец пути — это искомая вершина, мы закончили. Если нет, возвращаемся назад и двигаемся по другому пути до тех пор, пока не исследуем все варианты.
Мы следуем этому алгоритму применительно к каждой посещенной вершине.
Необходимость многократного повторения процедуры указывает на необходимость использования рекурсии для реализации алгоритма.
Вот JavaScript-код:
// при условии, что мы имеем дело со смежным списком
// например, таким: adj = {A: [B,C], B:[D,F], ... }
function dfs(adj, v, t) {
// adj - смежный список
// v - посещенный узел (вершина)
// t - пункт назначения
// это общие случаи
// либо достигли пункта назначения, либо уже посещали узел
if(v === t) return true
if(v.visited) return false
// помечаем узел как посещенный
v.visited = true
// исследуем всех соседей (ближайшие соседние вершины) v
for(let neighbor of adj[v]) {
// если сосед не посещался
if(!neighbor.visited) {
// двигаемся по пути и проверяем, не достигли ли мы пункта назначения
let reached = dfs(adj, neighbor, t)
// возвращаем true, если достигли
if(reached) return true
}
}
// если от v до t добраться невозможно
return false
}
Заметка: этот специальный DFS-алгоритм позволяет проверить, возможно ли добраться из одного места в другое. DFS может использоваться в разных целях. От этих целей зависит то, как будет выглядеть сам алгоритм. Тем не менее, общая концепция выглядит именно так.
Анализ DFS
Давайте проанализируем этот алгоритм. Поскольку мы обходим каждого «соседа» каждого узла, игнорируя тех, которых посещали ранее, мы имеем время выполнения, равное O(V + E).
Краткое объяснение того, что означает V+E:
V — общее количество вершин. E — общее количество граней (ребер).
Может показаться, что правильнее использовать V*E, однако давайте подумаем, что означает V*E.
V*E означает, что применительно к каждой вершине, мы должны исследовать все грани графа безотносительно принадлежности этих граней конкретной вершине.
С другой стороны, V+E означает, что для каждой вершины мы оцениваем лишь примыкающие к ней грани. Возвращаясь к примеру, каждая вершина имеет определенное количество граней и, в худшем случае, мы обойдем все вершины (O(V)) и исследуем все грани (O(E)). Мы имеем V вершин и E граней, поэтому получаем V+E.
Далее, поскольку мы используем рекурсию для обхода каждой вершины, это означает, что используется стек (бесконечная рекурсия приводит к ошибке переполнения стека). Поэтому пространственная сложность составляет O(V).
Теперь рассмотрим BFS.
Поиск в ширину
BFS следует концепции «расширяйся, поднимаясь на высоту птичьего полета» («go wide, bird’s eye-view»). Вместо того, чтобы двигаться по определенному пути до конца, BFS предполагает движение вперед по одному соседу за раз. Это означает следующее:

Вместо следования по пути, BFS подразумевает посещение ближайших к s соседей за одно действие (шаг), затем посещение соседей соседей и так до тех пор, пока не будет обнаружено t.

Чем DFS отличается от BFS? Мне нравится думать, что DFS идет напролом, а BFS не торопится, а изучает все в пределах одного шага.
Далее возникает вопрос: как узнать, каких соседей следует посетить первыми?
Для этого мы можем воспользоваться концепцией «первым вошел, первым вышел» (first-in-first-out, FIFO) из очереди (queue). Мы помещаем в очередь сначала ближайшую к нам вершину, затем ее непосещенных соседей, и продолжаем этот процесс, пока очередь не опустеет или пока мы не найдем искомую вершину.
Вот код:
// при условии, что мы имеем дело со смежным списком
// например, таким: adj = {A:[B,C,D], B:[E,F], ... }
function bfs(adj, s, t) {
// adj - смежный список
// s - начальная вершина
// t - пункт назначения
// инициализируем очередь
let queue = []
// добавляем s в очередь
queue.push(s)
// помечаем s как посещенную вершину во избежание повторного добавления в очередь
s.visited = true
while(queue.length > 0) {
// удаляем первый (верхний) элемент из очереди
let v = queue.shift()
// abj[v] - соседи v
for(let neighbor of adj[v]) {
// если сосед не посещался
if(!neighbor.visited) {
// добавляем его в очередь
queue.push(neighbor)
// помечаем вершину как посещенную
neighbor.visited = true
// если сосед является пунктом назначения, мы победили
if(neighbor === t) return true
}
}
}
// если t не обнаружено, значит пункта назначения достичь невозможно
return false
}
Анализ BFS
Может показаться, что BFS работает медленнее. Однако если внимательно присмотреться к визуализациям, можно увидеть, что они имеют одинаковое время выполнения.
Очередь предполагает обработку каждой вершины перед достижением пункта назначения. Это означает, что, в худшем случае, BFS исследует все вершины и грани.
Несмотря на то, что BFS может казаться медленнее, на самом деле он быстрее, поскольку при работе с большими графами обнаруживается, что DFS тратит много времени на следование по путям, которые в конечном счете оказываются ложными. BFS часто используется для нахождения кратчайшего пути между двумя вершинами.
Таким образом, время выполнения BFS также составляет O(V + E), а поскольку мы используем очередь, вмещающую все вершины, его пространственная сложность составляет O(V).
Аналогии из реальной жизни
Если приводить аналогии из реальной жизни, то вот как я представляю себе работу DFS и BFS.
Когда я думаю о DFS, то представляю себе мышь в лабиринте в поисках еды. Для того, чтобы попасть к цели мышь вынуждена много раз упираться в тупик, возвращаться и двигаться по другому пути, и так до тех пор, пока она не найдет выход из лабиринта или еду.

Упрощенная версия выглядит так:

В свою очередь, когда я думаю о BFS, то представляю себе круги на воде. Падение камня в воду приводит к распространению возмущения (кругов) во всех направлениях от центра.

Упрощенная версия выглядит так:

Выводы
- Поиск в глубину и поиск в ширину используются для обхода графа.
- DFS двигается по граням туда и обратно, а BFS распространяется по соседям в поисках цели.
- DFS использует стек, а BFS — очередь.
- Время выполнения обоих составляет O(V + E), а пространственная сложность — O(V).
- Данные алгоритмы имеют разную философию, но одинаково важны для работы с графами.
Прим. пер.: я не специалист по алгоритмам и структурам данных, поэтому при обнаружении ошибок, неточностей или некорректности формулировок, прошу написать в личку для исправления и уточнения. Буду признателен.
Благодарю за внимание.
Зачем вообще изучать графовые алгоритмы?
Графовые алгоритмы представляют собой последовательность шагов для обхода графа через вершины (узлы). Некоторые алгоритмы используются для поиска определенного узла или пути между двумя заданными узлами.
Данные алгоритмы применяют на сайтах социальных сетей, в моделировании конечного автомата, а также во многих других сферах. Я приложил свой исходный код для всех алгоритмов, про которые мы будем говорить ниже.
1. Поиск в ширину (Breadth First Searching)
Поиск в ширину — это рекурсивный алгоритм поиска всех вершин графа или дерева. Обход начинается с корневого узла и затем алгоритм исследует все соседние узлы. Затем выбирается ближайший узел и исследуются все неисследованные узлы. При использовании BFS для обхода любой узел графа можно считать корневым узлом.
Простой алгоритм для BFS, который нужно запомнить:
- Перейдите на соседнюю нерассмотренную вершину. Отметьте как рассмотренную. Отобразите это. Вставьте ее в очередь.
- Если смежная вершина не найдена, удалите первую вершину из очереди.
- Повторяйте шаг 1 и шаг 2, пока очередь не станет пустой.
Схематическое представление обхода BFS:
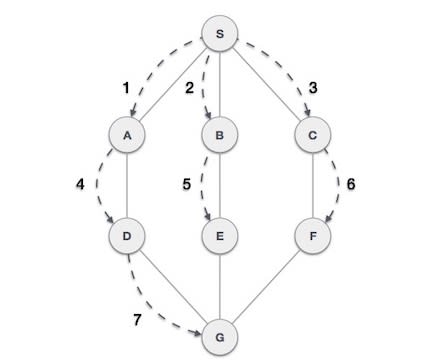
Ссылка на код: Поиск в ширину
2. Поиск в глубину (Depth First Searching)
Поиск в глубину или обход в глубину — это рекурсивный алгоритм поиска всех вершин графа или древовидной структуры данных.
Алгоритм поиска в глубину (DFS) осуществляет поиск вглубь графа, а также использует стек, чтобы не забыть «получить» следующую вершину для начала поиска, когда на любой итерации возникает тупик.
Простой алгоритм, который нужно запомнить, для DFS:
- Посетите соседнюю непосещенную вершину. Отметьте как посещенную. Отобразите это. Добавьте в стек.
- Если смежная вершина не найдена, то вершина берется из стека. Стек выведет все вершины, у которых нет смежных вершин.
- Повторяйте шаги 1 и 2, пока стек не станет пустым.
Схематическое представление обхода DFS:
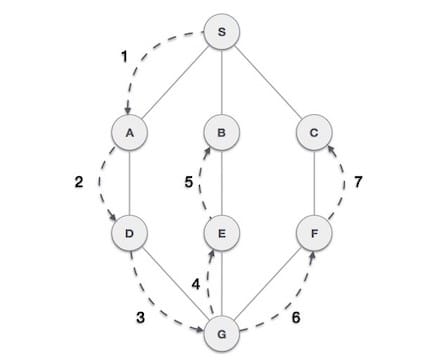
Ссылка на код: Поиск в глубину
Если хочешь подтянуть свои знания по алгоритмам, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:
- углубишься в теорию структур данных;
- научишься решать сложные алгоритмические задачи;
- научишься применять алгоритмы и структуры данных при разработке программ.
3. Топологическая сортировка (Topological Sorting)
Топологическая сортировка для ориентированного ациклического графа (DAG) — это линейное упорядочивание вершин, при котором вершина u предшествует v для каждого направленного ребра uv (в порядке очереди). Топологическая сортировка для графа невозможна, если граф не является DAG.
Для одного графа может применяться более одной топологической сортировки.
Простой алгоритм, который следует запомнить, для топологической сортировки:
1. Отметьте u как посещенную
2. Для всех вершин v, смежных с u, выполните:
2.1. Если v не посещенная, то:
2.2. Выполняем TopoSort (не забывая про стек)
2.3. Цикл выполнен
3. Запишите u в стек
Схематическое представление топологической сортировки:
Пример топологической сортировки для этого графа:
5 → 4 → 2 → 3 → 1 → 0
Ссылка на код: Топологическая сортировка
4. Обнаружение цикла с помощью алгоритма Кана (Kahn’s Algorithm)
Алгоритм топологической сортировки Кана — это алгоритм обнаружения циклов на базе эффективной топологической сортировки.
Работа алгоритма осуществляется путем нахождения вершины без входящих в нее ребер и удаления всех исходящих ребер из этой вершины.
Ссылка на код: Обнаружение цикла с использованием алгоритма Кана
5. Алгоритм Дейкстры (Dijkstra’s Algorithm)
Алгоритм Дейкстры позволяет найти кратчайший путь между любыми двумя вершинами графа. Он отличается от минимального остовного дерева тем, что кратчайшее расстояние между двумя вершинами может не включать все вершины графа.
Ниже проиллюстрирован алгоритм кратчайшего пути с одним источником. Здесь наличие одного источника означает, что мы должны найти кратчайший путь от источника ко всем узлам.
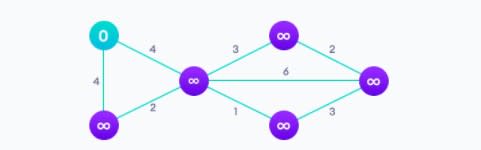
После применения алгоритма Дейкстры:
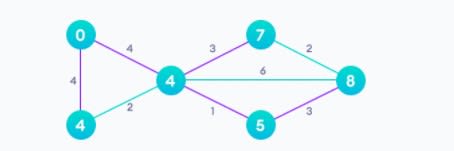
Ссылка на код: Алгоритм Дейкстры
6. Алгоритм Беллмана-Форда (Bellman Ford’s Algorithm)
Алгоритм Беллмана-Форда помогает нам найти кратчайший путь от вершины ко всем другим вершинам взвешенного графа. Он похож на алгоритм Дейкстры, но может обнаруживать графы, в которых ребра могут иметь циклы с отрицательным весом.
Алгоритм Дейкстры (не обнаруживает цикл с отрицательным весом) может дать неверный результат, потому что проход через цикл с отрицательным весом приведет к уменьшению длины пути. Дейкстра не применим для графиков с отрицательными весами, а Беллман-Форд, наоборот, применим для таких графиков. Беллман-Форд также проще, чем Дейкстра и хорошо подходит для систем с распределенными параметрами.
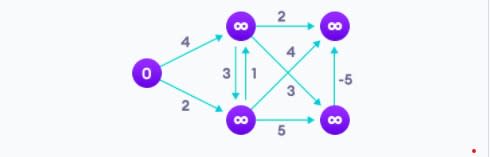
Результат алгоритма Беллмана-Форда:
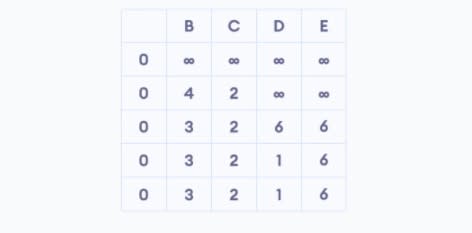
Ссылка на код: Алгоритм Беллмана Форда
7. Алгоритм Флойда-Уоршалла (Floyd-Warshall Algorithm)
Алгоритм Флойда-Уоршалла — это алгоритм поиска кратчайшего пути между всеми парами вершин во взвешенном графе. Этот алгоритм работает как для ориентированных, так и для неориентированных взвешенных графов. Но это не работает для графов с отрицательными циклами (где сумма ребер в цикле отрицательна). Здесь будет использоваться концепция динамического программирования.
Алгоритм, лежащий в основе алгоритма Флойда-Уоршалла:
Dij(k) ← min ( Dij(k-1), Dij(k-1)+Dkj(k-1))
Ссылка на код: Алгоритм Флойда-Уоршалла
8. Алгоритм Прима (Prim’s Algorithm)
Алгоритм Прима — это жадный алгоритм, который используется для поиска минимального остовного дерева из графа. Алгоритм Прима находит подмножество ребер, которое включает каждую вершину графа, так что сумма весов ребер может быть минимизирована.
Простой алгоритм для алгоритма Прима, который следует запомнить:
- Выберите минимальное остовное дерево со случайно выбранной вершиной.
- Найдите все ребра, соединяющие дерево с новыми вершинами, найдите минимум и добавьте его в дерево.
- Продолжайте повторять шаг 2, пока мы не получим минимальное остовное дерево.
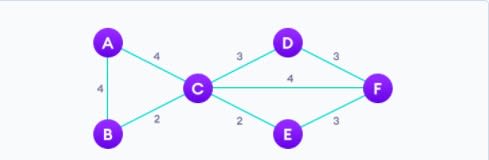
Получим:
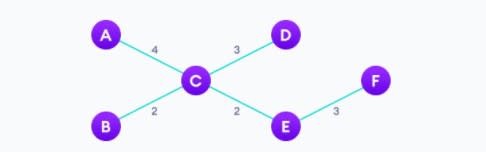
Ссылка на код: Алгоритм Прима
9. Алгоритм Краскала (Kruskal’s Algorithm)
Алгоритм Краскала используется для нахождения минимального остовного дерева для связного взвешенного графа. Основная цель алгоритма — найти подмножество ребер, с помощью которых мы можем обойти каждую вершину графа. Он является жадным алгоритмом, т. к. находит оптимальное решение на каждом этапе вместо поиска глобального оптимума.
Простой алгоритм Краскала, который следует запомнить:
- Сначала отсортируйте все ребра по весу (от наименьшего к наибольшему).
- Теперь возьмите ребро с наименьшим весом и добавьте его в остовное дерево. Если добавляемое ребро создает цикл, не берите такое ребро.
- Продолжайте добавлять ребра, пока не достигнете всех вершин и не будет создано минимальное остовное дерево.
Ссылка на код: Алгоритм Краскала
10. Алгоритм Косараджу (Kosaraju’s Algorithm)
Если мы можем достичь каждой вершины компонента из любой другой вершины этого компонента, то он называется сильно связанным компонентом (SCC). Одиночный узел всегда является SCC. Алгоритм Флойда-Уоршалла относится к методам полного перебора. Но для получения наилучшей временной сложности мы можем использовать алгоритм Косараджу.
Простой алгоритм Косараджу, который следует запомнить:
- Выполните обход графа DFS. Поместите узел в стек перед возвратом.
- Найдите граф транспонирования, поменяв местами ребра.
- Извлекайте узлы один за другим из стека и снова в DFS на модифицированном графе.
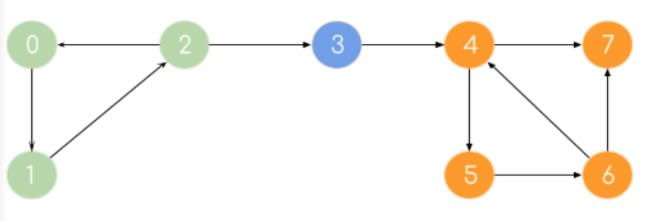
Получим:
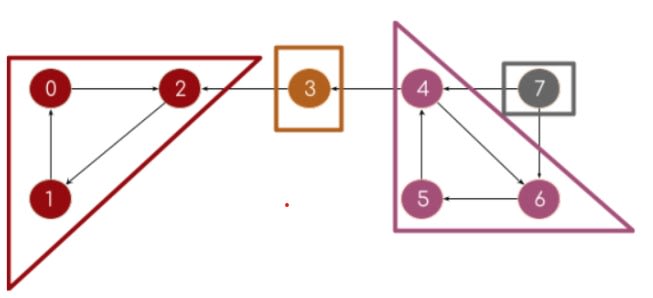
Ссылка на код: Алгоритм Косараджу
В этой статье мы познакомились с самыми важными алгоритмами, которые должен знать каждый программист, работающий с графами. Если хотите подтянуть или освежить знания по алгоритмам и структурам данных, загляни на наш курс «Алгоритмы и структуры данных», который включает в себя:
- живые вебинары 2 раза в неделю;
- 47 видеолекций и 150 практических заданий;
- консультации с преподавателями курса.
***
Материалы по теме
- 🌳 Деревья и графы: что это такое и почему их обязательно нужно знать каждому программисту
- ❓ Зачем разработчику знать алгоритмы и структуры данных?
- ❓ Пройди тест на знание алгоритмов и структур данных
