Все формулы для площадей полной и боковой поверхности тел
1. Площадь полной поверхности куба
a – сторона куба
Формула площади поверхности куба,(S):
2. Найти площадь поверхности прямоугольного параллелепипеда
a, b, c – стороны параллелепипеда
Формула площади поверхности параллелепипеда, (S):
3. Найти площадь поверхности шара, сферы
R – радиус сферы
π ≈ 3.14
Формула площади поверхности шара (S):
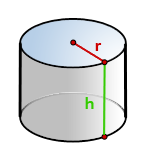
4. Найти площадь боковой и полной поверхности цилиндра
r – радиус основания
h – высота цилиндра
π ≈ 3.14
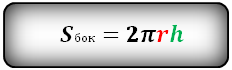
Формула площади боковой поверхности цилиндра, (Sбок):
Формула площади всей поверхности цилиндра, (S):
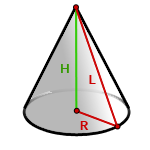
5. Площадь поверхности прямого, кругового конуса
R – радиус основания конуса
H – высота
L – образующая конуса
π ≈ 3.14
Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок):
Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (Sбок):
Формула площади полной поверхности конуса, через радиус (R) и образующую (L), (S):
Формула площади полной поверхности конуса, через радиус (R) и высоту (H), (S):
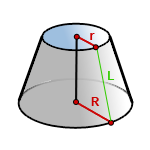
6. Формулы площади поверхности усеченного конуса
R – радиус нижнего основания
r – радиус верхнего основания
L – образующая усеченного конуса
π ≈ 3.14
Формула площади боковой поверхности усеченного конуса, (Sбок):
Формула площади полной поверхности усеченного конуса, (S):
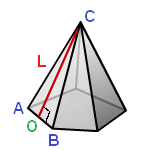
7. Площадь поверхности правильной пирамиды через апофему
L – апофема (опущенный перпендикуляр OC из вершины С, на ребро основания АВ)
P – периметр основания
Sосн – площадь основания
Формула площади боковой поверхности правильной пирамиды (Sбок):
Формула площади полной поверхности правильной пирамиды (S):
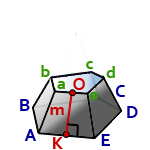
8. Площадь боковой поверхности правильной усеченной пирамиды
m – апофема пирамиды, отрезок OK
P – периметр нижнего основания, ABCDE
p – периметр верхнего основания, abcde
Формула площади боковой поверхности правильной усеченной пирамиды, (S):
9. Площадь поверхности шарового сегмента
R – радиус самого шара
h – высота сегмента
π ≈ 3.14
Формула площади поверхности шарового сегмента, (S):
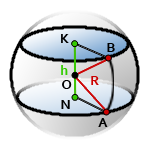
10. Площадь поверхности шарового слоя
h – высота шарового слоя, отрезок KN
R – радиус самого шара
O – центр шара
π ≈ 3.14
Формула площади боковой поверхности шарового слоя, (S):
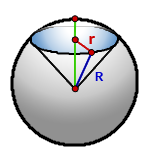
11. Площадь поверхности шарового сектора
R – радиус шара
r – радиус основания конуса = радиус сегмента
π ≈ 3.14
Формула площади поверхности шарового сектора, (S):
Подготовка к ЕГЭ по математике не может обойтись без изучения геометрии. Задачи на расчет площади и объема фигур, нахождение углов и длин сторон встречаются и в первой, и во второй части. В базовой математике ЕГЭ формулы на объем и площадь представлены в справочных материалах. Тем, кто сдает профильную, придется выучить их. Рассмотрим основную теорию.
Площадь — величина, которая есть у плоских фигур. Ее можно посчитать для квадрата, прямоугольника, параллелограмма, треугольника, ромба, трапеции, круга. Объем присущ трехмерным объектам, таким как куб, шар, параллелепипед, призма, пирамида, конус. Объемные тела условно делят на многогранники (состоят из нескольких многоугольников) и поверхности вращения (есть условная линия, вдоль которой вращается плоская фигура). На вычисление объема это не влияет.
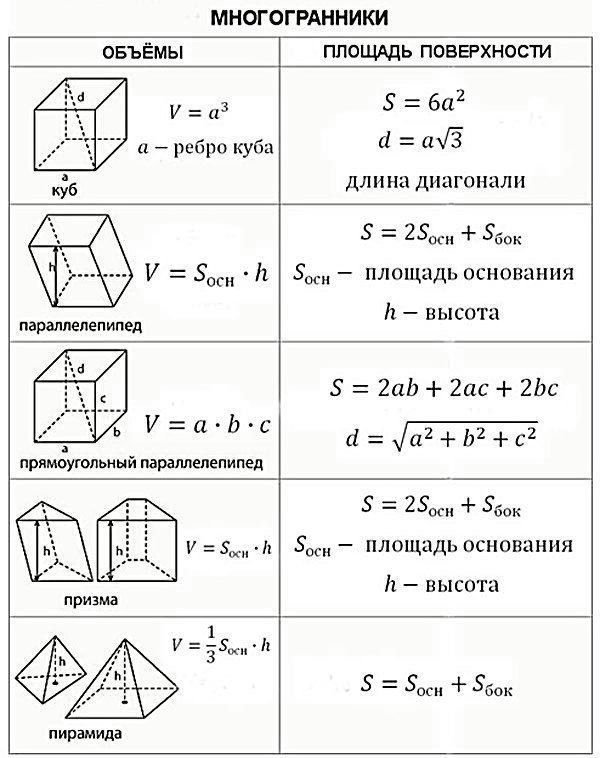
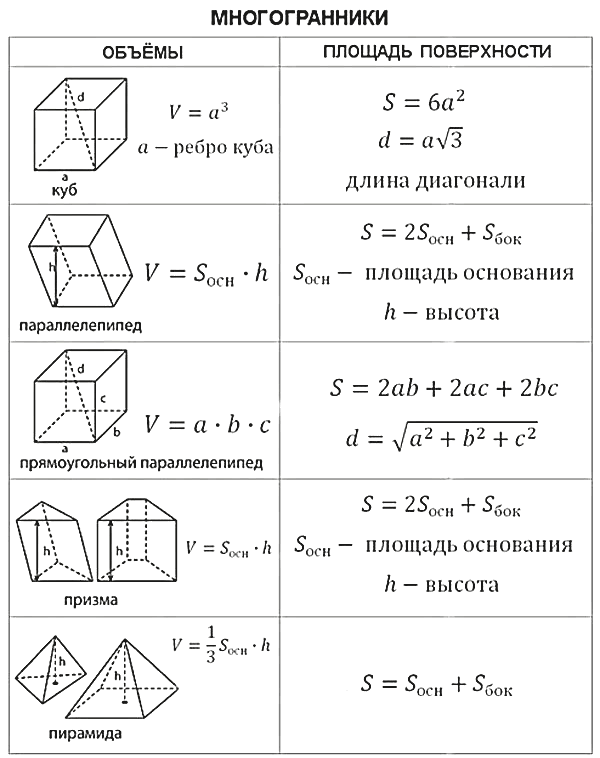
В таблицах представлены основные формулы объемов и площадей фигур для ЕГЭ. Мы советуем сохранить их себе, чтобы пользоваться при подготовке к ЕГЭ и быстро повторить теорию перед экзаменом.
В данной теме выложены вспомогательные картинки для учеников и студентов с формулами площадей и объемов фигур. Ниже расположены основные формулы, которые потребуются при решении задач по геометрии на нахождение объемов и площадей поверхности таких фигур, как квадрат, прямоугольник, параллелограмм, ромб, треугольник, прямоугольный треугольник, трапеция, круг, куб, параллелепипед, прямоугольный параллелепипед, призма, пирамида, цилиндр, конус и шар.

Все формулы по стереометрии для ЕГЭ
Формулы нахождения площадей поверхностей и объемов фигур.
|
Произвольная призма
Прямая призма
|
|
|
Прямоугольный параллелепипед
|
|
|
Произвольная пирамида
Правильная пирамида
|
|
|
Произвольная усеченная пирамида
Правильная усеченная пирамида
|
|
|
Цилиндр
|
|
|
Куб
|
|
|
Конус
|
|
|
Усеченный конус
|
|
|
Шаровая (или сферическая) поверхность
|
Смотри также:
- Формулы по планиметрии
- Основные формулы по математике
Решай с разбором и узнавай ответы:
- задание 13 по математике база
- задание 16 по математике база
- задание 8 по математике профиль
- задание 14 по математике профиль
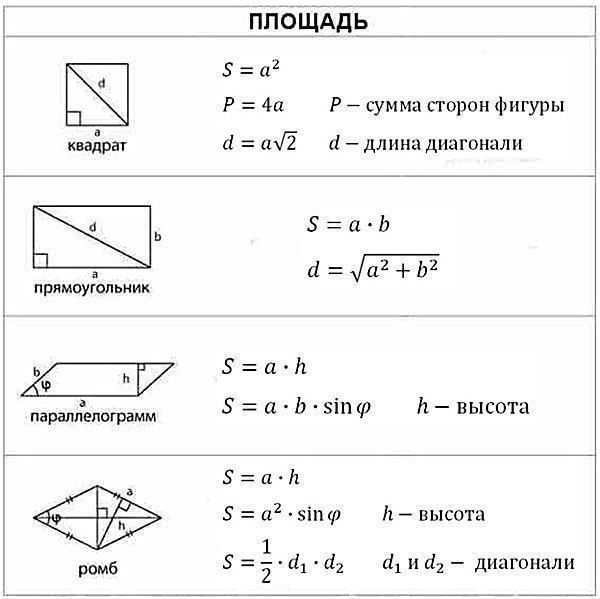
Формулы площадей
1.Площадь многоугольника.
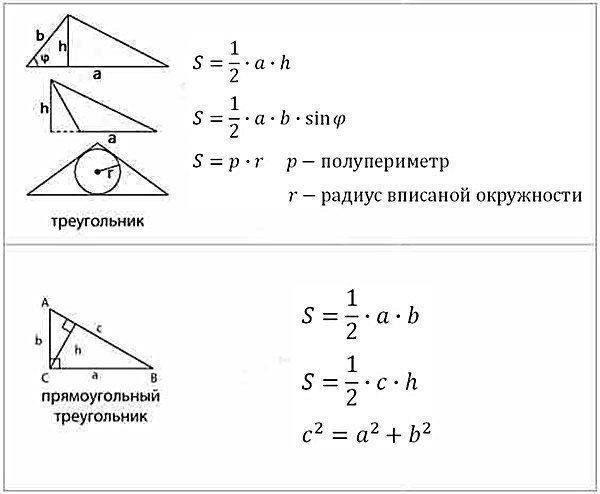
2.Площадь треугольника.
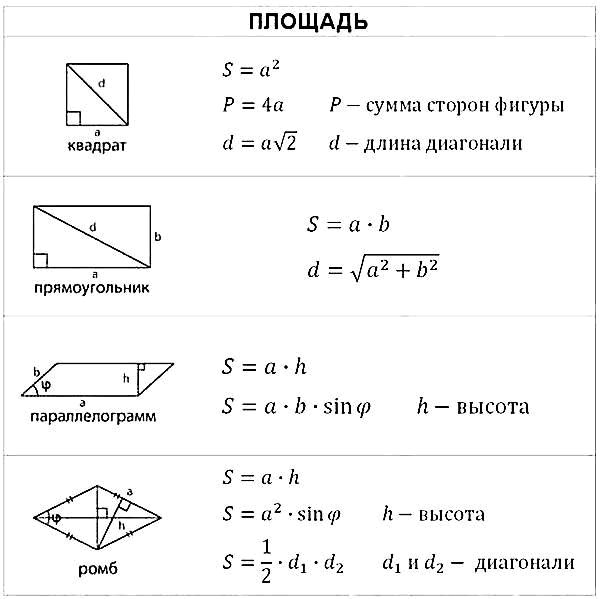
3.Площадь квадрата.
4.Площадь прямоугольника.
5.Площадь параллелограмма.
6.Площадь ромба.
7.Площадь трапеции.
8.Площадь четырехугольника.
9.Площадь круга.
10.Площадь кругового сектора.
11.Площадь эллипса.
Формулы объемов
1.Объем куба.
2.Объем параллелепипеда.
3.Объем призмы.
4.Объем пирамиды.
5.Объем усеченной пирамиды.
6.Объем цилиндра.
7.Объем правильной треугольной пирамиды.
8.Объем конуса.
9.Объем усеченного конуса.
10.Объем тетраэдра.
11.Объем шара.
12.Объем шарового сегмента и сектора.
1 2
3
4
5
6
7
8
Площадь многоугольника
Рассчитать площадь многоугольника вписанного в круг и описанного около круга
Радиус r
Число углов n
Sвп =
Sоп =
Площадь треугольника
Рассчитать площадь треугольника
Сторона а
Сторона а
Сторона b
Угол ɣ (0-90°)
°
S =
Площадь квадрата
Рассчитать площадь квадрата
Сторона а
S =
Площадь прямоугольника
Рассчитать площадь прямоугольника
Сторона а
Сторона b
S =
Площадь параллелограмма
Рассчитать площадь параллелограмма
Сторона а
Высота h
S =
Площадь ромба
Рассчитать площадь ромба
Сторона а
Угол α (0-90°)
°
S =
Площадь трапеции
Рассчитать площадь трапеции
Сторона а
Сторона b
Высота h
S =
Площадь четырехугольника
Рассчитать площадь четырехугольника
Диагональ d1
Диагональ d2
Угол
°
S =
Площадь круга
Рассчитать площадь круга, длину окружности
Радиус r
S =
L =
Площадь кругового сектора, длина дуги
Рассчитать площадь кругового сектора, длину дуги
Радиус R
Угол α (0-360°)
°
S =
L =
Площадь эллипса
Рассчитать площадь эллипса
Длина полуоси а
Репетитор: Васильев Алексей Александрович |
||||
|
|
Предметы: математика, физика, информатика, экономика, программирование. |
|||
Объем куба
Рассчитать объем и площадь поверхности куба
Сторона а
V =
S =
Объем параллелепипеда
Рассчитать объем параллелепипеда
Площадь основания S
Высота h
V =
Объем призмы
Рассчитать объем призмы
Площадь основания S
Высота h
V =
Объем пирамиды
Рассчитать объем пирамиды
Площадь основания S
Высота h
V =
Объем усеченной пирамиды
Рассчитать объем усеченной пирамиды
Площадь S1
Площадь S2
Высота h
V =
Объем цилиндра
Рассчитать объем цилиндра
Радиус основания R
Высота h
V =
Объем правильной треугольной пирамиды
Рассчитать объем правильной треугольной пирамиды
Сторона а
Высота h
V =
Объем конуса
Рассчитать объем конуса
Радиус основания R
Высота H
V =
Объем усеченного конуса
Рассчитать объем усеченного конуса
Радиус R1
Радиус R2
Высота H
V =
Объем тетраэдра
Рассчитать объем тетраэдра
Сторона а
V =
Объем шара
Рассчитать объем и площадь поверхности шара
Радиус R
V =
S =
Объем шарового сегмента и сектора
Рассчитать объем шарового сегмента
Радиус R
Высота H
V =
1 2
3
4
5
6
7
8
Куб – правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра куба равны.
Свойства куба:
1. В кубе $6$ граней и все они являются квадратами.
2. Противоположные грани попарно параллельны.
3. Все двугранные углы куба – прямые.
4. Диагонали равны.
5. Куб имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
6. Диагональ куба в $√3$ раз больше его ребра
$B_1D=AB√3$
7. Диагональ грани куба в $√2$ раза больше длины ребра.
$DC_1=DC√2$
Пусть $а-$длина ребра куба, $d-$диагональ куба, тогда справедливы формулы:
Объем куба: $V=a^3={d^3}/{3√3}$.
Площадь полной поверхности: $S_{п.п}=6а^2=2d^2$
Радиус сферы, описанной около куба: $R={a√3}/{2}$
Радиус сферы, вписанной в куб: $r={a}/{2}$
При увеличении всех линейных размеров куба в $k$ раз, его объём увеличится в $k^3$ раз.
При увеличении всех линейных размеров куба в $k$ раз, площадь его поверхности увеличится в $k^2$ раз.
Прямоугольный параллелепипед
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
1. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
$B_1D^2=AD^2+DC^2+C_1C^2$
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.
Чтобы были понятны формулы, введем обозначения:
$а$-длина;
$b$-ширина;
$с$-высота(она же боковое ребро);
$P_{осн}$-периметр основания;
$S_{осн}$-площадь основания;
$S_{п.п}$-площадь полной поверхности;
$V$-объем.
$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.
$S_{п.п}=2(ab+bc+ac)$.
Пирамида
Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) — треугольники, имеющие общую вершину.
Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.
$SO$ — высота.
Формулы вычисления объема и площади поверхности правильной пирамиды.
$h_a$ — высота боковой грани (апофема)
$S_{бок}={P_{осн}·h_a}/{2}$
$S_{п.п}=S_{бок}+S_{осн}$
$V={1}/{3}S_{осн}·h$
В основании лежат правильные многоугольники, рассмотрим их площади:
- Для равностороннего треугольника $S={a^{2}√3}/{4}$, где $а$ — длина стороны.
- Квадрат $S=a^2$, где $а$ — сторона квадрата.
Задачи на нахождение объема составного многогранника:
- Разделить составной многогранник на несколько параллелепипедов.
- Найти объем каждого параллелепипеда.
- Сложить объемы.
Задачи на нахождение площади поверхности составного многогранника.
— Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:
$S_{полн.пов.}=P_{осн}·h+2S_{осн}$
Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.
— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности правильной призмы разных видов (треугольной, четырехугольной и шестиугольной), а также, разберем примеры решения задач для закрепления материала.
Правильная призма – это прямая призма, основанием которой является правильный многоугольник. А прямой фигура является в том случае, если ее боковые грани перпендикулярны основаниям.
-
Формула площади правильной призмы
- 1. Общая формула
- 2. Площадь правильной треугольной призмы
- 3. Площадь правильной четырехугольной призмы
- 4. Площадь правильной шестиугольной призмы
- Примеры задач
Формула площади правильной призмы
1. Общая формула
Площадь (S) полной поверхности призмы равна сумме площади ее боковой поверхности и двух площадей основания.
Sполн. = Sбок. + 2Sосн.
Площадь боковой поверхности прямой призмы равняется произведению периметра ее основания на высоту.
Sбок. = Pосн. ⋅ h
Формула периметра и площади основания правильной призмы зависит от вида многогранника. Ниже мы рассмотрим самые популярные виды.
2. Площадь правильной треугольной призмы
Основание: равносторонний треугольник.
| Площадь | Формула |
| основание |  |
| боковая поверхность | Sбок. = 3ah |
| полная |  |
microexcel.ru
3. Площадь правильной четырехугольной призмы
Основание: квадрат.
| Площадь | Формула |
| основание | Sосн. = a2 |
| боковая поверхность | Sбок. = 4ah |
| полная | Sполн. = 2a2 + 4ah |
microexcel.ru
Примечание: Если высота правильной четырехугольной призмы равняется длине стороны ее основания, значит мы имеем дело с кубом, площадь одной грани которого равна a2. А так как все шесть граней куба равны, то полная площадь его поверхности равняется 6a2.
4. Площадь правильной шестиугольной призмы
Основание: правильный шестиугольник
| Площадь | Формула |
| основание |  |
| боковая поверхность | Sбок. = 6ah |
| полная |  |
microexcel.ru
Примеры задач
Задание 1:
Сторона правильной треугольной призмы равна 6 см, а ее высота – 8 см. Найдите полную площадь поверхности фигуры.
Решение:
Воспользуемся подходящей формулой, подставив в нее известные нам значения:
Задание 2:
Площадь полной поверхности правильной шестиугольной призмы составляет 400 см2. Найдите ее высоту, если известно, что сторона основания равна 5 см.
Решение:
Выведем выражение для нахождения высоты призмы из формулы ее полной площади:
Чтобы найти объем четырехугольной пирамиды с заданными параметрами, нужно знать ее высоту и площадь основания. Поскольку мы знаем, что основанием является грань куба, то площадь основания равна квадрату длины его ребра.
Для нахождения высоты четырехугольной пирамиды можно использовать теорему Пифагора. Если обозначить длину ребра куба как a, то длина полудиагонали его грани (расстояние от центра грани до ее вершины) будет равна √(a^2 + a^2) = √2a. Поскольку центр куба является вершиной пирамиды, то высота пирамиды будет равна расстоянию от центра куба до его грани, то есть a/2.
Таким образом, площадь основания четырехугольной пирамиды равна a^2, а ее высота равна a/2. Объем пирамиды можно найти, используя формулу:
V = (1/3) * S * h
где S – площадь основания, h – высота пирамиды.
Подставляя известные значения, получим:
V = (1/3) * a^2 * (a/2) = (a^3)/6
Так как объем куба равен 72, то a^3 = 72. Решая это уравнение, получаем a = 4√3.
Таким образом, длина ребра куба равна 4√3, площадь основания четырехугольной пирамиды равна (4√3)^2 = 48, а ее высота равна (4√3)/2 = 2√3.
Используя формулу для объема четырехугольной пирамиды, мы можем найти ее объем:
V = (1/3) * 48 * 2√3 = 32√3
Ответ: объем четырехугольной пирамиды равен 32√3.
Как найти площадь основания куба?
На этой странице вы найдете ответ на вопрос Как найти площадь основания куба?. Вопрос
соответствует категории Математика и уровню подготовки учащихся 1 – 4 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно
ознакомиться с вариантами ответов других посетителей страницы или обсудить с
ними интересующую тему. Здесь также можно воспользоваться «умным поиском»,
который покажет аналогичные вопросы в этой категории. Если ни один из
предложенных ответов не подходит, попробуйте самостоятельно сформулировать
вопрос иначе, нажав кнопку вверху страницы.

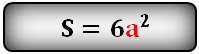



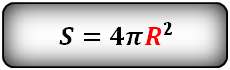






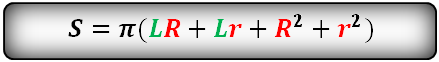
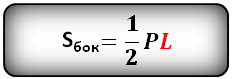
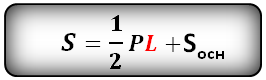
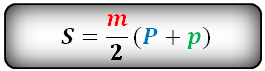




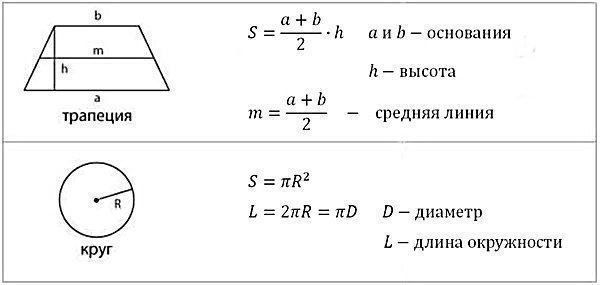
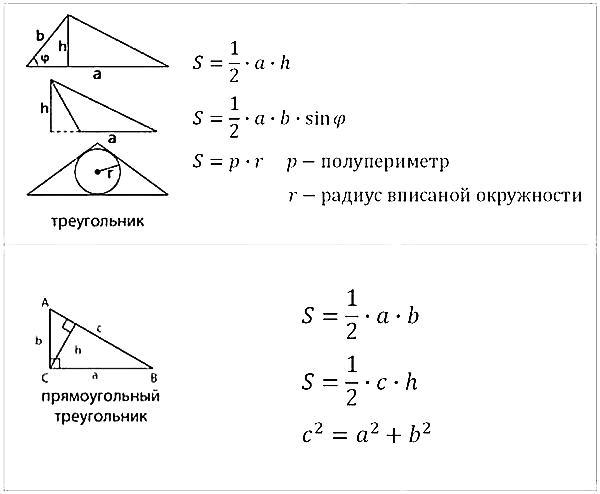
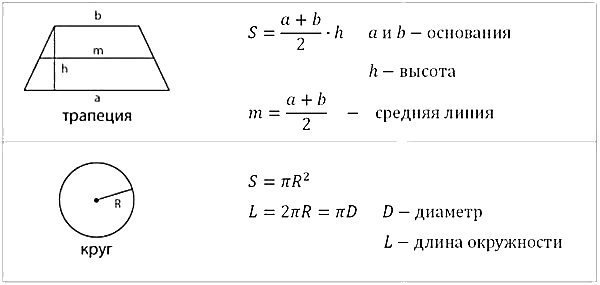













 2000 руб / 120 мин — подготовка к ЕГЭ и ГИА для школьников. 3000 руб / 120 мин — индивидуально (базовый уровень). 2000 руб / 120 мин — студенты.
2000 руб / 120 мин — подготовка к ЕГЭ и ГИА для школьников. 3000 руб / 120 мин — индивидуально (базовый уровень). 2000 руб / 120 мин — студенты.














