Команда “Газы!” была объявлена еще две недели назад. И что?! Легкие задачи порешали и расслабились?! Или вы думаете, что задачи на газы касаются только 28-х заданий ЕГЭ?! Как бы не так! Если газов пока еще не было в 34-х заданиях, это ничего не значит! Задач на электролиз тоже не было в ЕГЭ до 2018 года. А потом как врезали, мама не горюй! Обязательно прочитайте мою статью “Тайны задач по химии? Тяжело в учении – легко в бою!”. В этой статье очень подробно рассказывается о новых фишках на электролиз. Статья вызвала шквал самых разных эмоций у преподавателей химии. До сих пор мне и пишут, и звонят, и благодарят, и бьются в конвульсиях. Просто цирк с конями, в котором я – зритель в первом ряду.
Однако, вернемся к нашим баранам, вернее, Газам. Я прошла через огонь и воду вступительных экзаменов и знаю точно – хочешь завалить абитуриента, дай ему задачу на Газы. Почитайте на досуге сборник задач И.Ю. Белавина. Я процитирую одну такую “мозгобойню”, чтобы вам жизнь медом не казалась. Попробуйте решить.
И.Ю. Белавин, 2005, задача 229
“Два из трех газов (сероводород, водород и кислород) смешали и получили газовую смесь, плотность которой оказалась равной плотности оставшегося газа. Полученную газовую смесь вместе с равным ей объемом третьего газа под давлением поместили в замкнутый сосуд емкостью 4 л, содержавший азот при н.у. и нагревали при 600 С до окончания химических реакций, затем постепенно охладили. Определите массы веществ, содержавшихся в сосуде после охлаждения, если плотность газовой смеси в сосуде перед нагреванием равнялась 9,25г/л. (Ответ: m(S) = 7,5 г, m(SO2) = 15 г, m(Н2О) = 9 г)”
Ну как, решили? Нет?! А ваши репетиторы?! Извините, это был риторический вопрос. Кстати, мои ученики, абитуриенты 2003-2008 гг. такие задачи щелкали, как семечки, на экзаменах во 2-й медицинский (теперь РНИМУ им. Н.И. Пирогова). Надеюсь, вам понятно, что 34-м задачам ЕГЭ еще есть куда усложняться, perfectio interminatus est (нет предела совершенству), с газами нужно работать, работать и работать. Поэтому команду “Газы!” отменять рано. Итак, поехали!
Сегодня мы поговорим о газовых смесях, затронем понятие плотности газа (абсолютной и относительной), средней молярной массы, решим задачи: определение средней молярной массы и плотности газа по компонентам смеси и наоборот.
• Газовая смесь – смесь отдельных газов НЕ вступающих между собой в химические реакции. К смесям газов относятся: воздух (состоит из азота, кислорода, углекислого газа, водяного пара и др.), природный газ (смесь предельных и непредельных углеводородов, оксида углерода, водорода, сероводорода, азота, кислорода, углекислого газа и др.), дымовые газы (содержат азот, углекислый газ, пары воды, сернистый газ и др.) и др.
• Объемная доля – отношение объема данного газа к общему объему смеси, показывает, какую часть общего объема смеси занимает данный газ, измеряется в долях единицы или в процентах.
• Мольная доля – отношение количества вещества данного газа к общему количеству вещества смеси газов, измеряется в долях единицы или в процентах.
• Плотность газа (абсолютная) – определяется как отношение массы газа к его объему, единица измерения (г/л). Физический смысл абсолютной плотности газа – масса 1 л, поэтому молярный объем газа (22,4 л при н.у. t° = 0°C, P = 1 атм) имеет массу, численно равную молярной массе.
• Относительная плотность газа (плотность одного газа по другому) – это отношение молярной массы данного газа к молярной массе того газа, по которому она находится
• Средняя молярная масса газа – рассчитывается на основе молярных масс составляющих эту смесь газов и их объемных долей
Настоятельно рекомендую запомнить среднюю молярную массу воздуха Мср(в) = 29 г/моль, в заданиях ЕГЭ часто встречается.
Обязательно посетите страницу моего сайта “Изучаем Х-ОбХ-04. Закон Авогадро. Следствия из закона Авогадро. Нормальные условия. Молярный объем газа. Абсолютная и относительная плотность газа. Закон объемных отношений” и сделайте конспекты по теории. Затем возьмите бумагу и ручку и решайте задачи вместе со мной.
ВАНГУЮ: чует мое сердце, что ЕГЭ по химии 2019 года устроит нам газовую атаку, а противогазы не выдаст!
Задача 1
Определить плотность по азоту газовой смеси, состоящей из 30% кислорода, 20% азота и 50% углекислого газа.
Задача 2
Вычислите плотность по водороду газовой смеси, содержащей 0,4 моль СО2, 0,2 моль азота и 1,4 моль кислорода.
Задача 3
5 л смеси азота и водорода имеют относительную плотность по водороду 12. Определить объем каждого газа в смеси.
Несколько задач со страницы моего сайта
Задача 4
Плотность по водороду пропан-бутановой смеси равна 23,5. Определите объемные доли пропана и бутана
Задача 5
Газообразный алкан объемом 8 л (н.у.) имеет массу 14,28 г. Чему равна его плотность по воздуху
Задача 6
Плотность паров альдегида по метану равна 2,75. Определите альдегид
Ну как? Пошло дело? Если туго, вернитесь к задачам и решайте их самостоятельно до тех пор, пока не щелкнет! А для стимуляции – десерт в виде еще одной задачи И.Ю. Белавина на газы. Наслаждайтесь ее решением самостоятельно!
И.Ю. Белавин, 2005, задача 202
“Сосуд емкостью 5,6 л при н.у. заполнили метаном, затем нагрели до высокой температуры, в результате чего произошло частичное разложение метана. Определите массу образовавшейся сажи, если известно, что после приведения к нормальным условиям объем полученной газовой смеси оказался в 1,6 раза больше объема исходного метана, эта газовая смесь обесцвечивает бромную воду и имеет плотность по воздуху 0,2931. (Ответ: m(C) = 0,6 г)”
Задачи И.Ю. Белавина – это крутой драйв! Попробуйте порешать, и вы откажетесь от просмотра любых ужастиков, поскольку запасетесь адреналином надолго! Но нам нужно спуститься на землю к ЕГЭ, простому и надежному, как первый советский трактор. Кстати, у меня в коллекции припасено немало сюрпризов с газовыми фишками, собранными за все годы работы и бережно хранимыми. Думаю, пришло время сказать им: “И снова здравствуйте!”, поскольку ЕГЭ с каждым годом становится “все чудесатее и чудесатее”. Но это уже совсем другая история. Читайте мои статьи – и вы подстелите соломку под свою ЕГЭшную попу.
Вы готовитесь к ЕГЭ и хотите поступить в медицинский? Обязательно посетите мой сайт Репетитор по химии и биологии http://repetitor-him.ru. Здесь вы найдете огромное количество задач, заданий и теоретического материала, познакомитесь с моими учениками, многие из которых уже давно работают врачами. Позвоните мне +7(903)186-74-55, приходите ко мне на курс, на бесплатные Мастер-классы “Решение задач по химии”. Я с удовольствием вам помогу.
Репетитор по химии и биологии кбн В.Богунова
Решение задач на газовые смеси | Закон Авогадро
Задача 71.
При прохождении смеси равных объемов SO2 и О2 через контактный аппарат 90% молекул SO2 превращается в SO3. Определить состав (в процентах по объему) газовой смеси, выходящей из контактного аппарата.
Решение:
Уравнение реакции горения сернистого газа имеет вид:
2SO2 + O2 = 2SO3 .
Из уравнения реакции вытекает, что из двух молекул SO2 и одной молекулы O2 образуются две молекулы SO3. Известно, что из каждого литра SO2 превратилось в SO3 0,9л, при этом образовалось тоже 0,9л SO3. Кислорода на каждый литр прореагировало соответственно 0,45л О2 (0,9/2 = 0,45).
Таким образом, выходящая смесь газов из контактного аппарата, на каждый литр смеси состояла из 0,1л SO2 (1 – 0,9 = 0,1) и 0,55л О2 (1 – 0,45 = 0,55). Общий объём смеси, выходящей из контактного аппарата, составляет 1,55л (0,1 + 0,55 + 0,9 = 1,55).
Задача 72.
Смесь, состоящая из трех объемов Сl2 и одного объема H2, оставлена в закрытом сосуде на рассеянном свету при постоянной температуре. Через некоторое время содержание Сl2 в смеси уменьшилось на 20%. Изменилось ли давление в сосуде? Каков процентный состав смеси по объему?
Решение:
Уравнение реакции взаимодействия хлора с водородом имеет вид:
Cl2 + H2 = 2HCl
При взаимодействии одного моля хлора с одним моль водорода образуется два объёма хлороводорода, т. е. реакция идёт без изменения объёма. При нормальных условиях из трёх литров хлора в реакцию вступило 0,6л (3 . 0,2 = 0,6). Точно такое же количество водорода тоже вступило в реакцию. Таким образом, при взаимодействии 0,6л хлора и 0,6л водорода образовалось 1,2л хлороводорода (2 . 3 = 0,6). Так как реакция идёт без изменения объёма, то давление в системе тоже не изменится.
Находим процентный состав газовой смеси по формуле:
Ответ: не изменилось;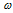
(Cl2) = 60%;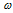(HCl) = 40%.
Задача 73.
При взаимодействии NН3 с Сl2 образуются хлороводород и азот. В каких объемных соотношениях взаимодействуют NH3 и С12 и каково отношение объемов получающихся газов?
Решение:
Уравнение реакции взаимодействия аммиака с хлором имеет вид:
2NH3 + 3Cl2 = 6HCl + N2
При взаимодействии аммиака с хлором из каждых двух объёмов аммиака и трёх объёмов хлора образуются шесть объёмов хлороводорода и один объём азота. Таким образом, аммиак и хлор взаимодействуют в объёмных отношениях 2 : 3 (2VNH3 : 3VCl), а отношение объёмов получающихся газов – 1 : 6 V(N2 : V(HCl).
Ответ: V(NH3) : V(Cl2) = 2 : 3; V(HCl) : V(N2) = 6 : 1.
Задача 74. Какой объем Н2 (при 17 °С и давлении 102,4кПа) выделится при растворении 1,5кг цинка в соляной кислоте?
Решение:
Уравнение реакции имеет вид:
Zn + 2HCl = ZnCl2 + H2↑
Зная мольную массу цинка (65,4г/моль) и мольный объём газа (22,4л), находим объём водорода, который выделится при растворении 1,5кг цинка из пропорции:
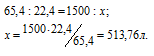
Затем приводим полученный объём к указанным условиям используя объединённое уравнение закона Бойля- Мариотта и Гей-Люссака, находим V0:
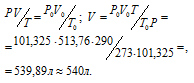
где P и V – давление и объём газа при температуре T = 290К (273 +17 = 290); P0 = 101,325 кПа; T0 = 273 К; P = 102,4 кПа; V0 -объём газа (н.у.) = 513,76 л.
Ответ: 540л.
Задача 75.
После взрыва смеси, состоящей из одного объема исследуемого газа и одного объема Н2, получился один объем водяного пара и один объем азота. Все измерения производились при одинаковых условиях. Найти формулу исследуемого газа.
Решение:
Молекулярная формула воды H2O, а азота – N2. Так как продукты реакции и исходные вещества состоят из одинаковых объёмов, то, учитывая, что образуются по одной молекуле воды и азота из одной молекулы водорода и одной молекулы исследуемого газа, можно предположить, что молекула исследуемого газа состоит из двух атомов азота и одного атома кислорода. Следовательно, формула исследуемого газа имеет вид N2O.
Ответ: N2O.
Задача 76
При одинаковых условиях взяты равные объемы N2 и O2. Каково соотношение масс обоих газов:
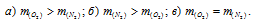
Решение:
Согласно закону Авогадро, в равных объёмах любых газов, взятых при одинаковых условиях (одной и той же температуре и одинаковом давлении) содержится одинаковое число молекул (6,02 . 1023). Поскольку M(O2) равен 32 г/моль, а M(N2) – 28г/моль, то m(O2) > m(N2)
Ответ: а).
Задача 77.
Смешали равные объемы Н2 и С12. Как изменится объем смеси после протекания реакции: а) не изменится;
б) увеличится в два раза; в) уменьшится в два раза?
Решение:
Уравнение реакции взаимодействия хлора с водородом имеет вид:
Cl2 + H2 = 2HCl
При взаимодействии одного моля хлора с одним моль водорода образуется два объёма хлороводорода, т.е. реакция идёт без изменения объёма. Поэтому объём смеси после протекания реакции не изменится.
Ответ: а).
Задача 78.
Каково соотношение объемов, занимаемых 1 моль НСI и 1 моль Сl2 (Т и Р одинаковы):
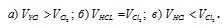
Решение:
Согласно закону Авогадро одно и тоже число молекул любого газа занимает при одинаковых условиях (температура и давление одинаковы) один и тот же объём. Вместе с тем 1 моль любого газа содержит одинаковое число молекул. Следовательно, при одинаковых условиях 1 моль любого газа занимает один и тот же объём. Этот объём называется мольным объёмом газа и при нормальных условиях (Т = 0 °С и Р = 101,325 кПа) равен 22,4л. Поэтому соотношение объёмов одного моля HCl и одного моля Cl2 (T и Р одинаковы):
V(HCl) = V(Cl2).
Ответ: б).
Задача 79.
При нагревании НВг полностью разлагается. При этом объём газа не изменяется. Каковы продукты реакции разложения: а) атомы Н и Вг; б) молекулы Н2 и Вг2 в) молекулы Н2 и атомы Br?
Решение:
Уравнение реакции термического разложения бромоводорода имеет вид:
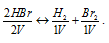
Таким образом, из двух молекул НВг образуются одна молекула Н2 и одна молекула Вг2, т.е. объём системы после реакции не изменяется. Следовательно, продуктами реакции термического разложения HBr являются газообразные Н2 и Вг2.
Ответ: б).
1.Находим
количество вещества газовой смеси: υ(смеси)=
=14/22,4=0,625(моль)
2.Вычисляем среднюю молярную массу смеси: М(смеси) = 
= 25,5:0,625= 40,8(г/моль)
3.
Находим объемную долю азота в смеси: Пусть x—объемная доля
азота в смеси, φ(N2)=x, тогда
(1-x)—объемная
доля оксида углерода(IV) в
смеси, φ (CO2)= 1-x
по формуле М(смеси)= φ(N2) × М(N2) + φ (CO2) × М(CO2)
40,8= x×28 +
(1-x) ×
44 откуда x=0,2
или x=20%
φ(N2)=20%
φ (CO2)=1-0,2=0,8
или 80%
4.
Определяем мольную долю азота в смеси. По закону Авогадро объемная доля газа
в смеси равна его мольной доле, поэтому φ(N2)= χ(N2)=0,2
или 20%
5.
Вычисляем массовую долю азота в смеси, на основе формулы χ(N2)= υ(N2)/ υ(смеси)
находим
количество вещества азота
υ(N2) = χ(N2) × υ(смеси)=0,2×0,625=0,125
(моль), тогда m(N2)= υ(N2) × M(N2)=
0,125×28=3,5(г)
ω(N2)=
= 3,5/25,5=0,137 или 13,7%
Все эти
действия можно объединить одной формулой ω(N2)= 
= 0,2 × 0,625 × 28/25,5=0,137
или
ω(N2)=
= 0,2 × 28/40,8 = 0,137 или 13,7%
Ответ:
φ(N2)=20%
; χ(N2)=20%
ω(N2)=13,7%
Концентрация объемная
Концентрация растворов является важной характеристикой, показывающей содержание растворенного вещества и растворителя в его составе. Выражается концентрация, как правило, в массовых (вес) и объемных (объем) процентах или долях.
Растворы и их концентрация
Под раствором следует понимать однородную (гомогенную систему), в состав которой входит один или несколько компонентов. Растворы могут быть газовыми, жидкими, твердыми. Концентрация раствора бывает качественной и количественной. Качественная концентрация определяет растворы насыщенные, ненасыщенные, перенасыщенные. Количественная концентрация показывает массу или объем содержания веществ в составе раствора.
Самый простой состав – это растворитель и растворенное вещество. Растворитель представляет собой вещество, которое при растворении не меняет свое состояние. Если смешиваются вещества в одинаковом агрегатном состоянии, к примеру, жидкость с жидкостью или газ с газом, растворителем будет компонент, которого больше. Образование раствора зависит от характера взаимодействия между частицами растворителя и растворенного вещества, их природой.
Чтобы определить соотношение растворенного вещества и растворителя в составе смеси и применяется такая характеристика, как концентрация. В зависимости от того, какая единица измерения выбрана, концентрация может быть объемной (содержание вещества в объеме раствора) или массовой (содержание вещества в единице массы раствора).
Объемные концентрации
Объемная доля вещества в общем объеме раствора выражается соотношением между объемом компонента, который нужно определить, и общим объемом всего раствора. Для измерения объемной концентрации используются доли или проценты. Значение концентрации указывается при определенных показателях температурного режима и давления.
Для выражения объемной доли используется следующая формула:
V(А) – объем вещества, V (смеси) – общий объем раствора.
Объемная доля, как правило, применяется в отношении газовых смесей. К примеру, содержание кислорода в воздухе составляет 21%, что означает объемную долю кислорода: φ(O2) = 21%. Применение объемной доли удобно потому, что объемное содержание газа в составе раствора газов, которые химически не взаимодействуют между собой, такая же, как молярная доля смеси. Это в достаточной мере точно выполняется, когда показатели давления и температуры не слишком высокие.
Для определения концентрации растворов определенных веществ используется ареометр. Он проградуирован непосредственно в концентрации смеси, а не в показателях ее плотности.
Объемная концентрация и объемная доля – безразмерные величины. Чтобы их выражать в большинстве случаев используются проценты, но могут также применяться такие единицы, как промилле, миллионные доли. Возможно также отображение единиц в таком виде: «% об.» или «об.%» (объемные проценты), однако рекомендуется писать конкретное указывать величину, к которой относится значение.
Вам могут быть интересны услуги
Расчет состава смесей по химическим формулам
Смеси бывают двухкомпонентные и многокомпонентные. Среди приемов, которые будут рассмотрены, можно выделить, пригодные только для двухкомпонентных смесей и те, которые подходят для расчета состава смесей с любым количеством компонентов.
Предлагаемые способы решения удобнее рассмотреть на конкретных примерах.
Задача 1.1. В каком объемном соотношении необходимо смешать водород и углекислый газ, чтобы получить газовую смесь по плотности равную воздуху.
А. Квадрат Пирса (правило креста). Как известно (закон Авогадро) , равные количества газов занимают равные объемы. Следовательно, если молярные массы газов равны, значит, равны и их плотности. Поэтому, нужно смешать водород и углекислый газ так, чтобы средняя молярная масса полученной газовой смеси была равна молярной массе воздуха (29 г/моль). Определив молярные массы H2 и СO2 , зная среднюю молярную массу воздуха, расставим их в виде треугольника:
H2 2
воздух 29
СO2 44
Найдем разницу в числах по диагонали 2-29=-27; 44-29=15. Отбросив минус, проставим их, в соответствии с диагональю, по которой они были определены 27 – напротив CO2; 15 – напротив H2:
H2 2 15
воздух 29
CO2 44 27
Cоотношение 15:27 и будет ответом. Ответ: Углекислый газ и водород необходимо смешать в объемном соотношении 15:27.
Б. Введем два неизвестных. Примем количество одного компонента за x, а второго – за y. Воспользуемся формулой n=m/M и, преобразовав, получим Mсм= mсм/nсм . Помня, что mcм=m(H2) + m(CO2), а nсм=n(H2) + n(CO2) получим 29=(2х + 44y)/(x + y). Упростив, получим, что 27х=15y. Полученное соотношение говорит о том что, водород с углекислым газом необходимо смешать в молярном (объемном) соотношении 27:15, что подтверждает ответ, полученный при решении способом А.
В. Примем количество одного из компонентов за 1 моль, а второго – за x. Данный способ позволяет рассчитать количество углекислого газа, требуемого на 1 моль водорода. Преобразования, описанные в Б варианте решения, позволяют получить следующее уравнение: 29=(2 + 44x)/1+x . Р 29 + 29x= 2 + 44x Р 27=15x . Полученное выражение означает, что водород с углекислым газом необходимо смешать в соотношении 27:15.
Г. Примем общее количество реагентов за 1 моль, а первого компонента за Х, следовательно, количество второго компонента будет равно 1-x. Воспользовавшись формулой nсм=mсм/Mсм, получим 1=(2х + 44(1-x))/29, Р 29=2x + 44 – 44x. Совершив необходимые преобразования, получим 42x=15 Р x=15/42, а 1-x=27/42 Р x/(1-x)=15/27. Полученный ответ подтверждает справедливость выбранного способа решения.
Д. Решение задачи с использованием понятия “доля”. Можно воспользоваться следующим правилом: вклад выделенной величины X, характеризующей каждый компонент смеси, в суммарную величину, характеризующую всю смесь, пропорционален его доле (которую в общем виде можно обозначить как e). Для смеси, состоящей из компонентов а, b, …,i, математически это правило можно выделить следующим образом:
X(a)•e(a) + X(b) •e(b) + … + X(i)•e(i)= X(см). (13)
Исходя их определения доли, необходимо помнить, что сумма долей всех компонентов смеси равна 1 или 100% (в зависимости от способа выражения). Выбор вида доли (массовая, объемная, мольная) определяется анализом условия каждой конкретной задачи.
Для решения задачи данным методом нужно определить характеристику, о которой идет речь в задании – это молярная масса смеси и составляющих компонентов. Приняв мольную долю H2 за x, а CO2 – за (1-x) получим выражение 29=2x + 44(1-x). Преобразовав, получим 42 x=15 Р x=15/42; 1-x=27/42, а отношение x/(1-x)=15:27.
Задача 1.2. Природный хлор представлен двумя изотопами 35Сl и 37Сl. Во сколько раз ядер 35Сl больше, чем ядер 37Сl?
Для решения представленной задачи подходят все описанные способы решения (А-Д). Однако, наиболее простым получается решение при использовании правила креста (А).
35Сl 35 1,5
35,5
37Cl 37 0,5
Полученное соотношение 1,5:0,5 свидетельствует, что атомов хлора с массовым числом 35 в три раза больше.
Задача 1.3. Какие массы 96% и 10% серной кислоты необходимо взять для получения 400 г 40% серной кислоты?
Подходят все способы решения (А-Д). Наиболее простым способом для решения задач подобного типа является правило креста (А):
96 30
40
10 56
30: 56 или 15:28 (на 15 массовых частей 96% серной кислоты нужно взять 28 частей 10% кислоты). Т.е. 15x + 28x=400 Р 43x=400, x=9,3. Масса 96% серной кислоты равна 15·9,3=139,5; Масса 10% серной кислоты равна: 28·9,3=260,5.
Рассмотрим способ решения этой задачи через введение двух неизвестных (Б).
Однако, в данном случае, удобнее оперировать с массами. Примем массу 96% серной кислоты за x, а 10% – за y. Тогда, из определения массовой доли (5) получим: 0,4=(0,96x + 0,10y)/(x + y) Р 0,4x + 0,4y = 0,96x + 0,10y Р 0,30y = 0,56x. C другой стороны x + y = 400.
Получив систему уравнений 0,30y = 0,56x
y = 400 – x,
решим ее 0,3 ·(400 – x) = 0,56x Р 120 – 0,3x = 0,56x Р 0,86x = 120 Р x=139,5, что вполне согласуется с ответом, полученным при решении задачи методом креста.
Задача 1.4. Найдите массовую долю этанола в водном растворе спирта, в котором содержание кислорода как элемента составляет 50%.
Подходят все способы, но проще задача решается методом креста:
Определив массовые доли кислорода в этаноле и в воде по уравнению (5).
Расставим их согласно правилу
этанол (wo%) 35 39
смесь (wo%) 50
вода (wo%) 89 15
Полученные значения показывают, что этанол с водой необходимо смешать в массовом соотношении 39:15. Отсюда, массовая доля этанола равна 39/(39+15)=0,722 или 72,2%.
Задача 1.5. Найдите массовую долю формальдегида в формалине (водный раствор формальдегида), в котором на 11 протонов приходится 9 нейтронов.
Решить эту задачу, используя правило креста (А), вряд ли удастся. Тем не менее, для ее решения подойдет любой из методов (Б-Д). Воспользуемся методом В, приняв количество формальдегида за 1, а воды за x. Подсчитаем суммарное количество протонов и суммарное количество нейтронов в означенных количествах веществ (в молекуле формальдегида на 16 протонов приходится 14 нейтронов, а в молекуле воды – на 10 протонов – 8 нейтронов). Суммарное количество протонов будет равно (в молях) (16 + 10x); а нейтронов (14 + 8x). Откуда, (16 + 10x)/(14 + 8x) = 11:9. Преобразовав уравнение, получим 144 + 90x = 154 + 88x Р 2x=10, а x=5. Полученный результат показывает, что на 1 моль формальдегида необходимо взять 5 моль воды. Воспользовавшись уравнением (5) найдем массовую долю формальдегида: w=30/(30 + 5·18)= 0,25 или 25%.
Задача 1.6. Определить объемную долю SO2 в смеси с SO3, в которой на 5 атомов серы приходится 12 атомов кислорода.
Для решения этой задачи подойдут все методы (Б-Д), кроме правила креста. Воспользуемся для ее решения методом Г. Примем общее количество газов за 1 моль, количество SO2 – за x моль, а SO3 – за (1-х)моль. Подсчитаем общее количество атомов серы – (x + (1-x)) и атомов кислорода – (2x + 3(1-x)). Разделив полученные выражения, приравняем их к требуемому значению: 1/(3-x)=5:12. Воспользовавшись правилом пропорции, получим: 15-5x=12 Р 5x=3. Полученное выражение свидетельствует, что мольная (для газов значит и объемная) доля SO2 составляет 3/5, а SO3 – 2/5 (60% и 40%, соответственно).
Задача 1.7: Определить массу 10 л (н. у.) газовой смеси, в которой на 1 молекулу метана приходится 2 молекулы этана, 3 молекулы пропана и 4 молекулы бутана.
1 способ: Для решения этой задачи подходит способ Д. Воспользовавшись уравнением 11, определим среднюю молярную массу смеси. Мольные доли метана, этана, пропана и бутана равны 0.1, 0.2, 0.3 и 0.4 соответственно. Поэтому, уравнение 11 приобретет вид Mсм=0.1·16 + 0.2·30 + 0.3·44 + 0.4·58. Р Мсм=44,8 г/моль. Воспользовавшись уравнениями (1) и (2) определим массу 10 л газовой смеси. m=10:22,4·44,8=20 г.
2 способ: Решение данной задачи возможно и через введение неизвестного. Определим объемы газов. Если, объем метана равен х, тогда объем этана – 2х, пропана – 3х, а бутана – 4х. Тогда х + 2х + 3х + 4х = 10 Р х = 1 л. Определив массы 1 л метана, 2 л этана, 3 л пропана и 4 л бутана, сложим их, найдя массу 10 л газовой смеси: 1:22,4·16 + 2:22,4·30 + 3:22,4·44 + 4:22,4·58 = 20 г.
Задача 1.8. Какую массу 5% раствора сульфата меди и медного купороса CuSO4·5H2O необходимо взять для получения 400 г 10% раствора сульфата меди?
Оптимальный способ решения данной задачи правило креста. Для использования данного способа необходимо определить массовую долю сульфата меди в кристаллогидрате: w=160/250=0,64.
Далее расположим полученные данные в виде креста
5 % р-р 5 54
смесь 10
СuSO4·5H2O 64 5
Находя разницу по диагонали, получим отношение масс при смешении. Таким образом, масса кристаллогидрата будет равна w (СuSO4·5H2O) ·400 = 54/(54+5) · 400= 366,1 г. Следовательно масса 5 %раствора будет равна 400 – 366,1 = 33,9 г
|
Высшая нервная деятельность
Значение коры больших полушарий.Высшая нервная деятельность (ВНД) — это деятельность коры больших полушарий головного мозга и ближайших к ней подкорковых образований, обеспечивающая наиболее совершенное приспособление (поведение) высокоорганизованных животных и человека к окружающей среде. В работе русского физиолога И. М. Сеченова «Рефлексы головного мозга» … |
Тонга
Королевство Тонга расположено на семисоткилометровой цепочке небольших островов в юго-западной части Тихого океана , к северу от Новой Зеландии .Это очень небольшое государство даже по масштабам Океании. Площадь его составляет всего 699 кв.км. |
|
Megrez 72 ED APO
Мы немножечко про него расскажем, и как всегда, покажем. Все фотографии (если находятся на нашем сервере;-)), как обычно, кликабельны и открываются в новом окне. ТТХ: объектив-дублет на особом стекле со следующими параметрами: D=72мм,F=432 мм , т.е. достаточно светосильный F, естественно FMC), весьма компактный ( в сложеном состоянии длина 300 мм) и довольно легковесный (2200 гр) … |
Шолохов М. А
Шолохов Михаил Александрович (1905, хутор Кружилин станицы Вёшенской Области войска Донского — 1984, станица Вёшенская Области войска Донского — 1984, станица Вёшенская Ростовской области), писатель, академик АН СССР (1939), Герой Социалистического Труда (1967, 1980). Автор посвященных драматическим судьбам донского казачества сборников рассказов («Донские рассказы», «Лазоревая степь», оба … |
