Сообщение от мадина2005
составляющую
Поскольку векторное произведение – исключительная привилегия трехмерного пространства, то имеет смысл освоить еще и такой прием.
Запишем равенство а=v+xb+yc, где вектор v – искомая ортогональная составляющая. Отсюда v=a-xb-yc. Коэффициенты х и у находим из условий (v,b)=0, (v,c)=0, что дает систему
(a,b)-x(b,b)-y(c,b)=0,
(a,c)-x(b,c)-y(c,c)=0.
0
Содержание:
Векторная алгебра
Векторная алгебра – это раздел векторного исчисления, изучающий линейные операции с векторами и их геометрические свойства; часть линейной алгебры, занимающаяся векторными пространствами; различные векторные алгебры XIX века (например, кватернионов, бикватернионов, сплит-кватернионов).
Векторы и линейные операции над ними
Займемся теперь таким важным как в самой математике, так и в ее многочисленных приложениях, понятием вектора.
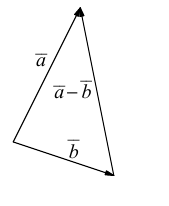
Определение: Вектором, на плоскости или в пространстве называется отрезок прямой с заданным на нем направлением, т. е. одна из его граничных точек считается начальной, а вторая – конечной.
Обозначать векторы мы будем строчными латинскими буквами
Длина отрезка, изображающего вектор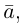
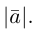
По определению, два вектора считаются равными, если один из них можно преобразовать в другой с помощью параллельного переноса.
Учитывая приведенное определение, всюду в дальнейшем мы без специальных оговорок будем перемещать вектор параллельным переносом в любую удобную для нас точку.
Два вектора 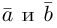
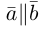
Аналогично, векторы а и b называются ортогональными (обозначение 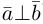
Три вектора называются компланарными, если после приведения их общему началу, они будут расположены в одной плоскости.
Углом между векторами 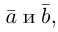
Два ненулевых вектора 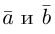
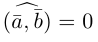
Введем теперь линейные операции над векторами.
а) Умножение числа на вектор.
Произведением действительного числа 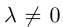
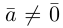
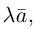
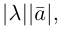
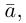
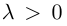
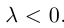
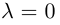
В частности, вектор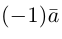
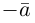
Если 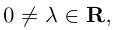
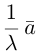
Из приведенного определения сразу же следует, что коллинеарные векторы 
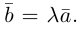
взять число 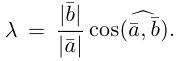
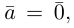
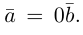
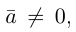
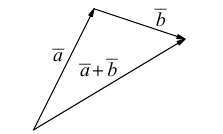
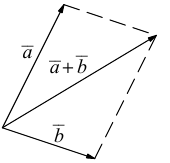
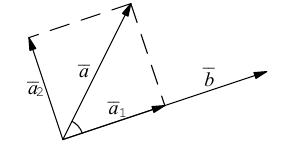
b) Сложение векторов.
Суммой двух векторов 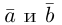
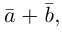
или по равносильному ему правилу параллелограмма
Вектор 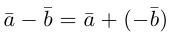
Свойства линейных операций над векторами аналогичны соответствующим свойствам действительных чисел.
Проекцией вектора 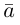
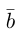
Геометрически очевидны следующие свойства проекции:
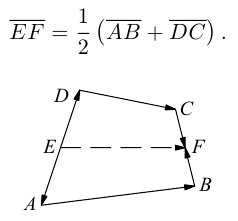
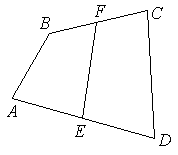
Пример №1
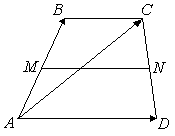
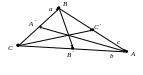
Пусть Е и F – середины сторон AD и ВС соответственно выпуклого четырехугольника ABCD. Доказать, что
Доказательство. Из четырехугольников EDCF и EABF по правил}’ сложения векторов получим:
Сложив данные равенства и учитывая, что 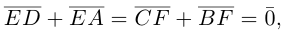
что и требовалось.
Базис и декартова система координат
Определение: Базисом на плоскости называется упорядоченная пара неколлинеарных векторов. Базисом в пространстве называется упорядоченная тройка некомпланарных векторов.
Обозначение: 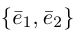
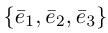
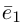
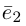
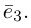
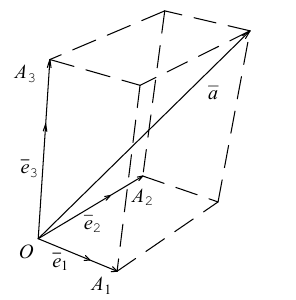
Теорема. Любой вектор единственным образом разлагается по базису, т. е. представляется в виде 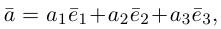
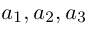
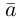
Приведем геометрическое доказательство этого утверждения.
Вектор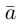
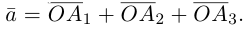
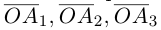
Если базис зафиксирован, то факт, что вектор а в этом базисе имеет координаты 
Из доказанной теоремы следует, что при выполнении линейных операций над векторами точно также преобразуются и их координаты, т. е. если 
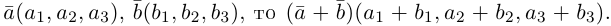
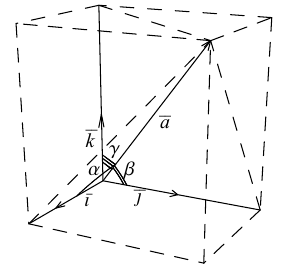
Рассмотрим теперь ортонормированный базис 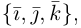
Как видно из чертежа, координаты вектора в ортонормированном базисе представляют собой проекции этого вектора на соответствующие орты. т. е.
Величины 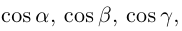
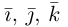
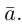
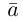
Очевидно также, что
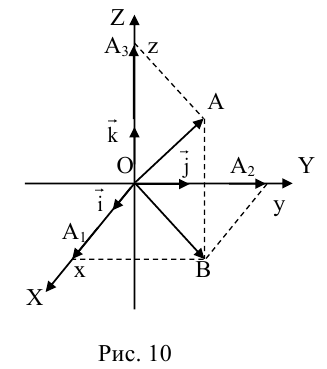
Свяжем теперь с ортонормированным базисом декартову (прямоугольную) систему координат. Для этого поместим начала ортов в некоторую точку О, ось Ох (абсцисс) направим вдоль орта 
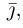
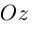
В выбранной системе координат координаты радиуса-вектора 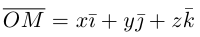
Если известны координаты начальной 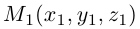
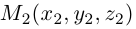
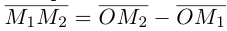
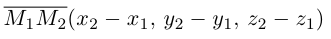
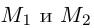
Найдем теперь координаты точки М, делящей отрезок с концами в точках 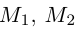
отношении 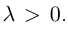
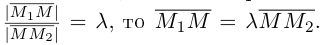
Следовательно, координаты искомой точки вычисляются по формулам:
Найдем, в частности, координаты середины отрезка. Здесь А = 1, поэтому
Пример №2
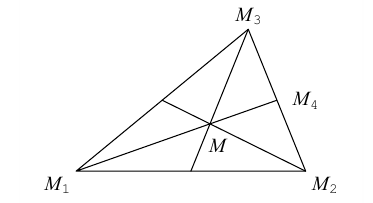
Треугольник задан координатами своих вершин 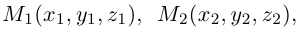
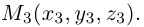
Пусть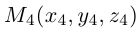
По известному свойству точки пересечения медиан 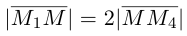
Подставив сюда найденные координаты точки 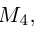
Таким образом, координаты точки пересечения медиан треугольника равны средним арифметическим соответствующих координат его вершин.
Замечание. Базисом n-мерного пространства 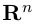
обладающая тем свойством, что любой вектор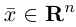
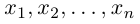
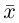
В качестве базиса в 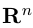
так как, очевидно, любой вектор 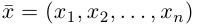
Скалярное произведение векторов
Определение: Скалярным произведением векторов 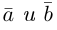
Из этого определения сразу же следует, что
и таким образом, если один из векторов имеет единичную длину, то их скалярное произведение равно проекции второго вектора на единичный.
Отметим основные свойства скалярного произведения.
Первые два и последнее свойства немедленно следуют из определения скалярного произведения, а третье и четвертое – из сформулированных в §1 свойств проекции.
Найдем теперь представление скалярного произведения в координатах. Пусть в орто-нормированном базисе 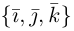
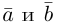
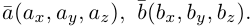
перемножим векторы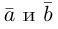
Таким образом, скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат векторов.
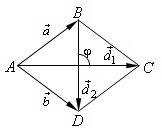
Пример №3
Разложить вектор 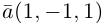
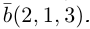
Решение.
Из чертежа следует, что 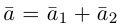
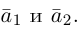
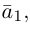
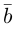
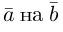
Тогда вторая ортогональная составляющая вектора 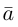
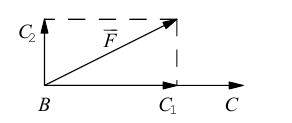
В заключение параграфа рассмотрим одно простое приложение скалярного произведения в механике. Пусть под действием постоянной силы 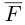
Найдем работу этой силы. Для этого разложим вектор силы 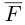
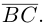
Составляющая 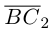
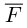
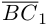
Окончательно, работа силы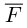
Замечание. Скалярным произведением векторов 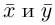
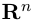
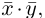
то
Несложной проверкой мы можем убедиться в том, что таким образом определенное скалярное произведение в 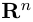
Длиной вектора 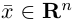
Векторы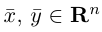
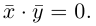
составляют ортонормированный базис пространства 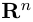
Любой вектор 
n-мерного пространства с координатами
Взяв еще одну точку 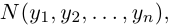
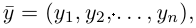
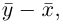
Таким образом переопределенное пространство 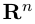
Совокупность точки О(0.0,…, 0) и ортонормированного базиса (1) называется декартовой системой координат евклидова пространства R”. Точка 0(0,0,… ,0) называется, естественно, началом координат.
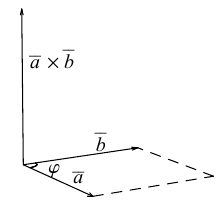
Векторное произведение векторов
Определение: Векторным произведением некоялинеарных векторов 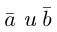

Из этого определения следует, что площадь параллелограмма, построенного на векторах 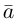
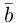

Сформулируем основные свойства векторного произведения.
Первые два свойства очевидным образом следуют из определения векторного произведения. Доказательство третьего ввиду его громоздкости мы приводить не будем.
Найдем формулу для вычисления векторного произведения в координатах. Пусть векторы 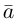
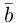
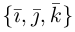
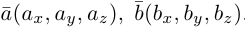
раскроем скобки в векторном произведении 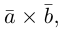
Полученный вектор мы можем записать в виде следующего символического определителя.
вычислять который удобно разложением по первой строке.
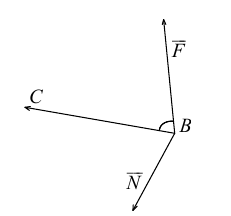
Пример №4
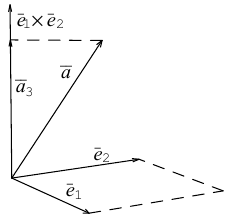
Найти составляющую вектора 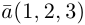
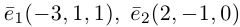
Решение.
Из чертежа видно, что искомая составляющая представляет собой вектор проекции данного вектора 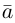

Переходим к вычислениям:
Тогда
Среди многочисленных приложений векторного произведения отметим его применение в механике при вычислении момента силы.
Итак, пусть сила 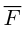
Смешанное произведение векторов
Определение: Смешанным произведением трех векторов 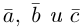
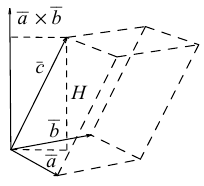
Выясним геометрический смысл смешанного произведения для тройки некомпланарных векторов.
По определению смешанного произведения
Поскольку 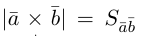
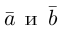
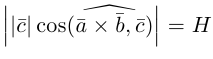
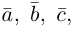
– объем параллелепипеда. Таким образом, абсолютная величина смешанного произведения трех векторов равна объему параллелепипеда, построенного на этих векторах.
Если векторы заданы своими координатами в ортонормированном базисе 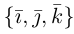
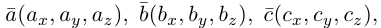
Следовательно (глава I. §2, пункт 3, свойство 7)), в координатах смешанное произведение вычисляется по формуле:
Докажем, пользуясь этой формулой, некоторые свойства смешанного произведения.
что следует из свойства 4) определителя (глава I. §2, пункт 3). Таким образом, в смешанном произведении можно менять местами знаки скалярного и векторного произведения, и поэтому для него используется более короткое обозначение 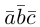
Эти свойства смешанного произведения также являются прямыми следствиями соответствующих свойств определителя.
Докажем еще одно, геометрическое свойство смешанного произведения.
Теорема. Три вектора 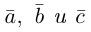
Доказательство. Докажем необходимость условия теоремы. Пусть векторы 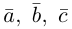
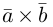
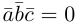
Следствие. Три вектора 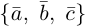
Заметим, кроме того, что, если 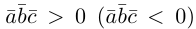
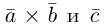
Пример №5
Доказать, что пять точек
расположены в одной плоскости.
Решение. Рассмотрим векторы 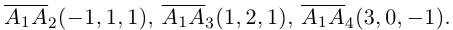
то по доказанной выше теореме эти векторы компланарны и, стало быть. точки 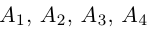
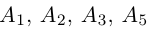
так как первая и третья строки в определителе пропорциональны. Плоскости 
Векторы и линейные операции над ними
Определение: Вектором называется направленный отрезок (рис. 1).
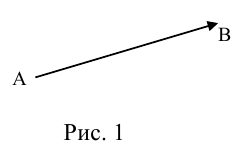
Рис. 1
Так как вектор определяется его началом и концом, то можно сформулировать эквивалентное данному определение.
Определение: Вектором называется упорядоченная пара точек.
Определение: Длина вектора 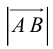
Определение: Два вектора называются равными, если они имеют равные длины и одинаково направлены. При этом одинаково направленными называются векторы, лежащие на параллельных прямых и имеющие одинаковые направления.
Из этого определения следует, что точка приложения вектора значения не имеет, то есть вектор не изменяется, если его перемещать параллельно самому себе, сохраняя длину. Такие векторы называются свободными.
Если начало и конец вектора совпадают, он называется нулевым:
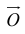
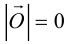
Определение: Векторы 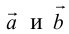
Так как направление нулевого вектора не определено, то он коллинеарен любому другому.
Определение: Векторы называются компланарными, если они параллельны одной плоскости.
Нулевой вектор компланарен любой системе компланарных векторов.
Линейные операции над векторами
Линейными называются операции сложения векторов и умножения на число.
Сложение
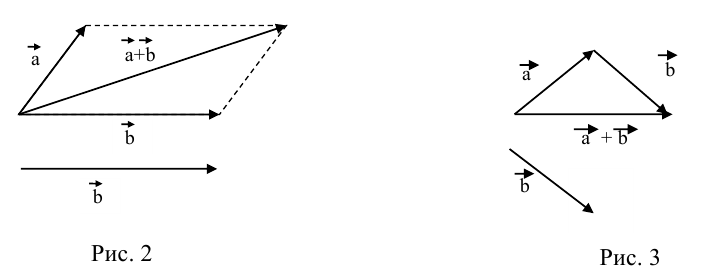
а) Правило параллелограмма (рис.2): начала 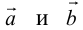
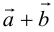
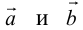
б) Правило треугольника (рис. 3): начало 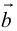
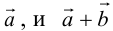
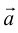
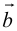
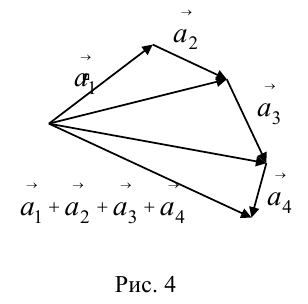
в) Правило сложения нескольких векторов (рис. 4).
Вектор 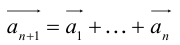
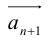
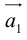
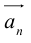
Умножение на число
Определение: Произведением вектора 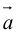
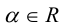
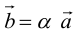
а) 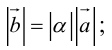
б) 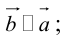
в)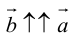
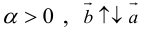
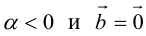
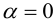
Произведение 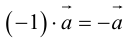
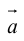
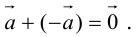
Определение: Разностью 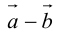
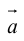
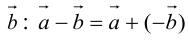
Начала 
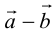
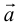
Свойства линейных операций
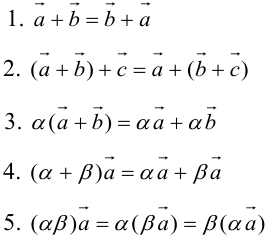
Определение: Результат конечного числа линейных операций над векторами называется их линейной комбинацией:
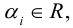
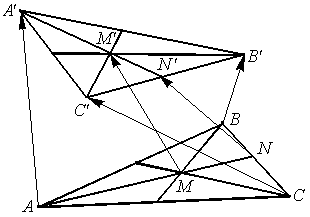
Пример №6
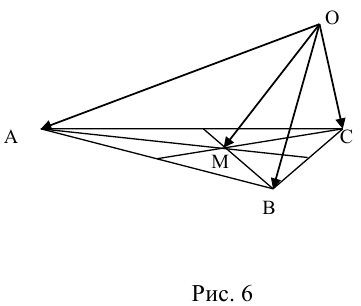
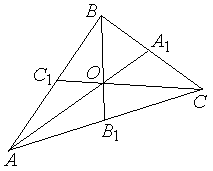
Пусть М – точка пересечения медиан треугольника АВС, а О – произвольная точка пространства. Представить 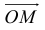
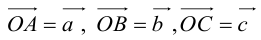
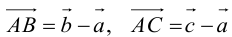
По правилу треугольника 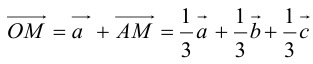
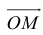
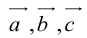
Теорема: Пусть 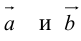
где коэффициенты (2.1) определяются единственным образом.
Представление вектора 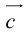
Доказательство:
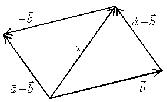
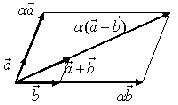
- Пусть среди
есть два коллинеарных, например:
- Пусть среди
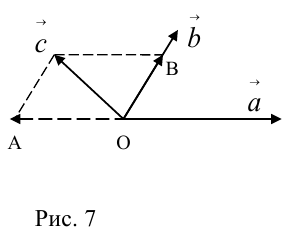
коллинеарных нет, тогда совместим начала всех трех векторов в одной точке. Построим параллелограмм, диагональ которого совпадает с
, а стороны параллельны прямым, на которых лежат
(рис. 7).
Тогда c 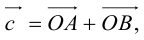
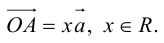
Докажем единственность разложения. Предположим, что 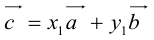
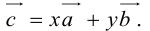
Если 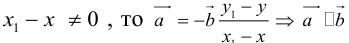
Теорема: Пусть 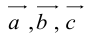
причем единственным образом.
Представление вектора 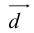
Доказать самостоятельно.
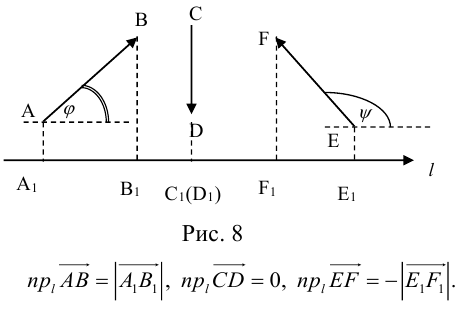
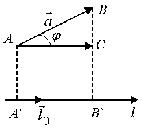
Проекция вектора на ось
Проекция вектора на ось — это скалярная величина (число), равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают; или число, противоположное длине геометрической проекции вектора, если направления геометрической проекции и оси — противоположные.
Координаты вектора
Осью называется направленная прямая.
Определение: Ортом оси 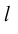
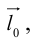
направление которого совпадает с направлением оси.
Определение: Ортогональной проекцией точки М на ось 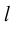
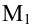
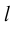
Определение: Ортогональной проекцией вектора 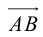
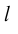
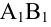
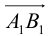
Определение: Углом между вектором и осью называется угол, на который нужно повернуть в положительном направлении ось до совпадения ее направления с направлением вектора (положительным считается поворот против часовой стрелки).
Очевидно, проекцию вектора на ось можно найти по формуле
Можно показать, что проекция линейной комбинации векторов равна та-
кой же линейной комбинации их проекций:
В частности, проекция суммы векторов равна сумме их проекций:
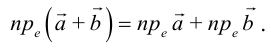
Рассмотрим прямоугольную декартову систему координат ХОY. Обозначим 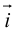
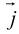

Аналогично в пространственной системе OXYZ 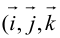
– разложение 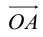
Таким образом, если задана прямоугольная декартова система координат (пдск), то со всяким пространственным вектором 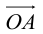
Определение: Координатами вектора 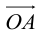
Таким образом, можно дать еще одно определение вектора.
Определение: Вектором называется упорядоченная тройка чисел (упорядоченная пара, если вектор плоский).
Пример №7
Если 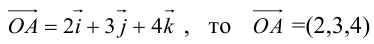
Так как, с одной стороны, вектор – объект, имеющий длину и направление, а с другой, – упорядоченная тройка чисел, то, зная длину и направление, можно определить его координаты и наоборот. Направление вектора в заданной системе координат характеризуется его направляющими косинусами (рис. 11):
Из этих формул очевидно следует основное свойство направляющих косинусов:
Если известны длина 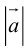
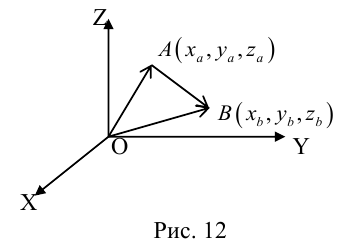
Пусть AB – произвольный вектор в системе OXYZ, OA,OB – радиус-векторы его начала и конца,
Тогда
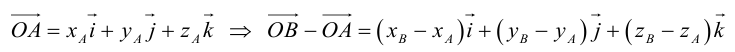
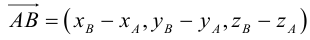
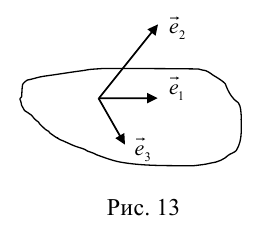
Определение: Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов (рис. 13).
Если 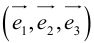
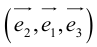
Определение: Базис называется прямоугольным декартовым, если базисные векторы взаимно перпендикулярны и длина каждого равна 1.
Такой базис принято обозначать
Из теоремы 2 следует, что всякий вектор 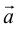
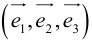
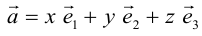
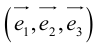
Определение: Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.
Если 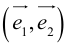
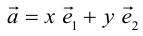
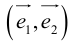
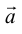
Определение: Базисом на прямой называется любой ненулевой вектор этой прямой.
Деление отрезка в данном отношении
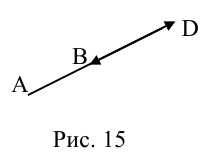
Рассмотрим задачу: дан отрезок AB . Найти точку D , которая делит AB в заданном отношении 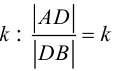
Введем прямоугольную декартову систему координат (пдск) OXYZ, тогда
Обозначим
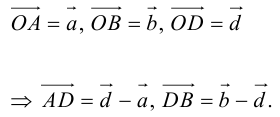
Так как 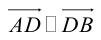
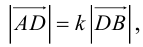
Переходя от этого векторного равенства к равенству соответствующих координат, получим:
ЗАМЕЧАНИЕ 1. Если D – середина отрезка AB , то k 1, поэтому
ЗАМЕЧАНИЕ 2. Если k < 0, 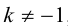
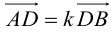
В этом случае
Скалярное произведение векторов
Определение: Скалярным произведением векторов 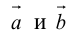
Скалярное произведение обозначается так: 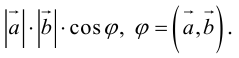
Так как 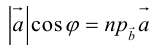
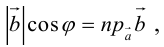
Свойства скалярного произведения
1.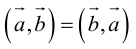
2.
Доказательство:
3.
Доказательство:
а) 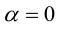
б)
в) 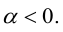
4.
Отсюда следует, что
Необходимым и достаточным условием перпендикулярности векторов является равенство нулю их скалярного произведения:
5.
Доказательство:
а) пусть
б) пусть
В первом и втором случаях один из сомножителей – нулевой вектор. Его направление не определено, поэтому можно считать, что 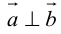
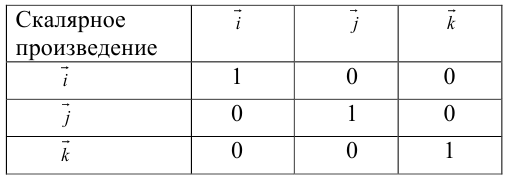
Используя свойства 4 и 5, составим таблицу вычисления скалярного произведения базисных векторов
Пусть в некоторой пдск 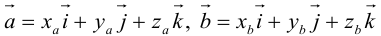
Таким образом,
Пример №8
Найти, при каком значении x векторы 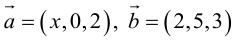
Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю (свойство 5), поэтому найдем скалярное произведение по формуле (2.5):
Пример №9
Найти угол между биссектрисой AD и медианой 
Так как 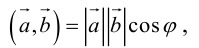
то
Найдем координаты векторов 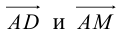
По теореме о биссектрисе внутреннего угла треугольника
Чтобы найти k , вычислим длины AC и AB :
Разделим отрезок CB в данном отношении по формулам (2.3):
отсюда
Заметим, что 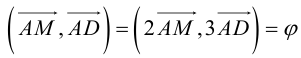
Пример №10
Найти
Воспользуемся свойствами 1–4 скалярного произведения:
Отсюда
ЗАМЕЧАНИЕ. Так как работа силы 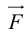
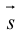
Определение векторного произведения векторов
Определение: Тройка некомпланарных векторов 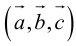
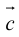
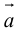
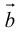
Определение: Векторным произведением вектора 
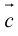
(
перпендикулярен плоскости векторов
и
).
- Направление
таково, что тройка
– правая.
Векторное произведение обозначается так:
ЗАМЕЧАНИЕ 1. Геометрический смысл векторного произведения: длина векторного произведения численно равна площади параллелограмма, построенного на этих векторах.
Это следует из того, что площадь параллелограмма равна произведению длин смежных сторон на синус угла между ними.
Заметим, что
Таким образом, длину вектора векторного произведения можно вычислить с помощью скалярного произведения по формуле
Пример №11
Найти площадь параллелограмма, построенного на векторах
По формуле (2.7):
ЗАМЕЧАНИЕ 2. Направление вектора 
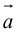
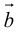
Свойства векторного произведения
1.
Доказательство:
а)пусть 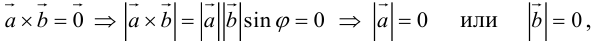
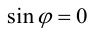
Его направление не определено, поэтому можно считать, что 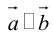
б)пусть
2. 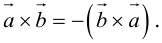
Доказательство: По определению направления векторов 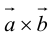
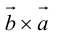
3.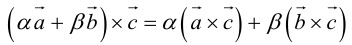
Векторное произведение также линейно и по второму сомножителю.
Используя определение и свойства 1 и 2, составим таблицу вычисления векторного произведения базисных векторов 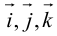
Пусть в некоторой пдск 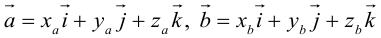
Заметим, что это выражение можно получить, вычислив символический определитель (сделать это можно по-разному, но лучше разложить по первой строке):
Таким образом,
Пример №12
Вычислить векторное произведение векторов
По формуле (2.8):
Заметим, что площадь треугольника, построенного на векторах 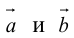
или
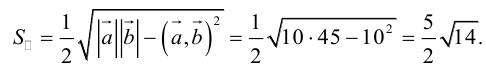
Пример №13
Вычислить площадь параллелограмма, построенного на векторах 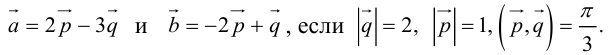
Так как 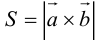
Отсюда
Определение смешанного произведения векторов
Определение: Смешанным произведением векторов 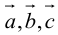
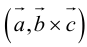
Смешанное произведение обозначается так:
Пусть в некоторой пдск
Обозначим
Тогда
по 7 свойству определителей.
Таким образом,
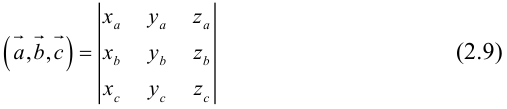
По определению скалярного произведения
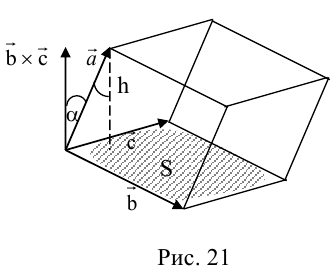
Совместим начала всех трех векторов в одной точке. Тогда (рис. 21)
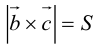
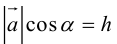
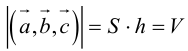
Геометрический смысл смешанного произведения: модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах-сомножителях, при этом 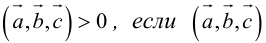
Свойства смешанного произведения
1. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения: 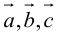
Доказательство: а) 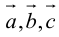
Если 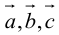
б)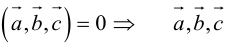
Во всех трех случаях 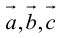
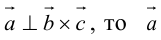
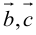
2. Круговая перестановка сомножителей в смешанном произведении не изменяет его величины. Перестановка соседних сомножителей изменяет его знак, не изменяя абсолютной величины:
Доказательство следует из формулы (2.9) и свойства 3 определителей, при этом круговая перестановка сомножителей соответствует двойной перемене строк в определителе, а потому оставляет его неизменным.
3. В смешанном произведении векторное и скалярное произведения можно менять местами:
Доказательство: из свойства 2 смешанного произведения и свойства 1 скалярного получим:
4. Смешанное произведение линейно по каждому из трех сомножителей.
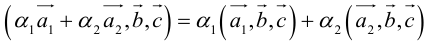
Доказательство следует из формулы (2.9) и свойств определителей.
Пример №14
Найти объем тетраэдра, построенного на векторах
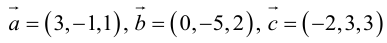
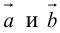
Объем тетраэдра в 6 раз меньше объема параллелепипеда, построенного на этих векторах, поэтому
Отсюда 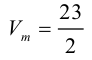
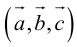
Чтобы найти высоту, воспользуемся формулой
По формуле (2.7)
Лекции по предметам:
- Математика
- Алгебра
- Линейная алгебра
- Геометрия
- Аналитическая геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика
Ортогональные векторы и условие ортогональности
В данной статье мы расскажем, что такое ортогональные векторы, какие существуют условия ортогональности, а также приведем подробные примеры для решения задач с ортогональными векторами.
Ортогональные векторы: определение и условие
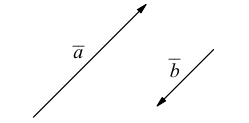
Ортогональные векторы — это векторы a ¯ и b ¯ , угол между которыми равен 90 0 .
Необходимое условие для ортогональности векторов — два вектора a ¯ и b ¯ являются ортогональными (перпендикулярными), если их скалярное произведение равно нулю.
Примеры решения задач на ортогональность векторов
Плоские задачи на ортогональность векторов
Если дана плоская задача, то ортогональность для векторов a ¯ = < a x × a y >и b ¯ = < b x × b y >записывают следующим образом:
a ¯ × b ¯ = a x × b x + a y × b y = 0
Задача 1. Докажем, что векторы a ¯ = < 1 ; 2 >и b ¯ = < 2 ; – 1 >ортогональны.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 1 × 2 + 2 × ( – 1 ) = 2 – 2 = 0
Ответ: поскольку произведение равняется нулю, то векторы являются ортогональными.
Задача 2. Докажем, что векторы a ¯ = < 3 ; – 1 >и b ¯ = < 7 ; 5 >ортогональны.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 3 × 7 + ( – 1 ) × 5 = 21 – 5 = 16
Ответ: поскольку скалярное произведение не равняется нулю, то и векторы не являются ортогональными.
Задача 3. Найдем значение числа n , при котором векторы a ¯ = < 2 ; 4 >и b ¯ = < n ; 1 >будут ортогональными.
Как решить?
Найдем скалярное произведение данных векторов:
a ¯ × b ¯ = 2 × n + 4 × 1 = 2 n + 4 2 n + 4 = 0 2 n = – 4 n = – 2
Ответ: векторы являются ортогональными при значении n = 2 .
Примеры пространственных задач на ортогональность векторов
При решении пространственной задачи на ортогональность векторов a ¯ = < 1 ; 2 ; 0 >и b ¯ = < 2 ; – 1 ; 10 >условие записывается следующим образом: a ¯ × b ¯ = a x × b x + a y × b y + a z × b z = 0 .
Задача 4. Докажем, что векторы a ¯ = < 1 ; 2 ; 0 >и b ¯ = < 2 ; – 1 ; 10 >являются ортогональными.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 1 × 2 + 2 × ( – 1 ) + 0 × 10 = 2 – 2 = 0
Ответ: поскольку произведение векторов равняется нулю, то они являются ортогональными.
Задача 5. Найдем значение числа n , при котором векторы a ¯ = < 2 ; 4 ; 1 >и b ¯ = < n ; 1 ; – 8 >будут являться ортогональными.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 2 × n + 4 × 1 + 1 × ( – 8 ) = 2 n + 4 – 8 = 2 n – 4 2 n – 4 = 0 2 n = 4 n = 2
Ответ: векторы a ¯ и b ¯ будут ортогональными при значении n = 2 .
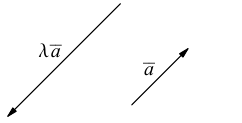
Ортогональность векторов. Перпендикулярность векторов.
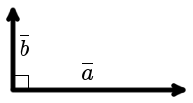
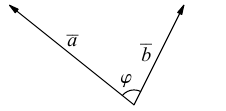
Вектора a и b называются ортогональными, если угол между ними равен 90°. (рис. 1).
 |
| рис. 1 |
Примеры задач на ортогональность векторов
Примеры плоских задач на ортогональность векторов
Так в случае плоской задачи для векторов a = < ax ; ay > и b = < bx ; by > , условие ортогональности запишется следующим образом:
Найдем скалярное произведение этих векторов:
a · b = 1 · 2 + 2 · (-1) = 2 – 2 = 0
Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Найдем скалярное произведение этих векторов:
a · b = 3 · 7 + (-1) · 5 = 21 – 5 = 16
Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.
Найдем скалярное произведение этих векторов:
a · b = 2 · n + 4 · 1 = 2 n + 4
2 n + 4 = 0
2 n = -4
n = -2
Ответ: вектора a и b будут ортогональны при n = -2.
Примеры пространственных задач на ортогональность векторов
Так в случае пространственной задачи для векторов a = < ax ; ay ; az > и b = < bx ; by ; bz >, условие ортогональности запишется следующим образом:
Найдем скалярное произведение этих векторов:
a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 – 2 + 0 = 0
Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Найдем скалярное произведение этих векторов:
a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0
Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Найдем скалярное произведение этих векторов:
a · b = 2 · n + 4 · 1 + 1 · (-8)= 2 n + 4 – 8 = 2 n – 4
2 n – 4 = 0
2 n = 4
n = 2
Ответ: вектора a и b будут ортогональны при n = 2.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Угол между векторами. Ортогональные проекции векторов
Угол между векторами
Углом между двумя ненулевыми векторами называется угол между равными им векторами, имеющими общее начало, не превосходящий по величине числа .
Пусть в пространстве даны два ненулевых вектора и (рис.1.22). Построим равные им векторы и . На плоскости, содержащей лучи и , получим два угла . Меньший из них, величина которого не превосходит , принимается за угол между векторами и .
Поскольку направление нулевого вектора не определено, то не определен и угол между двумя векторами, если хотя бы один из них нулевой. Из определения следует, например, что угол между ненулевыми коллинеарными векторами либо равен нулю (если векторы одинаково направлены), либо равен (если векторы противоположно направлены).
Ортогональные проекции векторов
Движение по любой прямой может быть в двух направлениях. Ориентированной прямой называется прямая, на которой выбрано направление, т.е. одно из направлений считается положительным, а противоположное — отрицательным. Для измерения длин отрезков на прямой задается масштабный отрезок, который принимается за единицу.
Ориентированная прямая с заданным масштабным отрезком называется осью.
Любой ненулевой вектор , принадлежащий прямой, называется направляющим вектором для данной прямой, поскольку задает на ней ориентацию. Направление вектора принимается за положительное, а направление противоположного вектора — за отрицательное. Кроме того, длину вектора — можно принять за величину масштабного отрезка на этой прямой. Поэтому можно сказать, что любой ненулевой вектор определяет ось — прямую, содержащую этот вектор, задавая на ней направление и масштабный отрезок.
Ортогональной проекцией вектора на ось, задаваемую вектором , называется его проекция на ось вдоль прямой (или вдоль плоскости), перпендикулярной данной оси. Ортогональную проекцию вектора на ось, задаваемую вектором , будем обозначать .
Ортогональную проекцию вектора на прямую (см. разд. 1.2.2 и рис. 1.13) будем обозначать .
Ортогональную проекцию вектора а на плоскость (см. разд. 1.2.2 и рис. 1.14) будем обозначать .
Разность между вектором и его ортогональной проекцией называют ортогональной составляющей:
— — ортогональная составляющая вектора относительно вектора ;
— — ортогональная составляющая вектора относительно прямой ;
— — ортогональная составляющая вектора относительно плоскости .
На рис. 1.23 изображены ортогональные проекции вектора :
— на прямую (или на ось , задаваемую вектором ) вдоль прямой (рис.1.23,а);
— на прямую (или на ось , задаваемую вектором ) вдоль плоскости (рис.1.23,б);
— на плоскость вдоль прямой (рис.1.23,в).
На рис. 1.23 изображены ортогональные составляющие вектора :
— относительно оси (вектора ): (рис.1.23,а);
— относительно плоскости (рис.1.23,в).
Для ортогональных проекций справедлива следующая теорема (см. теорему 1.1 в разд. 1.5).
Теорема 1.2 (об ортогональных проекциях вектора).
1. Если на плоскости заданы две взаимно перпендикулярные прямые и , то любой вектор на плоскости можно однозначно представить в виде суммы своих ортогональных проекций на эти прямые, т.е. (рис. 1.24,а).
2. Если в пространстве заданы три попарно перпендикулярные прямые и , пересекающиеся в одной точке, то любой вектор в пространстве можно однозначно представить в виде суммы своих ортогональных проекций на эти прямые, т.е. (рис. 1.24,6).
3. Квадрат длины вектора на плоскости или в пространстве равен сумме квадратов длин своих ортогональных проекций, т.е.
Первые два утверждения представляют собой частные случаи теоремы 1.1. Третье утверждение следует из теоремы Пифагора (для треугольника (рис. 1.24,а) или треугольников и (рис. 1.24,6)).
В формулировке теоремы 1.2 прямые можно заменить осями, задаваемыми попарно ортогональными векторами.
На рис.1.24,а проекции вектора на оси одновременно являются ортогональными составляющими: и . На рис. 1.24,6 вектор является проекцией вектора на плоскость , содержащую прямые и : , а вектор является ортогональной составляющей вектора относительно плоскости .
Алгебраическое значение длины проекции
Пусть – угол между ненулевым вектором и осью, задаваемой вектором , т.е. угол между ненулевыми векторами и .
Алгебраическим значением длины ортогональной проекции вектора на ось, задаваемую вектором , называется длина его ортогональной проекции , взятая с положительным знаком, если угол не превышает , и с отрицательным знаком, если угол больше , т.е.:
Например, для проекций, изображенных на рис. 1.25, 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAE8AAAAVBAMAAAD1D64kAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/cBBpYEhURAxkWFx4MHQtTUEJQAAAVlJREFUKM9jYKAAsBGrkKsATaB5AhZVRUpK+mKoQty3/LCpZDCu3YAqYDiB9QZWq4tBBHsEnO/PwCaNx6X7l8FYcgwMIgwMJlomWhOYnZarNECFmZ3KDMAMOzeogBQDgzwDQ46gZ4s420GRwANQhRsNHB9AWHbOEIWiDAyCDGDFFxuYJKZCTWSWZjAMgOoxUUZWKMTAsLCA6QNIqBWIeQWAZsJcl/IYVWFgAJMCA0No6FpQWDgwOMI9lHId6kYUhQwMJ4D44AGGe3B1YKvZ5MAeBylUnABRCAIHDdhEmZCdyMBwiYFNBkgJTuAWYeAHupEtBBTHiQX94qVgeSNPWDgk8IAiVd7LMYBVUFCBYVMCyFieW55fNEDS+9zgieTOQgOw1ZAY5xC3WQBJZJygkGJfhoikORUMEDeCAbvoTvypVB4a0twK+FPppkcvoTpucDoQl7CnRuOTBQA/mUGNQvQK+QAAAABJRU5ErkJggg==” style=”vertical-align: middle;” />, поскольку угол между векторами и острый, a , так как угол между векторами и тупой.
Некоторые свойства проекций векторов переносятся на алгебраические значения их длин, в частности:
1. — алгебраическое значение длины ортогональной проекции суммы векторов равно сумме алгебраических значений длин ортогональных проекций слагаемых;
2. — алгебраическое значение длины ортогональной проекции произведения вектора на число равно произведению этого числа на алгебраическое значение длины ортогональной проекции вектора
1. Из определения алгебраического значения длины ортогональной проекции следует (см. также рис.1.25), что , т.е. алгебраическое значение длины ортогональной проекции ненулевого вектора на ось равна произведению длины этого вектора на косинус угла между вектором и осью.
Ортогональную проекцию вектора на ось, задаваемую вектором , можно представить в виде
Если — единичный вектор, то .
2. Равенство можно использовать как определение косинуса угла между ненулевыми векторами и (или, что то же самое, косинуса угла между осями, заданными ненулевыми векторами и (рис. 1.26)).
3. Углом между ненулевым вектором и прямой называется угол между вектором и его ортогональной проекцией на прямую . Величина угла может быть найдена по формуле
4. Углом между ненулевым вектором и плоскостью называется угол между вектором и его ортогональной проекцией на плоскость . Величина угла может быть найдена по формуле
Пример 1.7. Основания и равнобокой трапеции равны и соответственно; точка — середина стороны (рис. 1.27). Найти алгебраические значения длин ортогональных проекций векторов и на ось, задаваемую вектором .
Решение. Пусть — высота трапеции, — точка пересечения прямых и . По свойству равнобокой трапеции ; из равенства треугольников и .
Обозначим через искомые алгебраические значения длин ортогональных проекций.Тогда из равенств
и свойства 1 алгебраических значений длин проекций следует:
[spoiler title=”источники:”]
http://ru.onlinemschool.com/math/library/vector/orthogonality/
http://mathhelpplanet.com/static.php?p=ugol-mezhdu-vektorami-i-ortogonalnye-proektsii-vektorov
[/spoiler]
В
ектор
– направленный отрезок.
Векторы коллинеарными,
если лежат на одной прямой, либо на
параллельных прямых.
Три вектора называются
компланарными,
если они лежат в одной плоскости или в
параллельных плоскостях.
– два вектора равны,
если они коллинеарны, имеют одинаковую
длину и направление.
Линейные операции над векторами
С
уммой
двух векторов
и
называется вектор, идущий из начала
вектора
в конец вектора
при условии, что начало вектора
приложено к концу вектора
(правило треугольника).
Свойства:
1
˚.
2˚.
3˚.
4
˚. Для
каждого вектора
существует противоположный ему вектор
,
такой, что
.
Разностью векторов
и
будет вектор
,
идущий из конца вектора
к концу вектора
.
Произведением
вектора
на вещественное число
.
Свойства операции умножения вектора
на число:
5
˚.
6˚.
7˚.
8˚.
Линейная зависимость векторов. Геометрические критерии линейной зависимости
Линейной комбинацией
векторов
называют выражение:
,
где
– произвольные действительные числа.
Система векторов
называется линейно зависимой, если
существуют действительные числа
,
такие, что хотя бы одно из них отлично
от нуля, и выполняется равенство:
.
(*)
В противном случае,
т.е. если линейная комбинация (*) обращается
в ноль только при всех
,
то система векторов называется линейно
независимой.
Если векторы линейно
зависимы, то любой
вектор может быть выражен в виде линейной
комбинации остальных.
Геометрические критерии линейной
зависимости
Система двух ненулевых
векторов
линейно зависима тогда, и только тогда,
когда векторы коллинеарны.
Система трех векторов
линейно зависима тогда и только тогда,
когда векторы компланарны.
Базис и координаты
Базисом в пространстве называются три
некомпланарных вектора, взятые в
определенном порядке.
Базисом на плоскости будем называть
два неколлинеарных вектора на этой
плоскости, взятые в определенном порядке.
Базисом на прямой будем называть любой
ненулевой вектор этой прямой.
Каждый
вектор может быть разложен по базису в
пространстве и это разложение единственно.
Коэффициенты разложения
вектора по базису называются координатами
вектора в данном базисе и в каждом базисе
определяются однозначно:
.
При сложении двух векторов
и
их координаты (относительно любого
базиса) складываются. При умножении
вектора
на любое число
все его координаты умножаются на это
число.
Системой координат
в пространстве называют совокупность
базиса
и некоторой точки, называемой началом
координат.
Вектор
,
идущий из начала координат в точку
,
называется радиус-вектором точки
.
Координатами точки
называются координаты вектора
.
Таким образом,
координаты радиус-вектора
и координаты точки
совпадают.
Ортонормированный базис. Декартова прямоугольная система координат
Пусть в качестве
базиса выбраны три взаимно перпендикулярных
вектора с длинами, равными единице.
Обозначения:
,
Т
акой
базис называется ортонормированным
(ОНБ). Векторы
называются базисными ортами. Зафиксируем
точку О
– начало координат и отложим от нее
векторы
.
Полученная система координат называется
прямоугольной
декартовой.
Координаты любого вектора в этом базисе
называются декартовыми координатами
вектора:
Прямые линии,
проведенные через начало координат по
направлениям базисных векторов,
называются координатными осями:
–
порождает
;
– порождает
;
–
порождает
.
Координаты точки М
(вектора
)
в декартовой системе координат по осям
,
,
называются соответственно абсциссой,
ординатой и аппликатой.
Декартовы прямоугольные координаты
вектора
равны проекциям этого вектора на оси
,
,
соответственно; другими словами,
,
,
.
Здесь
– углы, которые составляет вектор
с координатными осями
,
,
соответственно, при этом
,
,
называются направляющими косинусами
вектора
.
Вектор
представляет собой вектор единичной
длины данного направления, или орт
данного направления. Для направляющих
косинусов справедливо соотношение:
.
П
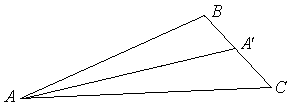
роекция
вектора
на ось l
–
величина А`В`
равна
,
где
– орт оси l.
Скалярным произведением
двух векторов называется число,
равное произведению длин этих векторов
на косинус угла между ними:
.
Если
,
,
то
.
Алгебраические и
геометрические свойства:
1°. Переместительное
свойство:
.
2°. Сочетательное
свойство:
3°. Распределительное
свойство:
,
.
4°.
,
если
,
и
,
если
.
5°.
;
.
6°.
.
7°.
=
,
.
8°.
:
– условие перпендикулярности.
9°.
,
– длина вектора.
10°.
,
,
– расстояние между двумя точками.
11°. Направляющие
косинусы вектора:
,
,
;
cos2
α
+ cos2
β
+ cos2
= 1
|
ПП 4.1. Векторы, базисы, координаты |
||
|
№ п/п |
Задание |
Ответ |
|
ПП 4 .№1 |
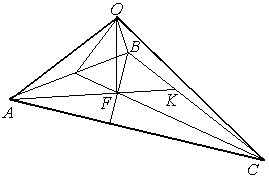
З и найдите координаты вектора – точка пересечения медиан основания РЕШЕНИЕ: Воспользуемся правилом треугольника:
Здесь – середина ребра находится на расстоянии длины медианы считая от вершины Но
Подставим в :
= |
= |
|
ПП 4 .№2 |
В пространстве заданы треугольники и и – точки пересечения медиан этих по базису векторов РЕШЕНИЕ:
Пусть – середина стороны – середина стороны
Найдем:
После последовательных подстановок
то есть |
= |
|
ПП 4 .№3 |
В треугольнике разложите биссектрису по базису векторов и РЕШЕНИЕ: Пусть , , лежит на стороне
Воспользуемся свойством биссектрисы и Отсюда следует, что
|
|
|
ПП 4. №4 |
В треугольнике через обозначена точка пересечения медиан. РЕШЕНИЕ:
О
|
|
|
ПП 4 .№5 |
Д считая от вершины. РЕШЕНИЕ:
Пусть – середина стороны , – середина стороны расстояние от вершины и поставим точку
Отложим от вершины по медиане расстояние и поставим точку . в базисе векторов и
Но это координаты и точка совпадают, это точка пересечения медиан, и она делит и в отношении считая от вершины. |
|
ПП 4 .№6 |
Т и – середины сторон и четырехугольника РЕШЕНИЕ:
Если – трапеция, стороны и параллельны, тогда
– свойство |
|
ПП 4.2. Переход к новому базису. |
||
|
ПП 4. №7 |
В пространстве векторы заданы своими координатами в базисе представляет собой базис в пространстве , в этом базисе, если РЕШЕНИЕ: Проверим, что – базис в пространстве :
значит – базис.
Найдем координаты в базисе двумя
1-й
2-й преобразования координат базиса к базису :
Найдем обратную матрицу:
Координаты вектора в новом базисе обозначим
|
или
|
|
ПП |
||
|
ПП 4 .№8 |
Применяя пространства ,
РЕШЕНИЕ:
Процесс ортогонализации строят новый, ортогональный базис по
Проделаем эту процедуру.
Осталось нормировать
|
, , . |
|
ПП 4.4. Декартов прямоугольный базис |
||
|
Направляющие косинусы и координаты |
||
|
ПП 4 .№9 |
В трапеции с основаниями и известны векторы и – середины сторон и . РЕШЕНИЕ:
|
3 |
|
ПП 4 .№10 |
Даны точки РЕШЕНИЕ:
|
-6 |
|
ПП 4 .№11 |
Дан модуль вектора и углы и , и соответственно. Вычислите проекции на координатные оси. РЕШЕНИЕ:
= |
|
|
ПП 4. №12 |
Даны векторы и РЕШЕНИЕ:
|
, , |
|
ПП 4 .№13 |
Может ли вектор , , ? РЕШЕНИЕ:
Для направляющих
|
да |
|
ПП 4. №14 |
Д треугольника . РЕШЕНИЕ: Координаты точки (середины ) |
7 |
|
ПП 4. №15 |
Коллинеарны ли и и РЕШЕНИЕ:
Пропорциональность не выполняется, векторы неколлинеарны. |
нет |
|
ПП 4.5. Скалярное произведение векторов |
||
|
ПП 4. №16 |
Найдите а) и б) РЕШЕНИЕ:
а)
|
а) |
|
ПП 4 |
Найдите РЕШЕНИЕ:
|
|
|
ПП 4. №18 |
Найдите косинус и , РЕШЕНИЕ:
|
-1 |
|
ПП 4. №19 |
Вычислите синус и РЕШЕНИЕ: Найдем косинус нужного угла:
Так как угол между |
|
|
ПП 4. №20 |
Для вектора найдите ортогональную составляющую и ортогональную составляющую в и РЕШЕНИЕ:
Найдем проекцию на орт :
вдоль равна и и .
в плоскости и лежит составляющая |
|
|
ПП 4. №21 |
Покажите, что сумма квадратов медиан РЕШЕНИЕ:
П
Осталось найти
|
|
ПП 4. №22 |
П ромб, если РЕШЕНИЕ:
и – ромб.
|
|
|
ПП 4. №23 |
Докажите, что вектор перпендикулярен вектору . РЕШЕНИЕ:
|
|
|
ПП 4. №24 |
Д Доказательство:
а) Рассмотрим , и
Пусть третья сторона
Теорема
б) При |
|
|
ПП 4. №25 |
Д РЕШЕНИЕ:
Пусть и – стороны ромба.
и – его диагонали.
так как для ромба |
17
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Векторы
- Действия над векторами
- Умножение вектора на число
- Скалярное произведение векторов
- Векторное произведение
- Смешенное произведение векторов
- Разложение вектора по базису
- Действия над векторами, заданными своими координатами
- Проекция вектора на ось
- Проекции вектора на оси координат
- Направляющие косинусы вектора
- Разложение вектора по ортам
- Действия над векторами, заданными в координатной форме
- Вектор – основные определения
- Операции над векторами и их свойства
- Сформулируем и докажем ещё одну важную для решения некоторых задач теорему.
- Координаты вектора
- Скалярное произведение векторов и его свойства
- Векторы и их решение
- Собственные числа и собственные векторы
- Векторная алгебра
- Векторы: основные определения, линейные операции
- Линейные операции над векторами
- Умножения вектора на скаляр
- Основные свойства проекции вектора на ось
- Прямоугольная система координат в пространстве. Координатная и алгебраическая формы задания векторов
- Скалярное, векторное, смешанное произведения векторов
- Векторное произведение двух векторов
- Смешанное произведение векторов, заданных в координатной форме
- Простейшие задачи аналитической геометрии
- Задача об определении площади треугольника
- Задача о деление отрезка в заданном отношении
Векторы
В математике вектором называют величину, которая характеризуется только числом и направлением. Так определённые векторы ещё называют свободными векторами. Примером физических величин, которые имеют векторный характер являются скорость, сила, ускорение. Геометрически вектор — это направленный отрезок, хотя правильней говорить про целый класс направленных отрезков, которые все параллельны между собой, имеют одинаковые длину и направление.
Векторы обозначают малыми латинскими буквами с чертой сверху 


Действия над векторами
Рассмотрим основные действия, определённые над векторами.
1. Сложение векторов. Суммой векторов 





Учитывая, что 

Вычитание векторов сводится к сложению противоположного вектора
Запишем основные свойства действий сложения векторов:
Заметим, что сумма нескольких векторов находится последовательным сложением двух из них, например:
Геометрически сумма нескольких векторов находится их последовательным отложением один за одним так, чтоб начало следующего совпадало с концом предыдущего. Суммой является вектор, который будет соединять начало первого с концом последнего (рис. 4). Если такая последовательность векторов даёт замкнутую ломаную то суммой векторов является 
Умножение вектора на число
Произведением вектора 


а) 
б) 




Запишем основные свойства действий умножения вектора на число:
Скалярное произведение векторов
Скалярным произведением 






Очевидно, что скалярное произведение двух ненулевых векторов будет равно нулю тогда и только тогда когда эти вектора перпендикулярны (ортогональны). Действительно, если 

Наоборот, если 

Например, скалярное произведение 
Запишем основные свойства действий скалярного умножения векторов:
Векторное произведение
Векторным произведением 



1) модуль вектора 


2) вектор 


3) вектор 





Модуль векторного произведения равен площади параллелограмма, построенного на векторах 







Приведём основные свойства векторного произведения:
1) векторное произведение 


2) от перестановки местами векторов-сомножителей векторное произведение меняет знак на противоположный: 
3) 
4) 
Физическое содержание векторного произведения такое. Если 







Смешенное произведение векторов
Смешенным произведением векторов 



Как результат скалярного произведения векторов 


Действительно, 




Объём V параллелепипеда, построенного на векторах 
Однако, знак смешенного произведения совпадает со знаком 




Из геометрического содержания смешенного произведения выходит, что
1) смешанное произведение равно нулю тогда и только тогда, когда перемноженные вектора копланарные (условие компланарных векторов);
2)
Учитывая коммутативность скалярного произведения и антикоммутативность векторного, для произвольных векторов 
Пример 1.
Доказать, что когда М — точка АВС и О — произвольные точки пространства, то выполняется равенство:
Решение.
Пусть 



тогда
Пример 2.
У прямоугольного параллелепипеда рёбра 




Решение.
Пусть 

рис. 9.
Далее,
Этим закончен “перевод” условия задачи на “язык” векторов.
Теперь произведём вычисления с векторами:
Наконец “переводим” полученные вектора равенства снова на “геометрический язык”. Поскольку 

Далее поскольку 




Разложение вектора по базису
Базисом на площади называют упорядоченную пару неколлинеарных векторов и точку отсчёта.
Теорема. Любой вектор 



Доказательство.
Пусть векторы 





Тогда по правилу параллелограмма 
Но 

Числа, которые стоят при базисных векторах в разложении вектора за двумя неколлинеарными векторами называют координатами вектора в данном базисе и обозначают 
Соответственно в пространстве базисом называется упорядоченная тройка некомпланарных векторов и точки отсчёта. Для четырёх некомпланарных векторов справедлива следующая теорема.
Теорема. Любой вектор 




Доказательство.
От точки О отложим векторы 


в котором вектор 
Числа х,у,z которые стоят при базисных векторах в разложении вектора по трём некомпланарным векторам называют координатами вектора в пространстве и обозначают 






Отсюда легко установить длину вектора как расстояние между двумя точками:
Действия над векторами, заданными своими координатами
1. При сложении двух, или более векторов их соответствующие координаты складываются:
Действительно:
2. При вычитании векторов соответствующие координаты вычитаются:
Доказательство аналогично предыдущему.
3. При умножении вектора на число все координаты умножаются на это число.
Правда, для вектора 

4. Скалярное произведение двух векторов 
Правда:
Поскольку 

5. Векторное произведение векторов 
6. Смешенное произведение трёх векторов 
Пример 1.
Зная координаты векторов 

Решение:
Ответ: 
Пример 2.
Зная координаты векторов 

Решение.
Ответ: 
Пример 3.
Зная координаты векторов 
а) скалярное произведение векторов
б) векторное произведение векторов
в) смешенное произведение векторов 
Решение.
Ответ:
На основании приведённых выше формул действий над векторами можно установить следующие условия и соотношения для нулевых векторов
1. Угол между векторами.
2. Условие перпендикулярности двух векторов:
(векторы перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю).
3. Условие коллинеарности двух векторов: 
4. Условие компланарности трёх векторов.
(три вектора компланарны тогда и только тогда, когда их смешенное произведение равно нулю).
5. Деление отрезка АВ в заданном отношении.
Если точка 

Если точка М делит отрезок АВ на пополам то 
Действия над векторами (теория)
а) Произведение вектора на число.
Определение 1. Произведением вектора 

который имеет длину 

Рис. 12.
Условие 
является условием коллинеарности двух векторов.
б) Сложение векторов.
Определение 2. Суммой двух векторов 






Рис. 13.
Понятно, что вектор 


Для векторной суммы справедливый переместительный закон
Легко убедиться, что для векторной суммы имеет место соединительный
закон 
Исходя из определения 2, легко находим сумму, например, четырех векторов 
Рис. 14.
Вектор 


в) Вычитание векторов.
Действие вычитание векторов можно рассматривать как обратное действие относительно сложения векторов.
Определение. Разностью 



Рис. 15.
Как видно из рис. 15, одна диагональ 




Дадим еще одно определение разности векторов.
Определение. Разностью двух векторов 


Проекция вектора на ось
Пусть имеем произвольную ось l на плоскости и некоторый вектор 
Рис. 16.
Опустим из начала A вектора и из конца B перпендикуляры на ось l. Основаниями перпендикуляров будут точки A1 и B1, которые называются проекциями точек A и B.
Величина A1B1 называется проекцией вектора 


Определение 1. Проекцией вектора 
Из точки A проведем прямую, параллельную оси l, которая пересечет отрезок BB1 в точке C. Вектор 


Определение 2. Проекция вектора на любую ось равна произведению длины этого вектора на косинус угла между осью и вектором.
Если угол φ острый, то проекция 

Свойства проекций.
1. Если векторы 


2. Проекция суммы векторов на любую ось равна сумме проекций слагаемых на ту же ось, то есть:
3. Проекция разности двух векторов на ось l равна разности величин проекций на ту же ось, то есть:
4. Если вектор 

Проекции вектора на оси координат
Рассматривается прямоугольная система координат Oxyz в пространстве и произвольный вектор 
Пусть 
Проекции x, y, z вектора 

Если заданы две точки A (x1; y1; z1) и B (x2; y2; z2), то координаты вектора 
x = x2 – x1, y = y2 – y1, z = z2 – z1 .
Рис. 17
Действительно, проведем через точки A и B плоскости, перпендикулярные оси Ox и обозначим точки их пересечения соответственно A1 и B1 (рис.17). Точки A1 и B1 имеют на оси Ox координаты x1 и x2 , но 
x = x2 – x1 . Аналогично доказывается, что y = y2 – y1, z = z2 – z1 .
Направляющие косинусы вектора
Пусть имеем вектор 
Рис. 18
Через точку M проведем плоскости, перпендикулярные к осям координат, и вместе с координатными плоскостями они образуют параллелепипед, диагональ которого — отрезок OM (рис.18). Через α, β, γ обозначим углы, которые образует вектор 


Квадрат диагонали прямоугольного параллелепипеда равна сумме квадратов длин трех его измерений.
Поэтому


Формула (2.8) выражает длину вектора через его координаты. Тогда на основе формул (2.7) и (2.8) получим
Отсюда для направляющих косинусов получаем

Для направляющих косинусов справедливо равенство 
Разложение вектора по ортам
Рассмотрим прямоугольную систему координат в пространстве и вектор, начало которого в точке O (рис.19) .
Рис. 19.
Обозначим орты осей координат Ox, Oy, Oz соответственно через 
Спроецируем вектор 
Из прямоугольника ODMC видно, что вектор 

Тогда

Вектор 
Векторы 




Подставляя эти значения в равенство (2.10), учитывая, что 

Слагаемые 

Тройка векторов 

Пример 1. Построить вектор 
Рис. 20.
Решение. Компоненты вектора 


соответствует прямоугольный параллелепипед, диагональ которого является искомый вектор (рис. 20).
Действия над векторами, заданными в координатной форме
Если векторы заданы в координатной форме, то действия сложения, вычитания, умножения вектора на число можно заменить простыми арифметическими операциями над координатами этих векторов по таким правилам.
Правило 1. При сложении векторов их одноименные координаты складываются
Пусть имеем векторы 





Сложив эти равенства, получим

Итак, координаты вектора 
Правило 2. Чтобы отнять от вектора 



Правило 3. Чтобы умножить вектор 


Пример 1. Найти вектор 
Решение. Выполним действия последовательно и найдем

Значит,
Вектор – основные определения
Определение вектора в пространстве ничем не отличается от определения вектора на плоскости.
Определение 1. Вектором называется направленный отрезок, т.е. отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.
Так же как и на плоскости, векторы обозначаются 
Определение 2. Длиной (или модулем) вектора 


Длина вектора 


Любая точка пространства также считается вектором, который называется нулевым. Начало такого вектора совпадает с его концом, а длина равна нулю. Обозначения нулевого вектора:
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Определение 3. Векторы 

Если ненулевые векторы 







Ясно, что сонаправленные векторы, в силу их определения, коллинеарны. Если два коллинеарных вектора не сонаправлены, то они называются противоположно направленными. Обозначения остаются обычными: 





Определение 4. Векторы 



Теорема 1. От любой тонки пространства можно отложить вектор, равный данному, и притом только один.
Доказательство этой теоремы аналогично доказательству соответствующей планиметрической теоремы.
Возможно вам будут полезны данные страницы:
Операции над векторами и их свойства
Операции над векторами в пространстве аналогичны соответствующим операциям на плоскости.
Пусть даны два вектора 








Теорема 2. Сумма 




Правило треугольника можно сформулировать и так: для любых трёх точек 
Кроме того, сумму двух неколлинеарных векторов с общим началом можно построить и по правилу параллелограмма: 




Все свойства операции сложения векторов, справедливые на плоскости, остаются справедливыми и в пространстве:
1)
2) 
3) 
Здесь 
Определение 5. Два ненулевых вектора называются противоположными, если их длины равны и эти векторы противоположно направлены.
Вектор, противоположный данному ненулевому вектору 
Определение 6. Разностью двух векторов 



Разность векторов 



Разность векторов 



Из законов сложения векторов следует, что сумма нескольких векторов не зависит от порядка слагаемых.
Умножение (произведение) вектора на число и его свойства, так же как и свойства операции сложения, не претерпевают изменений и в пространстве.
Определение 7. Произведением ненулевого вектора 








Таким образом, по определению, 






Свойства умножения вектора на число не отличаются от аналогичных свойств на плоскости:
-
— ассоциативность (сочетательный закон);
-
—дистрибутивность относительно сложения векторов (1-й распределительный закон);
-
— дистрибутивность относительно сложения чисел (2-й распределительный закон).
Здесь 


Справедлива также и лемма о коллинеарных векторах: если векторы 


что 

Сформулируем и докажем ещё одну важную для решения некоторых задач теорему.
Теорема 3. Пусть 



Доказательство
1. Из равенства 





2. Пусть 




З. Компланарные и некомпланарные векторы
Следующее понятие уже не имеет аналога в планиметрии.
Определение 8. Векторы называются компланарными, если лучи, задающие их направления, параллельны некоторой плоскости.
Замечание. Из определения 8 следует, что при откладывании от одной точки векторов, равных нескольким данным компланарным векторам, получим векторы, лежащие в одной плоскости. Таким образом, компланарные векторы лежат либо в одной плоскости, либо в параллельных плоскостях.
Очевидно, что любые два вектора компланарны и любые три вектора, два из которых коллинеарны, также являются компланарными (поясните). Рассмотрим теперь условия, при которых три вектора, из которых никакие два не коллинеарны, являются компланарными.
Теорема 4. Векторы 




Доказательство
1. Пусть векторы 
точки 
















Докажем, что векторы 






Отложим от произвольной точки 







Если векторы 






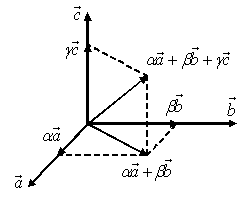
Следующая теорема, называемая теоремой о разложении вектора по трём некомпланарным векторам, является основной во всей элементарной (школьной) векторной алгебре.
Теорема 5. Любой вектор 




2. Пусть векторы 





















3. Докажем теперь, что разложение вектора 



Тогда
отсюда
– т. е. векторы
компланарны, что противоречит условию теоремы. Значит, наше допущение о ещё одном разложении неверно, т.е. разложение вектора
по данным векторам
единственно. Теорема доказана.
Итак, любой вектор 





Координаты вектора
Так же как и на плоскости, в пространстве помимо координат точки вводятся координаты вектора. Рассмотрим три попарно перпендикулярных вектора 












Свойства векторов пространства, заданных своими координатами, аналогичны соответствующим свойствам векторов на плоскости:
- Два вектора равны в том и только том случае, если равны их координаты.
- Координаты суммы (разности) двух векторов равны суммам (разностям) соответствующих координат этих векторов, т.е. для векторов
получаем
- При умножении вектора на число каждая его координата умножается на это число, т.е. для вектора
и действительного числа
получаем
Докажем, например, свойство 2. Так как 



Скалярное произведение векторов и его свойства
Определение скалярного произведения векторов 

Определение 11. Скалярным произведением векторов 

Теорема 8. Два ненулевых вектора 

Доказательство этой теоремы вытекает из формулы (9).
Определение 12. Скалярным квадратом вектора 


Так как 
Таким образом, длина вектора равна квадратному корню из его скалярного квадрата.
Замечание. Скалярное произведение есть число, поэтому грубой ошибкой явилась бы запись:
Если векторы 


Теорема 9. Скалярное произведение векторов равно сумме произведений их соответственных координат, т. е.
Доказательство. Отложим от произвольной точки 







итак как 


поэтому
Решение любой геометрической задачи на вычисление сводится, в сущности, к нахождению величин двух типов: расстояний и углов. Если в пространстве задан некоторый базис (в частности, прямоугольный), т. е. тройка некомпланарных векторов, то на основании теоремы 5 любой вектор пространства можно разложить по векторам этого базиса, причём единственным образом.
Если известны длины векторов, образующих базис, углы между ними и разложение некоторого вектора по векторам этого базиса, то, используя свойства скалярного произведения, можно определить длину такого вектора и угол, образуемый им с любым другим вектором, разложение которого по векторам этого базиса известно.
Таким образом, векторы позволяют находить решения довольно широкого класса геометрических задач, а умение определять разложение вектора по базисным векторам является важнейшим фактором их решения.
Для решения задач о разложении вектора по трём данным некомпланарным векторам, разумеется, необходимо, помимо теоремы 5, знание предшествующего ей материала.
Примеры с решением
Задача 1.
Основанием четырёхугольной пирамиды 






Решение (см. рис. 14).
1. 

2. Так как 


Ответ:
Заметим, что в разложении вектора 








Задача 2.
Пусть 


Решение (см. рис. 15). Пусть 






Ответ:
Векторы и их решение
Вектором называется направленный отрезок. Направление отрезка показывается стрелкой. Различают начало и конец отрезка.
Два вектора называются равными между собой, если каждый из них можно получить параллельными перенесениями другого.
Равные векторы являются параллельными (колинеарными), имеют одно и то же направление и одинаковую длину. Длина вектора 
Вектор называется нулевым (ноль- вектором), если он имеет нулевую длину, то есть его конец сходится с началом.
Чтобы найти сумму двух векторов 



Суммой 






Для складывания векторов имеют место такие законы:
1) переставной (коммутативный)
2) связующий
3) для каждого вектора 

4)
5) для некоторых двух векторов 

Если вектор 



Пусть вектор имеет начало в точке 





Если вектор 
Произведением вектора 






Любой вектор 
где 



Пример 1.73
Даны два вектора: 

Найти вектор
Решение
Признаком колинеарности двух векторов 

Скалярным произведением двух векторов 


Скалярное произведение можно записать в таком виде:
Если векторы 

Учитывая формулы (1.18) и (1.19), можно найти косинус угла между векторами 

Отсюда получается условие перпендикулярности двух векторов: если 

Среди свойств скалярного произведения отметим так:
Векторным произведением вектора 


1) длина вектора 
2) вектор 

3) из конца вектора 


Заметим, что 


В координатной форме векторное произведение векторов 

Смешанным или скалярно – векторным произведением трех векторов 



Если векторы 
Если известные координаты сомножителей 
Если три ненулевых 
Следует, в координатной форме условие компланарности трех ненулевых векторов имеет вид:
Решение примеров:
Пример 1.74
Заданы координатами точек 


1) вектор 
2) угол между векторами 
3) координаты вектора
4) объем пирамиды с вершинами в точках
Решение
1) По формуле (1.14) находим
тогда
2) Косинус угла между векторами 

Поскольку косинус угла отрицательный, то угол 
3) Координаты векторного произведения находим по формуле (1.22):
4) Чтобы найти объем пирамиды, найдем сначала смешанное произведение векторов, что выходят из одной вершины пирамиды:
Тогда объем пирамиды
Собственные числа и собственные векторы
Вектор – столбец 




Тут 



Координаты собственного вектора 

Собственный вектор обозначаются с точностью к постоянному множителю.
Решение примеров:
Пример 1.90.
Обозначить собственные определения и собственные векторы матрицы
Решение. Характеристические уравнения данной матрицы имеет вид (1.24):

отсюда получается, что матрица 





которое приводится к одному уравнению
Возьмем 
Следует, первый собственный вектор является
Второй вектор 

Эта система уравнений так же приводится к одному уравнению 


Таким образом, матрица 




Пример 1.91
Найти собственные векторы и собственные значения матрицы
Решение. Характеристическое уравнение
Раскрыв определитель получим:
Корень 


Система уравнений для определения собственных векторов имеет вид:
Последовательно подставим 

Фундаментальная система уравнений получается, если свободным переменным 
Получили два линейно независимые собственные векторы. Вся совокупность векторов, что соответствуют собственному значению 
Фундаментальная система решений получается, если взять
Векторная алгебра
Понятие «вектор» (от лат. vector – носитель), как отрезка, имеет определенную длину и определенное направление, впервые появилось в работах по построению числовых систем в ирландского математика Уильяма Гамильтона (1805-1865). Это понятие связано с объектами, которые характеризуются величиной и направлением, например, скорость, сила, ускорение. При этом скорость можно понимать в широком смысле: скорость изменения издержек производства, доходов, спроса, потребления и предложения и др. Вектор может указывать направление наибольшего возрастания или убывания функции, описывающей различные экономические процессы. Векторы, рассмотренные в данном разделе, является частным случаем 
Для графического изображения решения экономических задач на плоскости и в пространстве применяются средства аналитической геометрии. Аналитическая геометрия – математическая наука, объектом изучения которой являются геометрические фигуры, а предметом – установление их свойств средствами алгебры с помощью координатного метода. Теоретической базой этой науки является частично известна из школы векторная алгебра.
Основателем метода координат и, вместе с тем, аналитической геометрии является Рене Декарт (1596-1650) – французский философ, математик, физик и физиолог. Его именем и названа известная «декартова прямоугольная система координат», которая позволяет определить положение фигуры на плоскости и тела в пространстве.
После изучения данной темы вы сможете:
● использовать инструмент векторной алгебры для геометрического изображения и анализа объектов экономических процессов;
● применять уравнение прямой линии на плоскости для геометрической интерпретации зависимости между функциональному признаку и аргументом, что на нее влияет;
● применять уравнение кривых второго порядка при построении нелинейных математических моделей экономических задач;
● осуществлять геометрическую интерпретацию решений экономических задач с помощью поверхностей и плоскостей.
Векторы: основные определения, линейные операции
Выберем на произвольной прямой (в 






алфавита с чертой: 
Рис. 6.1
В применимых задачах естественных наук существенным является обстоятельство – где, в какой точке находится начало вектора. Например, результат действия силы зависит не только от ее величины и направления действия, но и от того, в какой точке она прикладывается.
Вектор, для которого фиксированная (не фиксирована) начальная точка называется связанным (свободным). Векторы, которые применяются в экономических задачах, как правило, не являются связанными, поэтому в дальнейшем будем рассматривать преимущественно свободные векторы
Длиной, или модулем, вектора называется длина соответствующего отрезка и обозначается одним из символов:
Нулевым вектором 0, или ноль-вектором, называется вектор, длина которого равна нулю, а направление его считается произвольным (неопределенным).
Единичным вектором 
Равными векторами называются векторы, которые принадлежат одной прямой или параллельным прямым, одинаково направлены и имеют равные длины.
Взаимно противоположными называются векторы, которые принадлежат одной прямой или параллельным прямым, имеют равные длины, но противоположно направлены. Вектор, противоположный вектору 

Коллинеарными называют векторы, которые принадлежат одной прямой или параллельным прямым.
Компланарными называются векторы, которые принадлежат одной плоскости или параллельным плоскостям.
Линейные операции над векторами
Будем считать, что векторы 



1. Суммой векторов 


Параллельный перенос можно осуществить и так, что объединятся начала векторов 

Рис. 6.2
Правило треугольника обобщается на произвольное конечное число векторов. Если параллельным переносом расположить векторы так, что конец предыдущего вектора (начиная с первого) является началом следующего, то результирующим будет вектор, соединяющий начало первого вектора слагаемого с концом последнего (рис. 6.3):
Рис. 6.3
Соответствующее правило называют правилом многоугольника.
Свойства суммы векторов:
1) переставная, или коммутативна:
2) соединительная, или ассоциативная:
3)
4)
Разницу 

Умножения вектора на скаляр
Пусть 










Рис. 6.4
При


Свойства умножения вектора на скаляр:
1) переставной или коммутативных закон:

2) соединительный, или ассоциативный закон:

3) распределительный или дистрибутивный закон:

4)
5)
Из определения умножения вектора на скаляр следует необходимое и достаточное условие коллинеарности двух векторов: вектора 

Известно, что три ненулевые векторы 


Рассмотрим понятие, имеет очень важное значение в теории векторов – проекции вектора на ось (прямую, имеет направление; заданное направление считать положительным, противоположное направление – отрицательным).
Компонентой вектора 





Рис. 6.5
Проекцией вектора 






Основные свойства проекции вектора на ось
1. Проекция вектора на ось 

2. Проекция суммы двух векторов на эту ось равна сумме их проекций на эту ось:
Это свойство обобщается на любое конечное число векторов.
3. Проекция на ось произведения вектора со скаляром равна произведению со скаляром проекции самого вектора на ось:
Прямоугольная система координат в пространстве. Координатная и алгебраическая формы задания векторов
Пусть в трехмерном векторном пространстве 


Рис. 6.6
Выберем в пространстве произвольную точку 





Под декартовыми прямоугольными координатами точки 

Точка 





Измерениями параллелепипеда есть модули координат точки 
Углы 


откуда:
Косинусы направляющих углов называются направляющими косинусами радиус-вектора 
1) направляющие косинусы являются координатами единичного радиус-вектора:
2) сумма квадратов направляющих косинусов вектора 
Понятие «координата», «направляющие углы», «направляющие косинусы» без изменений переносятся на любые свободные векторы, потому начало каждого из них параллельным переносом можно поместить в начало 
Координатами любого вектора 



Задача вектора тройкой его координат 
Для единичных векторов 

Длина произвольного вектора 
Найти длину и направляющие косинусы вектора
По формулам (6.5) имеем:
Установим связь между координатами вектора – числами – и его компонентами – векторами – с помощью единичных векторов 
Рис. 6.7
Компонентами вектора 


Следовательно, любой вектор 
Изображение вектора с 
Согласно свойствами операций над векторами, алгебраическая форма задания дает возможность установить результаты действий над векторами, заданными в координатной форме.
1. При добавлении (вычитании) двух векторов с 


Действительно, по свойствам ассоциативности и дистрибутивности имеем:
2. При умножении вектора 

Действительно, согласно распределительным свойствам умножения скаляра на сумму векторов имеем:
Скалярное, векторное, смешанное произведения векторов
Скалярным произведением двух векторов 



Вместо 


Для определения угла 







Основные свойства скалярного произведения векторов вытекают из его определения (6.7).
1. Скалярное произведение 
2. Скалярный квадрат вектора равен квадрату его модуля, то есть
3. Скалярное произведение подчиняется всем законам арифметики чисел относительно линейных операций:
4. Скалярное произведение двух векторов равно произведению модуля одного из них с проекцией второго на ось, направление которого определяется первым вектором:
Доказательство этого свойства основывается на определении (6.3).
Скалярное произведение векторов 

1. Вычислим скалярные произведения единичных векторов 

2. Находим произведение 
Раскрываем скобки и получаем:
Скалярное произведение двух векторов равно сумме произведений одноименных координат. Это полностью совпадает с определением скалярного произведения 
Как следствие из (6.12) при 
Определим угол между двумя ненулевыми векторами 

Следовательно, косинус угла между двумя векторами определяется формулой:
Отсюда
В результате с соотношением (6.13) получим критерий ортогональности двух векторов, заданных в координатной форме:
Критерием коллинеарности векторов 

Векторное произведение двух векторов
Пусть 








1) модуль его численно равен площади параллелограмма, построенного на векторах 

2) он перпендикулярный плоскости параллелограмма 



Рис. 6.9
Векторное произведение обозначается символами: 
Следовательно,
где 




Основные свойства векторного произведения вытекают из его определения.
1. Векторное произведение ненулевых векторов равно ноль-вектору тогда и только тогда, когда векторы 

Еще одним критерием коллинеарности векторов является равенство нулевому вектору их векторного произведения.
2. Векторные произведения с разным порядком сомножителей являются взаимно противоположными векторами:
Это означает, что векторное произведение не подчиняется переставному (коммутативному) закону.
3. Векторное произведение подчиняется ассоциативному закону относительно скалярного множителя и дистрибутивному закону относительно сложения:
где
Векторное произведение векторов 

1. Определяем векторные произведения ортов 
Векторное произведение одноименных векторов по свойству 1 дает ноль вектор:
Однако все векторные произведения разноименных единичных векторов будут давать единичные векторы:
Рис. 6.10
Рассмотрим, например, произведение 




2. Находим произведение 
Множители при 
Коэффициенты при единичных векторах в соотношении (6.20) являются координатами вектора 


Если символы 

Найдем векторное произведение векторов 
Модуль векторного произведения 

Смешанным произведением трех векторов 


Смешанное произведение можно обозначать тройкой векторов 





Геометрическая интерпретация смешанного произведения. Пусть 

Рис. 6.11
Вектор 





Согласно (6.11) скалярное произведение 



где 




Модуль смешанного произведения трех векторов численно равен объему параллелепипеда 
Основные свойства смешанного произведения вытекают из его определения и геометрической интерпретации.
1. Смешанное произведение ненулевых векторов равно нулю, если по крайней мере два из трех векторов коллинеарны или все три – компланарны, и наоборот.
Необходимым и достаточным условием компланарности трех ненулевых векторов является равенство нулю их смешанного произведения:

Свяжем с изображенными на плоскости векторами 
2. Циклическая перестановка трех сомножителей смешанного произведения не меняет его величины, а отрицательное перестановки меняет его знак на противоположный:
Смешанное произведение векторов, заданных в координатной форме
Пусть имеем три ненулевые векторы 
Полученная сумма произведений является расписанием определителя 3-го порядка, составленный из координат векторов, по элементам его третьей строки, то есть:
Векторы 

С помощью смешанного произведения векторов легко определить, относятся ли четыре точки 
Простейшие задачи аналитической геометрии
Задача об определении длины отрезка. Найти длину отрезка 

1. Введем в рассмотрение вектор 



2. Определим координаты вектора 


3. Находим модуль вектора 

Задача об определении площади треугольника
Найдем площадь треугольника, заданного координатами вершин:
По аксиомой стереометрии известно, что три точки в пространстве определяют плоскость и притом только одну. Для упрощения изложения, не нарушает общего подхода к решению задачи, договоримся рассматривать треугольник 



1. Введем в рассмотрение векторы:
и найдем их векторное произведение
По соотношению (6.20) имеем:
2. Вычислим модуль вектора 


Тогда для площади треугольника 
Знак 

Если треугольник принадлежит не плоскости 
Найдем площадь треугольника с вершинами 

Введем в рассмотрение векторы: 


Тогда

Задача о деление отрезка в заданном отношении
Пусть в пространстве заданы две точки 







Рис. 6.15
Число 
называется отношением, в котором точка 



Задача о деление отрезка в заданном отношении формулируется так: найти координаты точки 




Пусть точкам 




С этого векторного равенства найдем вектор
или в координатах:
Отсюда, если отрезок разделить на две равные части точкой 

Можно доказать, что координаты точки пересечения медиан треугольника, заданного координатами его вершин 
Лекции:
- Объем конуса
- Разложение на множители
- Деление многочлена на многочлен
- Правила дифференцирования
- Теорема Пифагора
- Асимптотическое поведение функций. Сравнение бесконечно малых функций
- Прямая линия на плоскости
- Выпуклость и вогнутость графика функции
- Матанализ для чайников
- Производные некоторых элементарных функций

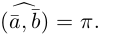
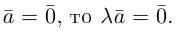
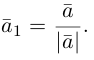
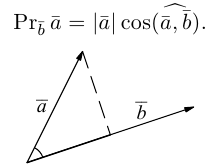
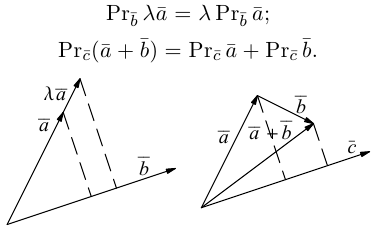
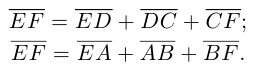
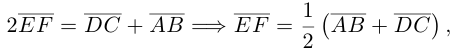
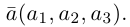
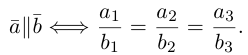
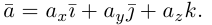
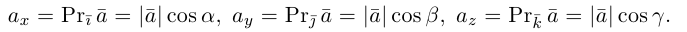
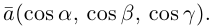
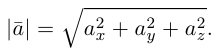
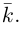

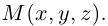
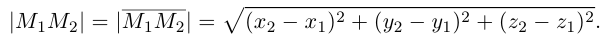
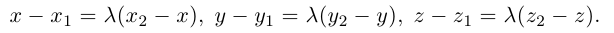
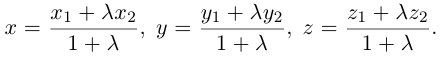
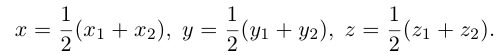
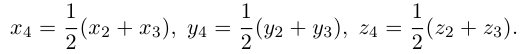
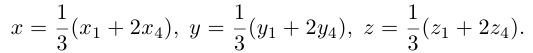
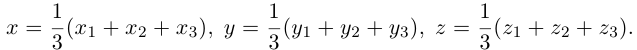


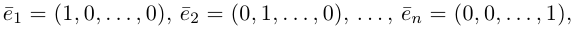
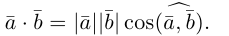
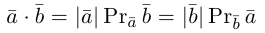
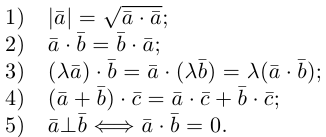
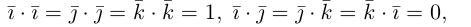
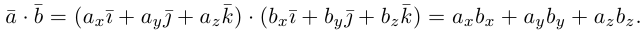
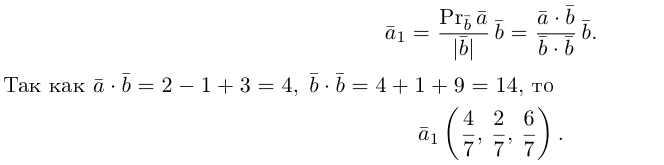
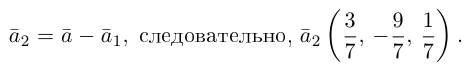
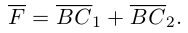
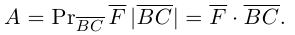
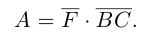
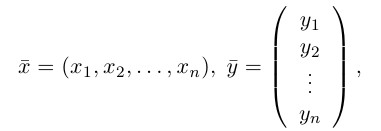
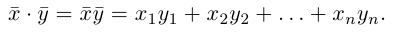
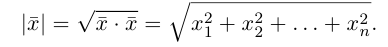
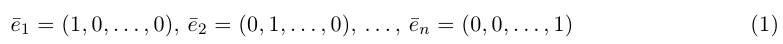
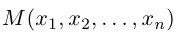

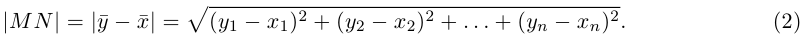
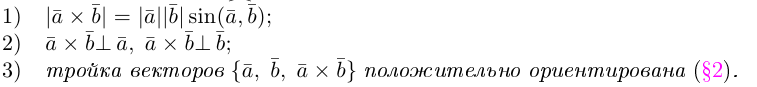
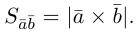
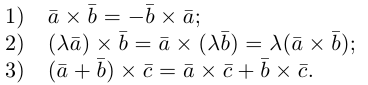
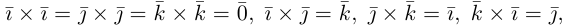
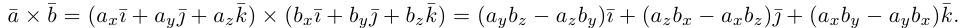
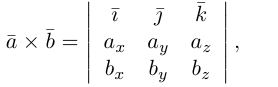
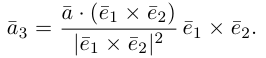
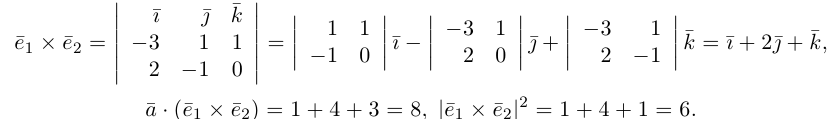
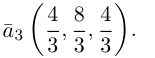
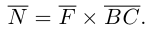
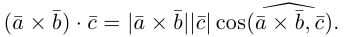
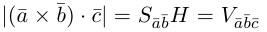
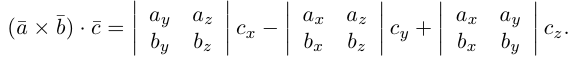
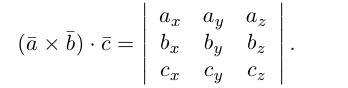
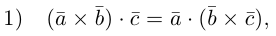
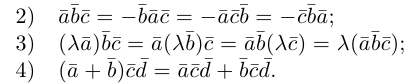
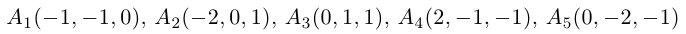
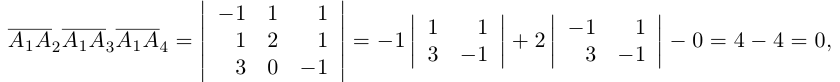
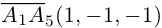
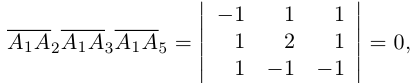

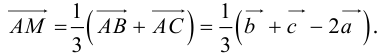
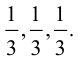
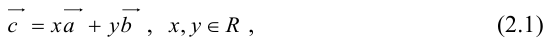
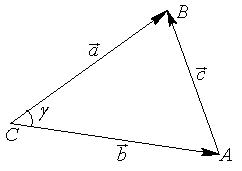
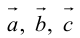 есть два коллинеарных, например:
есть два коллинеарных, например: 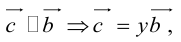
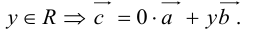
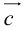 , а стороны параллельны прямым, на которых лежат
, а стороны параллельны прямым, на которых лежат 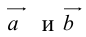 (рис. 7).
(рис. 7). 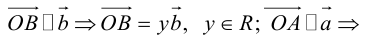
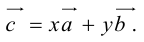
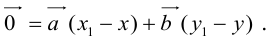
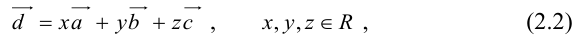
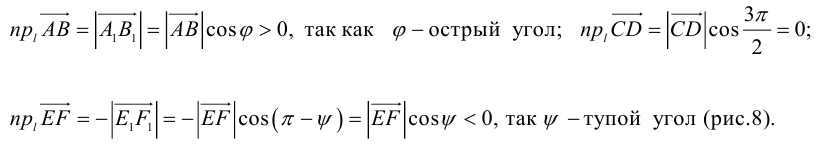
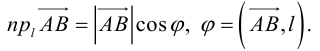
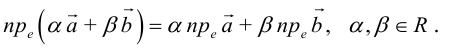
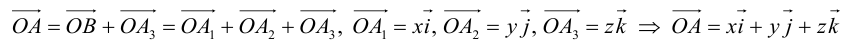
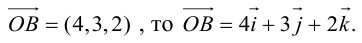
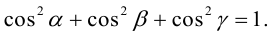
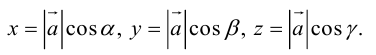
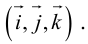
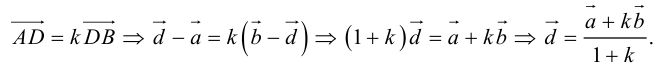
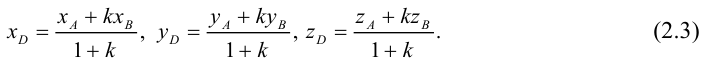
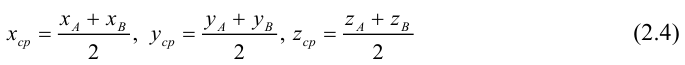
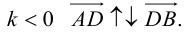
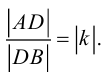
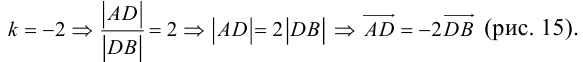
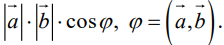
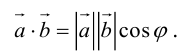
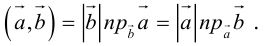
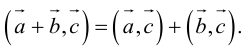
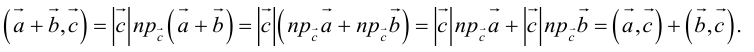
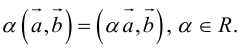
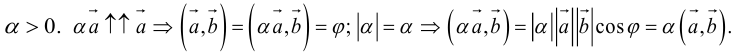
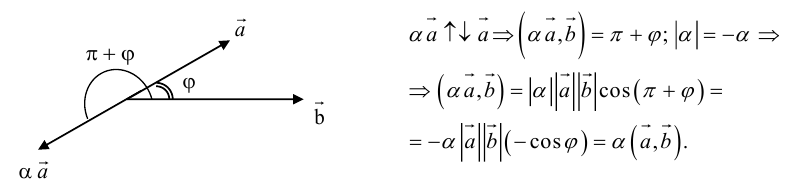
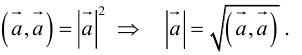
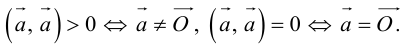
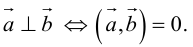
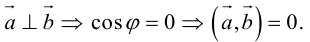
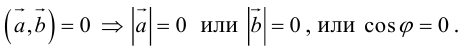
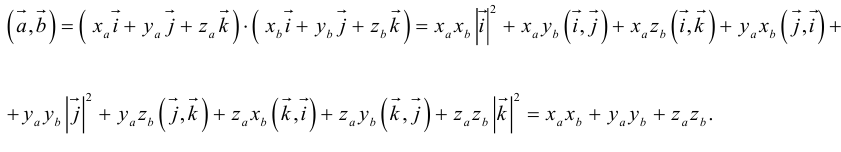

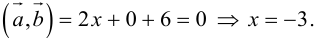

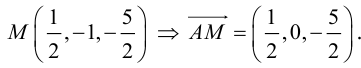
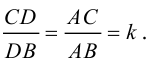
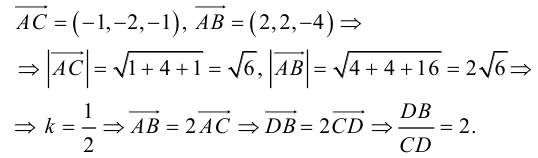
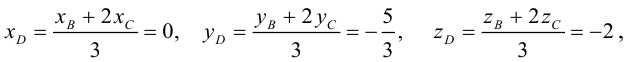
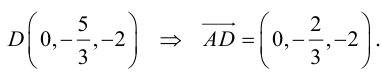
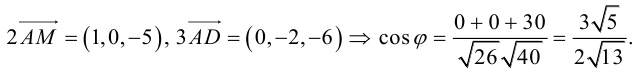
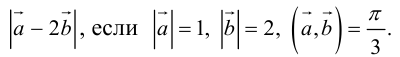
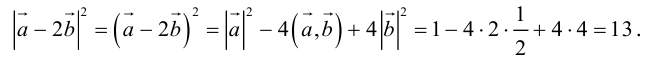
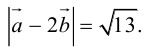
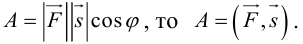
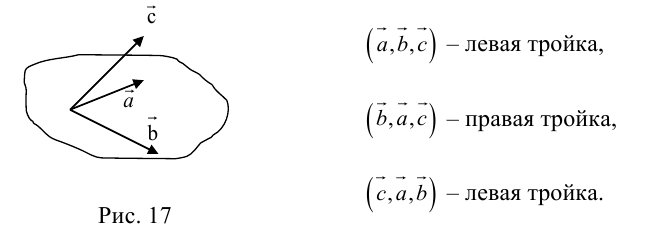
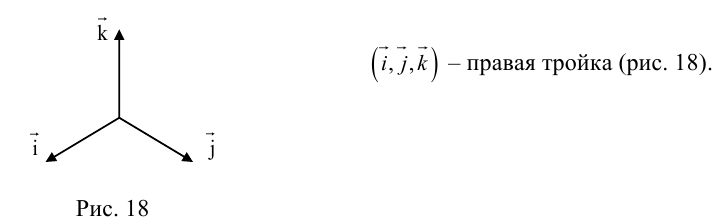
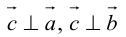 (
(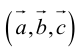 – правая.
– правая.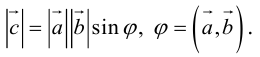
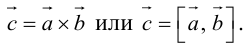
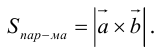
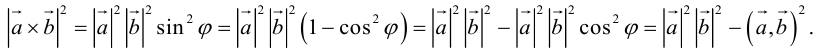
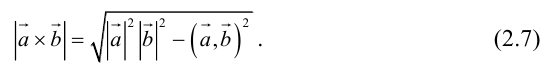
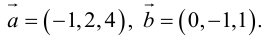
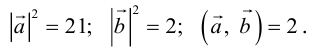
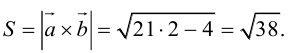
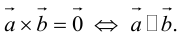
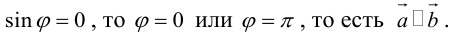
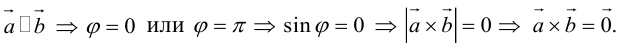
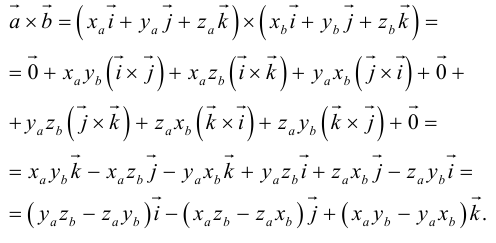
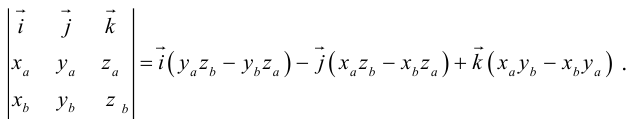
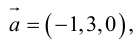
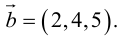
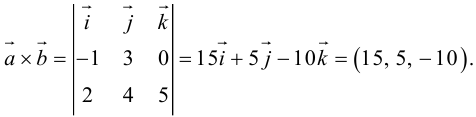
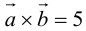
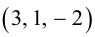
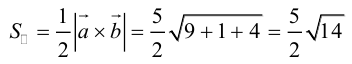
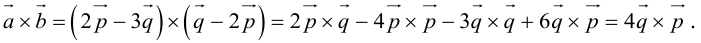
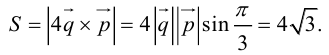
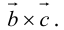
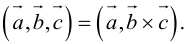
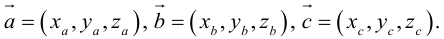
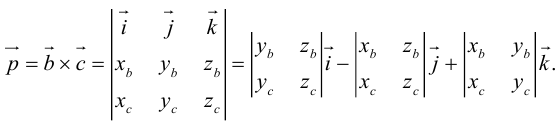
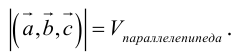
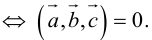
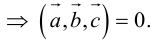
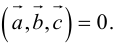
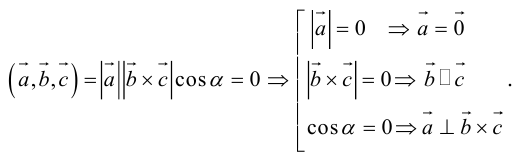
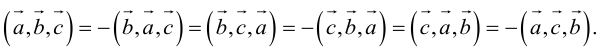
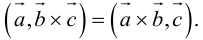
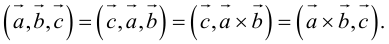
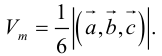
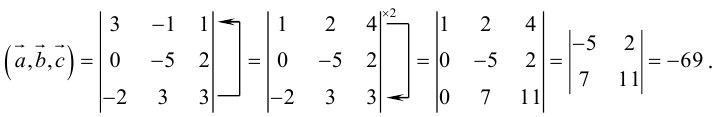
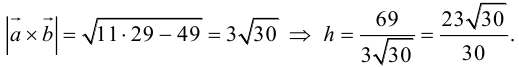
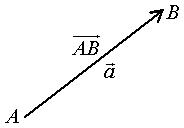
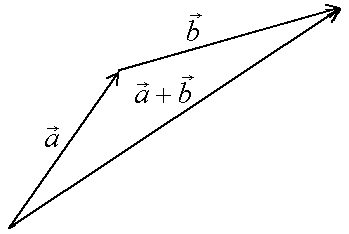
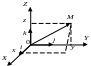
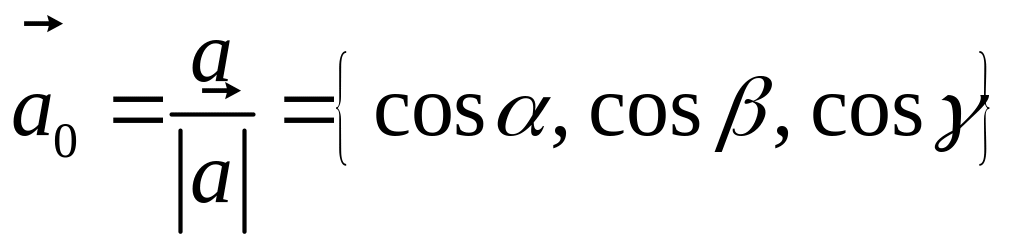
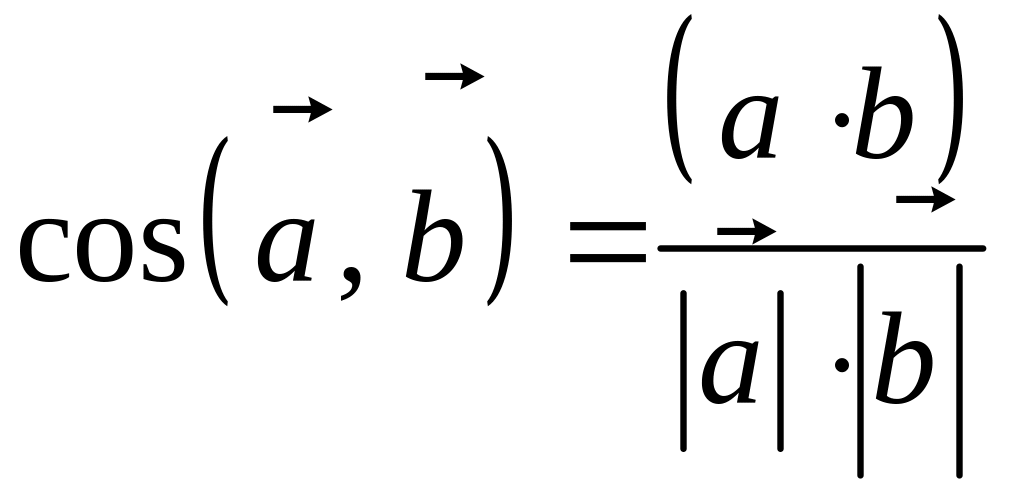
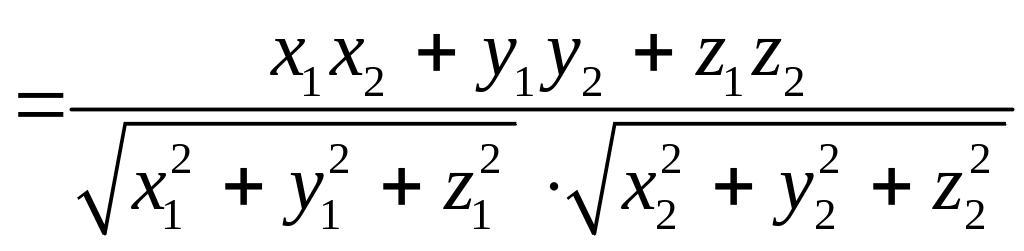
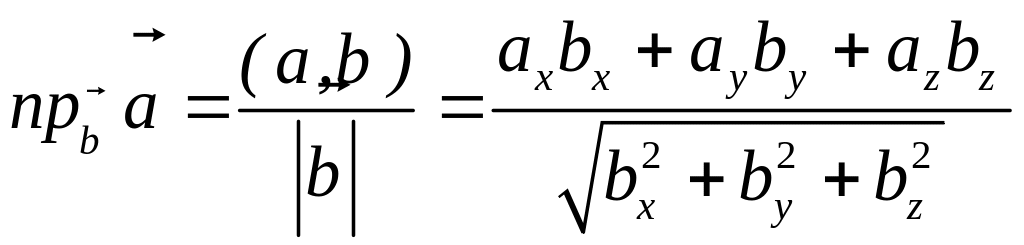
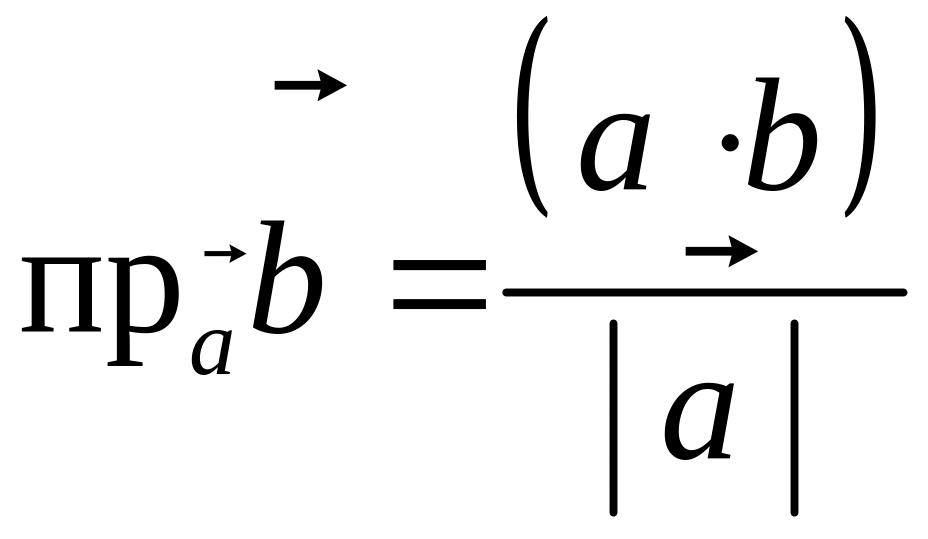
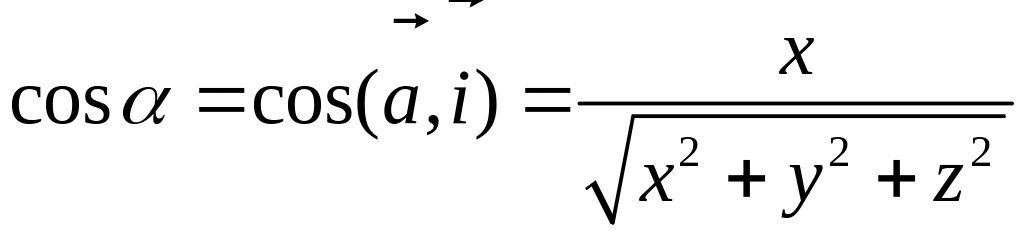
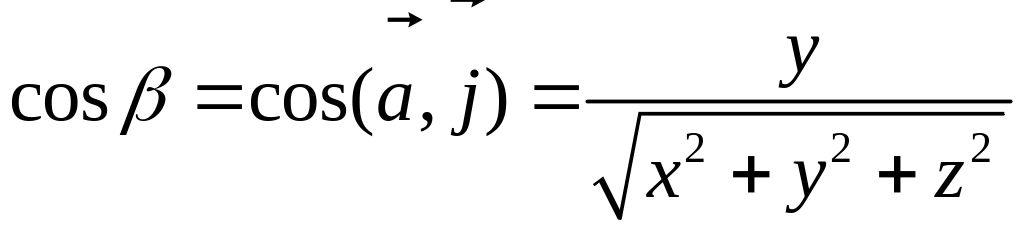
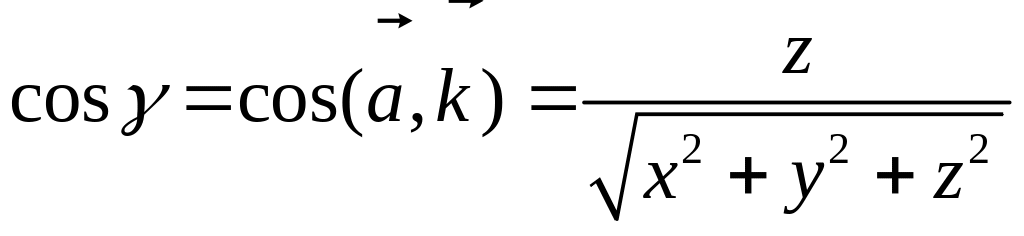
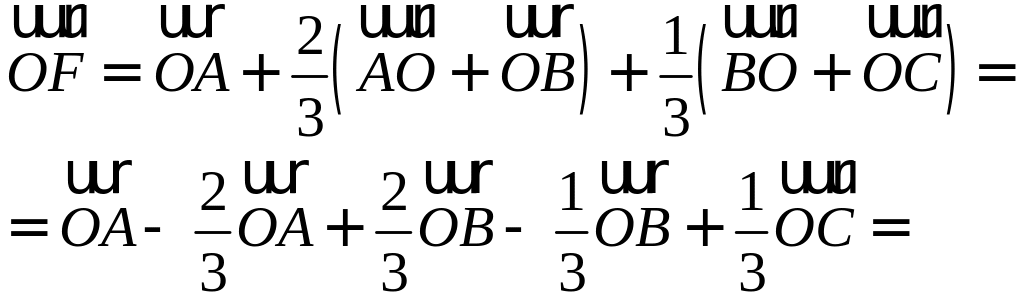
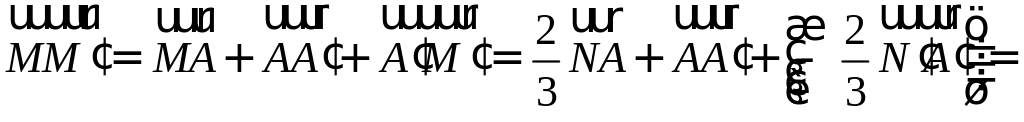
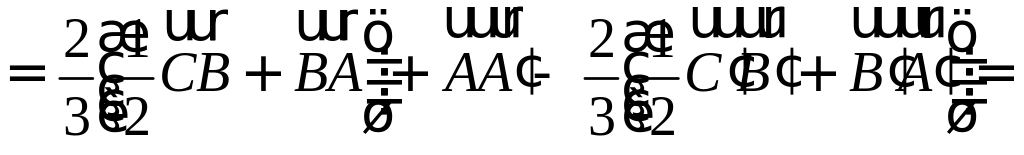
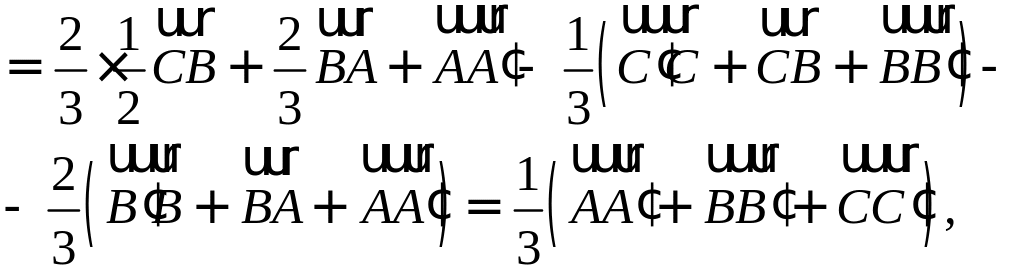
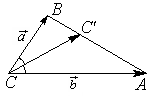
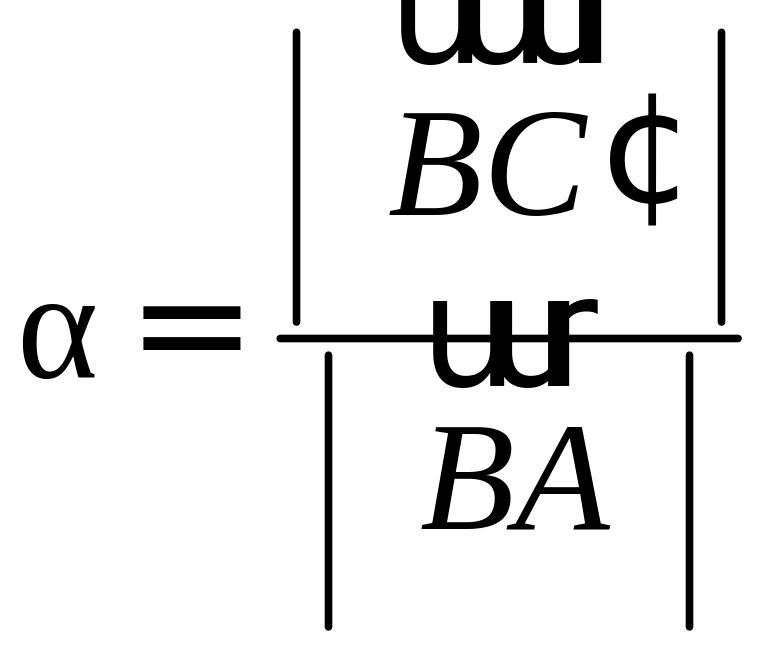
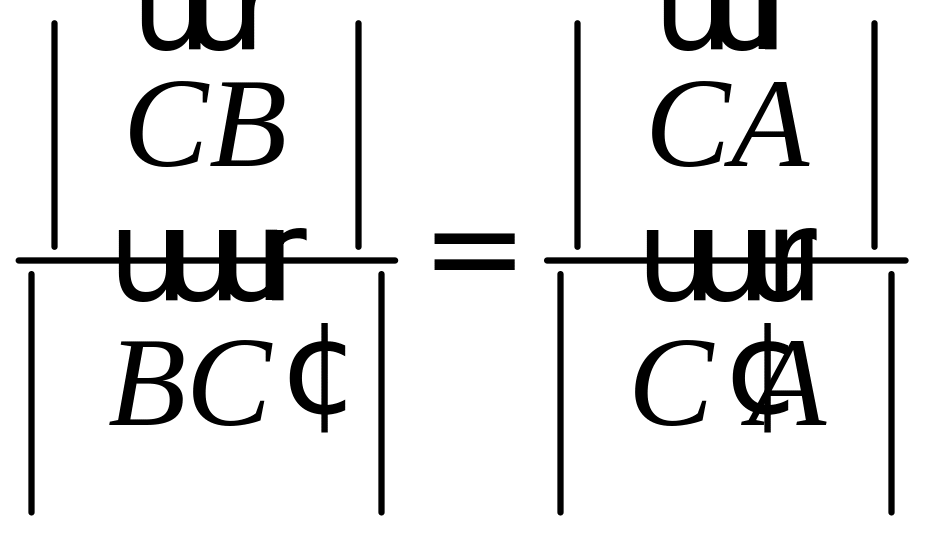
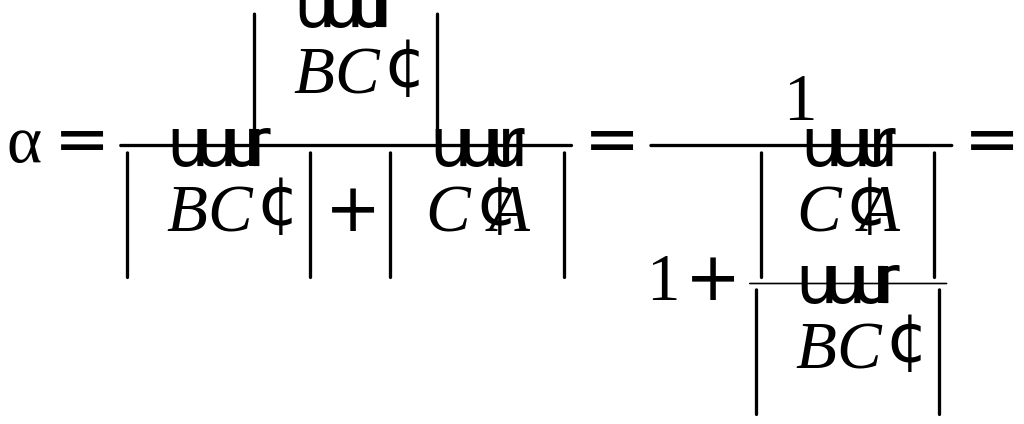
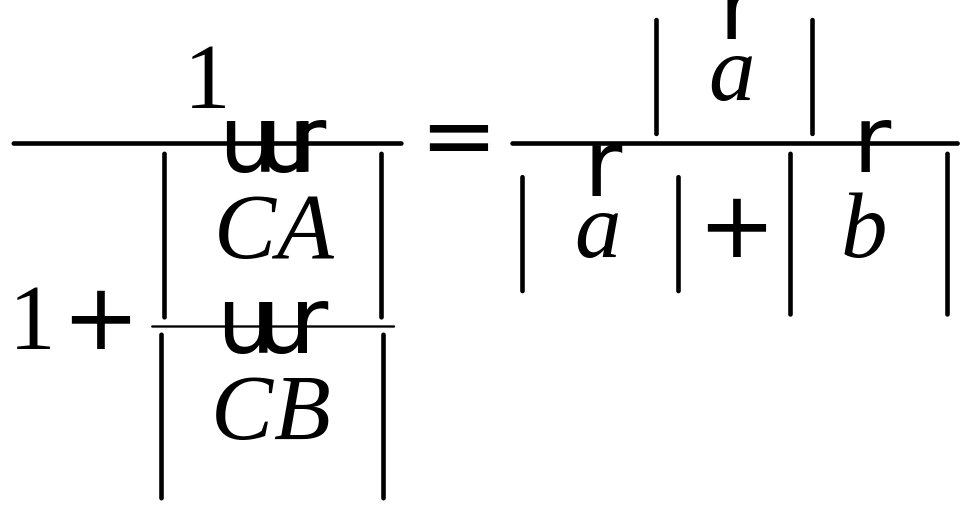
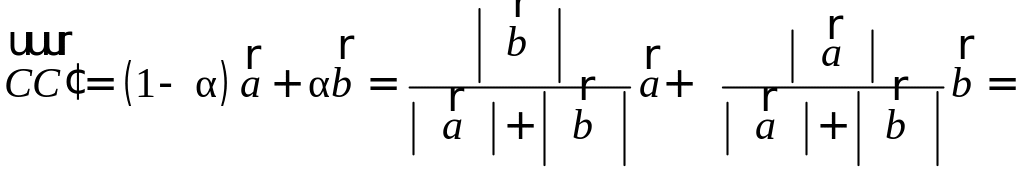
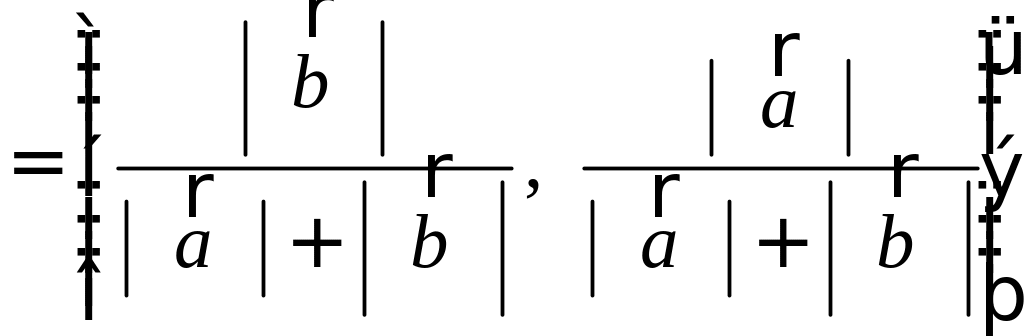
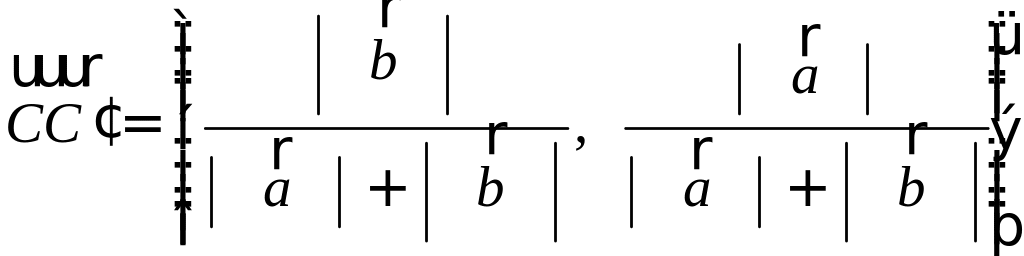
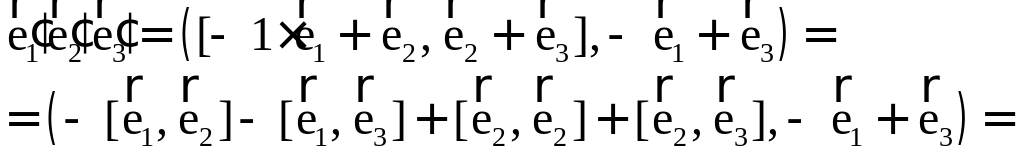
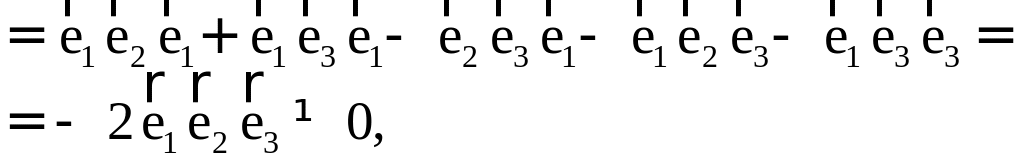
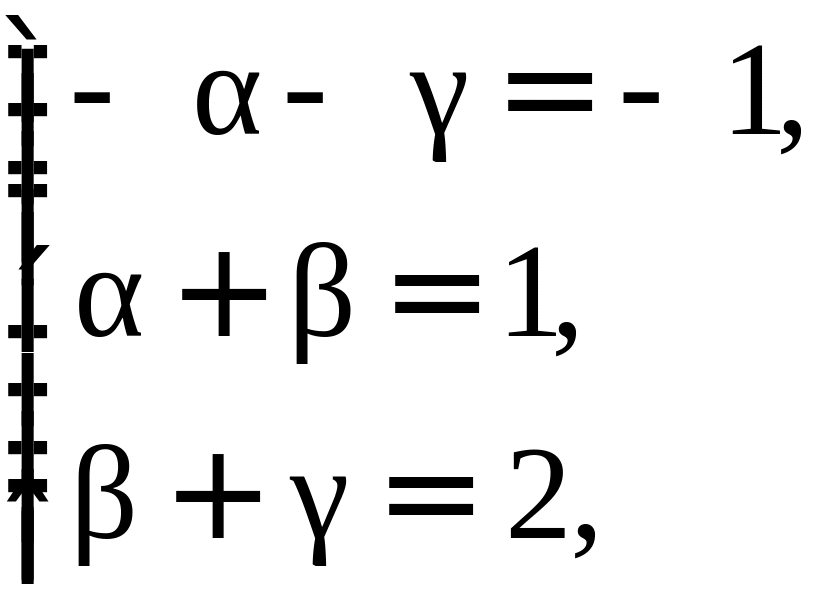
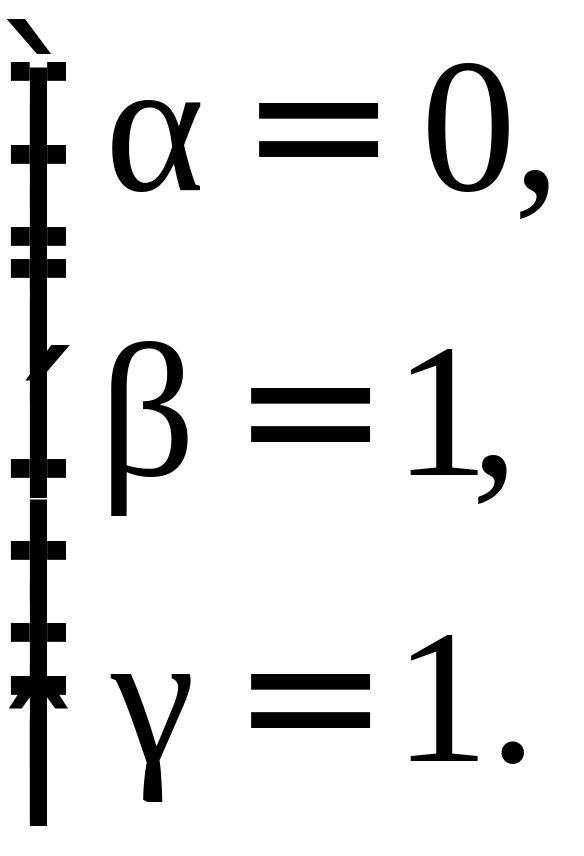
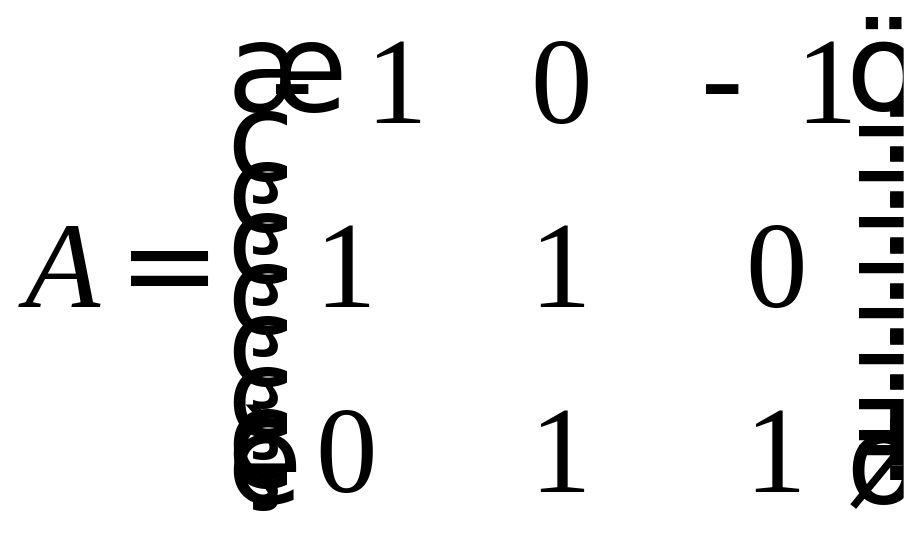
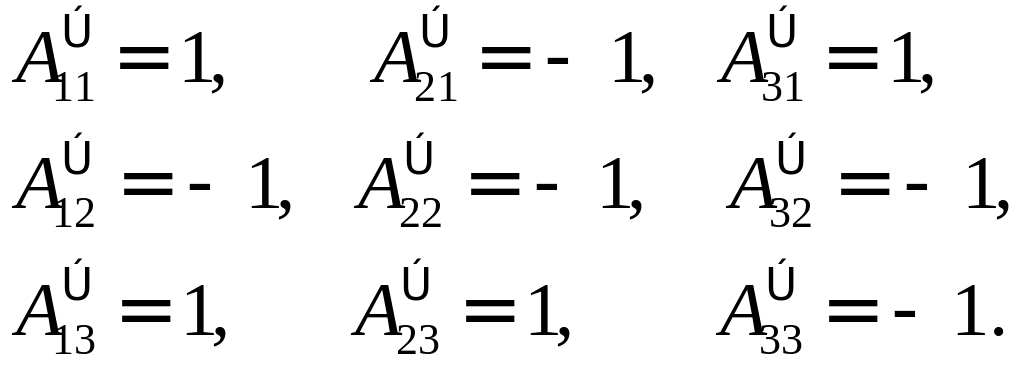
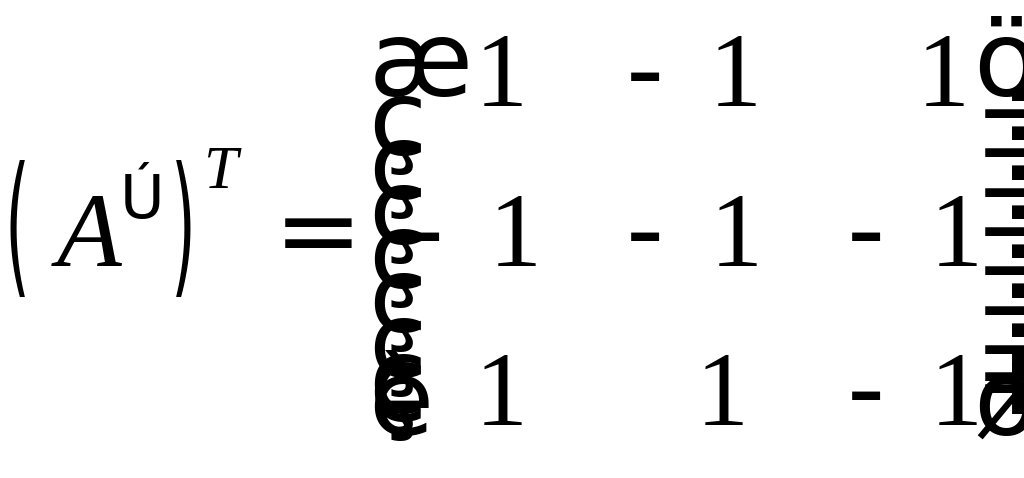
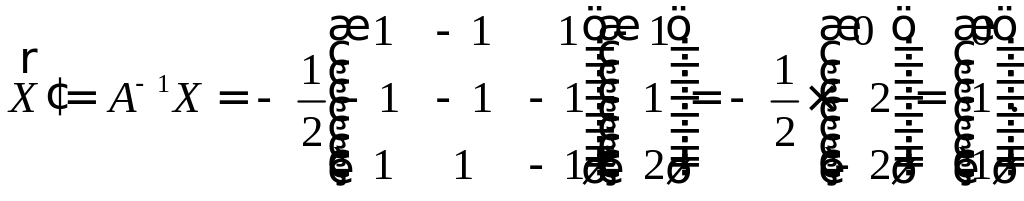
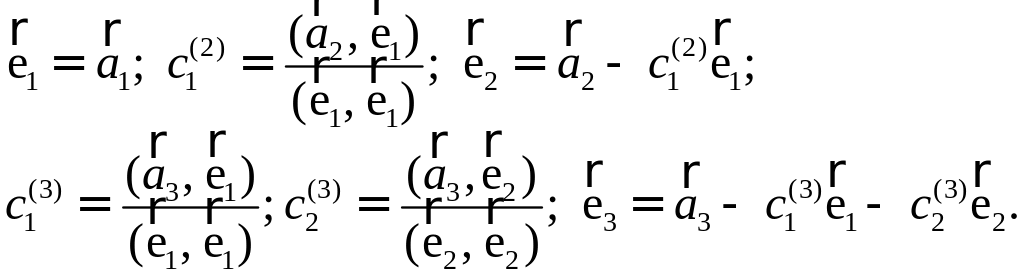
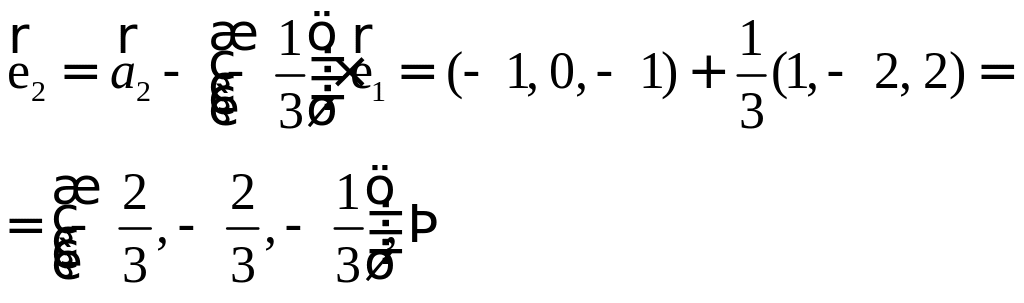
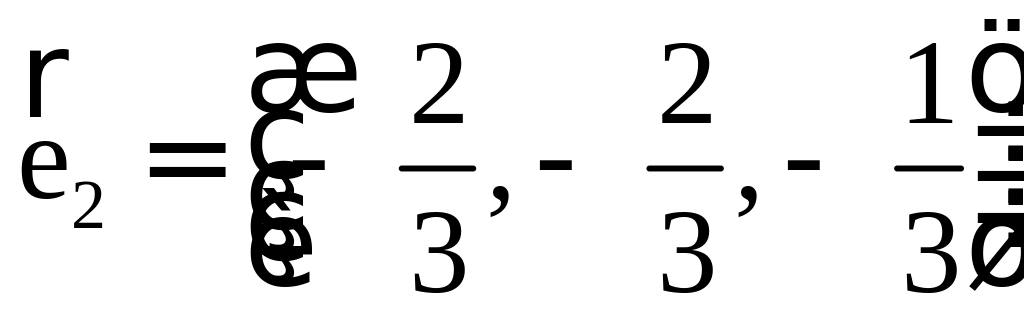
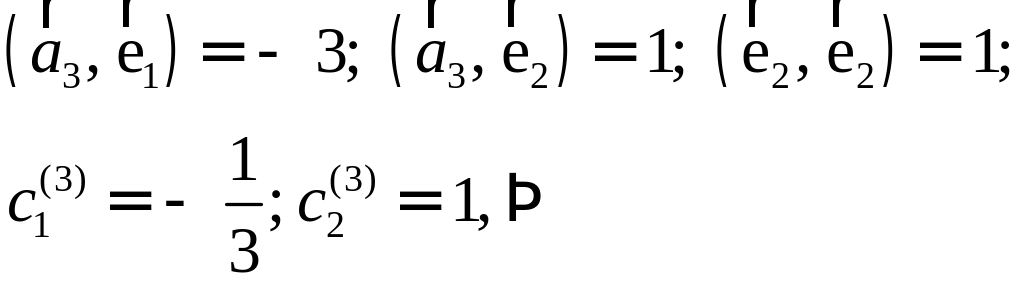
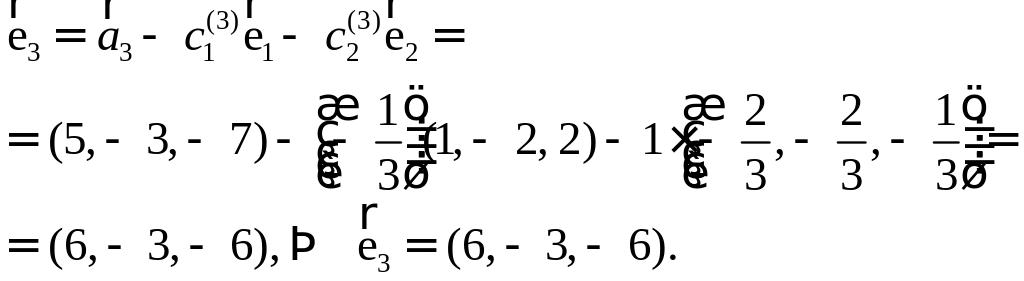

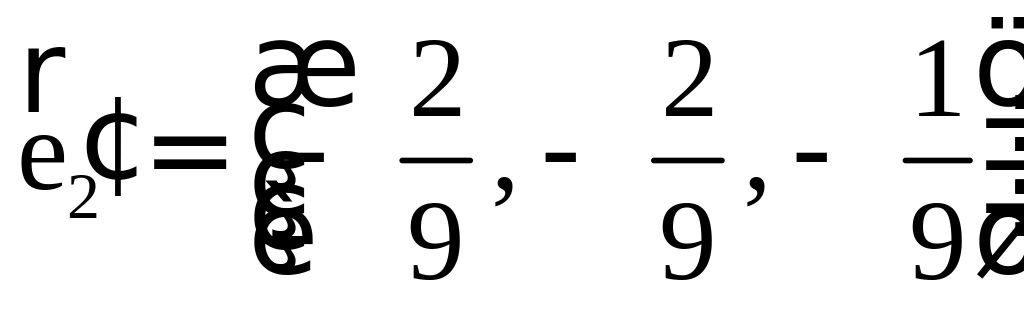
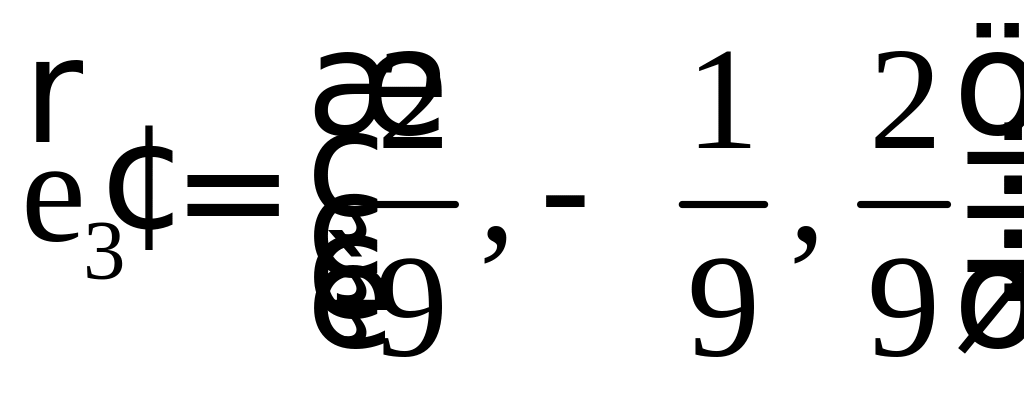
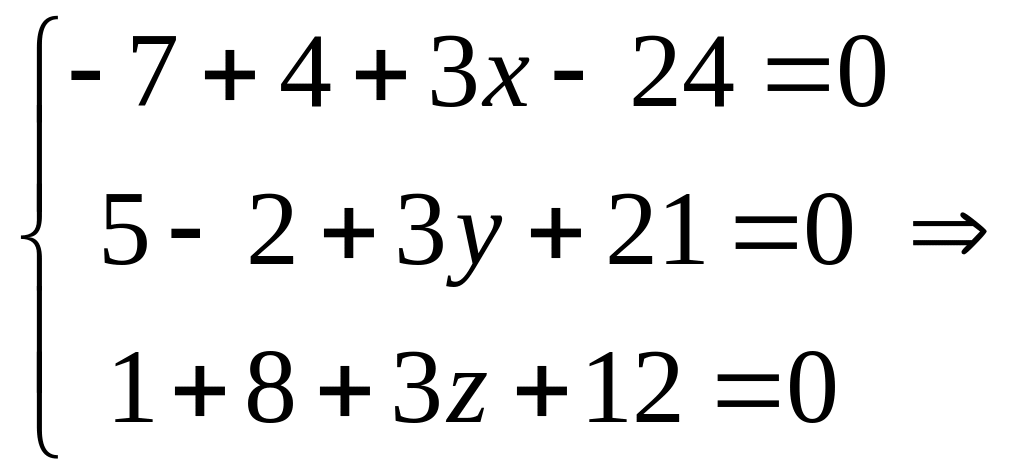
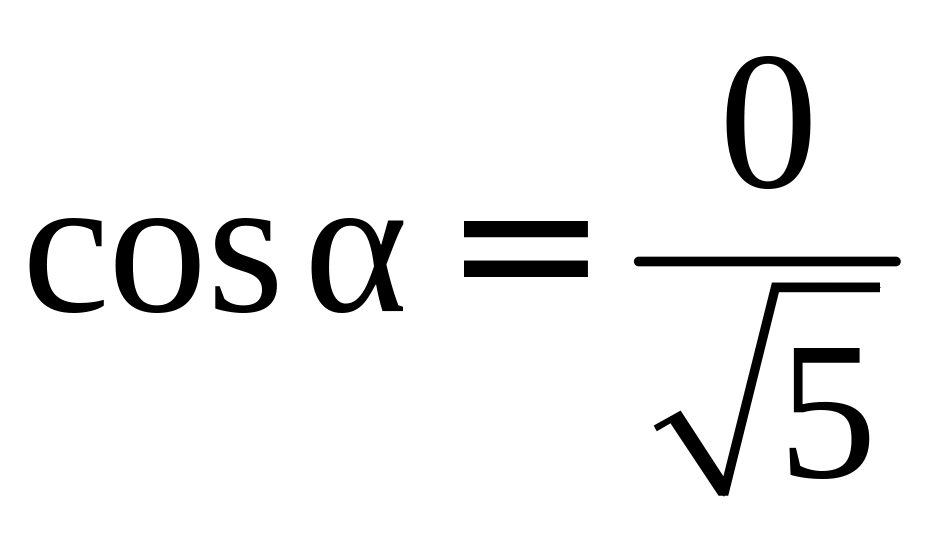
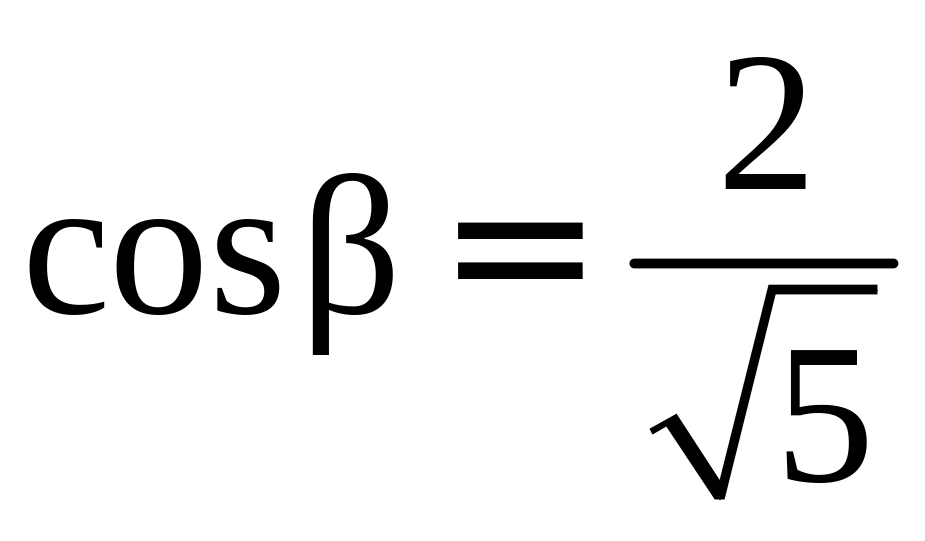
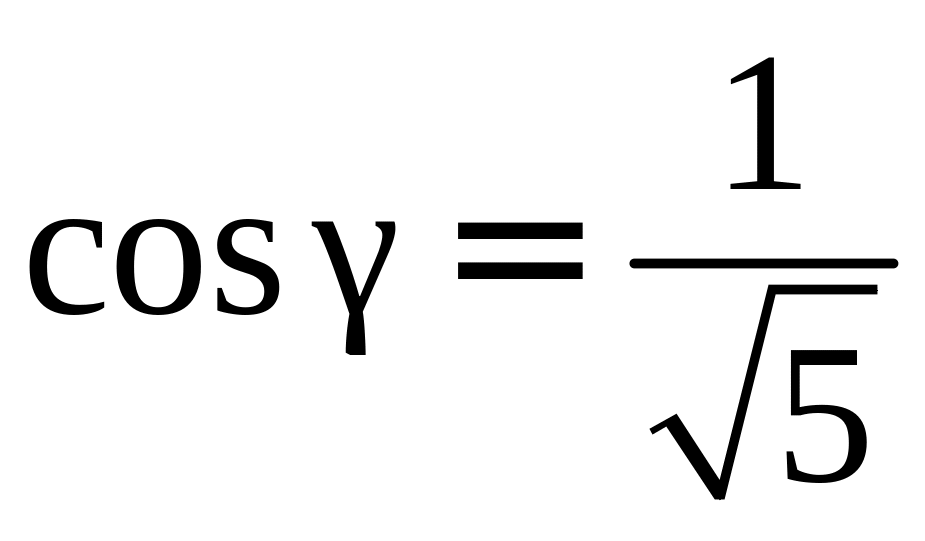
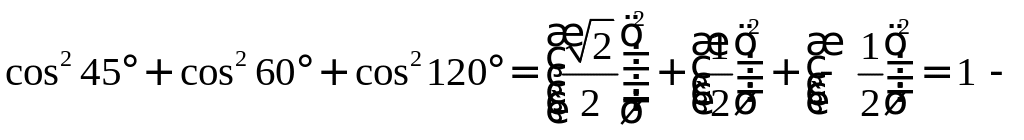
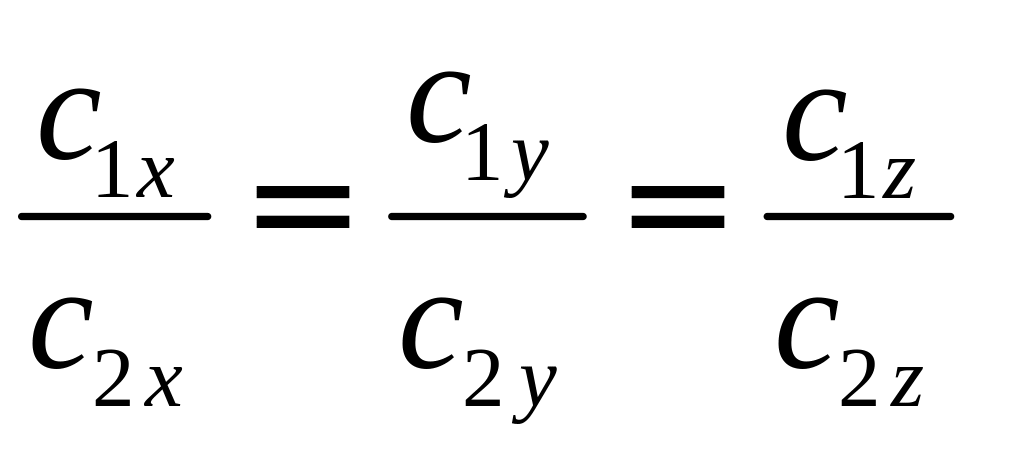
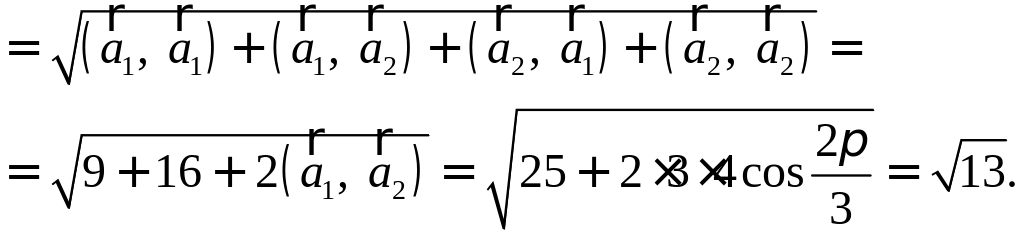
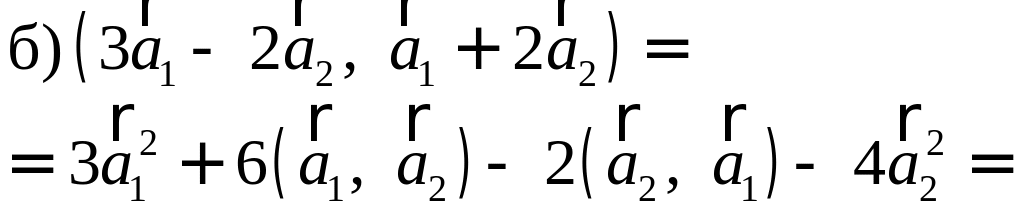
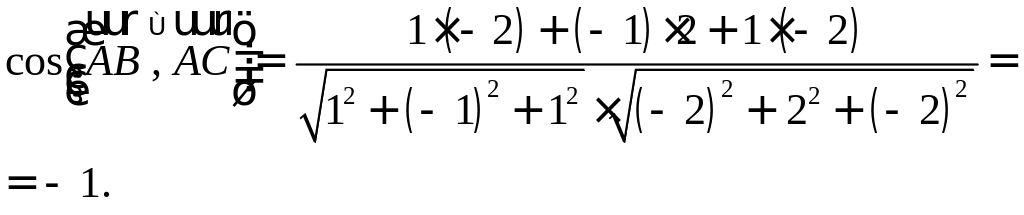
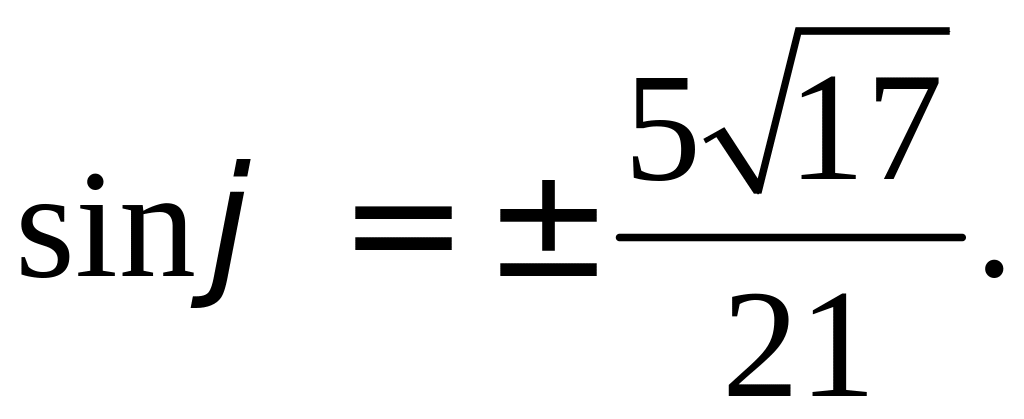
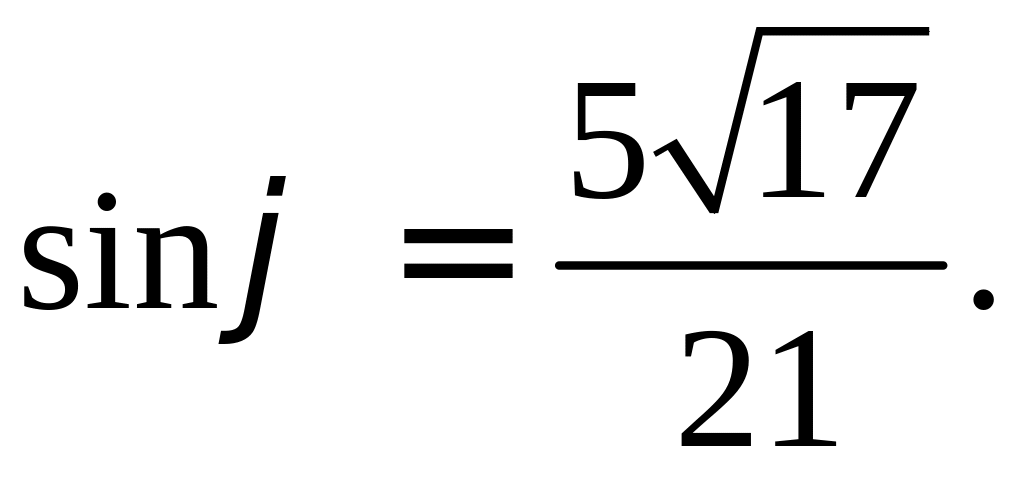
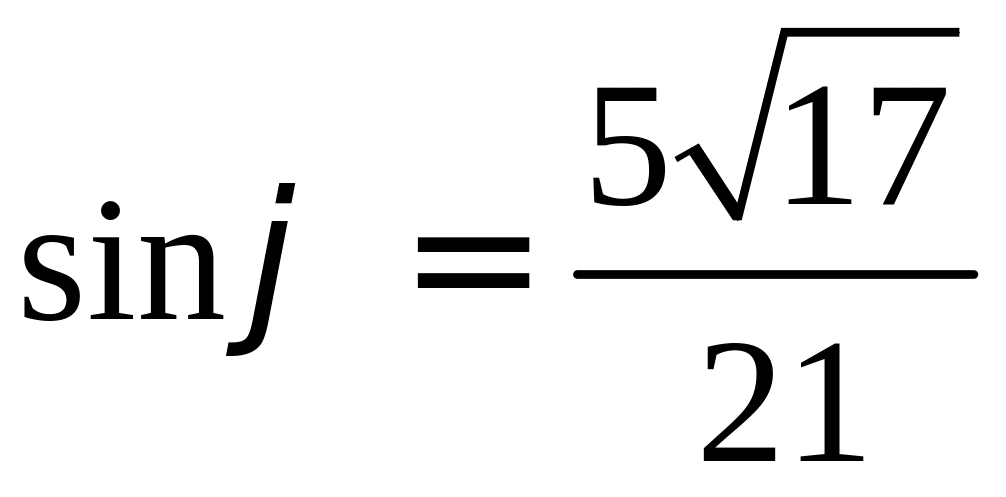
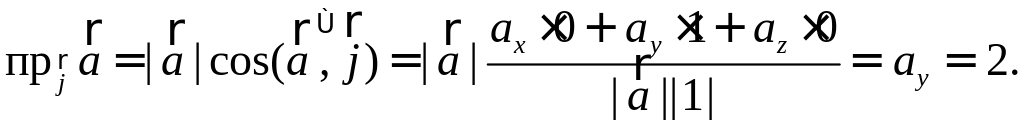
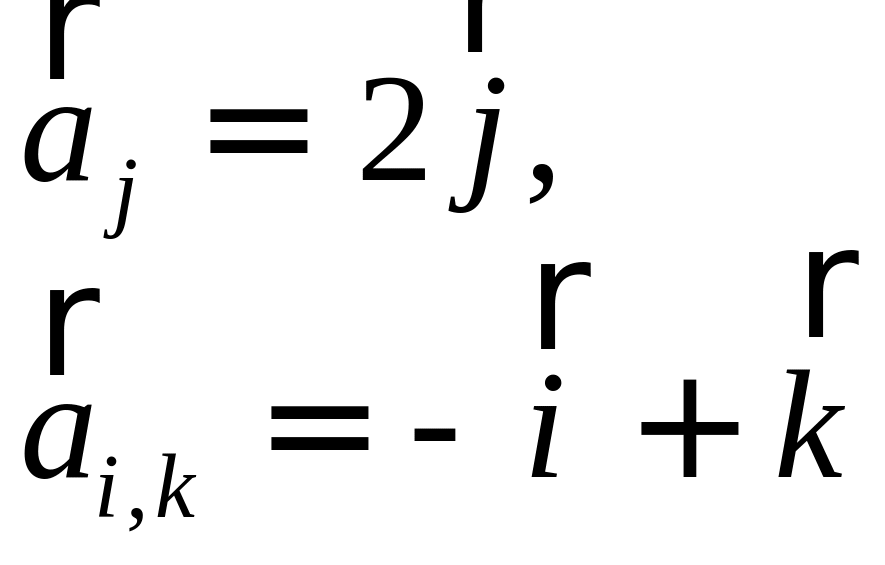
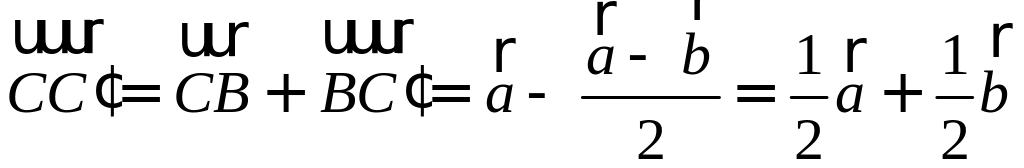
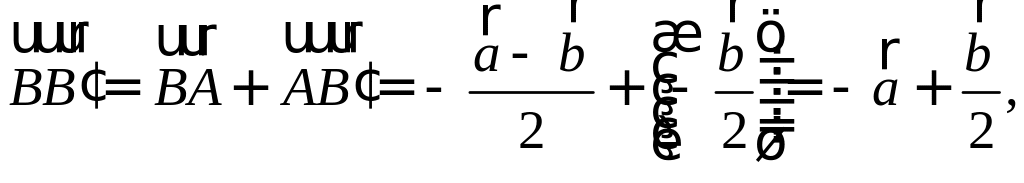
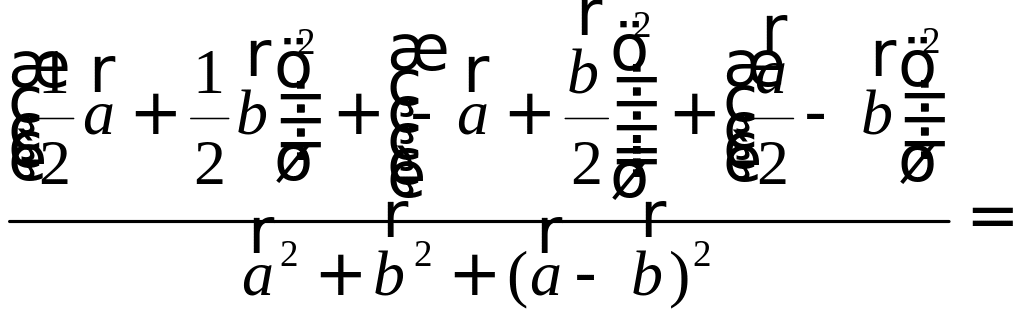
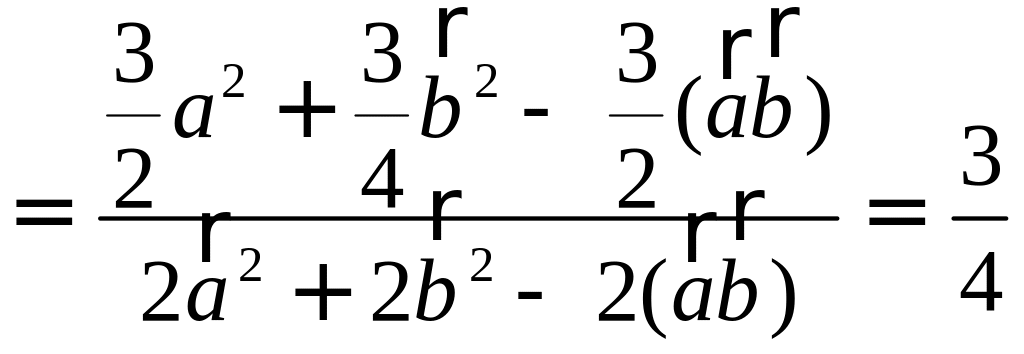

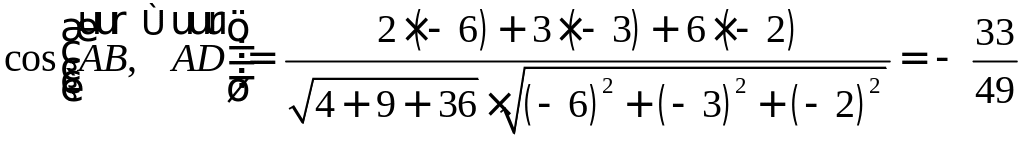
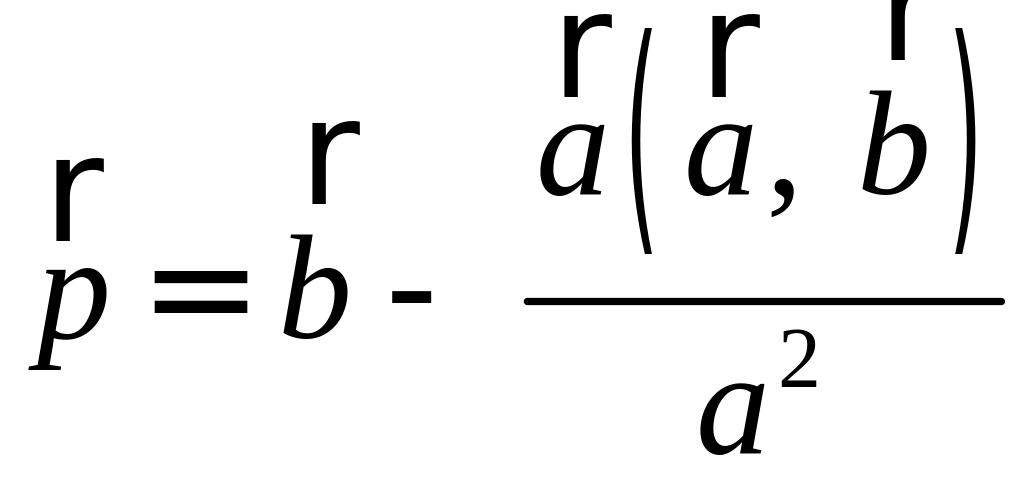
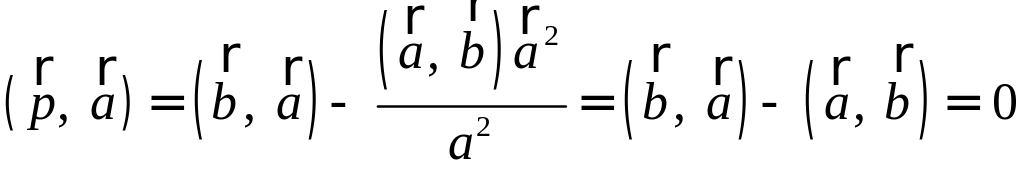
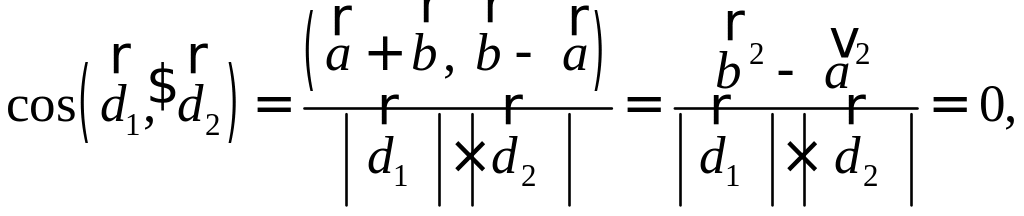























































































 — ассоциативность (сочетательный закон);
— ассоциативность (сочетательный закон); —дистрибутивность относительно сложения векторов (1-й распределительный закон);
—дистрибутивность относительно сложения векторов (1-й распределительный закон); — дистрибутивность относительно сложения чисел (2-й распределительный закон).
— дистрибутивность относительно сложения чисел (2-й распределительный закон).











 отсюда
отсюда 
 – т. е. векторы
– т. е. векторы  компланарны, что противоречит условию теоремы. Значит, наше допущение о ещё одном разложении неверно, т.е. разложение вектора
компланарны, что противоречит условию теоремы. Значит, наше допущение о ещё одном разложении неверно, т.е. разложение вектора  по данным векторам
по данным векторам  единственно. Теорема доказана.
единственно. Теорема доказана.

 получаем
получаем 
 и действительного числа
и действительного числа  получаем
получаем 












































































































































































































