Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 октября 2016 года; проверки требует 1 правка.
Состоя́тельная оце́нка в математической статистике — это точечная оценка, сходящаяся по вероятности к оцениваемому параметру.
Определения[править | править код]
по вероятности при
.
В противном случае оценка называется несостоятельной.
- Оценка
называется си́льно состоя́тельной, если
почти наверное при
.
На практике «увидеть» сходимость «почти наверное» не представляется возможным, поскольку выборки конечны. Таким образом, для прикладной статистики достаточно требовать состоятельности оценки. Более того, оценки, которые были бы состоятельными, но не сильно состоятельными, «в жизни» встречаются очень редко. Закон больших чисел для одинаково распределённых и независимых величин с конечным первым моментом выполнен и в усиленном варианте, всякие крайние порядковые статистики тоже сходятся в силу монотонности не только по вероятности, но и почти наверное.
Признак[править | править код]
- Если оценка сходится к истинному значению параметра “в среднем квадратичном” или если оценка асимптотически несмещенная и её дисперсия стремится к нулю, то такая оценка будет состоятельной.
Свойства[править | править код]
- Из свойств сходимостей случайных величин имеем, что сильно состоятельная оценка всегда состоятельна. Обратное, вообще говоря, неверно.
- Поскольку дисперсия состоятельных оценок стремится к нулю, часто со скоростью порядка 1/n, то состоятельные оценки сравниваются между собой асимптотической дисперсией случайной величины
(асимптотическое математическое ожидание этой величины равно нулю).
Связанные понятия[править | править код]
- Оценка называется суперсостоятельной, если дисперсия случайной величины
стремится к конечной величине. То есть скорость сходимости оценки к истинному значению существенно выше, чем у состоятельной оценки. Суперсостоятельными, например, оказываются оценки параметров регрессии коинтегрированных временных рядов.
Примеры[править | править код]
См. также[править | править код]
- Статистическая оценка
- Несмещенная оценка
- Эффективная оценка
-
Состоятельность оценки; примеры состоятельных и несостоятельных оценок
При
обработке выборки исследователь
интуитивно предполагает, что, чем больше
ее объем, тем ближе будет оценка к
истинному значению. Т.е. с ростом N,
ошибка в оценивании
![]()
должна стремиться к нулю. Это возможно,
если алгоритм оценки эффективно
использует ту информацию об искомом
параметре, которая содержится в выборке.
Формально
данное свойство определяется следующим
образом: оценка является состоятельной,
если
![]()
сходится по вероятности к
![]()
,
то есть:
Для
любого θ: NА
p→
при N → ∞
То
есть оценку параметра называют
состоятельной, если с ростом объёма
выборки N она сходится по вероятности
к оцениваемому параметру.
Несостоятельная
оценка – оценка, которая не сходится
по вероятности к оцениваемому параметру
с ростом выборки.
Сходимость
по вероятности в свою очередь означает,
что для любого, сколь угодно малого,
отличного от нуля
![]()
:
![]()
То
есть всегда найдется такой объем
выборки, который с вероятностью, близкой
к единице обеспечит необходимую величину
ошибки в оценивании
,
какой бы малой она не была.
На
практике «увидеть» сходимость «почти
наверное» не представляется возможным,
поскольку выборки конечны. Таким
образом, для прикладной статистики
достаточно требовать состоятельности
оценки.
Пример
состоятельной оценки:
При
анализе трафика, передаваемого с сервера
на компьютеры клиентов, производится
оценка среднего размера пакета
передаваемого по сети. Для этого из
общего потока выбирается N
пакетов,
размеры которых фиксируются и усредняются.
В данном примере случайная величина
![]()
характеризует размер пакета, искомый
параметр
– среднее значение
(т.е.
![]()
),
элементы выборки
![]()
– размеры зарегистрированных пакетов,
алгоритм оценивания
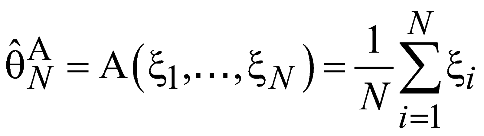
.
Проверим, является ли данная оценка
смещенной:
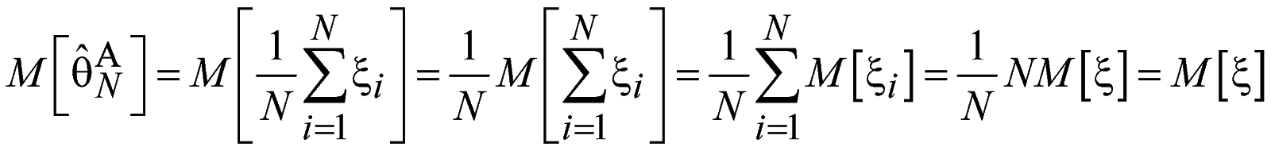
Таким
образом, данная оценка является
несмещенной, то есть
![]()
и
можно применить второе неравенство
Чебышева.
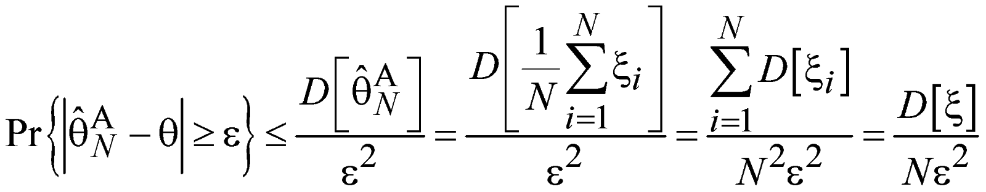
Очевидно,
что при конечной
![]()
для
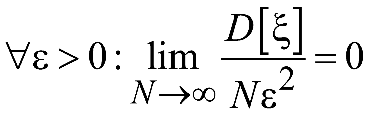
,
что доказывает состоятельность
рассмотренной оценки.
Выборочное
среднее
X=
1ni=1nXi
является сильно состоятельной
оценкой математического
ожидания Xi.
Вообще,
все (за редчайшими исключениями) оценки
параметров, используемые в
вероятностно-статистических методах
принятия решений, являются состоятельными.
-
Эффективность оценки; функции штрафа и риска
Предположим,
что для проведения эксперимента перед
исследователем стоит выбор одного из
двух алгоритмов оценивания искомого
параметра системы. Оба алгоритма
обеспечивают оценки несмещенные и
состоятельные. Как осуществить выбор
одного из них? Для ответа на этот вопрос
вводят третий параметр оценки – параметр
эффективности.
Прежде, чем дать формальное определение
эффективности, дадим ее качественную
интерпретацию. На рис. 1 для двух
гипотетических оценок приводятся
графики зависимости погрешности
оценивания от объема выборки. Не смотря
на то, что оба алгоритма обеспечивают
сколь угодно малую погрешность при
![]()
,
при конечном N
алгоритм 2 явно кажется более
предпочтительным, т.е. оценка 2 эффективнее
оценки 1.
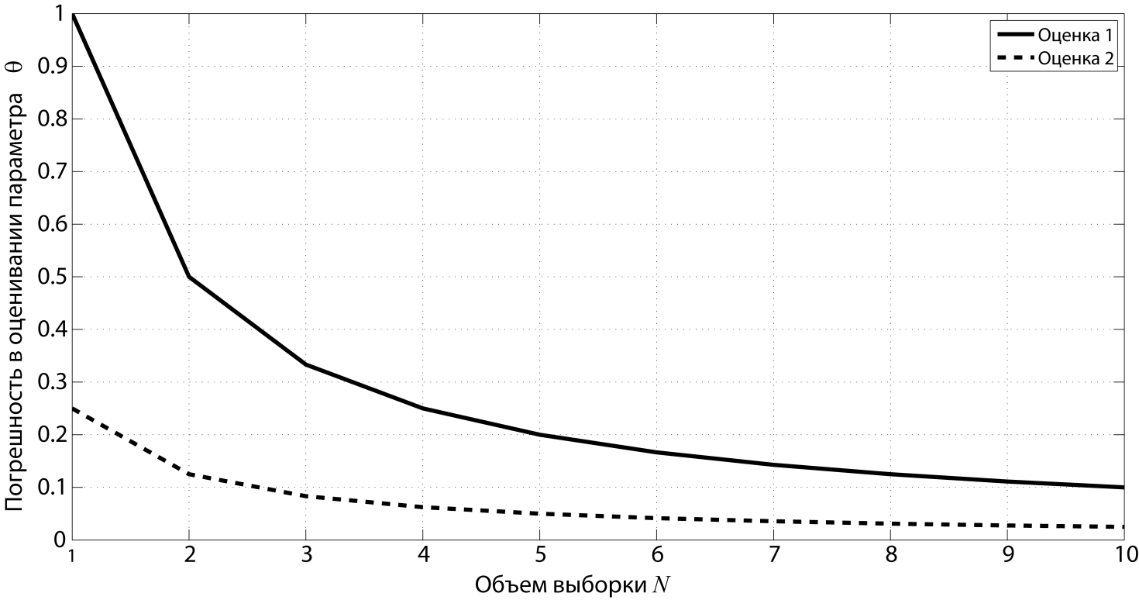
Рис.
1. Сравнение двух алгоритмов оценивания.
Чтобы
количественно измерять эффективность
введем несколько вспомогательных
функций.
Функцией
штрафа
![]()
называется функция, характеризующая
меру негативных последствий, возникающих
при той или иной ошибке e
оценивания параметра системы. Как
правило, чем больше
![]()
,
тем больше значение
.
Функция штрафа выбирается исходя из
специфики той предметной области, в
которой ведется статистический анализ
и может принимать достаточно сложный
вид.
Пример
иллюстрирующий функцию штрафа
По
данным Гидрометцентра проводится
оценка количества осадков, выпавших в
некотором регионе. Из количества осадков
рассчитывается тип и объем удобрений,
которые необходимо применить на
сельскохозяйственном поле. Известно,
что неправильно выбранный режим
удабривания приводит к падению количества
урожая. Тогда, функция штрафа может
иметь, например, вид, приведенный на
рис. 2.
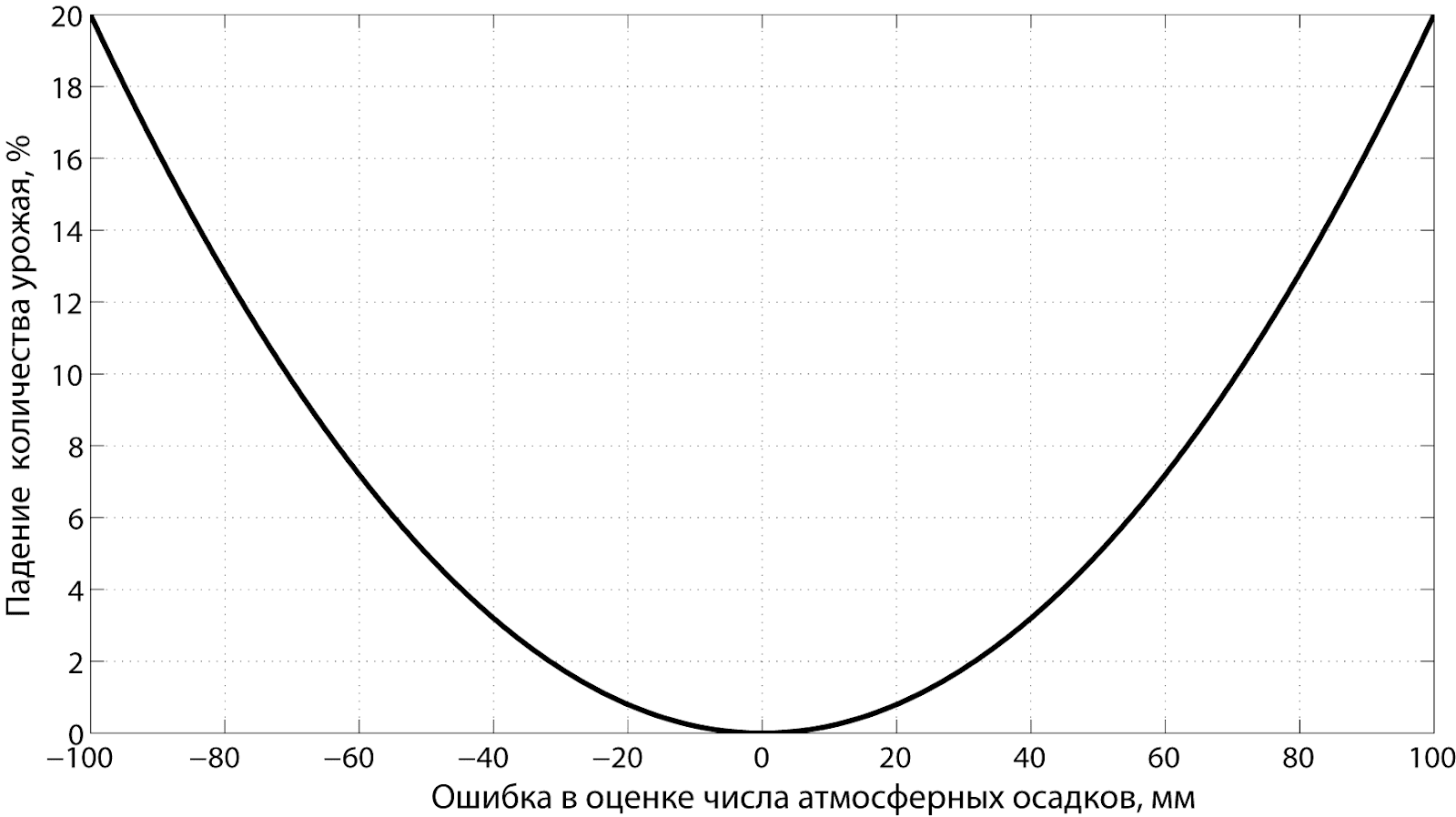
Рис.
2 Функция штрафа в примере, иллюстрирующем
функцию штрафа.
Пример
иллюстрирующий функцию штрафа 2
В
ходе работы телекоммуникационной
системы приемник периодически проводит
оценку мощности шумов, присутствующих
в канале. Этот уровень учитывается в
процессе декодирования принимаемого
сообщения. Известно, что ошибочно
введенная в декодер информация о шумах
повышает вероятность битовой ошибки
при приеме данных. При этом заниженная
оценка мощности приводит к существенно
большему ухудшению качества приема,
нежели завышенная. Типичная функция
штрафа приведена на рис. 3.
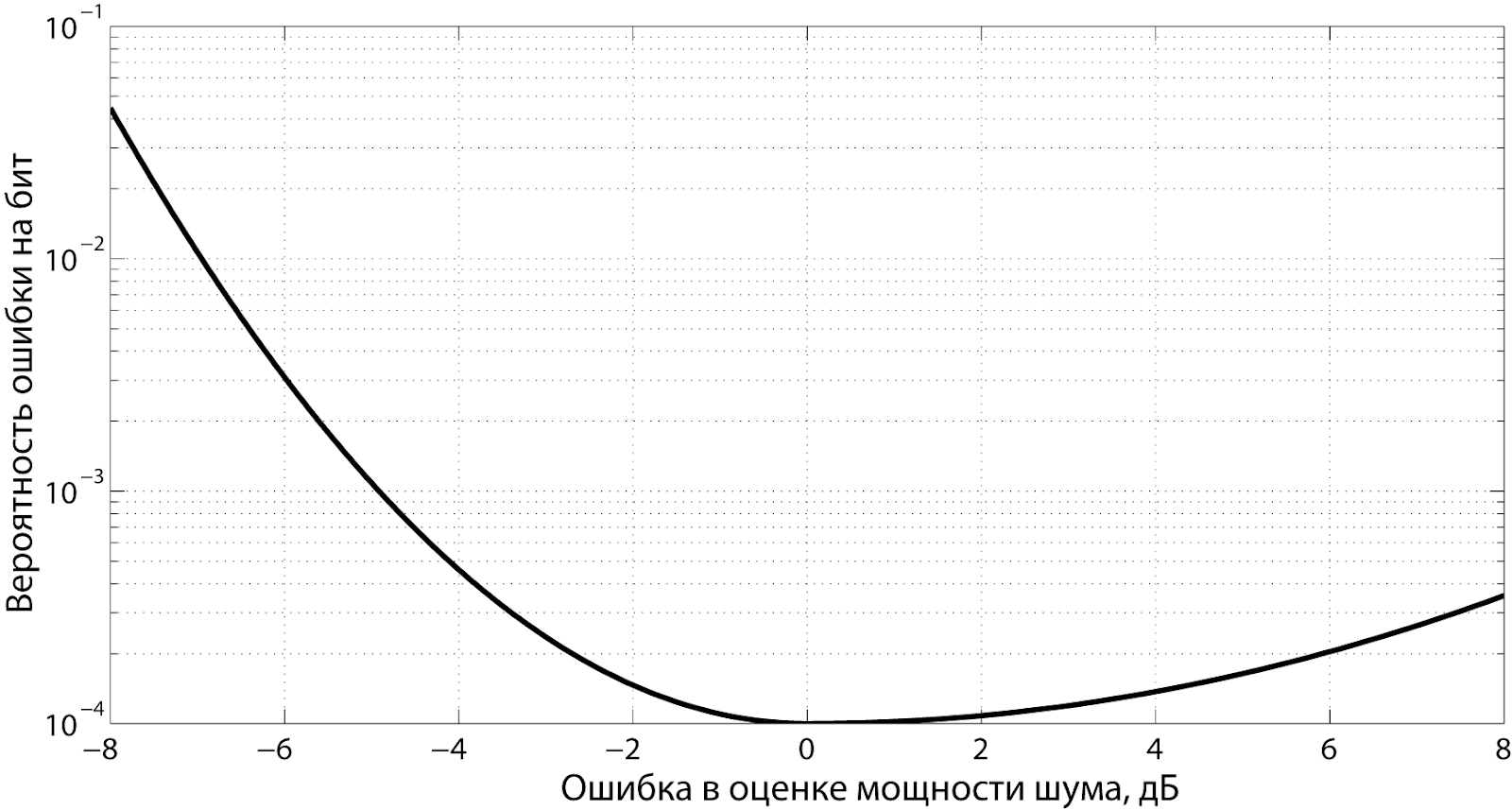
Рис.
3 Функция штрафа в примере, иллюстрирующем
функцию штрафа 2.
Как
правило, многие реальные функции штрафа
могут быть хорошо аппроксимированы
так называемой квадратичной
штрафной функцией
![]()
или абсолютной
штрафной функцией
![]()
.
Оценка
параметра является случайной величиной,
а, значит, ошибка в оценивании и величина
штрафа также являются случайными
величинами. Таким образом, вводят
функцию
риска:
![]()
.
Т.е.
функция риска характеризует средний
штраф, который заплатит исследователь
при использовании алгоритма
для оценки параметра
по выборке объема N.
Более эффективной является та оценка,
которая обеспечивает меньший риск.
Стоит
отметить, что для несмещенных оценок
в случае применения квадратичной
штрафной функции:
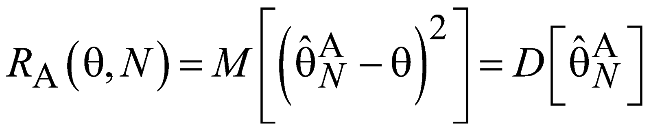
Т.е.
функция
риска совпадает с дисперсией оценки.
Как
можно видеть, функция риска зависит
как от объема выборки, так и от истинного
значения параметра
.
Таким образом, для различных диапазонов
значения
разные оценки могут оказаться более
или менее эффективными. При этом
ожидается, что для состоятельных оценок
![]()
(функция риска) убывает с ростом N.
Следующий пример иллюстрирует эту
зависимость:
Проводится
эксперимент, в ходе которого выясняется
вероятность потери пакета
при передаче по вычислительной сети.
Для этого по сети передаются N
тестовых пакетов, успешный прием или
потеря которых регистрируется на
приемной стороне. Вводится величина
,
равная единице, в случае, если i-й
пакет оказался утерянным, и нулю иначе.
Тогда воспользуемся следующей несложной
оценкой:
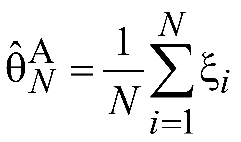
.
Найдем выражение
для случая применения квадратичной
штрафной функции. Очевидно, что
![]()
,
тогда:
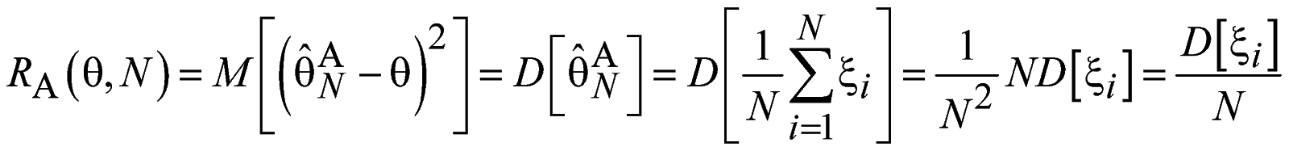
Т.к.
является Бернуллиевской случайной
величиной с параметром
,
то:
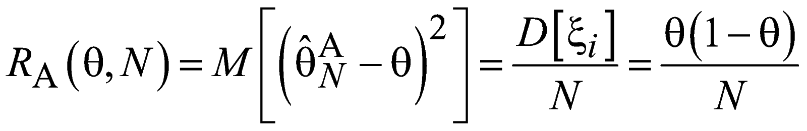
.
Соседние файлы в предмете Государственный экзамен
- #
- #
Содержание:
Точечные оценки:
Пусть случайная величина имеет неизвестную характеристику а. Такой характеристикой может быть, например, закон распределения, математическое ожидание, дисперсия, параметр закона распределения, вероятность определенного значения случайной величины и т.д. Пронаблюдаем случайную величину n раз и получим выборку из ее возможных значений 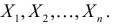
Существует два подхода к решению этой задачи. Можно по результатам наблюдений вычислить приближенное значение характеристики, а можно указать целый интервал ее значений, согласующихся с опытными данными. В первом случае говорят о точечной оценке, во втором – об интервальной.
Определение. Функция результатов наблюдений 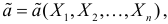
Для одной и той же характеристики можно предложить разные точечные оценки. Необходимо иметь критерии сравнения оценок, для суждения об их качестве. Оценка 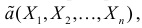 как функция случайных результатов наблюдений
как функция случайных результатов наблюдений 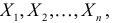 сама является случайной величиной. Значения
сама является случайной величиной. Значения 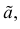 найденные по разным сериям наблюдений, могут отличаться от истинного значения характеристики
найденные по разным сериям наблюдений, могут отличаться от истинного значения характеристики 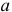 в ту или другую сторону. Естественно потребовать, чтобы оценка систематически не завышала и не занижала оцениваемое значение, а с ростом числа наблюдений становилась более точной. Формализация названных требований приводит к следующим понятиям.
в ту или другую сторону. Естественно потребовать, чтобы оценка систематически не завышала и не занижала оцениваемое значение, а с ростом числа наблюдений становилась более точной. Формализация названных требований приводит к следующим понятиям.
Определение. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемой величине: 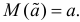 В противном случае оценку называют смещенной.
В противном случае оценку называют смещенной.
Определение. Оценка называется состоятельной, если при увеличении числа наблюдений она сходится по вероятности к оцениваемой величине, т.е. для любого сколь угодно малого 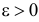
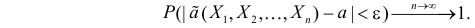
Если известно, что оценка 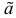 несмещенная, то для ее состоятельности достаточно, чтобы
несмещенная, то для ее состоятельности достаточно, чтобы
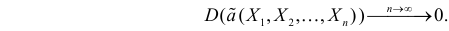
Последнее условие удобно для проверки. В качестве меры разброса значений оценки 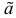 относительно
относительно 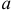 можно рассматривать величину
можно рассматривать величину 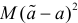 Из двух оценок предпочтительней та, для которой эта величина меньше. Если оценка имеет наименьшую меру разброса среди всех оценок характеристики, построенных по
Из двух оценок предпочтительней та, для которой эта величина меньше. Если оценка имеет наименьшую меру разброса среди всех оценок характеристики, построенных по 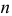 наблюдениям, то оценку называют эффективной.
наблюдениям, то оценку называют эффективной.
Следует отметить, что несмещенность и состоятельность являются желательными свойствами оценок, но не всегда разумно требовать наличия этих свойств у оценки. Например, может оказаться предпочтительней оценка хотя и обладающая небольшим смещением, но имеющая значительно меньший разброс значений, нежели несмещенная оценка. Более того, есть характеристики, для которых нет одновременно несмещенных и состоятельных оценок.
Оценки для математического ожидания и дисперсии
Пусть случайная величина имеет неизвестные математическое ожидание и дисперсию, причем 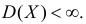 Если
Если 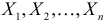 – результаты
– результаты 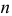 независимых наблюдений случайной величины, то в качестве оценки для математического ожидания можно предложить среднее арифметическое наблюдаемых значений
независимых наблюдений случайной величины, то в качестве оценки для математического ожидания можно предложить среднее арифметическое наблюдаемых значений 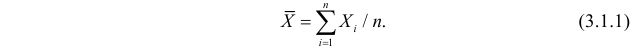
Несмещенность такой оценки следует из равенств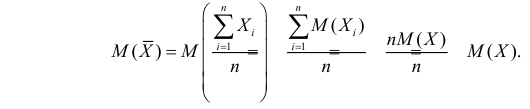
В силу независимости наблюдений 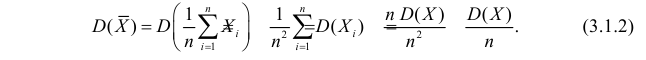
При условии 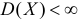 имеем
имеем 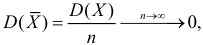 что означает состоятельность оценки
что означает состоятельность оценки 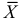 .
.
Доказано, что для математического ожидания нормально распределенной случайной величины оценка 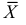 еще и эффективна.
еще и эффективна.
Оценка математического ожидания посредством среднего арифметического наблюдаемых значений наводит на мысль предложить в качестве оценки для дисперсии величину

Преобразуем величину 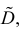 обозначая для краткости
обозначая для краткости 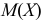 через
через 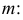
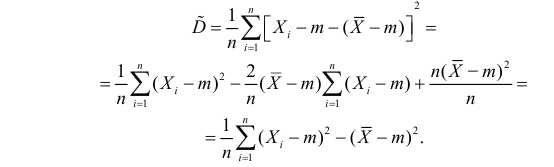
В силу (3.1.2) имеем 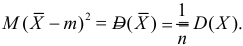 Поэтому
Поэтому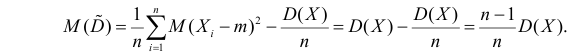
Последняя запись означает, что оценка 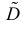 имеет смещение. Она систематически занижает истинное значение дисперсии. Для получения несмещенной оценки введем поправку в виде множителя
имеет смещение. Она систематически занижает истинное значение дисперсии. Для получения несмещенной оценки введем поправку в виде множителя 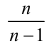 и полученную оценку обозначим через
и полученную оценку обозначим через 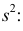
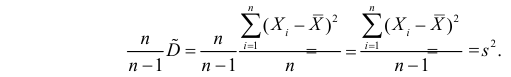
Величина
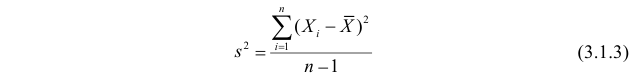
является несмещенной и состоятельной оценкой дисперсии.
Пример:
Оценить математическое ожидание и дисперсию случайной величины Х по результатам ее независимых наблюдений: 7, 3, 4, 8, 4, 6, 3.
Решение. По формулам (3.1.1) и (3.1.3) имеем 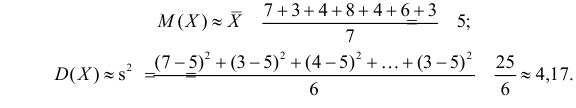
Ответ. 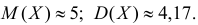
Пример:
Данные 25 независимых наблюдений случайной величины представлены в сгруппированном виде: 
Требуется оценить математическое ожидание и дисперсию этой случайной величины.
Решение. Представителем каждого интервала можно считать его середину. С учетом этого формулы (3.1.1) и (3.1.3) дают следующие оценки: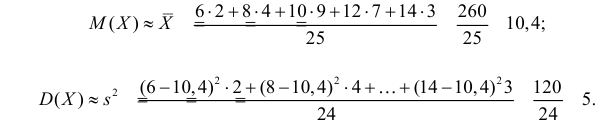
Ответ. 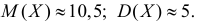
Метод наибольшего правдоподобия для оценки параметров распределений
В теории вероятностей и ее приложениях часто приходится иметь дело с законами распределения, которые определяются некоторыми параметрами. В качестве примера можно назвать нормальный закон распределения 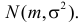 Его параметры
Его параметры 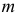 и
и 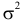 имеют смысл математического ожидания и дисперсии соответственно. Их можно оценить с помощью
имеют смысл математического ожидания и дисперсии соответственно. Их можно оценить с помощью 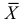 и
и 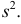 В общем случае параметры законов распределения не всегда напрямую связаны со значениями числовых 179 характеристик. Поэтому практический интерес представляет следующая задача.
В общем случае параметры законов распределения не всегда напрямую связаны со значениями числовых 179 характеристик. Поэтому практический интерес представляет следующая задача.
Пусть случайная величина Х имеет функцию распределения 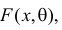 причем тип функции распределения F известен, но неизвестно значение параметра
причем тип функции распределения F известен, но неизвестно значение параметра 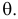 По данным результатов наблюдений нужно оценить значение параметра. Параметр может быть и многомерным.
По данным результатов наблюдений нужно оценить значение параметра. Параметр может быть и многомерным.
Продемонстрируем идею метода наибольшего правдоподобия на упрощенном примере. Пусть по результатам наблюдений, отмеченных на рис. 3.1.1 звездочками, нужно отдать предпочтение одной из двух функций плотности вероятности 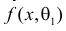 или
или 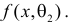
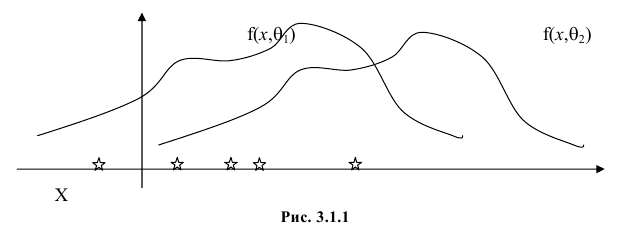
Из рисунка видно, что при значении параметра 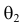 такие результаты наблюдений маловероятны и вряд ли бы реализовались. При значении же
такие результаты наблюдений маловероятны и вряд ли бы реализовались. При значении же 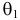 эти результаты наблюдений вполне возможны. Поэтому значение параметра
эти результаты наблюдений вполне возможны. Поэтому значение параметра 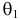 более правдоподобно, чем значение
более правдоподобно, чем значение 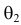 . Такая аргументация позволяет сформулировать принцип наибольшего правдоподобия: в качестве оценки параметра выбирается то его значение, при котором данные результаты наблюдений наиболее вероятны.
. Такая аргументация позволяет сформулировать принцип наибольшего правдоподобия: в качестве оценки параметра выбирается то его значение, при котором данные результаты наблюдений наиболее вероятны.
Этот принцип приводит к следующему способу действий. Пусть закон распределения случайной величины Х зависит от неизвестного значения параметра 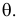 Обозначим через
Обозначим через 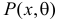 для непрерывной случайной величины плотность вероятности в точке
для непрерывной случайной величины плотность вероятности в точке 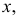 а для дискретной случайной величины – вероятность того, что
а для дискретной случайной величины – вероятность того, что 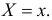 Если в
Если в 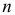 независимых наблюдениях реализовались значения случайной величины
независимых наблюдениях реализовались значения случайной величины 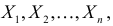 то выражение
то выражение 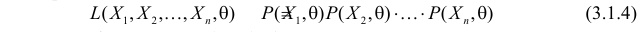
называют функцией правдоподобия. Величина 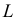 зависит только от параметра
зависит только от параметра 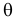 при фиксированных результатах наблюдений
при фиксированных результатах наблюдений 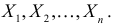 При каждом значении параметра
При каждом значении параметра 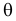 функция
функция  равна вероятности именно тех значений дискретной случайной величины, которые получены в процессе наблюдений. Для непрерывной случайной величины
равна вероятности именно тех значений дискретной случайной величины, которые получены в процессе наблюдений. Для непрерывной случайной величины  равна плотности вероятности в точке выборочного пространства
равна плотности вероятности в точке выборочного пространства 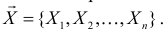
Сформулированный принцип предлагает в качестве оценки значения параметра выбрать такое 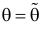 при котором
при котором  принимает наибольшее значение. Величина
принимает наибольшее значение. Величина 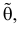 будучи функцией от результатов наблюдений
будучи функцией от результатов наблюдений 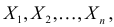 называется оценкой наибольшего правдоподобия.
называется оценкой наибольшего правдоподобия.
Во многих случаях, когда  дифференцируема, оценка наибольшего правдоподобия находится как решение уравнения
дифференцируема, оценка наибольшего правдоподобия находится как решение уравнения 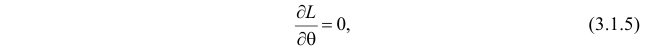
которое следует из необходимого условия экстремума. Поскольку  достигает максимума при том же значении
достигает максимума при том же значении 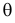 , что и
, что и  , то можно решать относительно
, то можно решать относительно 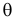 эквивалентное уравнение
эквивалентное уравнение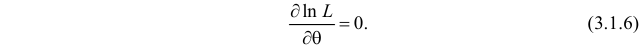
Это уравнение называют уравнением правдоподобия. Им пользоваться удобнее, чем уравнением (3.1.5), так как функция  равна произведению, а
равна произведению, а  – сумме, а дифференцировать
– сумме, а дифференцировать  проще.
проще.
Если параметров несколько (многомерный параметр), то следует взять частные производные от функции правдоподобия по всем параметрам, приравнять частные производные нулю и решить полученную систему уравнений.
Оценку, получаемую в результате поиска максимума функции правдоподобия, называют еще оценкой максимального правдоподобия.
Известно, что оценки максимального правдоподобия состоятельны. Кроме того, если для q существует эффективная оценка, то уравнение правдоподобия имеет единственное решение, совпадающее с этой оценкой. Оценка максимального правдоподобия может оказаться смещенной.
Метод моментов
Начальным моментом 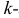 го порядка случайной величины Х называется математическое ожидание
го порядка случайной величины Х называется математическое ожидание 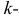 й степени этой величины, т.е.
й степени этой величины, т.е. 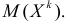 Само математическое ожидание считается начальным моментом первого порядка.
Само математическое ожидание считается начальным моментом первого порядка.
Центральным моментом 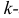 го порядка называется
го порядка называется 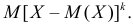 Очевидно, что дисперсия – это центральный момент второго порядка. Если закон распределения случайной величины зависит от некоторых параметров, то от этих параметров зависят и моменты случайной величины.
Очевидно, что дисперсия – это центральный момент второго порядка. Если закон распределения случайной величины зависит от некоторых параметров, то от этих параметров зависят и моменты случайной величины.
Для оценки параметров распределения по методу моментов находят на основе опытных данных оценки моментов в количестве, равном числу оцениваемых параметров. Эти оценки приравнивают к соответствующим теоретическим моментам, величины которых выражены через параметры. Из полученной системы уравнений можно определить искомые оценки.
Например, если Х имеет плотность распределения 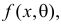 то
то 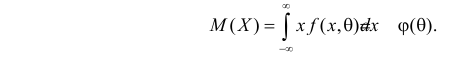
Если воспользоваться величиной 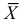 как оценкой для
как оценкой для 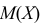 на основе опытных данных, то оценкой
на основе опытных данных, то оценкой 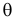 по методу моментов будет решение уравнения
по методу моментов будет решение уравнения 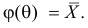
Пример:
Найти оценку параметра показательного закона распределения по методу моментов.
Решение. Плотность вероятности показательного закона распределения имеет вид 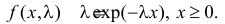 Поэтому
Поэтому 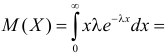
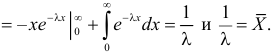 Откуда
Откуда 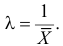
Ответ. 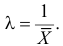
Пример:
Пусть имеется простейший поток событий неизвестной интенсивности 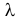 . Для оценки параметра
. Для оценки параметра 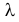 проведено наблюдение потока и зарегистрированы
проведено наблюдение потока и зарегистрированы 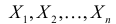 – длительности
– длительности  последовательных интервалов времени между моментами наступления событий. Найти оценку для
последовательных интервалов времени между моментами наступления событий. Найти оценку для 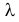 .
.
Решение. В простейшем потоке интервалы времени между последовательными моментами наступления событий потока имеют показательный закон распределения 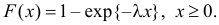 Так как плотность вероятности показательного закона распределения равна
Так как плотность вероятности показательного закона распределения равна 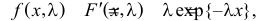 то функция правдоподобия (3.1.4) имеет вид
то функция правдоподобия (3.1.4) имеет вид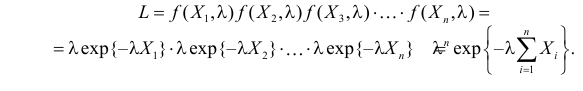
Тогда 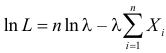 и уравнение правдоподобия
и уравнение правдоподобия 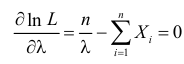 имеет решение
имеет решение 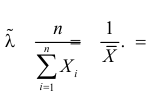
При таком значении 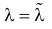 функция правдоподобия действительно достигает наибольшего значения, так как
функция правдоподобия действительно достигает наибольшего значения, так как 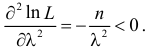
Ответ. 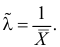
Определение. Пусть 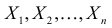 – результаты n независимых наблюдений случайной величины X. Если расставить эти результаты в порядке возрастания, то получится последовательность значений, которую называют вариационным рядом и обозначают:
– результаты n независимых наблюдений случайной величины X. Если расставить эти результаты в порядке возрастания, то получится последовательность значений, которую называют вариационным рядом и обозначают:

В этой записи 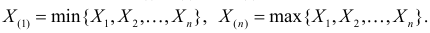
Величины 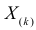 называют порядковыми статистиками.
называют порядковыми статистиками.
Пример:
Случайная величина Х имеет равномерное распределение на отрезке 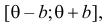 где
где  и
и  неизвестны. Пусть
неизвестны. Пусть 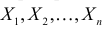 – результаты
– результаты  независимых наблюдений. Найти оценку параметра
независимых наблюдений. Найти оценку параметра  .
.
Решение. Функция плотности вероятности величины Х имеет вид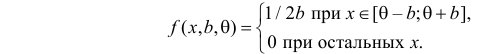
В этом случае функция правдоподобия 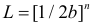 от
от  явно не зависит. Дифференцировать по
явно не зависит. Дифференцировать по  такую функцию нельзя и нет возможности записать уравнение правдоподобия. Однако легко видеть, что
такую функцию нельзя и нет возможности записать уравнение правдоподобия. Однако легко видеть, что  возрастает при уменьшении
возрастает при уменьшении  . Все результаты наблюдений лежат в
. Все результаты наблюдений лежат в 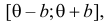 поэтому можно записать:
поэтому можно записать:
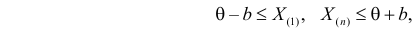
где 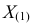 – наименьший, а
– наименьший, а 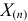 – наибольший из результатов наблюдений. При минимально возможном
– наибольший из результатов наблюдений. При минимально возможном 
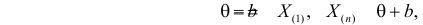
откуда 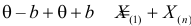 или
или 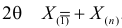
Оценкой наибольшего правдоподобия для параметра  будет величина
будет величина
Ответ. 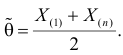
Пример:
Случайная величина X имеет функцию распределения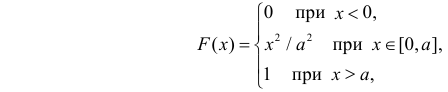
где 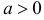 неизвестный параметр.
неизвестный параметр.
Пусть 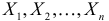 – результаты
– результаты  независимых наблюдений случайной величины X. Требуется найти оценку наибольшего правдоподобия для параметра
независимых наблюдений случайной величины X. Требуется найти оценку наибольшего правдоподобия для параметра 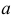 и найти оценку для M(X).
и найти оценку для M(X).
Решение. Для построения функции правдоподобия найдем сначала функцию плотности вероятности
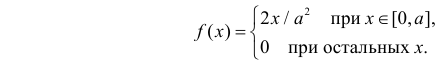
Тогда функция правдоподобия: 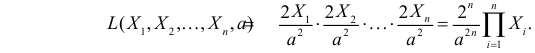
Логарифмическая функция правдоподобия: 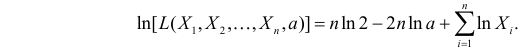
Уравнение правдоподобия

не имеет решений. Критических точек нет. Наибольшее и наименьшее значения  находятся на границе допустимых значений
находятся на границе допустимых значений  .
.
По виду функции  можно заключить, что значение
можно заключить, что значение  тем больше, чем меньше величина
тем больше, чем меньше величина  . Но
. Но  не может быть меньше
не может быть меньше 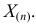 Поэтому наиболее правдоподобное значение
Поэтому наиболее правдоподобное значение 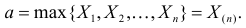
Так как 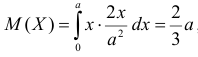 , то оценкой наибольшего правдоподобия для
, то оценкой наибольшего правдоподобия для 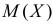 будет величина
будет величина 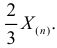
Ответ. 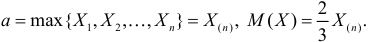
Пример:
Случайная величина Х имеет нормальный закон распределения 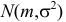 c неизвестными параметрами
c неизвестными параметрами 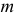 и
и 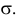 По результатам независимых наблюдений
По результатам независимых наблюдений 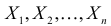 найти наиболее правдоподобные значения этих параметров.
найти наиболее правдоподобные значения этих параметров.
Решение. В соответствии с (3.1.4) функция правдоподобия имеет вид 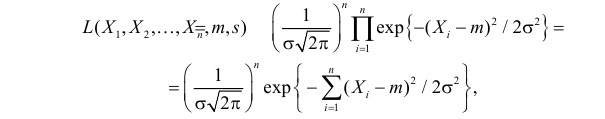
а логарифмическая функция правдоподобия: 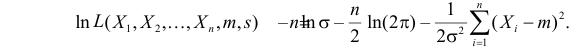
Необходимые условия экстремума дают систему двух уравнений: 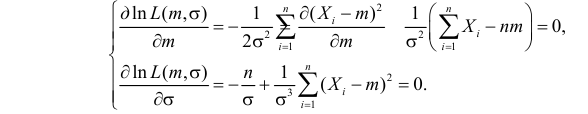
Решения этой системы имеют вид: 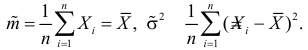
Отметим, что обе оценки являются состоятельными, причем оценка для 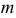 несмещенная, а для
несмещенная, а для 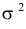 смещенная (сравните с формулой (3.1.3)).
смещенная (сравните с формулой (3.1.3)).
Ответ. 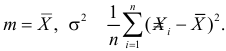
Пример:
По данным эксперимента построен статистический ряд:

Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения случайной величины X.
Решение. 1) Число экспериментальных данных вычисляется по формуле:
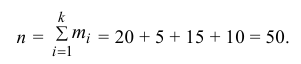
Значит, объем выборки n = 50.
2) Вычислим среднее арифметическое значение эксперимента:
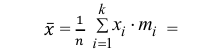
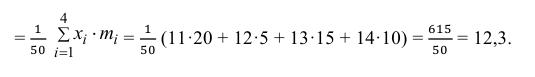
Значит, найдена оценка математического ожидания 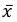 = 12,3.
= 12,3.
3) Вычислим исправленную выборочную дисперсию:
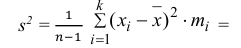
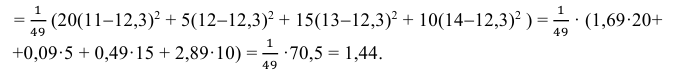
Значит, найдена оценка дисперсии: 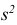 = 1,44.
= 1,44.
5) Вычислим оценку среднего квадратического отклонения:
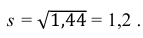
Ответ: 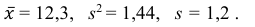
Пример:
По данным эксперимента построен статистический ряд:

Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения случайной величины X.
Решение. По формуле
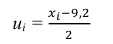
перейдем к условным вариантам:

Для них произведем расчет точечных оценок параметров:
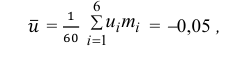
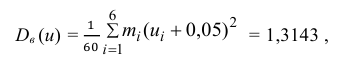
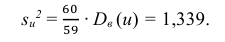
Следовательно, вычисляем искомые точечные оценки:
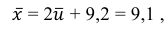
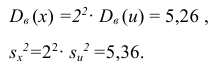
Ответ: 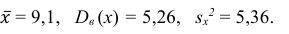
Пример:
По данным эксперимента построен интервальный статистический ряд:

Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения.
Решение. 1) От интервального ряда перейдем к статистическому ряду, заменив интервалы их серединами 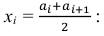

2) Объем выборки вычислим по формуле:
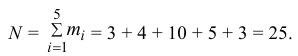
3) Вычислим среднее арифметическое значений эксперимента:
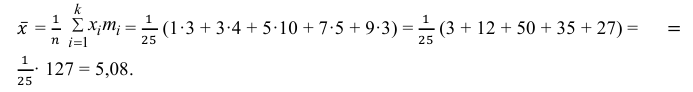
3) Вычислим исправленную выборочную дисперсию:
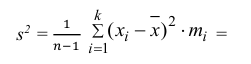
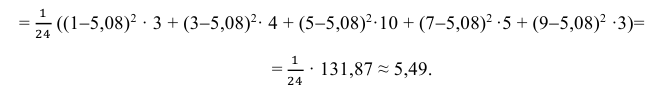
Можно было воспользоваться следующей формулой:
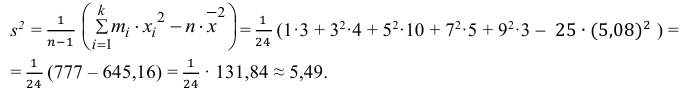
5) Вычислим оценку среднего квадратического отклонения:
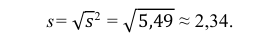
Ответ: 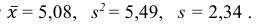
Пример:
Найти доверительный интервал с надежностью 0,95 для оценки математического ожидания M(X) нормально распределенной случайной величины X, если известно среднее квадратическое отклонение σ = 2, оценка математического ожидания 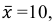 объем выборки n = 25.
объем выборки n = 25.
Решение. Доверительный интервал для истинного математического ожидания с доверительной вероятностью 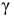 = 0,95 при известной дисперсии σ находится по формуле:
= 0,95 при известной дисперсии σ находится по формуле:
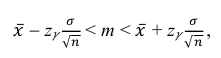
где m = M(X) – истинное математическое ожидание; 𝑥̅ − оценка M(X) по выборке; n – объем выборки; 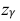 – находится по доверительной вероятности
– находится по доверительной вероятности 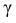 = 0,95 из равенства:
= 0,95 из равенства:
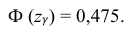
Из табл. П 2.2 приложения 2 находим: 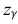 = 1,96. Следовательно, найден доверительный интервал для M(X):
= 1,96. Следовательно, найден доверительный интервал для M(X):
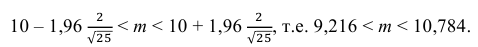
Ответ: (9,216 ; 10,784).
Пример:
По данным эксперимента построен статистический ряд:

Найти доверительный интервал для математического ожидания M (X) с надежностью 0,95.
Решение. Воспользуемся формулой для доверительного интервала математического ожидания при неизвестной дисперсии:
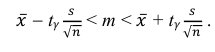
где n – объем выборки; 𝑥̅ оценка M(X); s – оценка среднего квадратического отклонения; 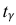 − находится по доверительной вероятности
− находится по доверительной вероятности 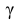 = 0,95.
= 0,95.
По числам 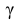 = 0,95 и n = 20 находим:
= 0,95 и n = 20 находим: 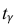 = 2,093.
= 2,093.
Теперь вычисляем оценки для M(X) и D(X):
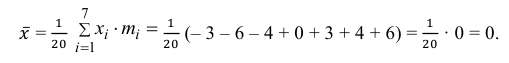
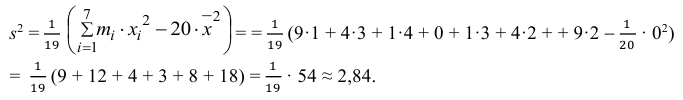
Следовательно, s ≈ 1,685. Поэтому искомый доверительный интервал математического ожидания задается формулой:
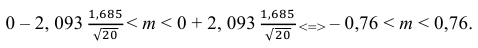
Ответ: (– 0,76; 0,76).
Пример:
По данным десяти независимых измерений найдена оценка квадратического отклонения 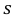 = 0,5. Найти доверительный интервал точности измерительного прибора с надежностью 99 %.
= 0,5. Найти доверительный интервал точности измерительного прибора с надежностью 99 %.
Решение. Задача сводится к нахождению доверительного интервала для истинного квадратического отклонения, так как точность прибора характеризуется средним квадратическим отклонением случайных ошибок измерений.
Доверительный интервал для среднего квадратического отклонения находим по формуле:
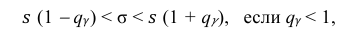
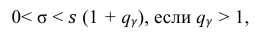
где 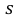 = 0,5 − оценка среднего квадратического отклонения;
= 0,5 − оценка среднего квадратического отклонения; 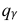 – число, определяемое из табл. П 2.4 приложения 2 по заданной доверительной вероятности
– число, определяемое из табл. П 2.4 приложения 2 по заданной доверительной вероятности 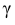 = 0,99 и заданному объему выборки n = 10.
= 0,99 и заданному объему выборки n = 10.
Находим: 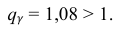
Тогда можно записать:
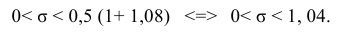
Ответ: (0; 1,04).
- Доверительный интервал для вероятности события
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Системы случайных величин
- Вероятность и риск
- Определения вероятности событий
- Предельные теоремы теории вероятностей
Что означает несмещенность, состоятельность и эффективность статистических оценок простыми словами?
Бизнес модели | 18.06.2022 |

Метки: Теория | Статистика | Матметоды в экономике
Постараемся объяснить, какой смысл кроется за этими терминами и связанными с ними математическими формулами.
Статистические методы используются в тех ситуациях, когда исследователь, не имея возможности изучить полную совокупность каких-либо объектов, стремится получить представление о ней, основываясь на выборочной совокупности. В этом случае также предполагаются, что выборка и полная (генеральная) совокупность не имеют друг с другом каких-либо значимых отличий. Также статистические методы необходимы, когда исследователь пытается на основе каких-либо прошлых данных сделать прогноз о том, что будет происходить в будущем.
Перед исследователем может быть поставлена задача описать функцию распределения в изучаемой генеральной совокупности (среднее, дисперсия, ковариация и пр.), либо задача описать зависимости между различными показателями в генеральной совокупности (коэффициенты регрессии, корректность самой регрессионной модели в целом и пр.), либо определить какие-то другие параметры изучаемой генеральной совокупности. При этом истинные значения параметров генеральной совокупности останутся исследователю недоступными – так как ему недоступна вся генеральная совокупность. В своих выводах и рассуждениях он будет опираться на оценочные значения (или оценки / estimations) данных параметров – то есть на их предположительные значения.
Термины несмещенность, состоятельность и эффективность показывают, насколько полученные оценочные значения параметров соответствуют их истинным значениям.
Как правило, если оценочное значение отвечает всем трем свойствам – значит, это наилучшая возможная оценка. Эту оценку можно использовать в практических целях – при прогнозировании, при принятии решений об определенных воздействиях на объект анализа и пр. Отметим также, что под оценкой обычно понимают математическую формулу (или метод), с помощью которой предлагается определять предположительное значение того или иного параметра. Если формула (метод) отвечают трем указанным выше свойствам, значит, его можно применять на практике.
Несмещенность, состоятельность и эффективность
Несмещенность (unbiasedness) – это свойство, которое означает, что математическое ожидание оценочного значения какого-то параметра будет равно истинному значению этого параметра. Если простыми словами, то наиболее вероятное значение параметра, подсчитанное на основе предложенной формулы, будет равно его истинному значению. То есть ожидается, что предложенная формула максимально точно, насколько это возможно, угадывает истинное значение изучаемого параметра. Например, если мы возьмем несколько выборок из генеральной совокупности (или проведем несколько экспериментов), то мы будем всегда получать похожие результаты и эти результаты будут максимально близки к истине. Как видим, несмещенность не означает, что полученное нами значение правильное, но вероятнее всего, что оно близко к нему.
Состоятельность (consistency) – это свойство, которое означает, что по мере увеличения размера выборки оценочное значение будет все больше и больше приближаться к истинному. Как правило, состоятельность – это дополнительное требование, которое накладывается на несмещенную оценку. Иными словами, если несмещенность гарантирует, что при использовании заданного метода исследователь окажется около истины, то состоятельность гарантирует, что по мере увеличения выборки он будет находиться все ближе и ближе к правде. То есть описывает признак сходимости оценки к истинному значению.
Эффективность (efficiency) – это свойство, означающее, что данная формула оценки искомого параметра дает наименьшую погрешность из всех возможных. Иными словами, эффективность – ещё более сильное условие, оно позволяет выбрать наилучший подход к определению значения искомого параметра из нескольких подходов, каждый из которых отвечает требованиям несмещенности и состоятельности. На практике во многих случаях достаточно несмещенности и состоятельности.
В чем отличие несмещенности от состоятельности
Важно понимать, что несмещенность и состоятельность – это два отдельных свойства. Из несмещенности никогда не вытекает состоятельность, и наоборот. Возможны ситуации, когда оценки несмещена, но несостоятельна, и наоборот, когда оценка смещена, но состоятельна.
Классический пример ситуации, когда оценка состоятельна, но смещена – это оценка дисперсии нормального распределения:
σ2оценка=(1/n)*∑(X-Xср.)
В данной формуле σ2оценка – оценочное значение дисперсии, n – количество наблюдений, X – значение одного наблюдения в выборке, Xср. – среднее значение по выборке. Сделав ряд математических преобразований, можно показать, что оценка в этом случае будет равна следующему значению:
σ2оценка=((n-1)/n)*σ2
σ2 – это истинное (искомое) значение оцениваемого параметра в генеральной совокупности. Из формулы хорошо видно, что какое n не подставляй, оценка никогда не будет равна истинному значению. Иными словами, данная оценка смещена. При этом из этой формулы также хорошо видно, что оценка состоятельна, т.к. при n стремящемся к бесконечности дробь (n-1)/n будет стремиться к единице, а оценка дисперсии будет равна истинному значению. Так как в данном случае мы знаем, что состоятельная оценка сходится к истинному значению, то в данном конкретном случае на больших выборках можно пользоваться данной формулой в практических целях – результат не будет сильно искажен. Но в общем случае, когда величину смещения оценить нельзя, смещенными, но состоятельными оценками пользоваться не рекомендуется.
Правильная формула, которая дает несмещенную и состоятельную оценку дисперсии в нормальном распределении, выглядит следующим образом:
σ2оценка=(1/(n-1))*∑(X-Xср.)
Возможна также обратная ситуация, когда оценка дает несмещенное значение, но не отвечает условию состоятельности. В этом случае увеличение выборки никак не повлияет на точность оценки.
Почему одни страны, города или компании добиваются экономического успеха, а другие – вынуждены влачить жалкое существование? Почему экономический рост такой слабый, а неравенство доходов все выше? Как новые технологии могут изменить глобальный экономический ландшафт? Присоединяйтесь к нашей группе ВКонтакте, чтобы получать больше информации о долгосрочных трендах в экономике и бизнесе.
Авторизация через:
Здесь пока нет комментариев. Чтобы их оставить, авторизуйтесь вверху страницы или с помощью аккаунта ВКонтакте либо зарегистрируйтесь .
1

Хорхе
Извините поторопился, исправил ошибки. Сейчас вроде верно, не бейте!) Снова поправил, с выводом сообразить не могу…
— Чт янв 13, 2011 23:20:59 —
Gortaur
, можно и посмеятся действительно
— Пт янв 14, 2011 00:10:48 —
Определение состоятельной оценки: Оценка  называется состоятельной, если
называется состоятельной, если 
Нам известно что
Условие 1: 
Условие 2:  .
.
По теореме Чебышева имеем: 
Применимо к задаче: 
Исходя из условия 1, получим: 
иходя из условия 2, получим:  или
или 
При  оценка
оценка  приближается к значению
приближается к значению  , а значит:
, а значит: = 0, следовательно оценка состоятельна ч.т.д.
= 0, следовательно оценка состоятельна ч.т.д.
Посмотрите пожалуйста – правильно?
