Процент это один из интересных и часто применяемых на практике инструментов. Проценты частично или полностью применяются в любой науке, на любой работе и даже в повседневном общении. Человек, хорошо разбирающийся в процентах, создаёт впечатление умного и образованного. В данном уроке мы узнаем, что такое процент и какие действия можно с ним выполнять.
Что такое процент?
В повседневной жизни дроби встречаются наиболее часто. Они даже получили свои названия: половина, треть и четверть соответственно.
Но есть ещё одна дробь, которая тоже встречается часто. Это дробь (одна сотая). Данная дробь получила название процент.
Дробь означает, что нечто разделено на сто частей и от этих ста частей взята одна часть. Значит процентом является одна сотая часть.
Процентом является одна сотая часть
Например, ![]() от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.
от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.
от одного метра уже составляет 2 сантиметра. В этот раз один метр разделили на сто частей и взяли оттуда не одну, а две части. А две части из ста составляют два сантиметра. Значит два процента от одного метра составляет 2 сантиметра.
Еще пример, ![]() от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.
от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.
Проценты встречались настолько часто, что люди заменили дробь ![]() на специальный значок, который выглядит следующим образом:
на специальный значок, который выглядит следующим образом:
Эта запись читается как «один процент». Она заменяет собой дробь ![]() . Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь
. Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь ![]() в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:
в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:
1% = ![]() = 0,01
= 0,01
Два процента в дробном виде будут записаны как , в виде десятичной дроби как 0,02 а с помощью специального значка два процента записывается как 2%.
2% = = 0,02
Как найти процент?
Принцип нахождения процента такой же, как и обычное нахождение дроби от числа. Чтобы найти процент от чего-либо, нужно это чего-либо разделить на 100 частей и полученное число умножить на нужный процент.
Например, найти 2% от 10 см.
Что означает запись 2% ? Запись 2% заменяет собой запись . Если перевести это задание на более понятый язык, то оно будет выглядеть следующим образом:
Найти от 10 см
А как решать подобные задания мы уже знаем. Это обычное нахождение дроби от числа. Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
Итак, делим число 10 на знаменатель дроби
Получили 0,1. Теперь 0,1 умножаем на числитель дроби
0,1 × 2 = 0,2
Получили ответ 0,2. Значит 2% от 10 см составляет 0,2 см. А если перевести 0,2 сантиметра в миллиметры, то получим 2 миллиметра:
0,2 см = 2 мм
Значит 2% от 10 см составляют 2 мм.
Пример 2. Найти 50% от 300 рублей.
Чтобы найти 50% от 300 рублей, нужно эти 300 рублей разделить на 100, и полученный результат умножить на 50.
Итак, делим 300 рублей на 100
300 : 100 = 3
Теперь полученный результат умножаем на 50
3 × 50 = 150 руб.
Значит 50% от 300 рублей составляет 150 рублей.
Если на первых порах сложно привыкнуть к записи со значком %, можно заменять эту запись на обычную дробную запись.
Например, те же 50% можно заменить на запись . Тогда задание будет выглядеть так: Найти
![]() от 300 рублей, а решать такие задачи для нас пока проще
от 300 рублей, а решать такие задачи для нас пока проще
300 : 100 = 3
3 × 50 = 150
В принципе, ничего сложного здесь нет. Если возникают сложности, советуем остановиться и заново изучить дроби и как их можно применять.
Пример 3. Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?
Здесь нужно найти 32% от 1200. Найденное число будет ответом к задаче. Воспользуемся правилом нахождения процента. Разделим 1200 на 100 и полученный результат умножим на искомый процент, т.е. на 32
1200 : 100 = 12
12 × 32 = 384
Ответ: 384 костюмов нового фасона выпустила фабрика.
Второй способ нахождения процента
Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.
Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.
Запись 50% заменяет собой запись ![]() , а если перевести эти
, а если перевести эти ![]() в десятичную дробь, то мы получим 0,5
в десятичную дробь, то мы получим 0,5
Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5
300 × 0,5 = 150
Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %
Нахождения числа по его проценту
Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.
Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:
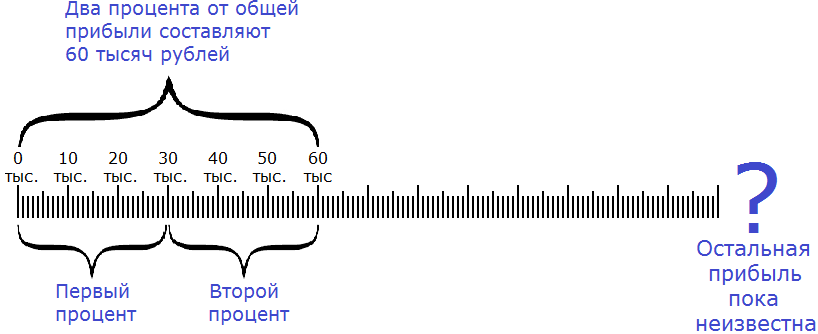
Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2
60 000 : 2 = 30 000
Мы нашли один процент от общей прибыли, т.е. ![]() . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100
. Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100
30 000 × 100 = 3 000 000
Мы нашли общую прибыль. Она составляет три миллиона.
Попробуем сформировать правило нахождения числа по его проценту.
Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.
Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.
Читаем первую часть правила:
Чтобы найти число по его проценту, нужно известное число разделить на данный процент
У нас известное число это 35, а данный процент это 7. Разделим 35 на 7
35 : 7 = 5
Читаем вторую часть правила:
и полученный результат умножить на 100
У нас полученный результат это число 5. Умножим 5 на 100
5 × 100 = 500
500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35
500 : 100 = 5
5 × 7 = 35
Получили 35. Значит задача была решена правильно.
Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.
Например, предыдущая задача может быть изложена так: число 35 это ![]() от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100
от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100
35 : 7 = 5
5 × 100 = 500
В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.
Задания для самостоятельного решения
Задание 1. Найдите 20% от числа 200
Задание 2. Найдите 34% от числа 1050
Задание 3. Найдите 25% от числа 80
Задание 4. Найдите 185% от числа 1,5
Задание 5. Найдите 150% от числа 1150
Задание 6. Представьте выражение 15% в виде обыкновенной дроби
Задание 7. Представьте выражение 25% в виде обыкновенной дроби
Задание 8. Представьте выражение 125% в виде обыкновенной дроби
Задание 9. Число 12 это 60% от какого-то числа. Найдите это число.
Задание 10. Число 40 это 20% от какого-то числа. Найдите это число.
Содержание материала
- Правильная и неправильная дробь
- Видео
- Дроби
- Нахождение части от целого (дроби от числа)
- Вычитание дробей
- Нахождение целого числа по дроби
- Как перевести десятичную дробь в обыкновенную или смешанную
- Применение нахождения дроби от числа для решения задач
- Нахождение числа по значению дроби
Правильная и неправильная дробь
Дробь, в которой числитель меньше знаменателя, называется правильной, а дробь, где числитель больше или равен знаменателю, — неправильной.

Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Для этого нужно умножить целую часть на знаменатель и к произведению прибавить числитель данной дроби. Полученная сумма будет числителем дроби, а знаменателем остается знаменатель дробной части.

Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления — это целая часть, остаток — это числитель, делитель — это знаменатель.

Дроби
Дроби вида $frac{n}{m}$ называют «обыкновенные дроби». В дроби $frac{n}{m}$ число над чертой называют числителем дроби, а число под чертой – знаменателем дроби.
Знаменатель показывает, на сколько долей делят, а числитель — сколько таких долей взято.
Таким образом, если нам нужно обозначить не один «кусочек» числа, а больше, мы просто пишем в верхней части дроби не единицу, а другое число, например, так:

Дроби нужно уметь читать правильно: числитель читается как количественное числительное женского рода (одна, две и т.д.), а знаменатель как порядковое числительное (вторая, пятая) и согласуется с первым числительным.Например: $frac{1}{2}$ — одна вторая, $frac{2}{5}$ — две пятых, $frac{6}{11}$ — шесть одиннадцатых.
На рисунке 6 изображён отрезок АВ, его длина 10 см, то есть 1 дм. Длина отрезка АС будет 1 см.

А какую долю составит сантиметр от метра?
Показать ответ
Скрыть
$frac{1}{100}$
А грамм от килограмма?
Показать ответ
Скрыть
$frac{1}{1000}$
Видео
Нахождение части от целого (дроби от числа)
Чтобы найти часть от целого, нужно число, соответствующее целому, разделить на знаменатель дроби, выражающей эту часть, и результат умножить на числитель той же дроби.
Задача нахождения части от целого по существу является задачей нахождения дроби от числа. Чтобы найти дробь (часть) от числа, необходимо число умножить на эту дробь.

Вычитание дробей
Алгоритм действий при вычитании двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Нахождение целого числа по дроби
Зная часть числа и сколько это составляет от целого числа, можно найти изначальное целое число. Это обратная задача к той, которую мы рассматривали в предыдущей теме. Там мы искали дробь от числа, деля это число на знаменатель дроби, и полученный результат умножая на числитель дроби.
А сейчас наоборот, зная дробь и сколько это составляет от числа, найти изначальное целое число.
Например, если  длины линейки составляют шесть сантиметров и нам говорят найти длину всей линейки, то мы должны понимать, что от нас требуют найти изначальное целое число (длину всей линейки) по дроби
длины линейки составляют шесть сантиметров и нам говорят найти длину всей линейки, то мы должны понимать, что от нас требуют найти изначальное целое число (длину всей линейки) по дроби  . Давайте решим эту задачу.
. Давайте решим эту задачу.
Требуется найти длину всей линейки по дроби  . Известно, что
. Известно, что  длины всей линейки составляют 6 см.
длины всей линейки составляют 6 см.
Мы уже знаем каким образом получились эти 6 см. Имелась какая-то длина, её разделили на пять частей, поскольку знаменатель дроби  это число 5. Затем было взято две части от пяти частей, поскольку числитель дроби
это число 5. Затем было взято две части от пяти частей, поскольку числитель дроби  это число 2.
это число 2.
Чтобы узнать длину всей линейки, сначала нужно узнать длину одной части. Как это узнать? Попробуем догадаться, внимательно изучив следующий рисунок:

Если две части длины линейки составляют 6 см, то нетрудно догадаться, что одна часть составляет 3 см. А чтобы получить эти 3 см, надо 6 разделить на 2
6 см : 2 = 3 см
Итак, мы нашли длину одной части. Одна часть из пяти или  длины линейки составляет 3 см. Если частей всего пять, то для нахождения длины линейки, нужно взять три сантиметра пять раз. Другими словами, умножить 3 см на число 5
длины линейки составляет 3 см. Если частей всего пять, то для нахождения длины линейки, нужно взять три сантиметра пять раз. Другими словами, умножить 3 см на число 5
3 см × 5 = 15
Мы нашли длину линейки. Она составляет 15 сантиметров. Это можно увидеть на следующем рисунке.

Видно, что пять частей из пяти или  составляют пятнадцать сантиметров.
составляют пятнадцать сантиметров.
Чтобы легче было находить число по его дроби, можно пользоваться следующим правилом:
Чтобы найти число по его дроби, нужно известное число разделить на числитель дроби, и полученный результат умножить на знаменатель дроби.
Пример 2. Число 20 это  от всего числа. Найдите это число.
от всего числа. Найдите это число.
Знаменатель дроби  показывает, что число, которое мы должны найти, разделено на пять частей. Если
показывает, что число, которое мы должны найти, разделено на пять частей. Если  этого числа составляет число 20, то для нахождения всего числа, сначала нужно найти
этого числа составляет число 20, то для нахождения всего числа, сначала нужно найти  (одну часть из пяти) от всего числа. Для этого 20 надо разделить на числитель дроби
(одну часть из пяти) от всего числа. Для этого 20 надо разделить на числитель дроби 
20 : 4 = 5
Мы нашли  от всего числа. Эта часть равна 5. Чтобы найти всё число, нужно полученный результат 5 умножить на знаменатель дроби
от всего числа. Эта часть равна 5. Чтобы найти всё число, нужно полученный результат 5 умножить на знаменатель дроби 
5 × 5 = 25
Мы нашли  от всего числа. Другими словами, нашли всё число, которое от нас требовали найти. Это число 25.
от всего числа. Другими словами, нашли всё число, которое от нас требовали найти. Это число 25.
Пример 3. Десять минут это  времени приготовления каши. Найдите общее время приготовления каши.
времени приготовления каши. Найдите общее время приготовления каши.
Знаменатель дроби  показывает, что общее время приготовления каши разделено на три части. Если
показывает, что общее время приготовления каши разделено на три части. Если  времени приготовления каши составляет десять минут, то для нахождения общего времени приготовления, нужно сначала найти
времени приготовления каши составляет десять минут, то для нахождения общего времени приготовления, нужно сначала найти  времени приготовления. Для этого 10 нужно разделить на числитель дроби
времени приготовления. Для этого 10 нужно разделить на числитель дроби 
10 мин : 2 = 5 мин
Мы нашли  времени приготовления каши.
времени приготовления каши.  времени приготовления каши составляют пять минут. Для нахождения общего времени приготовления, нужно 5 минут умножить на знаменатель дроби
времени приготовления каши составляют пять минут. Для нахождения общего времени приготовления, нужно 5 минут умножить на знаменатель дроби 
5 мин × 3 = 15 мин
Мы нашли  времени приготовления каши, то есть нашли общее время приготовления. Оно составляет 15 минут.
времени приготовления каши, то есть нашли общее время приготовления. Оно составляет 15 минут.
Пример 4.  массы мешка цемента составляет 30 кг. Найти общую массу мешка.
массы мешка цемента составляет 30 кг. Найти общую массу мешка.
Знаменатель дроби  показывает, что общая масса мешка разделена на четыре части. Если
показывает, что общая масса мешка разделена на четыре части. Если  массы мешка составляет 30 кг то для того, чтобы найти общую массу мешка нужно сначала найти
массы мешка составляет 30 кг то для того, чтобы найти общую массу мешка нужно сначала найти  массы мешка. Для этого 30 надо разделить на числитель дроби
массы мешка. Для этого 30 надо разделить на числитель дроби  .
.
30кг : 2 = 15кг
Мы нашли  массы мешка.
массы мешка.  массы мешка составляет 15 кг. Теперь, чтобы найти общую массу мешка, надо 15кг умножить на знаменатель дроби
массы мешка составляет 15 кг. Теперь, чтобы найти общую массу мешка, надо 15кг умножить на знаменатель дроби 
15кг × 4 = 60кг
Мы нашли  массы мешка. Другими словами, нашли общую массу мешка. Общая масса мешка цемента составляет 60 кг.
массы мешка. Другими словами, нашли общую массу мешка. Общая масса мешка цемента составляет 60 кг.
Как перевести десятичную дробь в обыкновенную или смешанную
Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:
- Записать дробь в виде десятичная дробь1
- Умножать числитель и знаменатель на 10 до тех пор, пока числитель не станет целым числом.
- Найти наибольший общий делитель и сократить дробь.
Например, переведем 0.36 в обыкновенную дробь:
- Записываем дробь в виде: 0.361
- Умножаем на 10 два раза, получим 36100
- Сокращаем дробь 36100 = 925
Применение нахождения дроби от числа для решения задач
В начале урока мы уже разобрали пример с тортом, сейчас посмотрим на другие примеры.
Задача 1
Остап зарабатывает 40 000 рублей в месяц.
Из них (mathbf{frac{1}{4}}) это подработка.
Сколько рублей Остапу приносит подработка?
Решение:
В данной случае числом будет являться сумма заработка за месяц — 40 000
Ну а дробью, очевидно, будет (mathbf{frac{1}{4}}).
Тогда, чтобы найти прибыль от подработки, надо просто умножить дробь на число.
(mathbf{40000cdotfrac{1}{4}=frac{40000}{4}=10000})
Ответ: 10 000 рублей.
Теперь рассмотрим что-нибудь посложнее.
Задача 2
Порфирий живет в комнате площадью 18 квадратных метров.
3 кровати занимают (mathbf{frac{1}{3}}) площади комнаты.
Какую площадь занимает одна кровать?
Решение:
Сначала найдем, какую площадь занимают 3 кровати, затем разделим это число на 3, чтобы получить площадь одной кровати.
1) (mathbf{18cdotfrac{1}{3}=frac{18}{3}=6}) (квадратных метров) занимают 3 кровати
2) (mathbf{6div3=2}) (квадратных метра) занимает одна кровать
Ответ: 2 квадратных метра.
Теперь посмотрим, как в задачах применяются проценты.
Задача 3
Пересвет работает на заводе и производит 100 деталей в день.
Начальник Елисей пообещал Пересвету выдать премию, если он будет делать на 20% деталей больше.
Сколько деталей в день должен делать Пересвет, чтобы получить премию?
Решение:
Для начала надо понять, на сколько в количественном измерении больше деталей нужно выпустить Пересвету, чтобы получить премию.
Для этого домножим текущее количество деталей на процент или долю, учитывая, что 20% — это 20 частей из 100, или иначе 0,20, и получим искомую прибавку.
1) (mathbf{20%=20div100=0.2})
2) (mathbf{100cdot0.2=20}) (деталей)- то, насколько больше деталей нужно производить
Теперь, чтобы найти общее количество деталей, надо прибавить эту прибавку к тому, что Пересвет производит уже сейчас.
3) (mathbf{100+20=120}) (деталей) в день нужно производить для получения премии
Ответ: 120 деталей.
В некоторых задачах нужно несколько раз применять нахождение процентов от числа.
Задача 4
Глубина реки в начале мая была равна 10 метрам, к началу июня она обмелела на 10%, а к началу июля еще на 15% относительно показателей начала июня. Вычислите, какая глубина реки была в начале июля.
Решение:
Исходное число- 10 метров, дробь задана в виде процентов.
Первым действием нужно будет найти глубину реки в начале июня.
Здесь можно пойти двумя разными путями:
I. Посчитаем, на сколько метров опустился уровень воды, а затем вычтем это из исходных показателей.
0) (mathbf{10%=10div100=0.1})
1) (mathbf{10-10cdot0.1=10-1=9}) (метров)- глубина реки в начале июня
II. Можно вместо того, чтобы считать разницу и вычитать ее, посчитать сколько процентов останется и найти сразу именно эту часть от исходного числа.
Учитывая, что всего у нас 100%, да если глубина уменьшилась на 10%, то осталось 90%.
0) (mathbf{100-10=90}) (процентов) останется
1) (mathbf{90%=90div100=0.9})
2) (mathbf{10cdot0.9=9}) (метров)- глубина реки в начале июня
Как мы видим, эти два подхода дают одинаковый результат.
Поэтому вы можете выбирать любой из них в зависимости от задачи и ваших предпочтений.
Таким образом, мы посчитали глубину в начале июня. Теперь нужно понять, какая будет глубина в начале июля, когда глубина уменьшится еще на 15 процентов.
Используем в этом случае второй способ.
3) (mathbf{100-15=85}) (процентов) останется в июле от уровня июня
4) (mathbf{85%=85div100=0.85})
5) (mathbf{0.85cdot9=7.65}) (метров) составит глубина реки в начале июля
Ответ: 7.65 метра.
Пройти тест Закрыть тест
Пройти тест и получить оценку можно после входа или регистрации Вход Регистрация
Нахождение числа по значению дроби
Если известно сколько число n занимает в числе m, и эта доля выражена в виде дроби, то для нахождения числа m используется формула:
m = m : a / b
Пример:
Один ряд кинозала вмещает 20 кресел, что составляет2 / 5
от всей вместимости зала. Определите, сколько всего посадочных мест в зале.
Решение
Общее количество кресел равняется:
20 :2 / 5
= 20 ⋅5 / 2
=20 ⋅ 5 / 2
= 50
Теги
Как найти часть от числа
Если же числитель нельзя без остатка разделить на заданную часть, то надо знаменатель умножить на размер этой части; С смешанной дробью: Проделываем тоже самое, как и с обыкновенной дробью, но только вначале нужно преобразовать смешанную дробь в обыкновенную. С десятичной дробью: Вычисление будет состоять из единственной операции деления. Десятичную дробь можно разделить на заданный размер части в столбик.
Как найти часть от числа
Итак, пусть нам дано некоторое целое число a. Нам необходимо найти, например, пятую часть от этого числа. Сделать это можно с помощью обыкновенных дробей:
- Поскольку нам необходимо найти пятую часть от числа, то мы ищем 1/5 от числа a.
- Чтобы найти 1/5 от числа a, мы должны умножить число a на часть, которую нам необходимо найти, то есть выполнить действие: a * 1/5 = a/5. То есть пятая часть от числа a — это a/5.
- При этом, если мы ищем часть от целого числа, то результат будет меньше, чем исходное число.
Могут быть разные задачи на нахождении части от целого: если необходимо найти, например, десятую часть от числа a, то надо a * 1/10 = a/10. Если требуется найти 1/8 от числа a, то надо a * 1/8 = a/8.
Нахождение любой части от целого выполняется умножением данного целого числа на часть, которую требуется найти.
Рассмотрим конкретный пример для ещё большего запоминания решения.
Как найти шестую часть от числа 36
Нам дано целое — число 36. Нам необходимо найти от него шестую часть, иначе — необходимо найти 1/6 от числа 36. Выполним действие умножение целого на часть: 36 * 1/6 = 6. Значит шестая часть от числа 36 — это число 6. Можно еще сказать следующее: число 36 ровно в шесть раз больше числа 6, или число 6 ровно в шесть раз меньше числа 36.
Как найти часть от числа и число по его части:)

Чтобы найти часть от числа, нужно число умножить на дробь, которая выражает эту часть.
1) Найти три пятых от числа 25 :
2) Найти одну сотую часть числа 312 :
3) В классе 30 учеников. Треть ребят занимается плаванием. Сколько человек занимаются плаванием?
Чтобы найти число по его части, нужно число поделить на дробь, которая выражает эту часть.
1) Есть некое число, четверть которого равна 12, найти это число.
2) Миша за день прочитал 25 страниц, что составляет десятую часть книги. Сколько страниц в книге?
25 : 0,1 = 250 : 1 = 250 страниц в книге
3) На киносеанс было продано 320 билетов. Шестая часть мест в зале оказалась свободна. Сколько мест в кинозале?
Нахождение дроби от числа
Дроби используют в математике, чтобы кратко обозначить часть рассматриваемой величины.
Но если есть часть, то обязательно есть и целое (то, отчего была взята эта часть).
Зная целое, можно найти его часть, указанную соответствующей дробью.
Запомните! ![]()
Чтобы найти дробь (часть) от числа, нужно это число умножить на данную дробь.
Пример. Рассмотрим задачу.
В книге 160 страниц. Юра прочитал
книги. Сколько страниц прочитал Юра?
Прежде всего найдём в задаче целое. Это — вся книга и в ней всего 160 страниц.
- 160 : 5 = 32 (стр.) — составляет
часть страниц.
- Числитель дроби равен 4 , значит взято 4 части.
- 32 · 4 = 128 (стр.) — составляют
книги.
Оба действия можно записать кратко, в соответствии с правилом нахождения части от целого.
Содержание
- Целое и часть
- Нахождение части по целому
- Нахождение целого по части
- Выражение части в долях целого
- Как найти часть от целого?
- Ответ или решение 2
- Как найти часть от целого
- Как найти третью часть от числа 75
- Как найти дробь от числа
- Как решать задачи с процентами
- Основные определения
- Типы задач на проценты
- Тип 1. Нахождение процента от числа
- Тип 2. Нахождение числа по его проценту
- Тип 3. Нахождение процентного отношения двух чисел
- Тип 4. Увеличение числа на процент
- Тип 5. Уменьшение числа на процент
- Тип 6. Задачи на простые проценты
- Тип 7. Задачи на сложные проценты
- Способы нахождения процента
- Деление числа на 100
- Составление пропорции
- Соотношения чисел
- Задачи на проценты с решением
Целое и часть
Нахождение части по целому

Для того чтобы найти некоторую часть числа, это число умножают на дробь, которое выражает эту часть.
По уставу сообщества, для того чтобы отчетное собрание являлось полномочным, присутствие на нем должно составлять, как правило, не менее двух третьих от общего числа персонала компании. В организации, проводящей данное собрание, общее число работающих в ней сотрудников составляет 120 человек. Требуется установить, при каком числе пришедших допускается проведение собрания?
Количество участников должно составить восемьдесят человек, что является двумя третями от ста двадцати человек:
Нахождение целого по части
Чтобы, найти целое число по значению данной его части, эту величину делят на дробь, которая выражает её часть.
Вес обработанной туши животного составляет три пятых общего живого веса. Нужно определить какой должен быть живой вес животного, чтобы его заготовленная туша весила 420 кг?
Живой вес животного составляет семьсот килограмм по отношению к туше:
Выражение части в долях целого
Чтобы выразить необходимую часть в долях целого, эту часть делят на исходное целое.
Чтобы узнать, какая часть сотрудников отсутствует, если известно, что четыре человека находятся вне расположения предприятия, а общее их число составляет 30 , нужно разделить четыре на тридцать:
Источник
Как найти часть от целого?
Ответ или решение 2
![]()
Для решения данного задания, вспомним, что Чтобы найти часть х от целого а, надо число а, соответствующее целому, разделить на знаменатель m и результат умножить на числитель k дроби, которая выражает эту часть. Например вычислим чему равна 1/4 часть от числа 20.
20 / 4 * 1 = 5 * 1 = 5
![]()
Как найти часть от целого
Итак, пусть нам дано некоторое целое число a. Нам необходимо найти половину от этого числа. Сделать это можно с помощью обыкновенных дробей:
- Обозначим целое за единицу, тогда половина от единицы — это 1/2. Значит нам надо найти 1/2 от числа a.
- Чтобы найти 1/2 от числа a, мы должны умножить число a на часть, которую нам необходимо найти, то есть выполнить действие: a * 1/2 = a/2. То есть половина от числа a — это a/2.
- При этом, если мы ищем часть от целого числа, то результат будет меньше, чем исходное число.
Могут быть разные задачи на нахождении части от целого: если необходимо найти, например, четверть от числа a, то надо a * 1/4 = a/4. Если требуется найти 1/8 от числа a, то надо a * 1/8 = a/8. Нахождение любой части от целого выполняется умножением данного целого числа на часть, которую требуется найти.
Рассмотрим пример.
Как найти третью часть от числа 75
Нам дано целое — число 75. Нам необходимо найти от него третью часть, иначе — необходимо найти 1/3. Выполним действие умножение целого на часть: 75 * 1/3 = 25. Значит третья часть от числа 75 — это число 25. Можно сказать и так: число 25 меньше числа 75 в три раза. Или: число 75 больше числа 25 в три раза.
Источник
Как найти дробь от числа

Одна из простой, но интересной темы – это как найти дробь от целого (от числа).
Как найти часть от целого? У нас есть какое-то значение и нам нужно найти долю или дробь от этого значения.
К примеру, пицца весит 540 г. Сколько весит кусок пиццы, если ее разделили на 6 одинаковых кусков?

Пиццу разрезали на 6 одинаковых кусков, значит, один кусок – это 1/6 от всей пиццы.
Начертим схему: чертим отрезок, разделим его на 6 равных частей. Удобнее начертить отрезок длиной 6 или 12 см (см. статью здесь).

Если пиццу разрезали, то и весь вес надо разделить: 540:6=90 (г)
Если нужно узнать вес двух кусков, т.е. 2/6

то эти 90 взять 2 раза: 90х2= 180 (г)
В итоге, 540 : 6 х 2, или, зная правила работы с дробями — 540 х 2/6.
Видим, что для того, чтобы найти 2/6 от целой пиццы нужно просто умножить общий вес на значение этой части — 2/6.
Как-то странно. Не правда ли? И, тем не менее: чтобы найти часть, мы умножаем, а не делим. Потому что если вспомнить, что дробь, вернее, горизонтальная черта дроби — это деление. Итак:


7/8 от 24 — 24:8х7=21
3/5 от 60 – 60:5х3=45
3/4 от 12 – 12:4х3=9
7/8 от 64 – 64:8х7=56
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 5 / 5. Количество оценок: 70
Источник
Как решать задачи с процентами

О чем эта статья:
Основные определения
Когда мы сравниваем разные части целого, мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Это удобно: отрезать половину пирога, пройти треть пути, закончить первую четверть в школе.
Чтобы сравнивать сотые доли, придумали процент (1/100): с латинского языка — «за сто».
Процент — это одна сотая часть от любого числа. Обозначается вот так: %.

Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить число на 100, как в примере выше.
А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например:
А вот, как перевести проценты в десятичную дробь — обратным действием:
Выразить дробь в процентах просто. Для перевода сначала превратим её в десятичную дробь, а потом используем предыдущее правило:

Типы задач на проценты
В 5, 6, 7, 8, 9 классах в задачках по математике на проценты сравнивают части одного целого, определяют долю части от целого, ищут целое по части. Давайте рассмотрим все виды задач на проценты.
Тип 1. Нахождение процента от числа
Чтобы найти процент от числа, нужно число умножить на процент.
Задача. За месяц на заводе изготовили 500 стульев. 20% изготовленных стульев не прошли контроль качества. Сколько стульев не прошло контроль качества?
Как решаем: нужно найти 20% от общего количества изготовленных стульев (500).
Из общего количества изготовленных стульев контроль не прошли 100 штук.
Тип 2. Нахождение числа по его проценту
Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.
Задачи по поиску процента по числу и числа по его проценту очень похожи. Чтобы не перепутать — внимательно читаем условия, иначе зайдем в тупик или решим неправильно. Если в задании есть слова «который», «что составляет» и «который составляет» — перед нами задача по нахождению числа по его проценту.
Задача. Школьник решил 38 задач из учебника. Что составляет 16% числа всех задач в книге. Сколько всего задач собрано в этом учебнике?
Как решаем: мы не знаем, сколько всего задач в учебнике. Но нам известно, что 38 задач составляют 16% от общего количества. Запишем 16% в виде дроби: 0,16. Далее известную нам часть целого разделим на ту долю, которую она составляет от всего целого.
38/0,16 = 38 * 100/16 = 237,5
Значит 237 задачи включили в этот сборник.
Тип 3. Нахождение процентного отношения двух чисел
Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100%.
Задача. В классе учится 25 человек. 10 из них — девочки. Сколько процентов девочек в классе?
Как решаем: возьмем алгоритм из правила выше:
10/25 * 100% = 2/5 * 100% = 2 * 100/5 = 40%
В классе учится 10 девочек — это 40%.
Тип 4. Увеличение числа на процент
Чтобы увеличить число на некоторое количество процентов, нужно найти число, которое выражает нужное количество процентов от данного числа, и сложить его с данным числом.
Формула расчета процента от числа выглядит так:
a = b * ((1 + c) / 100),
где a — число, которое нужно найти,
b — первоначальное значение,
c — проценты.
Задача. В прошлом месяце стикер-пак стоил 110 рублей. А в этом месяце на 12% больше. Сколько стоит стикер-пак?
Как решаем: подставим в формулу данные из условий задачи.
110 * (1 + 12/100) = 110 * 1,12 = 123,2.
Стоимость стикер-пака в этом месяце — 123 рубля 20 копеек.
Тип 5. Уменьшение числа на процент
Чтобы уменьшить число на несколько процентов, нужно найти число, которое выражает нужное количество процентов данного числа, и вычесть его от данного числа.
Формула расчета выглядит так:
a = b * ((1 — c) / 100),
где a — число, которое нужно найти,
b — первоначальное значение,
c — проценты.
Задача. В прошлом году школу закончили 100 ребят. А в это году выпускников на 25 меньше. Сколько выпускников в этом году?
Как решаем: подставим в формулу данные из условий задачи.
100 * (1 – 25/100) = 75
75 выпускников закончат школу в этом году.
Тип 6. Задачи на простые проценты
Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада или долга.
Формула расчета выглядит так:
S = а * ((1 + у * х)/ 100),
где a — исходная сумма,
S — сумма, которая наращивается,
x — процентная ставка,
y — количество периодов начисления процента.
Задача. Родители взяли в банке кредит 5000 рублей, чтобы купить тебе что-то классное. Кредит на год под 15% ежемесячно. Сколько денег они внесут через год?
Как решаем: подставим в формулу данные из условий задачи.
5000 * (1 + 12 * 15/100) = 14000
Родители через год внесут в банк 14000 рублей.
Тип 7. Задачи на сложные проценты
Сложные проценты — это метод расчета процентов, когда проценты прибыли прибавляют к сумме на остатке каждый месяц. В следующий раз проценты начисляют на эту новую сумму.
Формула расчета выглядит так:
S = а * ((1 + х)/100) y ,
где S — наращиваемая сумма,
a — исходная,
x — процентная ставка,
y — количество периодов начисления процента.
Задача. Папа взял в банке кредит 25000 рублей на 3 месяца под 15%. Нам нужно узнать, сколько денег придется заплатить банку по истечении срока кредита.
Как решаем: просто подставим в формулу данные из условий задачи:
25000 * (1 + 15/100)3 = 38021,875 — искомая сумма.
Онлайн обучение по математике для учеников с 1 по 11 классы! Уроки ведут лучшие преподаватели!
Способы нахождения процента
Универсальная формула для решения задач на проценты:
A * b = C,
где A — исходное число,
b — проценты, переведенные в десятичную дробь,
C — новое число.
Чтобы применить алгоритм, нужно прочитать задачу, отметить, какие два числа нам известны и найти третье.
Есть еще четыре способа поиска процентов. Рассмотрим каждый из них.
Деление числа на 100
При делении на 100 получается 1% от этого числа. Это правило можно использовать по-разному. Например, чтобы узнать процент от суммы, нужно умножить их на размер 1%. А чтобы перевести известное значение, следует разделить его на размер 1%. Этот метод отлично помогает в вопросе, как перевести целое число в проценты.
Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?
- Переведем 15% в рубли:
250 : 100 = 2,5 — это 1% от стоимости шоколада,
значит 2,5 * 15 = 37,5 — это 15%. - 250 — 37,5 = 212,5.
- 212,5
Ответ: выгоднее воспользоваться скидкой 15%.
Составление пропорции
Пропорция — определенное соотношение частей между собой.
С помощью метода пропорции можно рассчитать любые %. Выглядит это так:
Читается: a относится к b так, как с относится к d. Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение.
Рассмотрим пример. На сколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?
- Узнаем сколько стоит футболка сейчас в % соотношении:
100 — 14 = 86,
значит 1390 рублей это 86%. - Составим пропорцию:
1390 : 100 = х : 86,
х = 86 * (1390 : 100),
х = 1195,4. - 1390 — 1195,4 = 194,6.
Ответ: купить спортивную футболку выгоднее на 194,6 рубля.
Соотношения чисел
Есть случаи, при которых можно использовать простые дроби.
- 10% — десятая часть целого. Чтобы найти десять %, понадобится известное разделить на 10.
- 20% — пятая часть целого. Чтобы вычислить двадцать % от известного, его нужно разделить на 5.
- 25% — четверть целого. Чтобы вычислить двадцать пять %, понадобится известное разделить на 4.
- 50% — половина целого. Чтобы вычислить половину, нужно известное разделить на 2.
- 75% — три четверти целого. Чтобы вычислить семьдесят пять %, нужно известное значение разделить на 4 и умножить на 3.
Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?
- 100 — 25 = 75,
значит нужно заплатить 75% от первоначальной цены. - Используем правило соотношения чисел:
8500 : 4 * 3 = 6375.
Ответ: средств хватит, так как пиджак стоит 6375 рублей.
Задачи на проценты с решением
Как мы уже убедились, решать задачи на проценты совсем несложно. Для закрепления материала рассмотрим реальные примеры на проценты из учебников и несколько заданий для подготовки к ЕГЭ.
Задача 1. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?
76 : 100 = 0,76 — 1% от массы человека
Ответ: масса воды 53,2 кг
Задача 2. Цена товара понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой?
Обозначим первоначальную цену товара через х. После первого понижения цена станет равной.
Второе понижение цены составляет 25% от новой цены 0,6х, поэтому после второго понижения получим:
0,6х — 0,25 * 0,6x = 0,45x
После двух понижений изменение цены составит:
Так как величина 0,55x составляет 55% от величины x, то цена товара понизилась на 55%.
Задача 3. Четыре пары брюк дешевле одного пальто на 8%. На сколько процентов пять пар брюк стоят дороже, чем одно пальто?
По условиям задачи стоимость четырех пар брюк — это 92% от стоимости пальто
Получается, что стоимость одной пары брюк — это 23% стоимости пальто.
Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто.
Ответ: пять пар брюк на 15% дороже, чем одно пальто.
Задача 4. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Вычислить, какой процент в общий доход семьи приносит заработок жены.
По условиям задачи общий доход семьи напрямую зависит от доходов мужа. Благодаря увеличению зарплаты общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз 67% от общего дохода.
Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 — это и есть 4%, на которые уменьшился бы семейных доход.
Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии — это 4% дохода, то вся стипендия — это 6%.
А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100 – 67 – 6 = 27.
Ответ: заработок жены составляет 27%.
Задача 5. В свежих абрикосах 90% влаги, а в сухофрукте кураге только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?
Исходя из условия, в абрикосах 10% питательного вещества, а в кураге в концентрированном виде — 95%.
Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества.
На вопрос задачи мы ответим, если разделим одинаковое количество питательного вещества, которое содержится в разных объемах свежих абрикосов и кураги, на его процентное содержание в абрикосах.
Ответ: 190 кг свежих абрикосов потребуется для изготовления 20 кг кураги.
Источник
Adblock
detector
Процент — это одна сотая часть от любого числа. Обозначающим знаком является %.
Чтобы узнать, как перевести проценты в десятичную дробь, нужно убрать знак % и разделить известное на 100. Например, 18% — это 18 : 100 = 0,18.
А если нужно перевести натуральное число или десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например, 0,18 = 0,18 · 100% = 18%.
Выразить дробь в процентах просто. Для перевода сначала превратим ее в десятичную дробь, а далее используем предыдущее правило и переведём десятичную дробь в проценты.
Рассмотрим четыре известных способа поиска процентов.
Занимайтесь математикой в удовольствие вместе с нашими преподавателями на онлайн-курсах по математике для детей и подростков!
Найти процент от числа можно несколькими способами.
Найдем, чему равен 1%.
Умножим полученное значение на количество искомых процентов.
Пример: найти 12% от числа 48.
Переведем проценты в десятичную дробь.
Умножим число на полученную десятичную дробь.
Давайте снова найдем 12% от 48, но другим способом.
Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?
значит, 2,5 × 15 = 37,5 — это 15%.
Ответ: выгоднее воспользоваться скидкой 15%.
Составление пропорции
Равенство двух отношений называют пропорцией.
a : b = c : d или a/b = c/d
- a, d — крайние члены
- b, c — средние члены
Читается: а относится к b так, как с относится к d. Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение.
Рассмотрим пример. Насколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?
Как решаем:
Найдем, сколько рублей составляет выгода, то есть скидка в 14%. Обозначим стоимость футболки за 100%, значит 1390 рублей = 100%. Тогда 14% это х рублей. Получаем пропорцию:
1390 руб. = 100%
x руб. = 14%
Перемножим крест-накрест и найдем x:
x = 1390 × 14 : 100
x = 194,6
Ответ: выгода по скидке составила 194,6 рубля.
Соотношения чисел
Есть случаи, при которых можно использовать простые дроби. Например, 10% — это десятая часть целого. Чтобы найти 10% от числа a, нужно разделить его на 10. Собрали примеры соотношения чисел в таблице.
| Процент | Дробь | Как найти % от числа a |
|---|---|---|
| 10% | 1/10 | a : 10 |
| 20% | 1/5 | a : 5 |
| 25% | 1/4 | a : 4 |
| 50% | 1/2 | a : 2 |
| 75% | 3/4 | a : 4 × 3 |
Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?
Как решаем:
значит, нужно заплатить 75% от первоначальной цены.
Используем правило соотношения чисел:
75% — это 3/4 от числа, значит,
8500 : 4 × 3 = 6375 (рублей).
Ответ: средств хватит, так как пиджак стоит 6375 рублей.
Онлайн-калькулятор
Если вы уже знакомы со всеми правилами и умеете их с легкостью использовать, но ситуация срочная и нужно все быстро посчитать — можно обратиться за помощью к калькулятору. Нахождение ответа выглядит так:
- Для подсчета процента от суммы: вводим известное, равное 100%, знак умножения, нужный процент, знак %.
- Чтобы вычесть проценты: введем известное, равное 100%, знак минус, размер процентной доли и знак %.
Источник
Проценты
Процент это один из интересных и часто применяемых на практике инструментов. Проценты частично или полностью применяются в любой науке, на любой работе и даже в повседневном общении. Человек, хорошо разбирающийся в процентах, создаёт впечатление умного и образованного. В данном уроке мы узнаем, что такое процент и какие действия можно с ним выполнять.
Что такое процент?
В повседневной жизни дроби встречаются наиболее часто. Они даже получили свои названия: половина, треть и четверть соответственно.
Но есть ещё одна дробь, которая тоже встречается часто. Это дробь (одна сотая). Данная дробь получила название процент.
Дробь означает, что нечто разделено на сто частей и от этих ста частей взята одна часть. Значит процентом является одна сотая часть.
Процентом является одна сотая часть
Например,  от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.
от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.
от одного метра уже составляет 2 сантиметра. В этот раз один метр разделили на сто частей и взяли оттуда не одну, а две части. А две части из ста составляют два сантиметра. Значит два процента от одного метра составляет 2 сантиметра.
Еще пример,  от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.
от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.
Проценты встречались настолько часто, что люди заменили дробь  на специальный значок, который выглядит следующим образом:
на специальный значок, который выглядит следующим образом:
Эта запись читается как «один процент». Она заменяет собой дробь  . Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь
. Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь  в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:
в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:
1% =  = 0,01
= 0,01
Два процента в дробном виде будут записаны как , в виде десятичной дроби как 0,02 а с помощью специального значка два процента записывается как 2%.
Как найти процент?
Принцип нахождения процента такой же, как и обычное нахождение дроби от числа. Чтобы найти процент от чего-либо, нужно это чего-либо разделить на 100 частей и полученное число умножить на нужный процент.
Например, найти 2% от 10 см.
Что означает запись 2% ? Запись 2% заменяет собой запись . Если перевести это задание на более понятый язык, то оно будет выглядеть следующим образом:
А как решать подобные задания мы уже знаем. Это обычное нахождение дроби от числа. Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
Итак, делим число 10 на знаменатель дроби
Получили 0,1. Теперь 0,1 умножаем на числитель дроби
Получили ответ 0,2. Значит 2% от 10 см составляет 0,2 см. А если перевести 0,2 сантиметра в миллиметры, то получим 2 миллиметра:
Значит 2% от 10 см составляют 2 мм.
Пример 2. Найти 50% от 300 рублей.
Чтобы найти 50% от 300 рублей, нужно эти 300 рублей разделить на 100, и полученный результат умножить на 50.
Итак, делим 300 рублей на 100
Теперь полученный результат умножаем на 50
Значит 50% от 300 рублей составляет 150 рублей.
Если на первых порах сложно привыкнуть к записи со значком %, можно заменять эту запись на обычную дробную запись.
Например, те же 50% можно заменить на запись . Тогда задание будет выглядеть так: Найти  от 300 рублей, а решать такие задачи для нас пока проще
от 300 рублей, а решать такие задачи для нас пока проще
В принципе, ничего сложного здесь нет. Если возникают сложности, советуем остановиться и заново изучить дроби и как их можно применять.
Пример 3. Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?
Здесь нужно найти 32% от 1200. Найденное число будет ответом к задаче. Воспользуемся правилом нахождения процента. Разделим 1200 на 100 и полученный результат умножим на искомый процент, т.е. на 32
Ответ: 384 костюмов нового фасона выпустила фабрика.
Второй способ нахождения процента
Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.
Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.
Запись 50% заменяет собой запись  , а если перевести эти
, а если перевести эти  в десятичную дробь, то мы получим 0,5
в десятичную дробь, то мы получим 0,5
Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5
Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %
Нахождения числа по его проценту
Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.
Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:

Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2
60 000 : 2 = 30 000
Мы нашли один процент от общей прибыли, т.е.  . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100
. Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100
30 000 × 100 = 3 000 000
Мы нашли общую прибыль. Она составляет три миллиона.
Попробуем сформировать правило нахождения числа по его проценту.
Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.
Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.
Читаем первую часть правила:
Чтобы найти число по его проценту, нужно известное число разделить на данный процент
У нас известное число это 35, а данный процент это 7. Разделим 35 на 7
Читаем вторую часть правила:
и полученный результат умножить на 100
У нас полученный результат это число 5. Умножим 5 на 100
500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35
Получили 35. Значит задача была решена правильно.
Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.
Например, предыдущая задача может быть изложена так: число 35 это  от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100
от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100
В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.
Источник
Проценты
Процентом от некоторой величины называется одна сотая ее часть и обозначают один процент так: 1%.
Чтобы найти процент от некоторой величины, нужно разделить эту величину на 100.
Пример:
1% от 200 т равен 2 т, так как 200 : 100 = 2.
1% от 5 км равен 50 м, т.к. 1 км = 1 000 м, тогда 5 км = 5 000 м, а 5 000 м : 100 = 50 м.
Величина, от которой вычисляются проценты составляет 100 своих сотых долей, т.е. 100 %.
Например, если говорят, что учащийся выполнил 100% домашнего задания, значит, он выполнил все домашнее задание, которое ему было задано.
Любое число процентов можно записать в виде десятичной дроби или натурального числа.
Для этого нужно число, стоящее перед знаком %, разделить на 100.
Пример:
15% = 15 : 100 = 0,15;
60% = 60 : 100 = 0,60 = 0,6;
700% = 700 : 100 = 7;
23,5% = 23,5 : 100 = 0,235.
Обратите внимание: если у числа на конце справа стоит меньше двух нулей, то деление выполняем по правилу деления десятичных дробей на 100, т.е. перемещая запятую влево на две цифры, учитывая то, что у натурального числа запятую мы подразумеваем на конце справа.
Любую десятичную дробь или любое натуральное можно записать в процентах.
Для этого нужно десятичную дробь или натуральное число умножить на 100 и к результату приписать знак %.
Пример:
3,5 = 3,5 100 = 350%;
100 = 350%;
0,07 = 0,07 100 = 7%;
100 = 7%;
9 = 9 100 = 900%.
100 = 900%.
Обратите внимание: когда мы умножаем десятичную дробь на 100, то перемещаем запятую вправо на две цифры.
Чтобы найти несколько процентов от числа, нужно это число разделить на 100, а затем, полученный результат, умножить на число, стоящее перед знаком %.
Пример:
1) Найти 15% от числа 800.
800 : 100 = 8 — 1% от числа 800.
8 15 = 120 — 15% от числа 800.
15 = 120 — 15% от числа 800.
2) Найти 6% от числа 375.
375 : 100 = 3,75 — 1% от числа 375.
3,75 6 = 22,50 = 22,5 — 6% от числа 375.
6 = 22,50 = 22,5 — 6% от числа 375.
| × | 3 | 7 | 5 |
| 6 | |||
| 2 | 2 | 5 | 0 |
Чтобы найти число по его процентам, нужно разделить число, соответствующее известным процентам от числа, на число стоящее перед знаком % и полученный результат умножить на 100 или можно представить проценты в виде десятичной дроби и разделить значение процентов на эту дробь.
Пример:
Найдите число, если 20% этого числа равны 80?
1) 80 : 20 = 4 — 1% от числа.
2) 4 100 = 400.
100 = 400.
2) 80 : 0,2 = 800 : 2 = 400.
Ответ: 400.
Поделись с друзьями в социальных сетях:
Источник
