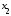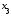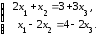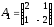Как найти совместность матрицы

Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность. Первая часть.

Исследовать систему линейных агебраических уравнений (СЛАУ) на совместность означает выяснить, есть у этой системы решения, или же их нет. Ну и если решения есть, то указать сколько их.

Нам понадобятся сведения из темы “Система линейных алгебраических уравнений. Основные термины. Матричная форма записи”. В частности, нужны такие понятия, как матрица системы и расширенная матрица системы, поскольку именно на них опирается формулировка теоремы Кронекера-Капелли. Как обычно, матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $widetilde{A}$.

Теорема Кронекера-Капелли

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. $rang A=rangwidetilde{A}$.

Напомню, что система называется совместной, если она имеет хоть одно решение. Теорема Кронекера-Капелли говорит вот о чём: если $rang A=rangwidetilde{A}$, то решение есть; если $rang Aneqrangwidetilde{A}$, то данная СЛАУ не имеет решений (несовместна). Ответ на вопрос о количестве этих решений даёт следствие из теоремы Кронекера-Капелли. В формулировке следствия использована буква $n$, которая равна количеству переменных заданной СЛАУ.

Следствие из теоремы Кронекера-Капелли

1. Если $rang Aneqrangwidetilde{A}$, то СЛАУ несовместна (не имеет решений).
2. Если $rang A=rangwidetilde{A} < n$, то СЛАУ является неопределённой (имеет бесконечное количество решений).
3. Если $rang A=rangwidetilde{A} = n$, то СЛАУ является определённой (имеет ровно одно решение).

Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения или нет, а если существуют – то сколько.

Пример №1

Исследовать СЛАУ $
left {begin{aligned}
& -3x_1+9x_2-7x_3=17;\
& -x_1+2x_2-4x_3=9;\
& 4x_1-2x_2+19x_3=-42.
end{aligned}right.$ на совместность. Если СЛАУ совместна, указать количество решений.

Решение

Чтобы выяснить наличие решений заданной СЛАУ, используем теорему Кронекера-Капелли. Нам понадобятся матрица системы $A$ и расширенная матрица системы $widetilde{A}$, запишем их:

$$
A=left( begin{array} {ccc}
-3 & 9 & -7 \ -1 & 2 & -4 \ 4 & -2 & 19
end{array} right);;

widetilde{A}=left( begin{array} {ccc|c}
-3 & 9 &-7 & 17 \ -1 & 2 & -4 & 9\ 4 & -2 & 19 & -42
end{array} right).
$$

Нужно найти $rang A$ и $rangwidetilde{A}$. Для этого есть много способов, некоторые из которых перечислены в разделе “Ранг матрицы”. Обычно для исследования таких систем применяют два метода: “Вычисление ранга матрицы по определению” или “Вычисление ранга матрицы методом элементарных преобразований”.

Способ №1. Вычисление рангов по определению.

Согласно определению, ранг – это наивысший порядок миноров матрицы, среди которых есть хоть один, отличный от нуля. Обычно исследование начинают с миноров первого порядка, но здесь удобнее приступить сразу к вычислению минора третьего порядка матрицы $A$. Элементы минора третьего порядка находятся на пересечении трёх строк и трёх столбцов рассматриваемой матрицы. Так как матрица $A$ содержит всего 3 строки и 3 столбца, то минор третьего порядка матрицы $A$ – это определитель матрицы $A$, т.е. $Delta A$. Для вычисления определителя применим формулу №2 из темы “Формулы для вычисления определителей второго и третьего порядков”:

$$
Delta A=left| begin{array} {ccc}
-3 & 9 & -7 \ -1 & 2 & -4 \ 4 & -2 & 19
end{array} right|=-21.
$$

Итак, есть минор третьего порядка матрицы $A$, который не равен нулю. Минор четвёртого порядка составить невозможно, так как для него требуется 4 строки и 4 столбца, а в матрице $A$ всего 3 строки и 3 столбца. Итак, наивысший порядок миноров матрицы $A$, среди которых есть хотя бы один не равный нулю, равен 3. Следовательно, $rang A=3$.

Нам требуется найти также и $rangwidetilde{A}$. Давайте посмотрим на структуру матрицы $widetilde{A}$. До черты в матрице $widetilde{A}$ находятся элементы матрицы $A$, причём мы выяснили, что $Delta Aneq 0$. Следовательно, у матрицы $widetilde{A}$ есть минор третьего порядка, который не равен нулю. Миноров четвёртого порядка матрицы $widetilde{A}$ составить мы не можем, поэтому делаем вывод: $rangwidetilde{A}=3$.

Так как $rang A=rangwidetilde{A}$, то согласно теореме Кронекера-Капелли система совместна, т.е. имеет решение (хотя бы одно). Чтобы указать количество решений, учтём, что наша СЛАУ содержит 3 неизвестных: $x_1$, $x_2$ и $x_3$. Так как количество неизвестных $n=3$, то делаем вывод: $rang A=rangwidetilde{A}=n$, поэтому согласно пункту №3 следствия из теоремы Кронекера-Капелли, система является определённой, т.е. имеет единственное решение.

Задача решена. Какие недостатки и преимущества имеет данный способ? Для начала поговорим о плюсах. Во-первых, нам понадобилось найти всего один определитель. После этого мы сразу сделали вывод о количестве решений. Обычно в стандартных типовых расчётах даются системы уравнений, которые содержат три неизвестных и имеют единственное решение. Для таких систем данный метод очень даже удобен, ибо мы заранее знаем, что решение есть (иначе примера не было бы в типовом расчёте). Т.е. нам остаётся только показать наличие решения наиболее быстрым способом. Во-вторых, вычисленное значение определителя матрицы системы (т.е. $Delta A$) пригодится после: когда станем решать заданную систему методом Крамера или с помощью обратной матрицы.

Однако метод вычисления ранга по определению нежелательно применять, если матрица системы $A$ является прямоугольной. В этом случае лучше применить второй метод, о котором пойдёт речь ниже. Кроме того, если $Delta A=0$, то мы ничего не сможем сказать о количестве решений заданной неоднородной СЛАУ. Может, СЛАУ имеет бесконечное количество решений, а может – ни одного. Если $Delta A=0$, то требуется дополнительное исследование, которое зачастую является громоздким.

Подводя итог сказанному, отмечу, что первый способ хорош для тех СЛАУ, у которых матрица системы квадратна. При этом сама СЛАУ содержит три или четыре неизвестных и взята из стандартных типовых расчетов или контрольных работ.

Способ №2. Вычисление ранга методом элементарных преобразований.

Подробно это метод описан в соответствующей теме. Мы станем вычислять ранг матрицы $widetilde{A}$. Почему именно матрицы $widetilde{A}$, а не $A$? Дело в том, что матрица $A$ является частью матрицы $widetilde{A}$, поэтому вычисляя ранг матрицы $widetilde{A}$ мы одновременно найдем и ранг матрицы $A$.

begin{aligned}

&widetilde{A} =left( begin{array} {ccc|c}
-3 & 9 &-7 & 17 \ -1 & 2 & -4 & 9\ 4 & -2 & 19 & -42
end{array} right) rightarrow left|text{меняем местами первую и вторую строки}right| rightarrow \

&rightarrow left( begin{array} {ccc|c}
-1 & 2 & -4 & 9 \
-3 & 9 &-7 & 17\
4 & -2 & 19 & -42
end{array} right)
begin{array} {l} phantom{0} \ r_2-3r_1\ r_3+4r_1 end{array} rightarrow

left( begin{array} {ccc|c}
-1 & 2 & -4 & 9 \
0 & 3 &5 & -10\
0 & 6 & 3 & -6
end{array} right)
begin{array} {l} phantom{0} \ phantom{0}\ r_3-2r_2 end{array}rightarrow\

&rightarrow left( begin{array} {ccc|c}
-1 & 2 & -4 & 9 \
0 & 3 &5 & -10\
0 & 0 & -7 & 14
end{array} right)

end{aligned}

Мы привели матрицу $widetilde{A}$ к ступенчатому виду. Полученная ступенчатая матрица имеет три ненулевых строки, поэтому её ранг равен 3. Следовательно, и ранг матрицы $widetilde{A}$ равен 3, т.е. $rangwidetilde{A}=3$. Делая преобразования с элементами матрицы $widetilde{A}$ мы одновременно преобразовывали и элементы матрицы $A$, расположенные до черты. Матрица $A$ также приведена к ступенчатому виду: $left( begin{array} {ccc}
-1 & 2 & -4 \
0 & 3 &5 \
0 & 0 & -7
end{array} right)$. Вывод: ранг матрицы $A$ также равен 3, т.е. $rang A=3$.

Так как $rang A=rangwidetilde{A}$, то согласно теореме Кронекера-Капелли система совместна, т.е. имеет решение. Чтобы указать количество решений, учтём, что наша СЛАУ содержит 3 неизвестных: $x_1$, $x_2$ и $x_3$. Так как количество неизвестных $n=3$, то делаем вывод: $rang A=rangwidetilde{A}=n$, поэтому согласно пункту №3 следствия из теоремы Кронекера-Капелли, система определена, т.е. имеет единственное решение.

Какие преимущества второго способа? Главное преимущество – это его универсальность. Нам совершенно неважно, является ли матрица системы квадратной или нет. Кроме того, мы фактически провели преобразования прямого хода метода Гаусса. Осталось лишь пару действий, и мы смогли бы получить решение данной СЛАУ. Честно говоря, второй способ нравится мне более первого, но выбор – это дело вкуса.

Ответ: Заданная СЛАУ совместна и определена.

Пример №2

Исследовать СЛАУ
$ left{ begin{aligned}
& x_1-x_2+2x_3=-1;\
& -x_1+2x_2-3x_3=3;\
& 2x_1-x_2+3x_3=2;\
& 3x_1-2x_2+5x_3=1;\
& 2x_1-3x_2+5x_3=-4.

end{aligned} right.$
на совместность.

Решение

Находить ранги матрицы системы и расширенной матрицы системы будем методом элементарных преобразований. Расширенная матрица системы: $widetilde{A}=left( begin{array} {ccc|c} 1 & -1 & 2 & -1\ -1 & 2 & -3 & 3 \ 2 & -1 & 3 & 2 \ 3 & -2 & 5 & 1 \ 2 & -3 & 5 & -4 end{array} right)$. Найдём требуемые ранги, преобразовывая расширенную матрицу системы:

$$
left( begin{array} {ccc|c}
1 & -1 & 2 & -1\
-1 & 2 & -3 & 3 \
2 & -3 & 5 & -4 \
3 & -2 & 5 & 1 \
2 & -1 & 3 & 2 end{array} right)
begin{array} {l} phantom{0}\r_2+r_1\r_3-2r_1\ r_4-3r_1\r_5-2r_1end{array}rightarrow

left( begin{array} {ccc|c}
1 & -1 & 2 & -1\
0 & 1 & -1 & 2 \
0 & -1 & 1 & -2 \
0 & 1 & -1 & 4 \
0 & 1 & -1 & 4 end{array} right)
begin{array} {l} phantom{0}\phantom{0}\r_3-r_2\ r_4-r_2\r_5+r_2end{array}rightarrow\
$$

$$
rightarrowleft( begin{array} {ccc|c}
1 & -1 & 2 & -1\
0 & 1 & -1 & 2 \
0 & 0 & 0 & 2 \
0 & 0 & 0 & 2 \
0 & 0 & 0 & 0 end{array} right)
begin{array} {l} phantom{0}\phantom{0}\phantom{0}\ r_4-r_3\phantom{0}end{array}rightarrow

left( begin{array} {ccc|c}
1 & -1 & 2 & -1\
0 & 1 & -1 & 2 \
0 & 0 & 0 & 2 \
0 & 0 & 0 & 0 \
0 & 0 & 0 & 0 end{array} right)
$$

Расширенная матрица системы приведена к ступенчатому виду. Ранг ступенчатой матрицы равен количеству её ненулевых строк, поэтому $rangwidetilde{A}=3$. Матрица $A$ (до черты) тоже приведена к ступенчатому виду, и ранг её равен 2, $rang{A}=2$.

Так как $rang Aneqrangwidetilde{A}$, то согласно теореме Кронекера-Капелли система несовместна (т.е. не имеет решений).

Ответ: система несовместна.

Пример №3

Исследовать СЛАУ

$$left{ begin{aligned}
& 2x_1+7x_3-5x_4+11x_5=42;\
& x_1-2x_2+3x_3+2x_5=17;\
& -3x_1+9x_2-11x_3-7x_5=-64;\
& -5x_1+17x_2-16x_3-5x_4-4x_5=-90;\
& 7x_1-17x_2+23x_3+15x_5=132.
end{aligned} right.$$

на совместность.

Решение

Приводим расширенную матрицу системы к ступенчатому виду:

$$
left( begin{array}{ccccc|c}
2 & 0 & 7 & -5 & 11 & 42\
1 & -2 & 3 & 0 & 2 & 17 \
-3 & 9 & -11 & 0 & -7 & -64 \
-5 & 17 & -16 & -5 & -4 & -90 \
7 & -17 & 23 & 0 & 15 & 132 end{array} right)
overset{r_1leftrightarrow{r_3}}{rightarrow}
$$

$$
rightarrowleft( begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 2 & 17\
2 & 0 & 7 & -5 & 11 & 42\
-3 & 9 & -11 & 0 & -7 & -64\
-5 & 17 & -16 & -5 & -4 & -90 \
7 & -17 & 23 & 0 & 15 & 132 end{array} right)
begin{array} {l} phantom{0}\ r_2-2r_1 \r_3+3r_1 \ r_4+5r_1 \ r_5-7r_1 end{array} rightarrow

left( begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 2 & 17\
0 & 4 & 1 & -5 & 7 & 8\
0 & 3 & -2 & 0 & -1 & -13\
0 & 7 & -1 & -5 & 6 & -5 \
0 & -3 & 2 & 0 & 1 & 13 end{array} right)
begin{array} {l} phantom{0}\ phantom{0}\4r_3+3r_2 \ 4r_4-7r_2 \ 4r_5+3r_2 end{array} rightarrow
$$

$$
rightarrowleft( begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 2 & 17\
0 & 4 & 1 & -5 & 7 & 8\
0 & 0 & -11 & 15 & -25 & -76\
0 & 0 & -11 & 15 & -25 & -76 \
0 & 0 & 11 & -15 & 25 & 76 end{array} right)
begin{array} {l} phantom{0}\ phantom{0}\phantom{0} \ r_4-r_3 \ r_5+r_2 end{array} rightarrow

left( begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 2 & 17\
0 & 4 & 1 & -5 & 7 & 8\
0 & 0 & -11 & 15 & -25 & -76\
0 & 0 & 0 & 0 & 0 & 0 \
0 & 0 & 0 & 0 & 0 & 0 end{array} right)
$$

Мы привели расширенную матрицу системы и саму матрицу системы к ступенчатому виду. Ранг расширенной матрицы системы равен трём, ранг матрицы системы также равен трём. Так как система содержит $n=5$ неизвестных, т.е. $rangwidetilde{A}=rang{A}lt{n}$, то согласно пункту №2 следствия из теоремы Кронекера-Капелли данная система является неопределённой, т.е. имеет бесконечное количество решений.

Ответ: система является неопределённой.

Во второй части мы разберём примеры, которые нередко включают в типовые расчёты или контрольные работы по высшей математике: исследование на совместность и решение СЛАУ в зависимости от значений параметров, входящих в неё.

Прежде чем пытаться выполнить решение системы линейных уравнений следует исследовать ее на совместность. Предварительное исследование упрощает анализ описывающих логистические и производственные процессы СЛАУ. Если система линейных уравнений совместна, у нее есть решения.

Совместность СЛАУ оценивается через применение теоремы Кронекера–Капели. В ходе анализа определяется равны ли ранги основной и расширенной матрицы, если равны, можно утверждать о наличии совместности, несовместность наблюдается во всех других случаях.

Если система является определенной у нее всего одно решение, у неопределенной несколько. Определенность совместной СЛАУ наблюдается в случае равенства ранга основной матрицы числу неизвестных.

Сначала исследуем совместность и установим количество решений, а затем найдём сами решения с помощью метода Гаусса. Записываем расширенную матрицу $$begin{pmatrix} 2&3&11&5 &|& 2 \ 1&1&5&2 &|& 1 \ 2&1&3&2 &|& -3 \ 1&1&3&4 &|& -3 end{pmatrix}.$$

Умножаем вторую строку на 2 и вычитаем из неё первую. Из третьей строки вычитаем первую. Умножаем четвертую строку на 2 и вычитаем от неё первую. $$begin{pmatrix} 2&3&11&5 &|& 2 \ 0&-1&-1&-1 &|& 0 \ 0&-2&-8&-3 &|& -5 \ 0&-1&-5&3 &|& -8 end{pmatrix}$$

Из третьей строки вычитаем вторую, умноженную на 2. Из четвертой строчки вычитаем вторую. $$begin{pmatrix} 2&3&11&5 &|& 2 \ 0&-1&-1&-1 &|& 0 \ 0&0&-6&-1 &|& -5 \ 0&0&-4&4 &|& -8 end{pmatrix}$$

Умножим четвертую строчку на 6 и вычтем из неё третью, умноженную на 4. $$begin{pmatrix} 2&3&11&5 &|& 2 \ 0&-1&-1&-1 &|& 0 \ 0&0&-6&-1 &|& -5 \ 0&0&0&28 &|& -28 end{pmatrix}$$ Разделим четвертую строку на 28 для дальнейшего удобства избавившись от крупных чисел.$$begin{pmatrix} 2&3&11&5 &|& 2 \ 0&-1&-1&-1 &|& 0 \ 0&0&-6&-1 &|& -5 \ 0&0&0&1 &|& -1 end{pmatrix}$$

Итак, матрица приведена к ступенчатой форме или как называют треугольный вид. Сделано это для того, чтобы определить ранг матрицы $A$ и её расширенной $(A|B)$. Подсчитываем количество ненулевых строк в обеих матрицах и получаем, что $rang A = rang (A|B) = 4$. Это означает по следствию теоремы Кронекера-Капелли, что СЛАУ совместна и имеет при этом одно решение.

По условию задачи требуется найти решение системы уравнений. Это означает, что нужно продолжить ход Гаусса в обратном направлении, чтобы найти $x_1,x_2,x_3, x_4$. Если бы в условии задачи это не было сказано, то это не потребовалось бы сделать и достаточно записать ответ о совместности системы. Продолжаем вычисления…

Из первой строки вычитаем четвертую, умноженную на 5. Ко второй строке прибавляем четвертую. К третьей строке прибавляем четвертую. $$begin{pmatrix} 2&3&11&0 &|& 7 \ 0&-1&-1&0 &|& -1 \ 0&0&-6&0 &|& -6 \ 0&0&0&1 &|& -1 end{pmatrix}$$Сразу делим третью строку на -6 для сокращения строки. $$begin{pmatrix} 2&3&11&0 &|& 7 \ 0&-1&-1&0 &|& -1 \ 0&0&1&0 &|& 1 \ 0&0&0&1 &|& -1 end{pmatrix}$$

Ко второй строке прибавляем третью. Из первой строки вычитаем третью, умноженную на 11. $$begin{pmatrix} 2&3&0&0 &|& -4 \ 0&-1&0&0 &|& 0 \ 0&0&1&0 &|& 1 \ 0&0&0&1 &|& -1 end{pmatrix}$$

К первой строке прибавляем вторую строчку, умноженную на 3. $$begin{pmatrix} 2&0&0&0 &|& -4 \ 0&-1&0&0 &|& 0 \ 0&0&1&0 &|& 1 \ 0&0&0&1 &|& -1 end{pmatrix}$$Делим первую строку на 2. Умножаем вторую строчку на (-1). $$begin{pmatrix} 1&0&0&0 &|& -2 \ 0&1&0&0 &|& 0 \ 0&0&1&0 &|& 1 \ 0&0&0&1 &|& -1 end{pmatrix}$$

Таким образом отсюда получаем решение системы линейных уравнений $$begin{bmatrix} x_1=-2 \ x_2=0 \ x_3=1 \ x_4=-1 end{bmatrix}.$$

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 ноября 2021 года; проверки требует 1 правка.

Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:

Для того чтобы линейная система являлась совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу её основной матрицы. Доказана Леопо́льдом Кро́некером, Альфре́до Капе́лли.

Название теоремы[править | править код]

В России это теорема Кронекера – Капелли, в Италии и англоязычных странах – теорема Руше-Капелли , в Испании и странах Латинской Америки – теорема Руше- Фробениуса.

Пояснения[править | править код]

Система уравнений разрешима тогда и только тогда, когда , где —
расширенная матрица, полученная из матрицы приписыванием столбца ^[1].

Доказательство (условия совместности системы)[править | править код]

Необходимость[править | править код]

Пусть система совместна. Тогда существуют числа такие, что . Следовательно, столбец является линейной комбинацией столбцов матрицы . Из того, что ранг матрицы не изменится, если из системы её строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что .

Достаточность[править | править код]

Пусть . Возьмём в матрице какой-нибудь базисный минор.
Так как , то он же будет базисным минором и матрицы .
Тогда, согласно теореме о базисном миноре, последний столбец матрицы будет линейной комбинацией базисных столбцов, то есть столбцов матрицы .
Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы .

Следствия[править | править код]

• Количество главных переменных системы равно рангу системы.
• Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.

См. также[править | править код]

• Матрица (математика)
• Кро́некер, Леопо́льд
• Капе́лли, Альфре́до

Примечания[править | править код]

Литература[править | править код]

• В. А. Ильин, Г. Д. Ким Линейная алгебра и аналитическая геометрия, М.: ТК Велби, Изд-во Проспект, 2007, 400с.
• Прасолов В. В. Задачи и теоремы линейной алгебры. — М.: Наука, 1996. — 304 с. — ISBN 5-02-014727-3.

1. Теорема Кронекера-Капелли о совместности системы линейных алгебраических уравнений.

Теорема
Кронекера-Капелли.

Для того, чтобы
система линейных алгебраических
уравнений была совместной (то есть имела
решение), необходимо и достаточно, чтобы
ранг исходной матрицы системы совпадал
с рангом расширенной матрицы, то есть
r(A)
= r(С).

1. если r(A)
   = r(С)=
   n,
   где n
   – число неизвестных системы, то данная
   система имеет единственное решение;

2. если r(A)
   = r(С)
   = k < n,
   то система имеет бесконечное множество
   решений;

3. если r(A)
   ≠ r(С),
   то система несовместна, то есть не имеет
   решений.

Если число неизвестных
больше числа уравнений, то система либо
не имеет решений, либо имеет их бесконечное
множество (если r(A)
= r(С)
= =k < n.)

Пример.
Исследовать систему уравнений на
совместность

Решение.

Запишем матрицу
системы А и определим ее ранг:

.

Так как матрица А
имеет порядок 34,
то r
(A)
≤ 3. Существует

4 различных минора
третьего порядка:

,

,

,

.

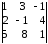
Легко проверить,
что все эти миноры равны нулю. Например:

==6ּ+11ּ

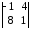
Так как минор
второго порядка
,то
r
(A)
= 2.

Рассмотрим
расширенную матрицу
.
Так как минор третьего порядка

==11ּ+5ּ=

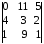
= –11ּ2+5ּ33=
–22+165=143 ≠ 0, то r(С)=3.

Следовательно, r
(A)
≠ r
(С), и по теореме Кронекера-Капелли
система несовместна, то есть не имеет
решений.

Действительно,
если первое уравнение системы умножить
на 3 и сложить со вторым уравнением, то
получим уравнение
.
Левая часть этого уравнения совпадает
с левой частью третьего уравнения
системы, а правые части у них разные.
Следовательно, система не имеет решений.

Пример.
Исследовать на совместность и решить
систему линейных алгебраических
уравнений

(2)

1. с помощью формул
   Крамера;

2. матричным методом.

Решение.

Запишем матрицу А
системы уравнений и определим ее ранг:

.

Так как
(третья
строка определителя является суммой
первых двух строк), то r(A)<
3. Рассмотрим какой-либо минор

второго порядка:

Рассмотрим
расширенную матрицу системы:
.

Найдем ее ранг.
Существуют 4 различных минора третьего
порядка:

,

,

,

.

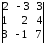
Легко проверить,
что все эти миноры равны нулю (в каждом
из них третья строка есть сумма первых
двух строк). Поэтому r
(С) < 3. Так как выше рассмотренный минор
второго порядка

принадлежит и матрице С, то

,
и по теореме Кронекера-Капелли исходная
система уравнений совместна (r(A)
= r(С)).
Но, так как r(A)
= r
(С) = 2 < 3, где 3 – число неизвестных
системы уравнений, то исходная система
имеет бесконечное множество решений.

Отличный от нуля
минор второго порядка

состоит из коэффициентов, стоящих при
неизвестных
и

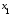
первого и второго уравнения. Следовательно,
первая и вторая строка матрицы А линейно
независимы, а третья выражается через
них (является их суммой). Поэтому третье
уравнение системы можно отбросить.

Так как элементы
данного минора – это коэффициенты при
и
,
то эти переменные будут базисными, а

«лишней» (свободной), поэтому перенесем
ее в правые части уравнений. В итоге
получим систему:

(3)

В данном случае
определитель матрицы системы

не равен нулю. Следовательно, существует
обратная матрица
,
и мы можем решить систему уравнений
матричным методом и по формулам Крамера.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #