Закон распределения вероятностей двумерной случайной величины
Законом
распределениядискретной двумерной
случайной величины![]() называют перечень возможных значений
называют перечень возможных значений
этой величины, т.е. пар чисел![]() ,
,
где![]() и
и![]()
![]() –
–
возможные значения величин![]() и
и![]() ,
,
соответственно, и вероятностей![]() их совместного появления
их совместного появления![]() .
.
Двумерная дискретная
случайная величина
![]() задается в видетаблицы распределения
задается в видетаблицы распределения
вида:
где первая строка
таблицы указывает возможные значения
составляющей
![]() ,
,
а первый столбец – все возможные значения
составляющей![]() .
.
Так как события
![]() (
(![]() ;
;![]() )
)
образуют полную группу, то![]() .
.
Зная закон
распределения двумерной дискретной
случайной величины, можно найти законы
распределения каждой из ее составляющих.
Так, например, вероятность того, что
![]() примет значение
примет значение![]() ,
,
равна![]() .
.
Совместная
функция распределения двух случайных
величин
Функция
![]() ,
,
определяющая для каждой пары чисел![]() вероятность того, что
вероятность того, что![]() примет значение меньшее
примет значение меньшее![]() ,
,
и при этом![]() примет значение меньшее
примет значение меньшее![]() ,
,
называетсясовместной функцией
распределениядвух случайных
величин![]() =
=![]() .
.
Геометрически это
равенство можно истолковать так:
![]() – это вероятность того, что случайная
– это вероятность того, что случайная
точка (![]() )
)
попадет в бесконечный квадрант с вершиной
(![]() ),
),
расположенный левее и ниже этой вершины.
Свойства совместной функции распределения двух случайных величин
-
Значения
совместной функции распределения
удовлетворяют неравенству:
![]() .
.
-
 –неубывающая
–неубывающая
функция по каждому аргументу, т.е.
![]() ,
,
если
![]() ;
;
![]() ,
,
если
![]() .
.
Совместная функция
распределения имеет следующие предельные
значения:
![]() ;
;![]() ;
;
![]() ;
;![]() .
.
-
При
 или
или совместная функция распределения
совместная функция распределения
системы становится функцией распределения
одной из составляющих: ;
;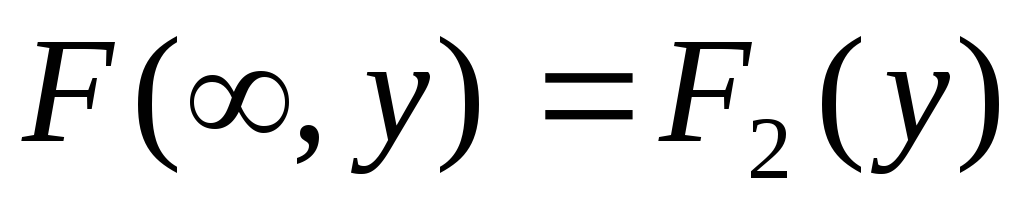
Плотность совместного распределения вероятностей непрерывной двумерной случайной величины
Непрерывную
двумерную случайную величину можно
задать с помощью плотности распределения.
Плотность совместного распределения
вероятностей![]() двумерной непрерывной случайной величины
двумерной непрерывной случайной величины
(![]() ,
,![]() )
)
– это вторая смешанная частная производная
от функции распределения![]() :
:
![]() .
.
Зная плотность
совместного распределения
![]() ,
,
можно найти совместную функцию
распределения![]() по формуле
по формуле![]()
следующей из
определения плотности распределения
двумерной непрерывной случайной величины
(![]() ,
,![]() ).
).
Смысл плотности
совместного распределения вероятностей:
вероятность попадания случайной точки
в прямоугольник (с вершиной в точке
![]() и сторонами
и сторонами![]() и
и![]() равна произведению
равна произведению![]() ,
,
когда стороны этого прямоугольника
стремятся к нулю.
В связи с этим,
вероятность попадания случайной точки
в произвольную область D
равна двойному интегралу по областиDот функции![]() :
:![]()
Свойства двумерной плотности вероятности
-
Двумерная плотность
вероятности неотрицательна:
 .
. -
Двойной несобственный
интеграл с бесконечными пределами от
двумерной плотности вероятности равен
единице: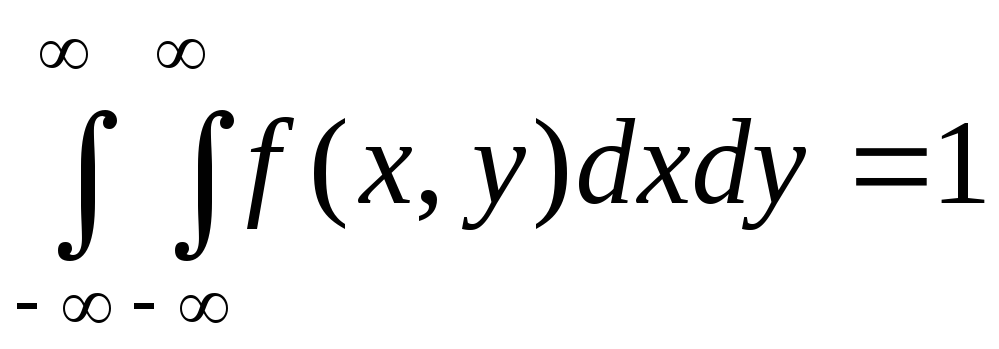 .
.
Независимые случайные величины
Две случайные
величины называются независимыми,
если закон распределения одной из них
не зависит от того, какие возможные
значения приняла другая величина.
Теорема.
Для того чтобы случайные величины![]() и
и![]() были
были
независимыми, необходимо и достаточно,
чтобы функция распределения системы
(![]() ,
,![]() )
)
была равна произведению функций
распределения составляющих:![]() .
.
Следствие.Для того чтобы случайные величины![]() и
и![]() были
были
независимыми, необходимо и достаточно,
чтобы плотность совместного распределения
системы (![]() ,
,![]() )
)
была равна произведению плотностей
распределения составляющих:![]() .
.
Двумерная непрерывная случайная величина
- Краткая теория
- Примеры решения задач
Краткая теория
Двумерной называют случайную величину
, возможные значения
которой есть пары чисел
. Составляющие
и
, рассматриваемые
одновременно, образуют систему двух случайных величин. Двумерную величину
геометрически можно истолковать как случайную точку
на плоскости
либо как случайный вектор
.
Непрерывной называют двумерную величину, составляющие которой непрерывны.
Законом распределения вероятностей двумерной случайной величины называют соответствие
между возможными значениями и их вероятностями.
Функция распределения двумерной случайной величины и ее свойства
Функцией распределения двумерной случайной величины
называют функцию
, определяющую для каждой
пары чисел
вероятность того, что
примет значение, меньшее
, и при этом
примет значение, меньшее
.
Свойство 1.
Значения
функции распределения удовлетворяют двойному неравенству:
Свойство 2.
есть неубывающая функция по каждому аргументу,
то есть:
если
если
Свойство 3.
Имеют место предельные соотношения:
1)
2)
3)
4)
Свойство 4.
При
функция распределения системы становится
функцией распределения составляющей
:
При
функция распределения системы становится
функцией распределения составляющей
:
Плотность распределения двумерной случайной величины и ее свойства
Плотностью совместного распределения вероятностей
двумерной непрерывной случайной величины
называют вторую смешанную частную производную
от функции распределения:
Зная
плотность совместного распределения
можно найти функцию распределения
по формуле:
Свойство 1.
Двумерная
плотность вероятности неотрицательна:
Свойство 2.
Двойной
несобственный интеграл с бесконечными пределами от двумерной плотности равен единице:
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Безусловные и условные законы распределения составляющих
Пусть
известна плотность совместного распределения вероятностей системы двух
случайных величин. Найдем плотности распределения каждой из составляющих.
Аналогично
находится плотность распределения составляющей
:
Итак,
плотность распределения одной из составляющих равна несобственному интегралу с
бесконечными пределами от плотности совместного распределения системы, причем
переменная интегрирования соответствует другой составляющей.
Пусть
– непрерывная двумерная случайная величина.
Условной
вероятностью
распределения составляющих
при данном значении
называют отношение плотности совместного
распределения
системы
к плотности распределения
составляющей
:
Аналогично
определяется условная плотность составляющей
при данном значении
:
Если
известна плотность совместного распределения
, то условные плотности
составляющих могут быть найдены по формулам:
Эти
формулы можно записать в виде:
Аналогично
определяется условная плотность составляющей
при данном значении
:
То есть
умножая закон распределения одной из составляющих на условный закон
распределения другой составляющей, найдем закон распределения системы случайных
величин.
Смежные темы решебника:
- Двумерная дискретная случайная величина
- Линейный выборочный коэффициент корреляции
- Парная линейная регрессия и метод наименьших квадратов
Примеры решения задач
Пример 1
Найти
плотность совместного распределения f(x,y) системы случайных величин (X,Y) по
известной функции распределения:
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
По определению плотности совместно
распределения:
Искомая плотность совместного распределения:
Пример 2
Найти
функцию распределения системы случайных величин F(x,y) по известной плотности
совместного распределения f(x,y):
Решение
Воспользуемся
формулой:
В нашем
случае:
Ответ:
Пример 3
Двумерная
случайная величина (X,Y) имеет равномерное распределение вероятностей в
треугольнике ABC. Определить функции плотности распределения
компонент этой случайной величины f(x), f(y), их математические
ожидания M(X), M(Y), дисперсии D(X), D(Y),
коэффициент корреляции rxy. Выяснить, являются ли
случайные величины X и Y независимыми?
A(0;0),B(-1;1),C(1;1)
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
где
– площадь треугольника
Разделим
область
на две равные части вдоль оси
, тогда из условия:
или
Тогда
плотность двумерной случайной величины
:
Вычислим
плотность составляющей
:
при
:
Откуда
плотность составляющей
:
Вычислим
плотность составляющей
:
при
Плотность
составляющей
:
Найдем
условную плотность составляющей
:
при
Следовательно,
случайные величины
и
зависимы
Найдем
математическое ожидание случайной величины
:
Найдем
дисперсию случайной величины
:
Найдем
математическое ожидание случайной величины
:
Найдем
дисперсию случайной величины
:
Найдем
математическое ожидание двумерной случайной величины
:
Тогда
ковариация:
Значит
коэффициент корреляции:
Следовательно,
случайные величины
и
– зависимые, но некоррелированные
Пример 4
Двумерная
случайная величина (X,Y) имеет плотность
распределения:
Найти
вероятность попадания значения (X,Y) в область x1≤x≤x2,
y1≤y≤y2, вероятность попадания значения X в
интервал x1≤x≤x2, математическое ожидание M[X] и
условное математическое ожидание M[Y⁄X=x].
a=8, b=2, x1=6, x2=9, y1=0, y2=4
Решение
Найдем
вероятность попадания в область
по формуле:
При
вычислении интеграла учитывается та часть области
, где
, т.е.
Плотность
вероятности для составляющей
имеет вид:
Если
или
, то
и
. При
находим:
Таким
образом, плотность имеет вид:
Тогда:
Условное математическое ожидание
определяется с
помощью условной плотности распределения
составляющей
Получаем:
Искомое
математическое ожидание:
- Краткая теория
- Примеры решения задач
Разумеется, на каждом вероятностном пространстве 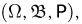 содержащем хотя бы один элементарный исход
содержащем хотя бы один элементарный исход 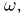 можно определить не одну случайную величину. На практике необходимость учета непредсказуемых воздействий также весьма редко приводит к рассмотрению только одной случайной величины. Обычно выделяют несколько случайных компонент и на их основе строят модель исследуемого явления. Классическим примером такого рода, описанным многими великими художниками слова, снова являются азартные игры. Игрок, даже имея самое твердое намерение сыграть только один раз, впадал в азарт (откуда и пошло само название «азартные игры») и, как правило, не уходил из-за игорного стола, пока совсем не разорялся. Здесь суммарный выигрыш игрока состоит из отдельных случайных величин — выигрышей его в каждой партии.
можно определить не одну случайную величину. На практике необходимость учета непредсказуемых воздействий также весьма редко приводит к рассмотрению только одной случайной величины. Обычно выделяют несколько случайных компонент и на их основе строят модель исследуемого явления. Классическим примером такого рода, описанным многими великими художниками слова, снова являются азартные игры. Игрок, даже имея самое твердое намерение сыграть только один раз, впадал в азарт (откуда и пошло само название «азартные игры») и, как правило, не уходил из-за игорного стола, пока совсем не разорялся. Здесь суммарный выигрыш игрока состоит из отдельных случайных величин — выигрышей его в каждой партии.
Итак, в этой главе мы обобщим результаты предыдущей главы на случай нескольких случайных величин. Естественно, для того чтобы над случайными величинами можно было производить различные действия (сложение, вычитание, умножение и т.п.), необходимо их задание на одном вероятностном пространстве.

Многомерная случайная величина
Пусть на одном и том же вероятностном пространстве 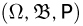 задано п случайных величин
задано п случайных величин 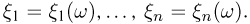 Совокупность случайных величин
Совокупность случайных величин 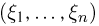 назовем многомерной (n-мерной) случайной величиной или случайным вектором.
назовем многомерной (n-мерной) случайной величиной или случайным вектором.
В дальнейшем для сокращения записи будем пользоваться также обозначением 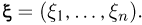
Пример:
На скачках, в которых участвуют 2 лошади, п человек заключают пари (между собой, группами и т.д.). Считая, что результат скачек случаен, причем с вероятностью 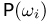 происходит элементарный исход
происходит элементарный исход 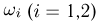 — к финишу первой пришла лошадь с номером i получаем, что каждому элементарному исходу
— к финишу первой пришла лошадь с номером i получаем, что каждому элементарному исходу 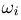 соответствует вектор
соответствует вектор 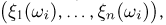 компонентами которого являются выигрыши 1-го, …, n-го участников пари.
компонентами которого являются выигрыши 1-го, …, n-го участников пари.
Пример:
Рассмотрим схему Бернулли, состоящую из п испытаний. Каждому элементарному исходу 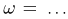 поставим в соответствие число
поставим в соответствие число 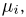 равное нулю, если в последовательности УНН…У на i-м месте стоит буква Н (в i-м испытании произошла неудача), и единице, если стоит буква У (произошел успех). Тогда случайная величина
равное нулю, если в последовательности УНН…У на i-м месте стоит буква Н (в i-м испытании произошла неудача), и единице, если стоит буква У (произошел успех). Тогда случайная величина 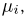 есть не что иное, как число успехов в i-м испытании. Совокупность случайных величин
есть не что иное, как число успехов в i-м испытании. Совокупность случайных величин 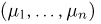 представляет собой n-мерный случайный вектор. Нетрудно видеть, что в данном случае существует взаимно однозначное соответствие между элементарными исходами
представляет собой n-мерный случайный вектор. Нетрудно видеть, что в данном случае существует взаимно однозначное соответствие между элементарными исходами 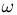 и значениями случайного вектора
и значениями случайного вектора 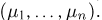 Действительно, элементарному исходу
Действительно, элементарному исходу 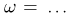 соответствует значение (1,0,0,…,1) случайного вектора
соответствует значение (1,0,0,…,1) случайного вектора  и, наоборот, случайный вектор
и, наоборот, случайный вектор  принимает значение (1,0,0,…, 1) только для элементарного исхода
принимает значение (1,0,0,…, 1) только для элементарного исхода 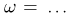 Ясно также, что суммарное число успехов
Ясно также, что суммарное число успехов 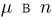 испытаниях Бернулли (см. пример 2 в гл. 5) представляет собой сумму чисел успехов в каждом испытании:
испытаниях Бернулли (см. пример 2 в гл. 5) представляет собой сумму чисел успехов в каждом испытании: 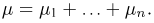
Пример:
Двумерной случайной величиной является вектор 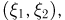 где
где 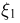 сумма очков, выпавших при бросании двух игральных костей, а
сумма очков, выпавших при бросании двух игральных костей, а 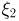 — сумма их квадратов. В этом случае различным элементарным исходам могут соответствовать одинаковые значения случайного вектора
— сумма их квадратов. В этом случае различным элементарным исходам могут соответствовать одинаковые значения случайного вектора 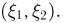 Например, двум элементарным исходам
Например, двум элементарным исходам 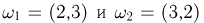 соответствует одно и то же значение вектора
соответствует одно и то же значение вектора 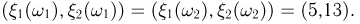
Пример:
Двумерными случайными величинами являются декартовы 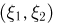 или полярные
или полярные 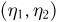 координаты точки падения частицы на плоский экран (см. пример 5 в гл.5). Случайные величины
координаты точки падения частицы на плоский экран (см. пример 5 в гл.5). Случайные величины 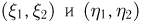 связаны соотношениями:
связаны соотношениями: 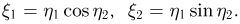
Пример:
Широта 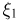 и долгота
и долгота 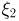 места падения метеорита на Землю представляют собой двумерный случайный вектор
места падения метеорита на Землю представляют собой двумерный случайный вектор 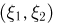 В эту модель можно ввести также третью координату
В эту модель можно ввести также третью координату 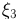 — время от начала наблюдений до момента падения первого метеорита на Землю
— время от начала наблюдений до момента падения первого метеорита на Землю 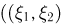 — координаты падения этого метеорита), если рассматривать процесс, протекающий во времени.
— координаты падения этого метеорита), если рассматривать процесс, протекающий во времени.
Совместная функция распределения
Функцией распределения (n-мерного) случайного вектора 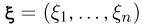 называется функция
называется функция 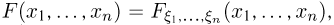 значение которой в точке
значение которой в точке  равно вероятности совместного осуществления (пересечения) событий
равно вероятности совместного осуществления (пересечения) событий 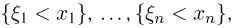 т.е.
т.е.
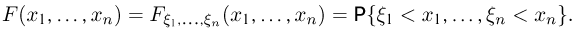
Функцию  называют также совместной функцией распределения случайных величин
называют также совместной функцией распределения случайных величин 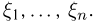
Для сокращения записи в дальнейшем для функции распределения 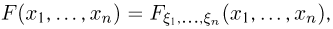 будем использовать также обозначения
будем использовать также обозначения 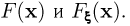
Далее мы будем в основном рассматривать двумерный случай. В большинстве приводимых далее результатов переход от двумерного к общему n-мерному случаю не должен вызвать каких-либо трудностей, а там, где могут возникнуть затруднения, приводятся дополнительные пояснения.
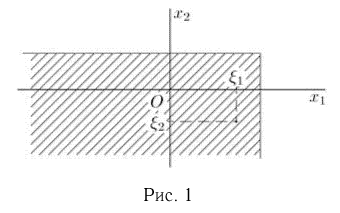
Совместная функция распределения двумерной случайной величины 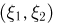 по определению, представляет собой не что иное, как вероятность попадания точки с координатами
по определению, представляет собой не что иное, как вероятность попадания точки с координатами 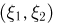 в область, заштрихованную на рис. 1.
в область, заштрихованную на рис. 1.
Выведем свойства совместной функции распределения, аналогичные свойствам функции распределения одномерной случайной величины.
Как и прежде, поскольку 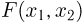 — вероятность, то
— вероятность, то
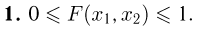
Следующее свойство является очевидным обобщением свойства 2 функции распределения одномерной случайной величины:
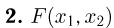 — неубывающая функция по каждому из аргументов
— неубывающая функция по каждому из аргументов 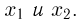
Поскольку события 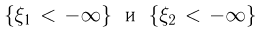 невозможны, а в результате пересечения невозможного события с любым событием, как мы знаем, также получается невозможное событие, то
невозможны, а в результате пересечения невозможного события с любым событием, как мы знаем, также получается невозможное событие, то
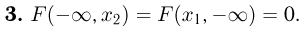
События 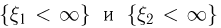 так же, как и их пересечение, достоверны. Значит,
так же, как и их пересечение, достоверны. Значит,
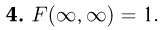
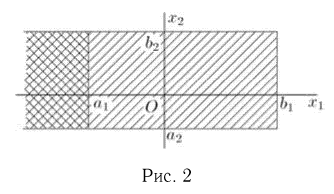
Найдем вероятность попадания двумерной случайной величины 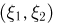 в прямоугольник
в прямоугольник 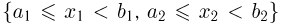 (рис. 2). Для этого сначала определим вероятность попадания в полуполосу
(рис. 2). Для этого сначала определим вероятность попадания в полуполосу 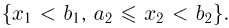 Но эта вероятность представляет собой вероятность попадания в квадрант
Но эта вероятность представляет собой вероятность попадания в квадрант 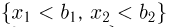 за вычетом вероятности попадания в квадрант
за вычетом вероятности попадания в квадрант 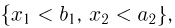 т. е.
т. е.
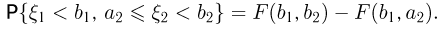
Теперь осталось заметить, что вероятность попадания в прямоугольник 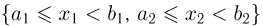 есть вероятность попадания в полуполосу
есть вероятность попадания в полуполосу 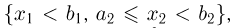 из которой вычтена вероятность попадания в полуполосу
из которой вычтена вероятность попадания в полуполосу 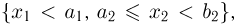 равная
равная 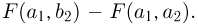 Окончательно получаем
Окончательно получаем
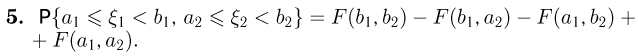
Подобно одномерному случаю доказывается и следующее свойство:
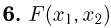 — непрерывная слева по каждому из аргументов
— непрерывная слева по каждому из аргументов 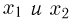 функция.
функция.
Наконец, последнее свойство устанавливает естественную связь между распределением случайного вектора 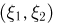 и распределениями
и распределениями
случайных величин 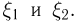 Событие
Событие 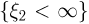 достоверно, поэтому
достоверно, поэтому 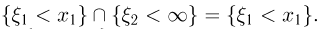 Аналогично
Аналогично 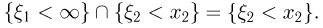 Значит,
Значит,
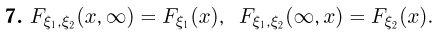
Отметим, что, в отличие от одномерного случая, не любая функция 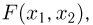 удовлетворяющая условиям 2-4 и 6, может являться совместной функцией распределения некоторой двумерной случайной величины. Для того чтобы это было возможно, необходимо потребовать также выполнение для любых
удовлетворяющая условиям 2-4 и 6, может являться совместной функцией распределения некоторой двумерной случайной величины. Для того чтобы это было возможно, необходимо потребовать также выполнение для любых 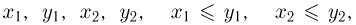 следующего дополнительного условия:
следующего дополнительного условия:
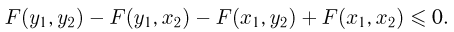
Дискретные двумерные случайные величины
Двумерная случайная величина 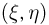 называется дискретной, если каждая из случайных величин
называется дискретной, если каждая из случайных величин 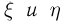 является дискретной. Ясно, что если случайная величина
является дискретной. Ясно, что если случайная величина 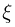 может принимать только значения
может принимать только значения 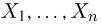 (для простоты мы ограничимся только конечным множеством значений), а случайная величина
(для простоты мы ограничимся только конечным множеством значений), а случайная величина 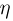 — значения
— значения 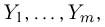 то двумерный случайный вектор
то двумерный случайный вектор 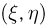 может принимать только пары значений
может принимать только пары значений 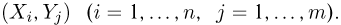
Так же, как и в одномерном случае, распределение двумерной дискретной случайной величины естественно описать с помощью перечисления всевозможных пар 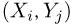 значений случайного вектора
значений случайного вектора 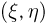 и соответствующих вероятностей, с которыми эти пары значений принимают случайные величины
и соответствующих вероятностей, с которыми эти пары значений принимают случайные величины 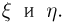 Такое перечисление удобно реализовать таблицей (табл. 1) с двумя входами. В верхней строке этой таблицы перечислены все возможные значения
Такое перечисление удобно реализовать таблицей (табл. 1) с двумя входами. В верхней строке этой таблицы перечислены все возможные значения  случайной величины
случайной величины 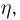 а в левом столбце — значения
а в левом столбце — значения  случайной величины
случайной величины 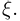 На пересечении столбца
На пересечении столбца 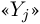 со строкой
со строкой 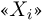 приведена вероятность
приведена вероятность 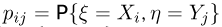 совместного осуществления событий
совместного осуществления событий 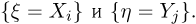 К этой таблице обычно добавляют еще одну строку
К этой таблице обычно добавляют еще одну строку 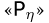 и столбец
и столбец 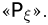 На пересечении столбца
На пересечении столбца 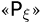 со строкой
со строкой 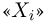 записывают число
записывают число 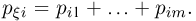 Но
Но 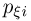 представляет собой не что иное, как вероятность случайной величине
представляет собой не что иное, как вероятность случайной величине 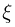 принять значение
принять значение 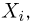 т.е.
т.е. 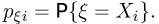 Таким образом, первый и последний столбцы таблицы дают нам ряд распределения случайной величины
Таким образом, первый и последний столбцы таблицы дают нам ряд распределения случайной величины 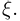 Аналогично в строке
Аналогично в строке 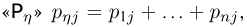 а первая и последняя строки в совокупности задают ряд распределения случайной величины
а первая и последняя строки в совокупности задают ряд распределения случайной величины 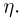 Для контроля правильности составления таблицы рекомендуется просуммировать элементы последней строки и последнего столбца. Если хотя бы одна из этих сумм не будет равна единице, то это означает, что при составлении таблицы была допущена ошибка.
Для контроля правильности составления таблицы рекомендуется просуммировать элементы последней строки и последнего столбца. Если хотя бы одна из этих сумм не будет равна единице, то это означает, что при составлении таблицы была допущена ошибка.
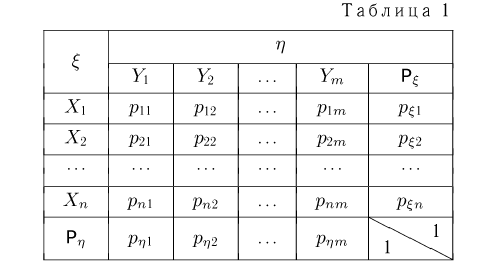
По табл. 1 нетрудно определить функцию распределения 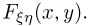 Ясно, что для этого необходимо просуммировать
Ясно, что для этого необходимо просуммировать 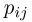 по всем тем значениям
по всем тем значениям 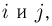 для которых
для которых 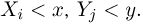 Иными словами,
Иными словами,
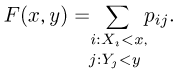
Пример:
В схеме Бернулли производится 2 испытания с вероятностью успеха р и вероятностью неудачи 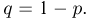 Выпишем распределение двумерного случайного вектора
Выпишем распределение двумерного случайного вектора 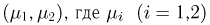 — число успехов в i-м испытании (см. пример 2). Каждая из случайных величин
— число успехов в i-м испытании (см. пример 2). Каждая из случайных величин 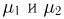 может принимать 2 значения: 0 или 1. Числа успехов в обоих испытаниях равны нулю тогда, когда произойдут две неудачи, а это в силу независимости испытаний происходит с вероятностью
может принимать 2 значения: 0 или 1. Числа успехов в обоих испытаниях равны нулю тогда, когда произойдут две неудачи, а это в силу независимости испытаний происходит с вероятностью 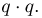 Поэтому
Поэтому 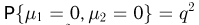 и на пересечении столбца «О» со строкой «О» нужно написать
и на пересечении столбца «О» со строкой «О» нужно написать 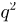 (табл. 2). Далее,
(табл. 2). Далее, 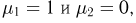 если в первом испытании произошел успех, а во втором — неудача, и, значит
если в первом испытании произошел успех, а во втором — неудача, и, значит 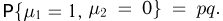 Аналогично заполняется второй столбец:
Аналогично заполняется второй столбец: 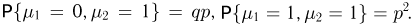 Наконец, на пересечении столбца
Наконец, на пересечении столбца 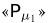 и строки «0» должно стоять
и строки «0» должно стоять 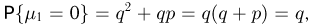 а на пересечении столбца
а на пересечении столбца 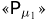 и строки
и строки 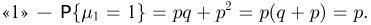 Таким же образом выписываем последнюю строку:
Таким же образом выписываем последнюю строку: 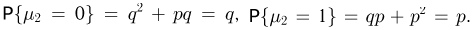 Проверяем правильность составления таблицы: сумма элементов последнего столбца
Проверяем правильность составления таблицы: сумма элементов последнего столбца 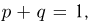 последней строки
последней строки 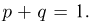 Значит, есть надежда, что таблица составлена правильно.
Значит, есть надежда, что таблица составлена правильно.
Построим теперь совместную функцию распределения 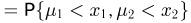 случайных величин
случайных величин 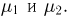 Поскольку при
Поскольку при 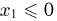 или
или 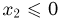 нет ни одного элементарного исхода
нет ни одного элементарного исхода 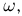 для которого
для которого 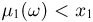 или
или 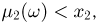 то событие
то событие 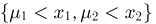 невозможно и, значит,
невозможно и, значит, 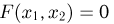 при
при 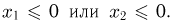 Далее, если
Далее, если 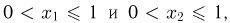 то событие
то событие 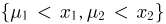 эквивалентно событию
эквивалентно событию 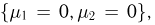 которое, как видно из табл.2, происходит с вероятностью
которое, как видно из табл.2, происходит с вероятностью 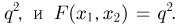 Если же
Если же 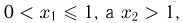 то событие
то событие 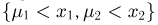 совпадает с объединением
совпадает с объединением
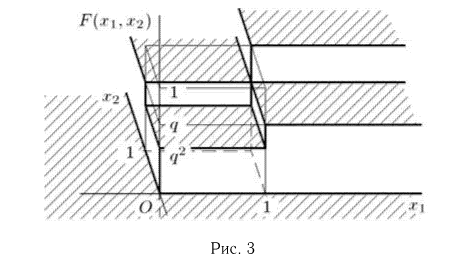
непересекающихся событий 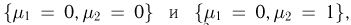 тогда
тогда 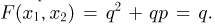 Аналогично,
Аналогично, 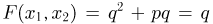 при
при 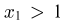 и
и 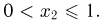 Наконец, если
Наконец, если 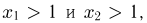 то событие
то событие 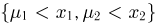 достоверно и, значит,
достоверно и, значит, 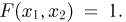 Функция распределения
Функция распределения 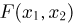 представляет собой поверхность в трехмерном пространстве, и ее не очень удобно изображать графически. Тем не менее такая попытка предпринята на рис. 3.
представляет собой поверхность в трехмерном пространстве, и ее не очень удобно изображать графически. Тем не менее такая попытка предпринята на рис. 3.
Пример:
Игральная кость размечена таким образом, что сумма очков на противоположных гранях равна 7 (т.е. 1-6, 2-5, 3-4). Случайная величина 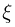 — число очков, выпавших на верхней грани, случайная величина —
— число очков, выпавших на верхней грани, случайная величина — 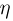 на нижней. И случайная величина
на нижней. И случайная величина 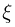 случайная величина
случайная величина 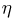 могут принимать любые целые значения от 1 до 6 с одинаковой вероятностью 1/6. Однако если случайная величина
могут принимать любые целые значения от 1 до 6 с одинаковой вероятностью 1/6. Однако если случайная величина 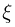 приняла значение 1 (на верхней грани выпало 1 очко), то единственным значением случайной величины
приняла значение 1 (на верхней грани выпало 1 очко), то единственным значением случайной величины 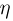 может быть только 6 (на нижней грани обязательно выпадет 6 очков). Значит, строка «1» табл.3 будет состоять из нулей, за исключением пересечения со столбцом «6»: на этом месте обязана стоять вероятность 1/6. Аналогично, строка «2» будет иметь единственный отличный от нуля элемент на пересечении со столбцом «5»,
может быть только 6 (на нижней грани обязательно выпадет 6 очков). Значит, строка «1» табл.3 будет состоять из нулей, за исключением пересечения со столбцом «6»: на этом месте обязана стоять вероятность 1/6. Аналогично, строка «2» будет иметь единственный отличный от нуля элемент на пересечении со столбцом «5»,
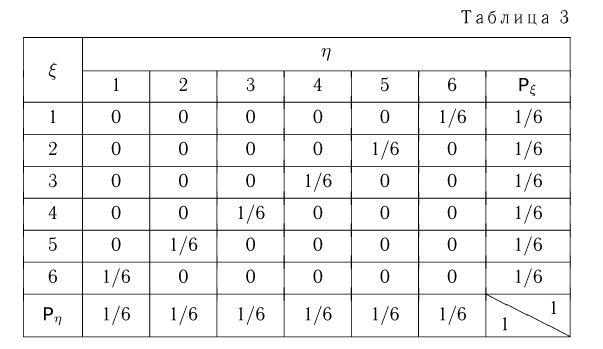
также равный 1/6 (на верхней грани выпало 2 очка, на нижней 5) и т.д. Столбец 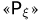 и строку
и строку 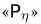 находим, суммируя соответствующие строки и столбцы; как и должно было быть, мы получаем в них одинаковые значения 1/6, соответствующие принципу классической вероятности.
находим, суммируя соответствующие строки и столбцы; как и должно было быть, мы получаем в них одинаковые значения 1/6, соответствующие принципу классической вероятности.
Предоставляем интересующемуся читателю самостоятельно построить совместную функцию распределения случайных величин 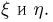
Непрерывные двумерные случайные величины
Непрерывной двумерной случайной величиной 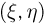 называется такая двумерная случайная величина
называется такая двумерная случайная величина 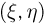 функция распределения которой
функция распределения которой 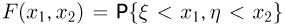 может быть представлена в виде
может быть представлена в виде
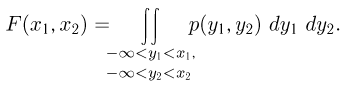
Здесь имеется в виду двукратный интеграл по области 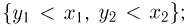 имеет место теорема Фубини, которая говорит, что этот двукратный интеграл можно представить в виде повторного, причем в любом порядке:
имеет место теорема Фубини, которая говорит, что этот двукратный интеграл можно представить в виде повторного, причем в любом порядке:
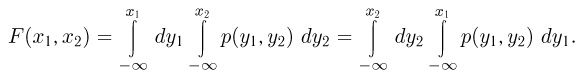
Функция 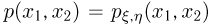 называется совместной плотностью распределения случайных величин
называется совместной плотностью распределения случайных величин 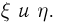
Так же, как и в одномерном случае, будем предполагать, что 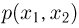 непрерывная (или «почти» непрерывная) функция по обоим аргументам. Тогда совместная плотность распределения представляет собой смешанную производную совместной функции распределения:
непрерывная (или «почти» непрерывная) функция по обоим аргументам. Тогда совместная плотность распределения представляет собой смешанную производную совместной функции распределения:
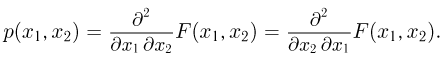
Нетрудно вывести следующие свойства совместной плотности распределения:
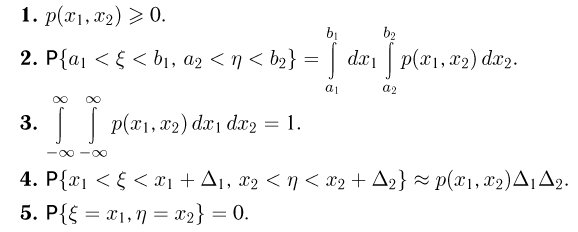
Кроме этих свойств, повторяющих свойства плотности распределения одномерной случайной величины, укажем дополнительные свойства совместной плотности распределения.
Пусть D — некоторая область на плоскости (рис.4).
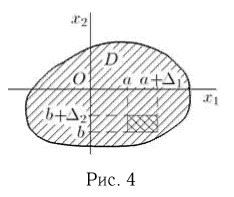
Тогда, как следует из свойства 4, вероятность попадания двумерной случайной величины 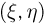 в малый прямоугольник
в малый прямоугольник 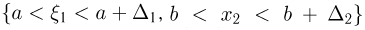 приближенно равна
приближенно равна 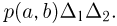 Поскольку попадания в непересекающиеся прямоугольники являются несовместными событиями, то, для того чтобы найти полную вероятность попадания двумерной случайной величины
Поскольку попадания в непересекающиеся прямоугольники являются несовместными событиями, то, для того чтобы найти полную вероятность попадания двумерной случайной величины 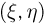 в область D, нужно просуммировать вероятности попадания во все «малые» прямоугольники, входящие в область D. Переходя к пределу, получаем для
в область D, нужно просуммировать вероятности попадания во все «малые» прямоугольники, входящие в область D. Переходя к пределу, получаем для 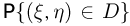 — вероятности попадания
— вероятности попадания 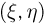 в область D — формулу
в область D — формулу
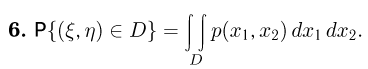
Далее, из свойства 7 совместной функции распределения и определения совместной плотности распределения имеем
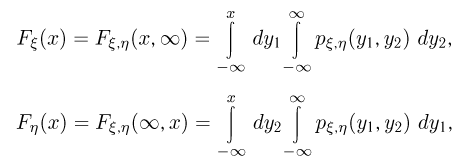
откуда, дифференцируя по x, получаем выражения для одномерных плотностей распределения случайных величин 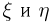
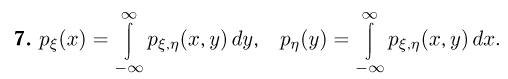
Пример:
Предположим, что в соответствии с принципом геометрической вероятности мы бросаем точку случайным образом в круг радиусом R с центром в начале координат (см. пример 10 в гл. 2). Пусть случайная величина 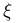 — абсцисса точки падения, а
— абсцисса точки падения, а 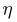 — ордината. Естественно, поскольку точка не может попасть за пределы круга, то
— ордината. Естественно, поскольку точка не может попасть за пределы круга, то 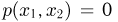 при
при 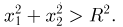 Для каждой области внутри круга (в частности, прямоугольника
Для каждой области внутри круга (в частности, прямоугольника 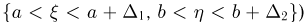 вероятность попадания пропорциональна площади этой области (равна
вероятность попадания пропорциональна площади этой области (равна 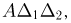 где А — коэффициент пропорциональности). Поэтому из свойства 4 совместной плотности распределения имеем:
где А — коэффициент пропорциональности). Поэтому из свойства 4 совместной плотности распределения имеем: 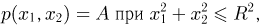 т.е. плотность распределения постоянна внутри
т.е. плотность распределения постоянна внутри
круга. Для определения постоянной А воспользуемся свойством 3 совместной плотности распределения. Поскольку 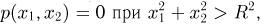 то
то
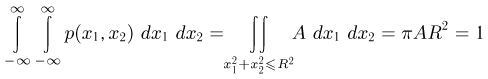
и, значит, 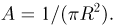 Итак,
Итак,

Нетрудно найти плотность распределения случайной величины 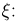
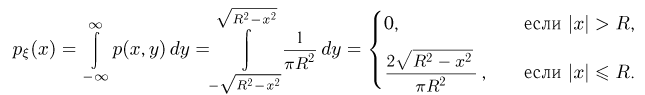
Аналогичное выражение получается и для 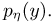
Для нахождения совместной функции распределения 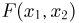 заметим, что в силу определения совместной плотности распределения
заметим, что в силу определения совместной плотности распределения
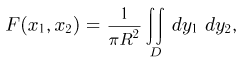
где область D представляет собой пересечение квадранта 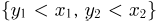 и круга
и круга 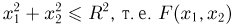 с точностью до множителя
с точностью до множителя 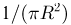 совпадает с площадью области D, имеющей двойную штриховку на рис. 5.
совпадает с площадью области D, имеющей двойную штриховку на рис. 5.
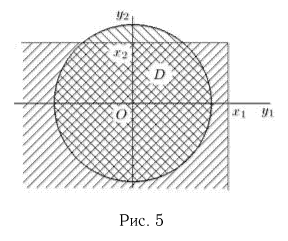
Мы думаем, читатель достаточно хорошо знаком с основами интегрального исчисления и может определить площадь области D для различных 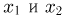 самостоятельно.
самостоятельно.
Предложенный выше вариант определения совместной плотности распределения 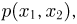 которую естественно назвать равномерной плотностью распределения внутри круга
которую естественно назвать равномерной плотностью распределения внутри круга 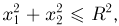 реализует первое решение примера 10 в гл.2. Во втором решении вероятность попадания одна и та же для областей, имеющих одинаковые приращения полярных координат: радиуса
реализует первое решение примера 10 в гл.2. Во втором решении вероятность попадания одна и та же для областей, имеющих одинаковые приращения полярных координат: радиуса 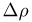 и угла
и угла 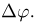 Переходя к декартовым координатам, получаем, что совместная плотность распределения
Переходя к декартовым координатам, получаем, что совместная плотность распределения 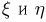 в этом случае должна иметь вид
в этом случае должна иметь вид
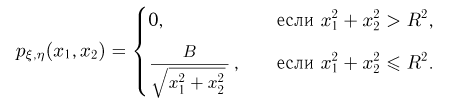
Предоставляем читателю определить нормировочную константу В, а также плотности распределения случайных величин 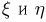 совместную функцию распределения
совместную функцию распределения 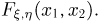
В заключение этого параграфа рассмотрим наиболее часто встречающееся на практике распределение непрерывной n-мерной случайной величины.
Многомерное нормальное (гауссово) распределение
Пусть 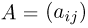 — положительно определенная симметрическая квадратная матрица порядка п (т. е.
— положительно определенная симметрическая квадратная матрица порядка п (т. е. 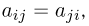 а все собственные значения матрицы А положительны). Обозначим через
а все собственные значения матрицы А положительны). Обозначим через 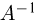 матрицу, обратную матрице А, а через
матрицу, обратную матрице А, а через 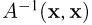 — квадратичную форму, порожденную матрицей
— квадратичную форму, порожденную матрицей 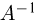 т.е.
т.е. 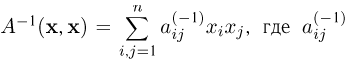 — элементы матрицы
— элементы матрицы 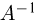 a
a 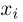 — i-я координата вектора
— i-я координата вектора 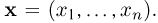 Пусть также задан n-мерный вектор
Пусть также задан n-мерный вектор 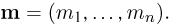 Скажем, что n-мерный непрерывный случайный вектор
Скажем, что n-мерный непрерывный случайный вектор 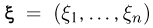 распределен по (невырожденному) нормальному закону, если его совместная плотность распределения
распределен по (невырожденному) нормальному закону, если его совместная плотность распределения  (определяется точно так же, как и совместная плотность распределения одномерной случайной величины:
(определяется точно так же, как и совместная плотность распределения одномерной случайной величины:
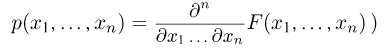
задается формулой
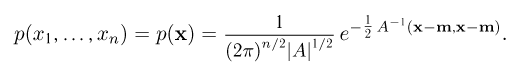
(Здесь 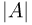 — определитель матрицы А.) Матрица А носит название ковариационной матрицы (матрицы ковариаций), а вектор m — вектора средних. Если матрица А (а значит, и матрица
— определитель матрицы А.) Матрица А носит название ковариационной матрицы (матрицы ковариаций), а вектор m — вектора средних. Если матрица А (а значит, и матрица 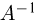 ) совпадает с единичной матрицей I, а вектор
) совпадает с единичной матрицей I, а вектор 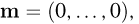 то
то
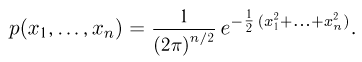
Такая плотность распределения по аналогии с одномерным случаем называется плотностью стандартного n-мерного нормального распределения (соответственно  — функция стандартного п-мерного нормального распределения).
— функция стандартного п-мерного нормального распределения).
Пусть  — n-мерный случайный вектор, распределенный
— n-мерный случайный вектор, распределенный
по (произвольному) нормальному закону. Тогда п— 1-мерный случайный вектор 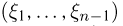 распределен также по нормальному закону с вектором средних
распределен также по нормальному закону с вектором средних 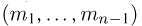 и ковариационной матрицей
и ковариационной матрицей 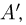 получаемой из матрицы А вычеркиванием последних строки и столбца (это можно показать непосредственно с помощью многомерного аналога свойства 7 совместной плотности распределения двумерной случайной величины:
получаемой из матрицы А вычеркиванием последних строки и столбца (это можно показать непосредственно с помощью многомерного аналога свойства 7 совместной плотности распределения двумерной случайной величины:
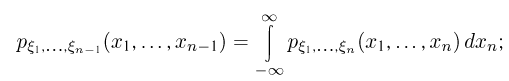
однако существенно проще для этой цели воспользоваться аппаратом характеристических функций, который частично будет рассмотрен нами в гл. 8). В частности, каждая из случайных величин 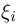 распределена по нормальному закону со средним
распределена по нормальному закону со средним 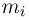 и средним квадратичным отклонением
и средним квадратичным отклонением 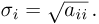
Рассмотрим теперь уравнение 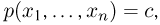 которое для плотности распределения n-мерного нормального распределения эквивалентно уравнению
которое для плотности распределения n-мерного нормального распределения эквивалентно уравнению
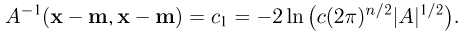
Для всех 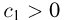 это уравнение в силу положительной определенности матрицы
это уравнение в силу положительной определенности матрицы 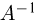 представляет собой уравнение n-мерного эллипсоида, называемого эллипсоидом рассеивания; его главные оси называются осями рассеивания (рис. 6).
представляет собой уравнение n-мерного эллипсоида, называемого эллипсоидом рассеивания; его главные оси называются осями рассеивания (рис. 6).
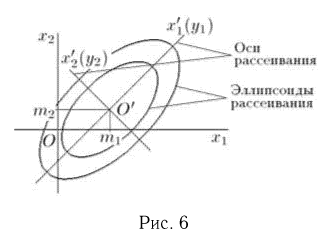
Будем трактовать n-мерный случайный вектор  как координаты случайной точки
как координаты случайной точки 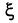 в n-мерном пространстве. Тогда, если мы выберем в n-мерном пространстве новую ортонормированную систему координат
в n-мерном пространстве. Тогда, если мы выберем в n-мерном пространстве новую ортонормированную систему координат  связанную с главными осями, то в этой системе новые координаты
связанную с главными осями, то в этой системе новые координаты 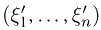 случайной точки
случайной точки 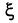 снова будут описываться n-мерным нормальным законом, имеющим нулевой вектор средних
снова будут описываться n-мерным нормальным законом, имеющим нулевой вектор средних 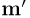 и диагональную матрицу ковариаций
и диагональную матрицу ковариаций 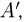 причем диагональные элементы
причем диагональные элементы 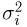 матрицы
матрицы 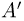 будут пропорциональны квадратам коэффициентов растяжения
будут пропорциональны квадратам коэффициентов растяжения 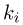 эллипсоида рассеивания по соответствующим осям рассеивания. Еще раз вводя новые координаты
эллипсоида рассеивания по соответствующим осям рассеивания. Еще раз вводя новые координаты 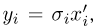 получаем, что в этой последней системе
получаем, что в этой последней системе  координаты случайной точки
координаты случайной точки 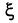 будут распределены по стандартному нормальному закону. Таким образом, делая обратные преобразования, можно трактовать (невырожденный) нормально распределенный вектор
будут распределены по стандартному нормальному закону. Таким образом, делая обратные преобразования, можно трактовать (невырожденный) нормально распределенный вектор 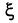 с произвольными вектором средних m и матрицей ковариаций А как координаты случайной точки
с произвольными вектором средних m и матрицей ковариаций А как координаты случайной точки 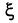 имеющей стандартное нормальное распределение, в некоторой (вообще говоря, не ортонормированной и даже не ортогональной) системе координат.
имеющей стандартное нормальное распределение, в некоторой (вообще говоря, не ортонормированной и даже не ортогональной) системе координат.
Разумеется, встречаются многомерные случайные величины, которые нельзя отнести ни к дискретному, ни к непрерывному типу. Так, у двумерной случайной величины 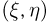 одна координата (допустим
одна координата (допустим 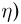 может быть дискретной, а другая
может быть дискретной, а другая 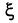 — непрерывной. Такую двумерную случайную величину удобно характеризовать набором функций
— непрерывной. Такую двумерную случайную величину удобно характеризовать набором функций 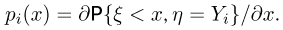
Пример:
Придя в кассу «Аэрофлота», клиент застает очередь из 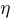 человек. Ясно, что
человек. Ясно, что 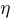 — дискретная случайная величина, принимающая значения 0, 1, 2,… Наряду с длиной очереди
— дискретная случайная величина, принимающая значения 0, 1, 2,… Наряду с длиной очереди 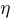 естественно рассмотреть и непрерывную случайную величину
естественно рассмотреть и непрерывную случайную величину 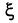 — общее время, проведенное клиентом в кассе. Если интервалы времени между приходами клиентов независимы (см. параграф 6) и имеют одно и то же экспоненциальное распределение с параметром
— общее время, проведенное клиентом в кассе. Если интервалы времени между приходами клиентов независимы (см. параграф 6) и имеют одно и то же экспоненциальное распределение с параметром 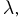 а длительность обслуживания каждого клиента кассиром также распределена экспоненциально с параметром
а длительность обслуживания каждого клиента кассиром также распределена экспоненциально с параметром 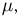 то, как показано в теории массового обслуживания, совместное распределение случайных величин
то, как показано в теории массового обслуживания, совместное распределение случайных величин 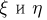 в установившемся режиме работы задается функциями
в установившемся режиме работы задается функциями
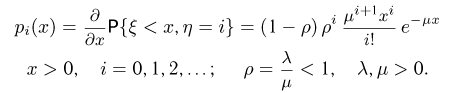
Ряд распределения случайной величины 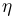 находим, проинтегрировав
находим, проинтегрировав 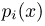 по х:
по х:
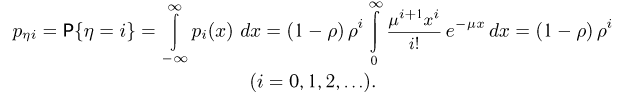
Итак, длина очереди 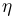 распределена по геометрическому закону. Аналогично, плотность распределения случайной величины
распределена по геометрическому закону. Аналогично, плотность распределения случайной величины 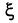 получаем, суммируя
получаем, суммируя 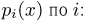
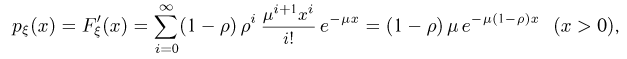
т. е. время 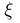 пребывания клиента в кассе имеет экспоненциальное распределение с параметром
пребывания клиента в кассе имеет экспоненциальное распределение с параметром 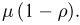
Еще более интересные явления возникают, если рассматривать случайные величины, имеющие явную функциональную зависимость.
Пример:
Пусть 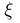 — непрерывная случайная величина с функцией распределения F(x) и плотностью распределения р(х). Рассмотрим двумерный случайный вектор
— непрерывная случайная величина с функцией распределения F(x) и плотностью распределения р(х). Рассмотрим двумерный случайный вектор 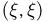 с одинаковыми координатами
с одинаковыми координатами 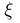 и совместной функцией распределения
и совместной функцией распределения 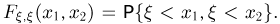 Ясно, что вектор
Ясно, что вектор 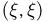 не является дискретным. Покажем, что
не является дискретным. Покажем, что 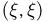 не может быть и непрерывной двумерной случайной величиной. Для этого заметим, что при
не может быть и непрерывной двумерной случайной величиной. Для этого заметим, что при 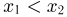 событие
событие 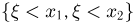 совпадает с событием
совпадает с событием 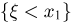 значит,
значит, 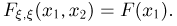
Но тогда
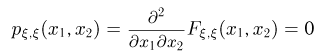
при 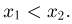 Аналогично,
Аналогично, 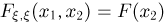 и
и
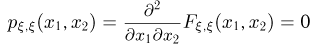
при 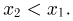
Таким образом, если бы у вектора 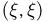 существовала плотность распределения, то она равнялась бы нулю всюду, кроме биссектрисы
существовала плотность распределения, то она равнялась бы нулю всюду, кроме биссектрисы 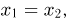 и, значит,
и, значит,
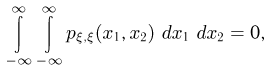
что противоречит свойству 3 совместной плотности распределения. Ясно, что причина этого явления кроется в том, что значения двумерного случайного вектора 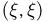 полностью сосредоточены на биссектрисе
полностью сосредоточены на биссектрисе 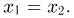
Условные распределения
Рассмотрим двумерную случайную величину 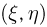 с совместной функцией распределения
с совместной функцией распределения 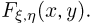 Пусть известно, что случайная величина
Пусть известно, что случайная величина 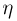 приняла значение у. Естественно задать вопрос: а что можно сказать при этом условии о распределении случайной величины
приняла значение у. Естественно задать вопрос: а что можно сказать при этом условии о распределении случайной величины 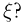 Ответ на этот вопрос дает условная функция распределения случайной величины
Ответ на этот вопрос дает условная функция распределения случайной величины 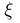 при условии
при условии 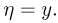 Как видно из самой постановки задачи, понятие условного распределения весьма схоже с понятием условной вероятности, разобранным в параграфе 1 гл. 3. Именно исходя из понятия условной вероятности, мы введем понятие условного распределения.
Как видно из самой постановки задачи, понятие условного распределения весьма схоже с понятием условной вероятности, разобранным в параграфе 1 гл. 3. Именно исходя из понятия условной вероятности, мы введем понятие условного распределения.
Начнем с наиболее простого случая. Пусть случайная величина 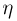 является дискретной. Назовем условной функцией распределения
является дискретной. Назовем условной функцией распределения 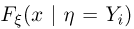 случайной величины
случайной величины 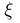 при условии
при условии 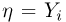 условную вероятность события
условную вероятность события 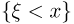 при условии события
при условии события 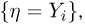 т.е. в соответствии с определением условной вероятности,
т.е. в соответствии с определением условной вероятности,
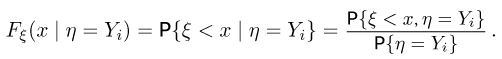
Условная функция распределения обладает всеми теми свойствами, которые присущи обычной (безусловной) функции распределения.
Пример:
Найдем условное распределение времени пребывания 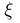 клиента в кассе «Аэрофлота» (пример 9) при условии, что в момент прихода он застает очередь
клиента в кассе «Аэрофлота» (пример 9) при условии, что в момент прихода он застает очередь 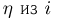 человек. В этом случае, как мы знаем,
человек. В этом случае, как мы знаем,
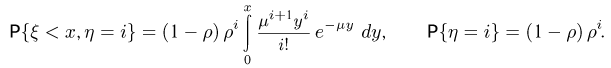
Таким образом,
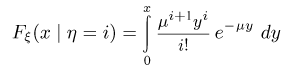
и, значит, условная функция распределения 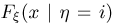 имеет условную плотность распределения
имеет условную плотность распределения
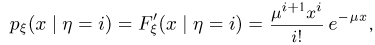
представляющую собой плотность гамма-распределения с параметрами 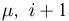 или, что то же самое, плотность распределения Эрланга порядка
или, что то же самое, плотность распределения Эрланга порядка 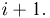
Если 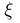 — также дискретная случайная величина, причем
— также дискретная случайная величина, причем 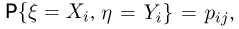 то удобно рассматривать условную вероятность
то удобно рассматривать условную вероятность 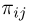 того, что случайная величина
того, что случайная величина 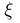 примет значение
примет значение 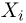 при условии
при условии 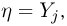 определяемую как условную вероятность события
определяемую как условную вероятность события 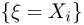 при условии события
при условии события 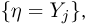 т.е.
т.е.
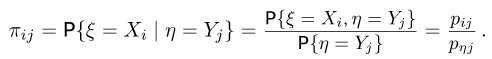
Обычно условное распределение дискретной случайной величины 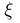 при условии дискретной случайной величины
при условии дискретной случайной величины 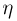 описывает табл. 4. Ясно, что элементы
описывает табл. 4. Ясно, что элементы 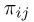 табл.4 получаются из элементов табл. 1 по формуле
табл.4 получаются из элементов табл. 1 по формуле 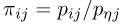 и, наоборот,
и, наоборот, 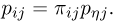
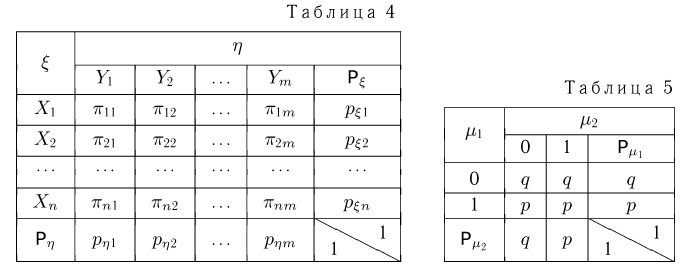
Пример:
Условное распределение случайной величины 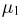 (числа успехов в первом испытании) при условии
(числа успехов в первом испытании) при условии 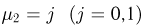 (числа успехов во втором испытании) из примера 6 задается табл. 5.
(числа успехов во втором испытании) из примера 6 задается табл. 5.
Пример:
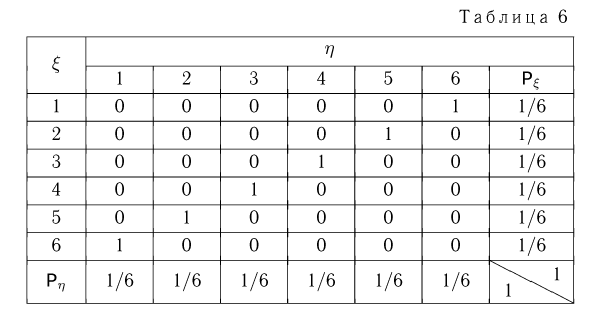
Условное распределение случайной величины 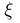 (числа очков, выпавших на верхней грани игральной кости) при условии
(числа очков, выпавших на верхней грани игральной кости) при условии 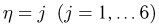 (числа очков, выпавших на нижней грани игральной кости) из примера 7 представлено в табл. 6.
(числа очков, выпавших на нижней грани игральной кости) из примера 7 представлено в табл. 6.
В общем случае условную функцию распределения случайной величины 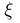 при условии
при условии 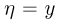 также естественно было бы определить формулой
также естественно было бы определить формулой
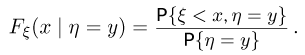
Однако это не всегда возможно (например, событие 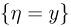 для непрерывной случайной величины имеет нулевую вероятность:
для непрерывной случайной величины имеет нулевую вероятность: 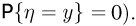 Поэтому попытаемся воспользоваться предельным переходом,
Поэтому попытаемся воспользоваться предельным переходом,
рассматривая вместо события 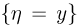 событие
событие 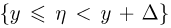 и устремляя
и устремляя  к нулю. Итак, определим сначала условную вероятность
к нулю. Итак, определим сначала условную вероятность
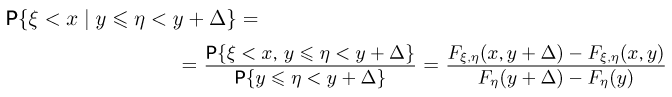
и назовем условной функцией распределения 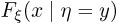 предел
предел
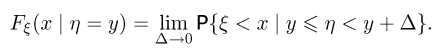
Оказывается, такой предел всегда существует (правда, в определенном смысле: это производная Радона-Никодима одной меры по другой. Производная Радона-Никодима определяется не однозначно, а с точностью до множества точек на прямой, вероятность попадания в которое случайной величины 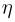 равна нулю. Впрочем, с неоднозначностью определения условной функции распределения мы фактически уже встречались в случае дискретной случайной величины
равна нулю. Впрочем, с неоднозначностью определения условной функции распределения мы фактически уже встречались в случае дискретной случайной величины 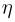 действительно, условную функцию распределения
действительно, условную функцию распределения 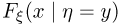 мы определяли только для
мы определяли только для 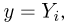 для остальных значений у мы могли бы задать
для остальных значений у мы могли бы задать 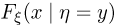 совершенно произвольным образом, поскольку все равно случайная величина
совершенно произвольным образом, поскольку все равно случайная величина 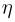 такие значения не принимает).
такие значения не принимает).
Если же случайная величина 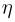 непрерывна, то условную функцию распределения можно определить следующим выражением:
непрерывна, то условную функцию распределения можно определить следующим выражением:
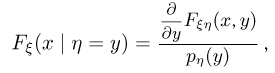
формально получаемым, если в выражении для 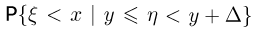 поделить числитель и знаменатель на
поделить числитель и знаменатель на  и устремить
и устремить  к нулю.
к нулю.
Пример:
Найдем условное распределение длины очереди 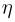 в кассу «Аэрофлота» в момент прихода клиента при условии, что общее время
в кассу «Аэрофлота» в момент прихода клиента при условии, что общее время 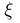 проведенное им в кассе, составило х (пример 9). Ответ дадим в терминах условного ряда распределения
проведенное им в кассе, составило х (пример 9). Ответ дадим в терминах условного ряда распределения 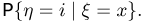 Тогда в обозначениях примера 9
Тогда в обозначениях примера 9
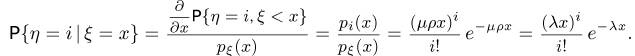
Таким образом, условное распределение очереди 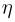 при условии
при условии 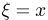 представляет собой распределение Пуассона с параметром
представляет собой распределение Пуассона с параметром 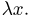
В наиболее важных для приложений случаях вектор 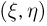 представляет собой двумерную непрерывную случайную величину с совместной плотностью распределения
представляет собой двумерную непрерывную случайную величину с совместной плотностью распределения 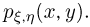 Тогда
Тогда
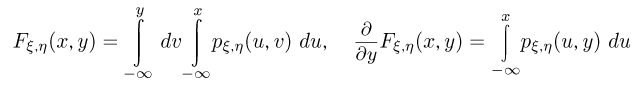
и значит,
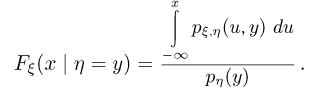
Нетрудно видеть, что условная функция распределения 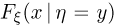 имеет производную по х, т. е. существует условная плотность распределения случайной величины
имеет производную по х, т. е. существует условная плотность распределения случайной величины 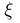 при условии
при условии 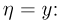
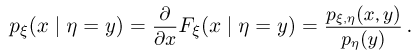
Пример:
Найдем условную плотность распределения случайной величины 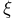 — абсциссы точки падения (из примера 8) при условии, что ордината
— абсциссы точки падения (из примера 8) при условии, что ордината 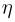 приняла значение у. Тогда, как мы знаем,
приняла значение у. Тогда, как мы знаем,
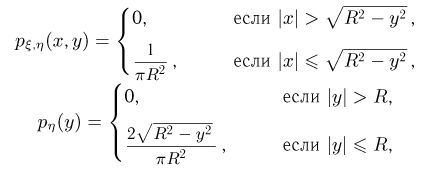
и при 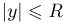
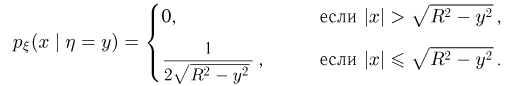
Таким образом, случайная величина 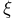 при условии
при условии 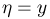 равномерно распределена на отрезке
равномерно распределена на отрезке 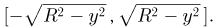 Если
Если 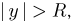 то условная плотность распределения
то условная плотность распределения 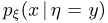 не определена; но это нас не должно волновать, поскольку случайная величина
не определена; но это нас не должно волновать, поскольку случайная величина 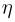 не может принимать значение, по модулю большее R.
не может принимать значение, по модулю большее R.
Рекомендуем читателю самостоятельно решить эту задачу для второго варианта определения плотности распределения из примера 8.
Пример:
Пусть 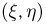 — двумерный нормальный вектор с матрицей ковариаций
— двумерный нормальный вектор с матрицей ковариаций
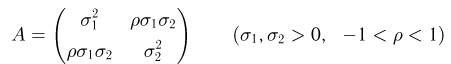
и вектором средних 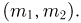 Найдем условную плотность распределения случайной величины
Найдем условную плотность распределения случайной величины 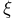 при условии
при условии 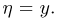 Для этого сначала определим
Для этого сначала определим 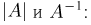
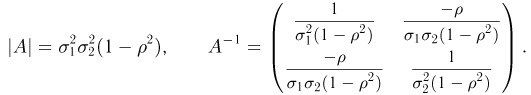
Теперь мы можем выписать совместную плотность распределения случайных величин 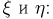
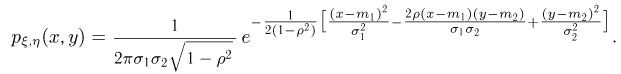
Далее, как нам известно,
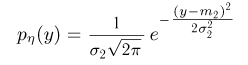
и, значит,
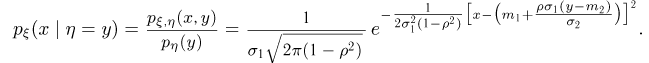
Таким образом, условное распределение 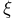 при условии
при условии 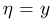 снова является нормальным со средним значением
снова является нормальным со средним значением 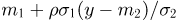 и средним квадратичным отклонением
и средним квадратичным отклонением 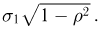
Независимые случайные величины
Назовем случайные величины 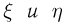 независимыми, если совместная функция распределения
независимыми, если совместная функция распределения 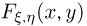 представляется в виде произведения одномерных функций распределения
представляется в виде произведения одномерных функций распределения 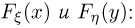
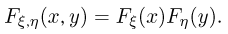
Понятие независимости случайных величин представляет собой перенос понятия независимости событий на случайные величины и опять-таки отражает отсутствие связи между случайными величинами 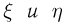 (хотя, повторяем еще раз,
(хотя, повторяем еще раз, 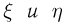 заданы на одном и том же вероятностном пространстве
заданы на одном и том же вероятностном пространстве 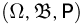 и в совокупности определяют двумерный случайный вектор
и в совокупности определяют двумерный случайный вектор 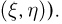 Иными словами, независимость случайных величин
Иными словами, независимость случайных величин 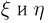 можно охарактеризовать следующим образом: зная значение, которое приняла случайная величина
можно охарактеризовать следующим образом: зная значение, которое приняла случайная величина 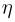 мы никакой новой информации о распределении случайной величины
мы никакой новой информации о распределении случайной величины 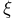 не получим. Отметим, что обычно независимость случайных величин вводится несколько иначе; в этом случае приведенное здесь определение выступает в роли необходимого и достаточного условия независимости.
не получим. Отметим, что обычно независимость случайных величин вводится несколько иначе; в этом случае приведенное здесь определение выступает в роли необходимого и достаточного условия независимости.
Совершенно аналогично определяется независимость произвольного числа случайных величин. Случайные величины  называются независимыми (в совокупности), если
называются независимыми (в совокупности), если
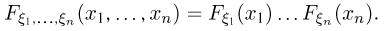
Разумеется, так же, как и для событий, из попарной независимости не следует независимость случайных величин в совокупности.
Пример:
Свяжем с бросанием правильного раскрашенного тетраэдра (пример 11 в гл. 3) три случайные величины: 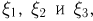 каждая из которых может принимать значения 0 или 1, причем
каждая из которых может принимать значения 0 или 1, причем 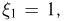 если тетраэдр упал на грань, в раскраске которой присутствует синий цвет, и
если тетраэдр упал на грань, в раскраске которой присутствует синий цвет, и 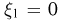 в противном случае. Аналогично,
в противном случае. Аналогично, 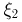 характеризует наличие красного цвета, а
характеризует наличие красного цвета, а 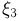 — зеленого. Нетрудно видеть, что случайные величины
— зеленого. Нетрудно видеть, что случайные величины 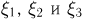 будут попарно независимы, но зависимы в совокупности.
будут попарно независимы, но зависимы в совокупности.
Пример:
Рассмотрим широту 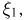 долготу
долготу 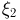 места падения метеорита на Землю и время
места падения метеорита на Землю и время 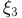 от начала наблюдений до момента его падения (см. пример 5). Предполагая, что каждый падающий метеорит имеет случайное направление, мы должны считать случайные величины
от начала наблюдений до момента его падения (см. пример 5). Предполагая, что каждый падающий метеорит имеет случайное направление, мы должны считать случайные величины 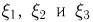 независимыми. Однако если Земля проходит через метеоритный поток определенного направления, уже нельзя пользоваться моделью с независимыми
независимыми. Однако если Земля проходит через метеоритный поток определенного направления, уже нельзя пользоваться моделью с независимыми 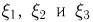 поскольку долгота места падения связана с тем, какой стороной к потоку метеоритов обращена Земля, т. е. в конечном счете со временем. Тем не менее и в этом случае широта
поскольку долгота места падения связана с тем, какой стороной к потоку метеоритов обращена Земля, т. е. в конечном счете со временем. Тем не менее и в этом случае широта 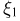 не будет зависеть от времени
не будет зависеть от времени 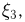 т.е. имеет место независимость случайных величин
т.е. имеет место независимость случайных величин 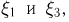 хотя случайные величины
хотя случайные величины 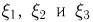 зависимы в совокупности. Предоставляем читателю самостоятельно поразмышлять над вопросом: какое направление должен иметь поток метеоритов, чтобы были независимыми между собой случайная величина
зависимы в совокупности. Предоставляем читателю самостоятельно поразмышлять над вопросом: какое направление должен иметь поток метеоритов, чтобы были независимыми между собой случайная величина 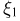 и случайный вектор
и случайный вектор 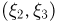 (широта не зависит от долготы и времени падения).
(широта не зависит от долготы и времени падения).
Пусть 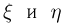 — независимые случайные величины. Рассмотрим событие
— независимые случайные величины. Рассмотрим событие 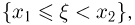 связанное со случайной величиной
связанное со случайной величиной 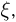 событие
событие 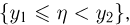 связанное со случайной величиной
связанное со случайной величиной 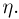 В силу независимости
В силу независимости 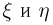
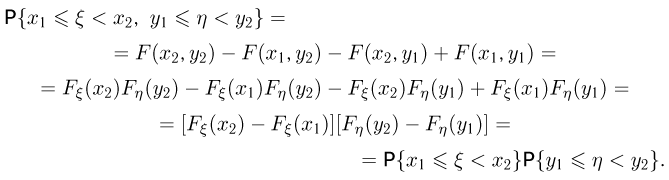
Таким образом, для независимых случайных величин независимы между собой не только события, связанные с попаданием случайных величин 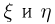 на интервалы
на интервалы 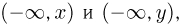 но и на любые интервалы
но и на любые интервалы 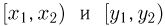 и, более того, в любые (измеримые) одномерные множества А и В.
и, более того, в любые (измеримые) одномерные множества А и В.
Для проверки независимости компонент многомерных дискретных и непрерывных случайных векторов обычно бывают удобными другие эквивалентные определения независимости (доказательство эквивалентности приводимых ниже определений предоставляем читателю). Так, дискретные случайные величины 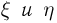 независимы, если для всех возможных значений
независимы, если для всех возможных значений 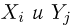
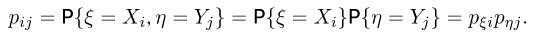
Пример:
В схеме Бернулли с двумя испытаниями (см. пример 6)
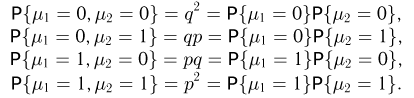
Таким образом, числа успехов 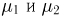 в первом и втором испытаниях представляют собой независимые случайные величины. Впрочем, иного и нельзя было ожидать из самого определения схемы Бернулли. Читатель может самостоятельно убедиться в том, что независимы в совокупности случайные величины
в первом и втором испытаниях представляют собой независимые случайные величины. Впрочем, иного и нельзя было ожидать из самого определения схемы Бернулли. Читатель может самостоятельно убедиться в том, что независимы в совокупности случайные величины  — числа успехов в первом,…, n-м испытаниях Бернулли.
— числа успехов в первом,…, n-м испытаниях Бернулли.
Непрерывные случайные величины 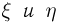 независимы, если для всех х и у
независимы, если для всех х и у
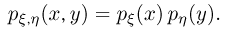
Отметим здесь же, что если независимые случайные величины 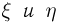 непрерывны, то и двумерная случайная величина
непрерывны, то и двумерная случайная величина 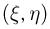 обязана быть непрерывной (ср. с примером 10).
обязана быть непрерывной (ср. с примером 10).
Пример:
Координаты двумерного нормального случайного вектора (см. пример 16) независимы тогда и только тогда, когда р = 0, т.е. матрицы 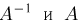 — диагональные. В этом можно без труда убедиться, сравнивая выражения для
— диагональные. В этом можно без труда убедиться, сравнивая выражения для 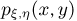 с произведением
с произведением 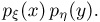 Аналогично, случайные величины
Аналогично, случайные величины 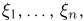 имеющие совместное n-мерное нормальное распределение, независимы (в совокупности) тогда и только тогда, когда матрица
имеющие совместное n-мерное нормальное распределение, независимы (в совокупности) тогда и только тогда, когда матрица 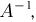 а значит, и ковариационная матрица А диагональны. Интересно отметить, что попарная независимость всех компонент
а значит, и ковариационная матрица А диагональны. Интересно отметить, что попарная независимость всех компонент 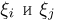 и нормального вектора
и нормального вектора 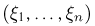 влечет за собой независимость случайных величин
влечет за собой независимость случайных величин 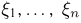 в совокупности(ср. с примером 17).
в совокупности(ср. с примером 17).
Для читателя, ознакомившегося с понятием условного распределения (параграф 5), приведем еще один критерий независимости случайных величин 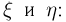 случайные величины
случайные величины 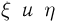 независимы тогда и только тогда, когда условное распределение (функция распределения
независимы тогда и только тогда, когда условное распределение (функция распределения 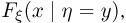 плотность распределения
плотность распределения 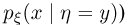 случайной величины
случайной величины 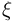 при условии
при условии 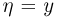 совпадает с безусловным распределением (функцией распределения
совпадает с безусловным распределением (функцией распределения 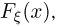 плотностью распределения
плотностью распределения 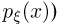 случайной величины
случайной величины 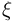 при всех значениях х и у. В частности, дискретные величины
при всех значениях х и у. В частности, дискретные величины 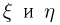 независимы тогда и только тогда, когда все условные вероятности
независимы тогда и только тогда, когда все условные вероятности 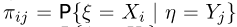 совпадают с безусловными вероятностями
совпадают с безусловными вероятностями 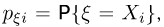 т.е. все столбцы табл.4 совпадают с последним.
т.е. все столбцы табл.4 совпадают с последним.
Пример:
В схеме Бернулли с двумя испытаниями (см. пример 6) числа успехов 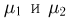 в первом и втором испытаниях независимы, поскольку в табл. 5 все три столбца совпадают. Этот факт нами уже был установлен другим способом в примере 19.
в первом и втором испытаниях независимы, поскольку в табл. 5 все три столбца совпадают. Этот факт нами уже был установлен другим способом в примере 19.
Пример:
Число очков 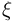 выпавших на верхней грани игральной кости, и число очков
выпавших на верхней грани игральной кости, и число очков 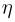 на нижней грани (см. пример 7) — зависимые случайные величины, поскольку вообще ни один из первых шести столбцов табл. 6 не совпадает с последним.
на нижней грани (см. пример 7) — зависимые случайные величины, поскольку вообще ни один из первых шести столбцов табл. 6 не совпадает с последним.
Пример:
В примере 11 показано, что условное распределение времени пребывания 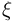 клиента в кассе «Аэрофлота» (см. пример 9) при условии, что в момент прихода он застает очередь
клиента в кассе «Аэрофлота» (см. пример 9) при условии, что в момент прихода он застает очередь 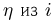 человек, является распределением Эрланга порядка
человек, является распределением Эрланга порядка 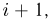 в то время как случайная величина
в то время как случайная величина 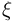 распределена по экспоненциальному закону. Таким образом,
распределена по экспоненциальному закону. Таким образом, 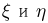 — зависимые случайные величины.
— зависимые случайные величины.
Пример:
Условная плотность распределения случайной величины 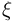 (абсциссы точки падения при равномерном бросании в круг, см. пример 8) при условии
(абсциссы точки падения при равномерном бросании в круг, см. пример 8) при условии 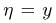 (ординаты точки падения), как следует из примера 15, равномерна, в то время как безусловная плотность распределения случайной величины
(ординаты точки падения), как следует из примера 15, равномерна, в то время как безусловная плотность распределения случайной величины 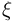 таковой не является. И в этом примере случайные величины
таковой не является. И в этом примере случайные величины 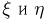 зависимы между собой.
зависимы между собой.
Функции от многомерных случайных величин
Функция от многомерной случайной величины определяется точно так же, как и функция от одномерной. Рассмотрим это понятие на примере двумерной случайной величины. Пусть на вероятностном пространстве 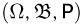 задана двумерная случайная величина
задана двумерная случайная величина 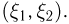 Предположим, что у нас имеется (измеримая) числовая функция
Предположим, что у нас имеется (измеримая) числовая функция 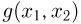 числовых аргументов
числовых аргументов 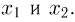 Случайную величину
Случайную величину 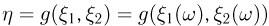 назовем функцией от двумерной случайной величины
назовем функцией от двумерной случайной величины 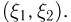
Функция 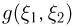 от двумерной дискретной случайной величины
от двумерной дискретной случайной величины 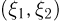 снова является дискретной случайной величиной, принимающей значения
снова является дискретной случайной величиной, принимающей значения 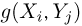 с вероятностью
с вероятностью 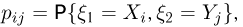 где
где 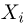 значения случайной величины
значения случайной величины 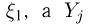 — случайной величины
— случайной величины 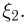 Разумеется, для того чтобы построить ряд распределения случайной величины
Разумеется, для того чтобы построить ряд распределения случайной величины 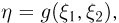 необходимо, во-первых, исключить все те значения
необходимо, во-первых, исключить все те значения 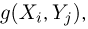 которые принимаются с вероятностью, равной нулю, а, во-вторых, объединить в один столбец все одинаковые значения
которые принимаются с вероятностью, равной нулю, а, во-вторых, объединить в один столбец все одинаковые значения 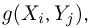 приписав этому столбцу суммарную вероятность.
приписав этому столбцу суммарную вероятность.
Пример:
Рассмотрим случайную величину 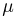 — суммарное число успехов в двух испытаниях Бернулли. Тогда
— суммарное число успехов в двух испытаниях Бернулли. Тогда 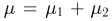 (см. пример 2) и
(см. пример 2) и 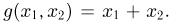 Поскольку случайные величины
Поскольку случайные величины 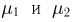 принимают только два значения 0 или 1, то случайная величина
принимают только два значения 0 или 1, то случайная величина 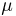 может принимать 4 значения:
может принимать 4 значения: 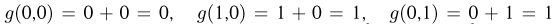 и
и 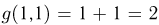 с вероятностями (см. пример 6)
с вероятностями (см. пример 6) 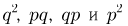 соответственно (табл. 7). Осталось заметить, что двум средним столбцам соответствует
соответственно (табл. 7). Осталось заметить, что двум средним столбцам соответствует

одно и то же значение 1 случайной величины 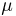 и их необходимо объединить. Окончательно получаем ряд распределения случайной величины
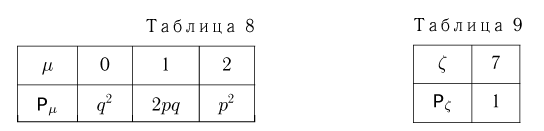
и их необходимо объединить. Окончательно получаем ряд распределения случайной величины 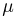 представленный в табл. 8.
представленный в табл. 8.
Естественно, мы получили, что суммарное число успехов 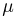 в двух испытаниях имеет распределение Бернулли.
в двух испытаниях имеет распределение Бернулли.
Пример:
Пусть 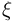 — число очков, выпавших на верхней грани игральной кости, а
— число очков, выпавших на верхней грани игральной кости, а 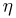 — на нижней (пример 7). Рассмотрим случайную величину
— на нижней (пример 7). Рассмотрим случайную величину 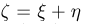 — суммарное число очков, выпавших на верхней и нижней гранях
— суммарное число очков, выпавших на верхней и нижней гранях 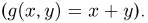 Тогда
Тогда 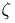 может принять любое целочисленное значение от 2 до 12. Так, например, значению
может принять любое целочисленное значение от 2 до 12. Так, например, значению 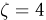 соответствует выпадение 1-3, 2-2 и 3-1 очков на верхней и нижней гранях. Однако нетрудно видеть из табл. 3. что все значения, кроме значения, равного семи, случайная величина
соответствует выпадение 1-3, 2-2 и 3-1 очков на верхней и нижней гранях. Однако нетрудно видеть из табл. 3. что все значения, кроме значения, равного семи, случайная величина 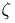 принимает с вероятностью, равной нулю, и их необходимо изъять из ряда распределения, а значение 7 случайная величина
принимает с вероятностью, равной нулю, и их необходимо изъять из ряда распределения, а значение 7 случайная величина 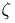 принимает в 6 случаях (1-6, 2-5, 3-4, 4-3, 5-2 и 6-1), причем каждый из этих случаев реализуется с вероятностью 1/6. Поэтому случайная величина
принимает в 6 случаях (1-6, 2-5, 3-4, 4-3, 5-2 и 6-1), причем каждый из этих случаев реализуется с вероятностью 1/6. Поэтому случайная величина 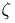 может принимать всего одно значение — 7 с вероятностью, равной единице, т.е. она имеет ряд распределения, представленный в табл. 9.
может принимать всего одно значение — 7 с вероятностью, равной единице, т.е. она имеет ряд распределения, представленный в табл. 9.
Собственно говоря, это было очевидно с самого начала, поскольку игральная кость размечена таким образом, что сумма очков на противоположных гранях равна семи. □
В том случае, когда 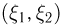 — двумерная непрерывная случайная величина с плотностью распределения
— двумерная непрерывная случайная величина с плотностью распределения 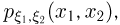 функция распределения случайной величины
функция распределения случайной величины 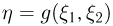 определяется формулой
определяется формулой
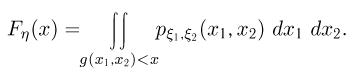
Область интегрирования в последней формуле состоит из всех 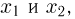 для которых
для которых 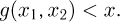
Пример:
Пусть 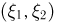 — двумерный случайный вектор, распределенный по стандартному нормальному закону. Найдем распределение случайной величины
— двумерный случайный вектор, распределенный по стандартному нормальному закону. Найдем распределение случайной величины 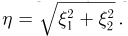 В этом случае
В этом случае 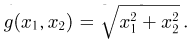 Очевидно, что
Очевидно, что
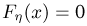 при
при 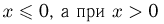
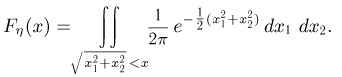
Последний интеграл удобно вычислить, переходя к полярным координатам 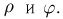 Тогда
Тогда 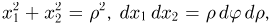 а область интегрирования превращается в круг
а область интегрирования превращается в круг 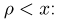
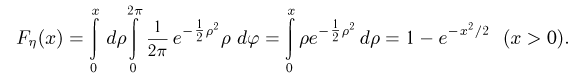
Это уже известное нам распределение Рэлея.
Полученный результат допускает многочисленные физические трактовки. Приведем одну из них. Если движущаяся в плоскости частица имеет случайные составляющие скорости, распределенные по двумерному стандартному нормальному закону, то абсолютная величина скорости распределена по закону Рэлея. Трехмерным аналогом распределения Рэлея (абсолютная величина скорости частицы, движущейся в трехмерном пространстве, причем составляющие скорости распределены по трехмерному стандартному нормальному закону) является распределение Максвелла, представляющее собой распределение случайной величины 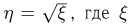 случайная величина, распределенная по закону
случайная величина, распределенная по закону 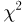 с тремя степенями свободы.
с тремя степенями свободы.
Особо важным для теории вероятностей представляется случай, когда 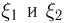 независимые случайные величины, а
независимые случайные величины, а 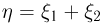 — их сумма. Тогда
— их сумма. Тогда 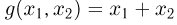 и в силу независимости
и в силу независимости 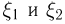
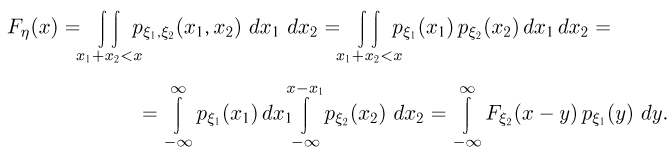
Дифференцируя последнюю формулу под знаком интеграла, получаем выражение для плотности 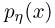 распределения суммы
распределения суммы 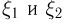
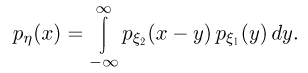
Последнее выражение носит название формулы свертки и должно быть хорошо известно читателю, знакомому с элементами теории преобразований Фурье.
Пример:
Случайные величины 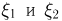 независимы и имеют гамма-распределения с параметрами
независимы и имеют гамма-распределения с параметрами 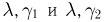 соответственно. Найдем плотность распределения суммы
соответственно. Найдем плотность распределения суммы 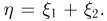 Ясно, что поскольку
Ясно, что поскольку 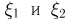 — положительные случайные величины, то случайная величина
— положительные случайные величины, то случайная величина 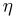 также положительна
также положительна
и 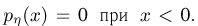 При х > 0, учитывая, что
При х > 0, учитывая, что 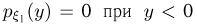 и
и 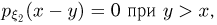 имеем по формуле свертки
имеем по формуле свертки
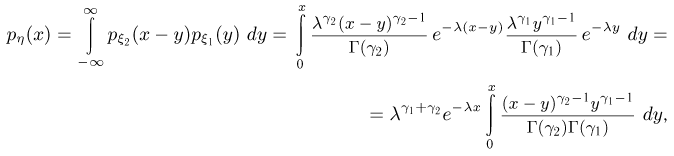
Г(x) введена в гл. 5, параграф 4. Делая замену 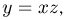 получаем
получаем
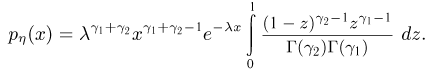
Интеграл, стоящий в последнем выражении, представляет собой так называемый 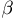 -интеграл, хорошо известный в теории специальных функций. Однако мы для его вычисления воспользуемся просто условием нормировки
-интеграл, хорошо известный в теории специальных функций. Однако мы для его вычисления воспользуемся просто условием нормировки
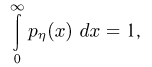
откуда
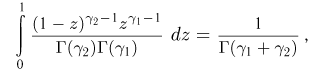
и получаем окончательно, что случайная величина 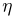 также имеет гамма-распределение с параметрами
также имеет гамма-распределение с параметрами 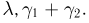 Отсюда, в частности, следует: если независимые случайные величины имеют распределения Эрланга порядков
Отсюда, в частности, следует: если независимые случайные величины имеют распределения Эрланга порядков 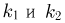 соответственно (с одинаковым параметром
соответственно (с одинаковым параметром 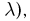 то их сумма также распределена по закону Эрланга порядка
то их сумма также распределена по закону Эрланга порядка 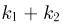 (также с параметром
(также с параметром 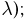 если независимые случайные величины имеют распределения
если независимые случайные величины имеют распределения 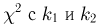 степенями свободы, то их сумма также имеет распределение
степенями свободы, то их сумма также имеет распределение 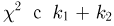 степенями свободы.
степенями свободы.
Пусть теперь с двумерным случайным вектором 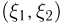 связана не одна, а две (можно рассматривать и большее количество) случайные величины
связана не одна, а две (можно рассматривать и большее количество) случайные величины 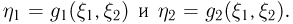 Тогда мы можем определить совместную функцию распределения случайных величин
Тогда мы можем определить совместную функцию распределения случайных величин 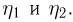 Так, для непрерывного двумерного случайного вектора
Так, для непрерывного двумерного случайного вектора 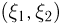
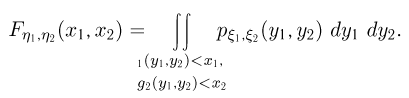
Если 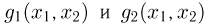 задают взаимно однозначное преобразование плоскости саму в себя (или в некоторую область G), причем обратные преобразования
задают взаимно однозначное преобразование плоскости саму в себя (или в некоторую область G), причем обратные преобразования 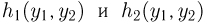 имеют непрерывные частные производные по
имеют непрерывные частные производные по 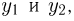 то плотности распределения случайных векторов
то плотности распределения случайных векторов 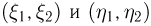 связаны между собой соотношениями
связаны между собой соотношениями
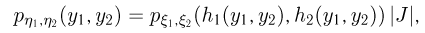
где
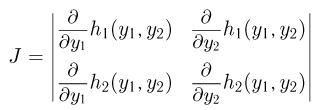
— якобиан преобразования 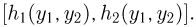 Это свойство вытекает из того факта, что
Это свойство вытекает из того факта, что 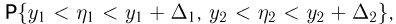 с одной стороны, приближенно равна
с одной стороны, приближенно равна 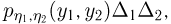 а с другой — приближенно равна
а с другой — приближенно равна 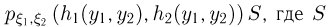 — площадь прообраза прямоугольника со сторонами
— площадь прообраза прямоугольника со сторонами 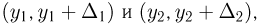 которая, как известно из курса математического анализа, в свою очередь приближенно равна
которая, как известно из курса математического анализа, в свою очередь приближенно равна 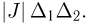
В частности, пусть 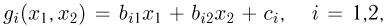 т.е. преобразование линейное, причем матрица
т.е. преобразование линейное, причем матрица 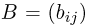 невырожденная. Тогда
невырожденная. Тогда
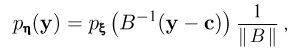
где 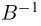 — обратная к B матрица, а
— обратная к B матрица, а 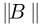 — модуль определителя матрицы B.
— модуль определителя матрицы B.
Пример:
Пусть 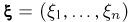 — (невырожденный) n-мерный случайный вектор, распределенный по нормальному закону с матрицей ковариаций
— (невырожденный) n-мерный случайный вектор, распределенный по нормальному закону с матрицей ковариаций 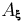 и вектором средних
и вектором средних 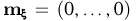 (этого всегда можно добиться, вводя случайный вектор
(этого всегда можно добиться, вводя случайный вектор 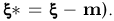 Введем новый случайный вектор
Введем новый случайный вектор 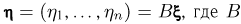 — некоторая невырожденная квадратная матрица порядка n (в этом случае случайные величины
— некоторая невырожденная квадратная матрица порядка n (в этом случае случайные величины 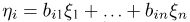 задаются линейными функциями
задаются линейными функциями 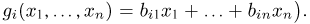 Тогда случайный вектор
Тогда случайный вектор 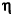 имеет плотность распределения
имеет плотность распределения
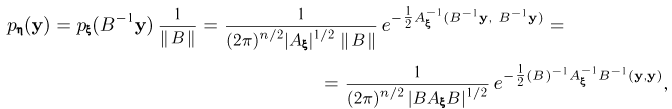
т. е. также распределен по нормальному закону с нулевым вектором средних 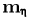 и матрицей ковариаций
и матрицей ковариаций  — матрица линейного преобразования
— матрица линейного преобразования 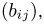 а В — транспонированная к В матрица. Из курса линейной алгебры известно, что всегда можно подобрать невырожденное преобразование В таким образом, чтобы матрица
а В — транспонированная к В матрица. Из курса линейной алгебры известно, что всегда можно подобрать невырожденное преобразование В таким образом, чтобы матрица 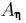 была единичной, т.е. вектор
была единичной, т.е. вектор 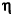 имел бы стандартное нормальное распределение. Таким образом, мы нашли второй способ (ср. с результатом параграфа 4) задания n-мерного нормального случайного вектора
имел бы стандартное нормальное распределение. Таким образом, мы нашли второй способ (ср. с результатом параграфа 4) задания n-мерного нормального случайного вектора 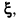 имеющего произвольный вектор средних m и матрицу ковариаций А, с помощью n-мерного стандартного нормального вектора
имеющего произвольный вектор средних m и матрицу ковариаций А, с помощью n-мерного стандартного нормального вектора 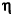
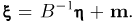 Отметим также, что если матрица
Отметим также, что если матрица 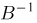 вырождена, то мы получаем так называемый вырожденный нормальный закон.
вырождена, то мы получаем так называемый вырожденный нормальный закон.
В дальнейшем нам понадобится следующее почти очевидное свойство функций от случайных величин. Пусть случайные величины 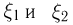 независимы, а функции
независимы, а функции 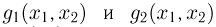 таковы, что
таковы, что 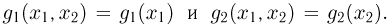 Тогда случайные величины
Тогда случайные величины 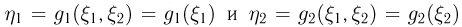 также независимы.
также независимы.
Действительно (предполагая, например, что 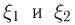 — непрерывные случайные величины), имеем
— непрерывные случайные величины), имеем
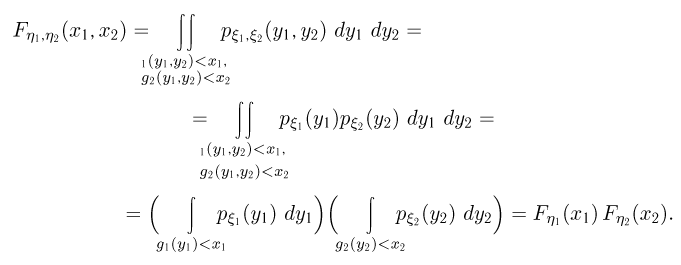
Как и все остальные свойства, рассмотренные в настоящем параграфе, это свойство без всяких комментариев переносится на случай произвольной размерности п случайного вектора 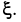
Пример:
Пусть 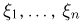 — независимые случайные величины, распределенные по стандартному нормальному закону. Тогда случайные величины
— независимые случайные величины, распределенные по стандартному нормальному закону. Тогда случайные величины 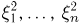 также независимы и распределены по закону
также независимы и распределены по закону 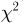 с одной степенью свободы (см. пример 12 в гл.5) и, как следует из примера 28, случайная величина
с одной степенью свободы (см. пример 12 в гл.5) и, как следует из примера 28, случайная величина 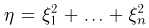 имеет распределение
имеет распределение 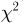 с n степенями свободы. Извлекая квадратный корень из получаем при
с n степенями свободы. Извлекая квадратный корень из получаем при 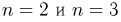 распределения Рэлея и Максвелла (см. пример 27).
распределения Рэлея и Максвелла (см. пример 27).
Решение заданий и задач по предметам:
- Теория вероятностей
- Математическая статистика
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Функции случайных величин
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Нормальный закон распределения
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Схема Бернулли
- Предельные теоремы теории вероятностей
- Оценки неизвестных параметров
- Генеральная совокупность

