Как найти совместную плотность случайных величин

Закон распределения вероятностей двумерной случайной величины

Законом
распределениядискретной двумерной
случайной величиныназывают перечень возможных значений
этой величины, т.е. пар чисел,
гдеи–
возможные значения величини,
соответственно, и вероятностейих совместного появления.

Двумерная дискретная
случайная величина
задается в видетаблицы распределения
вида:

где первая строка
таблицы указывает возможные значения
составляющей
,
а первый столбец – все возможные значения
составляющей.

Так как события
(;)
образуют полную группу, то.

Зная закон
распределения двумерной дискретной
случайной величины, можно найти законы
распределения каждой из ее составляющих.
Так, например, вероятность того, что
примет значение,
равна.

Совместная
функция распределения двух случайных
величин

Функция
,
определяющая для каждой пары чиселвероятность того, чтопримет значение меньшее,
и при этомпримет значение меньшее,
называетсясовместной функцией
распределениядвух случайных
величин=.

Геометрически это
равенство можно истолковать так:
– это вероятность того, что случайная
точка ()
попадет в бесконечный квадрант с вершиной
(),
расположенный левее и ниже этой вершины.

Свойства совместной функции распределения двух случайных величин

1. Значения
   совместной функции распределения
   удовлетворяют неравенству:

.

1. –неубывающая
   функция по каждому аргументу, т.е.

,
если
;

,
если
.

Совместная функция
распределения имеет следующие предельные
значения:

;;

;.

1. При
   илисовместная функция распределения
   системы становится функцией распределения
   одной из составляющих:;

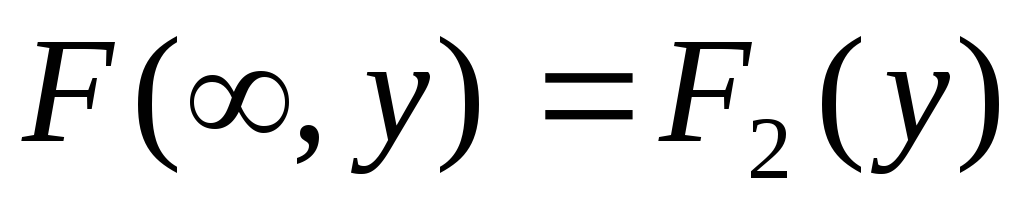
Плотность совместного распределения вероятностей непрерывной двумерной случайной величины

Непрерывную
двумерную случайную величину можно
задать с помощью плотности распределения.
Плотность совместного распределения
вероятностейдвумерной непрерывной случайной величины
(,)
– это вторая смешанная частная производная
от функции распределения:

.

Зная плотность
совместного распределения
,
можно найти совместную функцию
распределенияпо формуле

следующей из
определения плотности распределения
двумерной непрерывной случайной величины
(,).

Смысл плотности
совместного распределения вероятностей:
вероятность попадания случайной точки
в прямоугольник (с вершиной в точке
и сторонамииравна произведению,
когда стороны этого прямоугольника
стремятся к нулю.

В связи с этим,
вероятность попадания случайной точки
в произвольную область D
равна двойному интегралу по областиDот функции:

Свойства двумерной плотности вероятности

1. Двумерная плотность
   вероятности неотрицательна:
   .

2. Двойной несобственный
   интеграл с бесконечными пределами от
   двумерной плотности вероятности равен
   единице:.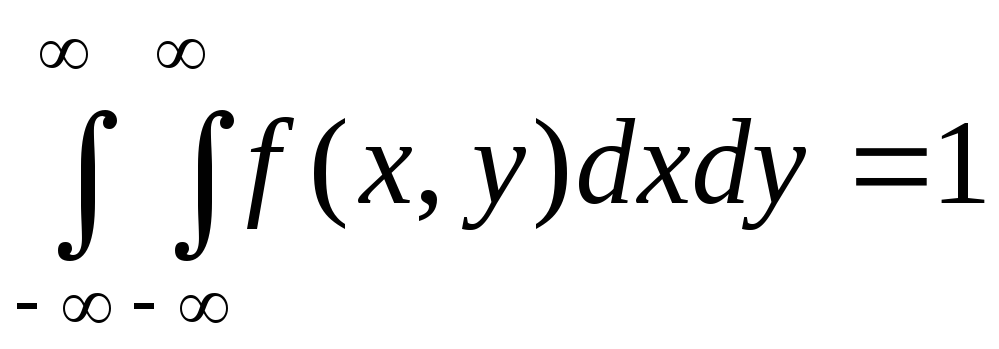

Независимые случайные величины

Две случайные
величины называются независимыми,
если закон распределения одной из них
не зависит от того, какие возможные
значения приняла другая величина.

Теорема.
Для того чтобы случайные величиныибыли
независимыми, необходимо и достаточно,
чтобы функция распределения системы
(,)
была равна произведению функций
распределения составляющих:.

Следствие.Для того чтобы случайные величиныибыли
независимыми, необходимо и достаточно,
чтобы плотность совместного распределения
системы (,)
была равна произведению плотностей
распределения составляющих:.

Двумерная непрерывная случайная величина

Ранее мы разобрали примеры решений задач для одномерной непрерывной случайной величины. Перейдем к более сложному случаю – двумерной непрерывной случайной величине $(X,Y)$ (или двумерному вектору). Кратко выпишем основы теории.

Система непрерывных случайных величин: теория

Двумерная непрерывная СВ задается своей функцией распределения $F(x,y)=P(Xlt x, Ylt y)$, свойства которой аналогичны свойствам одномерной ФР. Эта функция должна быть непрерывна, дифференцируема и иметь вторую смешанную производную, которая будет как раз плотностью распределения вероятностей системы непрерывных случайных величин:

$$
f(x,y)= frac{partial ^2}{partial x partial y} F(x,y)
$$

Зная плотность совместного распределения, можно найти одномерные плотности для $X$ и $Y$:

$$
f(x)= int_{-infty}^{infty} f(x,y) dy, quad f(y)= int_{-infty}^{infty} f(x,y) dx.
$$

Вероятность попадания случайного вектора в прямоугольную область можно вычислить как двойной интеграл от плотности (по этой области) или через функцию распределения:

$$P(x_1 le X le x_2, y_1 le Y le y_2) = F(x_2, y_2)-F(x_1, y_2)-F(x_2, y_1)+F(x_1, y_1).$$

Как и для случая дискретных двумерных СВ вводится понятие условного закона распределения, плотности которых можно найти так:

$$
f(x|y)=f_y(x)= frac{f(x,y)}{f(y)}, quad f(y|x)=f_x(y)= frac{f(x,y)}{f(x)} $$

Если для всех значений $(x,y)$ выполняется равенство

$$f(x,y) =f(x)cdot f(y),$$

то случайные величины $X, Y$ называются независимыми (их условные плотности распределения совпадают с безусловными). Для независимых случайных величин выполняется аналогичное равенство для функций распределений:

$$F(x,y) =F(x)cdot F(y).$$

Для случайных величин $X,Y$, входящих в состав случайного вектора, можно вычислить ковариацию и коэффициент корреляции по формулам:

$$
cov (X,Y)=M(XY)-M(X)M(Y)= int_{-infty}^{infty}int_{-infty}^{infty} (x-M(X))(y-M(Y)) f(x,y) dxdy, \
r_{XY} = frac{cov(X,Y)}{sqrt{D(X)D(Y)}}.
$$

В этом разделе мы приведем примеры задач с полным решением, где используются непрерывные двумерные случайные величины (системы случайных величин).

Примеры решений

Задача 1. Дана плотность распределения вероятностей системы
$$
f(x)=
left{
begin{array}{l}
C, mbox{ в треугольнике} O(0,0), A(4,0), B(4,1)\
0, mbox{ в остальных точках} \
end{array}
right.
$$
Найти:
$C, rho_1(x), rho_2(y), m_x, m_y, D_x, D_y, cov(X,Y), r_{xy}, F(2,10), M[X|Y=1/2]$.

Задача 2. Дана плотность распределения $f(x,y)$ системы $X,Y$ двух непрерывных случайных величин в треугольнике АВС.
1.1. Найдите константу с.
1.2. Найдите $f_X(x), f_Y(y)$ – плотности распределения с.в. Х и с.в. Y.
Выясните, зависимы или нет с.в. Х и Y. Сформулируйте критерий независимости системы непрерывных случайных величин.
1.3. Найдите математическое ожидание и дисперсию с.в. Х и с.в. Y. Поясните смысл найденных характеристик.
1.4. Найдите коэффициент корреляции с.в. Х и Y. Являются ли случайные величины коррелированными? Сформулируйте свойства коэффициента корреляции.
1.5. Запишите уравнение регрессии с.в. Y на Х и постройте линию регрессии в треугольнике АВС.
1.6. Запишите уравнение линейной среднеквадратичной регрессии с.в. Y на Х и постройте эту прямую в треугольнике АВС. $$ f(x,y)=csqrt{xy}, quad A(0;0), B(-1;-1), C(-1;0) $$

Задача 3. Интегральная функция распределения случайного вектора (X,Y):
$$
F(x)=
left{
begin{array}{l}
0, mbox{ при } x le 0 mbox{ или } yle 0\
(1-e^{-2x})(1-e^{-3y}), mbox{ при } x gt 0 mbox{ и } ygt 0\
end{array}
right.
$$
Найти центр рассеивания случайного вектора.

Задача 4. Плотность совместного распределения непрерывной двумерной случайной величины (Х, У)
$$f(x,y)=C e^{-x^2-2xy-4y^2}$$
Найти:
а) постоянный множитель С;
б) плотности распределения составляющих;
в) условные плотности распределения составляющих.

Задача 5. Задана двумерная плотность вероятности системы двух случайных величин: $f(x,y)=1/2 sin(x+y)$ в квадрате $0 le x le pi/2$, $0 le y le pi/2$, вне квадрата $f(x,y)=0$. Найти функцию распределения системы (X,Y).

Задача 6. Определить плотность вероятности, математические ожидания и корреляционную матрицу системы случайных величин $(X,Y)$, заданных в интервалах $0 le x le pi/2$, $0 le y le pi/2$, если функция распределения системы $F(x,y)=sin x sin y$.

Задача 7. Плотность вероятности системы случайных величин равна
$$f(x,y) = c(R-sqrt{x^2+y^2}), quad x^2+y^2 lt R^2.$$
Определить:
А) постоянную $c$;
Б) вероятность попадания в круг радиуса $alt R$, если центры обоих кругов совпадают с началом координат.

Задача 8. Совместная плотность вероятности системы двух случайных величин X и Y
$$f(x,y)=frac{c}{36+9x^2+4y^2+x^2y^2}.$$
Найти величину $с$; определить законы распределения $F_1(x)$, $F_2(y)$, $f_1(x)$, $f_2(y)$, $f(x/y)$; построить графики $F_1(x)$, $F_2(y)$; вычислить моменты $m_x$, $m_y$, $D_x$, $D_y$, $K_{xy}$.

Решебник по теории вероятности онлайн

Больше 11000 решенных и оформленных задач по теории вероятности:

Примеры решения задач

• Краткая теория
• Примеры решения задач