Содержание:
Формула полной вероятности:
Пусть событие А может произойти в результате появления одного и только одного события 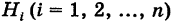
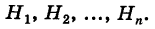
События этой группы обычно называются гипотезами.
Теорема: Вероятность события А равна сумме парных произведений вероятностей всех гипотез, образующих полную группу, на соответствующие условные вероятности данного события А, т. е.
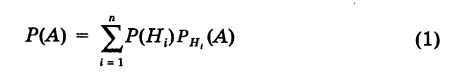
(формула полной вероятности), причем здесь

Доказательство. Так как
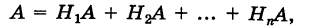
причем, ввиду несовместности событий 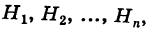 события
события 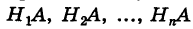 также несовместны, то на основании теорем сложения и умножения вероятностей имеем
также несовместны, то на основании теорем сложения и умножения вероятностей имеем
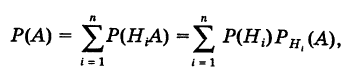
что и требовалось доказать.
Пример:
В магазин для продажи поступает продукция трех фабрик, относительные доли которых есть: I — 50%, II — 30%, III — 20%. Для продукции фабрик брак соответственно составляет: I — 2%, II — 3%, III — 5%. Какова вероятность того, что изделие этой продукции, случайно приобретенное в магазине, окажется доброкачественным (событие А)?
Решение:
Здесь возможны следующие три гипотезы: 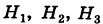 — приобретенная вещь выработана соответственно на I, II и III фабриках; очевидно, система этих гипотез полная, причем их вероятности
— приобретенная вещь выработана соответственно на I, II и III фабриках; очевидно, система этих гипотез полная, причем их вероятности
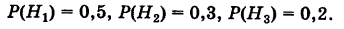
Соответствующие условные вероятности события А равны
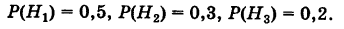
По формуле полной вероятности имеем
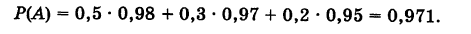
Формула Бейеса:
Пример:
Имеется полная группа несовместных гипотез
вероятности которых 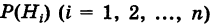 известны до опыта (вероятности априори). Производится опыт (испытание), в результате которого зарегистрировано появление события А, причем известно, что этому событию наши гипотезы приписывали определенные вероятности
известны до опыта (вероятности априори). Производится опыт (испытание), в результате которого зарегистрировано появление события А, причем известно, что этому событию наши гипотезы приписывали определенные вероятности 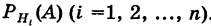 . Спрашивается, каковы будут вероятности этих гипотез после опыта (вероятности апостериори).
. Спрашивается, каковы будут вероятности этих гипотез после опыта (вероятности апостериори).
Например, очевидно, следует отбросить гипотезы, отрицающие появление события А. Вообще, проблема состоит в том, что, имея новую информацию, мы должны переоценить вероятности наших гипотез.
Иными словами, нам нужно определить условные вероятности
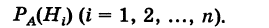
На основании теоремы умножения вероятностей имеем
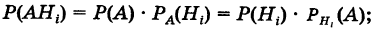
отсюда
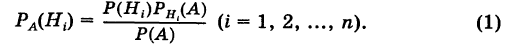
Для нахождения вероятности Р(А) можно использовать формулу полной вероятности
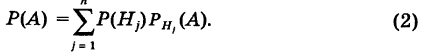
Отсюда имеем формулу вероятностей гипотез после опыта (<формулу Бейеса)
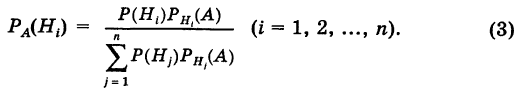
Пример:
Вероятность поражения самолета при одиночном выстреле для 1-го ракетного расчета (событие А) равна 0,2, а для 2-го (событие В) — 0,1. Каждое из орудий производит по одному выстрелу, причем зарегистрировано одно попадание в самолет (событие С). Какова вероятность, что удачный выстрел принадлежит первому расчету?
Решение:
До опыта возможны четыре гипотезы: 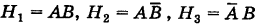
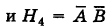 ; эти гипотезы образуют полную группу событий.
; эти гипотезы образуют полную группу событий.
Вероятности их, при независимом действии расчетов, соответственно равны
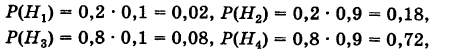
причем 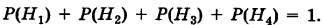
Условные вероятности для наблюдаемого события С при данных гипотезах будут
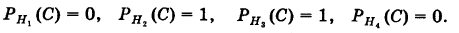
Следовательно, гипотезы 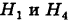 отпадают, а вероятности гипотез
отпадают, а вероятности гипотез 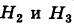 вычисляются по формуле Бейеса:
вычисляются по формуле Бейеса:
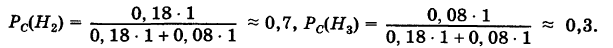
Таким образом, с вероятностью приблизительно 0,7 можно утверждать, что удачный выстрел принадлежит 1-му расчету,
Формула полной вероятности
Пусть событие А еще не произошло, но вскоре должно произойти. Событие А может протекать в различных условиях, относительно характера которых сделано  гипотез
гипотез 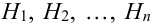 , образующих полную группу несовместных событий. Вероятности гипотез известны. Тогда вероятность события А равна сумме произведений вероятности каждой гипотезы на вероятность события при этой гипотезе:
, образующих полную группу несовместных событий. Вероятности гипотез известны. Тогда вероятность события А равна сумме произведений вероятности каждой гипотезы на вероятность события при этой гипотезе:
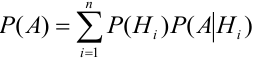 – формула полной вероятности.
– формула полной вероятности.
Доказательство.
По условию теоремы гипотезы 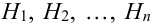 образуют полную группу несовместных событий, следовательно, событие А может произойти с одной и только с одной гипотезой:
образуют полную группу несовместных событий, следовательно, событие А может произойти с одной и только с одной гипотезой:
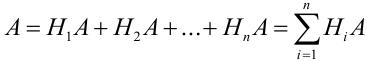 .
.
Т.к. гипотезы несовместны, то и комбинации 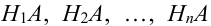 – несовместны. Применим теорему 1:
– несовместны. Применим теорему 1:
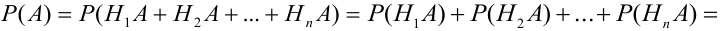
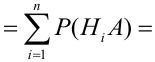 (события А и
(события А и  – зависимы, т.е. надо применить теорему 3) =
– зависимы, т.е. надо применить теорему 3) = 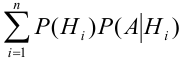 . (что и треб, доказать)
. (что и треб, доказать)
Пример:
Имеется пять урн:
2 урны состава 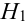 – по 2 белых шара и 1 черному,
– по 2 белых шара и 1 черному,
1 урна состава 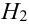 – 10 черных шаров,
– 10 черных шаров,
2 урны состава 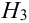 — по 3 белых и 1 черному шару.
— по 3 белых и 1 черному шару.
Наудачу выбирается урна, и из нее наудачу выбирается шар. Чему равна вероятность события А = {будет вынут белый шар}?
Решение.
Событие А еще не произошло. Шар может быть вынут из урн разных составов, следовательно, в алгебре событий событие А запишется в виде: 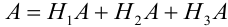 . Тогда по формуле полной вероятности:
. Тогда по формуле полной вероятности:
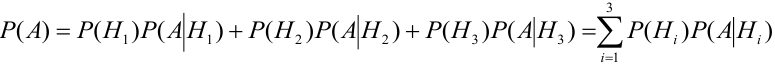 (*).
(*).
Найдем отдельно вероятности событий:
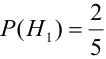 (две урны состава
(две урны состава 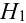 из пяти),
из пяти), 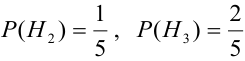 ,
,
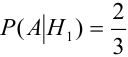 (в каждой урне состава
(в каждой урне состава 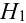 2 белых шара из трех),
2 белых шара из трех),
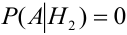 ( в урне состава
( в урне состава  белых шаров нет),
белых шаров нет),
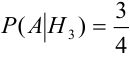 .
.
Подставим найденные вероятности в формулу (*): 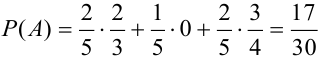 .
.
Формула полной вероятности и решение задач
Пример:
В двух одинаковых коробках имеется по 100 резисторов. В 1-й – 60 резисторов по 100 КОм, во 2-й 30 – резисторов по 100 КОм. Определить вероятность того, что взятый наугад из какой-либо коробки резистор будет 100 КОм.
Решение:
Пусть событие 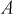 – достали резистор 100 КОм, гипотезы:
– достали резистор 100 КОм, гипотезы: 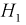 – выбрали 1-ю коробку,
– выбрали 1-ю коробку, 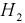 – выбрали 2-ю коробку. Так как коробки выбирали произвольно, то
– выбрали 2-ю коробку. Так как коробки выбирали произвольно, то 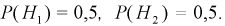 Условная вероятность того, что взяли резистор 100 КОм, при условии, что выбрана 1-я коробка –
Условная вероятность того, что взяли резистор 100 КОм, при условии, что выбрана 1-я коробка – 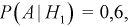 соответственно
соответственно 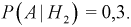 Тогда, применяя формулу (1.14) для
Тогда, применяя формулу (1.14) для 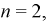 получаем
получаем 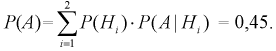
Пример №1
В первой коробке находится 20 деталей, из них 18 стандартных, во второй коробке – 10 деталей, из них 9 стандартных. Из второй коробки наудачу взята одна деталь и переложена в первую коробку.
Какова вероятность того, что деталь, наудачу извлечённая после этого из первой коробки, окажется стандартной?
Решение. Обозначим события:
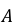 – из первой коробки извлечена стандартная деталь.
– из первой коробки извлечена стандартная деталь.
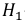 − из второй коробки в первую переложена стандартная деталь.
− из второй коробки в первую переложена стандартная деталь.
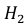 − из второй коробки в первую переложена нестандартная деталь.
− из второй коробки в первую переложена нестандартная деталь.
Событие А может наступить при условии наступления одного из событий 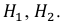 Эти события несовместны и образуют полную группу, т. е. являются гипотезами в формуле полной вероятности. Вероятность того, что из второй коробки извлечена стандартная деталь,
Эти события несовместны и образуют полную группу, т. е. являются гипотезами в формуле полной вероятности. Вероятность того, что из второй коробки извлечена стандартная деталь, 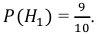
Вероятность того, что из второй коробки извлечена нестандартная деталь 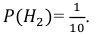
Условная вероятность того, что из первой коробки извлечена стандартная деталь, при условии, что из второй коробки в первую была переложена стандартная деталь, 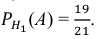
Условная вероятность того, что из первой коробки извлечена стандартная деталь, при условии, что из второй коробки в первую была переложена нестандартная деталь, 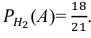
Искомая вероятность того, что из первой коробки будет извлечена стандартная деталь, по формуле полной вероятности равна:
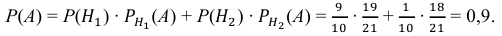 .
.
Ответ: 0,9.
Пример №2
Два станка производят одинаковые детали, которые поступают на общий конвейер. Производительность первого станка в два раза больше производительности второго станка. Первый производит 60 % деталей высшего сорта, а второй – 84 %. Наудачу взятая с конвейера деталь оказалась высшего сорта. Какова вероятность того, что эта деталь произведена на первом станке?
Решение. Обозначим события:
А – деталь, взятая с конвейера, оказалась высшего сорта.
Это событие наступит с одним из двух событий (гипотез):
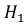 – эта деталь произведена на первом станке,
– эта деталь произведена на первом станке,
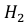 – эта деталь произведена на втором станке.
– эта деталь произведена на втором станке.
Поскольку производительность первого станка в два раза больше производительности второго станка, вероятности гипотез равны: 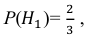
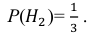
Условные вероятности события А даны: 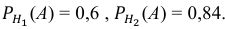
По формуле полной вероятности находим:
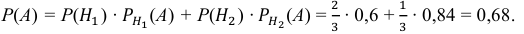
По формуле Байеса найдём условную вероятность того, что взятая наудачу деталь высшего сорта произведена на первом станке:
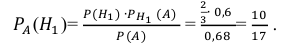
Ответ: 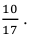
Пример №3
В ящике 20 белых и 10 чёрных шаров. Поочерёдно извлекают 4 шара, причём каждый извлечённый шар возвращают в ящик перед извлечением следующего. Какова вероятность того, что среди четырёх извлечённых шаров окажется два белых?
Решение. Вероятность извлечения белого шара одна и та же во всех четырёх испытаниях, так как каждый извлечённый шар возвращается в ящик: 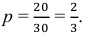
Тогда вероятность извлечения чёрного шара во всех четырёх испытаниях равна 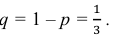
Используя формулу Бернулли, находим вероятность того, что из четырёх извлечённых шаров два шара будут белыми:
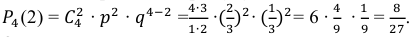
Ответ: 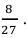
Пример №4
Вероятность поражения мишени при одном выстреле равна 0,8. Какова вероятность того, что при 100 выстрелах мишень будет поражена 75 раз?
Решение. По условию задачи 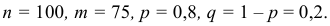
Так как n – достаточно большое число, воспользуемся локальной формулой Лапласа:
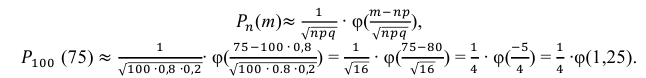
В таблице значений функции 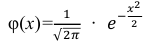 находим φ(1,25) =
находим φ(1,25) =
0,1826.
Следовательно, 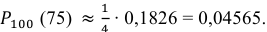
Ответ: 0,04565.
Пример №5
Вероятность поражения мишени при одном выстреле равна 0,8. Какова вероятность того, что при 100 выстрелах мишень будет поражена
а) не менее 75 раз и не более 90 раз?
б) не менее 75 раз?
в) не более 74 раз?
Решение.
Воспользуемся интегральной формулой Лапласа:
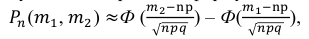
где 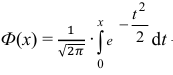 – функция Лапласа.
– функция Лапласа.
а) По условию задачи 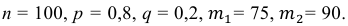 Тогда, воспользовавшись таблицей значений функции Ф(х), получаем:
Тогда, воспользовавшись таблицей значений функции Ф(х), получаем:
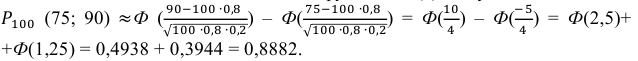
б) Требование того, чтобы событие наступило не менее 75 раз, означает следующее: число появлений события может быть равно либо 75, либо 76, … , либо 100.
Тогда следует принять 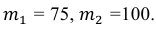 Воспользовавшись таблицей значений функции Лапласа Ф(х), получаем:
Воспользовавшись таблицей значений функции Лапласа Ф(х), получаем: 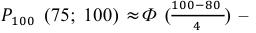
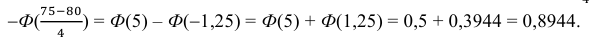
в) Событие “мишень поражена не более 74 раз” и событие “мишень поражена не менее 75 раз” являются противоположными. Поэтому сумма их вероятностей равна 1. Следовательно, искомая вероятность 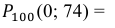
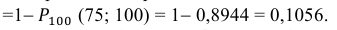
Ответ: а) 0,8882; б) 0,8944; в) 0,1056.
Пример №6
Учебник издан тиражом 100000 экземпляров.
Вероятность того, что один учебник сброшюрован неправильно, равна 0,0001. Какова вероятность того, что тираж содержит 5 бракованных книг?
Решение. По условию задачи n = 100000, p = 0,0001.
События “из n книг ровно m книг сброшюрованы неправильно”, где m = 0,1,2, … ,100000, являются независимыми. Так как число n велико, а вероятность p мала, вероятность 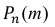 можно вычислить по формуле Пуассона:
можно вычислить по формуле Пуассона: 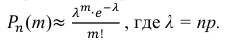
В рассматриваемой задаче 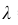 = 100000 ∙ 0,0001 = 10. Поэтому искомая вероятность
= 100000 ∙ 0,0001 = 10. Поэтому искомая вероятность 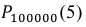 определяется равенством:
определяется равенством:
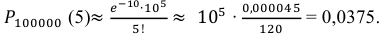
Ответ: 0,0375.
Формула Байеса (Бейеса)
Пусть событие А произошло, причем А могло протекать в различных условиях, относительно характера которых было сделано 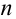 гипотез
гипотез 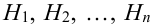 , образующих полную группу несовместных событий. Вероятности гипотез известны. Требуется узнать, как изменятся вероятности гипотез в связи с появлением события А. Т.е. надо найти условную вероятность
, образующих полную группу несовместных событий. Вероятности гипотез известны. Требуется узнать, как изменятся вероятности гипотез в связи с появлением события А. Т.е. надо найти условную вероятность 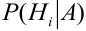 .
.
Решение:
По условию теоремы гипотезы 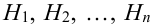 , образуют полную группу несовместных событий, следовательно событие .А произошло с одной и только с одной гипотезой:
, образуют полную группу несовместных событий, следовательно событие .А произошло с одной и только с одной гипотезой:
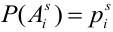 , причем события А и
, причем события А и 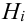 – зависимы, поэтому найдем вероятность произведения
– зависимы, поэтому найдем вероятность произведения 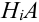 , воспользовавшись теоремой 3:
, воспользовавшись теоремой 3:
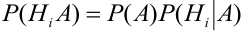 — (или, что то же самое) =
— (или, что то же самое) = 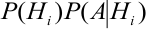 =
= 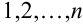 , отсюда
, отсюда
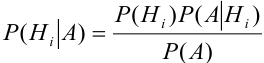 .
.
Выразим Р(А) с помощью формулы полной вероятности:
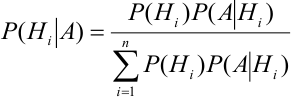 – формула Байеса.
– формула Байеса.
Пример №7
Имеется пять урн:
2 урны состава 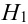 – по 2 белых шара и 3 черных шара,
– по 2 белых шара и 3 черных шара,
2 урны состава 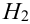 – по 1 белому и 4 черных шара,
– по 1 белому и 4 черных шара,
1 урна состава 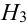 – 4 белых и 1 черный шар.
– 4 белых и 1 черный шар.
Из одной наудачу выбранной урны взят шар. Он оказался белым (событие А). Чему равна после опыта вероятность события, что шар вынут из урны третьего состава.
Решение.
Событие А произошло. Шар мог быть вынут из урн разных составов, следовательно, в алгебре событий событие А запишется в виде: 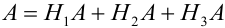 .
.
Найдем вероятности событий:
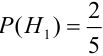 (две урны состава
(две урны состава 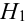 из пяти),
из пяти), 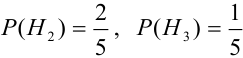 ,
,
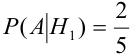 (в каждой урне состава
(в каждой урне состава 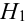 2 белых шара из пяти),
2 белых шара из пяти),
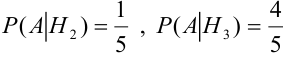 .
.
По формуле Байеса найдем условную вероятность  :
:
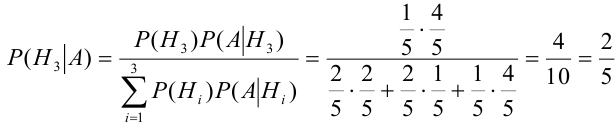 .
.
Пример №8
Вероятность дождливого дня в городе равна 0,2. Известно, что вероятность выиграть футбольный матч команде этого города в дождливый день равна 0,4, а в сухой – 0,7. Известно, что команда выиграла матч. Определить, что в этот день шел дождь.
Решение:
Событие  состоит в том, что команда выиграла матч. Гипотезы:
состоит в том, что команда выиграла матч. Гипотезы:  – шел дождь,
– шел дождь,  – дождя не было.
– дождя не было.
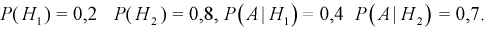
Чтобы ответить на вопрос, пересмотрим вероятность 1-й гипотезы с учетом результата опыта-появилось событие 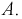 Определим апостериорную вероятность гипотезы
Определим апостериорную вероятность гипотезы 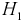 с учетом результата опыта (появилось событие
с учетом результата опыта (появилось событие 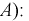
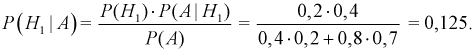
Из полученного результата видим, что с учетом события 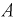 вероятность дождя в городе уменьшилась
вероятность дождя в городе уменьшилась 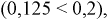 значит скорее всего дождя не было.
значит скорее всего дождя не было.
Независимые испытания
Под испытанием станем понимать осуществление определенного комплекса условий, в результате которого может произойти то или иное элементарное событие пространства 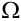 элементарных событий.
элементарных событий.
Определение 26. Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события А.
В каждом испытании вероятность появления события А одинакова.
Ряд задач связан с экспериментом, в котором проводятся последовательные независимые испытания, и наблюдается результат совместного осуществления тех или иных исходов каждого испытания.
Рассматривается последовательность п независимых испытаний, под которой будем понимать дискретное новое пространство 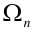 элементарных исходов, состоящее из точек
элементарных исходов, состоящее из точек 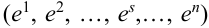 , где
, где 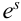 – произвольная точка пространства, отвечающая испытанию с номером s. В каждом испытании может произойти один из
– произвольная точка пространства, отвечающая испытанию с номером s. В каждом испытании может произойти один из  исходов:
исходов: 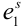 или
или 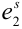 или ….
или …. 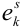 .
.
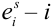 -тый исход в s-том испытании, где
-тый исход в s-том испытании, где  = 1, 2,…,
= 1, 2,…,  ; s = 1,2,…,
; s = 1,2,…,  .
.
Пример №9
Пусть испытание состоит в подбрасывании игральной кости. Пространство элементарных событий 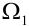 состоит из шести точек:
состоит из шести точек: 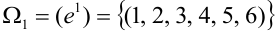 , т.е. шесть исходов. Если провести три испытания, то пространство
, т.е. шесть исходов. Если провести три испытания, то пространство 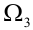 состоит из 216 точек.
состоит из 216 точек.
Обычно исходы обозначали большими заглавными буквами. Переобозначим! Пусть происходит  независимых испытаний: 1, 2,…, s,…,
независимых испытаний: 1, 2,…, s,…,  . В каждом испытании может произойти к исходов: 1-ый, 2, 3,…,
. В каждом испытании может произойти к исходов: 1-ый, 2, 3,…,  ,…,
,…,  -ый.
-ый.
Обозначим событие 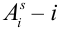 -тый исход в s-том испытании, где
-тый исход в s-том испытании, где  = 1,2,…,
= 1,2,…, ; s = 1,2,…,
; s = 1,2,…, . Эти к исходов – несовместные случайные события. Тогда для s-ого испытания можем записать:
. Эти к исходов – несовместные случайные события. Тогда для s-ого испытания можем записать:
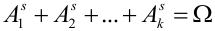 , причем
, причем 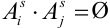 .
.
Обозначим вероятность  -ого исхода при s-том испытании через
-ого исхода при s-том испытании через 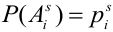 .
.
Пусть при первом испытании произошло событие под номером 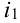 , при 2-ом – событие под номером
, при 2-ом – событие под номером 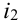 , …, при
, …, при  -ом – событие под номером
-ом – событие под номером 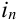 . Результат сразу
. Результат сразу  испытаний – событие, которое обозначим через произведение событий
испытаний – событие, которое обозначим через произведение событий 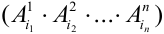 – цепочка результатов отдельных испытаний.
– цепочка результатов отдельных испытаний.
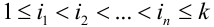 . Данное событие – цепочка состоит из всех точек
. Данное событие – цепочка состоит из всех точек 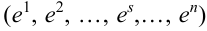 пространства
пространства 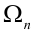 , для которых
, для которых 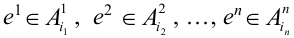 .
.
Испытания – независимые, следовательно, по теореме 4, имеет место равенство:
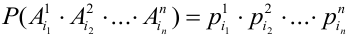
В случае, когда вероятности событий 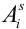 не зависят от номера испытаний,
не зависят от номера испытаний, 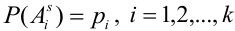 .
.
В силу несовместности и единственной возможности исходов, очевидно, что 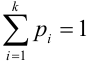 , так как
, так как 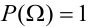 .
.
Теорема. Если данные 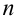 испытаний независимы, то любые
испытаний независимы, то любые 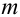 из них также независимы.
из них также независимы.
Теорема. Для того, чтобы 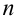 испытаний были независимы, необходимо и достаточно выполнения условия:
испытаний были независимы, необходимо и достаточно выполнения условия:
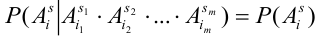 ,
,
для любой группы чисел 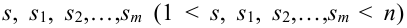 и
и 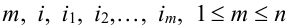 ,
, 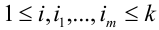 .
.
Формулы Бернулли
Пусть проводятся последовательные независимые испытания, и наблюдается результат совместного осуществления тех или иных исходов каждого испытания.
Схема независимых испытаний является математической моделью серии испытаний, повторяющихся при неизменных условиях. Такая схема называется полиномиальной.
Простейшим классом повторяющихся независимых испытаний является последовательность независимых испытаний с двумя исходами (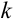 = 2): «успех», «неудача» и с неизменными вероятностями успеха – р и неудачи – q, где q = 1 – р, в каждом испытании. Такая схема называется биномиальной.
= 2): «успех», «неудача» и с неизменными вероятностями успеха – р и неудачи – q, где q = 1 – р, в каждом испытании. Такая схема называется биномиальной.
Определение 27. Независимые испытания при двух исходах называются испытаниями Бернулли.
Пример №10
Определить вероятность того, что в результате проведения 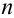 независимых испытаний некоторое событие А – успех (У) наступит ровно
независимых испытаний некоторое событие А – успех (У) наступит ровно  раз, если в каждом из этих испытаний данное событие наступает с постоянной вероятностью
раз, если в каждом из этих испытаний данное событие наступает с постоянной вероятностью 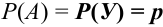 .
.
Решение.
Искомую вероятность обозначим 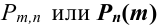 .
.
Событие А в данных испытаниях может появиться ровно  раз, причем, в разных последовательностях или комбинациях. Следовательно, остальные
раз, причем, в разных последовательностях или комбинациях. Следовательно, остальные 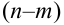 раз наступает противоположное событие
раз наступает противоположное событие 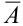 — неудача (Н), вероятность которого
— неудача (Н), вероятность которого 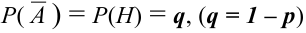 .
.
Сначала найдем вероятность того, что события У наступают при определенных  испытаниях. Элементарные события в этом случае естественно обозначать цепочками вида: УУУННУНН…УН (где У-
испытаниях. Элементарные события в этом случае естественно обозначать цепочками вида: УУУННУНН…УН (где У- штук, Н –
штук, Н – 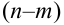 штук).
штук).
По условию данные события – независимые, следовательно, по теореме 4 для произведения независимых событий можем записать, что
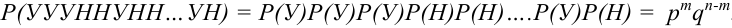 .
.
Число успехов и неудач задано. Можно менять только их расположения в цепочках, которое однозначно определяется выбором из  мест
мест  мест для успехов. Это можно сделать
мест для успехов. Это можно сделать 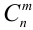 способами. Следовательно,
способами. Следовательно,
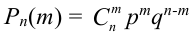 .
.
В данной задаче мы доказали теорему Бернулли.
Теорема Бернулли. Если  – число успехов в
– число успехов в  независимых испытаниях Бернулли, то вероятность того, что в результате проведения этих испытаний некоторое событие А наступит ровно
независимых испытаниях Бернулли, то вероятность того, что в результате проведения этих испытаний некоторое событие А наступит ровно  раз, находится по формуле:
раз, находится по формуле: 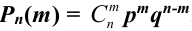 , которая называется формулой Бернулли.
, которая называется формулой Бернулли.
Следствие. 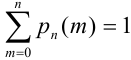 -так как события, состоящие в различном числе появления события А в серии
-так как события, состоящие в различном числе появления события А в серии  испытаний несовместны и образуют полную группу. Или можно было данное равенство объяснить так:
испытаний несовместны и образуют полную группу. Или можно было данное равенство объяснить так: 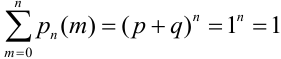 .
.
Пример №11
Пусть монета брошена 5 раз. Требуется найти вероятность того, что выпало ровно 3 орла.
Решение.
В каждом из 5 независимых испытаниях ( = 5) – бросании монеты – два исхода (
= 5) – бросании монеты – два исхода (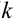 = 2: орел, решка), следовательно, это схема Бернулли с вероятностью успеха (выпал орел) и неудачи (выпала решка)
= 2: орел, решка), следовательно, это схема Бернулли с вероятностью успеха (выпал орел) и неудачи (выпала решка) 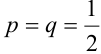 . Количество успехов:
. Количество успехов:  = 3.
= 3.
По формуле Бернулли 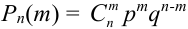 найдем искомую вероятность:
найдем искомую вероятность: 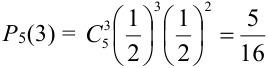 .
.
Замечания.
Замечание 1. Вероятность 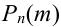 равна коэффициенту при
равна коэффициенту при 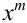 в разложении бинома
в разложении бинома 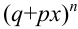 по степеням
по степеням 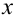 . В силу этого свойства совокупность вероятностей
. В силу этого свойства совокупность вероятностей 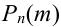 называют биномиальным законом распределения вероятностей, (будем изучать позднее)
называют биномиальным законом распределения вероятностей, (будем изучать позднее)
Замечание 2. Рассмотрим схему испытаний с произвольным количеством исходов. Пусть каждое из  независимых испытаний имеет
независимых испытаний имеет 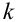 взаимно исключающих друг друга исходов, т.е. в каждом испытании может появиться одно из
взаимно исключающих друг друга исходов, т.е. в каждом испытании может появиться одно из 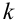 несовместных событий:
несовместных событий: 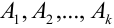 с вероятностями
с вероятностями 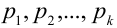 , не меняющимися от испытания к испытанию. Найдем вероятность появления в течении этих
, не меняющимися от испытания к испытанию. Найдем вероятность появления в течении этих  испытаний
испытаний 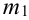 раз события
раз события 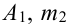 раза события
раза события 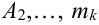 раз события
раз события 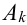 .
.  . Данная вероятность находится по формуле:
. Данная вероятность находится по формуле:
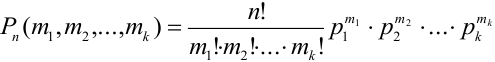 .
.
Эта совокупность вероятностей является коэффициентом при 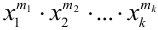 в разложении полинома
в разложении полинома 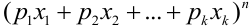 по степеням
по степеням 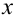 . Поэтому эту схему называют полиномиальной.
. Поэтому эту схему называют полиномиальной.
Например. При  подбрасываниях игральной кости получается полиномиальная схема с шестью исходами (
подбрасываниях игральной кости получается полиномиальная схема с шестью исходами (  = 6) и вероятностями
= 6) и вероятностями 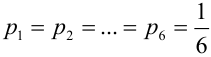 .
.
Если различать только «6» и «не 6», то получим схему Бернулли с двумя исходами ( = 2) и вероятностями успеха
= 2) и вероятностями успеха 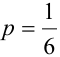 и неудачи
и неудачи 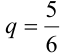 .
.
Замечание 3. При вычислении вероятности события, состоящего в том, что число успехов m лежит, например, между а и b, приходится находить числовые значения сумм вероятностей вида: 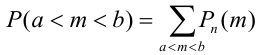 .
.
Например, вероятность того, что событие наступит а) менее  раз, b) более
раз, b) более  раз, с) не менее
раз, с) не менее  раз, d) не более
раз, d) не более  раз находятся соответственно по формулам:
раз находятся соответственно по формулам:
a) 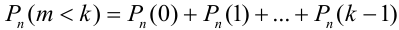 .
.
b) 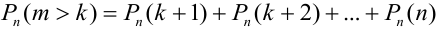 .
.
c) 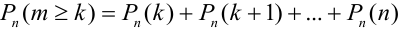 .
.
d) 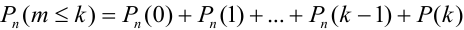 .
.
В некоторых случаях удобнее перейти к противоположному событию, например, 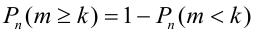 .
.
Пример №12
Пусть монета брошена 5 раз. Требуется найти вероятность того, что 1) менее двух раз выпал орел, 2) не менее двух раз выпал орел.
Решение.
Два исхода ( = 2: орел, решка) при 5 независимых испытаниях (n = 5) – схема Бернулли с вероятностью успеха и неудачи
= 2: орел, решка) при 5 независимых испытаниях (n = 5) – схема Бернулли с вероятностью успеха и неудачи 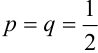 .
.
1) Орел выпал менее двух раз, значит, не выпал или выпал раз.
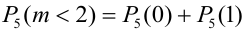 = (вероятности найдем по формуле Бернулли) =
= (вероятности найдем по формуле Бернулли) =
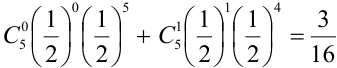
2) Орел выпал не менее двух раз, т.е. выпал два раза или три или четыре или пять:
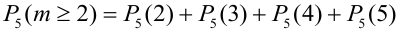 =(удобнее перейти к противоположному событию, т.е. «не менее двух», значит, противоположное событие: меньше двух, т.е. орел не выпал совсем или выпал один раз) =
=(удобнее перейти к противоположному событию, т.е. «не менее двух», значит, противоположное событие: меньше двух, т.е. орел не выпал совсем или выпал один раз) = 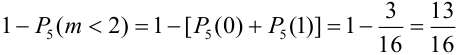 .
.
Замечание 4. В примере на формулу Бернулли вычисления проводятся очень легко, однако часто приходится вычислять вероятности при очень больших значениях n и m, например, при n = 1000, m = 500. Также затруднения при вычислении возникают при малых значениях р или q.
В этих случаях удается заменить формулу Бернулли какой-нибудь приближенной асимптотической формулой. Существуют три предельные теоремы, содержащие такие формулы.
Предельные теоремы в схеме Бернулли
Теорема Пуассона (асимптотическая формула для случая малых значений р)
Если вероятность наступления некоторого события А в n независимых испытаниях постоянна и равна р, причем  при
при  так, что
так, что 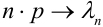 , где
, где 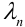 – среднее число появления события А в n испытаниях,
– среднее число появления события А в n испытаниях, 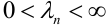 , то вероятность
, то вероятность 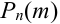 того, что в этих испытаниях событие А наступит ровно m раз, удовлетворяет при
того, что в этих испытаниях событие А наступит ровно m раз, удовлетворяет при  соотношению (или приближенно равна):
соотношению (или приближенно равна):
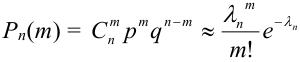
Замечания.
1. Часто формула Пуассона записывается в виде равенства, но надо помнить при этом, что оно верно при  :
:
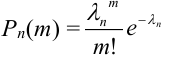 , при этом
, при этом 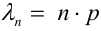 .
.
2. Формулой пользуются при больших n и малых р. Например, при n > 100, 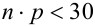 .
.
3. Теорема имеет место и в том случае, когда вероятность события А в каждом испытании равна нулю. В этом случае 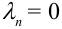 .
.
4. Существуют таблицы значений данной вероятности (стр. 410, 411 в задачнике Ефимова -Демидовича).
Пример №13
Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двумя и более пулями, если число выстрелов равно 5000.
Решение.
Считаем каждый выстрел за испытание и попадание в цель за событие. Количество испытаний n = 5000 (велико), р = 0,001 (мало). По формуле Бернулли считать сложно. Поэтому применим формулу Пуассона.
Найдем среднее число попаданий: 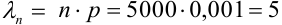 . Найдем заданную вероятность:
. Найдем заданную вероятность:
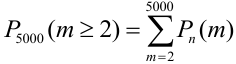 = (перейдем к противоположному событию: m < 2) =
= (перейдем к противоположному событию: m < 2) = 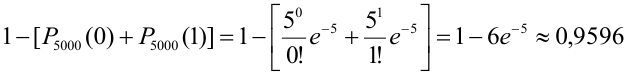 .
.
По точной формуле (формуле Бернулли) 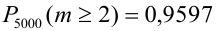 , т.е. ошибка невелика.
, т.е. ошибка невелика.
Локальная предельная теорема Муавра – Лапласа (асимптотическая формула для случая больших значений n и m)
Если вероятность наступления некоторого события А в n независимых испытаниях постоянна и равна р, (0 < р < 1), то вероятность 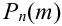 того, что в этих испытаниях событие А наступит ровно m раз, удовлетворяет при
того, что в этих испытаниях событие А наступит ровно m раз, удовлетворяет при  соотношению (или приближенно равна):
соотношению (или приближенно равна):
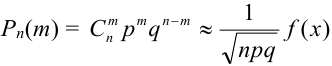 ,
,
где 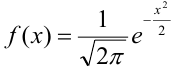 ,
, 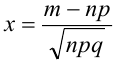 .
.
Замечания.
1. Часто формула Пуассона записывается в виде равенства, но надо помнить при этом, что оно верно при  :
:
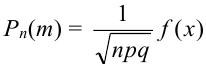
2. Формулой пользуются при больших n и m. Например, при п > 100, 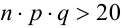 .
.
3. Из того, что  следует, что
следует, что 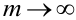 . Это означает, что n и m должны отличаться друг от друга не очень сильно. Например, для случая m = 0, теорема дает плохое приближение.
. Это означает, что n и m должны отличаться друг от друга не очень сильно. Например, для случая m = 0, теорема дает плохое приближение.
4. Существуют таблицы значений функции 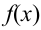 для положительных значений х (стр. 408 в задачнике Ефимова – Дсмидовича). Для отрицательных значений х используется та же таблица, так как
для положительных значений х (стр. 408 в задачнике Ефимова – Дсмидовича). Для отрицательных значений х используется та же таблица, так как 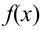 – четная функция:
– четная функция: 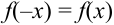 . Функцию
. Функцию 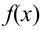 называют плотностью нормального распределения.
называют плотностью нормального распределения.
Пример №14
Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.
Решение.
Количество испытаний n = 243, количество успехов m = 70, вероятность успеха р = 0,25, вероятность неудачи q = 1 – 0,25 = 0,75.
По формуле Бернулли считать сложно. Так как n и m велики, поэтому применим формулу Муавра – Лапласа.
Найдем сначала х и 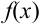 :
:
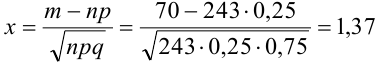 , тогда
, тогда 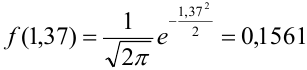 .
.
Можно было не считать значение 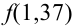 напрямую, а обратиться к таблице в учебнике.
напрямую, а обратиться к таблице в учебнике.
Подставим найденное значение 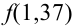 в формулу:
в формулу:
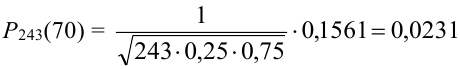 .
.
Предельная интегральная теорема Муавра – Лапласа (асимптотическая формула для случая, когда число успехов m лежит в некоторых пределах)
Теорема 1. Если m – число наступлений события А в n независимых испытаниях, в каждом из которых вероятность этого события равна р (0 < р < 1), то равномерно относительно а и b 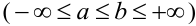 при
при 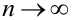 имеет место соотношение:
имеет место соотношение:
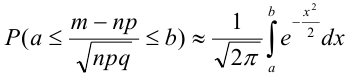 .
.
В некоторых источниках 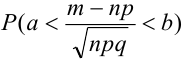 или
или 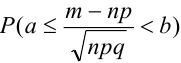 .
.
Ранее вывели, что 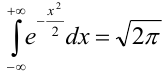 . Численное значение нашего интеграла можно найти с помощью таблиц (стр. 406 в задачнике Ефимова – Демидовича) для функции Лапласа Ф(х):
. Численное значение нашего интеграла можно найти с помощью таблиц (стр. 406 в задачнике Ефимова – Демидовича) для функции Лапласа Ф(х):
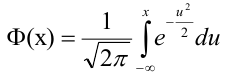 , где
, где 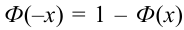 . Для тех значений х, которых нет в таблице, т.е для
. Для тех значений х, которых нет в таблице, т.е для 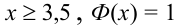
Либо, функция Лапласа может быть в виде: 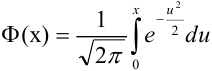 , где
, где 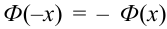 , для тех значений х, которых нет в таблице, т.е. для
, для тех значений х, которых нет в таблице, т.е. для 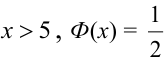 .
.
Теорема 2. (Теорема Муавра-Лапласа) Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие А наступит не менее 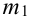 раза и не более
раза и не более 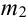 раз приближенно равна:
раз приближенно равна: 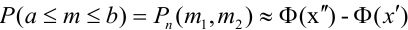 ,
,
где Ф(х) – функция Лапласа, значения 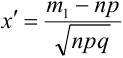 ,
, 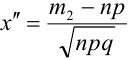 .
.
Теорема 3. (Закон больших чисел или теорема Бернулли).
При неограниченном увеличении числа однородных независимых опытов частота события будет сколь угодно мало отличаться от вероятности события в отдельном опыте.
Иначе, вероятность того, что отклонение относительной частоты наступления события 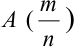 от постоянной вероятности события А (p) очень мало при
от постоянной вероятности события А (p) очень мало при 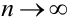 п —> оо стремится к 1.
п —> оо стремится к 1.
Доказательство.
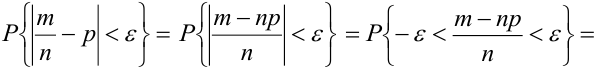
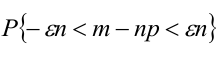 = (разделим все части неравенства на положительное число
= (разделим все части неравенства на положительное число 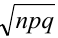 )
)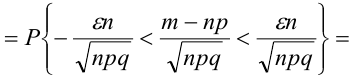
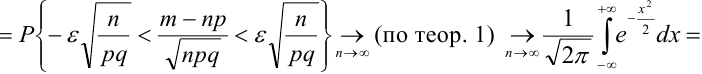
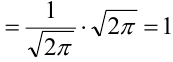 .
.
Пример №15
Вероятность появления события А в каждом из 100 независимых испытаний постоянна и равна 0,8. Найти вероятность того, что событие появиться не менее 75 раз и не более 90 раз.
Решение.
Количество испытаний n = 100, вероятность успеха р = 0,8, вероятность неудачи q = 1 – 0,8 = 0,2 , 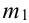 = 75,
= 75, 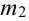 – 90.
– 90.
Найдем 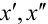 :
:
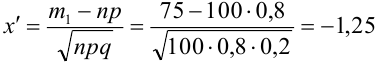 ,
, 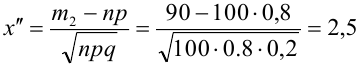 .
.
По теореме 2:
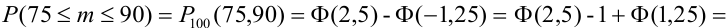 (по таблице для функции Лапласа) =
(по таблице для функции Лапласа) = 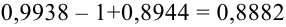 .
.
Наивероятнейшее число появления события в независимых испытаниях
Определение 28. Число 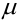 наступления события в независимых испытаниях, в каждом из которых вероятность появления события А равна р, называется наивероятнейшим, если вероятность того, что событие наступит в этих испытаниях
наступления события в независимых испытаниях, в каждом из которых вероятность появления события А равна р, называется наивероятнейшим, если вероятность того, что событие наступит в этих испытаниях 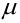 раз превышает или, по крайней мере, не меньше вероятности остальных возможных исходов испытаний.
раз превышает или, по крайней мере, не меньше вероятности остальных возможных исходов испытаний.
Наивероятнейшее число  определяется из двойного неравенства:
определяется из двойного неравенства:
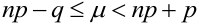 ,
,
причем 1) если (np – q) -дробное, то существует одно  , 2) если (nр- q) – целое, то существует два наивероятнейших числа, 3) если nр – целое, то
, 2) если (nр- q) – целое, то существует два наивероятнейших числа, 3) если nр – целое, то  = nр.
= nр.
Пример №16
Испытывается каждый из 15 элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, равна 0,9. Найти наивероятнейшее число элементов, которые выдержат испытание и вероятность этого числа.
Решение.
Количество испытаний n = 15, вероятность успеха р = 0,9, вероятность неудачи q = 0,1.
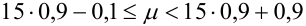 ,
, 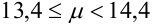 .
.
Т.к.  — целое число, то
— целое число, то  = 14— наивероятнейшее число элементов, выдержавших испытание. Вероятность этого числа найдем по формуле Бернулли:
= 14— наивероятнейшее число элементов, выдержавших испытание. Вероятность этого числа найдем по формуле Бернулли:
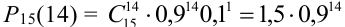 . (Удобнее было по локальной формуле Муавра – Лапласа).
. (Удобнее было по локальной формуле Муавра – Лапласа).
Всё о формуле полной вероятности
Пусть событие 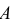 может произойти с одним и только с одним из несовместимых событий
может произойти с одним и только с одним из несовместимых событий 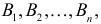 образующих полную группу. Иными словами, событие
образующих полную группу. Иными словами, событие 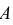 появится, если произойдет событие B1 и при этом появится событие
появится, если произойдет событие B1 и при этом появится событие 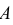 , или произойдет событие B2 и при этом появится событие
, или произойдет событие B2 и при этом появится событие 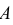 и т.д. Символическая запись этой фразы имеет вид
и т.д. Символическая запись этой фразы имеет вид
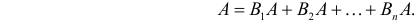
В силу несовместимости событий можно записать 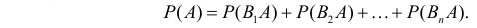
Используя теорему умножения вероятностей, получаем формулу 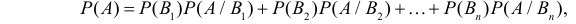
которая и называется формулой полной вероятности.
Обычно ее записывают кратко:
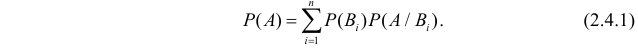
Пример №17
Имеется две коробки деталей, в каждой из которых по 10 деталей. В первой коробке среди деталей две низкого сорта, а во второй четыре низкосортных детали. Из первой коробки для нужд производства взяли наугад половину деталей, а оставшиеся высыпали во вторую коробку. Через некоторое время из второй коробки взяли наугад деталь. Какова вероятность того, что это деталь низкого сорта?
Решение. Обозначим через A событие, состоящее в выборе из второй коробки детали низкого сорта. Возможность этого выбора зависит от того, какие именно детали были добавлены во вторую коробку. На этот счет можно выдвинуть следующие предположения: B1 – во вторую коробку добавили пять годных деталей; B2 – добавили одну деталь низкого сорта и четыре доброкачественные; B3 – добавили две детали низкого сорта и три доброкачественные. Пять деталей во вторую коробку можно переложить 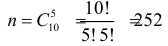 способами. Из них событию B1 благоприятствует
способами. Из них событию B1 благоприятствует 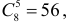 событию B2 —
событию B2 — 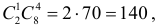 а событию B3 —
а событию B3 — 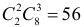 способов. Событие A произойдет, если появится событие B1 и после этого произойдет событие A или появится событие B2 и после этого произойдет событие A или появится B3 и после этого произойдет A. Символически:
способов. Событие A произойдет, если появится событие B1 и после этого произойдет событие A или появится событие B2 и после этого произойдет событие A или появится B3 и после этого произойдет A. Символически: 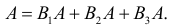 Учитывая несовместность событий
Учитывая несовместность событий  , имеем
, имеем 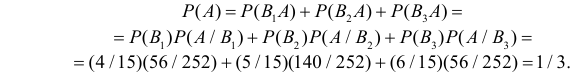
Ответ. 1/ 3.
Всё о Формуле Байеса
Пусть событие A может наступить только при появлении одного из несовместных событий 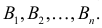 В этих условиях вероятность события A можно вычислить по формуле полной вероятности (2.4.1). События
В этих условиях вероятность события A можно вычислить по формуле полной вероятности (2.4.1). События  иногда называют «гипотезами», поскольку можно лишь предполагать какое именно из них произойдет. Предположим, что известны вероятности
иногда называют «гипотезами», поскольку можно лишь предполагать какое именно из них произойдет. Предположим, что известны вероятности 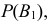
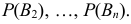
Проделан опыт, в результате которого событие A произошло. Тогда вероятности событий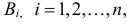 при условии появления события A определяются по формулам Байеса
при условии появления события A определяются по формулам Байеса
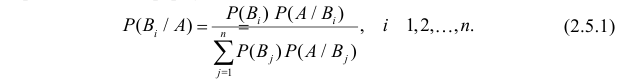
Формулы Байеса позволяют переоценивать вероятности гипотез (событий  ) с учетом информации, которую содержит в себе факт появления события A.
) с учетом информации, которую содержит в себе факт появления события A.
Пример №18
По каналу связи передается одна из последовательностей букв 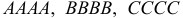 с вероятностями соответственно 0,5; 0,4; 0,1. Каждая передаваемая буква принимается правильно с вероятностью 0,8 и с вероятностями 0,1 и 0,1 за любую из двух других букв. Предполагается, что искажаются буквы при передаче независимо друг от друга. Найти вероятность того, что передано
с вероятностями соответственно 0,5; 0,4; 0,1. Каждая передаваемая буква принимается правильно с вероятностью 0,8 и с вероятностями 0,1 и 0,1 за любую из двух других букв. Предполагается, что искажаются буквы при передаче независимо друг от друга. Найти вероятность того, что передано 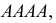 если принято
если принято 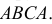
Решение. Для краткости записи формулы обозначим 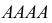 через
через 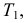
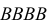 через
через 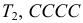 через
через 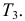 Тогда по формулам Байеса (2.5.1)
Тогда по формулам Байеса (2.5.1)

Ответ. 8/9.
Пример №19
Три стрелка производят по одному выстрелу в одну и ту же мишень. Вероятности попадания в мишень при одном выстреле для этих стрелков соответственно равны 0,8; 0,7; 0,6. Какова вероятность того, что третий стрелок промахнулся, если в мишени оказалось две пробоины?
Решение. Обозначим через А событие, состоящее в появлении двух пробоин в мишени. В отношении двух пробоин могут быть три предположения: В1 – попали первый и второй стрелки, а третий не попал, вероятность чего равна 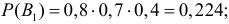 В2 – попали первый и третий, а второй не попал, вероятность чего равна
В2 – попали первый и третий, а второй не попал, вероятность чего равна 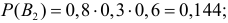 В3 – попали второй и третий, а первый не попал, вероятность чего равна
В3 – попали второй и третий, а первый не попал, вероятность чего равна 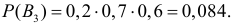
Заметим, что 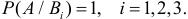 Тогда по формулам Байеса (2.5.1)
Тогда по формулам Байеса (2.5.1)
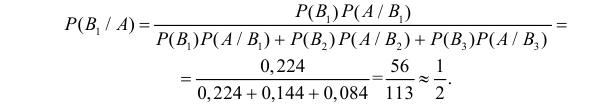
Ответ. 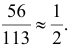
Пример №20
В партии из 10 изделий с равными шансами может оказаться от нуля до трех бракованных. Наугад взяли и проверили три изделия. Они оказались годными. Какова вероятность того, что остальные изделия в партии тоже годные?
Решение. Насчет содержания в партии бракованных изделий по условиям задачи может быть четыре предположения 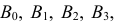 где
где 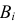 означает, что в партии
означает, что в партии 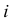 бракованных изделий. По условиям задачи все эти предположения равновозможны и поэтому имеют вероятности
бракованных изделий. По условиям задачи все эти предположения равновозможны и поэтому имеют вероятности 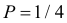 каждое. Обозначим через A факт проверки трех годных изделий. Требуется найти
каждое. Обозначим через A факт проверки трех годных изделий. Требуется найти 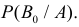
Заметим, что 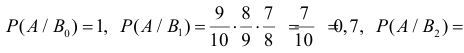
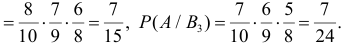 Поэтому по формулам Байеса (2.5.1)
Поэтому по формулам Байеса (2.5.1)
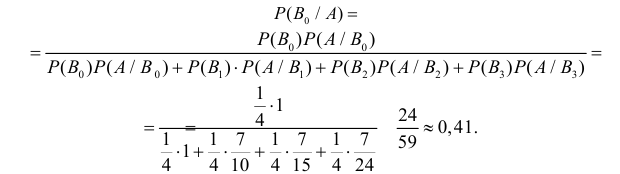
Ответ. 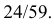
Пример №21
Вероятность того, событие B произойдет в течение часа, равна 0,9. Оказалось, что в течение первых 40 мин. событие B не произошло. Какова вероятность того, что это событие появится в оставшиеся 20 мин. времени?
Решение. В отношении события 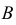 могут быть два предположения: либо оно появится
могут быть два предположения: либо оно появится 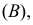 либо оно не появится
либо оно не появится 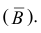 Обозначим через
Обозначим через 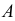 тот факт, что событие
тот факт, что событие 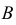 не появилось в течение первых 40 мин. Нас интересует вероятность
не появилось в течение первых 40 мин. Нас интересует вероятность 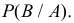 По формулам Байеса (2.5.1) получим
По формулам Байеса (2.5.1) получим
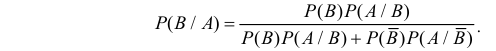
В задаче по умолчанию предполагается, что событие 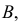 если оно происходит, то равновозможно его появление в любой момент данного часа. Поэтому по геометрическому определению вероятности
если оно происходит, то равновозможно его появление в любой момент данного часа. Поэтому по геометрическому определению вероятности 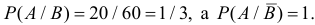 В итоге получаем, что
В итоге получаем, что
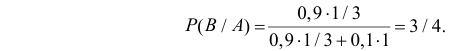
Ответ. 3/4.
Пример №22
В кошельке лежат четыре монеты. Три монеты обычных, а у четвертой на той и другой стороне изображен герб. Наугад взяли монету и подбросили три раза. Все три раза выпал герб. Какова вероятность того, что и при четвертом подбрасывании выпадет герб?
Решение. Обозначим через B1 – выбор монеты с одним гербом, через B2 – выбор монеты с двумя гербами. Априорные вероятности этих событий равны: 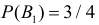 и
и 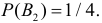
Обозначим через A – выпадение трех гербов подряд. Апостериорные вероятности по формулам Байеса равны: 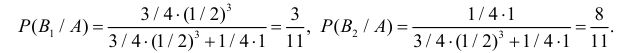
Тогда по формуле полной вероятности (2.4.1):
P(выпадения герба в четвертый раз)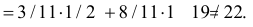
Ответ. 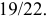
Подробное объяснение формулы полной вероятности
Постановка задачи: Пусть 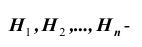 – полная система (группа) попарно несовместных событий (в дальнейшем эти события
– полная система (группа) попарно несовместных событий (в дальнейшем эти события 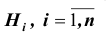 будем называть гипотезами) т. е.
будем называть гипотезами) т. е.  или что то же самое
или что то же самое  и пусть событие A может произойти лишь совместно с каким-либо одним из этих событий (гипотез).
и пусть событие A может произойти лишь совместно с каким-либо одним из этих событий (гипотез).
Требуется найти вероятность события A.
Выведем формулу решения этой задачи. Имеем
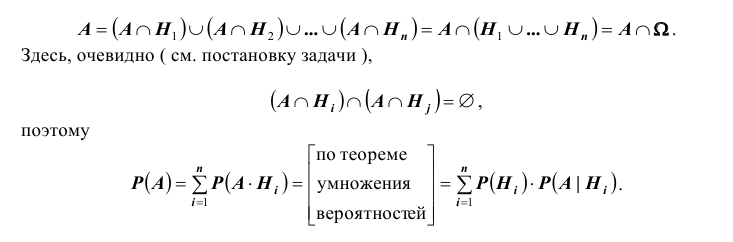
маршрутов (схема дорог). Какова вероятность того, что он попадет в пункт А ?
Решение. Как видим из схемы дорог, путь туриста обязательно проходит через один из пунктов 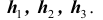 Тогда
Тогда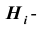 – гипотеза (предположение) которая состоит в том, что турист попал в пункт
– гипотеза (предположение) которая состоит в том, что турист попал в пункт  .
.
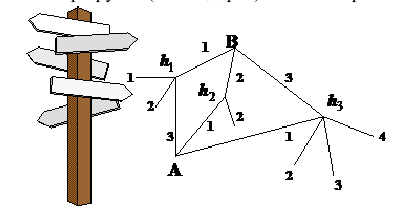
Заметим, что события (гипотезы) попарно несовместны и равновероятны, т.е., очевидно, образуют полную группу событий: во-первых,
попарно несовместны и равновероятны, т.е., очевидно, образуют полную группу событий: во-первых, , во-вторых
, во-вторых 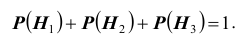 Событие A- турист попал в пункт А. Тогда, нетрудно
Событие A- турист попал в пункт А. Тогда, нетрудно
видеть (см. схему), что 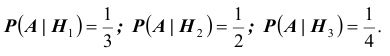 Значит, по формуле полной вероятности, получаем:
Значит, по формуле полной вероятности, получаем: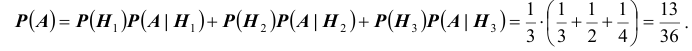

Пример №23 (о мудреце и властелине).
Властелин, разгневавшись на мудреца, приказал отрубить ему голову. Но затем, смягчившись, дал мудрецу возможность попытаться спастись. Итак, властелин взял 2 белых и 2 черных шара и предложил мудрецу распределить их по своему усмотрению по двум одинаковым урнам. После чего, палач сначала наугад выберет одну из урн, а затем также наугад, не глядя, вытащит из неё один шар. Мудрец будет помилован, если вытянутый шар оказался белым. Какую стратегию распределения шаров по урнам должен
выбрать мудрец, чтобы быть помилованным? Какова максимальная вероятность спастись мудрецу? Какая стратегия наименее выгодна для него?
Решение. Выдвинем гипотезы (предположения) 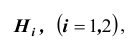 которые состоят в том, что палач вытащит шар из i – ой урны
которые состоят в том, что палач вытащит шар из i – ой урны 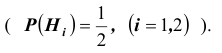 Очевидно, что эти события
Очевидно, что эти события 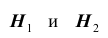 несовместны и их сумма является достоверным событием
несовместны и их сумма является достоверным событием 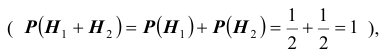 т.е. образуют полную группу (систему) событий. И пусть A- это событие состоящее в том, что
т.е. образуют полную группу (систему) событий. И пусть A- это событие состоящее в том, что
палачом вытянут белый шар. Далее, рассмотрим следующие варианты распределения мудрецом шаров по
урнам:
1). В первой урне 2 белых, а во второй 2 черных шара. Тогда 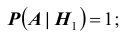
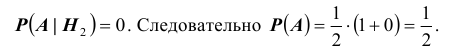
2 Хотим заметить, что далеко не всегда властелины были глупыми людьми, не знающими математики. Так, например, Наполеон был немного математиком, интересовался, в частности, геометрией. Он вёл дискуссии с Лагранжем и Лапласом, когда ещё не был правителем Франции.
Как-то в одной из таких дискуссий Лаплас резко оборвал Бонапарта: «Менее всего мы хотим от Вас, генерал, урока геометрии». В дальнейшем Лаплас стал его главным военным инженером. Наполеону приписывают теорему: «Если на сторонах произвольного треугольника во внешнюю сторону построены равносторонние треугольники, то их центры образуют равносторонний треугольник» – это так называемый вешний треугольник Наполеона.Так же ему приписывают один из знаменитых палиндромов (читается в обе стороны одинаково): «ABLE WAS I ERE I SAW ELBA» – я был силён, пока не увидел Эльбу.
2). В первой и во второй урнах по 1 белому и 1 черному шару. Тогда 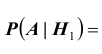
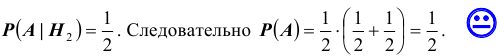
3). В первой урне 1 белый, а во второй 1 белый и 2 черных шара. Тогда 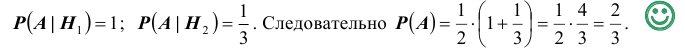
4). В первой урне 1 черный, а во второй 2 белых и 1 черный шары. Тогда 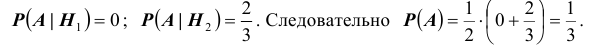
5). Первая урна оказалась пустой, т.е. все шары во второй урне. Тогда 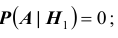
Как видим, наиболее предпочтительной является 3-я стратегия, ей соответствует вероятность быть помилованным равная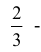 – действительно мудрое решение; наименее выгодна – последняя, 5 – я стратегия, где вероятность спастись равна
– действительно мудрое решение; наименее выгодна – последняя, 5 – я стратегия, где вероятность спастись равна 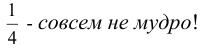
Вероятность гипотез. Формула Байеса
Постановка задачи: Пусть 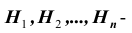 – полная система (группа) попарно несовместных событий (гипотез) т. е.
– полная система (группа) попарно несовместных событий (гипотез) т. е.
и пусть событие A может произойти лишь совместно с каким – либо одним из этих событий (гипотез) – ситуация аналогичная той, которая была ранее. И пусть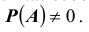 Требуется найти условную вероятность k – ой гипотезы при условии, что событие A произошло, т.е.
Требуется найти условную вероятность k – ой гипотезы при условии, что событие A произошло, т.е.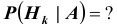 – переоценка гипотез.
– переоценка гипотез.
По теореме об умножении вероятностей
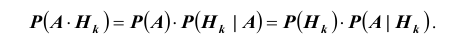 Следовательно
Следовательно 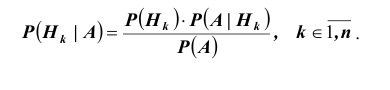
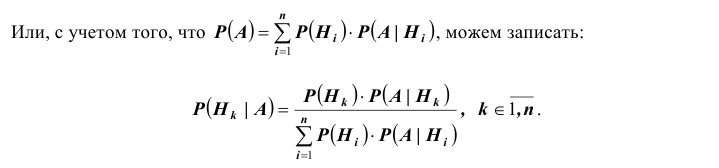
Полученная формула называется формулой Байеса (Бейеса) для переоценки гипотез. Другими словами: вероятность  гипотезы после испытания равна произведению вероятности
гипотезы после испытания равна произведению вероятности 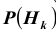 гипотезы до испытания на соответствующую ей условную вероятность
гипотезы до испытания на соответствующую ей условную вероятность 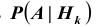 события, происшедшего при испытании, деленному на полную вероятность
события, происшедшего при испытании, деленному на полную вероятность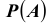 этого события.
этого события.
Пример №24
При обследовании больного имеется подозрение (т.е. делаются предположения или, что то же самое, выдвигаются гипотезы)
на одно из двух заболеваний 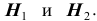 . Их вероятности в данных условиях равны
. Их вероятности в данных условиях равны 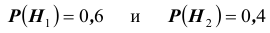 соответственно. Для уточнения диагноза назначается обследование, результатом которого будет отрицательная или положительная реакция. В случае болезни вероятность положительной реакции равна 0,9 , а в случае болезни
соответственно. Для уточнения диагноза назначается обследование, результатом которого будет отрицательная или положительная реакция. В случае болезни вероятность положительной реакции равна 0,9 , а в случае болезни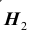 эта вероятность равна 0,5. Обследования проведены дважды и оба раза реакция оказалась отрицательной. Найти вероятность каждого заболевания.
эта вероятность равна 0,5. Обследования проведены дважды и оба раза реакция оказалась отрицательной. Найти вероятность каждого заболевания.

Решение. Во – первых, очевидно, что события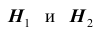 образуют полную группу событий. Действительно, эти события несовместны, так как у больного имеется подозрение только лишь на одно из двух заболеваний и сумма событий – есть достоверное событие (обследуемый болен):
образуют полную группу событий. Действительно, эти события несовместны, так как у больного имеется подозрение только лишь на одно из двух заболеваний и сумма событий – есть достоверное событие (обследуемый болен): 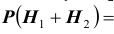 .
.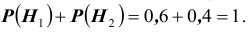 Во – вторых, если обозначить через A событие, которое состоит в том, что оба обследования дали отрицательный результат, то
Во – вторых, если обозначить через A событие, которое состоит в том, что оба обследования дали отрицательный результат, то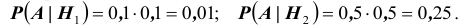 Таким образом, нетрудно видеть, что
Таким образом, нетрудно видеть, что
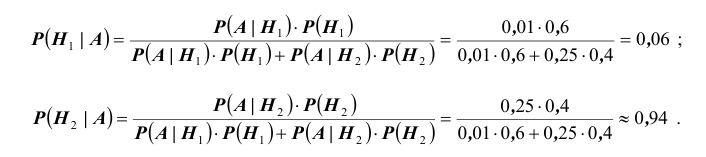
Как видим, при данных результатах обследования следует предполагать болезнь 
Повторение испытаний
Формула Бернулли (схема повторения опытов)
Опыты называются независимыми , если вероятность того или иного исхода каждого опыта не зависит от того, какие исходы имели другие опыты. Независимые опыты могут проводиться как в одинаковых условиях, так и в различных. В первом случае вероятность появления какого – либо события A во всех опытах одна и та же, во втором случае – она меняется от опыта к опыту. Ниже мы воспользуемся понятием сложного события, понимая под ним совмещение нескольких отдельных событий, которые называют простыми. Итак, пусть производится n независимых опытов в одинаковых условиях, в каждом из которых некоторое событие A может произойти с одной и той же вероятностью 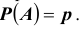 . Причём, каждый опыт (испытание) имеет лишь два исхода: событие A может появиться (произойти), либо не появиться. Условно, появление события A будем рассматривать как успех, а его не наступление (т.е. событие
. Причём, каждый опыт (испытание) имеет лишь два исхода: событие A может появиться (произойти), либо не появиться. Условно, появление события A будем рассматривать как успех, а его не наступление (т.е. событие 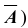 – как неудачу. Следовательно, вероятность не наступления события A в каждом испытании также постоянна и равна
– как неудачу. Следовательно, вероятность не наступления события A в каждом испытании также постоянна и равна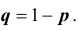 . Данная ситуация, или данная схема проведения опытов называется схемой Бернулли.
. Данная ситуация, или данная схема проведения опытов называется схемой Бернулли.
Итак, еще раз: схемой Бернулли называется последовательность n независимых испытаний, проводимых при одних и тех же условиях, в каждом из которых событие A либо происходит с постоянной вероятностью p , не зависящей от номера испытания, либо не происходит с вероятностью 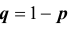
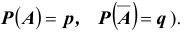
Ставятся задачи:
Задача №1. Найти вероятность 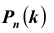 того, что в схеме Бернулли из n испытаний событие A произойдет ровно k раз
того, что в схеме Бернулли из n испытаний событие A произойдет ровно k раз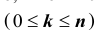 и, следовательно, не осуществится
и, следовательно, не осуществится 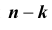 раз.
раз.
Задача № 2. Найти вероятность 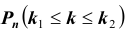 того, что в схеме Бернулли из n испытаний событие A произойдет не менее
того, что в схеме Бернулли из n испытаний событие A произойдет не менее 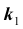 и не более
и не более 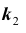 раз
раз
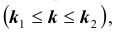 где
где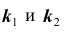 заданы.
заданы.
Задача № 3. Найти наивероятнейшее число 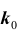 появления события A в схеме Бернулли из n испытаний, при котором
появления события A в схеме Бернулли из n испытаний, при котором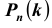 достигает наибольшего значения.
достигает наибольшего значения.
Решение №1.
Вероятность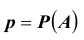 не зависит от номера испытания и, что также важно, не требуется чтобы событие A повторилось ровно k раз в определенной последовательности. Предположим, для определенности, что событие A произойдет подряд k раз, а в остальных
не зависит от номера испытания и, что также важно, не требуется чтобы событие A повторилось ровно k раз в определенной последовательности. Предположим, для определенности, что событие A произойдет подряд k раз, а в остальных 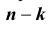 испытаниях – не произойдет. Используя теорему об умножении вероятностей, можем в этом случае записать:
испытаниях – не произойдет. Используя теорему об умножении вероятностей, можем в этом случае записать:
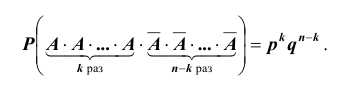
Таких несовместных событий столько, сколько сочетаний из n элементов по k элементов в каждом. Поэтому по теореме о вероятности суммы несовместных событий получим формулу, называемую формулой Бернулли:
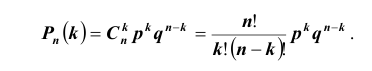
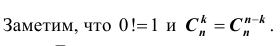 Легко видеть, что вероятность
Легко видеть, что вероятность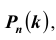 , вычисленная по формуле Бернулли, является коэффициентом при
, вычисленная по формуле Бернулли, является коэффициентом при 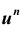 в разложении бинома
в разложении бинома 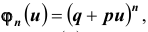 поэтому вероятность
поэтому вероятность 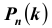 называется биномиальной, а функция
называется биномиальной, а функция 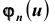 – производящей функцией для распределения вероятностей в схеме Бернулли из n испытаний. Разложение бинома Ньютона
– производящей функцией для распределения вероятностей в схеме Бернулли из n испытаний. Разложение бинома Ньютона 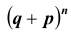 имеет вид:
имеет вид:

которую называют биномиальным законом распределения вероятностей события A в n испытаниях схемы Бернулли.
Заметим, что вероятность хотя бы одного появления события A в n испытаниях схемы Бернулли равна: 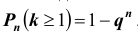 . Кстати, подумайте над
. Кстати, подумайте над
следующим вопросом: честное ли пари вам предлагают, если вы выиграете в том случае, когда при 24-х кратном бросании двух игральных костей хотя бы один раз одновременно появятся две шестёрки? Ответ дайте в конце пары.

(РЕШЕНИЕ. Вероятность одновременного выпадения двух шестерок при одном подбрасывании равна 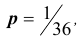 , следовательно – не выпадения равна
, следовательно – не выпадения равна 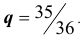 . Нетрудно видеть, что испытания, т.е. подбрасывания двух игральных костей 24 раза, удовлетворяют схеме Бернулли, следовательно вероятность одновременного появления двух шестерок хотя бы один раз равна
. Нетрудно видеть, что испытания, т.е. подбрасывания двух игральных костей 24 раза, удовлетворяют схеме Бернулли, следовательно вероятность одновременного появления двух шестерок хотя бы один раз равна 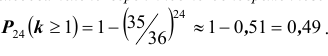 .То есть, пари нечестное.)
.То есть, пари нечестное.)
Другие примеры на применение формулы Бернулли, рассмотрим немного позднее, а именно после того, как решим задачи № 2 и № 3
Решение № 2.
Нетрудно показать, что вероятность 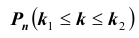 того, что в схеме Бернулли из n испытаний событие A произойдет не менее
того, что в схеме Бернулли из n испытаний событие A произойдет не менее 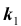 и не более
и не более 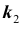 раз
раз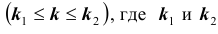 заданы, может быть вычислена по формуле:
заданы, может быть вычислена по формуле: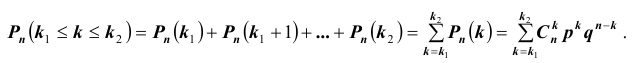
Решение № 3
Важной является задача № 3 о наивероятнейшем числе 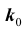 появления события A в схеме Бернулли из n испытаний.
появления события A в схеме Бернулли из n испытаний.
Рассмотрим отношение:
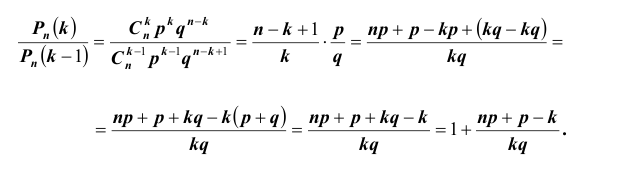
Из полученного следует, что:
1) если 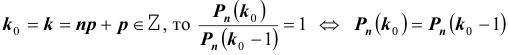 т.е. существует
т.е. существует
два максимума;
2) если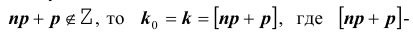 целая часть числа
целая часть числа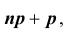 тогда
тогда 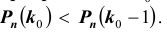

Пример №25
При некоторых условиях стрельбы вероятность p попадания в цель при одном выстреле равна
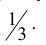 Произведено
Произведено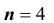 выстрела.
выстрела.
- а). Каково наивероятнейшее число попаданий в цель?
- б). Какова его вероятность?
- в). Какова вероятность двух попаданий?
- г). Какова вероятность хотя бы одного попадания?
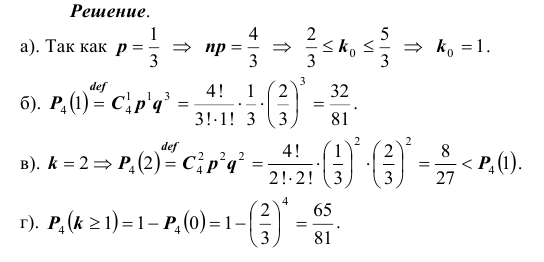
Пример №26
Некто Сэмюэль Пепайс обратился к Исааку Ньютону с вопросом: какое из событий наиболее вероятно –
- появление по крайней мере одной «шестерки» при подбрасывании 6-ти игральных костей;
- хотя бы двух «шестерок» при подбрасывании 12-ти;
- хотя бы трех «шестерок» при подбрасывании 18-ти?
Решение.
Вероятность q непоявления «шестерки» при одном подбрасывании, как известно, равна 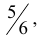 , следовательно, при шести подбрасываниях равна
, следовательно, при шести подбрасываниях равна 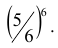
5 . Таким образом, вероятность появления по крайней мере одной «шестерки» при подбрасывании 6-ти игральных костей может быть найдена по формуле:
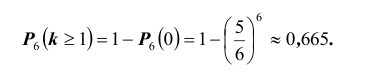
Событие «хотя бы две» противоположно событию «либо ни разу, либо один раз», т.е. 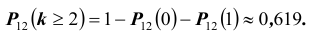
Событие «хотя бы три» противоположно событию «либо ни разу, либо один раз, либо два раза», т.е.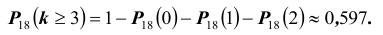
Таким образом, как видим, предпочтительнее первая стратегия – таким и был ответ Ньютона.
Замечу, что при больших значениях числа n испытаний в схеме Бернулли формула для подсчета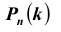 становится громоздкой для вычислений. В этих случаях пользуются асимптотическими формулами. Рассмотрим асимптотическую формулу Пуассона, которая справедлива при малых p и больших n (распределение редких событий в схеме Бернулли). Другими словами
становится громоздкой для вычислений. В этих случаях пользуются асимптотическими формулами. Рассмотрим асимптотическую формулу Пуассона, которая справедлива при малых p и больших n (распределение редких событий в схеме Бернулли). Другими словами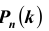 рассматривается как функция трех переменных n,k , p , при условии, что k – фиксировано, а n и p меняются
рассматривается как функция трех переменных n,k , p , при условии, что k – фиксировано, а n и p меняются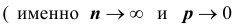
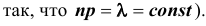
ТЕОРЕМА Пуассона 3. Пусть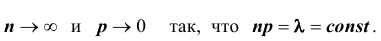 Тогда в схеме Бернулли
Тогда в схеме Бернулли 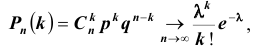 или то же самое
или то же самое 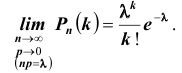
Доказательство

Что и требовалось доказать.
При доказательстве можно воспользоваться приближенной формулой Стирлинга.
Следствие: при указанных выше условиях, т.е. при 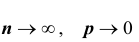 и
и 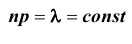 справедлива приближенная формула Пуассона:
справедлива приближенная формула Пуассона:
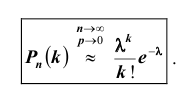
Пример №27
Телефонная станция обслуживает 800 абонентов. Для каждого абонента вероятность того, что в течении часа он позвонит на станцию равна p =0,01. Найти вероятность того, что четыре абонента позвонят на станцию в течении часа.
Решение 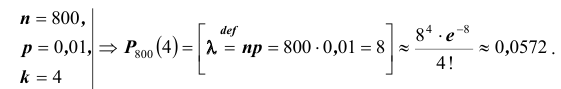
Теорема Муавра – Лапласа (локальная)
Остановлюсь еще на двух предельных теоремах в схеме Бернулли – локальной теореме Муавра – Лапласа (её доказательство получим как частный случай закона больших чисел – предельной теоремы Ляпунова, доказательство которой нам ещё предстоит провести) и интегральной теореме Муавра – Лапласа. Итак:

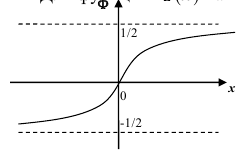
причем, во-первых, погрешность этой формулы есть величина порядка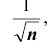 во-вторых, для функции
во-вторых, для функции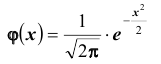 составлена таблица её значений. Для отрицательных значений аргумента пользуются той же таблицей, так как, очевидно,
составлена таблица её значений. Для отрицательных значений аргумента пользуются той же таблицей, так как, очевидно, 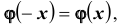 , то есть функция
, то есть функция 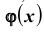 четная. Заметим также, что график функции
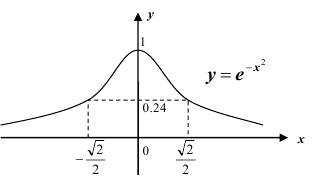
четная. Заметим также, что график функции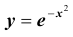 называется кривой Гаусса (см. рис.).
называется кривой Гаусса (см. рис.).
интегральная приближенная формула Лапласа ( при больших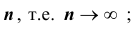
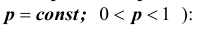

Для функции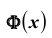 также есть табличные значения, когда
также есть табличные значения, когда 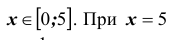 справедливо неравенство
справедливо неравенство 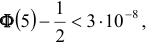
равносильно условию 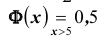 (график функции
(график функции 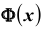 см. на рис.). Отметим, что точность растет с ростом произведения npq, и, обычно, пользуются этими формулами в случае, когда
см. на рис.). Отметим, что точность растет с ростом произведения npq, и, обычно, пользуются этими формулами в случае, когда 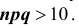
Замечание: если функция Лапласа записана в виде 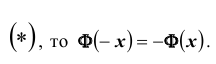 Иногда функция Лапласа может быть записана в виде
Иногда функция Лапласа может быть записана в виде
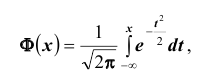
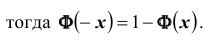 Отметим, что в схеме Бернулли рассматривались независимые испытания. Если же вероятность наступления события в k -ом опыте зависит от результата только предыдущего,
Отметим, что в схеме Бернулли рассматривались независимые испытания. Если же вероятность наступления события в k -ом опыте зависит от результата только предыдущего,  – ого опыта, то такая схема называется цепью Маркова.
– ого опыта, то такая схема называется цепью Маркова.
Формула полной вероятности и сложные задачи
В данном разделе мы рассмотрим более сложные задачи, имеющие большое практическое значение. Эти задачи встречается на практике в случае, если имеются несколько возможных сценариев развития событий (несколько вероятных гипотез). Известны как величины вероятности реализации каждого из сценариев, так и вероятность наступления интересующего нас события для любого из этих сценариев, а нас интересует, какова полная (совокупная) вероятность наступления интересующего нас события.
Предположим, что в результате опыта может произойти одно из n несовместных событий (гипотез) 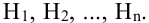 Пусть также имеется некоторое событие А и известны
Пусть также имеется некоторое событие А и известны 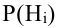 – вероятность гипотезы,
– вероятность гипотезы, 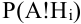 – условная вероятность события А при этой гипотезе). Тогда вероятность события А вычисляется по формуле полной вероятности:
– условная вероятность события А при этой гипотезе). Тогда вероятность события А вычисляется по формуле полной вероятности: 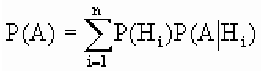
Пример №28
Из 40 деталей 10 изготовлены в первом цехе, 25 – во втором, а остальные – в третьем. Первый и третий цехи дают продукцию отличного качества с вероятностью 0,9, второй цех – с вероятностью 0,7. Какова вероятность того, что взятая наудачу деталь будет отличного качества?
Решение:
Обозначим событие А = {выбрана деталь отличного качества}, Hi= {выбранная деталь изготовлена в i цехе}, i = 1, 2, 3. Тогда 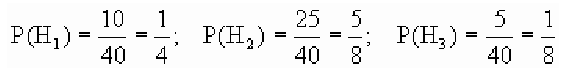
По условию задачи 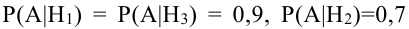 . По формуле полной вероятности находим искомую вероятность:
. По формуле полной вероятности находим искомую вероятность: 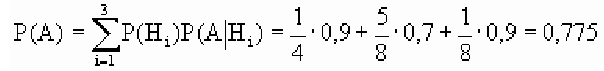
Пример №29
На рисунке изображена схема дорог. Найти вероятность того, что турист, вышедший из пункта А, попадет в пункт В, если на развилке он наугад выбирает любую дорогу (кроме обратной).
Решение:
Обозначим Нi = {приход туриста в пункт Hi}, i = 1, 2, 3, 4. Поскольку, выйдя из пункта А, он выбирает любую дорогу наугад, то 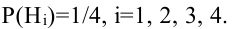
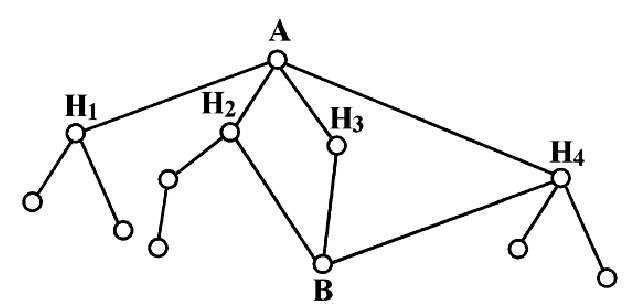
Исходя из схемы дорог, определяем, что 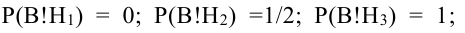
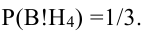
Таким образом, по формуле полной вероятности 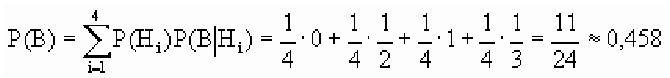
Пример №30
Из двенадцати лотерейных билетов пять выигрышных. Билеты вытягиваются по одному без возвращения. Какова вероятность того, что во второй раз вытянут выигрышный билет?
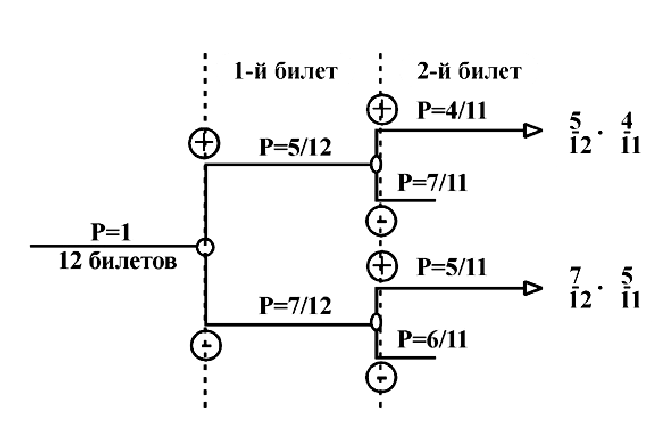
Решение:
Как обычно, вдоль каждой ветви “дерева вероятностей” значения вероятностей перемножаются, а затем значения на концах нужных веток между собой складываются. В результате получаем ответ: 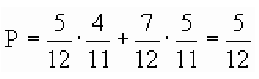
Случайные события независимые в совокупности
Следует различать попарно независимые случайные события и случайные события независимые в совокупности.
Определение: События называются попарно независимыми событиями, если любые два из них независимы.
Определение: События 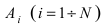 называются независимыми в совокупности, если каждое из них независимо от произведения любого числа остальных событий.
называются независимыми в совокупности, если каждое из них независимо от произведения любого числа остальных событий.
Замечание: Из определений видно, что из попарной независимости еще не следует, что эти события независимы в совокупности. Это означает, что условие независимости в совокупности является более сильным, чем условие попарной независимости случайных событий.
Теорема: Вероятность наступления хотя бы одного из событий 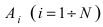 независимых в совокупности выражается формулой:
независимых в совокупности выражается формулой:
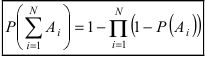 .
.
Доказательство: Обозначим через А событие, состоящее в том, что наступит хотя бы одно из событий 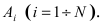 Очевидно, что противоположные события
Очевидно, что противоположные события 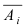 к событиям
к событиям 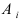 также будут независимы в совокупности. При этом событие
также будут независимы в совокупности. При этом событие 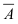 состоит в том, что в результате опыта не наступает ни одно из случайных событий
состоит в том, что в результате опыта не наступает ни одно из случайных событий 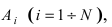 следовательно,
следовательно, 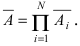 Так как события
Так как события 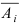 независимы в совокупности, то
независимы в совокупности, то 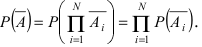 В силу того, что
В силу того, что 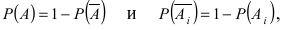 то
то 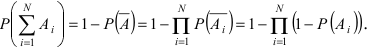
Пример №31
Пусть прибор содержит N последовательно соединенных блоков. Определить вероятность того, что цепь будет разорвана, если вероятность работы каждого блока равна р и она не зависит от работы других блоков.
Решение:
Пусть А – событие, которое состоит в том, что данная цепь разорвана. Это событие происходит, если выходит из строя хотя бы один из блоков, так как блоки включены последовательно. Противоположное событие состоит в том, что все блоки работают, т.е. 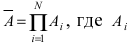 – событие, заключающееся в работе блока i. По условию задачи
– событие, заключающееся в работе блока i. По условию задачи 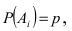 следовательно,
следовательно, 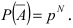 Таким образом, вероятность того, что цепь будет разорвана, равна
Таким образом, вероятность того, что цепь будет разорвана, равна 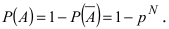
Теорема сложения вероятностей для совместных событий
Если случайные события одновременно появляются в условиях опыта, то имеет место следующая теорема.
Теорема: Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность их произведения:
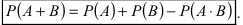
Доказательство: Пусть в результате опыта возможно n равно возможных, несовместных, элементарных исходов. При этом в 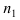 случаях наступает событие А, в
случаях наступает событие А, в 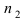 случаях – событие В, а в m случаях наступает и событие А, и событие B, т.е. событие
случаях – событие В, а в m случаях наступает и событие А, и событие B, т.е. событие 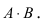 Таким образом, число исходов, в которых наступает или событие А , или событие В (т.е. событие А + В), равно
Таким образом, число исходов, в которых наступает или событие А , или событие В (т.е. событие А + В), равно 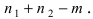 Согласно классическому определению вероятности вероятность суммы случайных, совместных событий А и В равна
Согласно классическому определению вероятности вероятность суммы случайных, совместных событий А и В равна
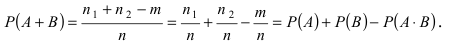
Замечание: Методом математической индукции вышеприведенная теорема может быть обобщена на любое число совместных событий, например, в случае 3 совместных событий А, В и С теорема принимает вид:
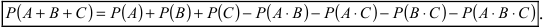
Пример №32
Найти вероятность того, что взятое наугад число из чисел от 10 до 20 делится или на 2, или на 3.
Решение:
Всего равновозможных, элементарных исходов 11 (числа от 10 включительно до 20 включительно). В 6 случаях (10, 12, 14, 16, 18, 20) число кратно 2; в 3 случаях (12, 15, 18) число кратно 3; в 2 случаях (12, 18) число кратно и 2, и 3. Пусть событие А состоит в том, что наугад взятое число кратно 2, а событие В состоит в том, что наугад взятое число кратно 3. Сложное событие С состоит в том, что наугад взятое число делится или на 2, или на 3, т.е. С = А + В. Следовательно, вероятность этого события равна:
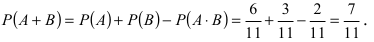
Все вышерассмотренные теоремы объединяются в теории вероятностей общим названием “основные теоремы теории вероятностей”.
Формула полной вероятности и события
Формула полной вероятности является следствием основных теорем теории вероятностей: теорем сложения и умножения вероятностей событий.
Пусть некоторое случайное событие А наступает с одним и только с одним из несовместных событий 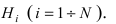
Определение: События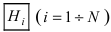 называются гипотезами, так как заранее неизвестно, какое из этих событий произойдет.
называются гипотезами, так как заранее неизвестно, какое из этих событий произойдет.
Теорема: Формула полной вероятности определяет вероятность случайного
события л, как сумму произведений вероятности каждой гипотезы 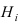 на условную вероятность события А при условии реализации гипотезы
на условную вероятность события А при условии реализации гипотезы 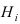 , т.е.
, т.е. 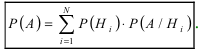
Доказательство: Событие А наступает с одним и только с одним из несовместных событий 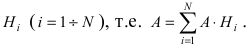 В силу того, что события
В силу того, что события 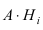 несовместны, то по теореме сложения вероятностей для несовместных событий имеем:
несовместны, то по теореме сложения вероятностей для несовместных событий имеем: 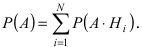 Используя теорему об умножении вероятностей зависимых событий, получаем искомую формулу:
Используя теорему об умножении вероятностей зависимых событий, получаем искомую формулу: 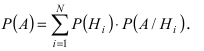
Пример №33
Пусть на сборку поступают детали с двух автоматических станков. Первый станок дает в среднем 0.3 % брака, а второй – 0.15 % брака. Производительность второго станка в два раза выше, чем первого станка. Найти вероятность того, что наугад взятая деталь окажется бракованной.
Решение:
Пусть событие А состоит в том, что наугад взятая деталь окажется бракованной. Тогда гипотеза 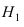 заключается в том, что эта деталь изготовлена на первом станке, а гипотеза
заключается в том, что эта деталь изготовлена на первом станке, а гипотеза 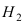 заключается в том, что эта деталь изготовлена на втором станке. Очевидно, что эти гипотезы являются несовместными событиями. В виду различной производительности станков обозначим через х количество деталей, изготовленных на первом станке, тогда на втором станке изготавливается 2х деталей. Общее число деталей, которые были изготовлены на обоих станках равна Зх. Следовательно, вероятности гипотез равны:
заключается в том, что эта деталь изготовлена на втором станке. Очевидно, что эти гипотезы являются несовместными событиями. В виду различной производительности станков обозначим через х количество деталей, изготовленных на первом станке, тогда на втором станке изготавливается 2х деталей. Общее число деталей, которые были изготовлены на обоих станках равна Зх. Следовательно, вероятности гипотез равны: 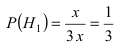 — для первой гипотезы и
— для первой гипотезы и 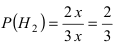 – для второй гипотезы.
– для второй гипотезы.
Вероятности события А при условии реализации первой и второй гипотез равны: 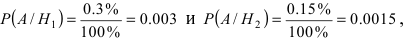 соответственно. Согласно формуле полной вероятности вероятность того, что наугад взятая деталь окажется бракованной, равна:
соответственно. Согласно формуле полной вероятности вероятность того, что наугад взятая деталь окажется бракованной, равна:
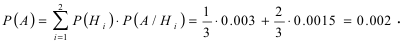
Формула вероятностей гипотез (формула Байеса)
Ниже будет получена формула, которая является следствием основных теорем теории вероятностей и формулы полной вероятности. Эта формула применяется для решения задач следующего типа. Пусть проводится эксперимент, в результате которого может появиться или не появиться событие л, которое наступает с одним и только с одним из несовместных событий  (
( ). Предположим, что события
). Предположим, что события 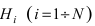 образуют полную группу и вероятности их появления
образуют полную группу и вероятности их появления 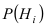 известны до проведения опыта. В результате проведения эксперимента событие А произошло. Используя этот факт, необходимо определить, какая из гипотез была ближе к истине, т.е. определить вероятность каждой гипотезы при условии реализации события А. Ответ на поставленный вопрос дает следующая теорема.
известны до проведения опыта. В результате проведения эксперимента событие А произошло. Используя этот факт, необходимо определить, какая из гипотез была ближе к истине, т.е. определить вероятность каждой гипотезы при условии реализации события А. Ответ на поставленный вопрос дает следующая теорема.
Теорема: Вероятность гипотезы 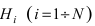 при условии реализации события А равна отношению произведения вероятности гипотезы на условную вероятность события А к паз ной вероятности события А:
при условии реализации события А равна отношению произведения вероятности гипотезы на условную вероятность события А к паз ной вероятности события А:
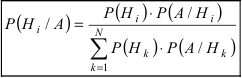
Доказательство: Событие А наступает с одним и только с одним из несовместных событий 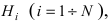 т.е. в каждом опыте происходит событие
т.е. в каждом опыте происходит событие 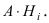 По теореме умножения вероятностей для зависимых событий:
По теореме умножения вероятностей для зависимых событий: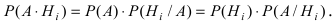
Следовательно, 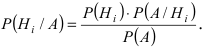 Воспользовавшись формулой полной вероятности, получим формулу Байеса:
Воспользовавшись формулой полной вероятности, получим формулу Байеса: 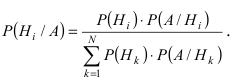
Пример №34
Однотипные пластмассовые детали изготавливаются на 3 прессах. Первый пресс выпускает 50 % всех деталей, второй – 40 %, третий – 10 % . При этом с первого пресса сходит в среднем 0.025 нестандартных деталей, со второго – 0.02 и с третьего – 0.015. Все детали поступают на сборку. Взятая наудачу деталь оказалась нестандартной. Какова вероятность того, что она изготовлена на первом прессе.
Решение:
Событие А состоит в том, что наудачу взятая деталь изготовлена на первом прессе. Гипотеза 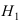 заключается в том, что эта деталь изготовлена на первом прессе, гипотеза
заключается в том, что эта деталь изготовлена на первом прессе, гипотеза 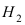 – на втором прессе, а гипотеза
– на втором прессе, а гипотеза 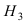 – на третьем прессе.
– на третьем прессе.
По условию задачи 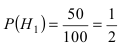 – для первой гипотезы,
– для первой гипотезы, 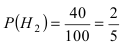 – для второй гипотезы и
– для второй гипотезы и 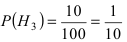 – для третьей гипотезы. Вероятности события А при условии реализации первой, второй и третьей гипотез, соответственно, равны:
– для третьей гипотезы. Вероятности события А при условии реализации первой, второй и третьей гипотез, соответственно, равны: 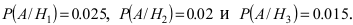 Согласно фор- муле пал ной вероятности вероятность того, что наугад взятая деталь окажется нестандартной, равна:
Согласно фор- муле пал ной вероятности вероятность того, что наугад взятая деталь окажется нестандартной, равна: 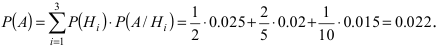
Используя формулу Байеса, получим 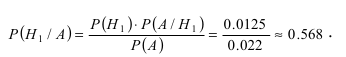
Независимые испытания и формула Бернулли
Пусть испытания повторяются n раз, причем событие А появляется в каждом опыте с одной и той же вероятностью р или не появляется с одной и той же вероятностью 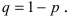
Определение: Испытания называются независимыми, если вероятность события А не зависит от того, какие события появились в предыдущих опытах, или появятся в последующих экспериментах.
Пример:
Независимы ли следующие испытания: а) многократное бросание кубика; б) извлечение карты из колоды без ее возвращения в колоду (выяснить самостоятельно).
Формула Бернулли
Теорема: Пусть проводится серия из n независимых испытаний, в каждом из которых событие А появляется с постоянной вероятностью 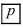 или не появляется с постоянной вероятностью
или не появляется с постоянной вероятностью 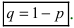 Тогда вероятность появления со- бытия А ровно m раз в серии из n независимых испытаний равна:
Тогда вероятность появления со- бытия А ровно m раз в серии из n независимых испытаний равна: 
Доказательство: Пусть 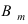 событие, состоящее в том, что в серии из n независимых испытаний событие А появится ровно m раз. Пусть
событие, состоящее в том, что в серии из n независимых испытаний событие А появится ровно m раз. Пусть 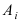 событие, описывающее появление события А в опыте i, а ему противоположное событие обозначим через
событие, описывающее появление события А в опыте i, а ему противоположное событие обозначим через 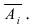 Так как вероятность появления события А в опыте i равна
Так как вероятность появления события А в опыте i равна 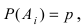 то вероятность появления противоположного события
то вероятность появления противоположного события 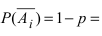
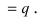 Для наступления события
Для наступления события 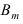 безразлично, в каких опытах произойдет событие A, а в каких – событие
безразлично, в каких опытах произойдет событие A, а в каких – событие 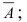 важно, чтобы число появлений события A в данной серии равнялось числу m. В качестве одного из вариантов чередования событий
важно, чтобы число появлений события A в данной серии равнялось числу m. В качестве одного из вариантов чередования событий 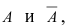 благоприятствующих появлению события
благоприятствующих появлению события 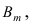 рассмотрим такое событие
рассмотрим такое событие 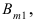 для которого событие А появится в m первых опытах и не появится в (n-m) последующих экспериментах, т.е.
для которого событие А появится в m первых опытах и не появится в (n-m) последующих экспериментах, т.е.
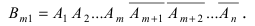
Воспользуемся теоремой умножения вероятностей для независимых событий, получим: 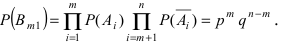 Аналогичные к
Аналогичные к  события отличаются от него только чередованием событий
события отличаются от него только чередованием событий  Все эти события равновероятны и их число равно количеству сочетаний из n элементов по m элементов, т.е.
Все эти события равновероятны и их число равно количеству сочетаний из n элементов по m элементов, т.е. 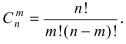 Таким образом, интересующее нас событие можно записать в виде
Таким образом, интересующее нас событие можно записать в виде 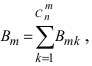 причем события
причем события 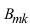 несовместны. По теореме сложения вероятностей несовместных событий вероятность изучаемого события равна
несовместны. По теореме сложения вероятностей несовместных событий вероятность изучаемого события равна 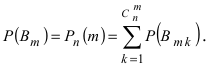 В правой части равенства суммируется
В правой части равенства суммируется 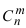 одинаковых слагаемых, следовательно,
одинаковых слагаемых, следовательно, 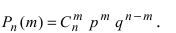 O5. Формула
O5. Формула  называется биномиальной или формулой Бернулли.
называется биномиальной или формулой Бернулли.
Пример №35
Монета подбрасывается 6 раз. Определить вероятность того, что герб выпадет а) 5 раз; б) от 2 до 4 раз.
Решение:
Вероятность выпадения герба не изменяется от опыта к опыту и равна 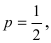 а, следовательно, вероятность выпадения решки равна
а, следовательно, вероятность выпадения решки равна 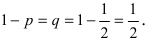 Для определения вероятности выпадения герба 5 раз в серии из 6 испытаний воспользуемся формулой Бернулли:
Для определения вероятности выпадения герба 5 раз в серии из 6 испытаний воспользуемся формулой Бернулли: 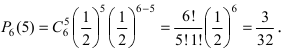 Событие, состоящее в том, что герб выпадет от 2 до 4 раз, соответствует события, которое состоит в том, что герб выпадет или 2 раза, или 3 раза, или 4 раза. Следовательно, вероятность
Событие, состоящее в том, что герб выпадет от 2 до 4 раз, соответствует события, которое состоит в том, что герб выпадет или 2 раза, или 3 раза, или 4 раза. Следовательно, вероятность 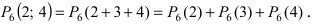 Вычислим соответствующие вероятности:
Вычислим соответствующие вероятности: 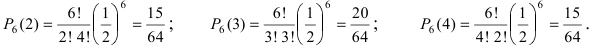 Таким образом, искомая вероятность равна
Таким образом, искомая вероятность равна 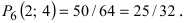
При больших значениях чисел m и n применение формулы Бернулли затруднительно, так как вычисление коэффициентов 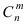 становится достаточно сложным. Поэтому при фиксированном значении т и в случае, когда вероятность появления события р<0.1, применяется формула Пуассона, а при р>0.1 – дифференциальная формула Муавра-Лапласа. Если
становится достаточно сложным. Поэтому при фиксированном значении т и в случае, когда вероятность появления события р<0.1, применяется формула Пуассона, а при р>0.1 – дифференциальная формула Муавра-Лапласа. Если 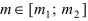 , то применяют интегральную формулу Муавра-Лапласа.
, то применяют интегральную формулу Муавра-Лапласа.
Формула Пуассона
Если при проведении серии испытаний по схеме Бернулли вероятность появления события А мала (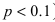 ), то при больших значениях чисел m и n применяют приближенную формулу Пуассона:
), то при больших значениях чисел m и n применяют приближенную формулу Пуассона: 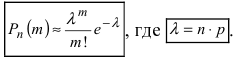
Формулы Муавра-Лапласа
Если при проведении серии испытаний по схеме Бернулли вероятность появления события А р>0.1, то при больших значениях чисел m и n применяют дифференциальную формулу Муавра-Лапласа: 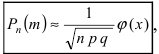 дифференциальная функция Муавра-Лапласа
дифференциальная функция Муавра-Лапласа 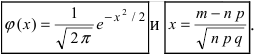
Замечание: В общем случае дифференциальная формула Муавра-Лапласа применяется при выполнении неравенств 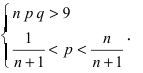
Если при проведении серии испытаний по схеме Бернулли числа m и n принимают большие значения, причем число m принимает значения от 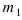 до
до 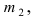 то применяют интегральную формулу Муавра-Лапласа:
то применяют интегральную формулу Муавра-Лапласа:
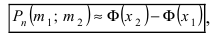 где
где 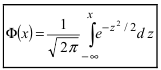 – интегральная функция Муавра-Лапласа и
– интегральная функция Муавра-Лапласа и 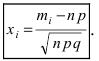
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
- Числовые характеристики случайных величин
- Комбинаторика – правила, формулы и примеры
- Классическое определение вероятности
- Геометрические вероятности
- Теоремы сложения и умножения вероятностей
Понравилось? Добавьте в закладки
Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В, записывается как $A subset B$.
События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записывается очевидно: А = В.
Суммой событий А и В называется событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.
Теорема о сложении вероятностей. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.
$$P(A+B)=P(A)+P(B).$$
Заметим, что сформулированная теорема справедлива для любого числа несовместных событий:
$$Pleft(sum_{i=1}^{n}A_i right)=sum_{i=1}^{n} P(A_i).$$
Если случайные события $A_1, A_2, …, A_n$ образуют полную группу несовместных событий, то имеет место равенство
$P(A_1)+P(A_2)+…+P(A_n)=1.$ Такие события (гипотезы) используются при решении задач на полную вероятность.
Произведением событий А и В называется событие АВ, которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.
Теорема о сложении вероятностей 2. Вероятность суммы совместных событий вычисляется по формуле
$$P(A+B)=P(A)+P(B)-P(Acdot B).$$
События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Теорема об умножении вероятностей. Вероятность произведения независимых событий А и В вычисляется по формуле:
$$P(Acdot B)=P(A)cdot P(B).$$
Вероятность произведения зависимых событий вычисляется по формуле условной вероятности.
Примеры решений задач с событиями
Пример. В первом ящике 1 белый и 5 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный.
Решение. Обозначим события: А – вынули белый шар из первого ящика,  ;
;
 – вынули черный шар из первого ящика,
– вынули черный шар из первого ящика,  ;
;
В – белый шар из второго ящика,  ;
;
 – черный шар из второго ящика,
– черный шар из второго ящика,  .
.
Нам нужно, чтобы произошло одно из событий  или
или  . По теореме об умножении вероятностей
. По теореме об умножении вероятностей
 ,
,  .
.
Тогда искомая вероятность по теореме сложения будет
 .
.
Пример. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) двойного промаха, в) хотя бы одного попадания; г) одного попадания.
Решение.
Пусть А – попадание первого стрелка,  ;
;
В – попадание второго стрелка,  .
.
Тогда  – промах первого,
– промах первого,  ;
;
 – промах второго,
– промах второго,  .
.
Найдем нужные вероятности.
а) АВ – двойное попадание, 
б) 
 – двойной промах,
– двойной промах,  .
.
в) А+В – хотя бы одно попадание,
 .
.
г)  – одно попадание,
– одно попадание,
 .
.
См. обучающую статью “решение задач о стрелках”
Пример. Решить задачу, применяя теоремы сложения и умножения. Мастер обслуживает 3 станка, работающих независимо друг от друга. Вероятность того, что первый станок потребует внимания рабочего в течение смены, равна 0,4, второй – 0,6, третий – 0,3. Найти вероятность того, что в течение смены: а) ни один станок не потребует внимания мастера, б) ровно 1 станок потребует внимания мастера.
Решение.
Вводим базовые независимые события $A_i$ = (Станок $i$ потребовал внимания рабочего в течение смены), $i=1, 2, 3$. По условию выписываем вероятности: $p_1=0,4$, $p_2=0,6$, $p_3=0,3$. Тогда $q_1=0,6$, $q_2=0,4$, $q_3=0,7$.
Найдем вероятность события $X$=(Ни один станок не потребует внимания в течение смены):
$$
P(X)=Pleft(overline{A_1} cdot overline{A_2} cdot overline{A_3}right)= q_1 cdot q_2 cdot q_3 =
0,6cdot 0,4 cdot 0,7 = 0,168.
$$
Найдем вероятность события $Z$= (Ровно один станок потребует внимания в течение смены):
$$
P(Z)= \ = P(A_1) cdot Pleft(overline{A_2} right) cdot Pleft(overline{A_3} right) + Pleft(overline{A_1}right) cdot P(A_2) cdot Pleft(overline{A_3} right) + Pleft(overline{A_1} right) cdot Pleft(overline{A_2} right) cdot P(A_3)=\
= p_1 cdot q_2 cdot q_3 + q_1 cdot p_2 cdot q_3 + q_1 cdot q_2 cdot p_3 =\ =
0,4cdot 0,4 cdot 0,7+0,6cdot 0,6 cdot 0,7+0,6cdot 0,4 cdot 0,3 = 0,436.
$$
См. обучающую статью “решение задач о станках”
Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.
Решение.
А – формула содержится в первом справочнике;
В – формула содержится во втором справочнике;
С – формула содержится в третьем справочнике.
Воспользуемся теоремами сложения и умножения вероятностей.
1. 
2.  .
.
3. 
Вероятность наступления хотя бы одного события
Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий?
Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.
Теорема. Вероятность появления хотя бы одного из событий $A_1, A_2, …, A_n$, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
$$
P(A)=1-Pleft(overline{A_1}right)cdot Pleft(overline{A_2}right)cdot … cdot Pleft(overline{A_n}right)= 1-q_1 cdot q_2 cdot … cdot q_n.
$$
Если события $A_1, A_2, …, A_n$ имеют одинаковую вероятность $p$, то формула принимает простой вид:
$$
P(A)=1-(1-p)^n=1-q^n.
$$
Примеры решений на эту тему
Пример. Вероятности попадания в цель при стрельбе из трех орудий таковы: p1 = 0,8; p2 = 0,7; p3 = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.
Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события  (попадание первого орудия),
(попадание первого орудия),  (попадание второго орудия) и
(попадание второго орудия) и  (попадание третьего орудия) независимы в совокупности.
(попадание третьего орудия) независимы в совокупности.
Вероятности событий, противоположных событиям  ,
,  и
и  (т. е. вероятности промахов), соответственно равны:
(т. е. вероятности промахов), соответственно равны:
 ,
,  ,
, 
Искомая вероятность  .
.
Пример. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А).
Решение. События “машина работает” и “машина не работает” (в данный момент) — противоположные, поэтому сумма их вероятностей равна единице: 
Отсюда вероятность того, что машина в данный момент не работает, равна 
Искомая вероятность 
Так как полученная вероятность весьма близка к единице, то на основании следствия из принципа практической невозможности маловероятных событий мы вправе заключить, что в данный момент работает хотя бы одна из машин.
Пример. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?
Решение. Обозначим через А событие “при n выстрелах стрелок попадает в цель хотя бы один раз”. События, состоящие в попадании в цель при первом, втором выстрелах и т. д., независимы в совокупности, поэтому применима формула  .
.
Приняв во внимание, что, по условию,  (следовательно,
(следовательно,  ), получим
), получим

Прологарифмируем это неравенство по основанию 10:

Итак,  , т.е. стрелок должен произвести не менее 5 выстрелов.
, т.е. стрелок должен произвести не менее 5 выстрелов.
См. обучающую статью “решение задач с хотя бы один…”
Зависимые и независимые случайные события.
Основные формулы сложения и умножения вероятностей
Понятия зависимости и независимости случайных событий. Условная вероятность. Формулы сложения и умножения вероятностей для зависимых и независимых случайных событий. Формула полной вероятности и формула Байеса.
Теоремы сложения вероятностей
Найдем вероятность суммы событий и
(в предположении их совместности либо несовместности).
Теорема 2.1. Вероятность суммы конечного числа несовместных событий равна сумме их вероятностей:
Пример 1. Вероятность того, что в магазине будет продана пара мужской обуви 44-го размера, равна 0,12; 45-го — 0,04; 46-го и большего — 0,01. Найти вероятность того, что будет продана пара мужской обуви не меньше 44-го размера.
Решение. Искомое событие произойдет, если будет продана пара обуви 44-го размера (событие
) или 45-го (событие
), или не меньше 46-го (событие
), т. е. событие
есть сумма событий
. События
,
и
несовместны. Поэтому согласно теореме о сумме вероятностей получаем
Пример 2. При условиях примера 1 найти вероятность того, что очередной будет продана пара обуви меньше 44-го размера.
Решение. События “очередной будет продана пара обуви меньше 44-го размера” и “будет продана пара обуви размера не меньше 44-го” противоположные. Поэтому по формуле (1.2) вероятность наступления искомого события
поскольку , как это было найдено в примере 1.
Теорема 2.1 сложения вероятностей справедлива только для несовместных событий. Использование ее для нахождения вероятности совместных событий может привести к неправильным, а иногда и абсурдным выводам, что наглядно видно на следующем примере. Пусть выполнение заказа в срок фирмой “Electra Ltd” оценивается вероятностью 0,7. Какова вероятность того, что из трех заказов фирма выполнит в срок хотя бы какой-нибудь один? События, состоящие в том, что фирма выполнит в срок первый, второй, третий заказы обозначим соответственно . Если для отыскания искомой вероятности применить теорему 2.1 сложения вероятностей, то получим
. Вероятность события оказалась больше единицы, что невозможно. Это объясняется тем, что события
являются совместными. Действительно, выполнение в срок первого заказа не исключает выполнения в срок двух других.
Сформулируем теорему сложения вероятностей в случае двух совместных событий (будет учитываться вероятность их совместного появления).
Теорема 2.2. Вероятность суммы двух совместных событий равна сумме вероятностей этих двух событий без вероятности их совместного появления:
Зависимые и независимые события. Условная вероятность
Различают события зависимые и независимые. Два события называются независимыми, если появление одного из них не изменяет вероятность появления другого. Например, если в цехе работают две автоматические линии, по условиям производства не взаимосвязанные, то остановки этих линий являются независимыми событиями.
Пример 3. Монета брошена два раза. Вероятность появления “герба” в первом испытании (событие ) не зависит от появления или не появления “герба” во втором испытании (событие
). В свою очередь, вероятность появления “герба” во втором испытании не зависит от результата первого испытания. Таким образом, события
и
независимые.
Несколько событий называются независимыми в совокупности, если любое из них не зависит от любого другого события и от любой комбинации остальных.
События называются зависимыми, если одно из них влияет на вероятность появления другого. Например, две производственные установки связаны единым технологическим циклом. Тогда вероятность выхода из строя одной из них зависит от того, в каком состоянии находится другая. Вероятность одного события , вычисленная в предположении осуществления другого события
, называется условной вероятностью события
и обозначается
.
Условие независимости события от события
записывают в виде
, а условие его зависимости — в виде
. Рассмотрим пример вычисления условной вероятности события.
Пример 4. В ящике находятся 5 резцов: два изношенных и три новых. Производится два последовательных извлечения резцов. Определить условную вероятность появления изношенного резца при втором извлечении при условии, что извлеченный в первый раз резец в ящик не возвращается.
Решение. Обозначим извлечение изношенного резца в первом случае, а
— извлечение нового. Тогда
. Поскольку извлеченный резец в ящик не возвращается, то изменяется соотношение между количествами изношенных и новых резцов. Следовательно, вероятность извлечения изношенного резца во втором случае зависит от того, какое событие осуществилось перед этим.
Обозначим событие, означающее извлечение изношенного резца во втором случае. Вероятности этого события могут быть такими:
Следовательно, вероятность события зависит от того, произошло или нет событие
.
Формулы умножения вероятностей
Пусть события и
независимые, причем вероятности этих событий известны. Найдем вероятность совмещения событий
и
.
Теорема 2.3. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
Следствие 2.1. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
Пример 5. Три ящика содержат по 10 деталей. В первом ящике — 8 стандартных деталей, во втором — 7, в третьем — 9. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.
Решение. Вероятность того, что из первого ящика взята стандартная деталь (событие ),
. Вероятность того, что из второго ящика взята стандартная деталь (событие
),
. Вероятность того, что из третьего ящика взята стандартная деталь (событие
),
. Так как события
,
и
независимые в совокупности, то искомая вероятность (по теореме умножения)
Пусть события и
зависимые, причем вероятности
и
известны. Найдем вероятность произведения этих событий, т. е. вероятность того, что появится и событие
, и событие
.
Теорема 2.4. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Следствие 2.2. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились.
Пример 6. В урне находятся 5 белых шаров, 4 черных и 3 синих. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его в урну. Найти вероятность того, что при первом испытании появится белый шар (событие ), при втором — черный (событие
) и при третьем — синий (событие
).
Решение. Вероятность появления белого шара при первом испытании . Вероятность появления черного шара при втором испытании, вычисленная в предположении, что при первом испытании появился белый шар, т. е. условная вероятность
. Вероятность появления синего шара при третьем испытании, вычисленная в предположении, что при первом испытании появился белый шар, а при втором — черный,
. Искомая вероятность
Формула полной вероятности
Теорема 2.5. Если событие наступает только при условии появления одного из событий
, образующих полную группу несовместных событий, то вероятность события
равна сумме произведений вероятностей каждого из событий
на соответствующую условную вероятность события
:
(2.1)
При этом события называются гипотезами, а вероятности
— априорными. Эта формула называется формулой полной вероятности.
Пример 7. На сборочный конвейер поступают детали с трех станков. Производительность станков не одинакова. На первом станке изготовляют 50% всех деталей, на втором — 30%, на третьем — 20%. Вероятность качественной сборки при использовании детали, изготовленной на первом, втором и третьем станке, соответственно 0,98, 0,95 и 0,8, Определить вероятность того, что узел, сходящий с конвейера, качественный.
Решение. Обозначим событие, означающее годность собранного узла;
,
и
— события, означающие, что детали сделаны соответственно на первом, втором и третьем станке. Тогда
Искомая вероятность
Формула Байеса
Эта формула применяется при решении практических задач, когда событие , появляющееся совместно с каким-либо из событий
, образующих полную группу событий, произошло и требуется провести количественную переоценку вероятностей гипотез
. Априорные (до опыта) вероятности
известны. Требуется вычислить апостериорные (после опыта) вероятности, т. е., по существу, нужно найти условные вероятности
. Для гипотезы
формула Байеса выглядит так:
Раскрывая в этом равенстве по формуле полной вероятности (2.1), получаем
Пример 8. При условиях примера 7 рассчитать вероятности того, что в сборку попала деталь, изготовленная соответственно на первом, втором и третьем станке, если узел, сходящий с конвейера, качественный.
Решение. Рассчитаем условные вероятности по формуле Байеса:
для первого станка
для второго станка
для третьего станка
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Совокупность – вероятность
Cтраница 1
Совокупность вероятностей ( 3) носит название гипергеомет-рического распределения.
[1]
Совокупность вероятностей (18.28) называется биномиальным распределением вероятностей.
[2]
Совокупность вероятностей Рт п называется биномиальным законом распределения.
[3]
Совокупность вероятностей Рг называется условным распределением числа точек пересечения G с прямой.
[4]
Для некоторой заданной совокупности вероятностей и для некоторых заданных каналов, кодирующей и декодирующей систем существует поддающаяся вычислению вероятность ошибки Ре, которая является вероятностью того, что некоторое сообщение будет закодировано и принято таким образом, что функция Л даст на выходе сообщение, отличное от переданного.
[5]
Отметим, что совокупность вероятностей, состоящую из п 1 биномиальных вероятностей, называют биномиальным законом распределения вероятностей.
[6]
Вероятность безотказной работы всего устройства в целом состоит из совокупности вероятностей безотказной работы узлов и систем, входящих в него. При этом необходимо иметь в виду, как в любом узле или системе соединены друг с другом детали: последовательно или параллельно. Последовательным считают такое соединение, когда отказ любой детали вызывает отказ всего узла или системы, а параллельным – когда отказ узла или системы наступает после выхода из строя всех параллельно соединенных деталей, входящих в них. Системы или узлы с параллельным соединением деталей называют резервированными.
[7]
Двусторонний дискретный канал без памяти с конечными алфавитами был определен с помощью совокупности вероятностей перехода P yi, yz xit х2, где х и хг являются входными буквами соответственно первого и второго конца канала, а z / i и у2 соответствующие буквы на его выходах. Каждая из этих букв принимает значение из соответствующего конечного алфавита.
[8]
Легко заметить, что вероятность Рп ( т) равна коэффициенту при хп в разложении бинома ( д – – рх) по степеням х; в силу этого свойства совокупность вероятностей Рп ( т) называют биномиальным законом распределения вероятностей.
[9]
Стандартная модель включает схему Кобаяши-Маскавы ( см. 8.4), согласно которой слабые взаимодействия между кварками с зарядами 2 / 3 и – 1 / 3 должны приводить к СР-несохранению, величина которого жестко связана с совокупностью вероятностей этих взаимодействий.
[10]
Показатели свойств, обуславливающих надежность, включая ремонтопригодность трубопровода, имеют вероятностный характер и характеризуются случайными величинами. Совокупность вероятностей всех значений, которые может принимать случайная величина, называется распределением вероятностей.
[11]
Полученная формула носит наименование формулы Бернулли. В силу этого свойства совокупность вероятностей Р ( т) называют биномиальным законом распределения вероятностей.
[12]
Иначе говоря, первоначальная вероятность величины / увеличивается или уменьшается в esl раз и образованные величины нормируются так, чтобы дать в сумме единицу. Для больших положительных значений s эта отклоненная совокупность вероятностей Qs ( Г) увеличивает вероятности Рг ( /) для положительных / и уменьшает их для / отрицательных.
[13]
На практике оказалось проще искать предельные доверительные интервалы, соответствующие абсолютному ( 100 %) уровню надежности. После этого поиск доверительных интервалов для всей совокупности вероятностей сводится к последовательному решению не более чем 2т х задач линейного программирования. В каждой из них ищется либо наибольшее, либо наименьшее возможное значение оценки ptj для одной выбранной субъективной вероятности. Нетрудно показать, что найденным таким образом границам доверительного интервала соответствует 100 % – ный уровень доверительной вероятности, трактуемой в обычном понимании.
[14]
Неравенство рх р2 остается справедливым и в том случае, когда разность р2 – pi близка к 1 и когда она близка к нулю. Но как это не парадоксально в принятых допущениях, на помощь нам приходит размерность решаемых задач: с ростом числа рассматриваемых следствий и альтернатив неопределенность числовой интерпретации отношений между величинами, задаваемых знаком или, в целом для совокупности вероятностей р / имеет тенденцию к снижению.
[15]
Страницы:
1
2
ВВЕДЕНИЕ
Многие вещи нам непонятны не потому, что
наши понятия слабы;
но потому, что сии вещи не входят в круг наших
понятий.
Козьма Прутков
Основная цель изучения математики в средних
специальных учебных заведениях состоит в том,
чтобы дать студентам набор математических
знаний и навыков, необходимых для изучения
других программных дисциплин, использующих в той
или иной мере математику, для умения выполнять
практические расчеты, для формирования и
развития логического мышления.
В данной работе последовательно вводятся все
базовые понятия раздела математики “Основы
теории вероятностей и математической
статистики”, предусмотренные программой и
Государственными образовательными стандартами
среднего профессионального образования
(Министерство образования Российской Федерации.
М., 2002г.), формулируются основные теоремы, большая
часть которых не доказывается. Рассматриваются
основные задачи и методы их решения и технологии
применения этих методов к решению практических
задач. Изложение сопровождается подробными
комментариями и многочисленными примерами.
Методические указания могут быть использованы
для первичного ознакомления с изучаемым
материалом, при конспектировании лекций, для
подготовки к практическим занятиям, для
закрепления полученных знаний, умений и навыков.
Кроме того, пособие будет полезно и студентам-
старшекурсникам как справочное пособие,
позволяющее быстро восстановить в памяти то, что
было изучено ранее.
В конце работы приведены примеры и задания,
которые студенты могут выполнять в режиме
самоконтроля.
Методические указания предназначены для
студентов заочной и дневной форм обучения.
ОСНОВНЫЕ ПОНЯТИЯ
Теория вероятностей изучает объективные
закономерности массовых случайных событий. Она
является теоретической базой для математической
статистики, занимающейся разработкой методов
сбора, описания и обработки результатов
наблюдений. Путем наблюдений (испытаний,
экспериментов), т.е. опыта в широком смысле слова,
происходит познание явлений действительного
мира.
В своей практической деятельности мы часто
встречаемся с явлениями, исход которых
невозможно предсказать, результат которых
зависит от случая.
Случайное явление можно охарактеризовать
отношением числа его наступлений к числу
испытаний, в каждом из которых при одинаковых
условиях всех испытаний оно могло наступить или
не наступить.
Теория вероятностей есть раздел математики, в
котором изучаются случайные явления (события) и
выявляются закономерности при массовом их
повторении.
Математическая статистика – это раздел
математики, который имеет своим предметом
изучения методов сбора, систематизации,
обработки и использования статистических данных
для получения научно обоснованных выводов и
принятия решений.
При этом под статистическими данными
понимается совокупность чисел, которые
представляют количественные характеристики
интересующих нас признаков изучаемых объектов.
Статистические данные получаются в результате
специально поставленных опытов, наблюдений.
Статистические данные по своей сущности
зависят от многих случайных факторов, поэтому
математическая статистика тесно связана с
теорией вероятностей, которая является ее
теоретической основой.
I. ВЕРОЯТНОСТЬ. ТЕОРЕМЫ СЛОЖЕНИЯ И
УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ
1.1. Основные понятия комбинаторики
В разделе математики, который называется
комбинаторикой, решаются некоторые задачи,
связанные с рассмотрением множеств и
составлением различных комбинаций из элементов
этих множеств. Например, если взять 10 различных
цифр 0, 1, 2, 3,: , 9 и составлять из них комбинации, то
будем получать различные числа, например 143, 431,
5671, 1207, 43 и т.п.
Мы видим, что некоторые из таких комбинаций
отличаются только порядком цифр (например, 143 и
431), другие – входящими в них цифрами (например, 5671
и 1207), третьи различаются и числом цифр (например,
143 и 43).
Таким образом, полученные комбинации
удовлетворяют различным условиям.
В зависимости от правил составления можно
выделить три типа комбинаций: перестановки,
размещения, сочетания.
Предварительно познакомимся с понятием факториала.
Произведение всех натуральных чисел от 1 до n
включительно называют n-факториалом и
пишут ![]() .
.
Пример 1.
Вычислить: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
Решение. а) ![]() .
.
б) Так как ![]() и
и
![]() , то можно
, то можно
вынести за скобки ![]()
Тогда получим
![]() .
.
в) ![]() .
.
Перестановки.
Комбинация из n элементов, которые отличаются
друг от друга только порядком элементов,
называются перестановками.
Перестановки обозначаются символом Рn,
где n- число элементов, входящих в каждую
перестановку. (Р – первая буква французского
слова permutation– перестановка).
Число перестановок можно вычислить по формуле
![]()
или с помощью факториала:
![]()
Запомним, что 0!=1 и 1!=1.
Пример 2. Сколькими способами можно
расставлять на одной полке шесть различных книг?
Решение. Искомое число способов равно числу
перестановок из 6 элементов, т.е.
![]() .
.
Размещения.
Размещениями из m элементов в n в каждом
называются такие соединения, которые отличаются
друг от друга либо самими элементами (хотя бы
одним), либо порядком из расположения.
Размещения обозначаются символом ![]() , где m–
, где m–
число всех имеющихся элементов, n– число
элементов в каждой комбинации. (А-первая
буква французского слова arrangement, что означает
“размещение, приведение в порядок”).
При этом полагают, что n![]() m.
m.
Число размещений можно вычислить по формуле
![]() ,
,
т.е. число всех возможных размещений из m
элементов по n равно произведению n последовательных
целых чисел, из которых большее есть m.
Запишем эту формулу в факториальной форме:
![]() .
.
Пример 3. Сколько вариантов распределения
трех путевок в санатории различного профиля
можно составить для пяти претендентов?
Решение. Искомое число вариантов равно числу
размещений из 5 элементов по 3 элемента, т.е.
![]() .
.
Сочетания.
Сочетаниями называются все возможные
комбинации из m элементов по n, которые
отличаются друг от друга по крайней мере хотя бы
одним элементом (здесь m и n-натуральные
числа, причем n ![]() m).
m).
Число сочетаний из m элементов по n
обозначаются ![]()
(С-первая буква французского слова combination
– сочетание).
В общем случае число из m элементов по n
равно числу размещений из m элементов по n,
деленному на число перестановок из n
элементов:
![]()
Используя для чисел размещений и перестановок
факториальные формулы, получим:
![]()
Пример 4. В бригаде из 25 человек нужно
выделить четырех для работы на определенном
участке. Сколькими способами это можно сделать?
Решение. Так как порядок выбранных четырех
человек не имеет значения, то это можно сделать ![]() способами.
способами.
Находим по первой формуле
![]() .
.
Кроме того, при решении задач используются
следующие формулы, выражающие основные свойства
сочетаний:
![]()
![]()
(по определению полагают ![]() и
и ![]() );
);
![]() .
.
1.2. Решение комбинаторных задач
Задача 1. На факультете изучается 16 предметов.
На понедельник нужно в расписание поставить 3
предмета. Сколькими способами можно это сделать?
Решение. Способов постановки в расписание трех
предметов из 16 столько, сколько можно составить
размещений из 16 элементов по 3.
![]() .
.
Задача 2. Из 15 объектов нужно отобрать 10
объектов. Сколькими способами это можно сделать?
Решение.
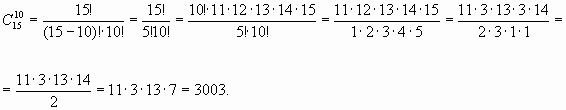
Задача 3. В соревнованиях участвовало четыре
команды. Сколько вариантов распределения мест
между ними возможно?
Решение.
![]() .
.
Задача 4. Сколькими способами можно составить
дозор из трех солдат и одного офицера, если
имеется 80 солдат и 3 офицера?
Решение. Солдат в дозор можно выбрать
![]()
способами, а офицеров ![]() способами. Так как с каждой командой
способами. Так как с каждой командой
из солдат может пойти любой офицер, то всего
имеется ![]()
способов.
Задача 5. Найти ![]() , если известно, что
, если известно, что ![]() .
.
Решение.
Так как ![]() , то
, то
получим
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
, ![]() .
.
По определению сочетания следует, что ![]() ,
, ![]() . Т.о.
. Т.о. ![]() .
.
Ответ: 9
1.3. Понятие о случайном событии. Виды
событий. Вероятность события
Всякое действие, явление, наблюдение с
несколькими различными исходами, реализуемое
при данном комплексе условий, будем называть испытанием.
Результат этого действия или наблюдения
называется событием.
Если событие при заданных условиях может
произойти или не произойти, то оно называется случайным.
В том случае, когда событие должно непременно
произойти, его называют достоверным, а в
том случае, когда оно заведомо не может
произойти,- невозможным.
События называются несовместными, если
каждый раз возможно появление только одного из
них.
События называются совместными, если в
данных условиях появление одного из этих событий
не исключает появление другого при том же
испытании.
События называются противоположными,
если в условиях испытания они, являясь
единственными его исходами, несовместны.
События принято обозначать заглавными буквами
латинского алфавита: А, В, С, Д, : .
Полной системой событий А1, А2, А3,
: , Аn называется совокупность
несовместных событий, наступление хотя бы одного
из которых обязательно при данном испытании.
Если полная система состоит из двух
несовместных событий, то такие события
называются противоположными и обозначаются А и ![]() .
.
Пример. В коробке находится 30
пронумерованных шаров. Установить, какие из
следующих событий являются невозможными,
достоверными, противоположными:
достали пронумерованный шар (А);
достали шар с четным номером (В);
достали шар с нечетным номером (С);
достали шар без номера (Д).
Какие из них образуют полную группу?
Решение. А – достоверное событие; Д –
невозможное событие;
В и С – противоположные события.
Полную группу событий составляют А и Д, В
и С.
Вероятность события, рассматривается как
мера объективной возможности появления
случайного события.
1.4. Классическое определение вероятности
Число, являющееся выражением меры объективной
возможности наступления события, называется вероятностью
этого события и обозначается символом Р(А).
Определение. Вероятностью события А
называется отношение числа исходов m,
благоприятствующих наступлению данного события А,
к числу n всех исходов (несовместных,
единственно возможных и равновозможных), т.е. ![]() .
.
Следовательно, для нахождения вероятности
события необходимо, рассмотрев различные исходы
испытания, подсчитать все возможные
несовместные исходы n, выбрать число
интересующих нас исходов m и вычислить отношение
m к n.
Из этого определения вытекают следующие
свойства:
Вероятность любого испытания есть
неотрицательное число, не превосходящее единицы.
Действительно, число m искомых событий
заключено в пределах ![]() . Разделив обе части на n, получим
. Разделив обе части на n, получим
![]() .
.
2. Вероятность достоверного события равна
единице, т.к. ![]() .
.
3. Вероятность невозможного события равна нулю,
поскольку ![]() .
.
Задача 1. В лотерее из 1000 билетов имеются 200
выигрышных. Вынимают наугад один билет. Чему
равна вероятность того, что этот билет
выигрышный?
Решение. Общее число различных исходов есть n=1000.
Число исходов, благоприятствующих получению
выигрыша, составляет m=200. Согласно формуле,
получим
![]() .
.
Задача 2. В партии из 18 деталей находятся 4
бракованных. Наугад выбирают 5 деталей. Найти
вероятность того, что из этих 5 деталей две
окажутся бракованными.
Решение. Число всех равновозможных независимых
исходов n равно числу сочетаний из 18 по 5 т.е.
![]()
Подсчитаем число m, благоприятствующих событию
А. Среди 5 взятых наугад деталей должно быть 3
качественных и 2 бракованных. Число способов
выборки двух бракованных деталей из 4 имеющихся
бракованных равно числу сочетаний из 4 по 2:
![]()
![]() .
.
Число способов выборки трех качественных
деталей из 14 имеющихся качественных равно
![]() .
.
Любая группа качественных деталей может
комбинироваться с любой группой бракованных
деталей, поэтому общее число комбинаций m
составляет
![]() .
.
Искомая вероятность события А равна отношению
числа исходов m, благоприятствующих этому
событию, к числу n всех равновозможных
независимых исходов:
![]() .
.
1.5. Теорема сложения вероятностей
несовместных событий
Суммой конечного числа событий называется
событие, состоящее в наступлении хотя бы одного
из них.
Сумму двух событий обозначают символом А+В, а
сумму n событий символом А1+А2+ : +Аn.
Теорема сложения вероятностей.
Вероятность суммы двух несовместных событий
равна ![]() сумме
сумме![]()
![]() вероятностей этих событий.
вероятностей этих событий.
![]() или
или
![]()
Следствие 1. Если событие А1, А2, :
,Аn образуют полную систему, то сумма
вероятностей этих событий равна единице.
![]() .
.
Следствие 2. Сумма вероятностей
противоположных событий ![]() и
и ![]() равна единице.
равна единице.
![]() .
.
Задача 1. Имеется 100 лотерейных билетов.
Известно, что на 5 билетов попадает выигрыш по 20000
руб., на 10 – по 15000 руб, на 15 – по 10000 руб., на 25 – по 2000
руб. и на остальные ничего. Найти вероятность
того, что на купленный билет будет получен
выигрыш не менее 10000 руб.
Решение. Пусть А, В, и С- события, состоящие в том,
что на купленный билет падает выигрыш, равный
соответственно 20000, 15000 и 10000 руб. так как события
А, В и С несовместны, то
![]() .
.
Задача 2. На заочное отделение техникума
поступают контрольные работы по математике из
городов А, В и С. Вероятность поступления
контрольной работы из города А равна 0,6, из
города В – 0,1. Найти вероятность того, что
очередная контрольная работа поступит из города С.
Решение. События “контрольная работа
поступила из города А“, “контрольная работа
поступила из города В” и “контрольная работа
поступила из города С” образуют полную систему,
поэтому сумма их вероятностей равна единице:
![]() , т.е.
, т.е. ![]() .
.
Задача 3. Вероятность того, что день будет
ясным, ![]() . Найти
. Найти
вероятность ![]()
того, что день будет облачным.
Решение. События “день ясный” и “день
облачный” противоположные, поэтому
![]() , т.е
, т.е ![]() .
.
1.6. Теорема умножения вероятностей
независимых событий
При совместном рассмотрении двух случайных
событий А и В возникает вопрос:
Как связаны события А и В друг с другом,
как наступление одного из них влияет на
возможность наступления другого?
Простейшим примером связи между двумя
событиями служит причинная связь, когда
наступление одного из событий обязательно
приводит к наступлению другого, или наоборот,
когда наступление одного исключает возможность
наступления другого.
Для характеристики зависимости одних событий
от других вводится понятие условной
вероятности.
Определение. Пусть А и В – два
случайных события одного и того же испытания.
Тогда условной вероятностью события А или
вероятностью события А при условии, что
наступило событие В, называется число ![]() .
.
Обозначив условную вероятность ![]() , получим формулу
, получим формулу
![]() ,
, ![]() .
.
Задача 1. Вычислить вероятность того, что в
семье, где есть один ребенок- мальчик, родится
второй мальчик.
Решение. Пусть событие А состоит в том, что в
семье два мальчика, а событие В – что один
мальчик.
Рассмотрим все возможные исходы: мальчик и
мальчик; мальчик и девочка; девочка и мальчик;
девочка и девочка.
Тогда ![]() ,
, ![]() и по формуле находим
и по формуле находим
![]() .
.
Событие А называется независимым от
события В, если наступление события В не
оказывает никакого влияния на вероятность
наступления события А.
Теорема умножения вероятностей
Вероятность одновременного появления двух
независимых событий равна произведению
вероятностей этих событий:
![]() .
.
Вероятность появления нескольких событий,
независимых в совокупности, вычисляется по
формуле
![]() .
.
Задача 2. В первой урне находится 6 черных и 4
белых шара, во второй- 5 черных и 7 белых шаров. Из
каждой урны извлекают по одному шару. Какова
вероятность того, что оба шара окажутся белыми.
Решение. Пусть ![]() – из первой урны извлечен белый шар;
– из первой урны извлечен белый шар; ![]() – из второй урны извлечен
– из второй урны извлечен
белый шар. Очевидно, что события ![]() и
и ![]() независимы.
независимы.
Так как ![]() ,
, ![]() , то по формуле
, то по формуле
![]() находим
находим
![]() .
.
Задача 3. Прибор состоит из двух элементов,
работающих независимо. Вероятность выхода из
строя первого элемента равна 0,2; вероятность
выхода из строя второго элемента равна 0,3. Найти
вероятность того, что: а) оба элемента выйдут из
строя; б) оба элемента будут работать.
Решение. Пусть событие А– выход из строя
первого элемента, событие В– выход их строя
второго элемента. Эти события независимы (по
условию).
а) Одновременное появление А и В есть
событие АВ. Следовательно,
![]() .
.
б) Если работает первый элемент, то имеет место
событие ![]()
(противоположное событию А– выходу этого
элемента из строя); если работает второй элемент-
событие В. Найдем вероятности событий ![]() и
и ![]() :
:
![]() ;
;
![]() .
.
Тогда событие, состоящее в том, что будут
работать оба элемента, есть ![]() и, значит,
и, значит,
![]() .
.
Полный вариант статьи.
