Практически всегда действует правило: чем выше возможная доходность, тем выше риски.
Но вот в обратную сторону правило работает не всегда, и это обидно: потенциальная доходность по активу так себе, а риск этого актива довольно высокий. Получается, для относительно невысокой доходности приходится рисковать так, будто вкладываешься в высокодоходный актив. В этом случае на помощь инвестору может прийти расчет соотношения «риск-доходность».
В статье я рассмотрю показатели, по которым можно оценить, насколько адекватно у определенного актива соотношение его риска и доходности. Вот какие показатели буду рассматривать:
- Коэффициент вариации — coefficient of variation.
- Коэффициент Шарпа — Sharpe ratio.
- Коэффициент информации — information ratio.
- Коэффициент Сортино — Sortino ratio.
- Коэффициент Трейнора — Treynor ratio.
Но прежде чем разбираться с показателями риска-доходности, нужно разобраться и с основой — с тем, как считаются сами доходность и риск.
Как считается доходность
Доходность — это показатель, характеризующий финансовый результат от инвестирования. Простыми словами, это процент от стоимости актива, который инвестор заработал «сверху». В общем виде доходность от вложения в финансовый актив считается так:
(Pt + 1 − Pt + CF) / Pt,
где Pt + 1 — цена актива сейчас или на момент продажи,
Pt — цена актива на момент покупки,
CF — промежуточный денежный поток, который принес актив за время владения им, — например, выплаченные дивиденды.
Бытовой пример: инвестор купил акцию за 100 $ и продал за 150 $, а за время владения получил 3 $ дивидендов. Доходность по формуле выше будет считаться так:
(150 − 100 + 3) / 100 = 0,53, или 53%
Для упрощения расчетов из формулы иногда убирают CF — промежуточные денежные потоки в виде дивидендов.
В зависимости от того, за какой период мы рассчитываем доходность, она может быть дневной, месячной, квартальной, годовой или общей.
Например, акции Apple 31 декабря 2016 стоили 27,4 $, а 30 сентября 2020 — 115,6 $. Посчитаем общую доходность за этот период:
(115,6 − 27,4) / 27,4 = 3,22, или 322%
Но доходность за все время владения инструментом не так показательна, если мы хотим сравнить активы, которыми владели в течение разных периодов. Например, один актив принес вам 11% за полгода, а второй — 30% за полтора года. Чтобы сравнить эффективность этих инструментов, их доходности нужно привести к общему знаменателю — годовой доходности. Годовая доходность показывает, сколько в среднем приносил актив за год владения им.
Для расчета годовой доходности можно использовать три подхода — в зависимости от того, какими данными владеет инвестор. Если есть сразу все данные, можно использовать любой из способов — результат будет одинаковый.
Если есть информация о доходности за каждый год владения активом, то доходность рассчитывается по следующей формуле:
((1 + r1) × (1 + r2) × (1 + r3) × (1 + rn))1/n − 1,
где rn — доходность за каждый анализируемый период,
n — количество периодов (лет).
Например, инвестор купил акцию компании за 100 $ и владел ею 3 года. За первый год стоимость акции выросла на 20%, во второй год — упала на 10% по отношению к прошлому периоду, а за третий год акции прибавили в цене 30%. Общая годовая доходность за эти три года будет считаться так:
((1 + 20%) × (1 − 10%) × (1 + 30%))1/3 − 1 = 11,98%
Кажется, что формула слишком сложная и что можно было бы просто взять доходность за каждый год, сложить и поделить на три — то есть посчитать среднее арифметическое. Но корректнее считать не среднее арифметическое, а среднее геометрическое — что и делает наша формула. И этому есть причина.
Для примера выше среднее арифметическое составило бы 13,33%:
(20% − 10% + 30%) / 3
Наше значение, полученное через среднее геометрическое, на 1,35 процентного пункта меньше. Геометрический показатель учитывает, что доходность неравномерна и меняется от года к году, — то есть такая доходность уже учитывает в себе некоторую волатильность.
Другими словами, чем выше волатильность актива, тем ниже будет значение среднего геометрического доходности к среднему арифметическому.
Для примера возьмем акции A и B и предположим, что за 4 года после покупки акции показали одинаковую итоговую доходность. Но на протяжении этих четырех лет вели себя по-разному: акции A росли более плавно, а акции B сильнее проседали и сильнее росли, то есть были более волатильными.
Котировки акций A и B за 4 года
| Покупка | Первый год | Второй год | Третий год | Четвертый год | |
|---|---|---|---|---|---|
| Акция A | 100 $ | 140 $ (+40%) | 150 $ (+7%) | 125 $ (−17%) | 180 $ (+44%) |
| Акция B | 100 $ | 70 $ (−30%) | 120 $ (+71%) | 100 $ (−17%) | 180 $ (+80%) |
Четвертый год
180 $ (+44%)
Четвертый год
180 $ (+80%)
Посчитаем данные для обоих активов: среднее арифметическое и среднее геометрическое, то есть годовую доходность.
Актив A:
Среднее арифметическое: (40% + 7% − 17% + 44%) / 4 = 18,5%.
Среднее геометрическое (годовая доходность): (1 + 40%) × (1 + 7%) × (1 − 17%) × (1 + 44%)1/4 = 15,8%.
Актив B:
Среднее арифметическое: (−30% + 71% − 17% + 80%) = 26%.
Среднее геометрическое (годовая доходность): (1 − 30%) × (1 + 71%) × (1 − 17%) × (1 + 80%)1/4 = 15,8%.
Среднее арифметическое актива А больше, чем актива В, — и если бы мы посчитали только среднее арифметическое, то сделали бы ложный вывод, что акции актива B выгоднее. Но ведь мы знаем, что это не так: в результате акции принесли одинаковую прибыль.
Годовая доходность по обеим акциям одинаковая — 15,8%. Но у акций B больше волатильность — и это выражается в разнице между средним арифметическим и средним геометрическим: чем она больше, тем больше волатильность.
В случае с акцией A разница между двумя арифметическим и геометрическим равна 2,8 процентных пункта. А у акции B эта разница составляет 10,4 процентных пункта — при равных доходностях по этой разнице можно сделать вывод, что акции B более волатильны.
Если известна совокупная доходность за весь срок владения, то формула для расчета годовой доходности будет выглядеть так:
(1 + Общая доходность)(365 / Количество дней владения активом) − 1
Например, инвестор купил акцию компании за 100 $, держал ее 714 дней, а на 715-й день продал и получил доходность 74% за весь период владения. Общая годовая доходность за рассматриваемый период будет считаться так:
(1 + 74%)(365 / 715) − 1 = 32,68%
Таким образом, на инвестициях в компанию инвестор заработал 32,68% годовых за рассматриваемый период.
Если известна начальная и конечная стоимость инвестиций, то общую годовую доходность можно вычислить по следующей формуле:
(Конечная стоимость актива / Начальная стоимость актива)(1 / Количество периодов) − 1
Например, инвестор купил 20 акций по 200 $ и решил удерживать их 2 года. За этот период компания каждый год выплачивала 1 $ дивидендов на акцию. На момент продажи цена акции составила 270 $. В этом случае общая годовая доходность будет такой:
((270 × 20 + 2 × 20) / 200 × 20)(1/2) − 1 = 16,62%
Совокупная доходность в данном кейсе составила 36%, а общая годовая доходность — 16,62%.
Как считается риск
Риск — это вероятность частичной или полной потери вложенного капитала. В классической портфельной теории риск вложения определяется как стандартное отклонение его доходности — то есть возможный разброс его фактической доходности вокруг средней доходности.
Предположим, в среднем акция растет на 10% в год, но при этом возможны отклонения на 5% в каждую сторону — то есть она может вырасти как на 15% в год, так и на 5%. Вот эти возможные отклонения нам и нужно рассчитать. Рассчитывается стандартное отклонение по следующей формуле:
где rn — доходность за n-й период, обычно годовая,
r̄ — среднее арифметическое доходности актива за все время владения,
n — количество периодов: если считаем по годовой доходности, то количество лет.
Например, инвестор владел активом 4 года — он знает доходность за каждый год и теперь хочет рассчитать стандартное отклонение доходности этого актива.
Доходность актива
| Период | Доходность |
|---|---|
| Первый год | −11,5% |
| Второй год | 15,9% |
| Третий год | 10% |
| Четвертый год | 7,2% |
Чтобы посчитать стандартное отклонение доходности, в первую очередь посчитаем — среднее арифметическое доходности:
(−11,5% + 15,9% + 10% + 7,2%) / 4 = 5,4%
Теперь можем подставить данные в формулу выше:
Стандартное отклонение составило 11,8%. Если допустить, что доходность акции нормально распределена, то по правилу трех сигм инвестор вправе ожидать, что с вероятностью 68,3% (одно стандартное отклонение — 68,3% вероятности) доходность акции в следующем году будет находиться в диапазоне от −6,4% до 17,2% — то есть от (5,4% − 11,8%) до (5,4% + 11,8%).
Чем сильнее значения фактической доходности отклоняются от ее среднего значения, тем больше стандартное отклонение, а значит, больше риск. Низкое значение стандартного отклонения означает, что годовые доходности лежат вблизи среднего значения и риск от вложения в актив невелик.
Формулу выше используют в случаях, если берутся котировки по акции не за весь период ее существования, а, предположим, за 2—3 года из возможных 10 лет, прошедших с момента первичного размещения акции на фондовом рынке. А если берутся котировки за весь период существования акции, то для расчета стандартного отклонения используется следующая формула — она отличается только знаменателем — берется полное количество периодов:
Анализируем на примере портфеля Баффетта
Итак, в общем виде мы рассмотрели понятия доходности и риска. Теперь я построю диаграмму «риск-доходность», чтобы проанализировать, какие активы показывают оптимальное отношение риска к доходности. Простыми словами, по диаграмме можно понять, какой актив дает максимальную доходность на единицу риска.
Для примера возьмем портфель Уоррена Баффетта: я взял те активы, по которым есть данные котировок за период с 2012 по 2020 год. По отчетным данным на 30 сентября 2020 года в портфель Баффетта входило 49 компаний, но лишь по 6 компаниям, составляющим существенную долю портфеля, были данные за нужный период.
6 крупнейших по весу компаний в портфеле Berkshire Hathaway на 30.09.2020
| Компания | Тикер | Вес актива в портфеле |
|---|---|---|
| Apple | AAPL | 47,78% |
| Bank of America | BAC | 10,63% |
| Coca-Cola | KO | 8,63% |
| American Express | AXP | 6,64% |
| Moody’s | MCO | 3,12% |
| US Bancorp | USB | 2,07% |
Вес актива в портфеле
47,78%
Вес актива в портфеле
10,63%
Вес актива в портфеле
8,63%
Вес актива в портфеле
6,64%
Вес актива в портфеле
3,12%
Вес актива в портфеле
2,07%
В расчетах для повышения точности я опираюсь на ежедневные котировки акций с 2012 по 2020 год — данные и расчеты представлены в гугл-таблице.
Еще для расчетов нам понадобится бенчмарк и безрисковая ставка. Бенчмарк — это портфель, с которым мы будем сравнивать эффективность наших активов. Обычно в качестве бенчмарка берут индекс на широкий рынок США — я взял ETF SPDR S&P 500.
Безрисковая ставка нужна для расчета показателей эффективности инвестиций: в ряде этих показателей она используется как доходность от вложения в безрисковый актив, то есть актив, риск наступления дефолта по которому стремится к нулю. Конечно, абсолютно безрисковых активов не существует, поэтому в качестве безрисковой ставки часто используют процентную ставку по государственным облигациям или определяют ее равной нулю. В качестве безрисковой ставки (RFR, risk-free rate) я взял 10-летние казначейские облигации США — 10-Year Treasury Constant Maturity Rate.
Шаги будут такие:
- Берем дневные доходности активов.
- Рассчитываем по ним среднюю годовую доходность и стандартное отклонение — как делали в разделе с расчетом риска.
- Строим карту «риск-доходность».
Показатели доходности и риска
| Компания | Тикер | Среднегодовая доходность | Стандартное отклонение |
|---|---|---|---|
| Apple | AAPL | 30,2% | 28,6% |
| Bank of America | BAC | 18,4% | 31,1% |
| Coca-Cola | KO | 10,0% | 18,3% |
| American Express | AXP | 15,0% | 29,3% |
| Moody’s | MCO | 27,1% | 27,7% |
| US Bancorp | USB | 10,8% | 26,1% |
| ETF S&P 500 | SPY | 15,5% | 16,8% |
| 10-Y Treasury Bonds | DGS10 | 2,1% | 0,0% |
Среднегодовая доходность
30,2%
Стандартное отклонение
28,6%
Среднегодовая доходность
18,4%
Стандартное отклонение
31,1%
Среднегодовая доходность
10,0%
Стандартное отклонение
18,3%
Среднегодовая доходность
15,0%
Стандартное отклонение
29,3%
Среднегодовая доходность
27,1%
Стандартное отклонение
27,7%
Среднегодовая доходность
10,8%
Стандартное отклонение
26,1%
Среднегодовая доходность
15,5%
Стандартное отклонение
16,8%
Среднегодовая доходность
2,1%
Стандартное отклонение
0,0%
Теперь строим карту по данным из таблицы: данные по среднегодовой доходности откладываем по вертикали, а по стандартному отклонению (риску) — по горизонтали.
Из диаграммы выше можно сделать ряд выводов относительно соотношения доходности и риска активов, определить наиболее предпочтительные и исключить наиболее убыточные из них: например, можно сделать вывод, что акции AAPL дают большую доходность, чем BAC и AXP, но при этом риск инвестирования в AAPL ниже.
Но зачастую неочевидно, какой из активов лучше, — в таком случае на помощь приходят показатели оценки соотношения риска и доходности.
Считаем индикаторы привлекательности активов
Индикаторы привлекательности активов приводят данные из таблицы выше к одному знаменателю: мы можем посчитать конкретные показатели для каждой бумаги и сравнить их. Разберем основные показатели.
Коэффициент вариации показывает величину риска, приходящуюся на единицу доходности. Он рассчитывается по следующей формуле:
CV = σ / r̄,
где σ — стандартное отклонение доходности актива,
r̄ — среднее арифметическое доходности актива.
Коэффициент вариации применяется для сравнения активов с разными доходностями и стандартными отклонениями. Применение показателя позволяет ранжировать активы по степени их рискованности. Чем больше значение показателя, тем выше риск инвестиций.
Коэффициент вариации для рассматриваемых акций
| Тикер | Среднегодовая доходность | Стандартное отклонение | Коэффициент вариации |
|---|---|---|---|
| AAPL | 30,2% | 28,6% | 0,95 |
| MCO | 27,1% | 27,7% | 1,03 |
| SPY | 15,5% | 16,8% | 1,09 |
| BAC | 18,4% | 31,1% | 1,70 |
| KO | 10,0% | 18,3% | 1,82 |
| AXP | 15,0% | 29,3% | 1,95 |
| USB | 10,8% | 26,1% | 2,40 |
Среднегодовая доходность
30,2%
Стандартное отклонение
28,6%
Коэффициент вариации
0,95
Среднегодовая доходность
27,1%
Стандартное отклонение
27,7%
Коэффициент вариации
1,03
Среднегодовая доходность
15,5%
Стандартное отклонение
16,8%
Коэффициент вариации
1,09
Среднегодовая доходность
18,4%
Стандартное отклонение
31,1%
Коэффициент вариации
1,70
Среднегодовая доходность
10,0%
Стандартное отклонение
18,3%
Коэффициент вариации
1,82
Среднегодовая доходность
15,0%
Стандартное отклонение
29,3%
Коэффициент вариации
1,95
Среднегодовая доходность
10,8%
Стандартное отклонение
26,1%
Коэффициент вариации
2,40
Можно сделать вывод относительно того, какой из активов несет больше или меньше риска. Теперь мы видим, что инвестиции в AAPL выгоднее не только инвестиций в BAC и AXP, но и вообще в любой из рассматриваемых активов: на единицу риска тут приходится наибольшая доходность. Самый рискованный актив — USB: на 1% доходности приходится 2,4% стандартного отклонения.
Коэффициент Шарпа показывает, во сколько раз избыточная доходность от инвестирования в портфель по сравнению с безрисковым активом выше уровня риска инвестиций. Избыточная доходность показывает, насколько доходность инвестиционного портфеля выше доходности безрискового актива, в роли которого чаще всего выступают государственные облигации.
Коэффициент Шарпа определяется по следующей формуле:
R̄x − R̄f / σx,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄f — средняя доходность безрискового актива за сопоставимый период,
σx — стандартное отклонение доходности актива за сопоставимый период.
Рассмотрим пример. Предположим, что средняя доходность по акции составляет 30% годовых при 20% стандартного отклонения, а средняя доходность по государственным облигациям США (безрисковый актив) равна 3% годовых. Тогда коэффициент Шарпа для нашей акции будет считаться так:
(30% − 3%) / 20% = 1,35
Это значение показателя говорит о высокой инвестиционной привлекательности нашей акции: доходность по ней выше доходности безрискового актива и превышает уровень риска.
Из формулы видно, что коэффициент Шарпа измеряет вознаграждение в виде средней избыточной доходности на единицу риска. Также следует отметить, что коэффициент был создан для анализа портфелей, а не отдельных инструментов, но все же его следует учитывать при отборе активов в портфель: он позволяет сделать вывод об эффективности вложения.
Критерии эффективности инвестиций на основе коэффициента Шарпа
| Критерий | Вывод по активу |
|---|---|
| Коэффициент Шарпа > 1 | Доходность инвестиций выше доходности безрискового актива и превышает уровень риска |
| 1 > коэффициент Шарпа > 0 | Риск инвестирования выше, чем доходность от инвестирования, — необходимо пересмотреть инвестиционное решение относительно этого актива или группы активов. Инвестирование в актив не приносит достаточной доходности |
| Коэффициент Шарпа < 0 | Доходность от инвестирования ниже доходности безрискового актива. Вероятно, лучше инвестировать в безрисковый актив |
Коэффициент Шарпа > 1
Доходность инвестиций выше доходности безрискового актива и превышает уровень риска
1 > коэффициент Шарпа > 0
Риск инвестирования выше, чем доходность от инвестирования, — необходимо пересмотреть инвестиционное решение относительно этого актива или группы активов. Инвестирование в актив не приносит достаточной доходности
Коэффициент Шарпа < 0
Доходность от инвестирования ниже доходности безрискового актива. Вероятно, лучше инвестировать в безрисковый актив
Рассмотрим результаты расчетов по коэффициенту Шарпа для акций в нашем примере.
Коэффициент Шарпа у акций из портфеля Баффетта
| AAPL | 0,98 |
| MCO | 0,90 |
| SPY | 0,79 |
| BAC | 0,52 |
| AXP | 0,44 |
| KO | 0,43 |
| USB | 0,33 |
Коэффициент информации характеризует соотношение риска-доходности актива или портфеля по сравнению с бенчмарком. Коэффициент расчетами напоминает коэффициент Шарпа, только вместо безрисковой ставки используется определенный эталон — бенчмарк. Бенчмарком могут выступать широкие рыночные индексы — MSCI, S&P 500, отраслевые индексы — DJA, собственноручно разработанные бенчмарки и так далее.
Иными словами, коэффициент информации — это отношение сверхдоходности к стандартному отклонению этой сверхдоходности у актива и бенчмарка. Коэффициент помогает понять, выгодно ли инвестировать в актив или набор активов — или проще и безопасней инвестировать в актив, выбранный бенчмарком. В нашем случае в качестве бенчмарка мы взяли ETF на S&P 500.
Формула выглядит так:
R̄x − R̄m / σx − m,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄m — средняя доходность бенчмарка за сопоставимый период,
σx − m — стандартное отклонение разности доходности актива и бенчмарка за сопоставимый период.
На примере AAPL и S&P 500 все будет выглядеть так:
В числителе: считаем разницу между средней доходностью акции AAPL (30,2% годовых) и средней доходностью индекса S&P 500 (15,5% годовых).
В знаменателе: сначала считаем разницу между дневными доходностями акции AAPL и индекса S&P 500, а потом по полученной совокупности дневных сверхдоходностей определяем стандартное отклонение и приводим дневное значение стандартного отклонения к годовому, перемножив дневное стандартное отклонение на корень из 252. Перемножаем на 252, так как в году 252 торговых дня. В нашей таблице этот расчет произведен на листе «Дневная доходность».
Итого получается:
(30,2% − 15,5%) / 21,28% = 0,69. Значение показателя выше 0,5 говорит о хорошей инвестиционной привлекательности акции.
Следует отметить, что этот коэффициент показывает эффективность активного управления, — при пассивном управлении, если мы просто покупаем индексный фонд и держим его, коэффициент будет равен нулю.
Чем больше значение коэффициента, тем выше избыточная «отдача» от инвестирования в определенный актив или портфель по сравнению с бенчмарком. Значение коэффициента информации в диапазоне от 0,5 до 0,74 считается хорошим, значение от 0,75 до 0,99 считается очень хорошим, а значение свыше 0,99 считается отличным. Ниже представлены результаты расчетов коэффициента информации для рассматриваемых акций.
Коэффициент информации у рассматриваемых акций
| AAPL | 0,69 |
| MCO | 0,63 |
| BAC | 0,13 |
| SPY | 0 |
| AXP | −0,02 |
| KO | −0,36 |
| USB | −0,26 |
Можно заметить, что для SPY (ETF на S&P 500) коэффициент информации равен нулю, так как он отражает движение рынка и не подразумевает сверхдоходности за активное управление. Напротив, хорошее значение коэффициента имеют акции AAPL и MCO, у которых на 1% стандартного отклонения сверхдоходности приходится 0,69 и 0,63% сверхдоходности соответственно. В случае с KO, AXP и USB отрицательные значения коэффициента связаны с отрицательными избыточными доходностями относительно бенчмарка.
Коэффициент Сортино — показатель, напоминающий коэффициент Шарпа, он отличается лишь расчетом риска. В коэффициенте Сортино для расчета риска учитываются только доходности актива ниже определенного уровня — чаще всего этот уровень определяется как доходность безрискового актива за сопоставимый период либо нулевая ставка.
Предполагается, что положительные отклонения доходностей — выше доходности безрискового актива — не несут риск, так как повышают доходность актива, — соответственно, учитывать их при расчете риска не нужно. Таким образом, для расчета стандартного отклонения необходимо выбрать только те дневные доходности, значение которых будет ниже доходности безрискового актива за этот же день. В нашей таблице все посчитано на листе «Кф. Сортино». Вот по какой формуле этот коэффициент рассчитывается:
R̄x − R̄f / σxd,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄f — средняя доходность безрискового актива за сопоставимый период,
σxd — стандартное отклонение доходности актива ниже заданного уровня.
Для примера рассмотрим логику, по которой фильтруются доходности для расчета риска по коэффициенту Сортино.
Месячные доходности акции и безрискового актива
| Период | Доходность акции | Доходность безрискового актива | Отфильтрованная доходность |
|---|---|---|---|
| 1 месяц | 0,16% | 0,18% | 0,16% |
| 2 месяц | −2,54% | 0,18% | −2,54% |
| 3 месяц | 0,29% | 0,18% | 0,00% |
| 4 месяц | 0,00% | 0,18% | 0,00% |
| 5 месяц | 2,24% | 0,18% | 0,00% |
| 6 месяц | −11,80% | 0,18% | −11,80% |
| 7 месяц | 14,10% | 0,18% | 0,00% |
| 8 месяц | 8,36% | 0,18% | 0,00% |
| 9 месяц | −2,14% | 0,18% | −2,14% |
| 10 месяц | 9,67% | 0,18% | 0,00% |
| 11 месяц | 7,00% | 0,18% | 0,00% |
| 12 месяц | 0,90% | 0,18% | 0,00% |
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,16%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
−2,54%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
−11,80%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
−2,14%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
В последней колонке оказались лишь те значения доходности акции, которые были ниже доходности безрискового актива за соответствующий период. Затем с помощью формулы стандартного отклонения рассчитываем риск по отфильтрованной доходности — он составит 3,54%. Среднемесячная доходность по акции — 2,19%, а среднемесячная доходность по безрисковому активу — 0,18%. Таким образом, коэффициент Сортино для акции из примера считается так:
(2,19% − 0,18%) / 3,54% = 0,57. Значение показателя ниже единицы указывает на то, что актив не обеспечивает должного уровня доходности на единицу нисходящего риска.
Чем больше значение коэффициента, тем выше вероятность безубыточности вложения и тем большей инвестиционной привлекательностью обладает рассматриваемый актив. Минимально допустимое значение показателя, определяющее инвестиционную привлекательность актива, — 1. Таким образом, на примере портфеля Баффетта допустимая и большая привлекательность у AAPL, MCO и SPY, а остальные же активы по коэффициенту Сортино непривлекательны, потому что не обеспечивают должного уровня доходности на единицу нисходящего риска.
Коэффициент Сортино у рассматриваемых акций
| AAPL | 1,59 |
| MCO | 1,40 |
| SPY | 1,19 |
| BAC | 0,86 |
| AXP | 0,73 |
| KO | 0,66 |
| USB | 0,53 |
Коэффициент Трейнора — еще один показатель, напоминающий коэффициент Шарпа и отличающийся только расчетом риска. В качестве риска берется коэффициент бета акции — он отражает волатильность актива по отношению к рынку. Коэффициент Трейнора показывает отношение сверхдоходности к рыночному риску.
Для расчета коэффициента бета акции используется следующая формула — рассчитанную бета акции можно найти на Yahoo Finance в разделе Summary на странице акции:
где σxm — ковариация между доходностью актива (портфеля) и доходностью рынка,
σm2 — дисперсия доходности рынка.
Методика расчета коэффициента бета акции раскрыта на листе «Дневная доходность» нашей таблицы, в столбце «Рыночный риск».
Коэффициент бета, находящийся в диапазоне от 0 до 1, свидетельствует о том, что акция движется в целом в одном направлении с рынком: если фондовый индекс растет, то растет и акция. Но значение коэффициента меньше 1 говорит о том, что актив менее чувствителен к движению рынка.
Коэффициент бета, равный 1, говорит о том, что движение актива полностью повторяет движение фондового индекса. Можно заметить, что значение 1 наблюдается у SPY, то есть у рыночного индекса.
Коэффициент бета больше 1 говорит о том, что динамика акции коррелирует с движением индекса, но при этом акция более чувствительно реагирует на любое движение рыночного индекса.
Коэффициент бета у рассматриваемых акций
| BAC | 1,38 |
| MCO | 1,26 |
| AXP | 1,26 |
| AAPL | 1,14 |
| SPY | 1,00 |
| USB | 1,15 |
| KO | 0,69 |
Зная коэффициент бета, доходность актива и доходность безрискового актива, мы можем рассчитать коэффициент Трейнора по следующей формуле:
R̄x − R̄f / βx,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄f — средняя доходность безрискового актива за сопоставимый период,
βx — коэффициент бета актива.
Допустим, необходимо рассчитать коэффициент Трейнора для акции USB — US Bancorp. Переходим на страницу компании на Yahoo Finance и находим Beta — 1,14 на момент написания статьи. Далее для расчета коэффициента Трейнора достаточно найти разницу между среднегодовой доходностью акции — 10,8% и среднегодовой доходностью безрискового актива — 2,1% и поделить полученное значение на бета акции.
Для акции USB:
(10,8% − 2,1%) / 1,14 = 0,076
Значение показателя выше нуля указывает на то, что инвестирование в актив более привлекательно, чем в рыночный индекс. Если коэффициент ниже нуля, то целесообразнее вкладывать в рыночный индекс, так как актив проигрывает рынку по соотношению риска и доходности. Таким образом, все акции портфеля инвестиционно привлекательны по этому показателю.
Коэффициент Трейнора у рассматриваемых акций
| AAPL | 0,24 |
| MCO | 0,20 |
| SPY | 0,13 |
| BAC | 0,12 |
| KO | 0,11 |
| AXP | 0,10 |
| USB | 0,08 |
Выводы
Теперь мы можем собрать сводную таблицу и оценить инвестиционную привлекательность активов на примере акций из портфеля Баффетта.
По данным из таблицы можно сделать вывод, что из рассмотренных активов наиболее привлекательны для инвестора Apple (AAPL), Moody’s (MCO) и SPDR S&P 500 (SPY).
Но важно помнить: кроме расчета индикаторов нужно оценивать перспективы отрасли и самой компании — и только когда картина собрана целиком, можно решать, инвестировать ли в компанию.
Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+
АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 (без ограничения срока действия).
ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.
Облигации считаются самым простым финансовым инструментом на бирже. Однако при этом у данных ценных бумаг есть свои нюансы, о которых должен знать каждый инвестор прежде, чем их купить. В этой статье расскажем о том, что такое доходность облигации, от чего она зависит и как её посчитать.
Что такое доходность облигации простыми словами
Облигация — долговое обязательство эмитента бумаги (того, кто её выпустил) перед держателем (тем, кто ей владеет). Эта бумага подтверждает, что тот, кто выпустил облигацию (компания или государство), одолжил капитал у инвестора с обещанием вернуть деньги с процентами в определённый срок.

Чтобы понимать, насколько прибыльна долговая бумага, инвестор должен уметь рассчитать её доходность. Если говорить простыми словами, доходом по облигации называется величина прибыли, полученная инвестором от вложений в ценную бумагу.
От чего зависит доход
Факторов, влияющих на доход облигации, много. Рассмотрим основные.
Рост котировок. Заработать инвестор может путём продажи бумаги по цене выше её покупки, так как облигациям, как и другим ценным бумагам на рынке, характерна волатильность.
Волатильность — показатель изменчивости цены актива за определённый промежуток времени.
Размер купона. Процент по облигации называется купоном. Эмитент облигации платит инвестору определённую сумму раз в месяц / квартал / год за то, что он одолжил у инвестора деньги.
По способу получения купонного дохода долговые бумаги бывают трёх видов:
- Купонная облигация. Инвестору в равные промежутки времени начисляется купонный платёж, а в конце срока обращения выплачивается обратно номинал бумаги.
- Облигация с плавающим купоном. Доходность по бумаге не фиксирована и изменяется вместе с внешними показателями: инфляцией, ключевой ставкой ЦБ и т. д.
- Дисконтная облигация. По ним не выплачиваются проценты за владение. Доходность бескупонной облигации фиксирована и формируется за счёт разницы между ценой покупки ниже номинала и первоначальной стоимостью облигации.
Погашение облигации. Это дата, в которую долговая бумага перестаёт торговаться на рынке. Как правило, в этот день эмитент выплачивает последний купон и возвращает инвестору номинал в полном размере.
Если инвестор приобрёл облигацию изначально ниже цены номинала, то при погашении, помимо купонов, он получит доход в виде курсовой разницы бумаги. Если же облигация покупалась по цене выше её первоначальной стоимости, то после выплаты номинала инвестор зафиксирует убыток.
Какие бывают виды
Чтобы выбрать облигацию, нужно сперва оценить её доходность. С одной стороны, инвестору не обязательно самостоятельно рассчитывать все показатели. Доходность бумаг можно узнать на сайтах Московской и Санкт-Петербургской бирж, а также в онлайн-приложении своего брокера.
С другой стороны, долговые бумаги не всегда продаются по номинальной стоимости. Соответственно, облигация может принести как больше прибыли, так и меньше ранее заявленным значениям. И чтобы правильно определить эту величину, необходимо различать виды доходности по облигациям.
Купонный доход
Данный показатель необходим, чтобы понимать, какой процент от номинала облигации (купон) начисляется каждый месяц / квартал / полгода / год.
Несмотря на то, что купонный доход выплачивается в определённые сроки, сумма купона начисляется инвестору ежедневно. Поэтому, если решите продать облигацию раньше следующего платежа, то уже начисленные неполные купоны вы не потеряете — следующий держатель облигации выплатит вам накопленный купонный доход (НКД) автоматически.
В этом примере есть и обратный эффект. Если вы только покупаете облигацию, то при выплате очередного купонного дохода часть полученной прибыли с вас спишут в пользу предыдущего владельца. Сумма списаний зависит от того, сколько дней прошло с момента выплаты прошлого купона.

Текущая доходность облигации
Если купонная доходность облигации определяется на основе номинала бумаги, то текущая учитывает только реальную цену приобретения бумаги на рынке.
Доходность к погашению облигации (простая)
Доходность к погашению облигации — экономический показатель, который отражает прибыльность бумаги на протяжении всего срока её обращения.
Простая доходность к погашению учитывает не только реальную цену покупки, но и ожидаемую стоимость погашения.
Если инвестор намерен владеть облигацией до конца её срока, то планируемая цена погашения бумаги будет равна её номиналу.
Эффективная к погашению
Эффективная доходность облигации — полный доход инвестора от вложений в долговую бумагу с учётом реинвестирования купонов по аналогичной купонной ставке.
Как рассчитать доходность облигации
Определить доходность долговой ценной бумаги можно 4 способами. Перед тем как считать доходность облигации, важно узнать некоторые данные:
- номинал облигации;
- размер купона / купонную ставку;
- срок погашения бумаги;
- рыночную стоимость облигации;
- частоту купонных выплат.
1 способ. Если покупать облигацию по номиналу и определять только купонный доход, потребуется следующая формула:
Купонный доход, за год = (Размер годовых купонов / Номинал) × 100%
Пример расчёта доходности облигации.
Эмитент выпустил облигацию номиналом 1000 руб. с ежеквартальной выплатой 25 руб. Определим купонный доход.
Купонный доход, за год = (25 руб. х 4 / 1000 руб.) х 100% = 10%
Таким образом, годовой купонный доход составляет 10%. Для простоты восприятия в данном случае учитывается тот факт, что инвестор приобрёл корпоративную облигацию по номиналу и держал её в своём инвестиционном портфеле весь срок обращения.
2 способ. При приобретении бумаги по цене, отличной от номинала, необходимо будет рассчитать текущую доходность облигации:
Доходность, годовых = (Купонный доход за год / Цена покупки облигации) × 100%
Пример расчёта справедливой доходности облигации.
Номинал долговой бумаги компании А равен 1000 р. Доходность по облигации составляет 8%. Купонный доход за год — 80 р. Инвестор покупает эту бумагу на вторичном рынке по цене 970 р. Определим её текущую доходность.
Доходность, годовых = (80 р. / 970 р.) х 100% = 8,24%
В данном случае показатель выше первоначальной купонной ставки, так как текущая стоимость облигации ниже номинала. По доходности бумага выглядит привлекательной, её необходимо покупать.
3 способ. Если же инвестор купил облигацию не по номиналу и знает, по какой цене он готов будет её продать, то его расчёт должен сводиться к формуле простой доходности облигации:
((Номинал − Полная цена покупки + Все купоны за период владения) / Полная цена покупки) × (365 / Количество дней до погашения) × 100%
Определим простую доходность к погашению долговой бумаги на основе следующего примера.
Номинал облигации — 1000 руб. Купон в размере 20 руб. выплачивается 4 раза в год (каждый квартал). Срок обращения — 2 года. Облигация начала торговаться на рынке 1 марта. При этом инвестор приобретает бумагу по цене 950 руб. 1 июня, сразу же после первой выплаты купона. Соответственно, предыдущему владельцу инвестор не перечисляет ничего из накопленного купонного дохода (НКД).
Купонов для выплат осталось 7 (4 раза х 2 года − 1 купон). Общая сумма оставшихся купонов — 140 руб. (7 х 20 р). Количество дней до погашения — 638 (365 х 2 года − 92 дня).
Примечание. Суммарно весенних дней в календаре — 92.
Считаем:
((1000 руб. − 950 руб. + 140 руб.) / 950 руб.) × (365 / 638) × 100% = 11,44%
Получается, что годовая доходность облигации составит 11,44% с учетом неполученного купона, но с ценовым дисконтом при покупке.
4 способ. Наиболее объективным и полным вариантом определения доходности облигации с учётом возможности реинвестирования купонных платежей можно считать формулу расчёта эффективной доходности:
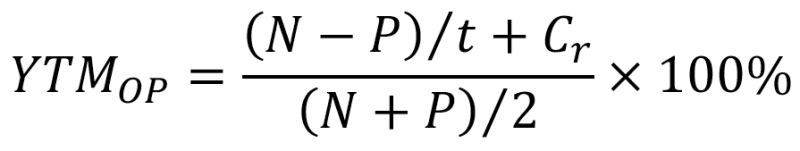
- YTMOP — доходность к погашению;
- Cr — сумма купонных выплат за год;
- P — текущая рыночная цена облигации;
- N — номинал облигации;
- t — лет до погашения.
Простой пример для расчёта эффективной доходности.
Номинал облигации — 1000 руб. Инвестор приобрел бумагу за 1020 руб. Ставка купона — 10%. Соответственно, сумма купонных выплат составит 100 руб. Срок обращения — 2 года.
Рассчитаем:
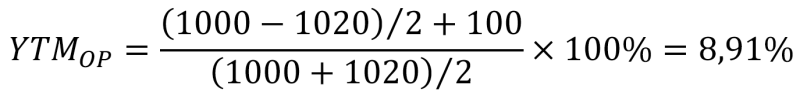
Итоговая доходность по бумаге составляет для инвестора не 10% годовых, а лишь 8,91%.
Налог на доход и комиссия брокера
По состоянию на 2022 год ставка НДФЛ по операциям с ценными бумагами равна 13%. Налоговым агентом на фондовом рынке является сам брокер. Это значит, что при продаже ценной бумаги из полученного инвестором дохода брокерская фирма автоматически вычтет сумму налога.

Если совокупный доход за год более 5 млн руб., то сумма превышения данного порога облагается НДФЛ по ставке 15%.
Помимо налогов, с инвестора также взимаются различные комиссии — сборы со стороны брокера. Их размер зависит от выбранного вами тарифа.
За что брокер может взимать комиссию:
- За ведение счёта. Как правило, российские брокеры взимают подобную комиссию, если клиент совершал хоть одну торговую операцию за месяц.
- За сделки. Это основной вид брокерской комиссии. Плата в пользу брокера взимается за каждую покупку и продажу ценной бумаги. У всех посредников величина сбора разная и может варьироваться в диапазоне от 0,05 до 0,1% от суммы сделки.
- За вывод средств. Согласно тарифу, брокер имеет право взимать с клиента фиксированный процент от величины вывода средств. Однако данная форма комиссии всё реже практикуется на рынке.
- За доступ к торговым платформам. Зачастую брокер не берёт комиссию за установку торгового терминала, разработанного брокерской компанией. Однако посредник может взять с инвестора фиксированную комиссию, если сумма депозита меньше заявленной для бесплатной установки ПО.
- Депозитарная комиссия. Когда инвестор откроет у посредника брокерский счёт, ему автоматически открывается и депозитарный счёт для учёта ценных бумаг. Сейчас почти все российские брокеры отказались от данной комиссии. Однако нередко этот вид комиссии может быть прописан в общих условиях тарифа.
Важно! Прежде чем выбрать брокера, тщательно ознакомьтесь с тарифными планами каждого. Зачастую в правилах пользования тарифом могут прописываться дополнительные комиссии за те или иные действия, совершаемые инвестором.
Почему меняется доходность к погашению?
Доходность к погашению облигации нередко в течение всего срока обращения изменяется. Причиной этому может быть изменчивость процентных ставок ЦБ, кризис в экономике, обострение политической обстановки в стране и в мире и многое другое.
Что происходит с доходностью облигации, когда цена облигации растёт?
Когда облигация начинает дорожать, то уровень её доходности падает.
Где посмотреть доходность к погашению облигации?
Наиболее эффективный и быстрый способ узнать доходность к погашению облигации — воспользоваться облигационным калькулятором на сайте биржи. Также можно посмотреть доходность в личном кабинете у брокера или рассчитать её значение самостоятельно.
Как рассчитать НКД по облигации?
Накопленный купонный доход по облигациям рассчитывается по следующей формуле:
НКД = Н × (С / 100) × Д / 365, где
- Н — величина номинала,
- С — годовая ставка купона,
- Д — число дней с момента прошедшей выплаты по купону.
3.7
Рейтинг статьи 3.7 из 5
Содержание статьи
Показать
Скрыть
Облигация — это долговая ценная бумага, по которой эмитент (тот, кто выпускает облигации) получает деньги в долг от инвестора. Взамен эмитент гарантирует, что выплатит инвестору в определенный срок стоимость облигации (номинал) и процент за пользование средствами (купонный доход) в будущем.
Облигации также называются бондами и считаются консервативным финансовым инструментом. Облигация подразумевает фиксированные условия, то есть эмитент обязан платить процент (купон) в четко фиксированные сроки и в фиксированном объеме. Их сравнивают с вкладами, но доходность облигаций обычно выше ставок по депозитам из-за наличия рыночных рисков и риска дефолта у компании-эмитента.
Доходность облигаций — это величина прибыли, которую инвестор получает в результате вложений в ценную бумагу. Таким образом, чтобы понять, насколько интересна та или иная облигация для вложений, инвестор должен уметь определять ее доходность.
Основные типы доходности облигаций
- Доходность бескупонной облигации
Бескупонная (дисконтная) облигация — это облигация, которая продается по цене ниже номинальной стоимости, а затем погашается по номиналу. Никаких других выплат держатели таких бумаг не получают. Доходность бескупонной облигации определяется разницей между ценой продажи и ценой покупки бумаги (как правило, при размещении такие облигации продаются инвесторам существенно дешевле номинала).
- Купонная доходность
Купонные облигации предполагают выплату держателям процентов (купона), которая производится с определенной периодичностью — например, раз в полгода или раз в год. Даты выплат установлены заранее, но размер купона со временем может изменяться. Купонная доходность определяется в процентах годовых и показывает прибыль, которую владелец облигации получит в качестве купонных выплат за год (при полугодовом купоне два раза в год выплачивается половина суммы). Это более широко распространенный вид доходности.
- Номинальная доходность
Номинальная доходность облигации показывает соотношение начисленного купона и номинальной стоимости ценной бумаги.
- Текущая доходность
Текущая доходность показывает соотношение начисляемого купона и актуальной рыночной цены облигации. При расчете этого показателя используется не номинальная стоимость бумаги, а ее текущая рыночная цена.
В случае краткосрочных вложений при расчете текущей доходности учитывают также накопленный купонный доход — часть купонных выплат, которая полагается предыдущему держателю облигации, но не была ему выплачена.
- Доходность к погашению (Yield to Maturity)
Доходность к погашению отражает прибыльность облигации на протяжении всего срока ее обращения, то есть показывает, сколько заработает инвестор, если купит облигации по текущей цене и не будет продавать раньше срока погашения. Простая доходность к погашению учитывает реальную цену покупки и стоимость бумаги на момент ее погашения. Эффективная доходность к погашению — это полный доход инвестора от вложений в облигацию с учетом реинвестирования полученных купонов на аналогичных условиях (по той же ставке купона). В реальности цена облигации меняется, поэтому и фактическая доходность будет отличаться.
- Доходность после удержания налогов
Доходы от облигаций облагаются налогом. Ставка налога в отношении доходов, полученных от облигаций, составляет 13%. Если сумма доходов превышает 5 млн рублей, ставка налога составит 15%. Для лиц, не являющихся резидентами России, ставка налога составляет 30%. Поэтому, чтобы понимать, какие реальные доходы может принести облигация, важно знать доходность после удержания налогов.
С помощью сервиса Банки.ру вы можете выбрать подходящие облигации.
Альтернатива валютным вкладам? Кто выпускает облигации в юанях и стоит ли их покупать
Практическая доходность все-таки одна — это доходность к погашению или оферте, говорит генеральный директор ИК «Иволга Капитал» Андрей Хохрин.
«Упрощенно, это купонная доходность, поделенная на рыночную стоимость облигации, уменьшенная или увеличенная на премию или дисконт рыночной цены облигации к ее номиналу, которые в свою очередь поделены на количество лет до погашения», — поясняет он.
Хохрин обращает внимание, что обычно при расчетах облигационных доходностей предполагается, что выплаченный купон реинвестируется в ту же облигацию. Многие эмитенты выплачивают купон ежемесячно, то есть при ставке купона 15% и его ежемесячной выплате доходность облигации достигнет уже 16%.
Управляющий по анализу банковского и финансового рынков ПСБ Дмитрий Грицкевич поясняет, что если по бумаге есть оферта, то доходность можно считать не к дате погашения, а к дате оферты. Оферта — это дата, в которую можно досрочно погасить номинал облигации.
Руководитель группы продаж и клиентских операций ПСБ Игорь Федосенко отмечает, что обычно инвесторы используют показатель доходности к погашению, когда планируют держать облигации до окончания срока обращения. В остальных случаях можно использовать текущую доходность — так проще сравнить облигации с разным сроком погашения. Купонную доходность, по его словам, используют преимущественно для оценки стоимости облигации до того, как она начнет торговаться на бирже.
Грицкевич добавляет, что для анализа привлекательности облигаций помимо доходности используют также спред к кривой ОФЗ — разницу между доходностью облигации и ОФЗ (облигации федерального займа) с соответствующими сроками и учетом рисков эмитента.
Как рассчитать доходность облигации
Доходность бескупонной облигации
Чтобы рассчитать доходность бескупонной облигации, нужно из номинальной стоимости облигации вычесть цену, по которой она приобреталась. В относительном выражении доходность вычисляется по формуле:
Д = (Н − Ц) / Ц * 100%, где:
- Д — доходность дисконтной облигации;
- Н — номинальная цена (цена погашения);
- Ц — цена покупки.
Пример: Лев приобрел облигацию Сбербанка номинальной стоимостью 1 000 руб. за 750 рублей с погашением в марте 2025 года. Через два года он получит 1000 руб., а его чистая прибыль составит 250 руб. Доходность облигации составляет:
1 000 руб. − 750 руб. = 250 руб., или (1 000 руб. — 750 руб.) / 750 руб. * 100% = 33,3% за два года или 16,65% годовых.
Купонная доходность
Для расчета купонной доходности нужно сумму купонных выплат поделить на стоимость облигации.
Номинальная купонная доходность
Для расчета номинальной купонной доходности применяется следующая формула:
Д = К / Н * 100%, где:
- К — сумма купонных выплат за период;
- Н — номинальная цена облигации.
Пример: Мария купила облигацию «Русала» за 1 000 руб., по которой предусмотрена выплата купона в размере 2,5% дважды в год.
Доходность облигации составляет:
(1 000 руб. /100% * 2,5% + 1 000 руб. / 100% * 2,5%) / 1 000 руб. * 100% = 5% годовых.
Текущая купонная доходность
Для расчета текущей купонной доходности применяется следующая формула:
Д = К / Ц * 100%, где:
- К — сумма купонных выплат за период;
- Ц — текущая рыночная цена облигации.
Пример: Светлана купила облигацию «Газпрома» номинальной стоимостью 1 000 руб. по рыночной цене 1 100 руб. По облигации предусмотрена выплата купона раз в год в размере 8% годовых.
Доходность облигации составит:
(1 000 руб. / 100% * 8%) / 1 100 руб. * 100% = 7,3% годовых.
Модифицированная текущая купонная доходность
В случае краткосрочных вложений учитывается также накопленный купонный доход:
Д = К / (Ц + НКД) * 100%, где:
- К — сумма купонных выплат за период;
- Ц — текущая рыночная цена облигации;
- НКД — накопленный купонный доход.
Накопленный купонный доход считается по формуле НКД = К * t / 365, где
- К — сумма купонных выплат за год;
- t — число дней от начала купонного периода.
Пример: Марина 1 марта купила облигацию «Роснефти» номинальной стоимостью 1 000 юаней за 1 100 юаней. По бумаге предусмотрена выплата купона в размере 1,5% дважды в год — 1 апреля и 1 октября, то есть 3% годовых. Марина заплатит предыдущему владельцу в качестве накопленного купонного дохода 12,5 юаней (1,5% от 1 000 юаней, купонный доход накопленный к 1 марта). Доходность облигации составит:
(1 000 юаней / 100% * 1,5% + 1 000 юаней / 100% *1,5%) / (1 100 юаней + 30 юаней * 152 / 365%) * 100% = 2,7%.
Доходность к погашению
При расчете такой доходности учитывается номинальная и рыночная цена, весь купонный доход и срок владения облигацией.
Простая доходность к погашению
Простая доходность к погашению рассчитывается по формуле:
Д = ((Н − Ц) + К) / Ц * 365 / t * 100%, где:
- Н — номинальная цена облигации (или цена ее продажи);
- Ц — рыночная цена бумаги при покупке;
- К — сумма купонных платежей за весь период владения бумагой;
- t — количество дней до погашения (продажи).
Пример: Иван 11 января 2021 года приобрел облигацию «Роснефти» номинальной стоимостью 1 000 рублей за 700 рублей. По облигации предусмотрена купонная выплата в размере 4% дважды в год (в мае и ноябре) или 8% годовых. 31 декабря 2022 г. Иван продал ценную бумагу за 900 рублей.
Доходность облигации составит:
((900 руб. − 700 руб.) + 1 000 / 100% * 4% * 4 раза) / 700 * 365 / 720 * 100% = 26,1%
Эффективная доходность к погашению
Эффективная доходность к погашению также учитывает реинвестирование полученных купонов. Формула будет выглядеть следующим образом:
Д= ((Н − Ц) + К) / Ц * 365 / t * 100% + ∑ИК, где
- Н — номинальная цена облигации (или цена ее продажи);
- Ц — рыночная цена бумаги при покупке;
- К — сумма купонных платежей за весь период владения бумагой;
- t — количество дней до погашения (продажи);
- ∑ИК — доход от реинвестирования купонных выплат.
Пример: Игорь 11 января 2021 года приобрел облигацию «Роснефти» номинальной стоимостью 1 000 рублей за 700 рублей. По облигации предусмотрена купонная выплата в размере 4% дважды в год (в мае и ноябре). Игорь инвестирует полученные купоны в приобретение облигаций на тех же условиях и держит до погашения. Дата погашения облигации — 31 декабря 2023 года. Доходность облигации составит:
Д = (( 1000 руб. − 700 руб.) + 1 000 / 100% * 4% * 6 раз) / 700 * 365 / 1 085 * 100% + ∑ИК = 26% + ∑ИК
При расчете показателя ∑ИК нужно учесть несколько последовательных реинвестиций купонных доходов, в результате чего появятся сложные проценты. Все это нужно учитывать в формуле при расчетах, что делает подсчет вручную трудоемким и нецелесообразным.
Поэтому при расчете эффективной доходности к погашению рекомендуем воспользоваться специальным онлайн-калькулятором. Например, на сайте Мосбиржи. Или онлайн-калькулятором облигационных доходностей на портале CBonds.ru (вкладка «Моделирование эмиссий»), отмечает Хохрин.
Самостоятельно эффективную доходность также можно посчитать в Excel через формулу ЧИСТВНДОХ, поясняет Грицкевич из ПСБ. Для этого нужно построить ряд с денежным потоком, включающим затраты на покупку облигации (с минусом), доходы от купона и погашения (с плюсом) и ряд дат.
Федосенко обращает внимание, что считать доходность к погашению самостоятельно инвестору необязательно — она есть в брокерских приложениях и на сайте биржи, где торгуются бумаги.
Как учитывать налоги при расчете доходности облигаций
НДФЛ взимается как с купонов, так и с дохода от прироста стоимости облигации (если они были проданы или погашены дороже, чем куплены), обращает внимание Хохрин. При этом, по его словам, обе базы налогообложения — купон и курсовая разница — не учитываются.
«Вы можете купить облигации по 105% от номинала и продать по 100% от номинала и за время владения получить 5% от их начальной стоимости в виде купона. С купона вы заплатите полный НДФЛ, по ставке 13–15%, который не сможете уменьшить на убыток от обесценения бумаг. Налог в этом примере сделает инвестицию убыточной», — отмечает эксперт.
Выбрать облигации в портфель
Грицкевич добавляет, что при покупке облигации в середине купонного периода инвестор выплачивает продавцу вместе с ценой облигации еще и НКД, при этом в дату выплаты весь размер купона облагается налогом. То есть инвестор уплачивает налог и за период, когда он не владел облигацией (с момента начала купонного периода и до момента покупки облигации на рынке).
Он также отмечает, что если ставка купона превышает ключевую ставку ЦБ РФ более чем на 5 процентных пунктов, то с превышения удерживается НДФЛ по ставке 35%. Если облигация валютная, то дополнительно удерживается налог на валютную переоценку.
Как рассчитать доходность после удержания налога
Руководитель налоговой дирекции УК «Альфа-Капитал» Константин Асабин отмечает, что финансовый результат, который должен быть уменьшен на размер НДФЛ — это предполагаемая доходность облигаций за вычетом комиссий и иных удержаний.
Как работают замещающие облигации и в чем интерес инвестора
«Если при доходе в 10% издержки обойдутся инвестору в 0,5%, финансовый результат составит 9,5%. Его нужно будет уменьшить на налог в 13%, что даст итоговый результат в 8,265%», — поясняет аналитик.
Как снизить налоговую нагрузку
Доходность облигаций учитывается в общем финансовом результате по соответствующему виду ценных бумаг, и такую доходность можно уменьшить на прямые расходы, которые несет инвестор (комиссии, сборы, иные удержания), говорит Асабин. Если работать с российским банком, брокером или управляющей компанией, все эти расходы обязательно учитываются, поясняет он.
По мнению Грицкевича, для оптимизации налоговой нагрузки с доходов за операции с облигациям лучше всего подходит индивидуальный инвестиционный счет (ИИС) типа А (вычет до 52 тыс. руб.). При этом можно написать заявление брокеру, чтобы купоны выплачивались не на брокерский, а на расчетный счет. Тогда купоны можно использовать в качестве пополнения ИИС (до 400 тыс. руб. в год).
Выбрать брокера для инвестиций
По словам Асабина, если инвестор не использует ИИС, для него доступен инвестиционный налоговый вычет. Он позволяет уменьшить налоговую базу до 3 млн руб. за каждый календарный год, в течение которого бумага принадлежала инвестору. Минимальный срок владения облигацией для получения вычета — 3 года.
О желании получить такой вычет нужно заранее, до окончания календарного года (налогового периода) известить банк, брокера или управляющую компанию. Если вычет через агента получить не удалось, необходимо подать налоговую декларацию.
Хохрин отмечает, что купонные доходы при расчете НДФЛ не сальдируются, а доходы и убытки от изменения цен разных облигаций в одном портфеле сальдируются (при условии, что инвестор их зафиксировал, то есть продал облигации). Это может быть маневром для оптимизации налоговой нагрузки, считает он. Грицкевич добавляет, что распространенным способом снижения НФДЛ является сальдирование убытков: уплаченный налог по купонам можно сальдировать с убытком по акциям и/или облигациям.
Подобрать облигации вы можете в этом разделе, выбрать подходящего брокера — здесь.
Еще по теме:
Как платить налоги с продажи акций
Как рассчитывать доходность инвестиций, чтобы зарабатывать больше
Это проще, чем кажется.

Зачем рассчитывать доходность
Накупить ценных бумаг и сколько‑то на них заработать довольно просто. Инвестору даже не надо никуда ходить — брокеры переехали в мобильные приложения, через которые можно приобрести разные активы на разных рынках.
Пока инвестор не знает, сколько именно он зарабатывает, ему трудно сохранить деньги или выгодно их вкладывать в будущем. Человек может думать, что у него отличные результаты, но внимательный расчёт покажет: не такие уж и отличные, особенно в сравнении с другими инструментами, поэтому нужно подумать о смене активов. Или наоборот: реальная доходность хорошая, и стоит продолжать в том же духе.
Для того чтобы всё это понять, нужно разобраться с относительной доходностью портфеля и подсчитать, сколько процентов годовых получает инвестор.
Как рассчитать годовую доходность инвестиций
Профессионалы используют сложные формулы вроде коэффициента Шарпа или коэффициента Трейнора. Частному инвестору это может пригодиться, но для начала будет достаточно таблички в Excel и нескольких чисел из приложения брокера.
Если инвестор завёл табличку и вносит туда все движения денег, даты, выплаты дивидендов и комиссии, то сможет всё удобно посчитать. Базовая формула выглядит так:
Прибыль (или убыток) по сделке + дивиденды − комиссии = доходность
Учесть активы
Допустим, инвестор девять месяцев подряд покупал и продавал ценные бумаги. Он знает, сколько денег пришло и ушло, помнит даты операций и не забыл всё подписать. В итоге у него есть простая таблица:
Инвестор покупал и продавал активы, вносил деньги на счёт и выводил их, поэтому правильно сначала посчитать чистую доходность. Достаточно просто подставить формулу ЧИСТВНДОХ (или XIRR, это то же самое).
Получается, что инвестор заработал 18,66% годовых. Это неплохо, потому что индекс S & P 500 за то же время вырос на 19,6%.
Заплатить комиссии
Брокеры берут процент с каждой операции, разве что конкретные суммы варьируются — лучше всего уточнить это в своём договоре со специалистом. Часто комиссии уже «вшиты» в отчёты, но иногда они идут дополнительной строкой. В таком случае лучше отдельно прописывать их в табличке.
Предположим, что инвестор платит 0,3% после каждой покупки или продажи актива. Если он учёл показатель заранее, то не придётся использовать новые формулы, сойдёт та же ЧИСТВНДОХ. Окажется, что заработано меньше.
Вычислить годовые проценты
Но инвестор рассчитал доходность портфеля только за то время, что вкладывал деньги. Это меньше года, а сравнивать объёмы прибыли принято в процентах годовых. Нужно добавить ещё одну формулу:
Чистая доходность × дни в году / дни инвестирования = годовая доходность
В нашем случае инвестор торговал ценными бумагами 236 дней. Применим формулу:
Годовая доходность вложений — 26,49%. Если инвестор сравнит её, например, с депозитами, то выяснится: прибыльность его активов выше в четыре‑пять раз, поэтому выгоднее продолжать размещать деньги таким способом. При этом индекс S & P 500 принёс 30,3% годовых за тот же период в 2021 году — возможно, что целесообразнее вложиться в фонды, которые за ним следуют.
Как рассчитать доходность инвестиций в будущем
Ни один аналитик, профессиональный инвестор или ясновидящий не сможет ответить точно. Но можно хотя бы попытаться оценить этот показатель с помощью исторической доходности.
Итак, инвестор заработал 18,66% годовых в 2021 году. Он изучил доходность своих активов за предыдущие 5–10 лет и понял: в среднем такой портфель приносил 13% годовых.
Не факт, что в будущем всё повторится. Тренды в экономике меняются, компании попадают под жёсткое регулирование, и всегда есть угроза кризиса.
Но инвестор всё учёл и предполагает, что в следующие 10 лет доходность сохранится на среднем уровне.
Деньги инвестора остаются на счету, потому что он копит на квартиру детям. Все полученные дивиденды человек реинвестирует обратно. В этом случае подключается магия сложного процента:
| Сумма на счёте, рубли | Доходность | Годовая прибыль, рубли | |
| 2022 | 90 400 | 13% | 10 400 |
| 2023 | 102 152 | 13% | 11 752 |
| 2024 | 115 431,76 | 13% | 13 279,76 |
| 2025 | 130 437,89 | 13% | 15 006,13 |
| 2026 | 147 394,81 | 13% | 16 956,92 |
| 2027 | 166 556,14 | 13% | 19 161,33 |
| 2028 | 188 208,44 | 13% | 21 652,30 |
| 2029 | 212 675,54 | 13% | 24 467,10 |
| 2030 | 240 323,36 | 13% | 27 647,82 |
| 2031 | 271 565,39 | 13% | 31 242,03 |
Если бы инвестор каждый год забирал прибыль и вновь вкладывал ту же сумму, то за 10 лет заработал бы 104 000 рублей. Но действия принесли ему 191 565 рублей — почти вдвое больше. Это называется сложным процентом, или капитализацией процентов.
Как не стоит считать доходность
Формулы чистой доходности и учёт комиссий позволяют увидеть «честные» числа. Потому что интуитивный способ расчёта — разделить нынешнюю стоимость портфеля на вложения — не поможет. Это подходит только в случае, если инвестор приобрёл активы, а ровно через год продал.
В реальности человек почти наверняка докупает в портфель что‑то новое или продаёт бумаги. Рассчитать доходность каждой отдельной инвестиции будет просто, но для всего портфеля, да ещё и с учётом комиссий, легче использовать формулы и табличку.
Как учитывать налоги от инвестиций
Налоги за инвестора в России платит брокер — поэтому можно даже не сразу заметить, что их списали. Но полезно всё-таки знать, сколько придётся отдать государству. Это зависит от того, какие активы и на какой срок приобретать.
Если акция, облигация или пай ETF куплены больше трёх лет назад, то можно смело их продавать и не платить налог на прибыль. Допустим, инвестор с планами на квартиру, которую он хочет купить через 10 лет, может вложиться и не волноваться, что обязательные отчисления повлияют на доходность.
Но если активы придётся продавать раньше, то налог с них всё-таки удержат — 13%. Кроме тех случаев, когда инвестор зафиксировал убыток: продал дешевле, чем купил. Если прибыль есть, то налог нужно заплатить, но только с разницы между покупкой и продажей.
Например, инвестор приобрёл акции компании «Первая» за 80 000 рублей, а в следующем году продал их за 100 000. За обе операции он отдал 0,3% комиссии брокеру, что тоже учитывается при расчётах. Заплатить придётся столько:
(100 000 − 300 − 80 000 − 240) × 0,13 = 2 529,8 рубля
Помимо этого, предстоят отчисления государству по дивидендам и купонам, тот же подоходный взнос в 13%. Допустим, дивиденды компании «Первая» составили 7 000 рублей — с инвестора удержат 910, что тоже отразится на доходности.
С учётом налогов инвестор потеряет 3% доходности своего портфеля — довольно много, и теперь вложение в индекс S & P 500 с годовой прибылью в 30,3% выглядит ещё более разумным. Хотя и это значение будет немного меньше — из‑за комиссий фондов и налогов.
Что стоит запомнить
- Если инвестор не считает доходность, то он не понимает, удачно ли вложил деньги и стоит ли изменить инвестиционный портфель.
- Рассчитывать прибыль, потери на комиссиях и налогах проще, если вести простейшую таблицу‑дневник в Excel.
- Инвестору лучше всего определять доходность с помощью формулы ЧИСТВНДОХ — она позволит учесть нерегулярные движения денег на брокерском счёте.
- Иногда выгоднее вложиться в несколько фондов или индексов, чем составлять собственный инвестиционный портфель.
Читайте также 🧐📈
- Как разобраться в финансовой отчётности компаний, если вы только начали инвестировать
- Стоит ли начинать инвестировать во время пандемии и кризиса
- Почему надо инвестировать в разных валютах, если хочется больше зарабатывать
- Как компании-единороги помогают грамотным инвесторам понять, где деньги
- Как пользоваться мультипликаторами, чтобы инвестировать в прибыльные и надёжные акции
