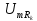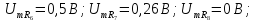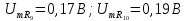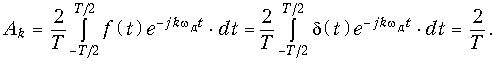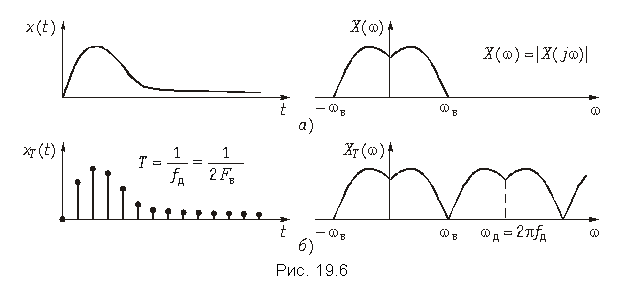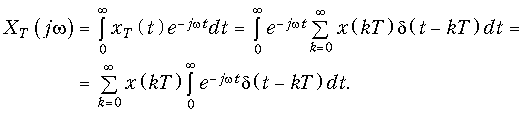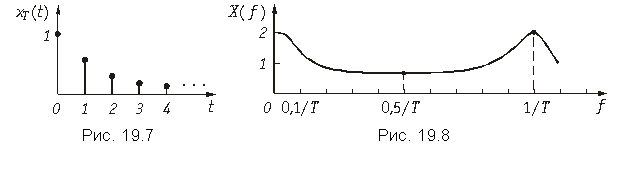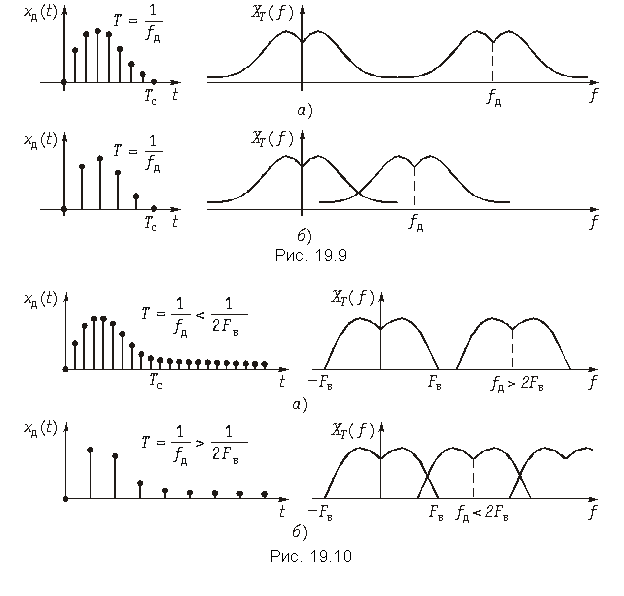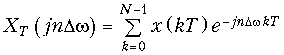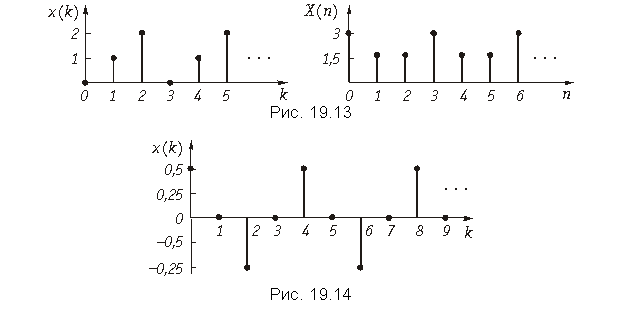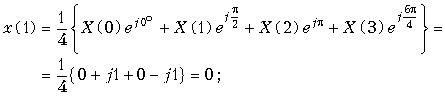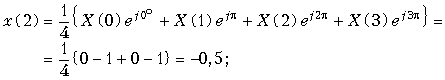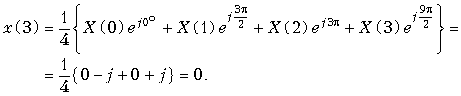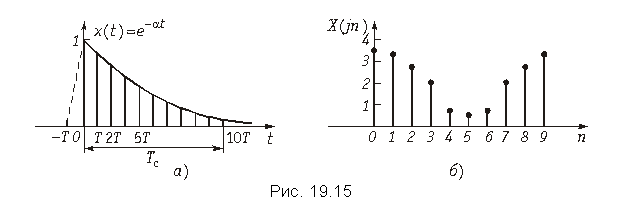Спектральный анализ сигналов
Время на прочтение
8 мин
Количество просмотров 264K
Не так давно товарищ Makeman описывал, как с помощью спектрального анализа можно разложить некоторый звуковой сигнал на слагающие его ноты. Давайте немного абстрагируемся от звука и положим, что у нас есть некоторый оцифрованный сигнал, спектральный состав которого мы хотим определить, и достаточно точно.
Под катом краткий обзор метода выделения гармоник из произвольного сигнала с помощью цифрового гетеродинирования, и немного особой, Фурье-магии.
Итак, что имеем.
Файл с отсчетами оцифрованного сигнала. Известно, что сигнал представляет собой сумму синусоид со своими частотами, амплитудами и начальными фазами, и, возможно, белый шум.
Что будем делать.
Использовать спектральный анализ для того, чтобы определить:
- количество гармоник в составе сигнала, а для каждой: амплитуду, частоту (далее в контексте числа длин волн на длину сигнала), начальную фазу;
- наличие/отсутствие белого шума, а при наличии, его СКО (среднеквадратическое отклонение);
- наличие/отсутствие постоянной составляющей сигнала;
- всё это оформить в красивенький PDF отчёт
с блэкджеком ииллюстрациями.
Будем решать данную задачу на Java.
Матчасть
Как я уже говорил, структура сигнала заведомо известна: это сумма синусоид и какая-то шумовая составляющая. Так сложилось, что для анализа периодических сигналов в инженерной практике широко используют мощный математический аппарат, именуемый в общем «Фурье-анализ». Давайте кратенько разберём, что же это за зверь такой.
Немного особой, Фурье-магии
Не так давно, в 19 веке, французский математик Жан Батист Жозеф Фурье показал, что любую функцию, удовлетворяющую некоторым условиям (непрерывность во времени, периодичность, удовлетворение условиям Дирихле) можно разложить в ряд, который в дальнейшем получил его имя — ряд Фурье.
В инженерной практике разложение периодических функций в ряд Фурье широко используется, например, в задачах теории цепей: несинусоидальное входное воздействие раскладывают на сумму синусоидальных и рассчитывают необходимые параметры цепей, например, по методу наложения.
Существует несколько возможных вариантов записи коэффициентов ряда Фурье, нам же лишь необходимо знать суть.
Разложение в ряд Фурье позволяет разложить непрерывную функцию в сумму других непрерывных функций. И в общем случае, ряд будет иметь бесконечное количество членов.
Дальнейшим усовершенствованием подхода Фурье является интегральное преобразование его же имени. Преобразование Фурье.
В отличие от ряда Фурье, преобразование Фурье раскладывает функцию не по дискретным частотам (набор частот ряда Фурье, по которым происходит разложение, вообще говоря, дискретный), а по непрерывным.
Давайте взглянем на то, как соотносятся коэффициенты ряда Фурье и результат преобразования Фурье, именуемый, собственно, спектром.
Небольшое отступление: спектр преобразования Фурье — в общем случае, функция комплексная, описывающая комплексные амплитуды соответствующих гармоник. Т.е., значения спектра — это комплексные числа, чьи модули являются амплитудами соответствующих частот, а аргументы — соответствующими начальными фазами. На практике, рассматривают отдельно амплитудный спектр и фазовый спектр.
Рис. 1. Соответствие ряда Фурье и преобразования Фурье на примере амплитудного спектра.
Легко видно, что коэффициенты ряда Фурье являются ни чем иным, как значениями преобразования Фурье в дискретные моменты времени.
Однако, преобразование Фурье сопоставляет непрерывной во времени, бесконечной функции другую, непрерывную по частоте, бесконечную функцию — спектр. Как быть, если у нас нет бесконечной во времени функции, а есть лишь какая-то записанная её дискретная во времени часть? Ответ на этот вопрос даёт дальнейшей развитие преобразования Фурье — дискретное преобразование Фурье (ДПФ).
Дискретное преобразование Фурье призвано решить проблему необходимости непрерывности и бесконечности во времени сигнала. По сути, мы полагаем, что вырезали какую-то часть бесконечного сигнала, а всю остальную временную область считаем этот сигнал нулевым.
Математически это означает, что, имея исследуемую бесконечную во времени функцию f(t), мы умножаем ее на некоторую оконную функцию w(t), которая обращается в ноль везде, кроме интересующего нас интервала времени.
Если «выходом» классического преобразования Фурье является спектр – функция, то «выходом» дискретного преобразования Фурье является дискретный спектр. И на вход тоже подаются отсчёты дискретного сигнала.
Остальные свойства преобразования Фурье не изменяются: о них можно прочитать в соответствующей литературе.
Нам же нужно лишь знать о Фурье-образе синусоидального сигнала, который мы и будем стараться отыскать в нашем спектре. В общем случае, это пара дельта-функций, симметричная относительно нулевой частоты в частотной области.
Рис. 2. Амплитудный спектр синусоидального сигнала.
Я уже упомянул, что, вообще говоря, мы рассматриваем не исходную функцию, а некоторое её произведение с оконной функцией. Тогда, если спектр исходной функции — F(w), а оконной W(w), то спектром произведения будет такая неприятная операция, как свёртка этих двух спектров (F*W)(w) (Теорема о свёртке).
На практике это означает, что вместо дельта-функции, в спектре мы увидим что-то вроде этого:
Рис. 3. Эффект растекания спектра.
Этот эффект именуют также растеканием спектра (англ. spectral leekage). А шумы, появляющиеся вследствие растекания спектра, соответственно, боковыми лепестками (англ. sidelobes).
Для борьбы с боковыми лепестками применяют другие, непрямоугольные оконные функции. Основной характеристикой «эффективности» оконной функции является уровень боковых лепестков (дБ). Сводная таблица уровней боковых лепестков для некоторых часто используемых оконных функций приведена ниже.
| Оконная функция | Уровень боковых лепестков (дБ) |
| Окно Дирихле (прямоугольное окно) | -13 дБ |
| Окно Ханна | -31.5 дБ |
| Окно Хэмминга | -42 дБ |
Основной проблемой в нашей задаче является то, что боковые лепестки могут маскировать другие гармоники, лежащие рядом.
Рис. 4. Отдельные спектры гармоник.
Видно, что при сложении приведённых спектров, более слабые гармоники как бы растворятся в более сильной.
Рис. 5. Чётко видна лишь одна гармоника. Нехорошо.
Другой подход к борьбе с растеканием спектра состоит в вычитании из сигнала гармоник, создающих это самое растекание.
То есть, установив амплитуду, частоту и начальную фазу гармоники, можно вычесть её из сигнала, при этом мы уберём и «дельта-функцию», соответствующую ей, а вместе с ней и боковые лепестки, порождаемые ей. Другой вопрос состоит в том, как же точно узнать параметры нужной гармоники. Недостаточно просто взять нужные данные из комплексной амплитуды. Комплексные амплитуды спектра сформированы по целым частотам, однако, ничто не мешает гармонике иметь и дробную частоту. В этом случае, комплексная амплитуда как бы расплывается между двумя соседними частотами, и точную её частоту, как и другие параметры, установить нельзя.
Для установления точной частоты и комплексной амплитуды нужной гармоники, мы воспользуемся приёмом, широко применяемым во многих отраслях инженерной практики – гетеродинирование.
Посмотрим, что получится, если умножить входной сигнал на комплексную гармонику Exp(I*w*t). Спектр сигнала сдвинется на величину w вправо.
Этим свойством мы и воспользуемся, сдвигая спектр нашего сигнала вправо, до тех пор, пока гармоника не станет ещё больше напоминать дельта-функцию (то есть, пока некоторое локальное отношение сигнал/шум не достигнет максимума). Тогда мы и сможем вычислить точную частоту нужной гармоники, как w0 – wгет, и вычесть её из исходного сигнала для подавления эффекта растекания спектра.
Иллюстрация изменения спектра в зависимости от частоты гетеродина показана ниже.
Рис. 6. Вид амплитудного спектра в зависимости от частоты гетеродина.
Будем повторять описанные процедуры до тех пор, пока не вырежем все присутствующие гармоники, и спектр не будет напоминать нам спектр белого шума.
Затем, надо оценить СКО белого шума. Хитростей здесь нет: можно просто воспользоваться формулой для вычисления СКО:
Автоматизируй это
Пришло время для автоматизации выделения гармоник. Повторим ещё разочек алгоритм:
1. Ищем глобальный пик амплитудного спектра, выше некоторого порога k.
1.1 Если не нашли, заканчиваем
2. Варируя частоту гетеродина, ищем такое значение частоты, при которой будет достигаться максимум некоторого локального отношения сигнал/шум в некоторой окрестности пика
3. При необходимости, округляем значения амплитуды и фазы.
4. Вычитаем из сигнала гармонику с найденной частотой, амплитудой и фазой за вычетом частоты гетеродина.
5. Переходим к пункту 1.
Алгоритм не сложный, и единственный возникающий вопрос — откуда же брать значения порога, выше которого будем искать гармоники?
Для ответа на этот вопрос, следует оценить уровень шума еще до вырезания гармоник.
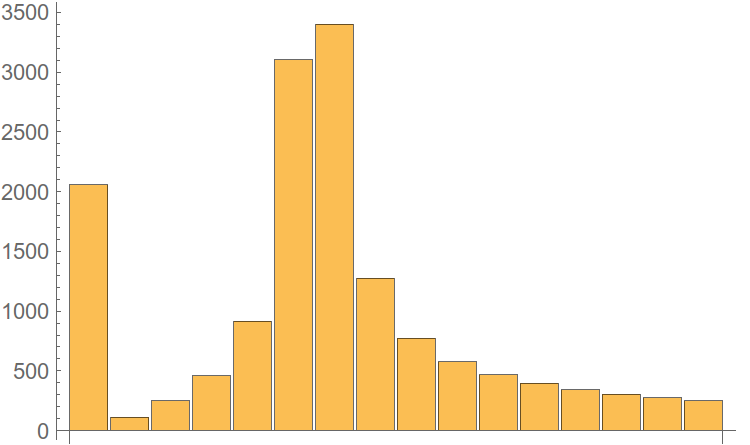
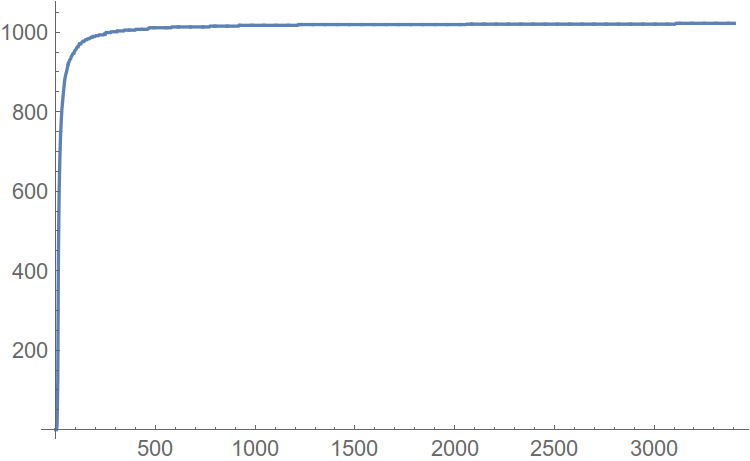
Построим функцию распределения (привет, мат. cтатистика), где по оси абсцисс будет амплитуда гармоник, а по оси ординат — количество гармоник, не превышающих по амплитуде это самое значение аргумента. Пример такой построенной функции:
Рис. 7. Функция распределения гармоник.
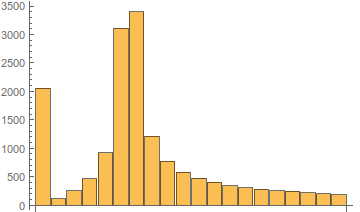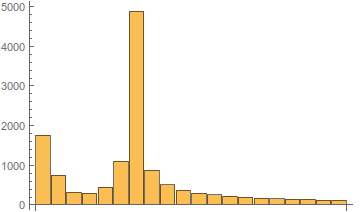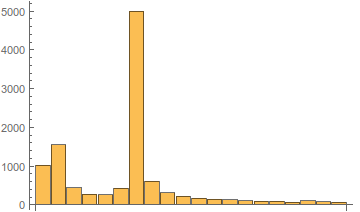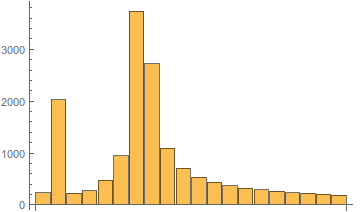
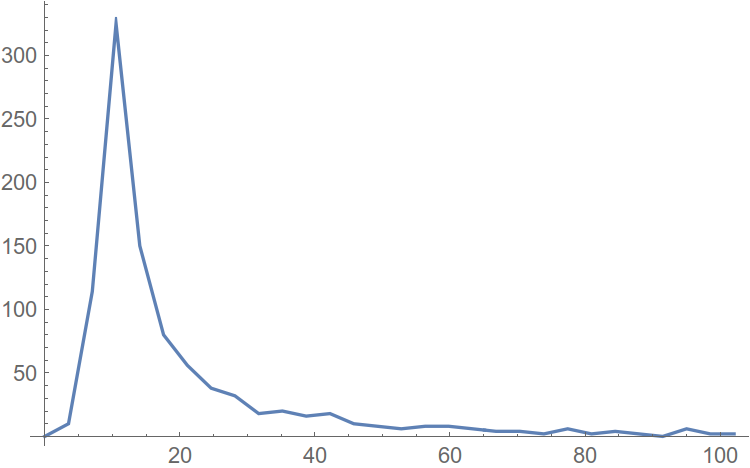
Теперь построим еще и функцию — плотность распределения. Т.е., значения конечных разностей от функции распределения.
Рис. 8. Плотность функции распределения гармоник.
Абсцисса максимума плотности распределения и является амплитудой гармоники, встречающейся в спектре наибольшее число раз. Отойдем от пика вправо на некоторое расстояние, и будем считать абсциссу этой точки оценкой уровня шума в нашем спектре. Вот теперь можно и автоматизировать.
Посмотреть на кусок кода, детектирующий гармоники в составе сигнала
public ArrayList<SynthesizableSignal> detectHarmonics() {
SignalCutter cutter = new SignalCutter(source, new Signal(source));
SynthesizableComplexExponent heterodinParameter = new SynthesizableComplexExponent();
heterodinParameter.setProperty("frequency", 0.0);
Signal heterodin = new Signal(source.getLength());
Signal heterodinedSignal = new Signal(cutter.getCurrentSignal());
Spectrum spectrum = new Spectrum(heterodinedSignal);
int harmonic;
while ((harmonic = spectrum.detectStrongPeak(min)) != -1) {
if (cutter.getCuttersCount() > 10)
throw new RuntimeException("Unable to analyze signal! Try another parameters.");
double heterodinSelected = 0.0;
double signalToNoise = spectrum.getRealAmplitude(harmonic) / spectrum.getAverageAmplitudeIn(harmonic, windowSize);
for (double heterodinFrequency = -0.5; heterodinFrequency < (0.5 + heterodinAccuracy); heterodinFrequency += heterodinAccuracy) {
heterodinParameter.setProperty("frequency", heterodinFrequency);
heterodinParameter.synthesizeIn(heterodin);
heterodinedSignal.set(cutter.getCurrentSignal()).multiply(heterodin);
spectrum.recalc();
double newSignalToNoise = spectrum.getRealAmplitude(harmonic) / spectrum.getAverageAmplitudeIn(harmonic, windowSize);
if (newSignalToNoise > signalToNoise) {
signalToNoise = newSignalToNoise;
heterodinSelected = heterodinFrequency;
}
}
SynthesizableCosine parameter = new SynthesizableCosine();
heterodinParameter.setProperty("frequency", heterodinSelected);
heterodinParameter.synthesizeIn(heterodin);
heterodinedSignal.set(cutter.getCurrentSignal()).multiply(heterodin);
spectrum.recalc();
parameter.setProperty("amplitude", MathHelper.adaptiveRound(spectrum.getRealAmplitude(harmonic)));
parameter.setProperty("frequency", harmonic - heterodinSelected);
parameter.setProperty("phase", MathHelper.round(spectrum.getPhase(harmonic), 1));
cutter.addSignal(parameter);
cutter.cutNext();
heterodinedSignal.set(cutter.getCurrentSignal());
spectrum.recalc();
}
return cutter.getSignalsParameters();
}
Практическая часть
Я не претендую на звание эксперта Java, и представленное решение может быть сомнительным как по части производительности и потреблению памяти, так и в целом философии Java и философии ООП, как бы я ни старался сделать его лучше. Написано было за пару вечеров, как proof of concept. Желающие могут ознакомиться с исходным кодом на GitHub.
Единственной сложностью стала генерация PDF отчёта по результатам анализа: PDFbox ну никак не хотел работать с кириллицей. К слову, не хочет и сейчас.
В проекте использовались библиотеки:
JFreeChart – отображение графиков
PDFBox – построение отчёта
JLatexMath – рендер Latex формул
В итоге, получилась довольно массивная программа (13.6 мегабайт), удобно реализующая поставленную задачу.
Есть возможность как вырезать гармоники вручную, так и доверить эту задачу алгоритму.
Всем спасибо за внимание!
Примеры сигналов для анализа
Пример отчёта, создаваемого программой.
Литература
Сергиенко А. Б. — Цифровая обработка сигналов
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ НАУКИ
РОССИЙСКОЙ
ФЕДЕРАЦИИ
ФЕДЕРАЛЬНО
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ
ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
МОСКОВСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПРИБОРОСТРОЕНИЯ
И ИНФОРМАТИКИ
В.
В. Филинов
Электроника
и схемотехника.
Расчёт
спектров электрических сигналов.
Учебно-методическое
пособие
Москва
– 2014
УДК
621.38
ББК
32.85
Рекомендовано
к изданию в качестве учебно-методического
пособия редакционно-издательским
советом МГУПИ
Рецензент:
д.т.н.
профессор Шкатов П. Н. (МГУПИ)
Филинов
В.В.
Электроника
и схемотехника. Расчет спектров
электрических сигналов.
Учебно-методическое пособие. М.: МГУПИ,
2014
Учебно-методическое
пособие предназначено для студентов
(бакалавров и специалистов) специальностей
по радиоэлектронике и информационной
безопасности, изучающих курс лекций
“Электроника и схемотехника”,
предназначено при подготовке к выполнению
практических и расчетно-графических
работ (РГР) по теме “Расчет спектров
электрических сигналов”. Приведены
примеры расчета спектров периодических
и непериодических сигналов, а также
задания для выполнения РГР. Полезно для
магистров и аспирантов технических
направлений МГУПИ.
Утверждено
и рекомендовано решением УМС факультета
«Приборостроения и радиоэлектроники»
МГУПИ в качестве учебно-методического
пособия.
©
Московский Государственный Университет
Приборостроения и Информатики, 2014
©
Филинов В.В., 2014
Оглавление
Стр.
Введение.
Необходимые формулы
………………………………………4
-
Спектры
амплитуд и фаз периодических сигналов
..…………6
Пример
1 ……………………………………………………………………6
Пример
2 …………………………………………………………………..10
Пример
3 …………………………………………………………………..11
Пример
4 …………………………………………………………………..12
Пример
5 …………………………………………………………………..13
Пример
6 …………………………………………………………………..14
Пример
7 …………………………………………………………………..16
Пример
8 …………………………………………………………………..17
Пример
9 …………………………………………………………………..18
Пример
10 …………………………………………………………………23
Пример
11 …………………………………………………………………24
-
Спектральная
плотность амплитуд и фаз периодических
сигналов
……..….…………..………………………..…….………………27
Пример
12 …………………………..……………………….……………27
Пример
13 …………………………..……………………….……………29
Пример
14 …………………………..……………………….……………31
Пример
15 …………………………..……………………….……………31
Пример
16 …………………………..……………………….……………33
Пример
17 …………………………..……………………….……………34
Пример
18 …………………………..……………………….……………36
Пример
19 …………………………..……………………….……………37
-
Литература
……………………………………………………………….39 -
Задания
для расчетно-географических
работ…………..………39
Необходимые
формулы.
Применительно
к периодическому гармоническому
напряжению
можно использовать разложение в ряд
Фурье:
(1)
Простейшим
периодическим сигналом является
гармоническое колебание вида
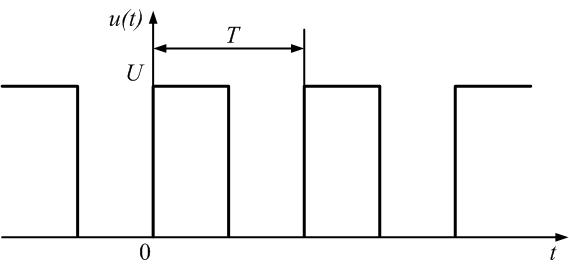
Разложение
последовательности прямоугольных
импульсов рис. 1.1 имеет вид:
(2)
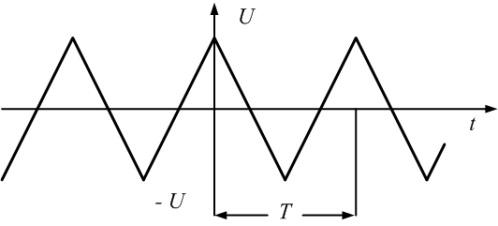
Разложение
последовательности пилообразных
импульсов рис. 1.2 имеет вид:
(3)
Две
равнозначные записи ряда Фурье:
Ряд Фурье в
комплексной форме:
Выражение
для комплексного спектра сигнала:
Ряд
Фурье периодической последовательности
прямоугольных импульсов амплитудой U
(рис. 1.5а)
имеет вид:
Напряжение
на участках цепи находят, используя
принцип суперпозиции, например напряжение
на резисторах:
Расчет
цепи от отдельных постоянной и
гармонических составляющих напряжения
проводится в символической форме. При
этом нужно иметь в виду, что на k-й
гармонике сопротивление индуктивности

а сопротивление емкости
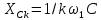
Интеграл
Фурье:
Уравнения
(10) и (11) являются основными в теории
спектров непериодических сигналов,
причем (10) называется прямым,
а (11) –
обратным
преобразованием Фурье (интегралом
Фурье).
Комплексная
придаточная функция по напряжению:
Из
выражений:
следует,
что спектральная плотность амплитуд
реакции цепи равна произведению
спектральной плотности амплитуд
воздействия АЧХ
цепи, а спектральная плотность фаз
реакции цепи равна сумме спектральной
плотности фаз
воздействия и ФЧХ
цепи.
-
Спектры амплитуд и фаз периодических сигналов.
Пример
1.
Определим параметры синусоид, формирующих
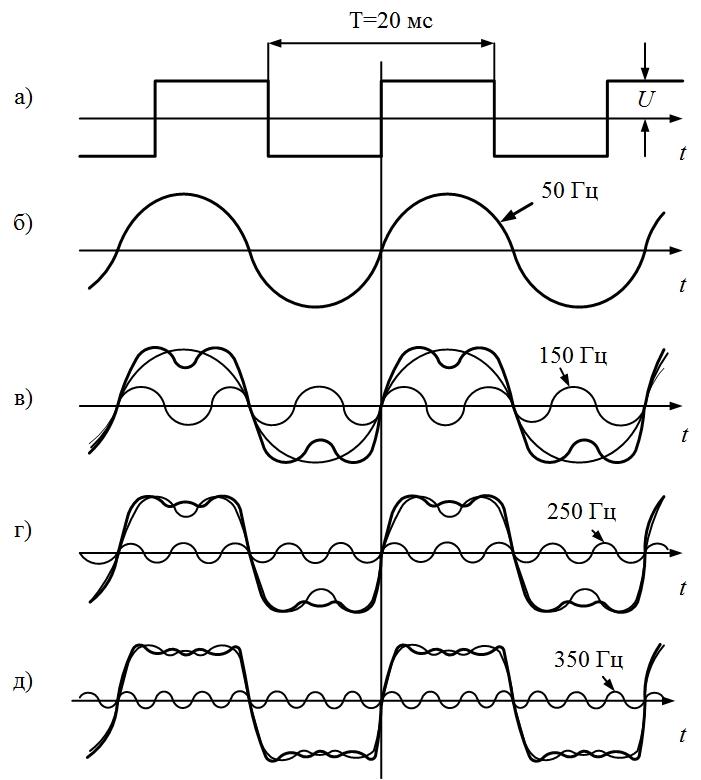
последовательности прямоугольных (рис.
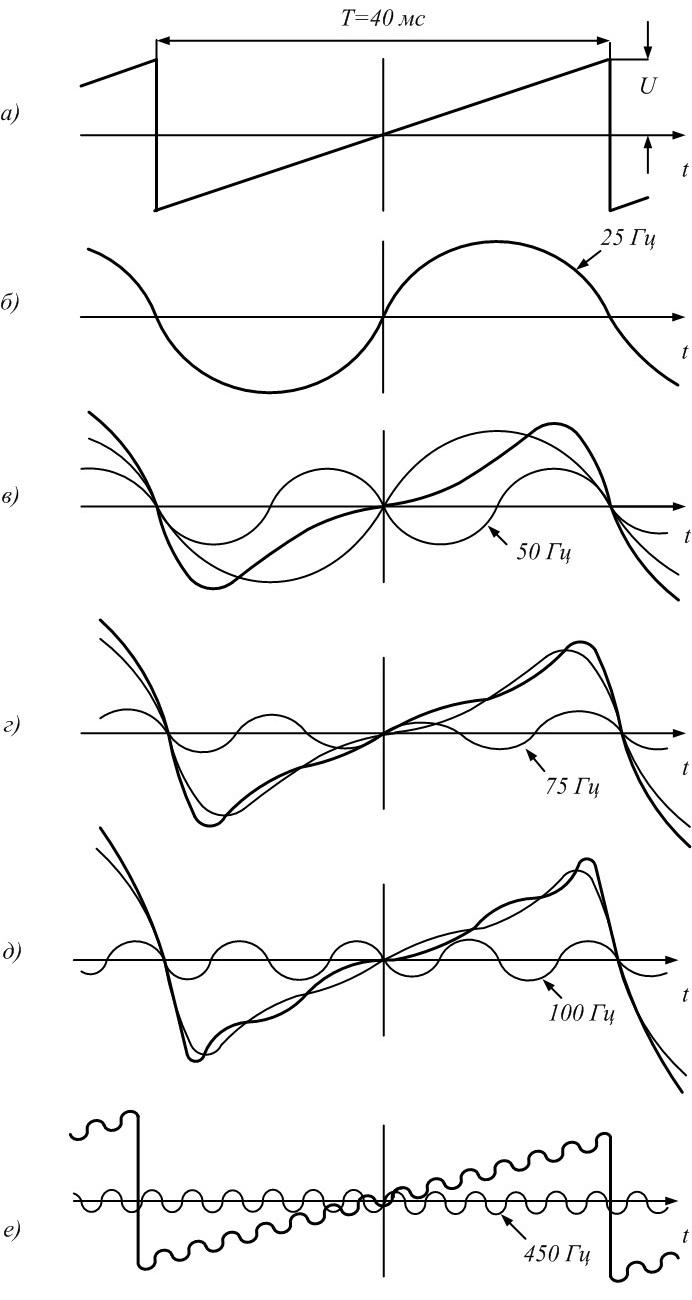
1.1, а) и пилообразных (рис. 1.2, а) импульсов,
имеющих амплитуду U = 10 В
и период Т = 20 мс.
а)
Для формирования периодической
последовательности прямоугольных
импульсов амплитуда основной синусоиды
должна быть
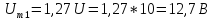
Частота
колебаний этой синусоиды обратно
пропорциональна периоду:
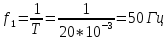
Круговая
частота

Таким образом, основная синусоида
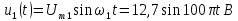
Все
последующие синусоиды в соответствии
с (2) должны иметь амплитуды в нечетное
количество раз меньшие, а частоты – в
это же нечетное количество раз большие,
чем у основной синусоиды:

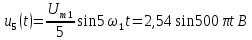
и
т.д.
Последовательность
прямоугольных импульсов, изображенных
на рис. 1.1, а,
–
это сумма синусоид:
.
Сигнал
изображен
на рис. 1.1, д.
6)
Для формирования последовательности
пилообразных импульсов необходимо,
чтобы амплитуда основной синусоиды
была, как мы уже знаем [1, 3], равна
Частота
основной синусоиды

Таким
образом,
Рис.
1.1. Последовательность прямоугольных
импульсов и образующие ее синусоиды
Рис.
1.2. Последовательность пилообразных
импульсов и образующие ее синусоиды
Таблица
1.1. Ряды Фурье наиболее часто встречающихся
сигналов
|
Сигнал |
Ряд |
|
|
|
|
|
|
|
|
|
|
|
k-четные; |
|
|
k-четные; |
|
|
|
Последующие
синусоиды в соответствии с (3) будут
иметь вид
и
т.д.
Последовательность
пилообразных импульсов – это сумма
синусоид:
.
Чем
больше синусоид используется при
формировании сигнала, тем ближе его
форма к пилообразной (рис. 1.е).
Пример
2.
Определим гармонический состав
последовательности треугольных
импульсов, изображенных на рис. 1.3,
имеющих амплитуду, U
= 10 B
и период Т = 10 мс.
Периодический
сигнал на рис. 1.3 отличается от сигнала
во второй строке табл. 1.1 на величину
постоянной составляющей
Частота
основной составляющей сигнала
или
Амплитуда
основной составляющей сигнала
рассчитывается по формуле, приведенной
в табл. 1.1, или по одной из формул (1):
Четная
функция (рис. 1.3) содержит только
косинусоиды, амплитуды и частоты
которых определяются по формулам,
приведенным во второй строке табл. 1.1.
Амплитуда
и частота третьей гармоники:
Рис.
1.3. Последовательность треугольных
импульсов
Амплитуда
и частота пятой гармоники:
Амплитуда
и частота седьмой гармоники:
и
т.д.
Гармонический
состав последовательности треугольных
импульсов (рис.1.3) имеет вид:
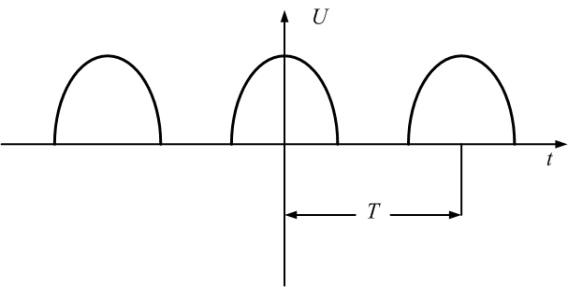
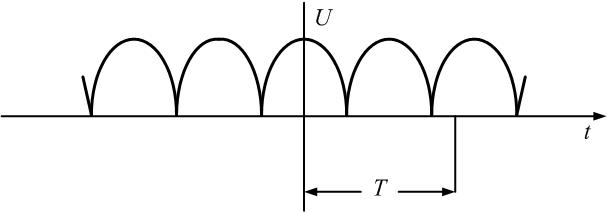
Пример
3.
Представим переменное напряжение,
выпрямленное двухполупериодным
выпрямителем (пятая строка табл. 1.1),
рядом Фурье в тригонометрической форме
(5).
Из
табл. 1.1 следует, что переменное напряжение
u(t) представлено рядом Фурье:
k
– четные.
Постоянная
составляющая напряжения u(
t)
рассчитывается по формуле

0,635U.
Нечетные
гармоники отсутствуют в ряде Фурье,
поскольку функция u(
t)–
четная.
Для
расчета амплитуд четных гармоник
нео6ходимо определить

1,27U.
Тогда амплитуда второй гармоники
Начальная
фаза второй гармоники равна нулю:
Амплитуда
четвертной гармоники
Фаза
четвертой гармоники
, так как в ряде Фурье перед слагаемым
стоит знак «минус».
Амплитуда
шестой гармоники
а
ее фаза, а также фазы десятой, четырнадцатой
и т.д. гармоник равны нулю.
Амплитуда
восьмой гармоники
а
ее начальная фаза, так же как и фазы
гармоник с номерами 12, 16, 20 и т.д., равна
180˚.
Тригонометрическая
форма ряда Фурье рассматриваемого
напряжения имеет вид:
.
Пример
4.
Представим ряд Фурье, полученный в
примере 3, в комплексной форме, ограничив
его восьмой гармоникой.
В
соответствии с (6) значения постоянной
составляющей и амплитуд гармоник
уменьшаются в 2 раза по сравнению со
значениями, которые 6ыли рассчитаны в
примере 3. Поэтому ряд Фурье в комплексной
форме имеет вид
Пример
5.
Построим спектр амплитуд и фаз
выпрямленного напряжения
(строка
5 табл, 1.1), имеющего амплитуду U
= 10 В и период Т = 10 мс.
При
решении примера 3 была получена
тригонометрическая форма ряда Фурье,
соответствующая выпрямленному напряжению:
.
Частота
основной составляющей сигнала
определяется
периодом колебаний:
В
спектре сигнала отсутствуют нечетные
гармоники, так как само колебание
является четной функцией. Частоты высших
гармоник с четными номерами кратны этим
номерам: частота второй гармоники равна
2
= 200 Гц, четвертой, шестой, восьмой гармоник
– 400, 600, 800 Гц соответственно и т.д.
Постоянная
составляющая
Амплитуды
четных гармоник спектра в соответствии
с выражениями, полученными для ряда
Фурье, имеют следующие значения:
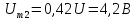

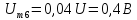
и
т.д.
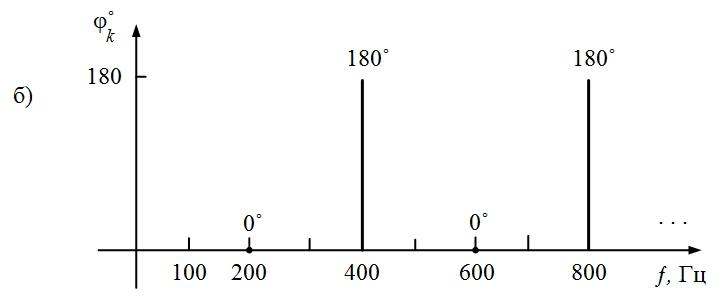
Фазы
гармоник поочередно принимают значения
0 и 180˚.
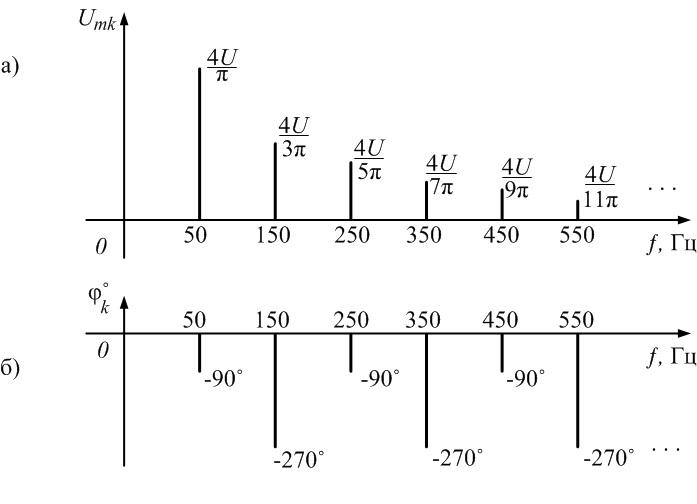
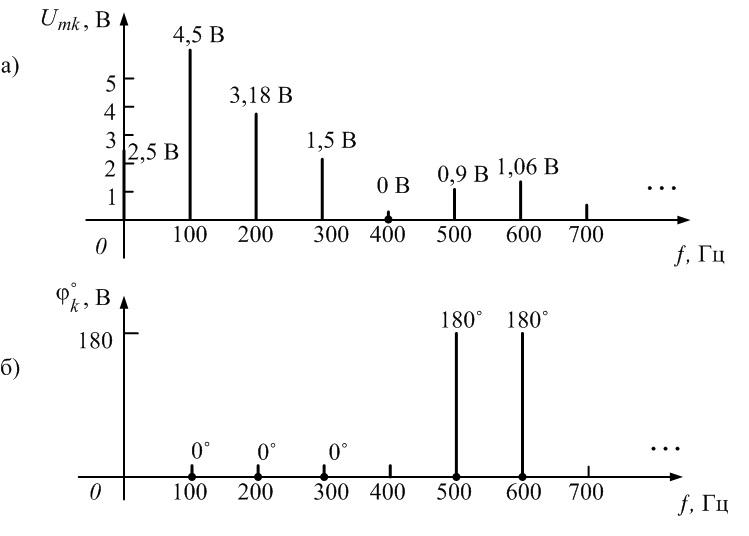
Рис.
1.4. Спектры амплитуд и фаз выпрямленного
напряжения
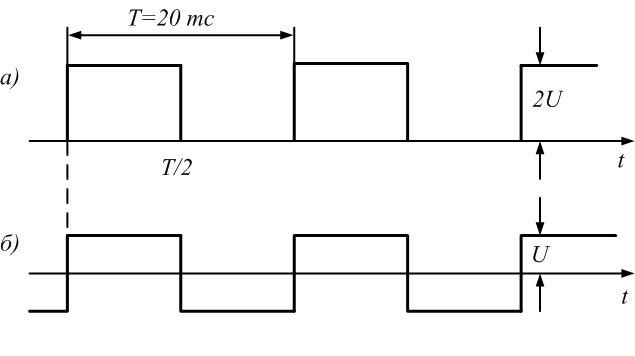
Пример
6.
Рассмотрим периодическую последовательность
прямоугольных импульсов, показанную
на рис. 1.5, а:
Рис.
1.5. Последовательности прямоугольных
импульсов
Она
имеет постоянную составляющую, равную
в соответствии с (1)
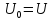
Коэффициенты
вычисляются
по формуле (1):
Здесь
6ыло учтено, что

1/Т.
Коэффициенты
вычисляются по формуле (1):
Выражение
удовлетворяет соотношению
Поэтому
Форма
ряда Фурье будет содержать только
синусоиды с нечетными гармоническими
частотами:
что,
естественно, с точностью до постоянной
составляющей U
совпадает с полученным ранее выражением
(2).
Переход
к форме ряда Фурье (5) дает
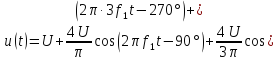
Спектр
такого сигнала без постоянной составляющей
показан на рис. 1.6:
Рис.
1.6. Спектры амплитуд и фаз сигнала рис.
1.5а
Пример
7.
Представим спектр сигнала
из примера 6 в комплексной форме.
Комплексный
спектр периодической последовательности
прямоугольных импульсов рассчитывается
по формуле (7):
Функция
имеет значения
Это
значит, что комплексный спектр
существует только для нечетных гармоник:
Заметим,
что в спектре
нет постоянной составляющей

которая рассчитывается по формуле (1) и
равна U.
Полученный
комплексный спектр
соответствует спектрам амплитуд и фаз,
изображенным на рис. 1.6.
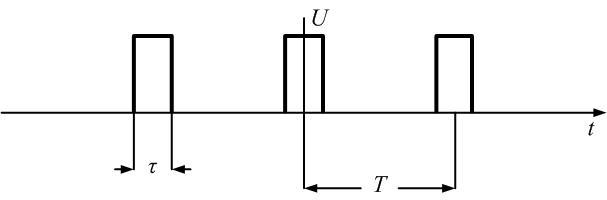
Пример
8.
Найдем спектр последовательности
прямоугольных импульсов, изображенных
на рис. 1.7.
Сигнал,
изображенный на рис. 1.7, имеет следующие
параметры: амплитуда U
= 10 В, длительность импульса τ= 10 мс,
период повторения импульсов Т
= 40 мс, скважность q
= Т/τ = 4. Спектр этого сигнала в форме
(Табл. 1.1, строка 6) имеет вид
Постоянная
составляющая
Частота
первой гармоники
Частоты
высших гармоник кратны 100 Гц. Амплитуды
первых шести гармоник, рассчитываемые
по формуле (3.28)
имеют
следующие значения:
Фазы
первой, второй, третьей гармоник равны
0˚, фазы пятой и шестой гармоник равны
180˚, так как при расчете
и
получены отрицательные значения.
Амплитуды и фазы последующих гармоник
рассчитывают аналогичным образом.
Причем, амплитуды гармоник, кратных
скважности q, т.е. четвертой, восьмой,
двенадцатой, шестнадцатой гармоник и
т.д., равны нулю. Спектры амплитуд и фаз
сигнала, изображенного на рис. 1.7,
приведены на рис. 1.8.
Рис.
1.7. Последовательность прямоугольных
импульсов со скважностью q = 4
Рис.
1.8. Спектр последовательности прямоугольных
импульсов со скважностью q = 4
Пример
9.
Определим напряжение на резисторе
в
последовательном колебательном контуре,
на который подается последовательность
прямоугольных импульсов (рис. 1.10).
Параметры элементов контура и сигнала
заданы: R = 2 Ом; L = 0,704 мГн; С = 4 мкФ; U = 5
В; Т = 1 мс; τ = 0,5 мс.
Найдем
параметры постоянной и гармонических
составляющих сигнала (рис. 1.10),
представленного рядом Фурье (8). Частота
первой гармоники
или
Частоты
третьей, пятой и т.д. гармоник равны
соответственно: 3
= 18,84 рад/с; 3
= 3 кГц; 5
= 31,4 рад/с; 5
= 5 кГц; … .
Амплитуды
четных гармоник равны нулю. Амплитуды
нечетных гармоник рассчитываются по
формуле (1):
.
Ряд
Фурье сигнала имеет вид:
Рис.
1.9. Последовательный колебательный
контур с источником периодического
сигнала
Рис.
1. 10. Последовательность прямоугольных
импульсов
Определим
резонансную частоту
и
контура
(рис. 1.9):
Резонанс
в контуре наступает на частоте третьей
гармоники входного напряжения.
Добротность
контура
Определим
гармонические составляющие тока в цепи
и напряжения на резисторе в каждой из
составляющих ряда Фурье схем, изображенных
на рис. 1.9.
Схема
последовательного колебательного
контура с источником постоянного
напряжения

= 2,5 В приведена на рис. 1.11. В этой цепи
сопротивление индуктивности равно
нулю, а сопротивление конденсатора
равно бесконечности, поэтому
= 0;
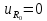
В
цепи, изображенной на рис. 1.12, в контур
включен источник напряжения, соответствующий
напряжению первой гармоники. Синусоидальное
напряжение
заменено
на комплексное

На частоте
= 1 кГц (
)
сопротивление индуктивности
а
сопротивление емкости
Рис.
1.11. Контур с источником постоянного
напряжения
Рис.
1.12. Контур с источником напряжения
первой гармоники
Комплексное
сопротивление цепи
Определим
комплексные значения тока
и напряжение
:
Это
соответствует составляющей синусоидального
напряжения (9) в исходной цепи:
На
третьей гармонике синусоидальный
источник заменяется источником
комплексного напряжения
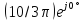
В результате имеем цепь, изображенную
на рис. 1.13.
На
частоте
= 3 кГц (
)
в цепи наступает резонанс напряжений.
Сопротивления индуктивности и емкости
равны по величине и противоположны по
знаку:
Комплексное
сопротивление цепи
= R = 2 Ом. Ток
Рис.
1.13. Контур с источником третьей гармоники
Рис.
1.14. Контур с источником напряжения
пятой гармоники
Напряжение
на резисторе
равно входному напряжению:

пятой гармонике синусоидальный источник
заменяется
источником комплексного напряжения
(рис. 1.14). На частоте
= 5 кГц (
)
сопротивления индуктивности и емкости
равны соответственно
и
Комплексное
сопротивление цепи
рассчитаем
по формуле:
Напряжение
на резисторе
Таким
образом, ряд Фурье напряжения на резисторе
имеет вид,
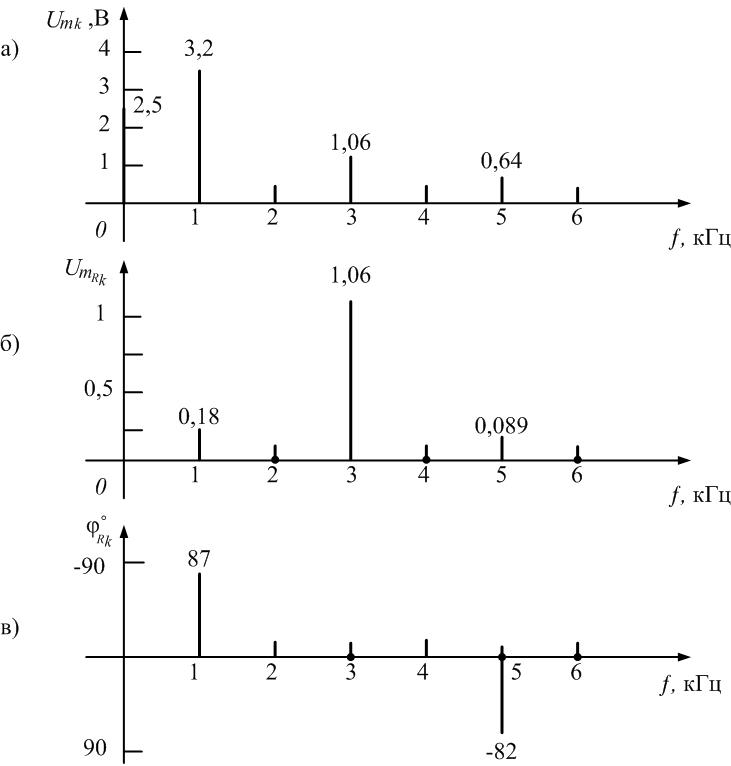
Рис.
1.15. Спектры амплитуд и фаз входного
напряжения и напряжения на резисторе
в колебательном контуре
Спектры
амплитуд и фаз этого напряжения изображены
на рис. 1.15
( 6, в).
Анализ спектра
показывает, что колебательный контур
выделил третью гармонику из входной
последовательности и подавил остальные
гармоники, т.е. явление резонанса можно
использовать для, выделения отдельных
гармоник из периодического несинусоидального
сигнала.
Пример
10.
Сравним спектры амплитуд (рис. 1.15) входной
последовательности прямоугольных
импульсов
и напряжения
на резисторе колебательного контура
из примера 9, чтобы определить коэффициенты
передачи по напряжению цепи на частотах
гармоник.
В
соответствии с формулой и рис. 1.15 (а),
постоянная составляющая
в спектре напряжения
равна 2,5 В. Амплитуды первой, третьей и
пятой гармоник имеют значения:
Постоянная
составляющая в спектре напряжения
на резисторе (рис. 3.15, б)
равна нулю, а амплитуды нечетных гармоник
равны соответственно
Коэффициенты
передачи по напряжению
на частотах гармоник рассчитаем по
формуле
На
частоте f
= 0 кГц получаем
= 0/2,5 = 0. На частоте f
= 1 кГц (частота основной составляющей)
= 0,18/3,2 = 0,056.
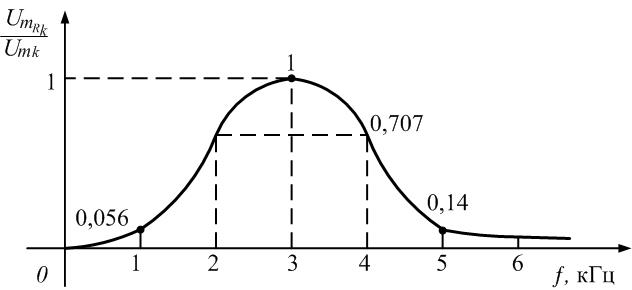
Рис.
1.16. Коэффициенты передачи по напряжению
на резисторе R на частотах гармоник
На
частоте
f=3
кГц (третья гармоника)
= 1,06/1,06 = 1.
На
частоте f=
5 кГц (пятая гармоника)
= 0,089/0,64= 0,14.
На
рис. 1.16 приведен график зависимости
коэффициента передачи контура от частоты
гармоник. На частоте резонанса коэффициент
передачи максимален и равен 1. На частотах
первой и пятой гармоник коэффициент
передачи резко уменьшается.
Пример
11.
Определим спектр амплитуд напряжения
на резисторе в цепи, изображенной на
рис. 1.17, а,
на вход которой поступает периодическая
последовательность прямоугольных
импульсов (рис. 1.17, б),
если заданы R
= 50 Ом, L
= 10 мГн, U
= 10 В, τ = 1 мс, Т = 4 мс.
Рис.
1.17. RL-цепь
и сигнал на ее входе
Найдем
комплексный спектр входного сигнала
u(t),
воспользовавшись (7):
Применив
формулу Эйлера, получим
Вычислим
амплитуды спектральных составляющих
Амплитуда
постоянной составляющей
Частота
основной составляющей
а
ее амплитуда
Аналогичным
образом определяются частоты и амплитуды
высших гармоник:
|
При |
k=2 |
2 |
|
|
k=3 |
3 |
|
|
|
k=4 |
4 |
|
|
|
k=5 |
5 |
|
|
|
k=6 |
6 |
|
|
|
k=7 |
7 |
|
|
|
k=8 |
8 |
|
|
|
k=9 |
9 |
|
|
|
k=10 |
10 |
|
Спектр
амплитуд
входного сигнала изображен на рис.
1.18, а.
Огибающая спектра амплитуд прямоугольных
импульсов изменяется по закону

нули спектра расположены на частотах,
кратных
=1 кГц (четвертая, восьмая, двенадцатая
и т.д. гармоники). Комплексная передаточная
функция цепи (рис. 1.17, а) определяется
по формуле
|
При |
k=0 |
|
|
k=1 |
|
|
|
k=2 |
|
|
|
k=3 |
|
|
|
k=4 |
|
|
|
k=5 |
|
|
|
k=6 |
|
|
|
k=7 |
|
|
|
k=8 |
|
|
|
k=9 |
|
|
|
k=10 |
|
Рис.
1.18. Спектры амплитуд последовательности
прямоугольных импульсов и напряжения
на резисторе в RL-цепи
и коэффициенты передачи цепи
График
зависимости коэффициента передачи
RL-цепи
от частоты изображен на рис. 3.18 (б).
Спектр
амплитуд
напряжения на резисторе, рассчитываем
в виде:
принимает
значения:
и
приведен на рис. 1.18 (в).
При обсуждении переменного тока в одной из предыдущих статей (ссылка) мы познакомились с понятием гармонической (синусоидальной) функции. А бывают ли негармонические функции и сигналы, и как с ними работать? В этом нам и предстоит сегодня разобраться. Кроме того, мы рассмотрим важнейшее понятие – амплитудно-частотную характеристику (АЧХ) сигналов.
Гармонические и негармонические сигналы.
И для начала чуть подробнее разберемся, как классифицируются сигналы. В первую очередь, нас интересуют периодические сигналы. Их форма повторяется через определенный интервал времени T, называемый периодом. Периодические сигналы в свою очередь делятся на два больших класса – гармонические и негармонические. Гармонический сигнал – это сигнал, который можно описать следующей функцией:
Здесь A – амплитуда сигнала, w – циклическая частота, а phi – начальная фаза. Может возникнуть логичный вопрос – разве синусоидальный сигнал не является гармоническим? Конечно, является, дело в том, что sinalpha = cos(frac{pi}{2}medspace-medspace alpha) – то есть сигналы отличаются начальной фазой, соответственно, синусоидальный сигнал не противоречит определению, которое мы дали для гармонических колебаний.
Вторым подклассом периодических сигналов являются негармонические колебания. Вот пример негармонического сигнала:
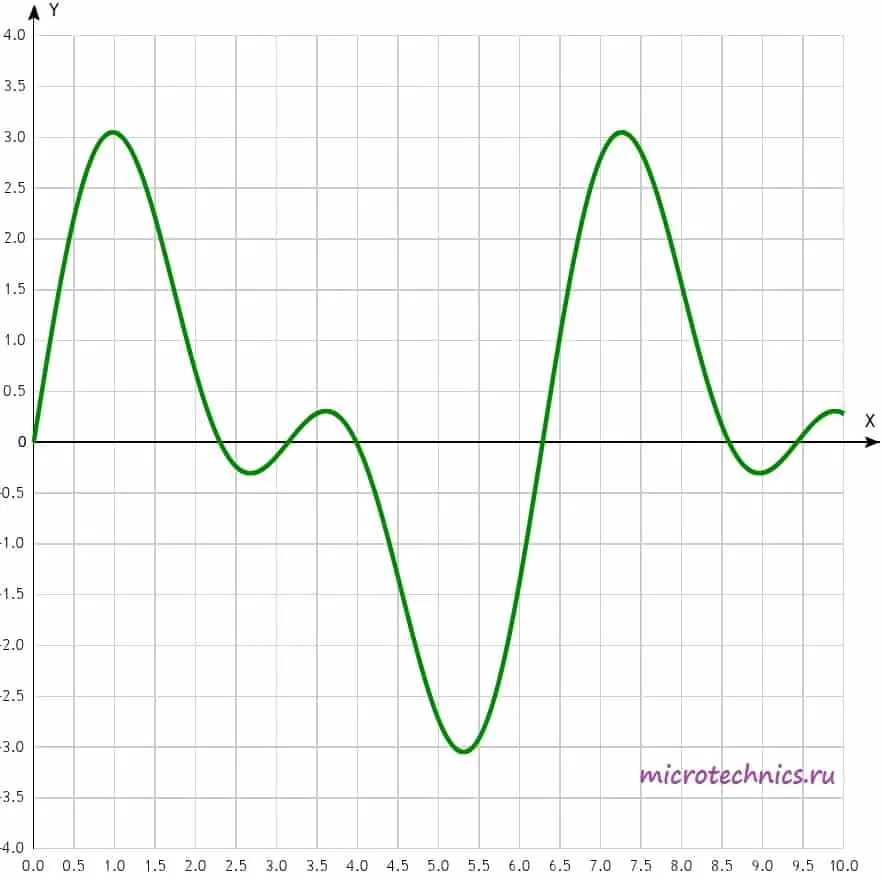
Как видите, несмотря на свой вид, сигнал остается периодическим, то есть его форма повторяется через интервал времени, равный периоду.
Для работы с такими сигналами и их исследования существует определенная методика, которая заключается в разложении сигнала в ряд Фурье. Суть состоит в том, что негармонический периодический сигнал (при выполнении определенных условий) можно представить в виде суммы гармонических колебаний с определенными амплитудами, частотами и начальными фазами. Важным нюансом является то, что все гармонические колебания, которые участвуют в суммировании, должны иметь частоты, кратные частоте исходного негармонического сигнала. Возможно это пока не совсем понятно, так что рассмотрим практический пример и разберемся подробнее. И для примера используем сигнал, который изображен на рисунке чуть выше. Его можно представить следующим образом:
u(t) = u_1(t) + u_2(t) = 2 sin(t) + 1.5 sin(2t)
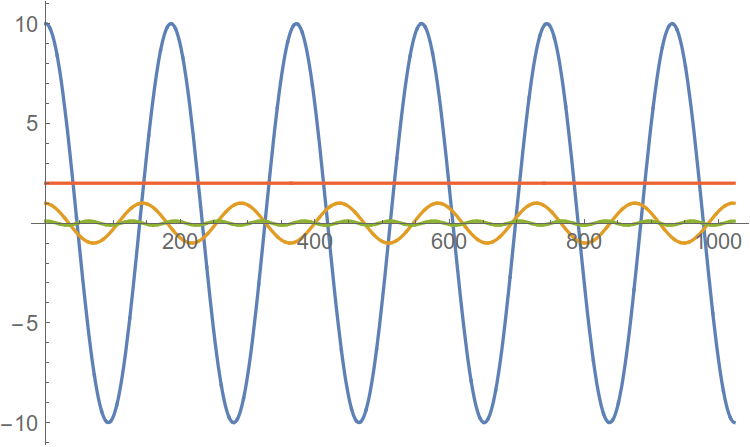
Давайте изобразим все эти сигналы на одном графике:
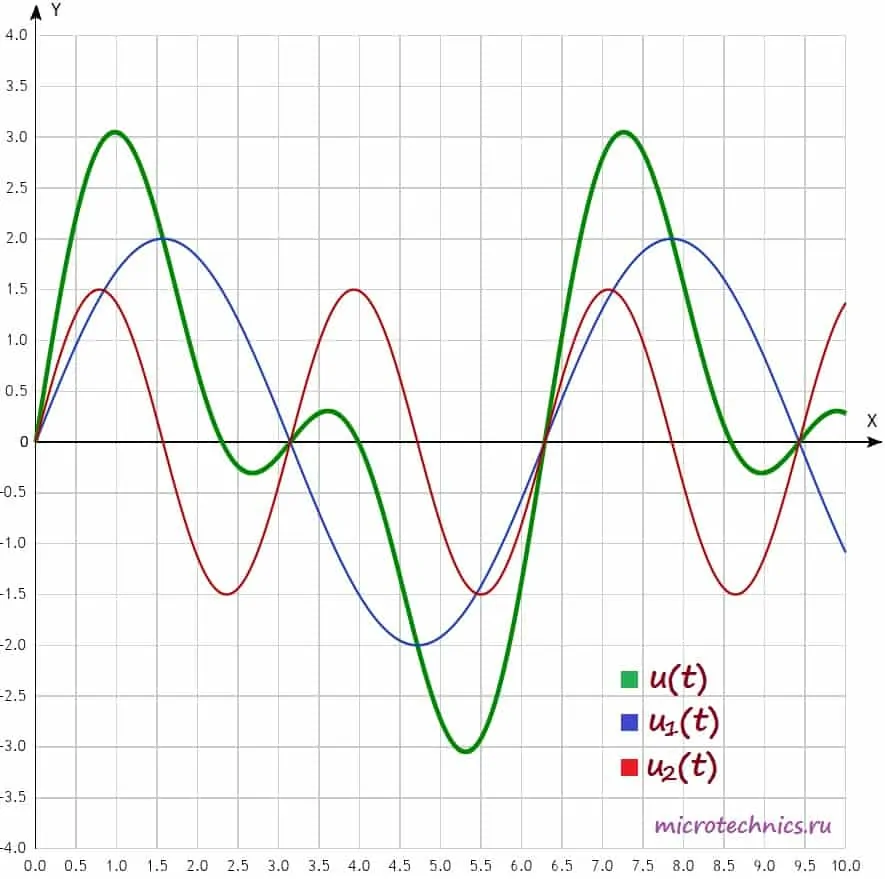
Функции u_1(t), u_2(t) называют гармониками сигнала, а ту из них, период которой равен периоду негармонического сигнала, называют первой или основной гармоникой. В данном случае первой гармоникой является функция u_1(t) (ее частота равна частоте исследуемого негармонического сигнала, соответственно, равны и их периоды). А функция u_2(t) = 1.5 sin(2t) представляет из себя ни что иное как вторую гармонику сигнала (ее частота в два раза больше). В общем случае, негармонический сигнал раскладывается на бесконечное число гармоник:
u(t) = U_0 + sum_{i=0}^{infty}{U_{k}thinspace sin(thinspace kwt + phi_kthinspace )}
Здесь U_k – амплитуда, а phi_k – начальная фаза k-ой гармоники. Как мы уже упомянули чуть ранее, частоты всех гармоник кратны частоте первой гармоники, собственно, это мы и наблюдаем в данной формуле. U_0 – это нулевая гармоника, ее частота равна 0, она равна среднему значению функции за период. Почему среднему? Смотрите – среднее значения функции синуса за период равно 0, а значит при усреднении в этой формуле все слагаемые, кроме U_0 будут равны 0 👍
Амплитудный спектр сигнала.
Совокупность всех гармонических составляющих негармонического сигнала называют спектром этого сигнала. Различают фазовый и амплитудный спектр сигнала:
- фазовый спектр сигнала – совокупность начальных фаз всех гармоник
- амплитудный спектр сигнала – амплитуды всех гармоник, из которых складывается негармонический сигнал
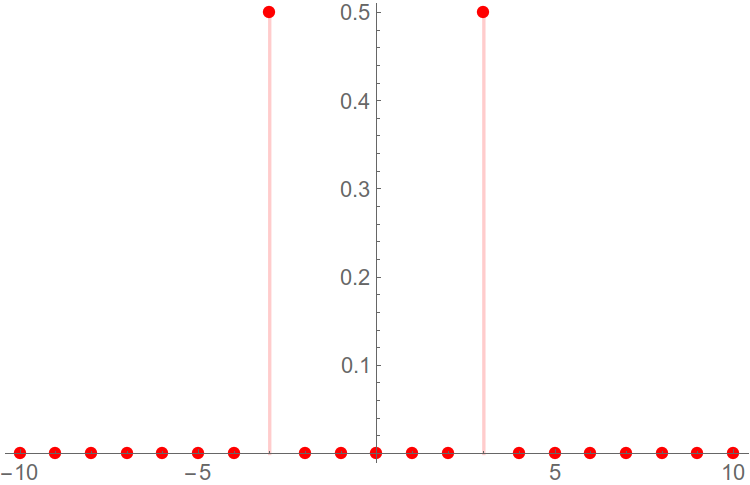
Давайте рассмотрим амплитудный спектр подробнее. Для визуального изображения спектра используют диаграммы, представляющие из себя набор вертикальных линий определенной длины (длина зависит от амплитуды сигналов). На горизонтальной оси диаграммы откладываются частоты гармоник:
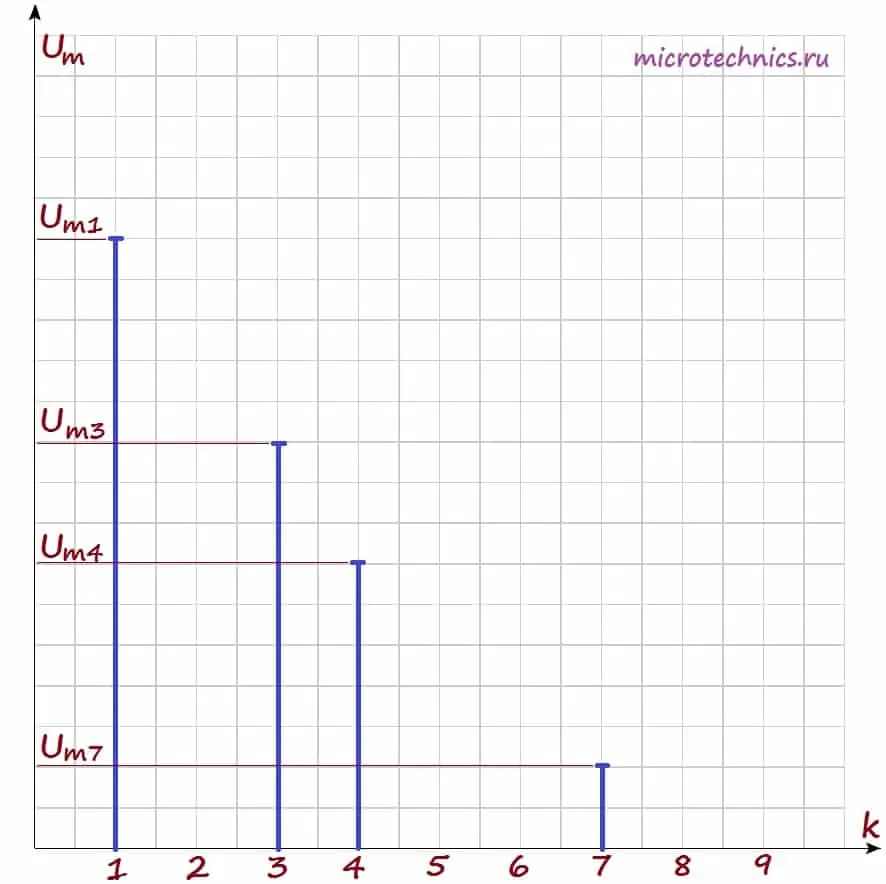
При этом на горизонтальной оси могут откладываться как частоты в Гц, так и просто номера гармоник, как в данном случае. А по вертикальной оси – амплитуды гармоник, тут все понятно. Давайте построим амплитудный спектр сигнала для негармонического колебания, которое мы рассматривали в качестве примера в самом начале статьи. Напоминаю, что его разложение в ряд Фурье выглядит следующим образом:
u(t) = u_1(t) + u_2(t) = 2 sin(t) + 1.5 sin(2t)
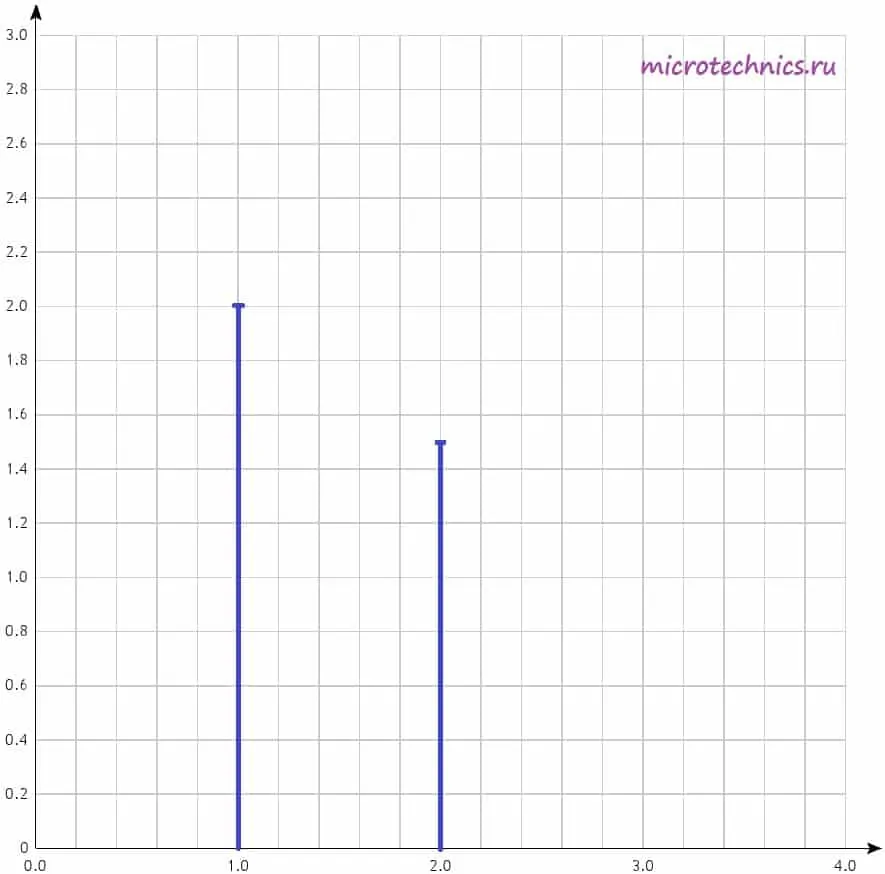
У нас есть две гармоники, амплитуды которых равны, соответственно, 2 и 1.5. Поэтому на диаграмме две линии, длины которых соответствуют амплитудам гармонических колебаний. Фазовый спектр сигнала строится аналогично, за той лишь разницей, что используются начальные фазы гармоник, а не амплитуды.
Итак, с построением и анализом амплитудного спектра сигнала мы разобрались. Давайте перейдем к следующей теме сегодняшней статьи – к понятию амплитудно-частотной характеристики.
Амплитудно-частотная характеристика (АЧХ).
АЧХ является важнейшей характеристикой многих цепей и устройств – фильтров, усилителей звука и т. д. Даже простые наушники имеют свою собственную амплитудно-частотную характеристику. Проанализируем, какой смысл она в себе несет…
АЧХ – это зависимость амплитуды выходного сигнала от частоты входного сигнала. Как мы выяснили в первой части статьи, негармонический периодический сигнал можно разложить в ряд Фурье. Но мы сейчас рассмотрим, в первую очередь, аудио-сигнал, и выглядит он следующим образом:
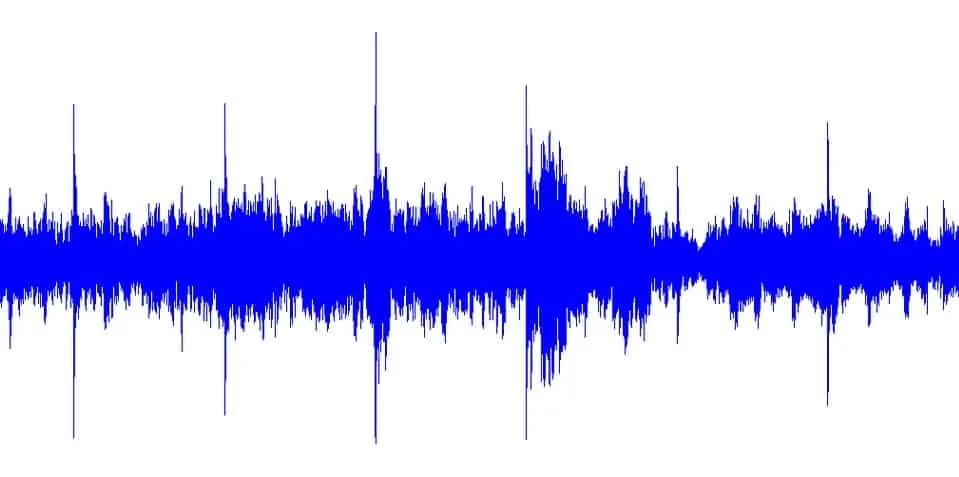
Как видите, ни о какой периодичности здесь не идет и речи. Но, к счастью, существуют специальные алгоритмы, которые позволяют представить звуковой сигнал в виде спектра входящих в него частот. Мы сейчас не будем подробно разбирать эти алгоритмы, это тема для отдельной статьи. Просто примем тот факт, что они позволяют нам осуществить такое преобразование.
Соответственно, мы можем построить диаграмму амплитудного спектра такого сигнала. А пройдя через какую-либо цепь (к примеру, через наушники при воспроизведении звука) сигнал будет изменен. Так вот амплитудно-частотная характеристика как раз и показывает, какие изменения будет претерпевать входной сигнал при прохождении через ту или иную цепь. Давайте детально обсудим этот момент.
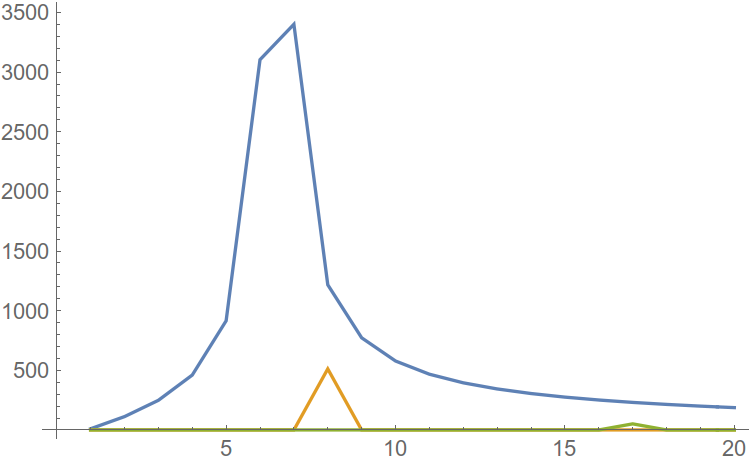
Итак, на входе мы имеем ряд гармоник. Амплитудная-частотная характеристика показывает, как изменится амплитуда той или иной гармоники при прохождении через цепь. Рассмотрим пример АЧХ:
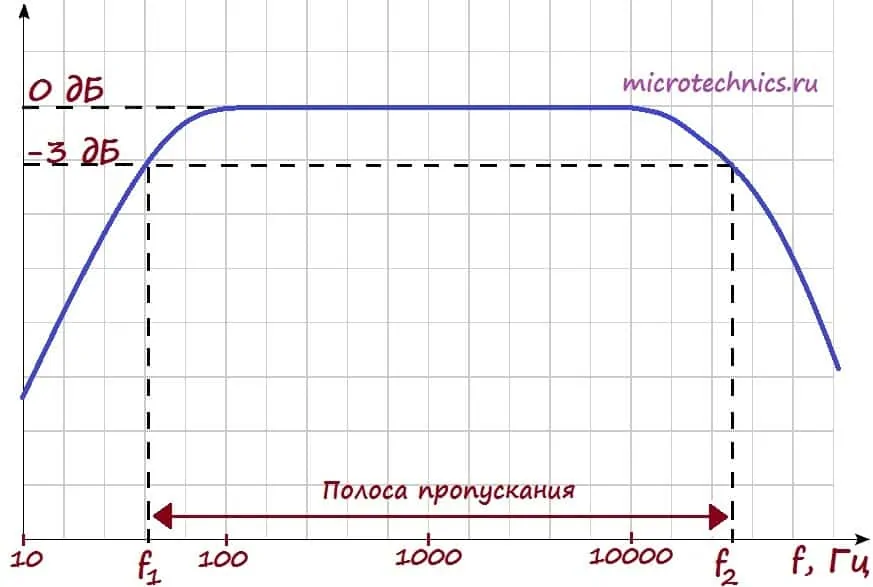
Разбираем поэтапно, что тут изображено. Начнем с осей графика АЧХ. По оси y мы откладываем величину выходного напряжения (или коэффициента усиления, как на данном рисунке). Коэффициент усиления мы считаем в дБ, соответственно величина, равная 0 дБ, соответствует усилению в 1 раз, то есть амплитуда сигнала остается неизменной.
По оси x откладываются частоты входного сигнала. Таким образом, в рассматриваемом случае для всех гармоник, частоты которых лежат в интервале от 100 до 10000 Гц, амплитуда не изменится. А сигналы всех остальных гармоник будут ослаблены.
На графике отдельно отмечены частоты f_1 и f_2. Их отличительной особенностью является то, что сигнал гармоник данных частот будет ослаблен в 1.41 раза (3 дБ) по напряжению. Это соответствует уменьшению по мощности в 2 раза . Полосу частот между f_1 и f_2 называют полосой пропускания. Получается следующая ситуация – сигналы всех гармоник, частоты которых лежат в пределах полосы пропускания устройства/цепи будут ослаблены менее, чем в 2 раза по мощности.
Практические примеры АЧХ аудио-устройств.
Частотный диапазон аудио-устройств обычно разбивают на низкие, средние и высокие частоты. Приблизительно это выглядит так:
- 20 Гц – 160 Гц – область низких частот
- 160 Гц – 1.28 КГц – область средних частот
- 1.28 КГц – 20.5 КГц – область высоких частот
Именно такую терминологию обычно можно встретить в разных программах-эквалайзерах, используемых для настройки звука. Теперь вы знаете, что красивые графики из таких программ являются именно амплитудно-частотными характеристиками, с которыми мы познакомились в сегодняшней статье. И в завершение статьи посмотрим на пару примеров АЧХ:
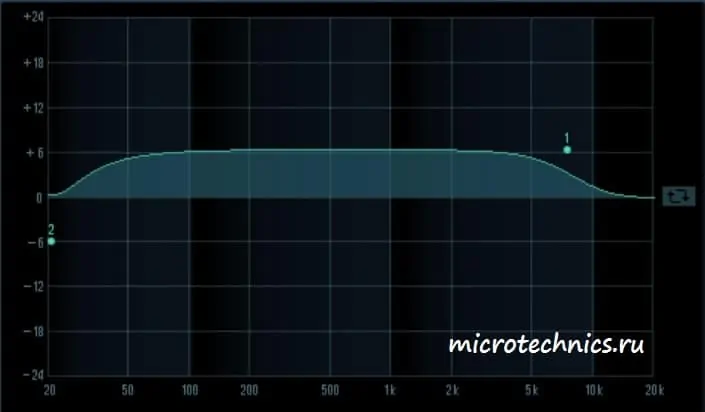
Здесь мы можем видеть амплитудно-частотную характеристику усилителя. Причем усилены будут преимущественно средние частоты диапазона.
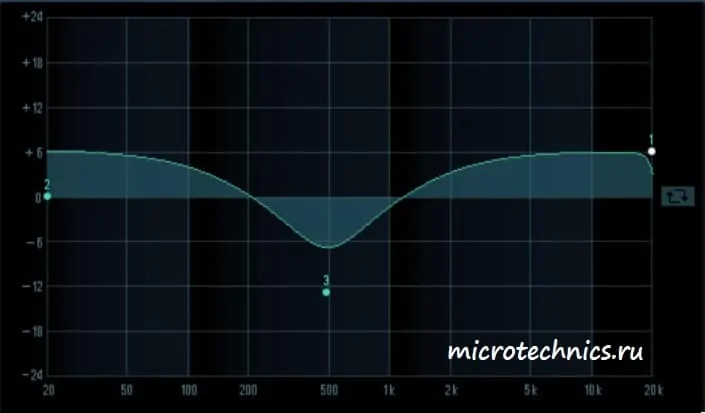
Во втором случае ситуация совсем другая – низкие и верхние частоты усиливаются, а в области средних частот для гармоник с частотой 500 Гц мы наблюдаем значительное ослабление.
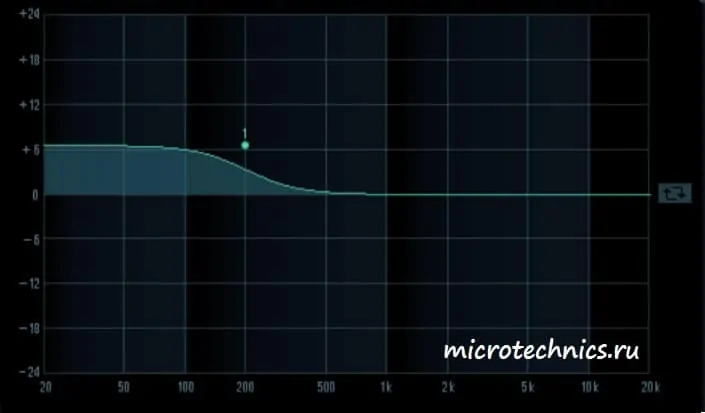
А теперь усиливаются только низкие частоты. Аудио-аппаратура с такой АЧХ будет обладать высоким уровнем басов.
На этом мы и заканчиваем нашу сегодняшнюю статью. Спасибо за внимание и ждем вас на нашем сайте снова 🤝
Преобразование Фурье для дискретного сигнала. Определим связь между спектром X(jw) аналогового сигнала x(t) и спектром XТ(jw) дискретного сигнала xТ(t), определенного моделью (19.2). Учитывая, что xТ(t) = x(t)f(t) согласно теоремы свертки (9.30) получим спектральную плотность дискретного сигнала
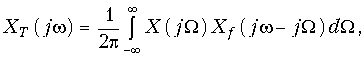
где Xf(jw) – спектральная плотность дискретизирующей последовательности (19.1).
Для нахождения Xf(jw) разложим f(t) в комплексный ряд Фурье (5.6):
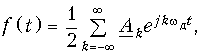
где wд = 2p/Т – частота дискретизации,
Отсюда согласно (9.42) получаем
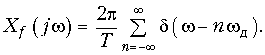
Подставив (19.6) в формулу (19.4) после изменения порядка интегрирования и суммирования и с учетом фильтрующего свойства d-функции окончательно получим
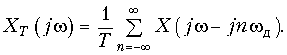
Из (19.7) следует важный вывод: спектр дискретного сигнала xT(t) (рис. 19.6 б) представляет собой сумму бесконечно большого числа «копий» спектра аналогового сигнала (рис. 19.6, а), расположенных на оси частот через одинаковые интервалы.
Следует отметь, что согласно (19.7) и рис. 19.6, б энергия спектра дискретного сигнала оказывается бесконечно велика, что является следствием идеализации реального сигнала моделью (19.2). Если же использовать вместо дискретизирующей последовательности (19.1) последовательность импульсов конечной энергии (например, прямоугольных импульсов), то получим спектр XТ(jw), энергия которого убывает с ростом w («копии» X(jw) с ростом w уменьшаются). В то же время следует еще раз подчеркнуть, что представление дискретного сигнала в форме (19.2) существенно упрощает анализ дискретных сигналов и цепей и широко используется в расчетах.
Спектр дискретного сигнала XТ(jw) можно найти и непосредственно из прямого преобразования Фурье (9.6) для дискретного сигнала (действует в момент t Õ 0).
Отсюда с учетом фильтрующего свойства d-функции получим прямое преобразование Фурье для дискретных сигналов.
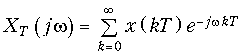
и обратное преобразование Фурье:
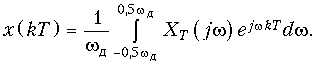
На практике в формулах (19.8), (19.9) часто вместо зависимости XТ(jw) рассматривают зависимости XТ(jf), которые легко можно получить путем замены w = 2pf.
Пример. Рассчитаем спектр дискретного сигнала, состоящего из одного отсчета xТ(t) = [a; 0; 0; 0; …].
Воспользуемся формулой (19.8), в которую подставим значения xt(t) заданного сигнала
.
Пример. Рассчитаем спектр экспоненциальной дискретной функции xТ(t) = 0,5k, k 0.
График дискретной функции xТ(t) приведен на рис. 19.7, а ее отсчеты можно записать в виде последовательности x{k} = {1; 0,5; 0,25; 0,125; 0,0625; …}.
Спектр дискретной экспоненты рассчитаем по формуле (19.8)
где для суммирования ряда использована формула
.
Используя формулу Эйлера , получим выражение для расчета спектра амплитуд X(f).
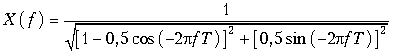
Для построения графика будем задавать значения f от 0 до 1/Т с шагом 0,1/T и рассчитывать X(f).
График спектра амплитуд X(f) экспоненциальной дискретной функции xT(t) = 0,5k приведен на рисунке 19.8.
Как видно из графика, спектр дискретного сигнала сплошной и периодический с периодом fд = 1/Т.
Следует отметить, что если не выполняется условие теоремы Котельникова: fд 2fв, то спектры в (19.7) частично перекрываются. На рис. 19.9, рис. 19.10 показан характер изменения спектра дискретного сигнала XT(f) при изменении частоты дискретизации сигнала xT(t), ограниченного во времени интервалом Tс (рис. 19.9) и неограниченного во времени (рис. 19.10).
Как следует из представленных графиков увеличение периода дискретизации T > 1/2Fв; Fд < 2Fв приводит к наложению смежных спектров в (19.7), что приводит к наложению спектра ХT(f). Эти искажения называются ошибками наложения. Чтобы их устранить необходимо частоту дискретизации увеличить до Fд 2Fв.
Пример. Рассчитаем интервал дискретизации и минимально допустимую частоту дискретизации сигнала, спектральная плотность которого равна нулю при значениях частоты выше 100 кГц.
Из условия задачи следует, что граничная частота спектра Fв равна 100 кГц. Тогда в соответствии с теоремой Котельникова имеем интервал дискретизации
.
Минимально допустимая частота дискретизации fд = 2Fв = 2×100 = 200 кГц.
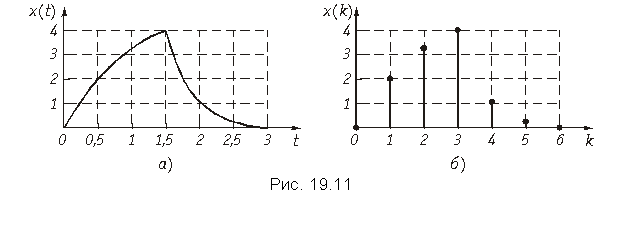
Пример. Определим дискретные отсчеты сигнала длительностью tи = 3 мс, приведенного на рис. 19.11, а, если в качестве граничной частоты спектра Fв принять значение 3/tи, выше которого все значения спектральной плотности уменьшаются более чем в 10 раз по сравнению с максимальным.
Хотя сигнал конечной длительности имеет бесконечный спектр частот, однако почти всегда можно определить граничную частоту спектра таким образом, чтобы отсекание частот превышающих Fв, привело к пренебрежимо малым изменениям энергии исходного сигнала. Такое условие задано в примере.
Граничная частота спектра Fв = 3/tи = 3/(3×103) = 1 кГц.
Интервал дискретизации T = 1/(2Fв) = 1/(2×1×103) = 0,5 мс.
Берем отсчеты сигнала, приведенного на рис. 19.11, а, через интервал времени T = 0,5 мс и получаем последовательность x{k} = {0; 2; 3,2; 4; 1; 0,3; 0}, изображенную графически на рис. 19.11, б.
Отметим, что аналоговый сигнал x(t) можно полностью восстановить по его дискретным отсчетам x(kT) с помощью ФНЧ, частота среза которого wс = 0,5wд = wв. Этот вывод хорошо иллюстрирует рис. 19.10, а из которого видно, что спектр сигнала на выходе ФНЧ совпадает со спектром аналогового сигнала x(t).
Дискретное преобразования Фурье. Как следует из формулы (19.7) XT(jw) имеет периодическую структуру с wд = 2p/T. Причем, как и спектр аналогового сигнала X(jw) спектр дискретного сигнала XT(jw) является сплошным (см. рис. 19.6, б). Вместе с тем при цифровой обработке сигналов используется не только дискретизация во времени, но и дискретизация в частотной области.
Для сигнала x(t) ограниченного во времени интервалом Tс (рис. 19.12, а) справедлива обратная теорема Котельникова, которая может быть получена из (19.3) путем заменыt ->w; wв->Tс/2; Т-> Dw:
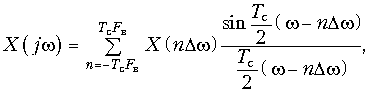
где Dw = 2p/Tс; Tс – длительность сигнала;X(nDw) – отсчеты спектра сигнала в частотной области.
Переходя к дискретному сигналу xT(t) (рис. 19.12, б) отметим, что общее количество отсчетов сигнала будет равно
где T = 2p/wд = p/wв.
Дискретный спектр (рис. 19.12, е) может быть получен путем периодического повторения последовательности {x(kT)} с периодом Tс = NT (рис. 19.12, в). При этом частотный интервал между дискретными отсчетами спектра (рис. 19.12, е) составляет
(19.11)
С учетом вышеизложенного дискретное преобразование Фурье (ДПФ) можно получить, если в преобразовании (19.8) сделать замену w = nDw. Тогда получим
или с учетом (19.11)
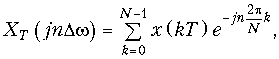
где n = 0; ±1; ±2; ± … N/2.
Для упрощения записи аргумент nDw и kT обычно заменяют индексом n и k соответственно и опускают индекс T, при этом (19.12) примет вид
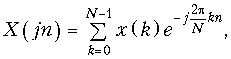
которое определяет прямое ДПФ.
С помощью (19.13) можно определить отсчеты спектра X(jn) по временным отсчетам сигнала x(k).
Обратное ДПФ можно получить из (19.13) воспользовавшись дуальностью прямого и обратного преобразований Фурье:
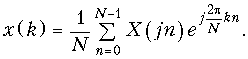
При k < 0 обратное преобразование Фурье определит x(k), расположенную слева от 0 (рис. 19.12, в).
Для ДПФ по аналогии с непрерывными преобразованиями Фурье справедливы основные теоремы и свойства.
В частности, свойство линейности
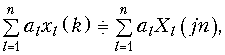
сдвиг дискретного сигнала:
(19.16)
т. е. сдвиг последовательности отсчетов сигнала на m интервалов приводит лишь к изменению фазового спектра дискретного сигнала.
Теорема свертки:
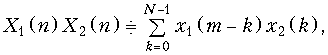
где N = N1 + N2; N1, N2 – число отсчетов х1 и х2 соответственно.
Аналогично можно записать и другие теоремы для ДПФ. Заметим, что ДПФ можно использовать для определения не только спектра дискретных сигналов, но и спектра аналоговых сигналов, для чего его необходимо дискретизировать согласно теоремы Котельникова (19.3).
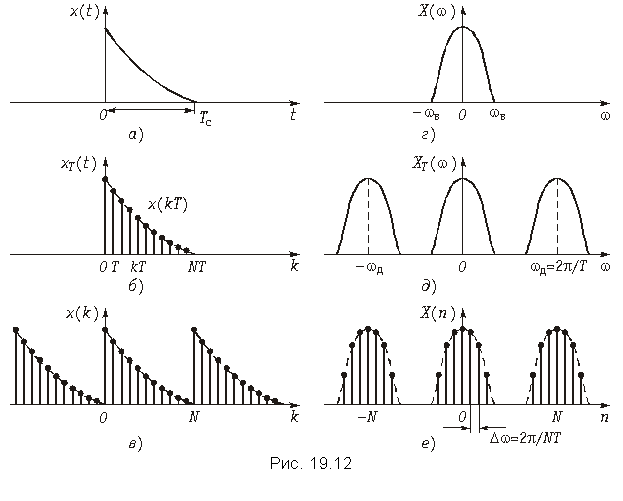
Пример. Рассчитаем ДПФ дискретного периодического сигнала, заданного тремя отсчетами x{k} = {0; 1; 2}.
Для расчета воспользуемся формулой ДПФ (19.13).
Поскольку
,
,
то ,
.
Графики заданного дискретного периодического сигнала x(k) и рассчитанного дискретного периодического спектра амплитуд X(n) приведены на рис. 19.13.
Пример. Рассчитаем значения дискретного сигнала x(k), ДПФ которого имеет вид X[n] = {0; 1; 0; 1}.
Значения дискретного сигнала x(k) будем рассчитывать по формуле (19.14)
;
График последовательности x{k} = {0,5; 0; –0,5; 0} приведен на рис. 19.14. Сигнал x(k) дискретный и периодический.
Пример. Определить с помощью ДПФ спектр аналогового сигнала, изображенного на рис. 19.15, а.
Ограничим длительность сигнала Tc, где (рис. 9.15, а). Например, при Tc = 3/a,
. Выберем число отсчетов N = 10, определим частоту дискретизации
Согласно (19.13) находим отсчеты спектра сигнала
и т.д.
В таблице приведены результаты расчета спектра,
|
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
X(jn) |
3.4 |
3.3 |
2.8 |
1.6 |
0.6 |
0.4 |
0.6 |
1.6 |
2.8 |
3.3 |
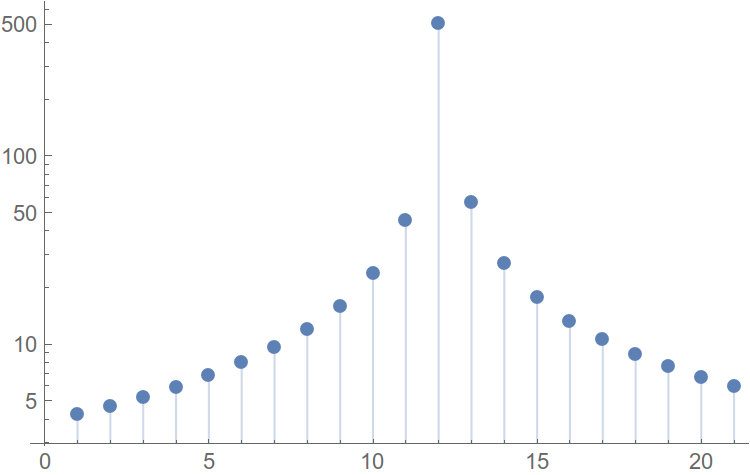
а на рис. 19.15, б спектр сигнала X(jn). Следует отметить, что с увеличением T (уменьшение числа отсчетов N) погрешность аппроксимации x(t) увеличивается (см. рис. 19.5, а).
Как следует из вышеприведенных примеров и формул (19.13), (19.14), для вычисления ДПФ содержащих N отсчетов необходимо осуществить в общем случае N2 операций с комплексными числами. Если длина обрабатываемых массивов достаточно велика, то вычисление ДПФ даже на современных быстродействующих ЭВМ занимает достаточно много времени. Для сокращения вычислений используют обычно алгоритм быстрого преобразования Фурье (БПФ). Существует много разновидностей БПФ. Здесь мы рассмотрим один алгоритм, основанный на прореживании по времени.
Быстрое преобразование Фурье. Положим, что число отсчетов N = 2q, где q – целое число. Разобьем дискретную последовательность отсчетов {x(k)} не две части:
четную {x(k)}чт = {x(2k)}
и нечетную {x(k)}нч = {x(2k + 1)}, где k = 0, 1, 2, … N/2 – 1.
Представим спектр (19.13) в виде
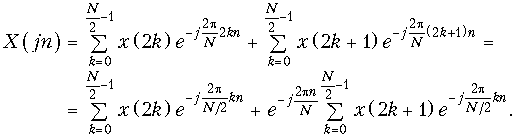
Из (19.18) следует, что
(19.19)
где n = 0, 1, 2, …, ((N/2) – 1).
Из (19.19) следует, что первая половина X(jn) (n = 0, 1, 2, …, (N/2) – 1) выражается через ДПФ двух частных последовательностей: Xчт(jn) и Xнч(jn). Вторую половину (n N/2) X(jn) можно найти, если учесть периодичность его четной и нечетной части с периодом N/2:
и соотношение (при n N/2):
при этом получим
(19.20)
Формула (19.19) и (19.20) лежит в основе БПФ. Как следует из этих формул для вычисления Xчт(jn) и Xнч(jn) требуется (N/2)2 операций и для выполнения операции умножения на exp{×} – N операций:
(19.21)
Для ДПФ (19.13) требуется операций, что существенно выше, чем NБПФ. Например, при N = 103, получаем NДПФ = 106, а NБПФ ~ 250×103, т. е. для БПФ требуется в четыре раза меньше операций, чем при ДПФ.
В общем случае число операций, необходимое в БПФ равно
(19.22)
и выигрыш по сравнению с ДПФ равно
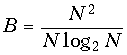
и может достигать сотен и тысяч раз при достаточно больших входных массивах N.
В заключении отметим, что сам процесс вычисления по формулам (19.18), (19.19) производят по итерационному принципу: последовательность отсчетов с четными и нечетными номерами снова разбивают на две части и т. д. Процесс разбиения продолжается до тех пор, пока не получится последовательность, состоящая из одного элемента (исходного ДПФ). Более подробно с алгоритмами БПФ можно ознакомиться в специальной литературе (см. например, Гольденберг Л.М., Матюшкин Б.Д., Поляк М.Н. Цифровая обработка сигналов. М. «Радио и связь. 1990).
7. Спектральный анализ периодических сигналов
7.1. Разложение периодических сигналов
по ортогональным функциям
Электрический сигнал 







Рис. 7.1
При расчете разнообразных сигналов удобно представить их взвешенной суммой заданных функций времени вида

где 



Рекомендуемые материалы
Чтобы разложение в ряд (7.1) было взаимно однозначным
144
функции 

где момент начала интегрирования 


Для ортогонального базиса коэффициенты разложения 

В математике и технике широко используются различные ортогональные наборы функций (базисы) и прежде всего гармонический базис

полиномы Чебышева, Лагранжа, Эрмита и др. В цифровой технике применяют ортогональные дискретные функции Уолша, Радамахера.
7.2. Ряд Фурье
Ряд Фурье для действительной периодической функции времени 
145

Компоненту ряда Фурье вида

называют 

– частота первой гармоники, 








146

Величины 


7.3. Спектры амплитуд и фаз периодического сигнала
Периодический сигнал 

то есть двумя в общем случае бесконечными наборами чисел.
Первый из них называют спектром амплитуд сигнала,

а второй – спектром фаз,

Спектры амплитуд и фаз не зависят от времени, а определяются формой сигнала 



147
не зависят от формы сигнала и определяются только периодом его повторения 

Рис. 7.2 тельности прямоугольных
импульсов с амплитудой 




а амплитуды синфазной и квадратурной составляющих –


Для амплитуды и начальной фазы 


148
Графики спектров амплитуд и фаз при условии 


Рис. 7.3
Переменная 

и спектральные диаграммы можно строить в координатах частоты гармоники, как показано на рис. 7.4 для спектра амплитуд.
Спектры имеют дискретный (линейчатый) характер, интервал частот между соседними гармониками одинаков и
149
равен 



Рис. 7.4 амплитуд гармоник. Формулу
огибающей можно получить из выражения для спектра амплитуд, подобного (7.20), при замене номера гармоники 

где 
В примере (7.20) получим

график показан на рис. 7.3а пунктирной линией. Характерной особенностью огибающей спектра амплитуд сигнала рис. 7.2 является наличие точек с нулевым значением (нулей огибающей), определяемых из уравнения

решение которого имеет вид
150

где 

7.4. Синтез сигнала по его спектру
Если известны спектры амплитуд и фаз, то с помощью ряда Фурье (7.13) можно получить сигнал как функцию времени. Бесконечная сумма на практике не реализуема и сигнал описывается конечной суммой гармоник,

Соответствующие кривые при 


Как видно, с увеличением 
7.5. Ряд Фурье в комплексной форме
Гармоники сигнала могут быть представлены своими комплексными амплитудами в виде

тогда исходный сигнал можно представить в виде ряда Фурье,

151
Рис. 7.5
Амплитуда 


а ее начальная фаза 

152

Комплексная амплитуда гармоники (2.27) позволяет существенно упростить расчеты спектров амплитуд и фаз за счет сокращения числа интегралов и с учетом того, что подынтегральное выражение с экспонентой часто интегрируется проще, чем с тригонометрической функцией.
Рассмотрим сигнал, показанный на рис. 7.6, тогда

Как видно, в данном примере комплексная амплитуда является действительной величиной, что обусловлено формой сигнала на рис. 7.2..Спектры амплитуд и фаз совпадают с ранее полученными значениями.
7.6. Влияние формы сигнала на спектры амплитуд и фаз
Спектры амплитуд и фаз сигнала взаимно однозначно связаны с его формой, которая определяется формой импульсов и их длительностью на периоде повторения.
На рис. 7.6 показана последовательность прямоугольных импульсов 



153
тельностью) фронт и срез импульса. Величину

называют скважностью импульсов. На рис. 7.7 приведены спектры амплитуд (рис. 7.7а) и фаз (рис. 7.7б)
Рис. 7.6 при 
Рис. 7.7
На рис. 7.8 приведены аналогичные зависимости при 
Рис. 7.8.
154
При фиксированном периоде повторения импульсов 

 |
Рассмотрим трапециидальный импульс, программа исследование которого в среде MathCAD показана на рис. 7.9. Спектральный анализ проводится с помощью стандартной процедуры спектрального анализа fft(s). Она построена на основе алгоритма быстрого преобразования Фурье (БПФ) и позволяет получить комплексные коэффициенты 


Период 

Как видно при сравнении графиков спектров амплитуд на рис. 7.7 и рис. 7.9, увеличение длительности фронта и среза импульса приводит к значительному ослаблению высших гармоник сигнала.
155
На рис. 7.10 показан пример программы расчета спектра амплитуд колоколообразного сигнала вида

для которого характерно наиболее плавное изменение значений во всем интервале времени.
Рис. 7.9.
График сигнала и его спектр амплитуд показаны в листинге программы на рис. 7.10. Как видно, спектр «гладкого» сигнала сосредоточен в области нижних частот, высшие гармоники практически отсутствуют.
Полученные выводы подтверждают результаты синтеза прямоугольных импульсов по ограниченному числу 
156
Рис. 7.10.
7.7. Свойства спектров сигналов
Свойства спектров сигналов часто формулируются в виде теорем.
Спектральное преобразование сигнала линейно, то есть комплексная амплитуда суммы сигналов равна сумме комплексных амплитуд гармоник каждого из суммируемых сигналов. На практике особый интерес представляет свойство (теорема) смещения сигнала во времени. Ее можно сформулировать следующим образом.
 |
157
Взяв модули левой и правой частей (7.30), получим

то есть спектр амплитуд не изменяется при задержке сиг-
нала во времени.
Вычислим аргументы обеих частей выражения (7.30),

то есть начальные фазы гармоник сигнала при временной задержке уменьшаются на величину 

Для доказательства теоремы смещения запишем

Проведем замену переменных 

На спектральные характеристики влияют свойства симметрии сигнала.
Рассмотрим четные функции времени, удовлетворяющие условию 


158
комплексная амплитуда 


а начальная фаза равна 0 или 

Для нечетной функции, удовлетворяющей условию 


комплексная амплитуда 


а начальная фаза равна 0 или 

Эти свойства иллюстрирует пример четного сигнала на рис. 7.2, для которого имеет место равенство (7.19). Его фазовый спектр со значениями 0 или 
Рассмотрим комплексные спектры двух сигналов 


Рис. 7.11.
Сигнал 

159
величину 


Комплексная амплитуда 


По теореме смещения можно найти комплексную амплитуду 


Тогда согласно свойству линейности комплексная амплитуда 


160
С другой стороны, при прямом вычислении (проведите расчеты самостоятельно) комплексная амплитуда 


что полностью совпадает с (7.46).
7.8. Мощность периодического сигнала
Пусть имеется сигнал 


Эту же величину можно выразить через гармоники сигнала с помощью равенства (теоремы) Парсеваля в виде

С помощью спектральных характеристик можно определить действующее значение 

7.9. Ширина спектра
Как видно по графикам спектров амплитуд рассмотренных сигналов, в целом наблюдается тенденция уменьшения
161
амплитуд гармоник с ростом их номера (частоты). Графики на рис. 7.5 показывают, что форма сигнала определяется сравнительно небольшим числом гармоник. Все это свидетельствует
о том, что для представления (даже достаточно точного) сигнала необходимо учитывать ограниченное число гармоник, которые занимают конечный интервал частот.
 |
Мощность сигнала определяется выражением (7.39). Для рассматриваемых видеосигналов наиболее интенсивные гармоники имеют номера от 1 до некоторой величины N, при этом их суммарная мощность равна

Как видно, с ростом 



Тогда можно определить число гармоник 


выражения

В результате можно определить ширину спектра 

162
В качестве примера рассмотрим последовательность прямоугольных импульсов, показанную на рис. 7.2 со спектром амплитуд, показанном на рис. 7.3а. (скважность импульсов 






Рис. 7.12
Этот же график в области значений от 0,9 до 1 показан на рис. 7.13. С ростом 


В инженерной практике рассмотренный расчет ширины спектра проводится редко, а используется ее инженерная оценка. Для импульсных сигналов с длительностью 
163
пример, рис. 7.2) ширина спектра определяется выражением


(сравните эти величины со значениями нулей огибающей спектра амплитуд).
Рис. 7.13
Множитель от 1 до 3 косвенно характеризует долю мощности сигнала, заключенную в полосе пропускания (единица примерно соответствует 

Оценки ширины спектра можно выразить через число гармоник,

где 

164
На практике чаще всего используются соотношения с единичным множителем вида
 |
В рассмотренном примере сигнала на рис. 7.2 скважность 

7.10. Задания для самостоятельного решения
Задание 7.1. Определите и постройте графики спектров амплитуд и фаз сигналов вида:





Задание 7.2. Определите спектры амплитуд и фаз сигналов, показанных на рис. 7.14, постройте их графики. Проведите расчет ширины спектра при 


165
Рис. 7.14
Задание 7.3. С помощью теоремы смещения проведите расчет спектров амплитуд и фаз сигнала, показанного на рис. 7.14а, воспользовавшись результатами, полученными для сигнала на рис.7.2.
Задание 7.4. Определите спектры амплитуд и фаз сигнала, показанного на рис.7.15, постройте их графики. Сравните спектр амплитуд со спектром гармонического сигнала, проанализируйте результаты.
Вычислите ширину спектра сигнала при 
Рис. 7.15
Задание 7.5. Определите спектры амплитуд и фаз сигналjd, показанного на рис.7.16, постройте их графики.
166
Рис. 7.16
Люди также интересуются этой лекцией: 2 Нефть и получение нефтепродуктов.
Задание 7.6. Определите спектры амплитуд и фаз сигнала, показанного на рис.7.17, постройте их графики.
Рис. 7.17
Проведите тот же расчет, представив сигнал на рис. 7.17 в виде суммы двух импульсных последовательностей, показанных на рис. 7.18, и используя свойство линейности.
Рис. 7.18

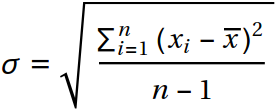

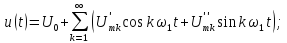
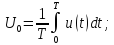
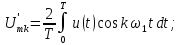

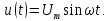
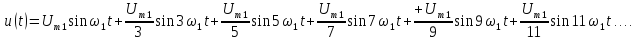
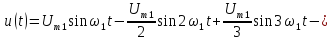
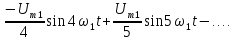


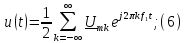

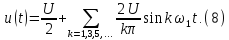

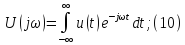
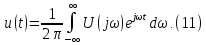
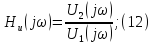
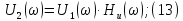
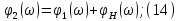


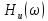
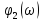


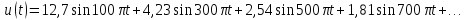

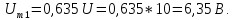



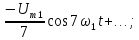
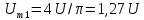
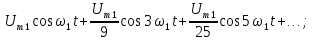


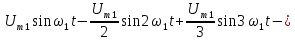

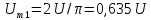
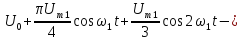
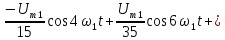


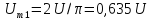
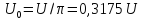
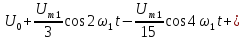

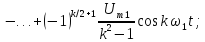
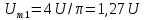

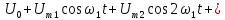
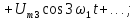
 ;
; ;
;
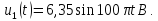

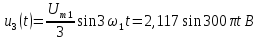
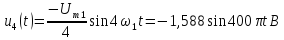

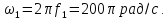
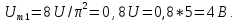


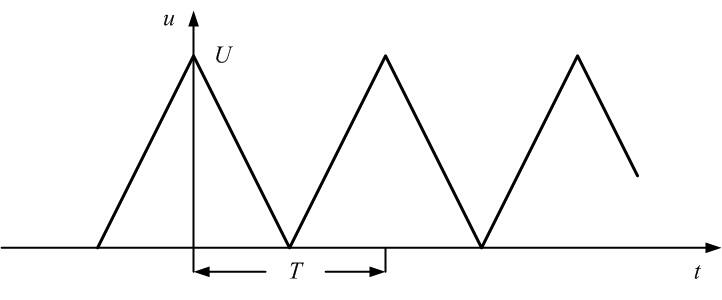

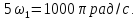
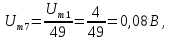


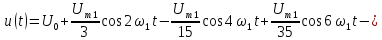
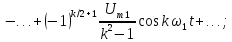
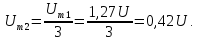

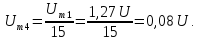
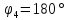
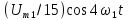


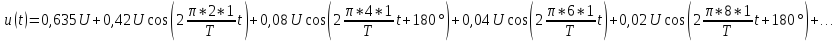
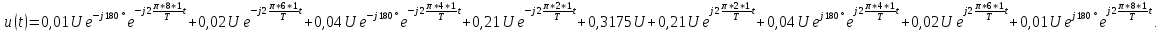
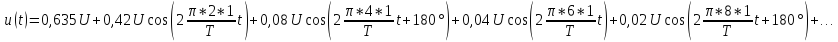
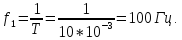
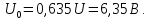


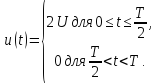
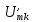



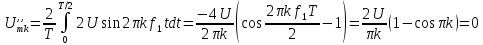
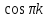
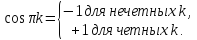
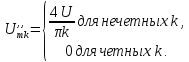
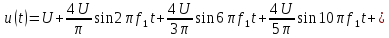








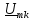
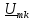
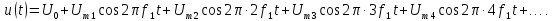
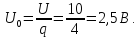

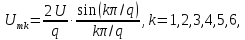

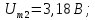

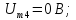
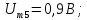
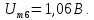


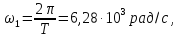
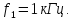

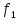



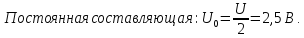
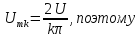
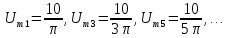

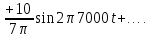

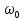
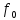
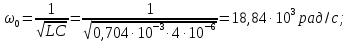



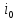
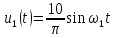
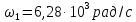
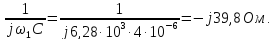


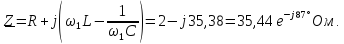






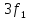
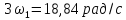


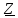

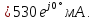




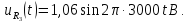
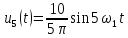





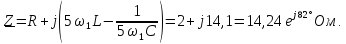
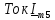
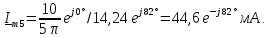
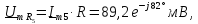
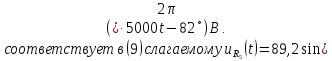

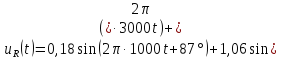

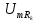
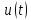

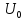

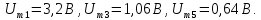
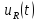
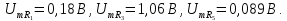

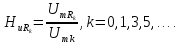

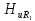
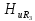
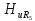
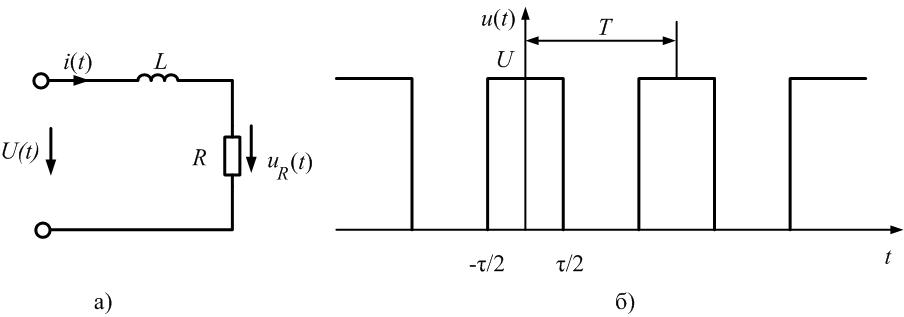

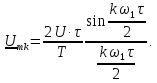
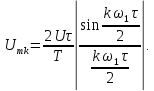
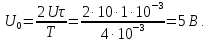

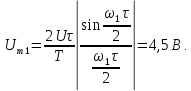
 =0,5
=0,5 =3,28
=3,28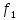 =0,75
=0,75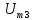 =1,5
=1,5 =1
=1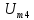 =0
=0 =1,25
=1,25 =0,9
=0,9 =1,5
=1,5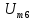 =1,06
=1,06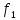 =1,75
=1,75 =0,64
=0,64 =2,0
=2,0 =0
=0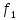 =2,25
=2,25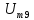 =0,5
=0,5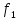 =2,5
=2,5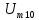 =0,64
=0,64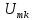

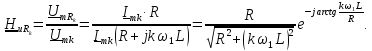
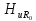 =1;
=1; =0,95;
=0,95;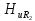 =0,85;
=0,85;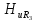 =0,73;
=0,73; =0,62;
=0,62; =0,54;
=0,54;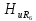 =0,47;
=0,47;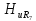 =0,41;
=0,41;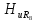 =0,37;
=0,37;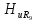 =0,33;
=0,33; =0,3.
=0,3.