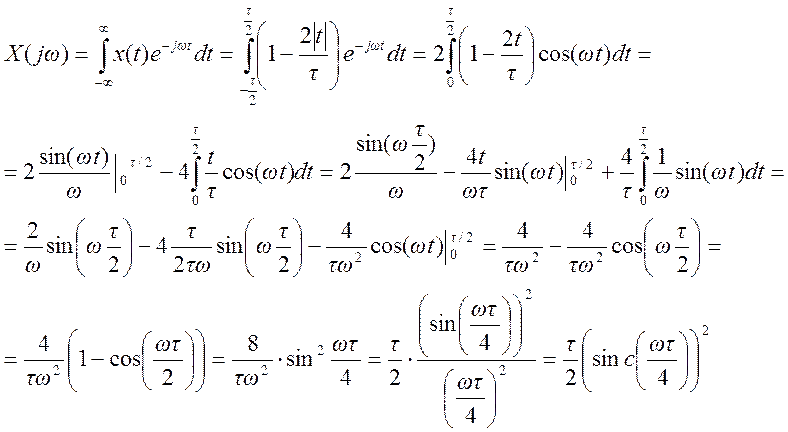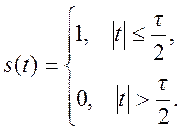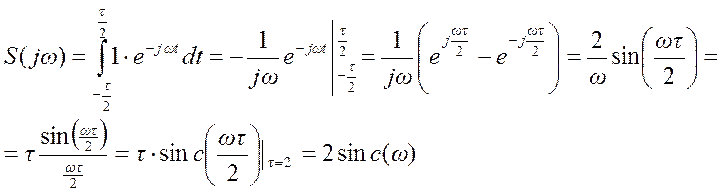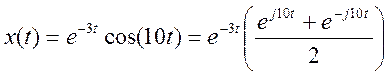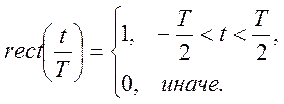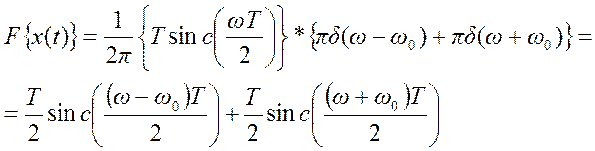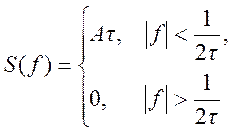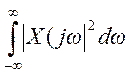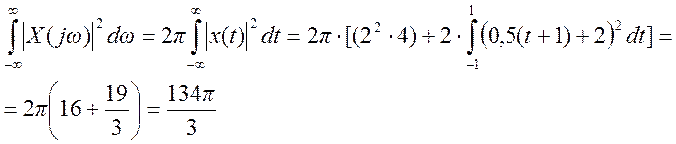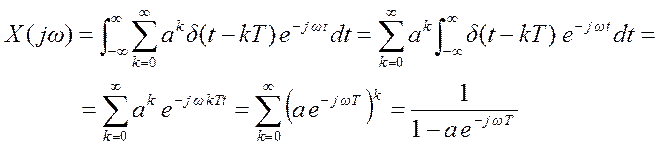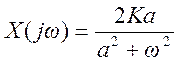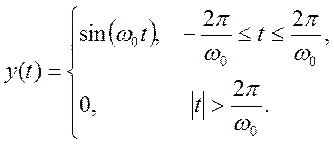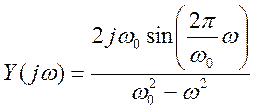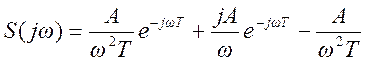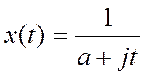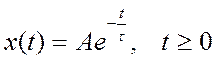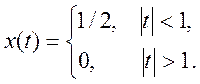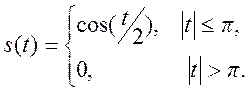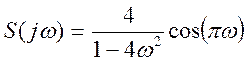Спектр симметричного треугольного импульса
Параметры
импульса приведены на рис. 1.8.4а.
Спектральную функцию проще всего найти,
используя теорему о спектре производной.
Для производной (рис. 1.8.4б)
спектральная функция равна
а

Рис.
1.8.4
Из
последнего равенства получаем окончательно
для спектра симметричного треугольного
импульса
Эта
спектральная функция является чётной
и вещественной
(рис.
1.8.4в).
Фазовый спектр чисто нулевой.
Спектр косинусоидального импульса
Косинусоидальный
импульс (рис. 1.8.5а)
записывается в виде
Рис.
1.8.5
После
двукратного дифференцирования сигнала
мы получим исходный сигнал, умноженный
наи две дельта функции
и
Дважды применяя теорему о спектре
производной, с учётом спектра двух
смещённых дельта-функций можем записать
откуда
Таким
образом, спектральная функция
косинусоидального импульса является
вещественной. АЧХ показана на рис.
1.8.5б.
Спектр одностороннего экспоненциального импульса
Такой
импульс задаётся функцией
п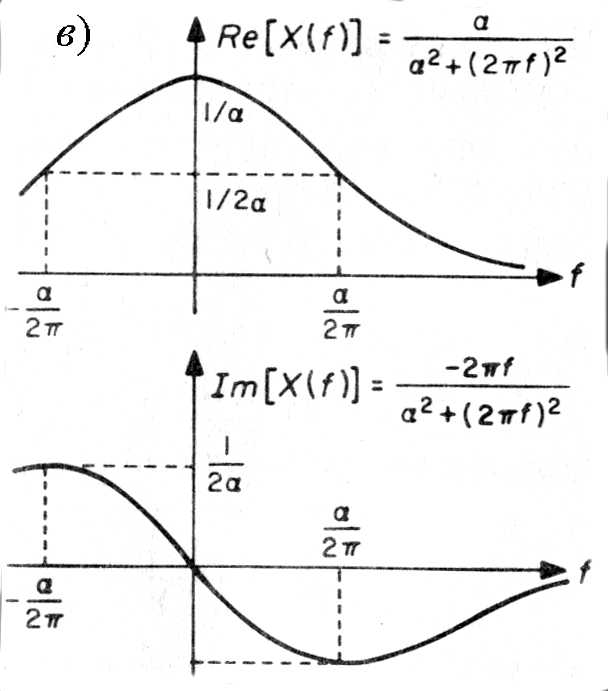
положительном вещественном значении
параметра
Рис.
1.8.6
Это
сигнал бесконечной длительности, однако
условие
обеспечивает быстрое уменьшение его
значений с ростом времени
(рис.
1.8.6а).
Спектральная
плотность
импульса
есть
комплексная функция
имеющая модуль (амплитудный спектр)
и
аргумент (фазовый спектр)
которые
изображены на рис. 1.8.6б.
Эквивалентным
заданием спектральной функции
является пара функций
и
графики которых представлены на рис.
1.8.6в.
Эти графики иллюстрируют свойство
симметрии преобразования Фурье любой
действительной функции.
и
являются чётными функциями, тогда как
и
– нечётными.
Спектр двустороннего экспоненциального импульса
Э
импульс задаётся функцией
к
показана на рис. 1.8.7а.
Его можно выразить через выше рассмотренный
односторонний импульсследующим образом:
С
учётом этого
Спектр
чисто вещественный и изображён на рис.
1.8.7б.
Рис. 1.8.7
Спектр колокольного импульса
Следующий
важный сигнал – колокольный или гауссов
импульс:
который
имеет бесконечную протяжённость (рис.
1.8.8а).
Эффективную длительность импульса
можно определить, например, из условия
Тогда получаем
Спектральная
плотность импульса
Рис.
1.8.8. а
–
гауссов импульс, б
– его спектр
Преобразуем
подынтегральное выражение так, чтобы
воспользоваться табличным интегралом
который
получается из условия нормировки
гауссова закона распределения. Выделяя
полный квадрат
можем
записать
Введём новую
переменную
тогда
и
т. е. спектральная
плотность гауссова импульса вещественна
и является гауссовой функцией частоты
(рис. 1.8.8б). Чем больше β тем короче
сигнал и тем шире его спектр.
Спектр короткого одиночного импульса
Функция
представляющая короткий импульс
произвольной формы, равна нулю вне
некоторого малого интервалаоколо
поэтому
площадь
импульса.
Здесь
учтено, что при малых
можно считать
Таким
образом, спектр короткого импульса есть
непрерывная функция частоты, имеющая
постоянное значение, равное площади
импульса, форма импульса может быть
произвольной.
Следует
заметить, что
мало отличается от единицы при
или
Отсюда
следует важный практический вывод:
короткий одиночный импульс произвольной
формы имеет сплошной спектр, который
может быть выражен постоянной величиной,
пропорциональной площади импульса, в
пределах того интервала частот, период
колебаний которых остается большим по
сравнению с длительностью импульса.
Соседние файлы в папке Литература ЦОС
- #
- #
- #
11.03.201672 б49dsplib.ru.txt
- #
- #
- #
- #
Основной задачей настоящего параграфа является пояснение свойств преобразований Фурье, приведенных в предыдущих параграфах, на примерах, важных для практики.
1. ПРЯМОУГОЛЬНЫЙ ИМПУЛЬС
Простейшее колебание, определяемое выражением

и представленное на рис. 2.14, а, получило широкое распространение как в технике, так и в теории сигналов и цепей. Применяя формулу (2.48), находим спектральную плотность (рис. 2.14, б)

Заметим, что произведение 

Таким образом, выражение (2.68) можно записать в форме

Здесь через 

При удлинении (растягивании) импульса расстояние между нулями функции 









На рис. 2.15 показаны отдельно графики модуля 





Рис. 2.14. Прямоугольный импульс (а) и его спектральная плотность (б)

Рис. 2.15. Модуль (а) и аргумент (б) спектральной плотности прямоугольного импульса

Рис. 2.16. Совмещение начала отсчета времени с фронтом прямоугольного импульса
При отсчете времени не от середины импульса (как на рис. 2.13), а от фронта (рис. 2.16) ФЧХ спектра импульса должна быть дополнена слагаемым 

2. ТРЕУГОЛЬНЫЙ ИМПУЛЬС
Представленный на рис. 2.17, а импульс определяется выражением

Прямое вычисление спектральной плотности треугольного импульса по формуле (2.48) хотя и несложно, все же несколько громоздко.
Для иллюстрации применения теорем о спектрах, приведенных в предыдущем параграфе, найдем сначала спектральную плотность функции, являющейся производной от заданного сигнала 





Рис. 2.17. К определению спектральной плотности треугольного импульса
Спектральная плотность отрицательного импульса, показанного на рис. 2.17, б, соответственно

Суммарная спектральная плотность двух импульсов

Спектральная плотность треугольного импульса, являющегося интегралом от функции 


Множитель 



Обобщение этого важного вопроса, основанное на использовании аппарата дельта-функций, дается в § 2.13.
3. КОЛОКОЛООБРАЗНЫЙ (ГАУССОВСКИЙ) ИМПУЛЬС (РИС. 2.18, а)
Представленный на рис. 2.18, а импульс определяется выражением

Этот импульс, совпадающий по форме с графиком нормального (гауссовского) закона распределения вероятностей, называется также гауссовским импульсом. Постоянная а имеет смысл половины длительности импульса, определяемой на уровне 


Применяя выражение (2.48), получаем

Для вычисления интеграла удобно в подынтегральной функции дополнить показатель степени до квадрата суммы

где величина d определяется из условия


Рис. 2.18. Колоколообразный (гауссовский) импульс (а) и его спектральная плотность (б) откуда

Таким образом, выражение (2.75) можно привести к виду

Переходя к новой переменной 

Учитывая, что входящий в это выражение интеграл равен 

где 
График этой функции изображен на рис. 2.18, б.
Полученный результат имеет важное значение для теории сигналов. Оказывается, что гауссовский импульс и его спектр выражаются одинаковыми функциями и обладают свойством симметрии: для получения одной из них по заданной другой достаточно заменить t на 



Гауссовскому спектру

соответствует гауссовский импульс

с длительностью 

Очевидно, что чем меньше длительность импульса 

4. ИМПУЛЬС ВИДА SINC(x)
На рис. 2.19, а изображен импульс, определяемый выражением

Вместо вычисления спектральной плотности по формуле (2.48) воспользуемся результатами п. 1 данного параграфа и свойством взаимной заменяемости 
Из рис. 2.14 очевидно, что после замены 



Рис 2.19. Импульс вида 
Для этого сопоставим абсциссу 





Уровень спектра, равномерный в полосе — 



Итак, окончательно

5. ГРУППА ОДИНАКОВЫХ И РАВНООТСТОЯЩИХ ИМПУЛЬСОВ
Спектральную плотность первого импульса в пачке (рис. 2.20) обозначим через 


Для группы из N импульсов в соответствии с принципом линейного суммирования спектров при сложении сигналов спектральная плотность

При частотах, отвечающих условию 

Таким образом, при частотах 

Рис. 2.20. Пачка одинаковых, равноотстоящих импульсов

Рис. 2.21. Модуль спектральной плотности пачки из трех (а) и четырех (б) импульсов
Это объясняется тем, что спектральные составляющие различных импульсов с указанными выше частотами складываются с фазовыми сдвигами, кратными 
При частотах же 


В качестве иллюстрации на рис. 2,21, а изображен спектр (модуль) пачки из трех прямоугольных импульсов, а на рис. 2.21, б — из четырех при интервале между соседними импульсами 

Задачи 3
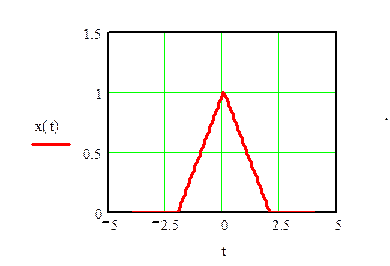
Определить
преобразование Фурье треугольного импульса и построить график его
амплитудного спектра
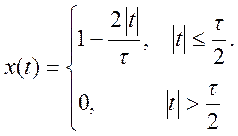
График для τ =4.
Решение.
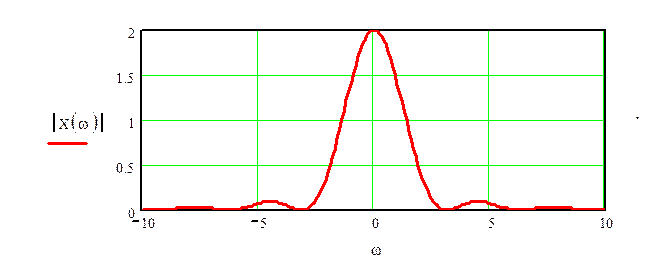
График амплитудного спектра
сигнала при
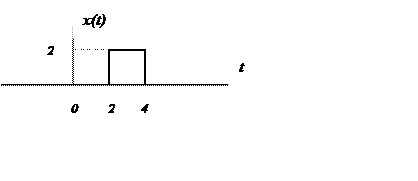
- Найти преобразование Фурье (спектр Фурье) сигнала
Решение.
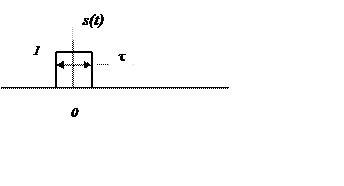
Определим спектр Фурье
прямоугольного импульса длительностью τ, симметричного относительного начала
координат.
Связь между сигналами x(t) и s(t) x(t) = 2s(t-3)
По свойству линейности и
временного сдвига преобразования Фурье
.
- Определить спектр Фурье сигнала
Решение.
Преобразование Фурье
правостороннего экспоненциального сигнала
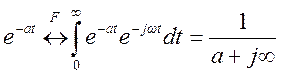
Поэтому 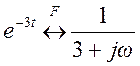
Согласно свойству частотного
сдвига
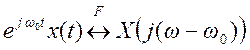
следовательно, для
преобразование Фурье
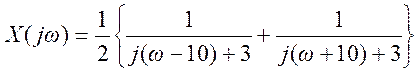
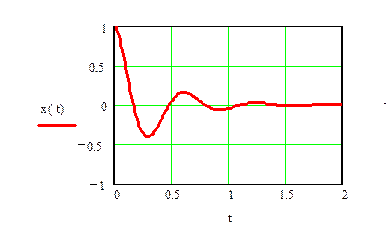
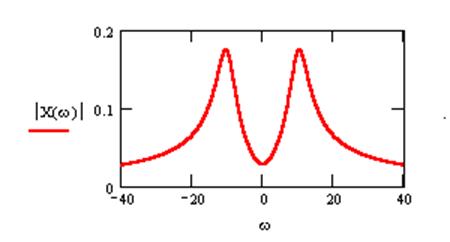
График амплитудного спектра сигнала
Комментарий: пики на частотах ω = ±10
соответствуют переносу
(сдвигу) спектра
сигнала в связи с его модуляцией
- Найти преобразование Фурье косинусоидального импульса
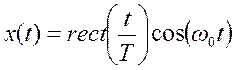
где
Решение
Преобразования Фурье
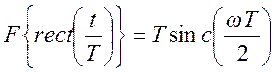
.
По свойству умножения
преобразования Фурье произведению сигналов во временной области соответствует
свертка их преобразований Фурье в частотной области
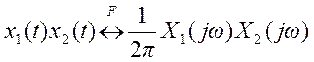
Поэтому
5. Определить спектр Фурье
сигнала 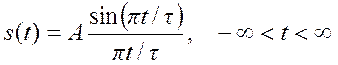
Решение.
Используем свойство дуальности
преобразования Фурье.
Если .
Прямоугольному импульсу x(t) с амплитудой А и длительностью , симметричному относительно начала
координат, соответствует преобразование Фурье
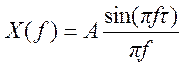
Следовательно, по свойству
дуальности сигналу
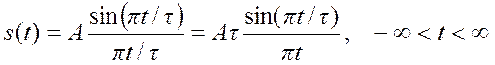
Фурье вида
Графики для А=1 и τ=2
6. Преобразование Фурье сигнала
имеет вид 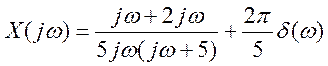
Найти вид сигнала во временной области.
Решение.
Представим как
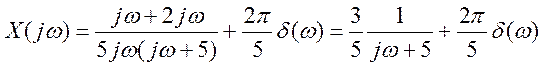
Используя таблицу преобразований
Фурье, определяем оригиналы во временной области, соответствующие слагаемым
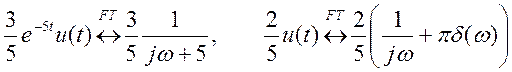
где u(t) – единичная
ступенчатая функция.
Поэтому 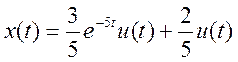
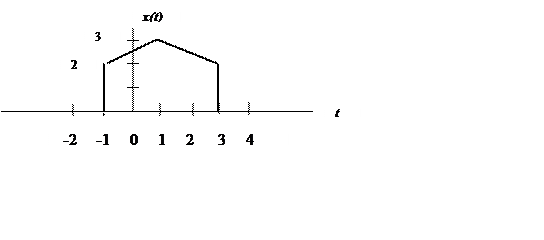
- Сигнал имеет вид
Найти
а) X(0),
б) 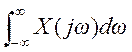
Решение.
а) 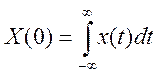
поэтому .
б) 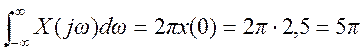
в) По теореме Парсеваля
8. Найти преобразование
Фурье сигнала
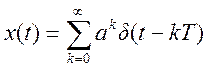
–
дельта – функция, .
Решение.
При преобразовании этого
выражения использовалась сумма геометрической прогрессии.
9. Вычислить свертку сигналов x(t) и h(t) с использованием
свойства свертки преобразования Фурье
– единичная ступенчатая
функция.
Решение.
Свертке 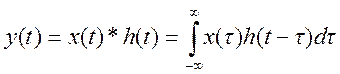
временной области соответствует произведение преобразований Фурье в частотной
области, т.е. .
Преобразование Фурье
односторонней экспоненты 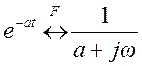
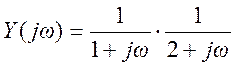
Разложим Y(jω) на простые
дроби
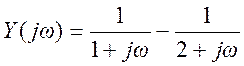
Применим к Y(jω) обратное
преобразование Фурье, получим .
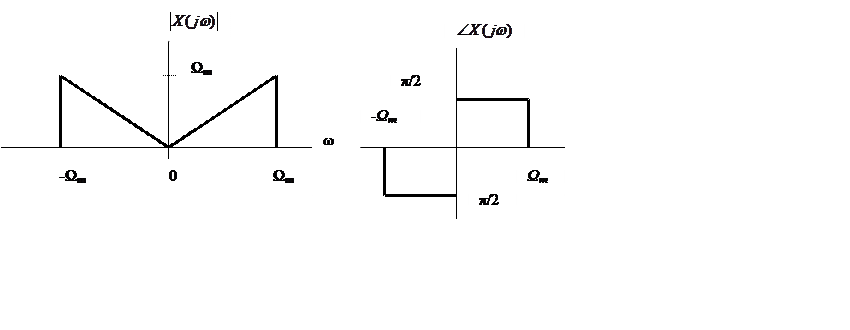
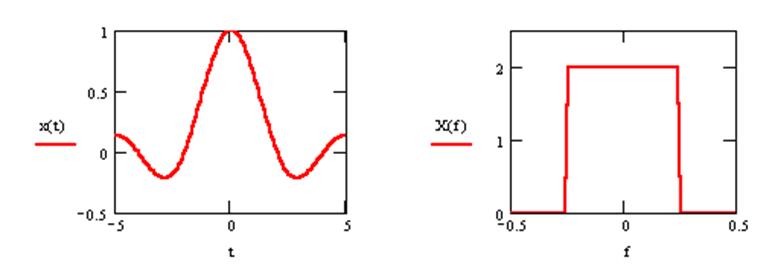
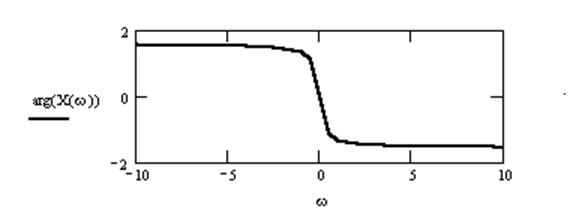
Заданы графики амплитудного и фазового спектров сигнала. Определить вид
сигнала во временной области.
Решение.
Предположим сигнал y(t) с равномерным
спектром следующего вида
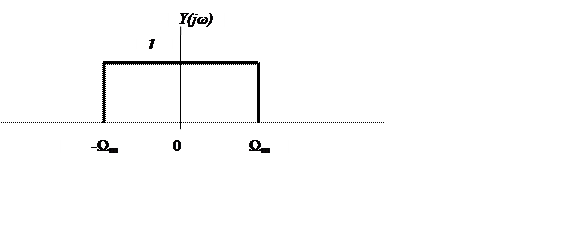 |
Это сигнал с единичной спектральной плотностью амплитуды в
полосе частот .
По свойству
дифференцирования преобразования Фурье .
Следовательно,
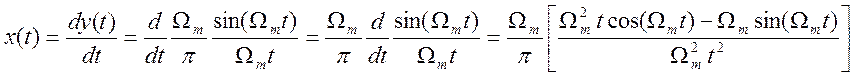
Задачи
для самостоятельного решения
- Определите преобразование Фурье и постройте (приближенно)
график амплитудного спектра сигнала
.
Ответ:
- Вычислите преобразование Фурье сигнала типа
синусоидального импульса
Ответ.
- Найдите спектр Фурье несимметричного треугольного импульса
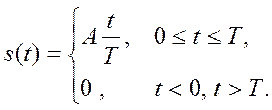
Ответ:
- Используя свойство дуальность преобразования Фурье,
определите спектр Фурье комплексного сигнала
Ответ:
- Определите преобразование Фурье сигнала непосредственным
вычислением и с помощью свойств линейности и временного сдвига
Ответ:
- Постройте (приближенно) график фазового спектра
одностороннего экспоненциального сигнала
Ответ: для А = 2,
7. Дано дифференциальное уравнение, связывающее вход x(t) и выход y(t) системы
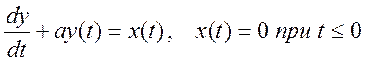
Найдите преобразование Фурье этого уравнения. Определите отношение
преобразований Фурье левой и правой части, т.е. 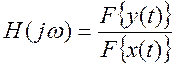
Постройте приближенные графики модуля и фазы этого отношения от частоты. Дайте
интерпретацию смысла функций на графиках.
Ответ. 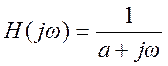
8. Найдите преобразование
Фурье и постройте приближенный вид графика амплитудного спектра следующего
сигнала
,
где u(t) – единичная
ступенчатая функция.
Ответ: 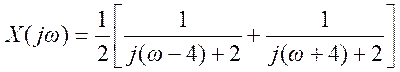
9. Найдите вид сигнала во временной
области, если преобразование Фурье сигнала имеет вид
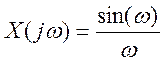
Ответ.
10. Постройте
амплитудный спектр сигнала
Ответ.
Спектральные плотности некоторых сигналов
Содержание
Обнаружили ошибку?
Выделите ее мышью
и нажмите

Спектральная плотность прямоугольного импульса
Рассмотрим спектральную плотность 





(1)
График прямоугольного импульса показан на рисунке 1а.

Рисунок 1. Спектральная плотность прямоугольного импульса
а — временно́й сигнал; б — спектральная плотность
Спектральная плотность 

(2)
где 

Приведем основные частотные свойства 
Спектральная плотность треугольного импульса
Рассмотрим треугольный импульс 


(3)
График треугольного импульса показан на рисунке 2а.

Рисунок 2. Спектральная плотность треугольного импульса
а — временно́й сигнал; б — спектральная плотность
Для рассмотрения спектральной плотности треугольного импульса мы не будем вычислять интеграл Фурье непосредственно, потому что это потребует громоздких выкладок, а воспользуемся свойством преобразования Фурье свертки двух сигналов.
Можно заметить, что треугольный импульс длительности 





Рисунок 3. Треугольный импульс как результат
свертки прямоугольных импульсов
Обратим внимание, что один из углов 

Для различного сдвига 



Таким образом, мы можем применить
свойство преобразования Фурье свертки сигналов
и записать спектральную плотность треугольного импульса как квадрат спектральной плотности 



(4)
График спектральной плотности треугольного импульса показан на рисунке 2б.
Приведем основные частотные свойства 
Спектральная плотность гауссова импульса
Гауссов импульс 
(5)
где 

График гауссова импульса при различном значении 


Рисунок 4. Спектральная плотность гауссова импульса
а — временно́й сигнал; б — спектральная плотность
Рассмотрим спектральную плотность гауссова импульса:
(6)
Преобразуем показатель экспоненты (6) следующим образом:
(7)
Тогда (6) с учетом (7):
(8)
Из курса математического анализа [1, стр. 401] известно, что:
(9)
Введем в выражении (8) замену переменной 


(10)
и с учетом (9) окончательно можно записать:
(11)
Можно заметить, что временно́й гауссов импульс 

График спектральной плотности гауссова импульса для различного значения параметра 
C увеличением 
Спектральная плотность экспоненциального импульса
Рассмотрим двусторонний экспоненциальный импульс 
(12)
где 

График двустороннего экспоненциального импульса при 


Рисунок 5. Спектральная плотность двустороннего экспоненциального импульса
а — временно́й сигнал; б — спектральная плотность
Как можно видеть из рисунка 5а, увеличение параметра 
Рассмотрим спектральную плотность 
(13)
Разобьем ось времени на положительную и отрицательную полуоси, и учтем что 
(14)
Объединим показатели экспонент в обоих интегралах и получим:
(15)
Таким образом, спектральная плотность двустороннего экспоненциального импульса (12) представляет собой вещественную функцию частоты, обладающую следующими свойствами.
На рисунке 5б показан вид спектральной плотности 



Рисунок 6. Односторонний экспоненциальный импульс
Рассмотрим теперь односторонний экспоненциальный импульс, который получается из двустороннего при обнулении значения отрицательной полуоси времени:
(16)
График одностороннего экспоненциального импульса показан на рисунке 6 при 

Спектральная плотность одностороннего экспоненциального импульса равна:
(17)
Приведем основные частотные свойства 
Поскольку спектральная плотность одностороннего экспоненциального импульса является комплексной функцией частоты 

(18)
На рисунке 7 показаны АЧХ и ФЧХ одностороннего экспоненциального импульса для различных значения параметра 

Рисунок 7. АЧХ и ФЧХ одностороннего экспоненциального импульса
а — АЧХ; б — ФЧХ
Спектральная плотность функции
Рассмотрим спектральную плотность сигнала вида 



Рисунок 8. Спектральная плотность функции 
а — временно́й сигнал; б — спектральная плотность
Для получения спектральной плотности сигнала 
свойством двойственности преобразования Фурье,
рассмотренным в
в предыдущем параграфе.
Тогда из выражения (2) можно записать:
(19)
Произведем замену переменных 



(20)
Вынесем множитель 

(21)
График спектральной плотности сигнала 
Важным частным случаем является 



Выводы
В данном разделе мы рассмотрели спектральные плотности некоторых непериодических сигналов: прямоугольного, треугольного, гауссова импульса,
а также одностороннего и двустороннего экспоненциальных импульсов.
Были приведены аналитические выражения для спектральных плотностей каждого из сигналов, а также их частотные свойства.
Смотри также
Представление периодических сигналов рядом Фурье
Преобразование Фурье непериодических сигналов
Свойства преобразования Фурье
Спектральные плотности некоторых сигналов
Список литературы
[1]
Кратные интегралы и ряды.
Москва, Наука, 1965, 608 c.
[2]
Баскаков, С.И.
Радиотехнические цепи и сигналы.
Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4
[3]
Гоноровский И.С.
Радиотехнические цепи и сигналы
Москва, Советское радио, 1977, 608 c.
[4]
Bracewell R.
The Fourier Transform and Its Applications
McGraw-Hills, 1986, 474 c. ISBN 0-07-007-015-6
Последнее изменение страницы: 12.05.2022 (19:42:52)
Страница создана Latex to HTML translator ver. 5.20.11.14
Тема 4: спектральное представление сигналов
Я согласен, что все состоит из атомов. Но какое нам до этого дело? Ведь мы занимаемся вопросом о природе богов!
Марк Туллий Цицерон. О природе богов.
Римский философ и политик (-I в.).
Это как сказать. Природа экономна. Если и богов она стряпает из атомов, то каждым сигналом в отдельности тем более заниматься не будет. А значит, они тоже из чего-то состоят!
Владимир Петухов. Взгляд с горы.
Осетинский геофизик Уральской школы (XX в.).
Содержание: 4.1. Разложение сигналов по гармоническим функциям. Понятие собственных функций. Ряд Фурье. Интеграл Фурье. Преобразование Лапласа. 4.2. Свойства преобразований Фурье. Линейность. Свойства четности. Изменение масштаба аргумента функции. Теорема запаздывания. Преобразование производной. Преобразование интеграла. Преобразование свертки. Преобразование произведения. Умножение сигнала на гармоническую функцию. Спектры мощности. 4.3. Спектры некоторых сигналов. Единичные импульсы. Гребневая функция. Спектр прямоугольного импульса. Треугольные импульсы. Экспоненциальный импульс. Функции Лапласа и Гаусса. Спектр косинусоиды. Литература.
4.1. Разложение сигналов по гармоническим функциям [1,21,24,25].
Рекомендуемые материалы
Спектральная (частотная) форма представления сигналов использует разложение сигнальных функций на гармонические составляющие. В качестве базисных функций разложения, в общем случае, принимаются комплексные экспоненциальные функции exp(jft), от которых с использованием формул Эйлера можно перейти к синус – косинусным функциям. Термин “частотная” обязан происхождением обратной переменной временного представления сигналов f = 1/|t|. Понятие частотного преобразования не следует связывать только с временными сигналами, т.к. математический аппарат преобразования не зависит от физического смысла независимых переменных. Так, например, при переменной “х”, как единице длины, значение f будет представлять собой пространственную частоту с размерностью 1/|х| – число периодических изменений сигнала на единице длины.
В математическом аппарате частотного анализа удобно использовать угловую частоту w = 2pf. Для процессов по другим независимым переменным в технической литературе вместо индекса частоты f часто используется индекс v, а для угловой частоты индекс k = 2pv, который называют волновым числом.
Понятие собственных функций. Удобство использования частотного представления сигналов заключается в том, что гармонические функции являются собственными функциями операций переноса, интегрирования, дифференцирования и других линейных операций, инвариантных по координатам.
Допустим, что исходная функция является линейной комбинацией функций синуса и косинуса:
s(х) = А sin(х)+B cos(х).
Осуществим произвольный сдвиг функции по аргументу на величину h. При этом получаем:
s(х+h) = C sin(х)+D cos(х),
C = А cos(h) – B sin(h),
D = A sin(h) + B cos(h),
где коэффициенты C и D, как и в исходном выражении коэффициенты А и В, не зависят от аргумента, при этом C2+D2 = А2+В2. Таким образом, при произвольном переносе функции по аргументу (а равно и при интегрировании, дифференцировании и других линейных преобразованиях) любую линейную комбинацию синуса и косинуса можно представить линейной комбинацией этих же функций.
Экспоненциальная комплексная запись гармонических функций делает это свойство еще нагляднее. Для произвольной гармонической функции имеем:
cos(wt-j) = A cos(wt)+B sin(wt),
где A = cos(j), B = sin(j), j – начальный фазовый угол колебания при t = 0. Переходя к комплексной записи данной функции с использованием тождеств Эйлера
cos(wt) = [ехр(jwt)+exp(-jwt)]/2, sin(wt) = [ехр(jwt)-exp(-jwt)]/2j,
получаем:
cos(wt-j) = C exp(jwt)+C*exp(-jwt),
где: C = 0,5 exp(-jj), C* = 0,5 exp(jj) – комплексно сопряженная с С величина. Применяя в качестве гармонической составляющей разложения сигнала функцию ехр(jwt), можно рассматривать вторую функцию ехр(-jwt), комплексно сопряженную с первой, как такую же составляющую, но с отрицательной частотой. Естественно, что отрицательная частота является чисто математической абстракцией, но нужно помнить, что пара таких комплексно сопряженных составляющих в сумме всегда дает вещественную функцию.
Экспоненциальные функции также являются собственными функциями линейных операций. Для операции переноса с использованием экспоненциальных функций:
exp[jw(t+h)] = exp(jwh)·exp(jwt) = H(w) exp(jwt),
где Н(w) = exp(jwh) – собственное значение операции переноса, независимое от переменной.
Для операции дифференцирования:
d[exp(jwt)]/dt = jw exp(jwt), H(w) = jw.
Для операции интегрирования:

В общем виде, для любых линейных операций:
Т[exp(jwt)] = H(w) exp(jwt),
где T[.] – произвольный линейный оператор, H(w) – собственное значение операции, независимое от аргумента.
У специалистов – практиков существует предубеждение против использования комплексных функций с их мнимыми частотами. Поэтому в дальнейшем будем использовать и вещественные функции, и их комплексные аналоги, по крайней мере, до тех пор, пока удобство использования последних не станет очевидным.
Ряд Фурье. Разложению в ряды Фурье подвергаются периодические сигналы. Как известно из математики, периодическую функцию любой формы, заданную на интервале одного периода Т = b-a и удовлетворяющую на этом интервале условиям Дирехле (ограниченная, кусочно-непрерывная, с конечным числом разрывов 1-го рода), можно представить в виде ряда Фурье:
s(t) =
где весовые коэффициенты S(nDw) ряда определяются по формуле:
S(nDw) = (1/T)
Ряд Фурье представляет собой ансамбль комплексных экспонент exp(jnDwt) с частотами, образующими арифметическую прогрессию. Функцию весовых коэффициентов S(nDw) принято называть комплексным спектром периодического сигнала или фурье-образом функции s(t). Спектр периодического сигнала является дискретной функцией, т.к. он определен только для целых значений n с шагом по частоте, обратным периоду: Dw = 2p/Т (или Df = 1/T). Первую частотную составляющую спектра при n = 1, равную w1 = 1×Dw = 2p/T (или f1 = 1/T), называют основной частотой сигнала (первой гармоникой), остальные частоты дискретного спектра nw1 при n>1 называют гармониками сигнала. Значения S(nDw) по положительным и отрицательным значениям n являются комплексно сопряженными.
Подынтегральную функцию экспоненты в выражении (4.1.2) с использованием тождества Эйлера (exp(-jwt)=cos(wt)-j×sin(wt)) можно разложить на синус – косинусные составляющие и выразить комплексный спектр в виде действительной и мнимой части:
S(nDw) = (1/T)
A(nDw) = (1/T) 
B(nDw) = (1/T) 
Рис. 4.1.1. Сигнал и его комплексный спектр.
На рис. 4.1.1 приведен пример периодического сигнала (треугольный импульс на интервале (3-5), повторяющийся с периодом Т=40) и форма действительной и мнимой части его спектра. Обратим внимание, что действительная часть спектра является четной относительно нуля функцией A(nDw) = A(-nDw), так как при вычислении значений A(nDw) по формуле (4.1.4) используется четная косинусная функция cos(nDwt) = cos(-nDwt). Мнимая часть спектра является нечетной функцией B(nDw) = -B(-nDw), так как для ее вычисления по (4.1.5) используется нечетная синусная функция sin(nDwt) = – sin(-nDwt).
Комплексные числа дискретной функции (4.1.3) могут быть представлены в виде модулей и аргументов комплексной экспоненты, что дает следующую форму записи комплексного спектра:
S(nDw) = R(nDw) exp[jj(nDw)], (4.1.3′)
R2(nDw) = A2(nDw)+B2(nDw),
j(nDw) = arctg(-B(nDw)/A(nDw)).
Рис. 4.1.2. Модуль и аргумент спектра.
Модуль спектра R(nDw) называют двусторонним спектром амплитуд, а аргумент спектра (последовательность фазовых углов j(nDw)) – двусторонним спектром фаз. Спектр амплитуд всегда представляет собой четную функцию: R(nDw) = R(-nDw), а спектр фаз нечетную: j(nDw) = -j(-nDw). Пример спектров приведен на рис. 4.1.2.
Если функция s(t) является четной, то все значения B(nDw) по (4.1.5) равны нулю (четные функции ортогональны синусным гармоникам) и спектр функции представлен только вещественными коэффициентами. Напротив, при нечетности функции s(t) обнуляются все значения коэффициентов А(nDw) (нечетные функции ортогональным косинусным гармоникам) и спектр является чисто мнимым. Этот фактор не зависит от выбора границ задания периода функции на числовой оси. На рис. 4.1.3 можно наглядно видеть ортогональность первой гармоники синуса и четной функции (А), косинуса и нечетной функции (В) в пределах одного периода. Учитывая кратность частот последующих гармоник первой гармонике спектра, ортогональность сохраняется для всех гармоник ряда Фурье
Рис. 4.1.3. Ортогональность функций.
При n = 0 имеем Во = 0 и получаем постоянную составляющую сигнала:
S(0) = Ao = Ro = (1/T) 
Тригонометрическая форма. Объединяя в (4.1.1) комплексно сопряженные составляющие (члены ряда, симметричные относительно центрального члена ряда S(0)), можно перейти к ряду Фурье в тригонометрической форме:
s(t) = Ао+2
s(t) = Ао+2
Значения An, Bn вычисляются по формулам (4.1.4-4.1.5), значения Rn и j – по формулам (4.1.3′).
Рис. 4.1.4. Спектр амплитуд
косинусных и синусных гармоник
Ряд (4.1.6) представляют собой разложение периодического сигнала s(t) на сумму вещественных элементарных гармонических функций (косинусных и синусных) с весовыми коэффициентами, удвоенные значения которых (т.е. значения 2×An, 2×Bn) не что иное, как амплитуды соответствующих гармонических колебаний с частотами nDw. Совокупность амплитудных значений этих гармоник образует односторонний физически реальный (только для положительных частот nDw) спектр сигнала, приведенный на рис. 4.1.4 (спектр треугольного сигнала рис. 4.1.1). Но такое графическое отображение спектра используется довольно редко.
Более широкое применение для отображения односторонних физически реальных спектров находит формула (4.1.6′). Спектр амплитуд при таком отображении называется амплитудно-частотным составом сигнала, а спектр фазовых углов – фазовой характеристикой гармоник сигнала. Для четных сигналов отсчеты ФЧХ могут принимать значения 0 и p, для нечетных соответственно ±p/2. Пример спектра (для треугольного сигнала на рис. 4.1.1) приведен на рис. 4.1.5.
Рис. 4.1.5. Спектр треугольного сигнала.
Ряды Фурье произвольных аналоговых периодических сигналов могут содержать бесконечно большое количество членов. Однако одним из важных достоинств преобразования Фурье является то, что при ограничении (усечении) ряда Фурье до любого конечного числа его членов обеспечивается наилучшее по средней квадратической погрешности приближение к исходной функции (для данного количества членов).
Аналогично в ряд Фурье может разлагаться и произвольная непериодическая функция, заданная на интервале (a,b), если нас не интересует ее поведение за пределами данного интервала. Однако следует помнить, что применение формул (4.1.1-4.1.6) автоматически означает периодическое продолжение данной функции за пределами заданного интервала (в обе стороны от него) с периодом Т = b-a.
Интеграл Фурье. Спектры непериодических сигналов конечной длительности (финитных), зарегистрированных на интервале Т, могут быть получены из уравнений для рядов Фурье как предельные значения функций суммирования при расширении периода Т до бесконечности.
Зададим периодическую последовательность импульсов и разложим импульс на одном периоде Т в ряд Фурье (формула 4.1.2). Не меняя положения импульса на интервале Т, увеличим значение Т в два раза (продлеваем интервал нулями), при этом формула (4.1.2) для вычисления спектра остается без изменения, но по ней рассчитывается в 2 раза большее количество гармоник с уменьшением в 2 раза частоты первой гармоники и шага Dw=2p/T. Увеличение интервала Т не влияет на результаты вычисления интеграла функции (4.1.2), т.к. интервал продления заполнен нулевыми значениями сигнала.
Рис. 4.1.6.
По существу, при увеличении периода Т без изменения финитного сигнала форма спектра по оси частот остается без изменения, изменяется только шаг дискретизации спектра и, за счет множителя 1/Т, в 2 раза уменьшаются значения спектра. Новые гармоники располагаются в интервалах между гармониками первого ряда. Пример измерения спектра при увеличении периода Т в 2 раза приведен на рис. 4.1.6.
Процесс можно продолжить дальнейшим последовательным увеличением периода, при этом спектр будет приближаться к непрерывной функции. В пределе, при T ® ¥, периодическая последовательность импульсов заменяется одиночным финитным сигналом, дискретные частоты nDw обращаются в непрерывные текущие значения w (Dw = 2p/T ® 0), суммирование амплитудных значений заменятся интегрированием, а сами значения спектра становятся бесконечно малыми (1/Т® 0). Для исключения последнего множитель 1/Т из расчетной формулы S(w) исключается, и интегральное преобразование Фурье приобретает следующий вид:
s(t) = (1/2p)
S(w) =
Формулу (4.1.8) обычно называют формулой прямого преобразования Фурье, а формулу (4.1.7) – обратного преобразования Фурье. Этими выражениями устанавливается взаимно однозначная связь сигнала и его спектра (спектральной плотности). Спектральные функции содержат ровно столько информации, сколько и исходный сигнал.
При преобразовании сигнала в пространство гармонических частот формулы прямого и обратного преобразований Фурье тождественны за исключением знака аргументов экспоненты:
s(t) = 
S(f) =
Рис. 4.1.7.
На рис. 4.1.7 сплошной кривой приведен пример непрерывного сигнала s(t), энергия которого сосредоточена на конечном интервале T = {0,25}. Если нас не интересует форма данного сигнала за пределами интервала Т, то спектр сигнала в виде ряда Фурье можно определить по формуле (4.1.2). При обратном преобразовании Фурье по формуле (4.1.1), т.е. при восстановлении сигнала по его спектру, в интервале Т будет восстановлен исходный сигнал s(t). Но если интервал для восстановления будет задан больше интервала Т, например равным 0-2Т, то за пределами этого интервала начнется периодическое повторение исходного сигнала, как это показано пунктиром на рис. 4.1.7. Если такой процесс нежелателен и за пределами интервала Т должны быть сохранены нулевые значения сигнала, то необходимо использовать интегральное преобразование Фурье (4.1.7-8). При этом следует учитывать особенности интегрального преобразования.
Спектральная функция S(w) представляет собой не спектр, а комплексную спектральную плотность сигнала, непрерывную на частотном интервале от – ¥ до ¥. Если s(t) – вещественная функция, то спектр этой функции является сопряжено симметричным относительно нулевой частоты
S(-w) = S*(w)
и содержит четную действительную и нечетную мнимую части:
Рис. 4.1.8.
S(w) = A(w) – jB(w), (4.1.9)
A(w) =
B(w) =
Как и в случае рядов Фурье, вещественные четные функции имеют вещественный четный спектр, представленный только спектральной функцией A(w), а вещественные нечетные – нечетный и только мнимый спектр, представленный спектральной функцией B(w).
Пример спектральной функции S(f) для сигнала s(t) на рис. 4.1.7 приведен на рис. 4.1.8. Как правило, графическое отображение спектральных функций выполняется в виде модуля и аргумента спектральной функции (амплитудного и фазового спектра), приведенных на рис. 4.1.9. Такое представление аналогично (4.1.3′):
R(w) = 
j(w) = arctg(-B(w)/A(w)), (4.1.13)
но в отношении функции модуля также имеет смысл спектральной плотности модуля.
Рис. 4.1.9.
Заметим также, что сопряженная симметричность спектральной функции позволяет в формулах (4.1.7)-(4.1.8) менять местами знаки аргументов в экспонентах, при этом изменяется только знак мнимой части и аргумента спектра.
Еще раз подчеркнем различие между спектрами и спектральными функциями сигналов. При практическом использовании формулы (4.1.8) для вычисления спектральных функций конечных сигналов, заданных на определенном интервале Т, пределы интегрирования обычно устанавливаются по границам интервала Т, так как нет необходимости выполнять интегрирование в бесконечных пределах, если за пределами интервала Т мы имеем нулевые (или незначимые) значения сигнала. Однако при сравнении формулы (4.1.8) с выражением (4.1.2) можно наглядно видеть, что значения интеграла (4.1.8) не нормируются на величину интервала Т. Отсюда следует, что числовые отсчеты значений модуля функции S(w) для определенных значений wi не являются амплитудными значениями соответствующих гармонических колебаний с частотой wi. Значения S(w) по сравнению со значениями функции S(nDw) по (4.1.2) при nDw = wi завышены на множитель Т. Это можно объяснить тем, что обратное преобразование Фурье по (4.1.1) представляет собой прямое суммирование гармоник с соответствующими амплитудами колебаний, в то время как интегрирование по (4.1.7) представляет собой предельное суммирование значений S(wi)×dwi, где dw = 2p/T (или, в обычном частотном представлении, df = 1/T) при Т Þ ¥.
Что касается спектра фазовых углов, то значения по (4.1.13) и по (4.1.3′) при nDw = wi полностью совпадают, так как их вычисление производится по отношению мнимой и действительной части спектра, наличие (или отсутствие) постоянного множителя в которых не меняет значение отношения.
Тригонометрическая форма интеграла Фурье (при объединении комплексно сопряженных частей спектральных функций):
s(t) = (1/2p)
s(t) = (1/2p)
Рис. 4.1.10.
Прямое и обратное преобразование Фурье подобны. Любая теорема, доказанная для прямого преобразования Фурье, справедлива и для обратного преобразования, и наоборот. Это непосредственно следует из выражений прямого и обратного преобразования Фурье, которые различаются только знаком в экспоненте. Особенно наглядно (см. рис. 4.1.10) это видно для четных сигналов (заданных функциями, симметричными относительно t = 0), для которых В(w) = 0 и, соответственно, фазовый спектр равен нулю:
s(t) = 2

В математическом анализе для упрощения записей используют символическую форму обозначения преобразования Фурье:
s(t) Û S(f), s(t) Û S(w),
где, в общем случае, как фурье-образ функции, так и она сама могут быть комплексными.
Для физических сигналов и их достаточно корректных математических моделей преобразование Фурье, как правило, всегда существует. С чисто математических позиций сигналу s(t) можно сопоставить спектральную плотность S(w), если существует интеграл:

Преобразование Лапласа. Если условие (4.1.15) не выполняется, то определенные приближения спектральных плотностей вычисляются с использованием специальных методов, одним из которых является преобразование Лапласа.
Рис. 4.1.11.
Допустим, что функция s(t) задана на интервале (0, ¥), равна нулю при t<0, а интеграл спектральной функции (4.1.8) расходится. Умножим s(t) на экспоненциальную функцию exp(-ct), где с – положительная константа, и выберем значение ‘с’ таким, чтобы произведение u(t) = s(t)×exp(-ct) удовлетворяло условию абсолютной интегрируемости. Сущность данной операции хорошо видна на рис. 4.1.11. Интегрируемость функции u(t) может быть установлена для любой функции s(t) соответствующим выбором коэффициента ‘c’. При этом спектральная плотность функции u(t) может быть вычислена по формуле (4.1.8):
U(w,c) = 
После объединения экспоненциальных функций это выражение можно переписать следующим образом:
U(c+jw) = 
Соответствующее обратное преобразование Фурье функции U(c+jw):
(1/2p)
Для восстановления функции s(t) достаточно умножить обе части данного выражения на exp(ct), объединить экспоненциальные множители под интегралом и заменить переменную интегрирования w на c+jw:
s(t) = (1/2p)
Обозначим комплексную переменную c+jw в выражениях (4.1.16-17) через р и получим общепринятую форму прямого и обратного преобразования Лапласа:
S(p) = 
s(t) = (1/2p)
Рис. 4.1.12. Сигнал и его спектральная функция Лапласа при p=0.0005+jw.
Сигнальную функцию s(t) в преобразованиях Лапласа обычно называют оригиналом, а ее спектральную функцию S(p) – изображением оригинала. Пример спектральной функции Лапласа для оригинала – сложного и неограниченного во времени сигнала, состоящего из каузальной суммы трех гармоник, приведен на рис. 4.1.12. По спектральной функции Лапласа можно выделить эти три основных частоты сигнала и оценить соотношение их амплитуд. Ширина пиков спектральной функции при выделении “чистых” гармоник зависит от значения коэффициента ‘c’ и уменьшается при его уменьшении.
Если вместо р в изображениях оригинала подставить переменную jw, то будут получены спектральные функции, полностью идентичные преобразованию Фурье каузальных функций (имеющих нулевые значения при t<0).
4.2. Свойства преобразований Фурье [1,17,21].
Рис. 4.2.1. Сигналы и их спектры. s0(k)=s1(k)+s2(k) Û S1(w)+S2(w) = S0(w).
Свойствами преобразований Фурье определяется взаимное соответствие трансформации сигналов и их спектров.
1. Линейность. Преобразование Фурье относится к числу линейных интегральных операций, т.е. спектр суммы сигналов равен сумме спектров этих сигналов. Пример суммирования сигналов и его отображения в суммирования спектров приведен на рис. 4.2.1:


|
Сигнал s(t) |
Спектр S(w) |
|
Четный |
Вещественный, четный |
|
Нечетный |
Мнимый, нечетный |
|
Произвольный |
Действительная часть – четная. Мнимая часть – нечетная |
2. Свойства четности преобразования определяются косинусными (четными, действительными) и синусными (нечетными, мнимыми) частями разложения и подобием прямого и обратного преобразований.
На рис. 4.2.2. приведены примеры, поясняющие свойства четности преобразования. Сигнал s1(k) является четным, s1(k) = s1(-k), и имеет только вещественный четный спектр (мнимая часть спектральной функции представлена нулевыми значениями). Сигнал s2(k) = -s2(-k) нечетный и имеет мнимый нечетный спектр, а нулевыми значениями представлена его действительная часть. Сигнал s3(k) образован суммой сигналов s1(k) и s2(k). Соответственно, спектральная функция сигнала представлена и действительной четной частью (принадлежащей s1(k)), и мнимой нечетной частью (принадлежащей s2(k)). При обратном преобразовании Фурье раздельно действительной и мнимой части спектра S3(w), равно как и любых других комплексных спектров, будут раздельно восстановлены четная и нечетная части исходного сигнала.
Рис. 4.2.2. Свойства четности преобразования.
Заметим, что исходный произвольный сигнал может быть задан в одностороннем варианте (в интервале 0-Т), но четная и нечетная части этого сигнала занимают интервал от –Т до Т, при этом на левой половине числовой оси (от –Т до 0) эти два сигнала компенсируют друг друга, давая нулевые значения.
3. Увеличение масштаба аргумента функции приводит к уменьшению масштаба ее фурье-образа и наоборот. Действительно, если s(t) Û S(w), то при изменении длительности сигнала с сохранением его формы, т.е. для сигнала с новым аргументом f(x) = s(at) при x=at, получаем:
s(at) Û

s(at) Û (1/a) S(w/a). (4.2.2′)
Выражение (4.2.2′) действительно при а>0. При а<0 происходит зеркальный поворот сигнала относительно вертикальной оси, а замена переменной t=x/a вызывает перестановку пределов интегрирования и, соответственно, изменение знака спектра:
s(at) Û -(1/a) S(w/a). (4.2.2”)
Обобщенная формула изменения масштаба:
s(at) Û (1/|a|) S(w/a), a ≠ 0 (4.2.2)
Если под аргументом функции и ее спектра понимать определенные физические единицы, например, время – частота, то отсюда следует: чем короче по своей длительности сигнал, тем шире по частоте его спектр, и наоборот. Это можно наглядно видеть на рис. 4.2.1. для сигналов s1(k) и s2(k) и их спектров S1(w) и S2(w).
Действительно и обратное всем известное явление. Сирена поезда имеет определенный спектр частот. Но воспринимаемый спектр сирены резко изменяется с высоких частот на более низкие при прохождении поезда мимо наблюдателя. Аргумент частотной оси (1/t) не изменяется, но за счет эффекта Доплера происходит расширение спектра воспринимаемого сигнала при набегании на наблюдателя и сжатие при уходе от наблюдателя. Если сигнал записать и замерить период его колебаний, то можно убедиться, что период колебаний на временной оси при набегании сирены меньше периода колебаний при ее уходе. На основе именно этого эффекта доказывается расширение Вселенной.
От изменения аргумента функций следует отличать изменение масштаба представления функций, хотя для него действительна та же формула (4.2.2). Изменение масштаба аргументов изменяет только оцифровку числовых осей представления сигналов и их спектров, но не изменяет самих сигналов и спектров. Так, при масштабе оси времен t=1 секунда, масштаб оси частот f=1/t=1 герц, а при t=1 мксек f=1/t=1 МГц (t=at, f=1/at, a=10-6).
Что касается возможности изменения длительности сигналов без изменения его формы (сжатие или расширение), то оно не может выполняться линейными системами с постоянными параметрами.
4. Теорема запаздывания. Запаздывание (смещение) сигнала по аргументу функции на интервал to приводит к изменению фазочастотной функции спектра (фазового угла всех гармоник) на величину wto без изменения модуля (амплитудной функции) спектра. Применяя замену переменной t-to = x, получаем:
s(t-to) Û

Совершенно очевидно, что при сдвиге сигнала амплитуды составляющих его гармоник изменяться не должны. С учетом того, что |exp(-jwto|=1, это следует и из (4.2.3):
|S(w)exp(-jwto)| = |S(w)|.
Фазовый спектр сдвигается на -wto с линейной зависимостью от частоты:
S(w)exp(-jwto) = R(w)exp[j(j(w)] exp(-jwto) = R(w)exp[j(j(w)-wto)]. (4.2.4)
Рис. 4.2.3. Изменение спектра сигнала при его сдвиге.
Пример двух одинаковых сигналов, сдвинутых относительно друг друга на to=1, и соответствующих данным сигналам спектров приведен на рис. 4.2.3.
5. Преобразование производной (дифференцирование сигнала):
s(t) = d[y(t)]/dt = d[

=
Таким образом, дифференцирование сигнала отображается в спектральной области простым умножением спектра сигнала на оператор дифференцирования сигнала в частотной области jw, что эквивалентно дифференцированию каждой гармоники спектра. Умножение на jw приводит к обогащению спектра производной сигнала высокочастотными составляющими (по сравнению с исходным сигналом) и уничтожает составляющие с нулевой частотой.
Рис. 4.2.4. Спектры сигнала и его производной.
Пример сигнала, его производной и соответствующих им спектров приведен на рис. 4.2.4. По изменению аргумента спектра (для четного исходного сигнала он был нулевым) можно видеть, что для всех гармоник спектра появляется сдвиг фаз на p/2 (900) для положительных частот, и на -p/2 (-900) для отрицательных частот.
В общем случае, для кратных производных:
dn[y(t)]/dtn = (jw)nY(w). (4.2.6)
6. Преобразование интеграла сигнала в частотной области при известном спектре сигнала может быть получено из следующих простых соображений. Если имеет место s(t) = d[y(t)]/dt Û jw Y(w) = S(w), то должна выполняться и обратная операция: y(t) =

Оператор интегрирования в частотной области (1/jw) при w>1 ослабляет в амплитудном спектре высокие частоты и при w<1 усиливает низкие. Фазовый спектр сигнала смещается на -900 для положительных частот и на 900 для отрицательных. Пример модуля спектра сигнала и его интегральной функции приведены на рис. 4.2.5.
Рис. 4.2.5. Сигналы и амплитудные спектры сигналов.
Формула (4.2.7) справедлива для сигналов с нулевой постоянной составляющей. При интегрировании сигналов с определенным значением постоянной составляющей С=const в правой части выражения (4.2.7) появляется дополнительное слагаемое преобразования Фурье постоянной составляющей C, которое представляет собой, как будет показано ниже, дельта-функцию на нулевой частоте с весовым коэффициентом, равным значению С:
y(t) = (1/jw)S(w) + C·d(wo).
7. Преобразование свертки сигналов y(t) = s(t) * h(t):
Y(w) =

Y(w) =

По теореме запаздывания (4.2.3):

Отсюда: Y(w) =
s(t) * h(t) Û S(w)H(w). (4.2.8)
Рис. 4.2.6. Сигналы и амплитудные спектры сигналов.
Пример выполнения свертки в частотной области приведен на рис. 4.2.6. Отметим, что частотное представление H(w) импульсного отклика h(t) линейной системы (или соответствующей линейной операции) имеет смысл частотной передаточной функции системы и позволяет определить сигнал на выходе системы (в частотной форме представления) при задании произвольного сигнала (в частотной форме) на ее входе. По существу, функция H(w) представляет собой распределение по частоте коэффициента пропускания частотных составляющих сигнала с входа на выход системы (операции).
8. Преобразование произведения сигналов y(t) = s(t)h(t) непосредственно следует из подобия прямого и обратного преобразований Фурье:
s(t)·h(t) Û S(w) * H(w). (4.2.9)
Таким образом, свертка функций в координатной форме отображается в частотном представлении произведением фурье-образов этих функций. И наоборот, произведение функций отображается сверткой их фурье-образов.
9. Умножение сигнала на гармоническую функцию заполняет сигнал гармонической частотой и формирует радиоимпульс. Без учета начальной фазы гармоники:
s(t) = u(t) cos(wot).
Спектр радиоимпульса:
S(w) =

= ½

= ½ U(w) exp(jwot) + ½ U(w) exp(-jwot). (4.2.10)
Спектры сигналов обычно низкочастотные и сосредоточены в центре частотной оси. Частота гармоники заполнения, как правило, много больше максимальной частоты гармоник сигнала. Из (4.2.10) следует, что спектр сигнала раздваивается (с коэффициентом ½) и смешается влево и вправо по оси частот на частоты ±wo. Особенно наглядно это видно для четных сигналов и приведено на рис. 4.2.7.
Рис. 4.2.7. Радиоимпульс и его амплитудный спектр.
10. Спектры мощности. Если функция s(t) имеет фурье-образ S(w), то спектральная плотность мощности данной функции определяется выражениями:
w(t) = s(t)s*(t) = |s(t)|2 Û |S(w)|2 = S(w)S*(w) = W(w). (4.2.11)
Спектр мощности – вещественная неотрицательная четная функция, которую очень часто называют энергетическим спектром. Спектр мощности, как квадрат модуля спектра сигнала, не содержит фазовой информации о частотных составляющих, а, следовательно, восстановление сигнала по спектру мощности невозможно. Это означает также, что сигналы с различными фазовыми характеристиками могут иметь одинаковые спектры мощности. В частности, сдвиг сигнала не отражается на его спектре мощности.
Полная энергия спектра сигнала:
Es = (1/2p)

Для функций мощности взаимодействия сигналов в частотной области соответственно имеем частотные спектры мощности взаимодействия сигналов:
Wxy(w) = X(w) Y*(w),
Wyx(w) = Y(w) X*(w),
Wxy(w) = W*yx(w).
Функция Wxy(w) комплексная, даже если обе функции x(t) и y(t) вещественны, при этом Re[Wxy(w)] – четная функция, а Im[Wxy(w)] – нечетная. Отсюда полная энергия взаимодействия сигналов определяется только реальной частью спектра,
Exy = (1/2p)

и всегда является вещественным числом.
Равенство Парсеваля. Так как координатное и частотное представления по существу только разные математические отображения одного и того же сигнала, то равной должна быть и энергия сигнала в двух представлениях, откуда следует:


т.е. энергия сигнала равна интегралу модуля его частотного спектра – сумме энергий всех частотных составляющих сигнала. Аналогично для энергии взаимодействия сигналов:


Из равенства Парсеваля следует инвариантность скалярного произведения сигналов и нормы относительно преобразования Фурье:
(x(t),y(t)) = (X(f),Y(f)), ||x(t)||2 = ||X(f)||2.
Не следует забывать, что при представлении спектров в круговых частотах (по w) в правой части приведенных равенств должен стоять множитель 1/2p.
4.3. Спектры некоторых сигналов [1,16].
1. Единичные импульсы. Функция d(t), центрированная относительно t = 0, значения которой по определению равны нулю при t ¹ 0, a интеграл от – ¥ до ¥ равен 1, имеет равномерное спектральное распределение в бесконечной полосе частот от 0 до ¥:
ТF[d(t)] =
Рис. 4.3.1. Спектр функции d(t-2)
Это следует и из свойства свертки функций, поскольку свертка функции с бесконечно коротким импульсом с единичной площадью не должна приводить к изменению функции:
s(t) * d(t) = s(t).
Выполняя преобразование Фурье правой и левой части данного выражения, имеем:
S(w)H(w) = S(w),
что может быть реализовано только при H(w) = 1.
Отсюда следует также, что дельта-функцию можно записать в виде обратного преобразования Фурье:
d(t) = (1/2p)
С учетом теоремы запаздывания (4.2.3), для обобщенной функции Дирака соответственно имеем:
d(t-t) Û exp(-jwt). (4.3.1′)
Пример спектра функции приведен на рис. 4.3.1.
Рис. 4.3.2.
Для единичного импульса с площадью, равной Р:
Р×d(t) Û Р. (4.3.1′)
Если спектром весовой дельта-функции является константа, то на основе дуальности преобразования Фурье спектром константы должна быть весовая дельта-функция в нуле частотной оси.
С Û С×d(w).
Представить графически эту операцию для непрерывных функций невозможно. Но для дискретных спектральных функций с использованием единичного импульса Кронекера она имеет вполне реальный смысл (рис. 4.3.2).
2. Гребневая функция ШT(t) представляет собой последовательность импульсов Дирака с периодом Т = 1/F, где F- частота следования импульсов:
ШТ(t) =
Спектр гребневой функции (с учетом теоремы запаздывания при Df = 1/T = F) также последовательность импульсов Дирака:
ШТ(t) = (1/Т)


3. Спектр прямоугольного импульса Пr(t) амплитудой U и длительностью r (рис. 4.3.2). При расположении начала координат по центру импульса:
Пr(w) =

Пr(w) = rU sin(wr/2)/(wr/2) = rU sinc(wr/2). (4.3.4)
Вид функций Пr(w) приведен на рис. 4.3.3. Представлена только часть частотного диапазона, в остальной части диапазона постепенно затухающие флюктуации спектров, которые, чисто теоретически, простираются до бесконечности.

Рис. 4.3.3. Спектры П – импульсов. Рис. 4.3.4. Спектры П-импульсов
Как и следовало ожидать, для вещественной и четной динамической П-функции спектр сигнала также является вещественной и четной функцией частоты. Спектр имеет лепестковый характер, и ширина лепестков (по пересечениям нулевой линии) обратно пропорциональна длительности импульсов и равна 2p/r. Значение спектральной плотности на нулевой частоте равно площади импульсов.
Функция вида sin(x)/x в анализе сигналов встречается довольно часто и имеет специальное обозначение: sinc(x) = sin(x)/x. Она называется интегральным синусом или функцией отсчетов.
На рис. 4.3.4 приведены нормированные по площади спектры этих же импульсов. При сравнении спектров с рис. 4.3.2 можно наглядно видеть характер зависимости ширины спектров (по ширине главного максимума) от длительности импульсов. Нетрудно также заметить, что форма спектра П – импульсов остается практически постоянной и только “растягивается” по шкале частоты при уменьшении длительности импульсов. Чем шире сигнал, тем короче его спектр.
Если прямоугольный импульс начинается в момент времени to, то имеем:
П(w)= U
Рис. 4.3.5. Спектр задержанного П-импульса
Это выражение может быть получено непосредственно из (4.3.4) с использованием теоремы смещения. Вид функций П(w) при r = 50 и to = 50 приведен на рис. 4.3.5.
Как видно на рисунке, спектр сигнала, несимметричного относительно t = 0, имеет две части: четную действительную A(w) = Re(П(w)), и нечетную мнимую B(w) = Im(П(w)),. Модуль спектра R(w) = |П(w)| всегда четный, имеет только положительные значения и полностью повторяет |Пr(w)| четного импульса (при смещении начала координат в центр импульса).
При изменении величины сдвига импульса модуль спектра остается без изменений, т.к. амплитуда частотных составляющих сигнала зависит только от его формы и не меняется от места расположения сигнала на координатной оси. Сдвиг сигнала определяет его фазовый спектр, пример которого для задержанного П-импульса приведен на рис. 4.3.6. Заметим, что фактический спектр имеет непрерывный характер. Пилообразная форма кривых на рис. 4.3.6 объясняется периодическим сбросом действительных значений фазы сигнала на величину p.
Учитывая, что значения функций на отрицательных частотах спектра всегда в одном и том же порядке однозначно соотносится со значениями на положительных частотах (четные функции А(w) и R(w), нечетные функции B(w) и j(w)), в дальнейшем двусторонние спектры сигналов будем приводить только для области положительных частот.
Рис. 4.3.6. Фазовый спектр задержанного
П-импульса (to = 50, r = 50)
Для количественной характеристики соотношения формы сигналов и их спектров применяют понятие базы сигнала. Под ним понимают произведение эффективных значений длительности сигнала и ширины его спектра. Конкретное значение базы сигнала зависит от способа определения этих параметров. Для сигналов простой формы значение базы обычно составляет несколько единиц. Если для прямоугольного импульса эффективную ширину спектра принять по длительности центрального пика (2p/r), то значение базы сигнала будет равно 2p.
Длительности сигналов и ширина их спектров связаны принципом неопределенности, которым устанавливается, что значение их произведения (база сигналов) не может быть меньше 1. Этим устанавливается, что не может существовать коротких сигналов с узким спектром. Напротив, максимальное значение базы сигналов не ограничивается, и могут существовать сигналы с большой базой, имеющие как большую длительность, так и широкий спектр.
Рис. 4.3.6. Форма импульсов.
Если прямоугольные импульсы повторяются с периодом Т, то соответственно при Dw = 1/Т имеем:
Пr(kDw) = (rU/T) sinc(kDwr/2)exp(-jkDw(to-r/2)). (4.3.6)
Как и положено, спектр периодического сигнала дискретен по w, а при снятии нормировки спектра на длительность периода (умножением на Т) огибающая спектра повторяет выражение (4.3.5).
4. Треугольные импульсы длительностью r по основанию с площадью, равной Р, могут быть получены сверткой двух прямоугольных импульсов длительностью r/2 с амплитудой 2Р/r, откуда:
s(t) = Пr/2(t) * Пr/2(t) Û S(w) = Пr/2(w)Пr/2(w),
S(w) = P sinc2(wr/4).
Рис. 4.3.7. Спектры импульсов.
Спектр треугольного импульса также имеет лепестковую структуру с шириной лепестков 4p/r. Соответственно, база треугольного импульса равна 4p. Спектральная функция за счет квадратирования интегрального синуса имеет только положительные значения.
Аналогично можно получить и спектры трапеций (при разной длительности П-импульсов).
Примеры импульсов и сопоставление формы их нормированных спектров (делением значений S(w) на площадь импульсов – значение S(0)) приведены на рис. 4.3.6 и 4.3.7.
Заметим, что обратная операция – аппроксимация спектра сигнала произведением спектров простых сигналов с последующим переводом спектров в координатную область, позволяет представить сложный исходный сигнал в виде свертки более простых сигналов.

Рис. 4.3.8. Рис. 4.3.9. Спектр импульса.
5. Экспоненциальный импульс s(t) = U exp(-at), t ³ 0, a > 0. Функция exp(-at) только условно может быть названа импульсом, т.к. определена и при t Þ ¥, но при а > 0 она достаточно быстро затухает (рис. 4.3.8). Преобразование Фурье экспоненциального импульса, как произвольного одностороннего сигнала, имеет действительную и мнимую части:
S(w) = U

Рис. 4.3.10. Рис. 4.3.11.
Функция S(w) бесконечна по частоте. Модуль и аргумент спектра (фазовая характеристика в градусах) приведены на рис. 4.3.9.
6. Функции Лапласа и Гаусса:
Для функции Лапласа (экспонента по модулю t) имеем следующее преобразование:
U exp(-a|t|) Û 2aU/(a2+w2), a>0. (4.3.8)
Форма функции (при U=1, а=0.1) и ее вещественный спектр (функция четная и представлена только действительной частью) приведены на рис. 4.3.10.
Преобразование для центрированной функции Гаусса:
U exp(-pt2) Û U
Спектр центрированной функции Гаусса – также функция Гаусса. Форма функции (при U=1, а=0.0.003) и ее вещественный спектр приведены на рис. 4.3.11. Если эффективную длительность и ширину спектра гауссовых функций определять по уровню 1/е от максимума (t=2/а, Dw=a), то база сигнала равна 4.
Сравнивая на рисунках 4.3.10 и 11 функции Лапласа и Гаусса и их спектры (с учетом масштаба последних), нетрудно заметить, что чем более плавно изменяются значения сигнала (меньше его дифференциал), тем более низкочастотным является спектр сигнала.
7. Спектр косинусоиды с частотой wo может быть определен с помощью свойства смещения:
(1/2) d(w-wo) Û (1/2) exp(-jwot),
(1/2) d(w+wo) Û (1/2) exp(jwot),
(1/2) [d(w-wo)+d(w+wo)] Û cos(wot). (4.3.7)
Cпектр косинусоиды вещественен и представляет собой два импульса Дирака, расположенных симметрично относительно w = 0 на частотах -wo и wo (рис. 4.3.12).









 Определить
Определить