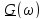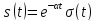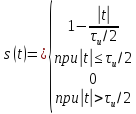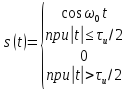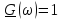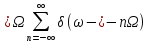Как найти спектральную плотность сигнала

1. Примеры определения спектральной плотности сигналов

Ниже
приводится краткое описание некоторых
сигналов и опре­деляются их спектральные
плотности. При определении спектраль­ных
плотностей сигналов, удовлетворяющих
условию абсолютной интегрируемости,
пользуемся непосредственно формулой
(4.41).

Спектральные
плотности ряда сигналов приведены в
табл. 4.2.

1)
Импульс
прямоугольной формы
(табл. 4.2, поз. 4). Колебание, изобра­женное
на рис. (4.28, а), можно записать в виде

.

Его
спектральная плотность

График
спектральной плотности

(рис.
4.28, а) построен на основе прове­данного
ранее анализа спектра периодической
последовательности однополярных,
прямоугольных импульсов (4.14). Как видно
из (рис. 4.28, б), функция
обра­щается
в нуль при значениях аргумента
=
n,
где п –
1,
2, 3, … — лю­бое целое число. При этом
угловые частоты равны
 = .

Рис.
4.28. Импульс прямоугольной формы (а) и
его спектральная плотность (б)

Спектральная
плотность импульса при
численно равна его площади, т.еG(0)=A.
Это положение справедливо для импульса
s(t)
произвольной
формы. Действительно, полагая в общем
выражении (4.41)
= 0,
получим

т.
е. площадь импульса s(t).

Таблица
4.3.

№ п/п	Сигнал s(t)	Спектральная плотность
1	2	3	4	5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16		–
17

При
растягивании импульса расстояние между
нулями функциисокращается, т. е. происходитсжатие
спектра. Значение
при
этом возра­стает. Наоборот, при сжатии
импульса происходит расширение
его спектра а значение
уменьшается.
На (рис. 4.29, а, б)
приведены графики амплитудного
и
фазового и
спектров
прямоугольного импульса.

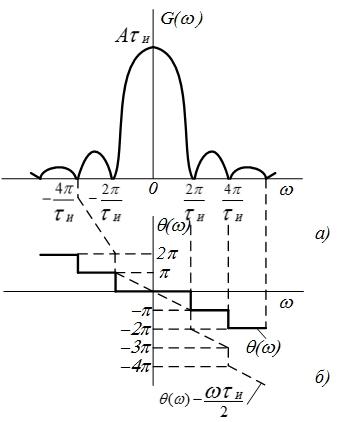
Рис. 4.29. Графики
амплитудного (а) Рис. 4.30. Импульс
прямоугольной формы, и фазового
(б) спектров сдвинутый
на время

При
сдвиге импульса вправо (за­паздывание)
на время
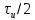(рис. 4.30) фазовый спектр изменяется на
величи­ну,
определяемую аргументом множителяexp()
(табл.
4.2, поз. 9). Результирующий фазовый спектр
запаздывающего импульса изо­бражен
на рис. 4.29, б пунктирной ли­нией.

2) Дельта-функция

(табл.
4.3, поз. 9). Спектральную плотность
– функции находим по формуле (4.41),
используя фильтрующее свойствоδ-функции:

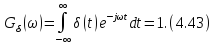
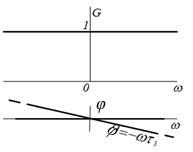
Таким
образом, амплитудный спектр
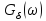равномерный и определяется пло­щадьюδ-функции
[= 1], а фазовый спектр равен нулю [= 0].

Обратным
преобразованием Фурье от функции
= 1 пользуются как одним из определенийδ-функции:

или

Пользуясь
свойством временного сдвига (табл. 4.2,
поз. 9), определяем спект­ральную
плотность функции
,
запаздывающей
на время
относительно:

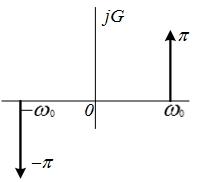
Амплитудный
и фазовый спектры функции

показаны
в табл. 4.3,
поз. 10. Обратное преобразование Фурье
от функции

имеет
вид

3)
Гармоническое
колебание
(табл. 4.3, поз. 12). Гармони­ческое
колебание не является абсолютно
интегрируемым сигналом. Тем не ме­нее
для определения его спектральной
плотностиприменяют
прямое пре­образование Фурье, записывая
формулу (4.41) в виде:

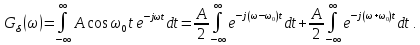
Тогда
с учетом (4.47) получаем

где

δ(ω)
– дельта-функции, смещенные по оси
частот на частоту
,
соответственно вправо и влево относительно.
Как видно из (4.48), спектральная плотность
гармонического колебания с конечной
амплитудой принимает бесконечно боль­шое
значение на дискретных частотахи.

Выполняя
аналогичные преобразования, можно
получить спектральную плотность
колебания

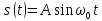
(табл.
4.3, поз. 13)

(4.49)

4)
Функция
вида

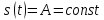
(табл.
4.3, поз. 11)

Спектральная
плотность
сигнала в виде постоянного уровня А
определяется по формуле (4.48), положив

=
0:

5)
Единичная
функция
(или единичный скачок)

(табл.
4.3, поз. 8).
Функция

не
является абсолютно интегрируемой. Если
представить

как
предел экспоненциального импульса
,т.
е.

то
спектральную плотность
функции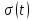можно
определить как предел спектральной
плотности экспоненциального импульса
(табл. 4.3, поз. 1)
при
:

Припервое слагаемое в правой части этого
выражения равно нулю на всех частотах,
кроме= 0, где оно обращается в бесконечность,
а площадь под функцией
равна
постоянной величине

Поэтому
пределом первого слагаемого можно
считать функцию
.
Преде­лом второго слагаемого является
функция.
Окончательно получим

Наличие
двух слагаемых в выражении (4.51) согласуется
с представлением функции

в
виде
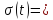1/2+1/2sign(t).Постоянной
составляющей 1/2 со­гласно (4.50)
соответствует спектральная плотность
,
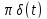а нечетной функции
—
мнимое значение спектральной плотности
.

При
анализе воздействия единичного скачка

на
цепи, передаточная функция которых при

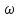
= 0
равна нулю (т. е. на цепи, не пропускающие
по­стоянный ток), в формуле (4.51) можно
учитывать только второе слагаемое,
представляя спектральную плотность
единичного скачка в виде

6)
Комплексный
экспоненциальный сигнал
(табл.
4.3, поз. 16). Если представить функциюв виде

то
на основании линейности преобразования
Фурье и с учетом выражений (4.48) и (4.49)
спектральная плотность комплексного
экспоненциального сигнала

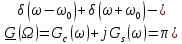
Следовательно,
комплексный сигнал
обладает несимметричным спект­ром,
представленным одной дельта-функцией,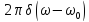
смещенной на частотувправо относительно.

7)
Произвольная
периодическая функция.
Представим произвольную перио­дическую
функцию

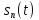
(рис.
4.31, а) комплексным рядом Фурье

где
—
частота следования импульсов.

Коэффициенты
ряда Фурье

выражаются
через значения спектральной плотности

одиночного
импуль­са s(t)
на
частотах

(n=0,±1,
±2, …). Подставляя (4.55) в (4.54) и поль­зуясь
соотношением (4.53), определяем спектральную
плотность
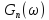перио­дической
функции:

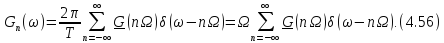
Согласно
(4.56) спектральная плотность
произвольной
периодической функции
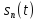имеет вид последовательности-функций,
смещенных друг от­носительно друга,
на частоту

(рис.
4.31, б). Коэффициенты при δ-функциях
изменяются в соответствии со спектральной
плотностьюодиночного им­пульсаs(t)
(пунктирная
кривая на рис. 4.31,б).

8)
Периодическая
последовательность δ-функций
(табл. 4.3, поз. 17).
Спект­ральная плотность
периодической последовательности
–функций

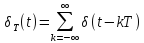
определяется
по формуле (4.56) как частный случай
спектральной плотности периодической
функции

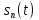
при

= 1:

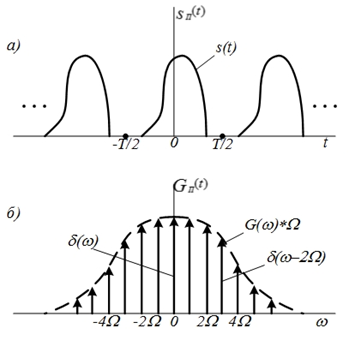
Рис.4.31. Произвольная
последовательность импульсов (а) и её
спектральная плотность (б)

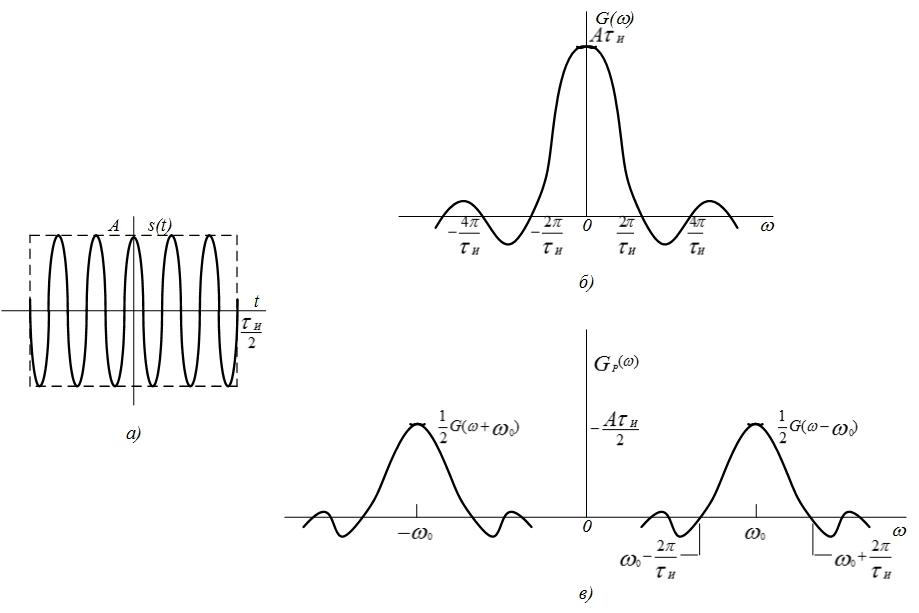
Рис.
4.32. Радиосигнал (а), спектральные плотности
радиосигнала (в) и его огибающей (б)

и
имеет вид периодической
последовательности δ-функций,
умноженных на ко­эффициент
.

9)
Радиосигнал
с прямоугольной огибающей.
Радиосигнал, представленный на (рис.
4.32,а), можно записать как

Согласно
поз. 11 табл.4.2 спектральная плотность
радиосигнала
полу­чается путем сдвига спектральной
плотности
прямоугольной
огибающей по оси частот на
вправо
и влево с уменьшением ординат в два
раза, т. е.

Это
выражение получается из (4.42) путем замены
частоты
на частоты–
сдвиг вправо и— сдвиг влево. Преобразование спектра
огибающейпоказано
на (рис. 4.32, б, в).

Примеры расчета
спектров непериодических сигналов
приведены так же в [7].

Соседние файлы в папке РАДИОТЕХНИКА

• #
• #
• #

Спектральные плотности некоторых сигналов

Содержание

Обнаружили ошибку?
Выделите ее мышью
и нажмите

Спектральная плотность прямоугольного импульса

Рассмотрим спектральную плотность  прямоугольного импульса  длительности  и амплитуды . Функция  описывает прямоугольный импульс длительности  и единичной амплитуды:

(1)

График прямоугольного импульса показан на рисунке 1а.

Рисунок 1. Спектральная плотность прямоугольного импульса
а — временно́й сигнал; б — спектральная плотность

Спектральная плотность  прямоугольного импульса  равна:

(2)

где . График спектральной плотности  прямоугольного импульса показан на рисунке 1б.
Приведем основные частотные свойства .

Спектральная плотность треугольного импульса

Рассмотрим треугольный импульс  длительности  и амплитуды :

(3)

График треугольного импульса показан на рисунке 2а.

Рисунок 2. Спектральная плотность треугольного импульса
а — временно́й сигнал; б — спектральная плотность

Для рассмотрения спектральной плотности треугольного импульса мы не будем вычислять интеграл Фурье непосредственно, потому что это потребует громоздких выкладок, а воспользуемся свойством преобразования Фурье свертки двух сигналов.

Можно заметить, что треугольный импульс длительности  и амплитуды  может быть представлен как результат свертки прямоугольного импульса  длительности  и амплитуды  c самим собой, как это показано на рисунке 3.

Рисунок 3. Треугольный импульс как результат
свертки прямоугольных импульсов

Обратим внимание, что один из углов  маркирован черным квадратиком для того, чтобы показать инверсию во времени сдвинутого сигнала , входящего в интеграл свертки.

Для различного сдвига  мы будем иметь линейно нарастающую площадь (заштрихованная область) произведения  сигнала  и его сдвинутой инверсной во времени копии .

Таким образом, мы можем применить

свойство преобразования Фурье свертки сигналов

и записать спектральную плотность треугольного импульса как квадрат спектральной плотности  прямоугольного импульса  длительности  и амплитуды :

(4)

График спектральной плотности треугольного импульса показан на рисунке 2б.
Приведем основные частотные свойства .

Спектральная плотность гауссова импульса

Гауссов импульс  задается выражением:

(5)

где  — амплитуда, а  — положительный параметр, который задает ширину импульса.

График гауссова импульса при различном значении  и  показан на рисунке 4а.

Рисунок 4. Спектральная плотность гауссова импульса
а — временно́й сигнал; б — спектральная плотность

Рассмотрим спектральную плотность гауссова импульса:

(6)

Преобразуем показатель экспоненты (6) следующим образом:

(7)

Тогда (6) с учетом (7):

(8)

Из курса математического анализа [1, стр. 401] известно, что:

(9)

Введем в выражении (8) замену переменной , тогда , пределы интегрирования остаются неизменными при положительном значении . Тогда (8) можно представить как:

(10)

и с учетом (9) окончательно можно записать:

(11)

Можно заметить, что временно́й гауссов импульс  имеет спектральную плотность , которая также описывается гауссовской функцией.

График спектральной плотности гауссова импульса для различного значения параметра  показан на рисунке 4б.
C увеличением  увеличивается ширина гауссова импульса во временно́й области, и сужение спектральной плотности. При этом, убывание импульса во времени и по частоте носит экспоненциальный характер.

Спектральная плотность экспоненциального импульса

Рассмотрим двусторонний экспоненциальный импульс , который задается выражением:

(12)

где  — амплитуда, а  — положительный параметр, который определяет ширину импульса.
График двустороннего экспоненциального импульса при  и различном значении параметра  показан на рисунке 5а.

Рисунок 5. Спектральная плотность двустороннего экспоненциального импульса
а — временно́й сигнал; б — спектральная плотность

Как можно видеть из рисунка 5а, увеличение параметра  приводит к сужению импульса во временно́й области.

Рассмотрим спектральную плотность  двустороннего экспоненциального импульса:

(13)

Разобьем ось времени на положительную и отрицательную полуоси, и учтем что  для отрицательной полуоси времени. Тогда (13) можно записать:

(14)

Объединим показатели экспонент в обоих интегралах и получим:

(15)

Таким образом, спектральная плотность двустороннего экспоненциального импульса (12) представляет собой вещественную функцию частоты, обладающую следующими свойствами.

На рисунке 5б показан вид спектральной плотности  при различном значении . Можно видеть, что при увеличении параметра , спектральная плотность сужается (импульс во временно́й области —расширяется).

Рисунок 6. Односторонний экспоненциальный импульс

Рассмотрим теперь односторонний экспоненциальный импульс, который получается из двустороннего при обнулении значения отрицательной полуоси времени:

(16)

График одностороннего экспоненциального импульса показан на рисунке 6 при  и различном .

Спектральная плотность одностороннего экспоненциального импульса равна:

(17)

Приведем основные частотные свойства  одностороннего экспоненциального импульса:

Поскольку спектральная плотность одностороннего экспоненциального импульса является комплексной функцией частоты , то можно представить  в виде амплитудно- и фазочастотной характеристик:

(18)

На рисунке 7 показаны АЧХ и ФЧХ одностороннего экспоненциального импульса для различных значения параметра .

Рисунок 7. АЧХ и ФЧХ одностороннего экспоненциального импульса
а — АЧХ; б — ФЧХ

Спектральная плотность функции

Рассмотрим спектральную плотность сигнала вида , где  — параметр определяющий ширину главного лепестка функции , как это показано на рисунке 8а.

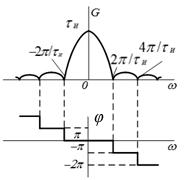
Рисунок 8. Спектральная плотность функции 
а — временно́й сигнал; б — спектральная плотность

Для получения спектральной плотности сигнала  воспользуемся

свойством двойственности преобразования Фурье,

рассмотренным в
в предыдущем параграфе.
Тогда из выражения (2) можно записать:

(19)

Произведем замену переменных  и , а также обозначим , откуда :

(20)

Вынесем множитель  из под оператора преобразования Фурье, и окончательно спектральная плотность сигнала  равна:

(21)

График спектральной плотности сигнала  показан на рисунке 8б.

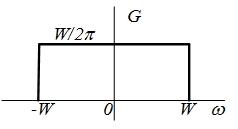
Важным частным случаем является , тогда  будет иметь спектральную плотность , что соответствует частотной характеристике идеального фильтра нижних частот. Временно́й сигнал   определяет импульсную характеристику идеального фильтра нижних частот.

Выводы

В данном разделе мы рассмотрели спектральные плотности некоторых непериодических сигналов: прямоугольного, треугольного, гауссова импульса,
а также одностороннего и двустороннего экспоненциальных импульсов.

Были приведены аналитические выражения для спектральных плотностей каждого из сигналов, а также их частотные свойства.

Смотри также

Представление периодических сигналов рядом Фурье
Преобразование Фурье непериодических сигналов
Свойства преобразования Фурье

Спектральные плотности некоторых сигналов

Список литературы

[1]

Кратные интегралы и ряды.
Москва, Наука, 1965, 608 c.

[2]

Баскаков, С.И.
Радиотехнические цепи и сигналы.
Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4

[3]

Гоноровский И.С.
Радиотехнические цепи и сигналы
Москва, Советское радио, 1977, 608 c.

[4]

Bracewell R.
The Fourier Transform and Its Applications
McGraw-Hills, 1986, 474 c. ISBN 0-07-007-015-6

Последнее изменение страницы: 12.05.2022 (19:42:52)

Страница создана Latex to HTML translator ver. 5.20.11.14

1.3.1. Спектральная плотность энергии

1.3.2. Спектральная плотность мощности

Спектральная плотность (spectral density) характеристик сигнала – это распределение энергии или мощности сигнала по диапазону частот. Особую важность это понятие приобретает при рассмотрении фильтрации в системах связи. Мы должны иметь возможность оценить сигнал и шум на выходе фильтра. При проведении подобной оценки используется спектральная плотность энергии (energy spectral density – ESD) или спектральная плотность мощности (power spectral density – PSD).

1.3.1. Спектральная плотность энергии

Общая энергия действительного энергетического сигнала , определенного в интервале описывается уравнением (1.7). Используя теорему Парсеваля [1], мы можем связать энергию такого сигнала, выраженную во временной области, с энергией, выраженной в частотной области:

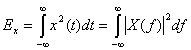, (1.13)

где – Фурье-образ непериодического сигнала . (Краткие сведения об анализе Фурье можно найти в приложении А.) Обозначим через прямоугольный амплитудный спектр, определенный как

(1.14)

Величина является спектральной плотностью энергии (ESD) сигнала . Следовательно, из уравнения (1.13) можно выразить общую энергию путем интегрирования спектральной плотности по частоте.

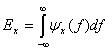(1.15)

Данное уравнение показывает, что энергия сигнала равна площади под на графике в частотной области. Спектральная плотность энергии описывает энергию сигнала на единицу ширины полосы и измеряется в Дж/Гц. Положительные и отрицательные частотные компоненты дают равные энергетические вклады, поэтому, для реального сигнала , величина представляет собой четную функцию частоты. Следовательно, спектральная плотность энергии симметрична по частоте относительно начала координат, а общую энергию сигнала можно выразить следующим образом.

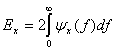(1.16)

1.3.2. Спектральная плотность мощности

Средняя мощность действительного сигнала в периодическом представлении определяется уравнением (1.8). Если – это периодический сигнал с периодом , он классифицируется как сигнал в периодическом представлении. Выражение для средней мощности периодического сигнала дается формулой (1.6), где среднее по времени берется за один период .

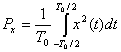(1.17,а)

Теорема Парсеваля для действительного периодического сигнала [1] имеет вид

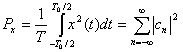, (1.17,б)

где члены являются комплексными коэффициентами ряда Фурье для периодического сигнала (см. приложение А).

Чтобы использовать уравнение (1.17,6), необходимо знать только значение коэффициентов . Спектральная плотность мощности (PSD) периодического сигнала , которая является действительной, четной и неотрицательной функцией частоты и дает распределение мощности сигнала по диапазону частот, определяется следующим образом.

(1.18)

Уравнение (1.18) определяет спектральную плотность мощности периодического сигнала как последовательность взвешенных дельта-функций. Следовательно, PSD периодического сигнала является дискретной функцией частоты. Используя PSD, определенную в уравнении (1.18), можно записать среднюю нормированную мощность действительного сигнала.

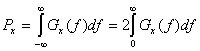(1.19)

Уравнение (1.18) описывает PSD только периодических сигналов. Если – непериодический сигнал, он не может быть выражен через ряд Фурье; если он является непериодическим сигналом в периодическом представлении (имеющим бесконечную энергию), он может не иметь Фурье-образа. Впрочем, мы по-прежнему можем выразить спектральную плотность мощности таких сигналов в пределе. Если сформировать усеченную версию непериодического сигнала в периодическом представлении , взяв для этого только его значения из интервала (), то будет иметь конечную энергию и соответствующий Фурье-образ . Можно показать [2], что спектральная плотность мощности непериодического сигнала определяется как предел.

(1.20)

Пример 1.1. Средняя нормированная мощность

а) Найдите среднюю нормированную мощность сигнала , используя усреднение по времени.

б) Выполните п. а путем суммирования спектральных коэффициентов.

Решение

а) Используя уравнение (1.17,а), имеем следующее.

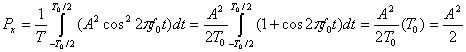
б) Используя уравнения (1.18) и (1.19), получаем следующее.

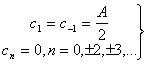(см. приложение А)

В статистической радиотехнике и физике при изучении детерминированных сигналов и случайных процессов широко используется их спектральное представление в виде спектральной плотности, которая базируется на преобразовании Фурье.

Если процесс имеет конечную энергию и квадратично интегрируем (а это нестационарный процесс), то для одной реализации процесса можно определить преобразование Фурье как случайную комплексную функцию частоты:

(1)

Однако она оказывается почти бесполезной для описания ансамбля. Выходом из этой ситуации является отбрасывание некоторых параметров спектра, а именно спектра фаз, и построении функции, характеризующей распределение энергии процесса по оси частот. Тогда согласно теореме Парсеваля энергия

(2)

Функция характеризует, таким образом, распределение энергии реализации по оси частот и называется спектральной плотностью реализации. Усреднив эту функцию по всем реализациям можно получить спектральную плотность процесса.

Перейдем теперь к стационарному в широком смысле центрированному случайному процессу , реализации которого с вероятностью 1 имеют бесконечную энергию и, следовательно, не имеют преобразования Фурье. Спектральная плотность мощности такого процесса может быть найдена на основании теоремы Винера-Хинчина как преобразование Фурье от корреляционной функции:

(3)

Если существует прямое преобразование, то существует и обратное преобразование Фурье, которое по известной определяет :

(4)

Если полагать в формулах (3) и (4) соответственно и , имеем

(5)

(6)

Формула (6) с учётом (2) показывает, что дисперсия определяет полную энергию стационарного случайного процесса, которая равна площади под кривой спектральной плотности. Размерную величину можно трактовать как долю энергии, сосредоточенную в малом интервале частот от до . Если понимать под случайный (флуктуационный) ток или напряжение, то величина будет иметь размерность энергии [В²/Гц] = [В²с]. Поэтому иногда называют энергетическим спектром. В литературе часто можно встретить другую интерпретацию: – рассматривается как средняя мощность, выделяемая током или напряжением на сопротивлении 1 Ом. При этом величину называют спектром мощности случайного процесса.

Свойства спектральной плотности[править | править код]

• Энергетический спектр стационарного процесса (вещественного или комплексного) – неотрицательная величина:

.

(7)

• Энергетический спектр вещественного стационарного в широком смысле случайного процесса есть действительная и чётная функция частоты:

.

(8)

См. также[править | править код]

• Спектральная плотность мощности
• Спектральная плотность излучения
• База сигнала

Литература[править | править код]

• Зюко, А. Г., Кловский, Д. Д., Назаров, М. В., Финк, Л. М. Теория передачи сигналов. — М.: Связь, 1980. — 288 с.
• Тихонов, В. И., Харисов, В. Н. Статистический анализ и синтез радиотехнических устройств и систем. — М.: Радио и связь, 2004. — 608 с. — ISBN 5-256-01701-2.
• Тихонов, В. И., Бакаев, Ю. Н. Статистическая теория радиотехнических устройств. — М.: ВВИА им. проф. Н. Е. Жуковского, 1978. — 420 с.