Алексей . Малеев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Спин ядра
Спин ядра ($I$) складывается из спинов нуклонов и их орбитальных моментов. (Определяя спин, называют одно число, которое указывает максимальную проекцию спина на произвольную ось $Z$).
Спин нуклона – $I_p=I_n=frac{1}{2}$, следовательно, величина спина ядра может иметь целое или полуцелое значение, что зависит от четного или нечетного количества нуклонов в ядре. Так, спин ядра атома водорода равен $I_p=frac{1}{2}$.
Если ядро стабильно, и оно находится в основном состоянии, то $Ile frac{9}{2}$. Моменты импульса основной части нуклонов в ядре взаимно компенсируют друг друга, имея антипараллельную ориентацию. Для всех ядер, имеющих четное количество протонов и нейтронов в основном состоянии $I=0. $
Существование собственного момента импульса ядра было предположено Паули в виде постулата. В соответствии с данной гипотезой ядро имеет собственный момент импульса $overrightarrow{I}$. Спиновый момент ядра квантуется. Максимальное значение проекции $overrightarrow{I}$ на избранное направление и обозначают через $I$ и называют спином ядра. Его нельзя путать с длиной вектора момента импульса $left|overrightarrow{I}right|$.
Полная длина вектора $overrightarrow{I}$ определена правилом квантования момента импульса:
где квантовое число $I$ принимает значения: $I=L+S;;L+S-1;dots ,left|l-Sright|.$
Так, спин протона равен $frac{1}{2}$, при этом длина вектора спина протона в единицах $hbar $:
Разница между спином ($I$) и $left|Iright|$ связана с поперечной компонентой у вектора $overrightarrow{I}$ по отношению к избранному направлению. Ее направление не определено, но длина имеет определенную величину. При этом исключение составляет случай, когда $overrightarrow{I} =0.$
Магнитный момент нуклонов и ядра
Орбитальное перемещение протонов в ядре атома ведет к тому, что магнитный момент ядер атомов отличен от нуля. Помимо этого, нуклоны обладают собственным магнитным моментом, который связан со спином как:
где $g_N$ — $g$ — фактор нуклона, ${mu }_{NB}=frac{q_ehbar }{2m_p}=5,05cdot {10}^{-27}frac{Дж}{Тл}- $ядерный магнетон Бора ($m_p$- масса протона или масса ядра). Для протона $g_papprox 5,6$, для нейтрона $g_napprox -3,8.$ То, что нейтрон, не имея заряда, имеет магнитный момент неравный нулю, говорит о том, что он обладает пространственной структурой.
«Спин и магнитный момент нуклонов и ядра. Сверхтонкая структура атомных спектров» 👇
Так как проекция спинов нуклонов на некоторую ось $Z$ равна $frac{1}{2}$, то проекцией магнитных моментов на ось $Z$ является величина:
Ядерный магнетон Бора является естественной единицей магнитного момента ядра. Его формула совпадает с формулой для магнетона Бора (${mu }_B$), где масса электрона заменена на массу протона. В результате:
Замечание 1
Итак, магнитный момент ядер вызван спиновыми магнитными моментами нуклонов и магнитными моментами, которые возникают благодаря орбитальным движениям протонов. При этом вектор магнитного момента не совпадает с вектором момента количества движения. В результате магнитного взаимодействия, которое присутствует между орбитальным и спиновым моментами, суммарный магнитный момент совершает прецессию относительно результирующего момента количества движения. Средний по времени суммарный магнитный момент — составляющая магнитного момента направлен по моменту количества движения ядра.
Сверхтонкая структура атомных спектров
Взаимодействие магнитных моментов электронов в атоме с ядром ведет к дополнительному расщеплению энергоуровней. Как результат: линии тонкой структуры дополнительно расщепляются, возникает сверхтонкая структура линий спектра. Данное расщепление весьма мало (около тысячных нм). Его наблюдают при помощи спектральных приборов, которые имеют высокую разрешающую способность.
Сверхтонкая структура была открыта Майкельсоном в $1891$ г. при помощи интерферометра Фабри и Перо. Позднее, было выявлено, что некоторые линии спектра имеют более $10$ близко расположенные компоненты. К $1910$ г. был получен большой объем экспериментальных данных, однако его объяснение стало возможным только после создания квантовой теории.
Первые измерения спинов и магнитных моментов ядер были изначально получены при исследовании сверхтонкой структуры линий спектра. Данный метод не был точен и утратил свое значение на сегодняшний момент. Все сведения о спинах и магнитных моментах в дальнейшем получали методом ядерного магнитного резонанса.
Гипотеза Паули предполагала, что сверхтонкая структура линий спектра появляется вследствие взаимодействия магнитного момента атомного ядра с магнитным полем, которое создано электронной оболочкой (орбитальным и спиновым моментами электронов). Помимо этого ядро может обладать электрическим квадрупольным моментом, электрическими и магнитными мультиполями, которые взаимодействуют с электронной оболочкой. Данная гипотеза полностью подтверждена. Основную роль играет магнитный дипольный момент ядра. Он взаимодействует с магнитным полем электронной оболочки, которая окружает ядро. Это взаимодействие ведет к расщеплению энергетических уровней. С этим связана (в основном) сверхтонкая структура энергоуровней и линий спектра.
Замечание 2
Отметим, что в спектральном приборе наблюдают сверхтонкая структура не энергетических уровней, а спектральных линий. Каждая линия спектра сверхтонкой структурой появляется как результат перехода атома с одного подуровня на другой. Допустимые переходы определены правилами отбора.
Интенсивности линий спектра сильно зависят от кратности вырождения энергетических уровней, между которыми идут квантовые переходы.
Пример 1
Задание: Ядро составлено из двух нуклонов. Полные моменты этих нуклонов равны: $j_1=frac{5}{2}$ и $j_2=frac{3}{2}$ , какие значения может принимать момент количества движения ядра ($I$), которое составлено из вышеупомянутых нуклонов?
Решение:
Если составить ядро из $2$ нуклонов с полными моментами $j_1=frac{5}{2}$ и $j_2=frac{3}{2}$, то момент количества движения ядра может быть равен одному из целых чисел, равного длине стороны треугольника, две остальные стороны которого равны $j_1$ и $j_2$, то есть запишем:
[j_1+j_2le Ile left|j_1-j_2right|left(1.1right).]
Так как выполняется неравенство (1.1), то:
[frac{5}{2}+frac{3}{2}le Ile left|frac{5}{2}-frac{3}{2}right|to 4le Ile 1left(1.2right).]
Так как длина стороны треугольника не может быть больше суммы (4) или меньше разности (1), то механический момент ядра в нашем случае может иметь значения:
[I=1,2,3,4.]
Ответ: $I=1,2,3,4.$
Пример 2
Задание: Какое явление получило название азотной катастрофы?
Решение:
До того, как были открыты нейтроны, считали, что ядро составлено из протонов и электронов. Рассмотрим ядро атома азота: $N^{14}_7.$ Если ядро содержит протоны и электроны, то в нем содержится: $14$ протонов и $7$ электронов:
[14p+7e^-=21 (частица) left(2.1right).]
Спины протона и электрона равны $frac{1}{2}hbar .$ Получается, что спин ядра азота должен быть полуцелым. Эмпирически же получалось, что величина спина ядра азота равна $1$. Данный факт и получил наименование: «азотная катастрофа».
Так, измерение значений спинов ядер подтолкнуло к выводу о том, что электроны не входят в состав ядер атомов.
На самом деле, ядро атома азота содержит $7$ протонов и $7$ нейтронов:
[7p+7n=14 left(частицright).]
Получается, что спин ядра атома азота будет целым.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
1. Спин ядра
Ядро,
как пространственно ограниченная и
связанная система взаимодействующих
между собой нуклонов, в определенных
случаях может рассматриваться в целом
как одна микрочастица. Так как нуклоны,
из которых состоит ядро, обладают
собственным механическим моментом, или
спином, а также совершают движение
относительно друг друга (орбитальное
движение относительно центра инерции
ядра), то и ядра должны иметь собственный
механический момент (далее просто
момент) или спин.
Спин
ядра
![]()
есть
векторная сумма полных моментов
![]()
отдельных нуклонов, каждый из которых
складывается из орбитального момента![]()
и собственного момента (спина) нуклона
![]()
,
так что
|
|
(1.6.1) |
Возможна
другая схема сложения моментов отдельных
нуклонов, дающая другой результат, когда
сначала отдельно суммируются векторы
спинов, а затем векторы орбитальных
моментов всех нуклонов, и полученные
два вектора складываются. Однако,
поскольку ядерные силы не центральны
(см. §1.9 п.7) и в ядре существует
спин-орбитальное взаимодействие (см.
§2.3 п.1), то по этой причине в теории ядра
используют первую схему.
Естественной
единицей измерения момента импульса в
квантовой механике служит постоянная
Планка ħ = 1,0546·10-34 Дж·с,
имеющая размерность момента импульса.
Вектор момента любых микрочастиц, как,
впрочем, и спин ядра, обладает своеобразными
свойствами.
1.
Абсолютная величина вектора момента
любой изолированной физической величины
может принимать только дискретные
значения:
|
| |
(1.6.2) |
где I – положительное
число, либо целое, либо полуцелое:
|
I = 0, 1/2, 1, 3/2, … |
(1.6.3) |
Число
I называют обычно
величиной момента или квантовым числом
момента. Следует особо отметить различие
между модулем вектора
и
квантовым числом I,
так как последнее является одним из
чисел (1.6.3), используемых в формуле
(1.6.2) для нахождения модуля вектора
![]()
.
Когда говорят: «момент
1/2», то имеют в виду именно
это квантовое число в формуле (1.6.2).
Нуклоны (и электрон тоже) имеют квантовое
число спина s = 1/2 (спин
равен 1/2).
В
формуле (1.6.1) квантовое число lk
для орбитального момента всегда целое
число, lk
= 0, 1, 2, и т.д.
2.
Мгновенное значение вектора механического
момента любой микрочастицы не имеет
смысла по той же причине, по которой в
квантовой механике не имеет смысла
мгновенное значение вектора импульса.
Строго фиксированное значение может
иметь только абсолютная величина вектора
момента (1.6.2) и одна из его пространственных
проекций, обычно называемой проекцией
на ось Z, которая
обозначается как Iz.
Проекция момента Iz
может принимать случайным образом одно
из (2I + 1) значений,
уменьшающихся на единицу:
|
Iz |
(1.6.4) |
Реализация
любой возможной проекции из набора
(1.6.4) оказывается равновероятной.
Число
возможных проекций на ось Z
четно, если
I – полуцелое
число, и нечетно, если I
– целое число. Знак плюс или минус в
(1.6.4) означает ориентацию вектора момента
на выбранное направление оси Z
в пространстве. Однако величины
проекций Ix
и Iy
оказываются совершенно неопределенными1
и флуктуируют относительно нулевого
среднего значения. Учитывая, что
|
|
(1.6.5) |
имеем
|
|
(1.6.6) |
Т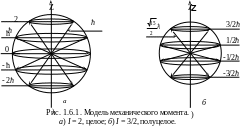
аким
образом, квадраты проекций вектора
момента на оси Х и Y
не равны нулю. По этой причине проекция
момента Iz
всегда меньше абсолютной величины
вектора механического момента, т.е.
направление вектора
никогда
не может совпадать с осью Z.
Действительно, согласно (1.6.4), максимальное
значение
![]()
=
![]()
тогда как согласно (1.6.2)
![]()
.
Все перечисленные выше свойства вектора
механического момента обычно демонстрируют
с помощью квазиклассической модели
(рис. 1.6.1), которая находится в определенном
согласии со свойствами квантовомеханического
вектора момента. Вектор момента, величина
которого вычисляется с помощью (1.6.2),
прецессирует относительно оси Z
с некоторой угловой скоростью и может
ориентироваться вдоль или против
направления оси Z
только таким образом, чтобы его проекция
на ось Z была равна
одному из значений от +Iћ
до –Iћ через
единицу. Этот вектор никогда не может
ориентироваться точно по направлению
оси Z, поскольку его
величина, как отмечено выше, не равна
Iћ. Поэтому, помимо
величины вектора момента, сохраняющейся
во времени величиной является только
одна проекция вектора – проекция на
ось Z. Полное число
проекций Iz
вектора момента на рис.1.6.1 равно
(2I + 1).
3.
Модуль вектора момента
![]()
сложной
системы, составленной из двух подсистем
с моментами
![]()
и
![]()
,
вычисляется из выражения
|
|
(1.6.7) |
обычным образом через свои квантовые
числа
![]()
.
Сложение векторов
и
есть сложение их проекций как алгебраических
чисел. Для получения всех возможных
проекций вектора
на ось Z каждая из
проекций вектора
складывается
с каждой из проекций вектора
.
Таких проекций вектора
оказывается всего (2I1
+ 1)(2I2 + 1), которые
будут образовывать (2Im
+ 1) векторов
![]()
,
Im
= min{I1,I2},
со следующими значениями квантовых
чисел:
|
|
(1.6.8) |
Соотношение
(1.6.8) определяет правило сложения моментов
в квантовой механике.
Поскольку
каждое значение проекции из
(2I1 + 1)(2I2 + 1)
возможных реализуется с равной
вероятностью, то относительная вероятность
образования состояния со спином
![]()
из возможного набора значений (1.6.8)
составит
|
|
(1.6.9) |
т.е. равна отношению числа возможных
проекций вектора
![]()
к полному числу проекций возможных
значений вектора
![]()
.
Величина g называется
статистическим фактором или статистическим
весом.
4.
Любая векторная величина
![]()
,
характеризующая физические свойства
микрочастицы, пропорциональна вектору
момента
:
|
|
(1.6.10) |
где а – константа, полностью
характеризующая вектор.
В
отношении спинов различных ядер
наблюдаются следующие опытные
закономерности:
а) Для
ядер с четными А спины всегда целые, а
при нечетном А – всегда полуцелые.
б)
Четно-четные ядра (А –
четное) в основном состоянии имеют спин
равный нулю. Этот факт дает основания
полагать, что одноименные нуклоны с
одинаковыми величинами, но противоположно
направленными векторами
![]()
полных моментами, объединяются в пары
(эффект спаривания, см. §1.4 п.3) и суммарный
момент импульса ядра оказывается равным
нулю.
в)
Нечетно-нечетные ядра (А –
четное) имеют целочисленный спин. Это
указывает на то, что разноименные нуклоны
объединяются в пары с одинаковым
направлением векторов механического
момента, создавая целочисленный момент
(см. §1.11).
г)
Ядра с нечетным А имеют полуцелый спин
в пределах от 1/2 до
9/2, что крайне мало по сравнению с суммой
абсоютных значений полных моментов
(см.
(1.6.1)) отдельных нуклонов для
большинства ядер. По-видимому
векторы
полных
механических моментов для большинства
одноименных нуклонов попарно компенсируются
и не участвуют в создании спина ядра.
Как найти спин атома?
4.1. Определение спина
- если A – чётное, то J = n (n = 0, 1, 2, 3,…), т. е. …
- если A – нечётное, то J = n + 1/2, т. е. …
- чётно-чётные ядра в основном состоянии имеют значение спина J= 0, что указывает на взаимную компенсацию моментов нуклонов в основном состоянии ядра – особое свойство межнуклонного взаимодействия.
Как определить спин и четность ядра?
Спин ядра указывается числом, а чётность — знаком плюс для чётных или знаком минус для нечётных состояний. Этот знак ставится справа сверху от числа, указывающего спин.
Что показывает спин?
Спином называют собственный момент импульса частицы. Момент импульса характеризует количество вращательного движения, то есть спин характеризует тот факт, что частицы ведут себя так, будто бы они вращаются вокруг своей оси.
Чему равен спин электрона?
Протоны, электроны и нейтроны обладают спином. Каждый непарный электрон имеет спин равный 1/2.
Какие частицы относятся к Нуклонам?
Нукло́ны (от лат. nucleus «ядро») — общее название для составляющих атомное ядро протонов и нейтронов. С точки зрения электромагнитного взаимодействия протон и нейтрон — разные частицы, так как протон электрически заряжен, а нейтрон — нет.
Что такое изотопы?
Изото́пы (от др. -греч. ισος — «равный», «одинаковый», и τόπος — «место») — разновидности атомов (и ядер) какого-либо химического элемента, которые имеют одинаковый атомный (порядковый) номер, но при этом разные массовые числа.
Чему равен спин нейтрона?
Нейтрон и протон имеют собственный момент количества движения (спин), величина которого равна ½ ћ, где ћ – модифицированная постоянная Планка. Поскольку нуклоны могут двигаться в ядре по некоторым орбитам, они обладают также орбитальными моментами количества движения.
Зачем нужны квантовые числа?
Квантовые числа – целые или дробные числа, определяющие возможные значения физических величин, характеризующих квантовую систему (молекулу, атом, атомное ядро, элементарную частицу). Квантовые числа отражают дискретность (квантованность) физических величин, характеризующих микросистему.
Что называется спином электрона?
Спин (от англ. spin – вращаться) – собственный момент количества движения элементарной частицы, имеющий квантовую природу и не связанный с её перемещением в пространстве как целого.
Чему равен спин ядра?
Это ее внутренняя характеристика. Нейтрон и протон имеют собственный момент количества движения (спин), величина которого равна ½ ћ, где ћ – модифицированная постоянная Планка. Поскольку нуклоны могут двигаться в ядре по некоторым орбитам, они обладают также орбитальными моментами количества движения.
Чему равен спин фотона?
Корпускулярная модель электромагнитного взаимодействия приписывает фотону спин, равный ±1; это означает, что спиральность фотона равна
Какие частицы не относятся к Нуклонам?
Нукло́ны (от лат. nucleus — ядро) — общее название для протонов и нейтронов. С точки зрения электромагнитного взаимодействия протон и нейтрон разные частицы, так как протон электрически заряжен, а нейтрон — нет.
Что такое нуклоны и нуклиды?
НУКЛИД — общее название атомных ядер (и атомов), характеризующихся числом протонов в ядре Z, числом нейтронов N и общим числом нуклонов A = Z + N, которое называется массовым числом. Обозначается химическим символом Н с индексами .
Что такое изотоп простыми словами?
Изотопы (от греческих слов isos «одинаковый» и topos «место») это атомы одного химического элемента с разным числом нейтронов в ядре.
Что такое изотопы и их примеры?
Изотопы – атомные ядра, имеющие одинаковое число протонов Z, разное число нейтронов N и, следовательно, разное массовое число A = Z + N. Пример: изотопы кальция Са (Z = 20) — 38Ca, 39Ca, 40Ca, 41Ca, 42Ca. Радиоактивные изотопы — ядра-изотопы, испытывающие радиоактивный распад.
Какое свойство одинаково у протона и нейтрона?
Настолько одинаковым, что, с точки зрения ядерных сил, протон и нейтрон можно считать как бы двумя проявлениями одной и той же частицы — нуклона: протон — это электрически заряженный нуклон, а нейтрон — нейтральный нуклон.
Что показывает главное квантовое число?
главное квантовое число, n pranc.
НА ГЛАВНУЮ СТРАНИЦУ
Спин и четность ядра
Механистическая модель строения ядер атомов позволяет вернуть
спину первоначальный механический смысл. Спин ядра представляет собой сумму
спинов составляющих ядро нуклонов с учетом знака спина. Спин нуклона –
механический момент вращения. Его величина зависит от скорости вращения нуклона
вокруг собственной оси и от расстояния до оси измерения, чаще всего являющейся
и осью симметрии ядра. Так как собственное вращение нуклона постоянно, то
изменяться может только расстояние до оси измерения.
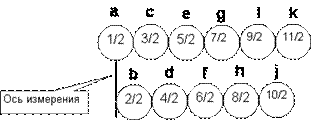

Рисунок 1. Спин нуклона в зависимости от расстояния до
оси
При плотной упаковке расстояние до оси измерения
принимает только дискретные величины, кратные радиусу нуклона. Соответственно,
спин нуклона тоже может иметь только дискретные значения, так как, согласно
данной модели, все вектора моментов вращения параллельны оси измерения. Для
точного подсчета спина ядра достаточно знать точное расстояние от каждого
нуклона до оси симметрии и ориентацию спина нуклона. Это возможно при наличии
графического изображения пространственной конфигурации ядра. Но с графическим
изображением не всегда удобно работать. Иногда необходимо использовать
математическое либо символьное описание. Существующее символьное описание
электронных оболочек для данного случая явно не подходит – нет четкой системы
обозначений. Обозначение должно естественным образом указывать на относительную
координату нуклона в ядре.
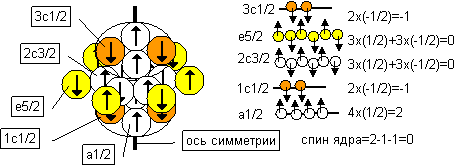
Рисунок 2. Пример вычисления спина ядра
При плотной упаковке нуклоны располагаются слоями. Для
удобства символьного описания, присвоим каждому слою уникальное обозначение,
используя буквы латинского алфавита последовательно. Начальную
букву алфавита используем для обозначения нуклонов, находящихся на оси
симметрии. Последующие буквы алфавита будем последовательно использовать для
обозначения нуклонов, находящихся на последующих дискретных расстояниях
(орбитах) от оси симметрии (измерения). Нуклоны, находящиеся на орбите ‘c’,
кроме вращения вокруг собственной оси могут еще вращаться по орбите вокруг оси
симметрии (2-3 нуклона с одинаковым направлением спина). В этом случае
суммарный спин нуклона уменьшается до значения “1/2”. Во всех остальных
случаях нуклоны не имеют орбитального вращения и имеют суммарный спин согласно
рисунку выше.
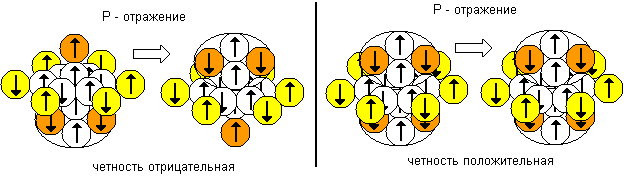
Рисунок 3. Пример вычисления четности ядра
Четность ядра тоже вычисляется легко. При инверсии
координат каждого нуклона (x на –x, y на –y, z на –z, то есть при P-отражении)
конфигурация ядра с отрицательной четностью изменяется, а конфигурация ядра с
положительной четностью не изменяется. Направление спина нуклона при P-отражении
не меняется. На рисунке ниже приведены примеры вычисления четности. Во втором
случае отраженные ядра полностью идентичны, поэтому четность положительная. В
первом случае отраженные ядра внешне похожи, если одно из ядер развернуть на
180 градусов. Но физическими свойствами они все же будут отличаться, так как не
совпадает направление спинов у шести нуклонов. Поэтому у этих ядер четность
отрицательная. Отраженные ядра имеют одинаковый по абсолютной величине спин, но
направление спина противоположное при одинаковой ориентации ядер в пространстве.
Владимир Яковлев, lun1@list.ru , http://logicphysic.narod.ru ,
январь 2008 года
