Для описания положения электрона в электронной оболочке используют четыре квантовых числа. Здесь мы не будем углубляться в квантово-механические подробности и опишем только утилитарный смысл данных чисел. Набор, состоящий из четырёх квантовых чисел – это «адрес» электрона в электронной оболочке.
Главное квантовое число `n` – определяет полную энергию электрона на энергетическом уровне и показывает, из скольких энергетических уровней состоит электронная оболочка атома. Принимает целочисленные положительные значения от `1` до `oo`. В периодической таблице Д. И. Менделеева `n` равно номеру периода.
Орбитальное квантовое число `l` показывает, сколько энергетических подуровней составляют данный уровень и характеризует форму орбиталей. Принимает значения от `0` до `(n-1)`.
При `n=1`, `l` принимает только одно значение `0` (этому числовому значению соответствует буквенное `s`), следовательно, на первом энергетическом уровне только один подуровень – `s`. Орбиталь `s`-подуровня имеет сферическую форму (рис. 1).
При `n=2`, `l` принимает два значения: `0` `(s)` и `1` `(p)`. Энергетический уровень состоит из двух подуровней – `s` и `p`. Форма `p`-орбитали похожа на объёмную восьмёрку (рис. 1).
При `n=3`, `l` принимает уже три значения: `0` `(s)`; `1` `(p)` и `2` `(d)`. Таким образом, на третьем уровне три подуровня. Орбитали `d`-подуровня имеют форму двух перекрещённых объёмных восьмёрок либо объёмной восьмерки с перемычкой (рис. 1).
При `n=4`, значений `l` уже четыре, следовательно, и подуровней на четвёртом уровне четыре. К перечисленным выше добавляется `3` `(f)`. Орбитали `f`-подуровня имеют более сложную, объёмную, форму.
Магнитное квантовое число `ml` определяет число орбиталей на каждом подуровне и характеризует их взаимное расположение.
Принимает значения `-l` до `+l`, включая `0`.
При `l=0`, `m_l` принимает только одно значение – `0`. Следовательно, орбиталь, находящаяся на данном подуровне (`s`-подуровне), только одна. Мы уже знаем, что она имеет форму сферы с центром в начале координат.
При `l=1`, `m_l` принимает три значения: `−1`; `0`; `+1`. Значит, орбиталей на данном подуровне (`p`-подуровне) три. Так как `p`-орбитали представляют из себя объёмные восьмёрки (то есть линейной структуры), располагаются они в пространстве по осям координат, перпендикулярно друг другу (`p_x`, `p_y`, `p_z`).
При `l=2`, `m_l` принимает уже пять значений: `−2`; `−1`; `0`; `+1`; `+2`. То есть на `d`-подуровне располагаются пять орбиталей. Это плоскостные структуры, в пространстве занимают пять положений.
При `l=3`, то есть на `f`-подуровне, орбиталей становится семь, так как `m_l` – принимает семь значений (от `−3` до `+3` через `0`). Орбитали являются более сложными объёмными структурами, и взаимное их расположение еще более сложно.
Спиновое квантовое число `m_s` характеризует собственный момент количества движения электрона и принимает только два значения: `+1//2` и `-1//2`.
Электронная ёмкость подуровня (максимальное количество электронов на подуровне) может быть рассчитана по формуле `2(2l+1)`, а уровня – по формуле `2n^2`.
Всё вышесказанное можно обобщить в Таблице 2.
Таблица 2. Квантовые числа, атомные орбитали и число электронов на подуровнях (для `n<=4`)
|
`n` |
`l` |
Обозначение орбитали |
`ml` |
Число орбиталей |
Число электронов на подуровне |
|
`1` |
`0` |
`1s` |
`0` |
`1` |
`2` |
|
`2` |
`0` `1` |
`2s` `2p` |
`0` `−1`; `0`; `+1` |
`1` `3` |
`2` `6` |
|
`3` |
`0` `1` `2` |
`3s` `3p` `3d` |
`0` `−1`; `0`; `+1` `−2`; `−1`; `0`; `+1`; `+2` |
`1` `3` `5` |
`2` `6` `10` |
|
`4` |
`0` `1` `2` `3` |
`4s` `4p` `4d` `4f` |
`0` `−1`; `0`; `+1` `−2`; `−1`; `0`; `+1`; `+2` `−3`; `−2`; `−1`; `0`; `+1`; `+2`; `+3` |
`1` `3` `5` `7` |
`2` `6` `10` `14` |
Химические свойства элементов и их соединений определяются электронным строением валентного уровня их атомов. Именно с участием электронов валентного уровня возникают химические связи между атомами и образуется соединение (вещество). Поэтому важно понимать правила заполнения электронных оболочек, строение валентного уровня и составлять электронную конфигурацию атомов элементов.
In physics, the spin quantum number is a quantum number (designated s) that describes the intrinsic angular momentum (or spin angular momentum, or simply spin) of an electron or other particle. It has the same value for all particles of the same type, such as s = 1/2 for all electrons. It is an integer for all bosons, such as photons, and a half-odd-integer for all fermions, such as electrons and protons. The component of the spin along a specified axis is given by the spin magnetic quantum number, conventionally written ms.[1] The value of ms is the component of spin angular momentum, in units of the reduced Planck constant ħ, parallel to a given direction (conventionally labelled the z–axis). It can take values ranging from +s to −s in integer increments. For an electron, ms can be either ++1/2 or −+1/2 .
The phrase spin quantum number was originally used to describe the fourth of a set of quantum numbers (the principal quantum number n, the azimuthal quantum number ℓ, the magnetic quantum number m, and the spin magnetic quantum number ms), which completely describe the quantum state of an electron in an atom.
Some introductory chemistry textbooks describe ms as the spin quantum number,[2][3] and s is not mentioned since its value 1/2 is a fixed property of the electron, sometimes using the variable s in place of ms.[4] Some authors discourage this usage as it causes confusion.[4] At a more advanced level where quantum mechanical operators or coupled spins are introduced, s is referred to as the spin quantum number, and ms is described as the spin magnetic quantum number[5] or as the z-component of spin sz.[6]
Spin quantum numbers apply also to systems of coupled spins, such as atoms that may contain more than one electron. Capitalized symbols are used: S for the total electronic spin, and mS or MS for the z-axis component. A pair of electrons in a spin singlet state has S = 0, and a pair in the triplet state has S = 1, with mS = −1, 0, or +1. Nuclear-spin quantum numbers are conventionally written I for spin, and mI or MI for the z-axis component.
The name “spin” comes from a physical spinning of the electron about an axis, as proposed by Uhlenbeck and Goudsmit. However, this simplistic picture was quickly realized to be unrealistic, physically, because it would require the electrons to rotate faster than the speed of light.[7] It was therefore replaced by a more abstract quantum-mechanical description.
Key points[edit]
- Quantum numbers give complete information about the electron in an atom, i.e., energy, position, size, shape and orientation of that orbital and the direction of spin. The direction of spin is described by spin quantum number.
- The electron in an atom not only moves around the nucleus, but also spins about its own axis. This number gives the information about the direction of spinning of the electron present in any orbital.
- The spin angular momentum is an intrinsic property, like rest mass and charge.
- The magnitude spin quantum number of an electron cannot be changed.
- The spin may lie in 2s + 1 = 2 orientations.
- Each type of subatomic particle has fixed spin quantum numbers like 0, 1 /2, 1, 3 /2, … etc.
- The spin value of an electron, proton, neutron is 1 /2.
- The particles having half-integral value ( 1 /2, 3 /2 …) of spin are called fermions.
- The particles having integral value (0, 1, 2…) of spin are called bosons.
Magnetic nature of atoms and molecules[edit]
The spin quantum number helps to explain the magnetic properties of atoms and molecules. A spinning electron behaves like a micromagnet with a definite magnetic moment. If an atomic or molecular orbital contains two electrons, then their magnetic moments oppose and cancel each other.
If all orbitals are doubly occupied by electrons, the net magnetic moment is zero and the substance behaves as diamagnetic; it is repelled by the external magnetic field. If some orbitals are half filled (singly occupied), the substance has a net magnetic moment and is paramagnetic; it is attracted by the external magnetic field.
History[edit]
Early attempts to explain the behavior of electrons in atoms focused on solving the Schrödinger wave equation for the hydrogen atom, the simplest possible case, with a single electron bound to the atomic nucleus. This was successful in explaining many features of atomic spectra.
The solutions required each possible state of the electron to be described by three “quantum numbers”. These were identified as, respectively, the electron “shell” number n, the “orbital” number ℓ, and the “orbital angular momentum” number m. Angular momentum is a so-called “classical” concept measuring the momentum[citation needed] of a mass in circular motion about a point. The shell numbers start at 1 and increase indefinitely. Each shell of number n contains n2 orbitals. Each orbital is characterized by its number ℓ, where ℓ takes integer values from 0 to n − 1, and its angular momentum number m, where m takes integer values from +ℓ to −ℓ. By means of a variety of approximations and extensions, physicists were able to extend their work on hydrogen to more complex atoms containing many electrons.
Atomic spectra measure radiation absorbed or emitted by electrons “jumping” from one “state” to another, where a state is represented by values of n, ℓ, and m. The so-called “transition rule” limits what “jumps” are possible. In general, a jump or “transition” is allowed only if all three numbers change in the process. This is because a transition will be able to cause the emission or absorption of electromagnetic radiation only if it involves a change in the electromagnetic dipole of the atom.
However, it was recognized in the early years of quantum mechanics that atomic spectra measured in an external magnetic field (see Zeeman effect) cannot be predicted with just n, ℓ, and m.
In January 1925, when Ralph Kronig was still a Columbia University Ph.D. student, he first proposed electron spin after hearing Wolfgang Pauli in Tübingen. Werner Heisenberg and Pauli immediately hated the idea: They had just ruled out all imaginable actions from quantum mechanics. Now Kronig was proposing to set the electron rotating in space. Pauli especially ridiculed the idea of spin, saying that “it is indeed very clever but of course has nothing to do with reality”. Faced with such criticism, Kronig decided not to publish his theory and the idea of electron spin had to wait for others to take the credit.[8] Ralph Kronig had come up with the idea of electron spin several months before George Uhlenbeck and Samuel Goudsmit, but most textbooks credit these two Dutch physicists with the discovery.
Pauli subsequently proposed (also in 1925) a new quantum degree of freedom (or quantum number) with two possible values, in order to resolve inconsistencies between observed molecular spectra and the developing theory of quantum mechanics.
Shortly thereafter Uhlenbeck and Goudsmit identified Pauli’s new degree of freedom as electron spin.
Electron spin[edit]
A spin- 1 /2 particle is characterized by an angular momentum quantum number for spin s = 1 /2. In solutions of the Schrödinger-Pauli equation, angular momentum is quantized according to this number, so that magnitude of the spin angular momentum is
The hydrogen spectrum fine structure is observed as a doublet corresponding to two possibilities for the z-component of the angular momentum, where for any given direction z:
whose solution has only two possible z-components for the electron. In the electron, the two different spin orientations are sometimes called “spin-up” or “spin-down”.
The spin property of an electron would give rise to magnetic moment, which was a requisite for the fourth quantum number. The electron spin magnetic moment is given by the formula:
where
- e is the charge of the electron
- g is the Landé g-factor
and by the equation:
where 
When atoms have even numbers of electrons the spin of each electron in each orbital has opposing orientation to that of its immediate neighbor(s). However, many atoms have an odd number of electrons or an arrangement of electrons in which there is an unequal number of “spin-up” and “spin-down” orientations. These atoms or electrons are said to have unpaired spins that are detected in electron spin resonance.
Detection of spin[edit]
When lines of the hydrogen spectrum are examined at very high resolution, they are found to be closely spaced doublets. This splitting is called fine structure, and was one of the first experimental evidences for electron spin. The direct observation of the electron’s intrinsic angular momentum was achieved in the Stern–Gerlach experiment.
Stern–Gerlach experiment[edit]
The theory of spatial quantization of the spin moment of the momentum of electrons of atoms situated in the magnetic field needed to be proved experimentally. In 1922 (two years before the theoretical description of the spin was created) Otto Stern and Walter Gerlach observed it in the experiment they conducted.
Silver atoms were evaporated using an electric furnace in a vacuum. Using thin slits, the atoms were guided into a flat beam and the beam sent through an in-homogeneous magnetic field before colliding with a metallic plate. The laws of classical physics predict that the collection of condensed silver atoms on the plate should form a thin solid line in the same shape as the original beam. However, the in-homogeneous magnetic field caused the beam to split in two separate directions, creating two lines on the metallic plate.
The phenomenon can be explained with the spatial quantization of the spin moment of momentum. In atoms the electrons are paired such that one spins upward and one downward, neutralizing the effect of their spin on the action of the atom as a whole. But in the valence shell of silver atoms, there is a single electron whose spin remains unbalanced.
The unbalanced spin creates spin magnetic moment, making the electron act like a very small magnet. As the atoms pass through the in-homogeneous magnetic field, the force moment in the magnetic field influences the electron’s dipole until its position matches the direction of the stronger field. The atom would then be pulled toward or away from the stronger magnetic field a specific amount, depending on the value of the valence electron’s spin. When the spin of the electron is ++ 1 /2 the atom moves away from the stronger field, and when the spin is −+ 1 /2 the atom moves toward it. Thus the beam of silver atoms is split while traveling through the in-homogeneous magnetic field, according to the spin of each atom’s valence electron.
In 1927 Phipps and Taylor conducted a similar experiment, using atoms of hydrogen with similar results. Later scientists conducted experiments using other atoms that have only one electron in their valence shell: (copper, gold, sodium, potassium). Every time there were two lines formed on the metallic plate.
The atomic nucleus also may have spin, but protons and neutrons are much heavier than electrons (about 1836 times), and the magnetic dipole moment is inversely proportional to the mass. So the nuclear magnetic dipole momentum is much smaller than that of the whole atom. This small magnetic dipole was later measured by Stern, Frisch and Easterman.
Electron paramagnetic resonance[edit]
For atoms or molecules with an unpaired electron, transitions in a magnetic field can also be observed in which only the spin quantum number changes, without change in the electron orbital or the other quantum numbers. This is the method of electron paramagnetic resonance (EPR) or electron spin resonance (ESR), used to study free radicals. Since only the magnetic interaction of the spin changes, the energy change is much smaller than for transitions between orbitals, and the spectra are observed in the microwave region.
Derivation[edit]
For a solution of either the nonrelativistic Pauli equation or the relativistic Dirac equation, the quantized angular momentum (see angular momentum quantum number) can be written as:
where
Given an arbitrary direction z (usually determined by an external magnetic field) the spin z-projection is given by
where ms is the secondary spin quantum number, ranging from −s to +s in steps of one. This generates 2 s + 1 different values of ms.
The allowed values for s are non-negative integers or half-integers. Fermions have half-integer values, including the electron, proton and neutron which all have s = ++ 1 /2 . Bosons such as the photon and all mesons) have integer spin values.
Algebra[edit]
The algebraic theory of spin is a carbon copy of the angular momentum in quantum mechanics theory.
First of all, spin satisfies the fundamental commutation relation:
where 
Next, the eigenvectors of 

where 
Energy levels from the Dirac equation[edit]
In 1928, Paul Dirac developed a relativistic wave equation, now termed the Dirac equation, which predicted the spin magnetic moment correctly, and at the same time treated the electron as a point-like particle. Solving the Dirac equation for the energy levels of an electron in the hydrogen atom, all four quantum numbers including s occurred naturally and agreed well with experiment.
Total spin of an atom or molecule[edit]
For some atoms the spins of several unpaired electrons (s1, s2, …) are coupled to form a total spin quantum number S.[9][10] This occurs especially in light atoms (or in molecules formed only of light atoms) when spin–orbit coupling is weak compared to the coupling between spins or the coupling between orbital angular momenta, a situation known as L S coupling because L and S are constants of motion. Here L is the total orbital angular momentum quantum number.[10]
For atoms with a well-defined S, the multiplicity of a state is defined as 2S + 1 . This is equal to the number of different possible values of the total (orbital plus spin) angular momentum J for a given (L, S) combination, provided that S ≤ L (the typical case). For example, if S = 1, there are three states which form a triplet. The eigenvalues of Sz for these three states are +1ħ, 0, and −1ħ .[9] The term symbol of an atomic state indicates its values of L, S, and J .
As examples, the ground states of both the oxygen atom and the dioxygen molecule have two unpaired electrons and are therefore triplet states. The atomic state is described by the term symbol 3P, and the molecular state by the term symbol 3Σ−
g.
Nuclear spin[edit]
Atomic nuclei also have spins. The nuclear spin I is a fixed property of each nucleus and may be either an integer or a half-integer. The component mI of nuclear spin parallel to the z–axis can have (2I + 1) values I, I–1, …, –I. For example, a 14N nucleus has I = 1, so that there are 3 possible orientations relative to the z–axis, corresponding to states mI = +1, 0 and −1.[11]
The spins I of different nuclei are interpreted using the nuclear shell model. Even-even nuclei with even numbers of both protons and neutrons, such as 12C and 16O, have spin zero. Odd mass number nuclei have half-integral spins, such as 3/ 2 for 7Li, 1 /2 for 13C and 5/ 2 for 17O, usually corresponding to the angular momentum of the last nucleon added. Odd-odd nuclei with odd numbers of both protons and neutrons have integral spins, such as 3 for 10B, and 1 for 14N.[12] Values of nuclear spin for a given isotope are found in the lists of isotopes for each element. (See isotopes of oxygen, isotopes of aluminium, etc. etc.)
See also[edit]
- Total angular momentum quantum number
- Rotational spectroscopy
- Basic quantum mechanics
References[edit]
- ^ Pauling, Linus (1960). The nature of the chemical bond and the structure of molecules and crystals: an introduction to modern structural chemistry. Ithaca, N.Y. ISBN 0-8014-0333-2. OCLC 545520.
- ^ Petrucci, Ralph H.; Harwood, William S.; Herring, F. Geoffrey (2002). General Chemistry (8th ed.). Prentice Hall. p. 333. ISBN 0-13-014329-4.
- ^ Whitten, Kenneth W.; Galley, Kenneth D.; Davis, Raymond E. (1992). General Chemistry (4th ed.). Saunders College Publishing. p. 196. ISBN 0-03-072373-6.
- ^ a b Perrino, Charles T.; Peterson, Donald L. (1989). “Another quantum number?”. J. Chem. Ed. 66 (8): 623. doi:10.1021/ed066p623. ISSN 0021-9584.
- ^ Atkins, Peter; de Paula, Julio (2006). Atkins’ Physical Chemistry (8th ed.). W.H. Freeman. p. 308. ISBN 0-7167-8759-8.
- ^ Banwell, Colin N.; McCash, Elaine M. (1994). Fundamentals of Molecular Spectroscopy. McGraw-Hill. p. 135. ISBN 0-07-707976-0.
- ^ Halpern, Paul (2017-11-21). “Spin: The quantum property that should have been impossible”. Forbes. Starts with a bang. Retrieved 2018-03-10.
- ^ Bertolotti, Mario (2004). The History of the Laser. CRC Press. pp. 150–153. ISBN 978-1-4200-3340-3. Retrieved 22 March 2017.
- ^ a b Merzbacher, E. (1998). Quantum Mechanics (3rd ed.). John Wiley. pp. 430–431. ISBN 0-471-88702-1.
- ^ a b Atkins, P.; de Paula, J. (2006). Physical Chemistry (8th ed.). W.H. Freeman. p. 352. ISBN 0-7167-8759-8.
- ^ Atkins, Peter; de Paula, Julio (2006). Atkins’ Physical Chemistry (8th ed.). W.H. Freeman. p. 515. ISBN 0-7167-8759-8.
- ^ Cottingham, W.N.; Greenwood, D.A. (1986). An introduction to nuclear physics. Cambridge University Press. pp. 36, 57. ISBN 0-521-31960-9.
External links[edit]
- Weiss, Michael (2001). “Full treatment of spin – including origins, evolution of spin theory, and details of the spin equations”. Department of Mathematics. UC Riverside.
Квантовые числа это числовое значение квантовой переменной определенного объекта (пример: электронная частица, ядра, атомы), которое характеризует его.
Квантовое число (полностью) характеризует состояние этой частицы.
Согласно современным взглядам стационарные состояния атома или термы характеризуются четырьмя квантовыми числами:
- Главным,
- Орбитальным,
- Магнитным,
- Спиновым.

Что такое квантовые числа
При развитии теории Бора оказалось, что для полной характеристики стационарных состояний атома должно учитываться наличие у электронов не только круговых, но и эллиптических орбит (Зоммерфельд), а также и некоторые другие условия, которые увеличивают количество дозволенных энергетических уровней.
Главное квантовое число п определяет дозволенные энергетические уровни атома или в соответствии с моделью Резерфорда—Бора порядковые номера орбит и их радиусы (для эллиптических орбит — большую полуось).
Главное квантовое число может принимать значение любого числа натурального ряда:
n = 1, 2, 3..
Главное квантовое число
В одномерной модели атома энергия электрона может принимать только определенные значения, иначе говоря — она квантована.
Энергия электрона в реальном атоме также величина квантованная.
Возможные энергетические состояния электрона в атоме определяются величиной главного квантового числа п, которое может принимать положительные целочисленные значения: 1, 2, 3… и т. д.
Наименьшей энергией электрон обладает при п =1, с увеличением п энергия электрона возрастает.
Поэтому состояние электрона, характеризующееся определенным значением главного квантового числа.
Принято называть энергетическим уровнем электрона в атоме:
при п = 1 электрон находится на первом энергетическом уровне, при п = 2 — на втором и т. д.
Главное квантовое число определяет и размеры электронного облака.
Для того чтобы увеличить размеры электронного облака, нужно часть его удалить на большее расстояние от ядра.
Этому препятствуют силы электростатического притяжения электрона к ядру, преодоление которых требует затраты энергии.
Поэтому большим размерам электронного облака соответствует более высокая энергия электрона в атоме и, следовательно, большее значение главного квантового числа п.
Электроны же, характеризующиеся одним и тем же значением главного квантового числа, образуют в атоме электронные облака приблизительно одинаковых размеров.
Поэтому можно говорить о существовании в атоме электронных слоев, или электронных оболочек, отвечающих определенным значениям главного квантового числа.
Для энергетических уровней электрона в атоме (т. е. для электронных слоев, или оболочек), соответствующих различным значениям п, приняты следующие буквенные обозначения:
| Главное квантовое число n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Обозначение энергетического уровня | K | L | M | N | O | P | Q |
Что определяет побочное квантовое число
Орбитальное или побочное квантовое число l определяет дозволенные значения момента количества движения lэ электрона по орбите.
В модели Бора—Зоммерфельда — дозволенные соотношения малой b и большой а полуосей эллиптических орбит (рис. , а):
b/a = (l + 1)/n
где п — главное квантовое число.
Орбитальное квантовое число
Орбитальное квантовое число l может принимать значения любых целых чисел в пределах от нуля до числа на единицу меньшего главного квантового числа п : l = 0, 1, 2, … , п — 1
Для основной орбиты атома водорода (квантовые числа атома водорода) п = 1 и l = (п — 1) = 0; b/a = 1/n = 1; эта орбита — круговая.
Если п > 1, то орбита имеет форму круга при l = (п — 1). Для примера на рис. , б показана группа орбит с главным квантовым числом n = 3 при трех значениях орбитального квантового числа:
l = 0 (b/a = 1/3), l = 1, (b/a = 2/3) и l = 2, (b/a = 1).
Не только энергия электрона в атоме (и связанный с ней размер электронного облака) может принимать лишь определенные значения.
Произвольной не может быть и форма электронного облака. Она определяется орбитальным квантовым числом l (его называют также побочным, или азимутальным), которое может принимать целочисленные значения от 0 до (n — 1), где n — главное квантовое число.
Различным значениям n отвечает разное число возможных значений l.
Так. при n = 1 возможно только одно значение орбитального квантового числа — нуль (l = 0), при n — 2 l может быть равным 0 или I, при n—3 возможны значения l, равные 0, 1 и 2, вообще, данному значению главного квантового числа п соответствуют n различных возможных значении орбитального квантового числа.
Вывод о том, что формы атомных электронных облаков не могут быть произвольными, вытекает из физического смысла квантового числа l.
Именно оно определяет значение орбитального момента количества движения электрона; эта величина, как и энергия, является квантованной физической характеристикой состояния электрона в атоме.
Напомним, что орбитальным моментом количества движения М частицы движущейся вокруг центра вращения по некоторой орбите, зазывается произведение mυr, где m — масса частицы, υ — ее скорость, r — радиус-вектор, соединяющий центр вращения с частицей (рис. 7). Важно отметить, что М векторная величина; направление этого вектора перпендикулярно плоскости, в которой расположены векторы υ и r.
Определенной форме электронного облака соответствует вполне определенное значение орбитального момента количества движения электрона М.
Но поскольку М может принимать только дискретные значення, задаваемые орбитальным квантовым числом l, то формы электронных облаков не могут быть произвольными: каждому возможному значению l соответствует вполне определённая форма электронного облака.
Мы уже знаем, что энергия электрона в атоме зависят от главного квантового числа n. В атоме водорода энергия электрона полностью определяется значением n. Однако в многоэлектронных
атомах энергия электроне зависит и от значения орбитального квантового числа l.
Поэтому состояния электрона, характеризующиеся различными значениями l, принято называть энергетическими подуровнями электрона в атоме. Этим подуровням подуровням присвоены следующие буквенные обозначения:
| Орбитальное квантовое число | 0 | 1 | 2 | 3 |
| Обозначение энергетического подуровни | s | p | d | f |
В соответствии с этими обозначениями говорят об s— подуровне, р-подуровне и т, д.
Электроны, характеризующиеся значениями побочного квантового числя 0, 1, 2 и 3, называют соответственно s— электронами, р-электронами, d— электронами и f— электронами.
При данном значений главного квантового числя n наименьшей энергией обладают s- электроны, затем р-, d— и f—электроны,
Состояние электрона в атоме, отвечающее определенным значениям n и l, записывается следующим образом: сначала цифрой указывается значение главного квантового числа, а затем буквой— орбитального квантового числа.
Так, обозначение 2р относится к электрону, у которого n = 2 и l = 1, обозначение 3d — к электрону, у которого n = 3 и l = 2.
Магнитное квантовое число
Магнитное квантовое число т1 определяет пространственную ориентировку электронных орбит, которая должна удовлетворять дозволенный значениям проекции орбитального момента, на некоторое направление.
В качестве такого направления рассматривается направление внешнего (действующего на атом) магнитного поля.
Движущийся вокруг ядра электрон образует элементарный круговой ток, имеющий собственное магнитное поле.
В результате взаимодействия внешнего магнитного поля с этим полем плоскость орбиты электрона ориентируется в пространстве определенным образом.
Дозволенными являются те положения орбиты, при которых численное значение l‘э проекции вектора lЭ момента количества движения электрона на направление магнитного поля (рис, справа) кратно величине h/2π : l ‘э = ml (h/2π), где ml — магнитное квантовое число.
Магнитное квантовое число тl может принимать значения любых целых положительных и отрицательных чисел в пределах от 0 до орбитального квантового числа l : тl = 0, ± 1, ±2, ±3, … ± l .
Пример магнитного квантового числа
Для примера на рис. (справа) показано расположение орбиты электрона с некоторыми заданными главным и орбитальным квантовыми числами п и l и различным магнитным квантовым числом, которое изменяется в пределах тl = +1; тl = + 2 и тl — +3 (при отрицательных значениях этих чисел плоскости орбит поворачиваются на 180°).
Таким образом, при данных главном п и орбитальном l квантовых числах электрон в атоме, находящемся под действием магнитного поля, может двигаться по орбитам, имеющим в пространстве (2l + 1) различных положений.
Этим положениям соответствуют свои энергетические уровни и, следовательно, линии в спектре (расщепление спектральных линий в магнитном поле называется явлением Зеемана).
Спиновое квантовое число
 Спиновое квантовое число ms определяет дозволенные направления вектора спина электронов.
Спиновое квантовое число ms определяет дозволенные направления вектора спина электронов.
Тело, вращающееся вокруг своей оси (как, например, волчок), имеет собственный момент количества движения или момент вращения, с которым связаны особые механические свойства тела.
Такие же свойства имеет электрон (и другие элементарные частицы), хотя понятие о вращении вокруг своей оси к ним не применимо, вследствие отсутствия у них определенной внутренней структуры.
Поэтому электрону так же приписывается собственный момент количества движения, который называется спином.
Экспериментально установлено, что спин S электрона численно равен половине величины h/2π : S = ± (1/2)(h/2). С другой стороны, спин электрона приравнивается произведению спинового квантового числа ms на величину h/2π, т. е.
S = ms(h/2π)
Отсюда следует, что спиновое квантовое число электрона имеет только два значения:
ms = ±1/2
Эти значения обусловливают две дозволенные ориентировки проекции S’ вектора спина S электрона на направление орбитального момента l: параллельную ms= +1/2 (рис. 2, а) и антипараллельную ms = — 1/2 (рис. 2, б).
Квантовые числа сохраняют свое значение и в атомах с большим числом электронов, хотя общая система обозначения состояний (термов) атома при этом усложняется.
Магнитное и спиновое квантовые числа
Размеры и формы электронных облаков в атоме могут быть не любыми, а только такими, которые соответствуют возможным значениям квантовых чисел n и l.
Из уравнения Шредингера следует, что и ориентация электронного облака в пространстве не может быть произвольной: она определяется значением третьего, так называемого магнитного квантового числа m.
Магнитное квантовое число может принимать любые целочисленные значения — как положительные, так и отрицательные — в пределах от +l до —l.
Таким образом, для разных значений l число возможных значений m различно.
Так, для s — электронов (l = 0) возможно только одно значение m (m = 0); для р — электронов (l = 1) возможны три различных значения m (—1, 0, +1); при l = 2 (d — электроны) m может принимать пять различных значений (—2, —1, 0, +1, +2).
Вообще, некоторому значению l соответствует (2l + 1) возможных значений магнитного квантового числа, т. е. (2l + 1) возможных расположений электронного облака в пространстве.
Состояние электрона в атоме, характеризующееся определенными значениями квантовых чисел n, l и m, т. с. определенными размерами, формой и ориентацией в пространстве электронного облака, получило название атомной электронной орбитали.
Исследования атомных спектров привели к выводу, что, помимо квантовых чисел n, l и m, электрон характеризуется еще одной квантованной величиной, не связанной с движением электрона вокруг ядра, а определяющей его собственное состояние.
Эта величина получила название спинового квантового числа или просто спина (от английского spin — кручение, вращение); спин обычно обозначают буквой s.
Спин электрона может иметь только два значения: +1/2 или — 1/2; таким образом, как и в случае остальных квантовых чисел, возможные значения спинового квантового числа различаются на единицу.
Кроме орбитального момента количества движения, определяемого значением l, электрон обладает и собственным моментом количества движения, что можно упрощенно рассматривать как результат вращения электрона вокруг своей оси.
Проекция собственного момента количества движения электрона на избранное направление (например, на ось z) и называется спином.
Четыре квантовых числа — n, I, т и s — полностью определяют состояние электрона в атоме.
Электронные оболочки
Группировка энергетических уровней атома (или орбит электронов по Боровской модели) происходит в соответствии со значением главного и побочного квантовых чисел.
Электроны с одинаковым главным числом п образуют электронные оболочки, которые принято обозначать следующими буквами:
n=1 2 34567.
К L М N О Р Q
Электроны, принадлежащие к определенной оболочке, образуют несколько подоболочек в соответствии с их орбитальным квантовым числом l.
Значение этого числа и соответствующих ему подоболочек часто обозначают следующими буквами (буквы заимствованы из названий спектральных линий):
l = 0 1 2 3 4 5
s р d f g h
Поскольку орбитальное квантовое число принимает значения от 0 до (п — 1), число подоболочек равняется порядковому номеру п оболочки. Оболочка К состоит из одной подоболочки s: Оболочка L состоит из двух подоболочек s и р, оболочка М — из трех: s, р,d, и т. д.
Количество электронов в подоболочке обусловливается магнитным и спиновым квантовыми числами.
Принцип Паули
При этом выполняется принцип Паули: в атоме не может быть двух электронов, находящихся в тождественных состояниях движения, другими словами, не может быть больше одного электрона с четырьмя одинаковыми квантовыми числами.
Поскольку при заданном орбитальном числе l магнитное число тl может иметь (2l + 1) значений и при каждом из них спиновое число ms может иметь два значения, отличающихся знаком, общее количество возможных состояний при этом будет 2•(2l + 1).
Следовательно, подоболочка s (l = 0) может содержать только два электрона, различающиеся знаком спина; подоболочка р (l =1) — шесть электронов, различающихся тремя магнитными числами и при каждом из них двумя спиновыми; подоболочка d (l = 2) — десять, и т. д.
Число электронов в подоболочке указывается как показатель степени у буквы, ее обозначающей.
Электронная оболочка пример
 Например, электронная оболочка К атома водорода, содержащая только один электрон, обозначается 1s. Оболочка содержит одну круговую орбиту.
Например, электронная оболочка К атома водорода, содержащая только один электрон, обозначается 1s. Оболочка содержит одну круговую орбиту.
У гелия на этой же оболочке находится два электрона, отличающиеся спиновыми числами:
1s2
(рис. 3, а, на котором слева показано схематическое, а справа — условное изображение оболочек).
Второй период таблицы Менделеева
У элементов второго периода таблицы Менделеева появляется вторая оболочка L. Она может состоять из двух подоболочек s и р.
Сначала заполняется подоболочка 2s (эллиптическая орбита): у лития одним электроном 1s22s, у бериллия — двумя (с разными спиновыми числами) ls22s2 (рис. 3, б).
Затем заполняется подоболочка 2р (круговые орбиты) электронами с разными значениями магнитного квантового числа: у бора и углерода с ml = 0, у азота и кислорода с ml = + 1, у фтора и неона с тl = —1 (см. таблицу).
Таким образом, у неона подоболочка 2р заполнена шестью электронами:
ls22s22p6
(рис. 3, в).
У натрия появляется третья оболочка М с одним электроном 1s22s22p63s (рис. 3, г), и т. д.
Последовательность заполнения электронных оболочек сохраняется только у атомов первых 18 элементов.
Затем этот порядок усложняется: в одних случаях новый слой может начинать заполняться раньше, чем окончится заполнение предыдущего, в других случаях, наоборот, происходит заполнение оставшихся мест в предыдущей оболочке при неизменном числе электронов в наружном слое.
Количество электронов в наружной оболочке во всех случаях изменяется только от 1 до 8.
Наибольшее возможное число N электронов в оболочке соответствует условию:
N = 2п2,
где п — главное квантовое число (для оболочки К —2, для L — 8, М — 18).
Это условие выполняется только для первых четырех оболочек (К — N), для остальных — полное число электронов не достигает максимально возможного.
Сходство строения электронных оболочек
Сопоставление модели строения электронной оболочки атомов отдельных элементов с расположением их в периодической системе Д. И. Менделеева показывает, что периодичность повторения свойств элементов связана со сходством строения их электронных оболочек.
Число электронных оболочек соответствует номеру периода таблицы, к которому данный элемент принадлежит.
В каждом периоде физико-химические свойства элементов связаны с числом электронов во внешнем слое, поэтому при образовании каждого нового слоя они повторяются.
Таким образом установленная Менделеевым периодичность свойств элементов получила новое обоснование в строении электронных оболочек атомов.
Принципиальное квантовое число (обозначается буквой » n’)
-
Это относится к основной электронной оболочке. Это дает вероятное расстояние электрона от ядра. Большее значение » n’ означает большее расстояние между электроном и ядром.
-
Он также обозначает размер орбиты и энергетический уровень электрона. Таким образом, большее » n’ означает больший размер орбиты и, следовательно, указывает на больший атомный радиус.
-
Если радиус атома велик, сила притяжения между электроном и ядром не так сильна. Следовательно, энергия ионизации, энергия, необходимая для удаления электронов, меньше по сравнению с атомами с малыми радиусами.
-
Значением » n’ является любое положительное целое число. Он не может быть нулем и не может быть отрицательным целым числом, потому что атом не может иметь нулевую энергию или отрицательную энергию. Когда n = 1, он обозначает самую внутреннюю оболочку или первую основную оболочку, которая является основным состоянием или оболочкой с наименьшей энергией. Он может иметь такие значения, как n=1, 2, 3, 4…
-
Электрон может получить энергию и перейти к более высоким оболочкам за счет поглощения энергии или фотонов, и поэтому значение » n » увеличивается.
-
Если он теряет энергию, он возвращается к более низким оболочкам, и значение » n » уменьшается, вызывая излучение фотонов.
Азимутальное квантовое число (обозначается » ℓ’)
-
Также известное как квантовое число орбитального/углового момента, оно относится к подоболочке, к которой принадлежит электрон. Значение » ℓ » указывает на конкретную подоболочку; s, p, d и f, каждая из которых имеет уникальную форму.
-
Он также обозначает форму данной орбиты. Значение » ℓ’ указывает общее количество угловых узлов на орбите.
-
Значение » ℓ’ может быть больше или равно нулю и меньше или равно n-1.
ℓ = 0, 1, 2, 3, 4… (Н-1)
-
Значение «ℓ’ зависит от значения «n». Если n= 3, » ℓ «может иметь значения 0, 1 и 2. Когда ℓ = 0, это означает, что подрешетка «s». Когда ℓ= 1, это означает подоболочку «p», а когда ℓ= 2, это означает подоболочку «d». Для n= 3 возможными подоболочками являются 3s, 3p и 3d.
Магнитное квантовое число (обозначается » mℓ’)
-
Каждый электрон находится в оболочке. Каждая оболочка разделена на подоболочки, и каждая подоболочка дополнительно разделена на орбитали.
-
Он определяет количество орбиталей в подоболочке и ориентацию этих орбиталей.
-
Это дает проекцию углового момента, соответствующего орбите, вдоль заданной оси.
-
На следующем рисунке показана ориентация орбиталей в соответствии с соответствующими квантовыми числами.
-
Значение ‘m «зависит от значения» ℓ’. Магнитные квантовые числа могут иметь в общей сложности (2 ℓ + 1) значения. Для заданного значения ‘ℓ’ магнитное квантовое число может иметь значения в диапазоне от –l до +l. таким образом, это может быть положительное целое число, ноль и отрицательное целое число. Следовательно, значение «mℓ» косвенно зависит от значения » n’.
Квантовое число спина электрона (обозначается буквой «м»)
-
Это не зависит от других квантовых чисел, таких как значения n, ℓ и ml.
-
Он дает информацию о направлении, в котором электрон вращается по заданной орбите. Электрон вращается, как волчок на орбитали. Он может вращаться по часовой стрелке или против часовой стрелки.
-
Он может иметь значения +1/2 и -1/2.
-
Положительное значение ms (+1/2) указывает на восходящий спин электрона и называется «спин вверх». Он представлен .
-
Отрицательное значение ms (-1/2) указывает на нисходящий спин электрона и называется «спином вниз». Он представлен .
-
Электроны сначала занимают орбитали поодиночке, а затем объединяются в пары. На каждой орбите может поместиться максимум два электрона, и их ориентация будет противоположной друг другу. Если один электрон находится в положении спина вверх, то другой будет вращаться вниз. Это объясняется на следующем рисунке.
-
Это также говорит о том, обладает ли атом способностью создавать магнитные поля или нет. Из-за спина электрон ведет себя как маленький магнит.
-
Если в атоме все электроны спарены на орбиталях, их спины с противоположными значениями уравновешивают друг друга, и атом считается диамагнитным. Если мы сложим их спины, общая сумма будет равна нулю, и они отталкивают магнитные поля.
Электронная конфигурация Mg в основном состоянии (все электроны спарены, поэтому его диамагнитность).
-
Если атом содержит неспаренные электроны на орбиталях, электрон на орбитали имеет чистый спин, и спины не уравновешивают друг друга. В результате атом имеет чистый спин и притягивается магнитным полем. Такие атомы называются парамагнитными. Электронная конфигурация O- — У него 1 неспаренный электрон, поэтому он парамагнитный.
Спектр электромагнитного излучения

В связи с тем что радиусы электронных оболочек у атомов различных элементов обратно пропорциональны их порядковому номеру, у элементов с высоким номером орбиты электронов расположены значительно ближе к ядру.
Поэтому разность энергий между соседними уровнями, на которых находятся внутренние электроны, значительно выше, чем для внешних электронов, и для перевода их с одной орбиты на другую, особенно у атомов с высоким порядковым номером, требуется энергия, измеряемая сотнями и тысячами электрон-вольт.
Излучение, которое получается при этом, имеет значительно более высокую частоту и относится уже к дальнему ультрафиолетовому и рентгеновскому.
Торможение электронов
Имеется еще один механизм электромагнитного излучения — это торможение быстро движущихся электронов электрическим полем атома, внутри которого они пролетают. Фотоны излучения при этом имеют высокую энергию и относятся преимущественно к рентгеновскому излучению.
Еще большую энергию фотонов, чем рентгеновское излучение, и, следовательно, меньшую длину волны имеет гамма-излучение радиоактивных веществ, источником которого является атомное ядро.
Виды оптического излучения
В таблице приведены некоторые данные (частота, длина волны, энергия фотонов), характеризующие различные виды оптического излучения, рентгеновского и гамма-излучения.
| Элемент | Квантовые числа | Обозначение | |||
| п | l | тl | тs | ||
| Н | К
(n= 1) |
s
(l = 0) |
0 | + 1/2 | 1s |
| Не | -1/2 | 1s2 | |||
| Li | L
(n = 2) |
s
(l = 0) |
0 | + 1/2 | 1s22s |
| Be | -1/2 | 1s2 2s2 | |||
| В | р
(l = 1) |
0 | + 1/2 | ls22s22p | |
| С | -1/2 | 1s2 2s22p2 | |||
| N | +1 | + 1/2 | 1s2 2s22p3 | ||
| О | -1/2 | 1s2 2s2 2p4 | |||
| F | —1 | + 1/2 | 1s2 2s2 2p5 | ||
| Ne | -1/2 | ls22s22p6 | |||
| Вид излучения | Длина волны | Частота в гц | Энергия фотона в ЭВ | |||
| от | до | от | до | от | до | |
| Инфракрасное | 400 мк | 0,76 мк | 7,5•1011 | 3,94• 1014 | 0,0031 | 1,65 |
| Видимое | 760 ммк | 380 ммк | 3,94• 1014 | 7,9• 1014 | 1,65 | 3,3 |
| Ультрафиолетовое | 380 ммк | 10 ммк | 7,9• 1014 | 3,0• 1016 | 3,3 | 124 |
| Рентгеновское | 10 ммк | 0,001 ммк | 3,0•1016 | 3,0•1020 | 124 | 1,2•106 |
| Гамма | 0,1 ммк | не определен | 3,0•1018 | 1,2•104 |
На рис. 3 приведен общий спектр электромагнитных волн, расположенных в порядке убывания длины волны. Разделение спектра на отдельные участки имеет условный характер, поэтому во многих случаях отдельные виды излучения перекрывают границы участков.
Часто задаваемые вопросы и ответы квантовые числа?
Что такое главное квантовое число?
Главное квантовое число — целое число, для водорода и водородоподобных атомов определяет возможные значения энергии.
В случаях сложных атомов нумерует уровни энергии с фиксированным значением азимутального ( орбитального) квантового числа.
Какие числа относятся квантовым числам?
Квантовые числа иногда делят на те, которые связаны с перемещением описываемого объекта в обычном пространстве (к ним, например, относятся введённые выше n, l, m ), и те, которые отражают «внутреннее» состояние частицы. К последним относится спин и его проекция ( спиральность ).
Какие значения квантовых чисел имеют квантовые электроны?
Согласно правилу Хунда электроны в квантовых ячейках располагаются следующим образом:
Значения главного, побочного и спинового квантовых чисел у электронов одинаковы и равны n=4, l=2, ms=+1/2. Рассматриваемые электроны отличаются значениями квантовых чисел ml.
Что такое азимутальное квантовое число?
В случаях сложных атомов нумерует уровни энергии с фиксированным значением азимутального ( орбитального) квантового числа n = l + 1 , l + 2 , l + 3 .
Является первым в ряду квантовых чисел, который включает в себя главное, орбитальное и магнитное квантовые числа, а также спин.
Статья на тему Квантовые числа
Материалы портала onx.distant.ru
Квантовые числа
Общая характеристика квантовых чисел
Принцип (запрет) Паули
Правило Хунда
Примеры решения задач
Задачи для самостоятельного решения
Общая характеристика квантовых чисел
Главное квантовое число n характеризует энергию электрона в атоме и размер электронной орбитали. Оно соответствует также номеру электронного слоя, на котором находится электрон. Совокупность электронов в атоме с одинаковым значением главного квантового числа n называют электронным слоем (энергетическим уровнем). n – принимает значения 1, 2, 3, …, ∞ . Энергетические уровни обозначают прописными латинскими буквами:
| Значение n | 1 | 2 | 3 | 4 | 5 | 6 |
| Обозначение слоя | K | L | M | N | O | P |
Различия в энергиях электронов, принадлежащих к различным подуровням данного энергетического уровня, отражает побочное (орбитальное) квантовое число l. Электроны в атоме с одинаковыми значениями n и l составляют энергетический подуровень (электронную оболочку). Максимальное число электронов в оболочке Nl:
Nl = 2(2l + 1). (1)
Побочное квантовое число принимает целые значения 0, 1, … (n – 1). Обычно l обозначается не цифрами, а буквами:
| Значение l | 0 | 1 | 2 | 3 | 4 |
| Обозначение орбитали | s | p | d | f | g |
Орбиталь – пространство вокруг ядра, в котором наиболее вероятно нахождение электрона.
Побочное (орбитальное) квантовое число l характеризует различное энергетическое состояние электронов на данном уровне, форму орбитали, орбитальный момент импульса электрона.
Таким образом, электрон, обладая свойствами частицы и волны, движется вокруг ядра, образуя электронное облако, форма которого зависит от значения l. Так, если l = 0, (s-орбиталь), то электронное облако имеет сферическую симметрию. При l = 1 (p-орбиталь) электронное облако имеет форму гантели. d-орбитали имеют различную форму: dz2 — гантель, расположенная по оси Z с тором в плоскости X – Y, dx2 — y2 — две гантели, расположенные по осям X и Y; dxy, dxz, dyz, — две гантели, расположенные под 45o к соответствующим осям.

- Формы электронных облаков для различных состояний электронов в атомах
Магнитное квантовое число ml характеризует ориентацию орбитали в пространстве, а также определяет величину проекции орбитального момента импульса на ось Z. ml принимает значения от +l до — l, включая 0. Общее число значений ml равно числу орбиталей в данной электронной оболочке.
Магнитное спиновое квантовое число ms характеризует проекцию собственного момента импульса электрона на ось Z и принимает значения +1/2 и –1/2 в единицах h/2p (h – постоянная Планка).
Принцип (запрет) Паули
В атоме не может быть двух электронов со всеми четырьмя одинаковыми квантовыми числами. Принцип Паули определяет максимальное число электронов Nn, на электронном слое с номером n:
Nn = 2n2. (2)
На первом электронном слое может находиться не более двух электронов, на втором – 8, на третьем – 18 и т. д.
Правило Хунда
Заполнение энергетических уровней происходит таким образом, чтобы суммарный спин был максимальным. Например, три р-электрона на орбиталях р-оболочки располагаются следующим образом:
![]()
Таким образом, каждый электрон занимает одну р-орбиталь.
Примеры решения задач
Задача 1. Охарактеризуйте квантовыми числами электроны атома углерода в невозбужденном состоянии. Ответ представьте в виде таблицы.
Решение. Электронная формула атома углерода: 1s22s22p2. В первом слое атома углерода находятся два s-электрона с антипараллельными спинами, для которых n = 1. Для двух s-электронов второго слоя n = 2. Спины двух р-электронов второго слоя параллельны; для них m s= +1/2.
| № электрона | n | l | ml | ms |
| 1 | 1 | 0 | 0 | +1/2 |
| 2 | 1 | 0 | 0 | –1/2 |
| 3 | 2 | 0 | 0 | +1/2 |
| 4 | 2 | 0 | 0 | –1/2 |
| 5 | 2 | 1 | 1 | +1/2 |
| 6 | 2 | 1 | 0 | +1/2 |
Задача 2. Охарактеризуйте квантовыми числами внешние электроны атома кислорода в основном состоянии. Ответ представьте в виде таблицы.
Решение. Электронная формула атома кислорода: 1s22s22p4. Во внешнем слое у этого атома находятся 6 электронов 2s22p4. Значения их квантовых чисел приведены в таблице.
| № электрона | n | l | ml | ms |
| 1 | 2 | 0 | 0 | +1/2 |
| 2 | 2 | 0 | 0 | –1/2 |
| 3 | 2 | 1 | 1 | +1/2 |
| 4 | 2 | 1 | 0 | +1/2 |
| 5 | 2 | 1 | –1 | +1/2 |
| 6 | 2 | 1 | 1 | –1/2 |
Задача 3. Охарактеризуйте квантовыми числами пять электронов, находящихся в состоянии 4d. Ответ представьте в виде таблицы.
Решение. Согласно правилу Хунда электроны в квантовых ячейках располагаются следующим образом:
![]()
Значения главного, побочного и спинового квантовых чисел у электронов одинаковы и равны n=4, l=2, ms=+1/2. Рассматриваемые электроны отличаются значениями квантовых чисел ml.
| № электрона | n | l | ml | ms |
| 1 | 4 | 2 | 2 | +1/2 |
| 2 | 4 | 2 | 1 | +1/2 |
| 3 | 4 | 2 | 0 | +1/2 |
| 4 | 4 | 2 | –1 | +1/2 |
| 5 | 4 | 2 | –2 | +1/2 |
Задача 4. Рассчитайте максимальное число электронов в электронном слое с n = 4.
Решение. Максимальное число электронов, обладающих данным значением главного квантового числа, рассчитываем по формуле (2). Следовательно, в третьем энергетическом уровне может быть не более 32 электронов.
Задача 5. Рассчитайте максимальное число электронов в электронной оболочке с l = 3.
Решение:
Максимальное число электронов в оболочке определяется выражением (1). Таким образом, максимальное число электронов в электронной оболочке с l = 3 равно 14.
Задачи для самостоятельного решения
1. Охарактеризуйте квантовыми числами электроны атома бора в основном состоянии. Ответ представьте в виде таблицы:
| № электрона | n | l | ml | ms |
| 1 | ? | ? | ? | ? |
| 2 | ? | ? | ? | ? |
| 3 | ? | ? | ? | ? |
| 4 | ? | ? | ? | ? |
| 5 | ? | ? | ? | ? |
| № электрона | n | l | ml | ms |
| 1 | 1 | 0 | 0 | +1/2 |
| 2 | 1 | 0 | 0 | –1/2 |
| 3 | 2 | 0 | 0 | +1/2 |
| 4 | 2 | 0 | 0 | –1/2 |
| 5 | 2 | 1 | 1 | +1/2 |
2. Охарактеризуйте квантовыми числами d-электроны атома железа в основном состоянии. Ответ представьте в виде таблиц:
Расположение 3d-электронов атома железа на орбиталях:
| ? | ? | ? | ? | ? |
Значения квантовых чисел этих электронов:
| № электрона | n | l | ml | ms |
| 1 | ? | ? | ? | ? |
| 2 | ? | ? | ? | ? |
| 3 | ? | ? | ? | ? |
| 4 | ? | ? | ? | ? |
| 5 | ? | ? | ? | ? |
| 6 | ? | ? | ? | ? |
Шесть 3d-электронов атома железа располагаются на орбиталях следующим образом
![]()
Квантовые числа этих электронов приведены в таблице
| № электрона | n | l | ml | ms |
| 1 | 3 | 2 | 2 | +1/2 |
| 2 | 3 | 2 | 1 | +1/2 |
| 3 | 3 | 2 | 0 | +1/2 |
| 4 | 3 | 2 | — 1 | +1/2 |
| 5 | 3 | 2 | — 2 | +1/2 |
| 6 | 3 | 2 | 2 | — 1/2 |
3. Каковы возможные значения магнитного квантового числа ml, если орбитальное квантовое число l = 3?
Ответ: ml = +3; +2; +1; 0, — 1, — 2, — 3.
4. Охарактеризуйте квантовыми числами находящиеся во втором электронном слое электроны:
![]()
![]()
Ответ представьте в виде таблицы:
| № электрона | n | l | ml | ms |
| 1 | ? | ? | ? | ? |
| 2 | ? | ? | ? | ? |
| 3 | ? | ? | ? | ? |
| 4 | ? | ? | ? | ? |
| 5 | ? | ? | ? | ? |
| 6 | ? | ? | ? | ? |
| 7 | ? | ? | ? | ? |
Ответ: Электронная конфигурация 2s22p5. Главное квантовое число для всех электронов равно 2. Для s электронов l = 0, для р-электронов l = 1.
| № электрона | n | l | ml | ms |
| 1 | 2 | 0 | 0 | +1/2 |
| 2 | 2 |
0 |
0 | — 1/2 |
| 3 | 2 | 1 | 1 | +1/2 |
| 4 | 2 | 1 | 0 | +1/2 |
| 5 | 2 | 1 | — 1 | +1/2 |
| 6 | 2 | 1 | 1 | — 1/2 |
| 7 | 2 | 1 | 0 |
— 1/2 |
5. Определите максимальное число электронов на электронном слое, для которого главное квантовое число n = 6.
6. Определите максимальное число электронов на электронной оболочке, для которой побочное квантовое число l = 4.
7. Определите максимальное число электронов на третьем слое.
8. Определите максимальное число электронов на 5d электронной оболочке.
9. Какие значения может принимать орбитальное (побочное) квантовое число l?
Олег Лебедь
Эксперт по предмету «Химия»
Задать вопрос автору статьи
Введение
Состояние каждого электрона в атоме описывается волновой функцией, которая называется атомной орбиталью (или уровнем) и характеризуется тремя квантовыми числами. Соответствующие волновые функции выводятся из уравнения Шредингера и должны удовлетворять следующим требованиям: непрерывность, однозначность и конечность каждой волновой функции. При нарушении хотя бы одного из этих требований волновая функция оказывается непригодной для описания состояния электронов в атоме. Следовательно, дискретность энергетических состояний, в которых могут находиться электроны в атоме, является прямым следствием уравнения Шредингера. То же касается и трех квантовых чисел.
Главное квантовое число
Главное квантовое число может принимать любое целочисленное значение:
Но атомы известных в настоящее время элементов в стационарном состоянии (т.е. невозбужденные) не содержат электроны, для описания которых необходимы были бы атомные орбитали (уровни) с $n > 7$. Поэтому, в общем случае, реальным верхним пределом изменения главного квантового числа является значение $7$. Главное квантовое число характеризует энергию электрона на соответствующей орбитали. Или, проще говоря, степень удаленности данной орбитали от ядра атома (рис. 1). Чем меньше $n$, тем больше энергия связи электрона с ядром, т.е. тем большее, при прочих равных условиях, количество энергии требуется для удаления этого электрона из атома (эта энергия называется энергией ионизации).
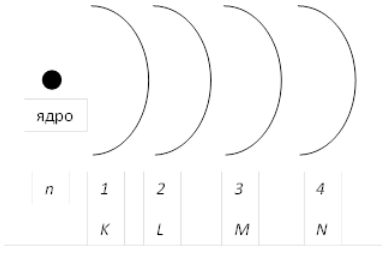
Рисунок 1. Схема раположений орбиталей атома
Забегая вперед, стоит сказать, что иногда для краткости записи электронной конфигурации атома вместо главного квантового числа используется буквенное обозначение соответствующих орбиталей (рис. 1): $K (n = 1)$, $L (n = 2)$, $M (n = 3)$, $N (n = 4)$, и так далее по алфавиту.
Орбитальное квантовое число
Орбитальное квантовое число $l$ может принимать значения от $0 до(n – 1)$:
Таким образом, $l$ для первых четырех значений главного квантового числа $n$ принимает следующие значения:

Рисунок 2.
«Квантование» 👇
Орбитальное квантовое число определяет форму соответствующего электронного облака (рис. 4). В записи электронной конфигурации атома оно обозначается по первым буквам английских наименований соответствующих спектральных линий $(sharp – s$, $principal – p$, $diffuse – d$, $fundamental – f$):

Рисунок 3.
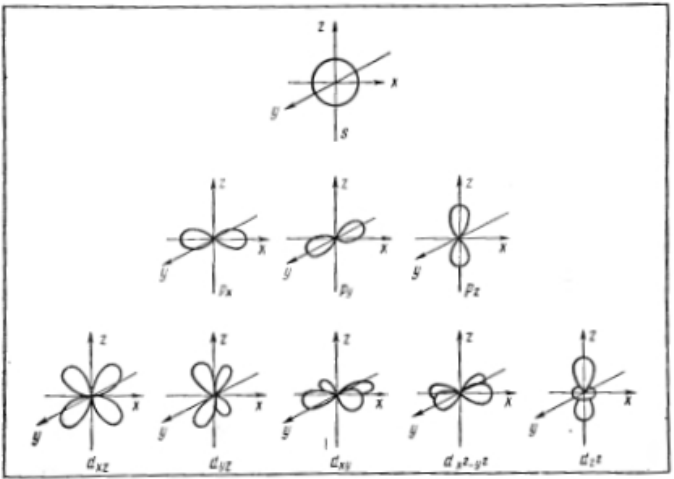
Рисунок 4. Формы электронных облаков атомных $s-$, $p-$, $d-$ орбиталей и их пространственное расположение
Таким образом, для каждого значения $n$ возможны строго определенные (по количеству и характеру) атомные орбитали (подуровни):
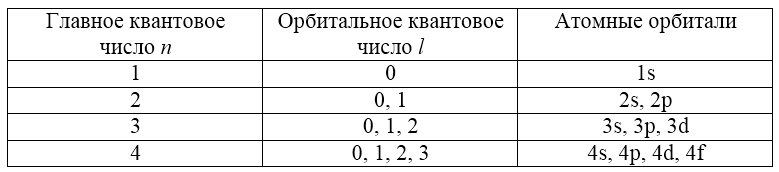
Рисунок 5.
Причем значения энергии электронов на соответствующих орбиталях таковы, что подуровень $4s$ расположен ближе к ядру, чем $3d$. Это правило пригодится при решении задач на составление электронных конфигураций атомов.
Магнитное квантовое число
Магнитное квантовое число m может принимать любые целочисленные значения от $+l$ до $-l$, включая $0$, и характеризует расположение соответствующей орбитали в пространстве атома:
Количество значений магнитного квантового числа определяется значением орбитального квантового числа $l$ и равно $(2l + 1)$:

Рисунок 6.

При заданных значениях $n$ и $l$ все возможные атомные орбитали независимо от значений m имеют одинаковую энергию, т.е. являются вырожденными. Кратность вырождения определяется числом атомных орбиталей с одинаковой энергией, т.е. числом значений m при заданном значении $l$. Таким образом, $s$-состояние электрона является вырожденным ($m = 0$), $p$-состояние – трехкратновырожденным ($m = 1$, $0$, $-1$), $d$- состояние – пятикратновырожденным, и.т.д.
Физический смысл магнитного квантового числа схематично представлен на рис. 7, где клетки – это, по сути, места, которые могут быть заняты электронами.
Спиновое квантовое число
Кроме всего прочего, электроны в атоме отличаются собственным моментом количества движения, который условно можно представить как вращение вокруг собственной оси. Это вращение характеризуется спиновым квантовым числом s, которое может иметь лишь два значения $+1/2$ и $-1/2$ (условно говоря, вращение по часовой стрелке и против часовой стрелки).
Примеры решения типовых задач
Пример 1
Записать электронную конфигурацию атома гелия в основном состоянии.
Решение. Главное квантовое число $n = 1$, орбитальное квантовое число $l = n – 1 = 0$, что соответствует s-состоянию. Таким образом, электронная конфигурация атома гелия $1s^2$, где индекс $2$ указывает на число электронов, занимающих орбиталь $1s$.
Пример 2
Записать электронную конфигурацию атома железа с порядковым номером $26$.
Решение. В соответствии с порядком заполнения атомных орбиталей имеем $1s^22s^22p^63s^23p^64s^23d^6$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме






![{displaystyle [S_{i},S_{j}]=i hbar epsilon _{ijk} S_{k} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0a5b23972acdc47ffb28ee19015a0fc4f180d97)
![{displaystyle left[S_{i},S^{2}right]=0 }](https://wikimedia.org/api/rest_v1/media/math/render/svg/12f311610f445def9662755454c783f4fd0916af)



