Все курсы > Анализ и обработка данных > Занятие 6 (часть 1)
В реальных данных встречаются не только ошибки, но и пропущенные значения (missing values). При этом не все алгоритмы машинного обучения умеют работать с данными, в которых есть пропуски.
Вначале немного теории.
Типы пропусков
В 1976 году математик Дональд Рубин (Donald B. Rubin) предложил следующую классификацию пропущенных значений.
Полностью случайные пропуски
Полностью случайные пропуски (missing completely at random, MCAR) предполагают, что вероятность появления пропуска никак не связана с данными. Такие пропуски возникают, например, если измерительный прибор неисправен и случайным образом не записал часть наблюдений, или если один из образцов крови, изучаемых в лаборатории, оказался поврежден и по этой причине его характеристики выпали из исследования.
Интересно посмотреть на эту классификацию с точки зрения условной вероятности. Введем обозначения.
- П — пропуски в данных (missing data)
- Н — наблюдаемые значения, то есть те данные, которые мы собрали (observed data)
- О — отсутствующие значения, или те данные, которые собрать не удалось (unobserved data)
Тогда полностью случайные пропуски можно выразить следующим образом.
P (П | Н, О) = константа
Какими бы ни были наблюдаемые и отсутствующие значения, вероятность пропусков всегда одинакова, так как они, эти пропуски, полностью случайны.
Эту же идею можно выразить и так.
P (П | Н, О) = P (П)
Считается, что в реальности наблюдать полностью случайные пропущенные значения очень сложно. Какие-либо закономерности (то есть связь с наблюдаемыми или отсутствующими значениями) все равно существуют. Это приводит нас ко второй категории пропусков.
Случайные пропуски
Случайные пропуски (missing at random, MAR) — вероятность появления пропуска зависит от некоторой известной нам переменной. Например, отсутствие ответа на определенный вопрос анкеты может зависеть от возраста респондента. Молодые охотнее отвечают на вопрос, люди более пожилого возраста скорее избегают ответа.
Если мы знаем об этой особенности, то можем, правильно собирая и корректируя данные, добиться большей объективности.
Вероятность появления таких пропусков с учетом наблюдаемых и отсутствующих значений можно представить как функцию от наблюдаемых значений.
Р (П | Н, О) = $f$(Н)
В нашем примере, такой функцией является функция возраста респондентов, $f$(возраст).
Неслучайные пропуски
Неслучайные пропуски (missing not at random, MNAR) — вероятность появления пропуска зависит, в том числе, от фактора, о котором мы ничего не знаем. Например, у весов может быть верхний предел измерения и любой образец выше этого предела автоматически не записывается. В опросах общественного мнения MNAR возникает, когда люди с более активной жизненной позицией (переменная, которую мы не измеряем) чаще дают ответы на вопросы интервьюера.
В таком случае условная вероятность пропусков зависит от функции, которая может учитывать как наблюдаемые, так и, что более важно, отсутствующие значения.
Р (П | Н, О) = $f$(Н, O)
Проблема опять же в том, что мы не знаем, что это за функция, а значит не знаем как именно появились пропущенные значения. Теперь перейдем к практике.
Откроем ноутбук к этому занятию⧉
Выявление пропусков
В первую очередь подготовим необходимые данные. Сегодня мы снова будем работать с датасетом «Титаник».
|
# импортируем датасет Титаник titanic = pd.read_csv(‘/content/train.csv’) |
Базовые методы
Метод .info()
Рассмотрим базовые методы обнаружения пропусков. В первую очередь, можно использовать метод .info(). Этот метод соотносит максимальное количество записей в датафрейме с количеством записей в каждом столбце.
|
# применим этот метод к нашему датасету titanic.info() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
<class ‘pandas.core.frame.DataFrame’> RangeIndex: 891 entries, 0 to 890 Data columns (total 12 columns): # Column Non-Null Count Dtype — —— ————– —– 0 PassengerId 891 non-null int64 1 Survived 891 non-null int64 2 Pclass 891 non-null int64 3 Name 891 non-null object 4 Sex 891 non-null object 5 Age 714 non-null float64 6 SibSp 891 non-null int64 7 Parch 891 non-null int64 8 Ticket 891 non-null object 9 Fare 891 non-null float64 10 Cabin 204 non-null object 11 Embarked 889 non-null object dtypes: float64(2), int64(5), object(5) memory usage: 83.7+ KB |
Как мы видим, всего в датасете может быть до 891 записи. При этом в столбцах Age, Cabin и Embarked записей меньше, а значит есть пропуски.
Также обратите внимание на одну особенность Питона. Столбец Age логично преобразовать в тип int, однако из-за того, что в нем есть пропущенные значения, сделать этого не получится. Для количественных данных с пропусками доступен только тип float.
|
# попробуем преобразовать Age в int titanic.Age.astype(‘int’) |
Конечно, если столбцов много, результат метода .info() становится трудно воспринимать.
Методы .isna() и .sum()
Можно последовательно использовать методы .isna() и .sum().
|
# .isna() выдает True или 1, если есть пропуск, .sum() суммирует единицы по столбцам titanic.isna().sum() |
|
PassengerId 0 Survived 0 Pclass 0 Name 0 Sex 0 Age 177 SibSp 0 Parch 0 Ticket 0 Fare 0 Cabin 687 Embarked 2 dtype: int64 |
Процент пропущенных значений
Также не сложно посчитать процент пропущенных значений.
|
# для этого разделим сумму пропусков в каждом столбце на количество наблюдений, # округлим результат и умножим его на 100 (titanic.isna().sum() / len(titanic)).round(4) * 100 |
|
PassengerId 0.00 Survived 0.00 Pclass 0.00 Name 0.00 Sex 0.00 Age 19.87 SibSp 0.00 Parch 0.00 Ticket 0.00 Fare 0.00 Cabin 77.10 Embarked 0.22 dtype: float64 |
Теперь нам гораздо проще оценить «масштаб бедствия».
Библиотека missingno
Библиотека missingno предоставляет удобные средства для визуальной оценки пропусков.
|
# импортируем библиотеку missingno с псевдонимом msno import missingno as msno |
Кроме того, для повышения качества визуализации сделаем стиль графиков seaborn основным.
В первую очередь на пропуски можно посмотреть с помощью столбчатой диаграммы (функция msno.bar()).
На этом графике мы четко видим процент (слева) и абсолютное количество (справа и сверху) заполненных значений.
При этом столбчатая диаграмма не дает информации о том, где именно больше всего пропущенных значений. Другими словами, есть ли в пропусках какая-то закономерность или нет.
Для этого подойдет матрица пропущенных значений (функция msno.matrix()).
Распределение пропущенных значений в датасете «Титаник» выглядит случайным, закономерностью были бы пропуски, например, только в первой половине наблюдений.
При этом обратите внимание, мы говорим про случайность внутри столбцов с пропусками. О том, зависят ли пропуски от значений других столбцов, мы поговорим ниже.
Матрица корреляции пропущенных значений
Еще один интересный инструмент — матрица корреляции пропущенных значений (nullity correlation matrix).
По сути, она показывает насколько сильно присутствие или отсутствие значений одного признака влияет на присутствие значений другого.
Если мы знаем, в каких столбцах есть пропуски, то можем просто последовательно применить к ним методы .isnull() и .corr().
|
titanic[[‘Age’, ‘Cabin’, ‘Embarked’]].isnull().corr() |
В тех случаях, когда мы не знаем, в каких столбцах есть пропущенные значения, то можем использовать код ниже (взят из документации⧉ к библиотеке).
|
df = titanic.iloc[:, [i for i, n in enumerate(np.var(titanic.isnull(), axis = ‘rows’)) if n > 0]] df.isnull().corr() |
Значения корреляции могут быть от −1 (если значения одного признака присутствуют, значения другого — отсутствуют) до 1 (если присутствуют значения одного признака, то присутствуют значения и другого). Более подробно про корреляцию мы поговорим при изучении взаимосвязи переменных.
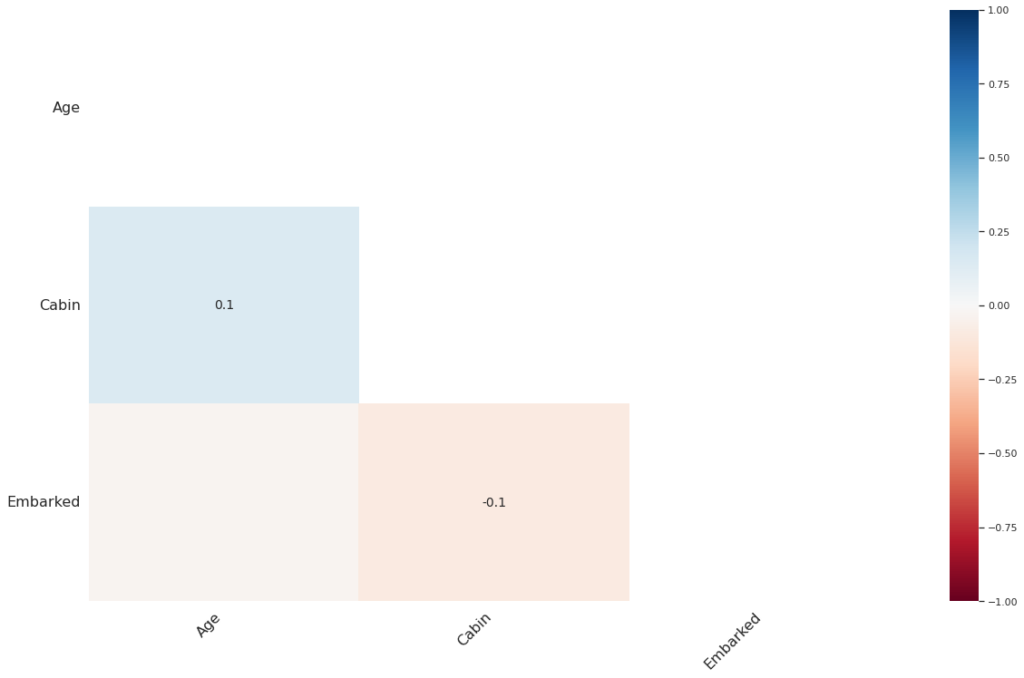
Визуально, корреляцию пропущенных значений можно представить с помощью тепловой карты (heatmap). Для этого есть функция msno.heatmap().
Мы видим, что корреляция пропусков близка к нулю для всех признаков. Другими словами, пропуски одного признака не влияют на пропуски другого.
Теперь рассмотрим стратегии работы с пропусками. По большому счету их две: удаление и заполнение. У обоих подходов есть свои достоинства и недостатки.
Удаление пропусков
Во многих случаях удаление пропусков (missing values deletion) может оказаться неплохим решением, потому что в этом случае мы не «портим» данные.
Удаление пропущенных значений хорошо работает (позволяет качественно обучить алгоритм), если мы считаем, что пропуски носят полностью случайный характер (MCAR). Единственным ограничением в этом случае будет достаточность данных для обучения после удаления пропусков.
Удаление строк
Удаление строк (deleting rows или listwise deletion, также называется анализом полных наблюдений, complete case analysis), в которых есть пропуски — наиболее очевидный подход к работе с пропущенными значениями. Рассмотрим этот способ на практике.
В датасете «Титаник» только два пропущенных значения в столбце Embarked. Удалим соответствующие строки.
|
# удаление строк обозначим через axis = ‘index’ # subset = [‘Embarked’] говорит о том, что мы ищем пропуски только в столбце Embarked titanic.dropna(axis = ‘index’, subset = [‘Embarked’], inplace = True) |
|
# убедимся, что в Embarked действительно не осталось пропусков titanic.Embarked.isna().sum() |
Удаление строк не стоит применять, если пропущенные значения зависят от какого-либо неизвестного нам фактора (MNAR). Например, если на вопрос анкеты не склонны отвечать менее активные граждане, удаление строк с пропусками оставит в данных только определенную группу населения (появится bias, искажение) и алгоритм не будет репрезентативен.
Кроме того, если в одном из столбцов большой процент пропусков, построчное удаление просто оставит нас без данных. В датасете «Титаник» это относится к столбцу Cabin. В этом случае, если мы выбираем стратегию удаления данных, разумнее удалить сам столбец.
Удаление столбцов
Удаление столбцов (column deletion) несложно выполнить с помощью метода .drop(). Например, удалим столбец Cabin, в котором более 77 процентов пропусков.
|
# передадим в параметр columns тот столбец, который хотим удалить titanic.drop(columns = [‘Cabin’], inplace = True) |
|
# убедимся, что такого столбца больше нет titanic.columns |
|
Index([‘PassengerId’, ‘Survived’, ‘Pclass’, ‘Name’, ‘Sex’, ‘Age’, ‘SibSp’, ‘Parch’, ‘Ticket’, ‘Fare’, ‘Embarked’], dtype=’object’) |
Попарное удаление пропусков
Попарное удаление пропусков (pairwise deletion или, как еще говорят, анализ доступных данных, available case analysis) проще понять, если представить, что мы не удаляем пропуски, а игнорируем их или используем только доступные значения.
Расчет метрик. Принципа игнорирования пропусков придерживаются очень многие функции и методы в Питоне. Например, используем методы .groupby() и .count() для того, чтобы посчитать количество мужчин и женщин на борту и выведем данные по каждому из оставшихся признаков.
|
sex_g = titanic.groupby(‘Sex’).count() sex_g |
Как вы видите, если верить столбцу Age, пассажиров на борту меньше, чем если руководствоваться данными, например, столбца PassengerId.
|
# сравним количество пассажиров в столбце Age и столбце PassengerId sex_g[‘PassengerId’].sum(), sex_g[‘Age’].sum() |
Это значит, что метод .count() игнорировал пропуски. То же самое касается, например, метода .mean() или метода .corr().
|
# метод .mean() игнорирует пропуски и не выдает ошибки titanic[‘Age’].mean() |
|
# то же можно сказать про метод .corr() titanic[[‘Age’, ‘Fare’]].corr() |
Построение модели. Преимуществом при построении модели будет то, что мы по максимуму используем имеющиеся данные. Например, у нас есть два признака, и в первом есть пропуск у четвертого наблюдения (с индексом «три»), а во втором — у пятого.

Если мы построим первую модель (A) на основе признака 1 (и соответственно удалим только четвертое наблюдение), а вторую (B) — на основе признака 2 (удалив пятое), то избежим необходимости каждый раз удалять два наблюдения и терять информацию.
Недостаток заключается в том, что эти модели по сути построены на разных данных (в реальности мы конечно удалим больше одного наблюдения в каждом случае), а значит сравнение моделей будет некорректным.
Заполнение пропусков
Как уже было сказано выше, удаление пропусков не всегда возможно. В этом случае прибегают к заполнению пропусков (missing values imputation). Подготовим данные.
|
# еще раз загрузим датасет “Титаник”, в котором снова будут пропущенные значения titanic = pd.read_csv(‘/content/train.csv’) # возьмем лишь некоторые из столбцов titanic = titanic[[‘Pclass’, ‘Sex’, ‘SibSp’, ‘Parch’, ‘Fare’, ‘Age’, ‘Embarked’]] # закодируем столбец Sex с помощью числовых значений map_dict = {‘male’ : 0, ‘female’ : 1} titanic[‘Sex’] = titanic[‘Sex’].map(map_dict) # посмотрим на результат titanic.head() |
Одномерные методы
Одномерные методы (Single Imputation) — это заполнение с использованием данных одного столбца. Другими словами, чтобы заполнить пропуски мы берем данные того же признака.
Заполнение константой
Количественные данные. Самый простой способ работы с пропусками в количественных данных — заполнить пропуски константой. Например, нулем (подходит для алгоритмов, чувствительных к масштабу признаков).
Воспользуемся методом .fillna().
|
# вначале сделаем копию датасета fillna_const = titanic.copy() # заполним пропуски в столбце Age нулями, передав методу .fillna() словарь, # где ключами будут названия столбцов, а значениями – константы для заполнения пропусков fillna_const.fillna({‘Age’ : 0}, inplace = True) |
Заполнение константой позволяет не сокращать размер выборки, однако может внести системную ошибку в данные. Сравним медианный возраст до и после заполнения пропусков нулями.
|
titanic.Age.median(), fillna_const.Age.median() |
При использовании алгоримов, основанных на деревьях решений, пропуски можно заполнить значением, не встречающимся в выборке. Если все значения признака положительные, то пропуски заполняются, например, −1.
Категориальные данные. Для категориальных признаков в некоторых случаях можно провести дополнительное исследование. В частности, в датасете «Титаник» есть два пассажира с неизвестным портом посадки.
|
# найдем пассажиров с неизвестным портом посадки # для этого создадим маску по столбцу Embarked и применим ее к исходным данным missing_embarked = pd.read_csv(‘/content/train.csv’) missing_embarked[missing_embarked.Embarked.isnull()] |
При этом в Интернете⧉ можно найти информацию о том, что обе пассажирки (Mrs Stone и ее служанка Amelie Icard) зашли на борт в порту Southampton (S).
Для заполнения строковым значением также подойдет метод .fillna().
|
# метод .fillna() можно применить к одному столбцу # два пропущенных значения в столбце Embarked заполним буквой S (Southampton) fillna_const.Embarked.fillna(‘S’, inplace = True) |
Конечно, такая информация о пропущенных значениях бывает доступна далеко не всегда.
|
# убедимся, что в столбцах Age и Embarked не осталось пропущенных значений fillna_const[[‘Age’, ‘Embarked’]].isna().sum() |
|
Age 0 Embarked 0 dtype: int64 |
Вместо метода .fillna() можно использовать инструмент библиотеки sklearn, который называется SimpleImputer. Создадим объект этого класса и обучим модель.
|
# сделаем копию датасета const_imputer = titanic.copy() # импортируем класс SimpleImputer из модуля impute библиотеки sklearn from sklearn.impute import SimpleImputer # создадим объект этого класса, указав, # что мы будем заполнять константой strategy = ‘constant’, а именно нулем fill_value = 0 imp_const = SimpleImputer(strategy = ‘constant’, fill_value = 0) # и обучим модель на столбце Age # мы используем двойные скобки, потому что метод .fit() на вход принимает двумерный массив imp_const.fit(const_imputer[[‘Age’]]) |
|
SimpleImputer(fill_value=0, strategy=’constant’) |
Теперь применим эту модель для заполнения пропусков.
|
# также используем двойные скобки с методом .transform() const_imputer[‘Age’] = imp_const.transform(const_imputer[[‘Age’]]) # убедимся, что пропусков не осталось и посчитаем количество нулевых значений const_imputer.Age.isna().sum(), (const_imputer[‘Age’] == 0).sum() |
В конце раздела мы проведем сравнение эффективности различных методов заполнения пропусков и столбец Embarked нам уже не понадобится.
|
# удалим его const_imputer.drop(columns = [‘Embarked’], inplace = True) # и посмотрим на размер получившегося датафрейма const_imputer.shape |
|
# посмотрим на результат const_imputer.head(3) |
Заполнение средним арифметическим или медианой
Количественные данные можно заполнить средним арифметическим или медианой (Statistical Imputation). Вначале воспольуемся методом .fillna().
|
# сделаем копию датафрейма fillna_median = titanic.copy() # заполним пропуски в столбце Age медианным значением возраста, # можно заполнить и средним арифметическим через метод .mean() fillna_median.Age.fillna(fillna_median.Age.median(), inplace = True) # убедимся, что пропусков не осталось fillna_median.Age.isna().sum() |
У такого простого и понятного подхода тем не менее есть ряд недостатков.
- Во-первых, когда в данных появляется большое количество одинаковых близких к среднему значений, мы снижаем ценную вариативность в данных.
- Кроме того, такое заполнение пропусков может быть некорректно. Ниже мы рассмотрим пример данных кредитного скоринга, где, если заполнить пропуски в столбце «Стаж» средним значением или медианой, молодой сотрудник может получить больший стаж, чем у него есть на самом деле, а сотрудник в возрасте, меньший.
Еще раз обратимся к столбцу Age в датасете «Титаник» и рассмотрим распределение возраста до и после заполнения медианой.
|
# изменим размер последующих графиков sns.set(rc = {‘figure.figsize’ : (10, 6)}) # скопируем датафрейм median_imputer = titanic.copy() # посмотрим на распределение возраста до заполнения пропусков sns.histplot(median_imputer[‘Age’], bins = 20) plt.title(‘Распределение Age до заполнения пропусков’); |
Посмотрим на среднее арифметическое и медиану.
|
median_imputer[‘Age’].mean().round(1), median_imputer[‘Age’].median() |
Используем класс SimpleImputer библиотеки sklearn для заполнения пропусков этим медианным значением.
|
# создадим объект класса SimpleImputer с параметром strategy = ‘median’ # (для заполнения средним арифметическим используйте strategy = ‘mean’) imp_median = SimpleImputer(strategy = ‘median’) # применим метод .fit_transform() для одновременного обучения модели и заполнения пропусков median_imputer[‘Age’] = imp_median.fit_transform(median_imputer[[‘Age’]]) # убедимся, что пропущенных значений не осталось median_imputer.Age.isna().sum() |
Посмотрим на распределение возраста и его медианное значение после заполнения пропусков.
|
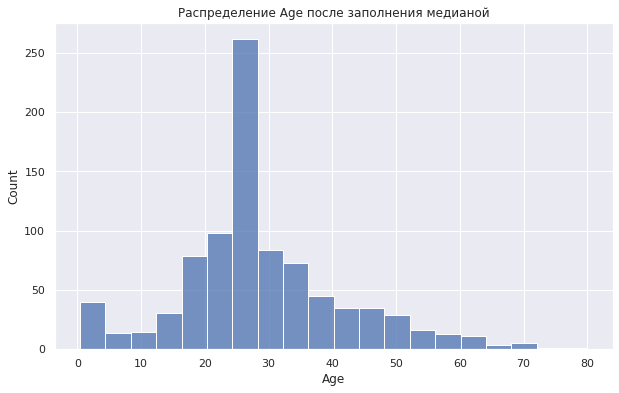
# посмотрим на распределение после заполнения пропусков sns.histplot(median_imputer[‘Age’], bins = 20) plt.title(‘Распределение Age после заполнения медианой’); |
|
# посмотрим на метрики после заполнения медианой median_imputer[‘Age’].mean().round(1), median_imputer[‘Age’].median() |
|
# столбец Embarked нам опять же не понадобится median_imputer.drop(columns = [‘Embarked’], inplace = True) # посмотрим на размеры получившегося датафрейма median_imputer.shape |
Как мы видим, распределение притерпело существенные изменения. В частности, у нас появилось очень много медианных значений, которые доминируют в распределении возраста.
Заполнение внутригрупповым значением
Справиться с этой проблемой можно, в частности, через более сложный способ заполнения пропусков количественного признака — вначале разбить пассажиров на категории (bins), например, по полу или классу каюты, вычислить медианное значение для каждой категории и только потом заполнять им пропущенные значения.
Выполним группировку с помощью метода .groupby() и найдем медианный возраст каждой группы.
|
# скопируем датафрейм median_imputer_bins = titanic.copy() |
|
# сгруппируем пассажиров по полу и классу каюты Age_bins = median_imputer_bins.groupby([‘Sex’, ‘Pclass’]) # найдем медианный возраст с учетом получившихся групп Age_bins.Age.median() |
|
Sex Pclass 0 1 40.0 2 30.0 3 25.0 1 1 35.0 2 28.0 3 21.5 Name: Age, dtype: float64 |
Применим lambda-функцию к объекту SeriesGroupBy и заменим пропуски соответствующим медианным значением.
|
# объект SeriesGroupBy находится в переменной Age_bins.Age, # применим к нему lambda-функцию через метод .apply() median_imputer_bins.Age = Age_bins.Age.apply(lambda x: x.fillna(x.median())) |
Убедимся, что в столбце Age не осталось пропусков.
|
# проверим пропуски в столбце Age median_imputer_bins.Age.isna().sum() |
Посмотрим на распределение.
|
sns.histplot(median_imputer_bins[‘Age’], bins = 20) plt.title(‘Распределение Age после заполнения внутригрупповой медианой’); |
Мы видим, что медианное значение доминирует гораздо меньше.
|
# столбец Embarked нам не понадобится median_imputer_bins.drop(columns = [‘Embarked’], inplace = True) # посмотрим на размеры получившегося датафрейма median_imputer_bins.shape |
Рассмотрим другие методы.
Заполнение наиболее частотным значением
Для заполнения пропусков в категориальных данных подойдет метод заполнения наиболее часто встречающимся значением (модой). Если пропусков немного, этот метод вполне обоснован. При большом количестве пропусков, можно попробовать создать на их основе новую категорию.
Подготовим данные и посмотрим на распределение категорий в столбце Embarked.
|
# скопируем датафрейм titanic_mode = titanic.copy() # посмотрим на распределение пассажиров по порту посадки до заполнения пропусков titanic_mode.groupby(‘Embarked’)[‘Survived’].count() |
|
Embarked C 168 Q 77 S 644 Name: Survived, dtype: int64 |
Модой будет порт Southampton (что одновременно является верным для заполнения пропусков значением, однако, опять же, в большинстве случаев мы не можем этого знать наверняка).
Воспользуемся классом SimpleImputer для заполнения пропусков.
|
# создадим объект класса SimpleImputer с параметром strategy = ‘most_frequent’ imp_most_freq = SimpleImputer(strategy = ‘most_frequent’) # применим метод .fit_transform() к столбцу Embarked titanic_mode[‘Embarked’] = imp_most_freq.fit_transform(titanic_mode[[‘Embarked’]]) # убедимся, что пропусков не осталось titanic_mode.Embarked.isna().sum() |
Проверим результат.
|
# количество пассажиров в категории S должно увеличиться на два titanic_mode.groupby(‘Embarked’)[‘Survived’].count() |
|
Embarked C 168 Q 77 S 646 Name: PassengerId, dtype: int64 |
Примечание. Приведу еще один простой способ найти моду. Его можно использовать совместно с методом .fillna() для заполнения пропусков.
|
titanic.Embarked.value_counts().index[0] |
В случае если у нас есть существенное количество пропусков в категориальной переменной мы можем задуматься над созданием отдельной категории для пропущенных значений.
Очевидно, каким бы одномерным методом мы ни воспользовались, мы всегда ограничены данными одного признака.
|
# для работы с последующими методами столбец Embarked нам уже не нужен titanic.drop(columns = [‘Embarked’], inplace = True) |
Перейдем ко второй части занятия.
В одной из таблиц сохраняются заранее сгенерированные серийные номера (последовательности).
При сохранении этих серийных номеров, некоторые из них могут быть “потеряны”, т.е образуются пропуски. Моя задача, найти эти пропуски в сохранённых серийных номерах.
Например, в таблице последовательность чисел: (7001, 7002, 7004, 7005, 7006, 7010).
В этой последовательности, с 7001 до 7010, отсутствуют (7003, 7007, 7008, 7009).
Есть ли в БД какая-то встроенная функция, которая найдёт эти пропуски чисел? Если нет, то какой алгоритм решения задачи?
Свободный перевод How to check any missing number from a series of numbers? от участника @Samcoder
задан 14 июл 2020 в 16:25
1
Попробуйте так:
SELECT t1.n+1 as "From", MIN(t2.n)-1 as "To"
FROM testdata t1
JOIN testdata t2 ON t1.n < t2.n
GROUP BY t1.n
HAVING t1.n+1 < MIN(t2.n)
/
Результат для последовательности как в вопросе:
From To
---------- ----------
7003 7003
7007 7009
Свободный перевод ответа от участника @Patrick
ответ дан 14 июл 2020 в 16:39
0xdb0xdb
51.4k194 золотых знака56 серебряных знаков232 бронзовых знака
Решение, если граничные значения последовательности неизвестны:
with testdata as (
select column_value n
from sys.odciNumberList (7001, 7002, 7004, 7005, 7006, 7010)
)
select nmin-1+level missing
from (
select min (n) nmin, max (n) nmax
from testdata
) connect by level <= nmax-nmin+1
minus
select n from testdata
/
MISSING
----------
7003
7007
7008
7009
Свободный перевод ответа от участника @Rob van Wijk
ответ дан 14 июл 2020 в 16:25
0xdb0xdb
51.4k194 золотых знака56 серебряных знаков232 бронзовых знака
Учитывая, что заполнение коллекций почти всегда упорядочено, то есть, в первом элементе минимальное значение, а в последнем – максимальное, то на чистом PL/SQL решается так:
var rc refcursor
declare
nt1 numtab := numtab (7001, 7002, 7004, 7005, 7006, 7010);
nt2 numtab := numtab ();
res numtab;
begin
nt2.extend (nt1(nt1.last) - nt1(nt1.first) + 1);
for ix in 1 .. nt1(nt1.last) - nt1(nt1.first) + 1 loop
nt2 (ix) := nt1 (nt1.first) + ix -1; end loop;
res := nt2 multiset except nt1;
open :rc for select column_value missing from table (res);
end;
/
MISSING
----------
7003
7007
7008
7009
ответ дан 14 июл 2020 в 20:32
0xdb0xdb
51.4k194 золотых знака56 серебряных знаков232 бронзовых знака
В предыдущие дни проблемы в данных обычно заключались в том, что их больше, чем нужно: дубли или фейковые данные избыточны для анализа.
Важно! Если вы не сделали практику в теме «Data раскопки. Анализируем редкие значения», то предварительно требуется открыть решение задания предыдущего дня, скачав его ниже.
lgpРешение практического задания. День 9.lgp
Сегодня будет рассмотрена обратная проблема — пропуски, т.е. отсутствие данных. Их можно разделить на 2 вида:
- Отсутствие значений в полях;
- Пропуски строк в таблицах.
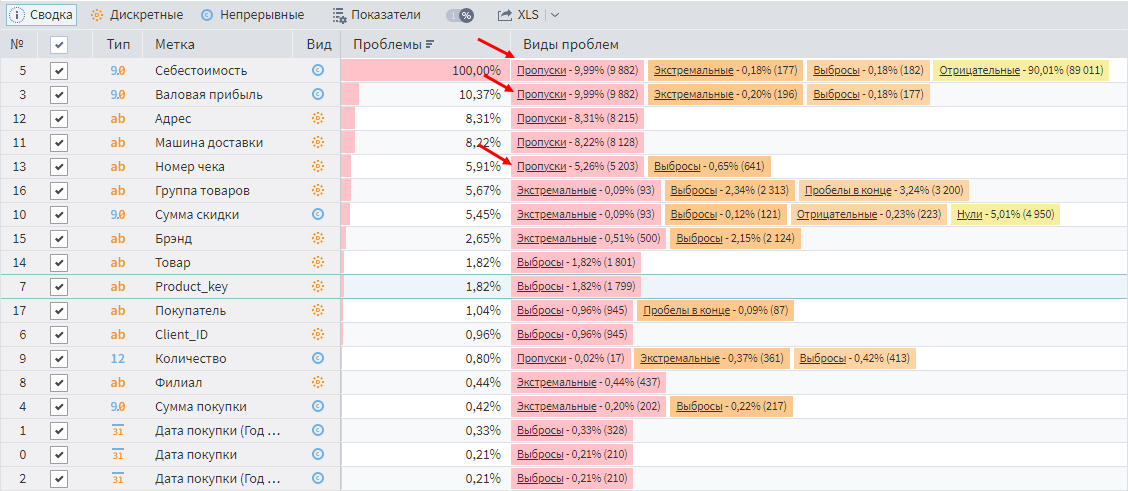
Первый тип проблем легко обнаружить с помощью визуализатора Качество данных. Если просмотреть данные по клиентским транзакциям, то наличие пропусков сразу бросится в глаза.
Пропуски в данных
Реакция на проблему зависит от целей анализа. Иногда пропуски можно игнорировать. Например, на отсутствие значений в полях адреса и машин доставки можно не обращать внимание, если не интересуют вопросы транспортировки.
А вот пропуски в себестоимости игнорировать нельзя. Особенно если учесть, что анализируется Валовая прибыль, являющаяся суммой между между Суммой продаж и Себестоимостью. Себестоимость задается отрицательной.
Если в арифметических расчетах имеется null-значение, то результат тоже будет пустым. Как следствие для некоторых записей валовая прибыль отсутствует, и данный показатель по всей базе получится заниженным.
Также стоит обратить внимание на пропуски в поле Номер чека. Оно используется для расчета количества транзакций, что, в свою очередь, учитывается при вычислении среднего чека. Таким образом, получается заниженное количество транзакций и завышенное значение среднего чека.
Возникновение пропусков в полях
Причин обычно две: технические проблемы или брак бизнес-процесса.
Технические причины
К возникновению пропусков в номере чека привела типичная техническая проблема. В компании используется контрольно-кассовое оборудование разных производителей. Данные с них попадают в единую базу. Часть оборудования формировала номер чека как число, а часть – как микс числа и текстовых символов.
При этом в консолидированной базе под хранение номера чека отведено числовое поле. В результате часть значений, которые удалось конвертировать в число, попали в базу, а часть — стала пустым (null) значением.
Ошибки бизнес-процесса
Еще одной частой причиной пропусков является человеческий фактор, усугубленный сложным бизнес-процессом.
Например, сотрудник, принимающий товар от поставщиков, должен прописывать его закупочную стоимость в учетной системе, но регулярно этого не делает. Причины могут быть разные: не успевает или забывает, лень, нет корректных данных на момент ввода, анализ себестоимости вне его зоны ответственности…
Поэтому контроль качества вводимых данных лучше всего автоматизировать. В частности, с забывчивостью можно бороться настройкой обязательных полей в учетных системах. Правда, это не спасает от фейковых данных, когда в обязательное поле Телефон вписывают +123456789.
Человеческий фактор нельзя игнорировать. Его влияние слишком велико. Значит, все, что может собираться и проверяться автоматически, должно быть автоматизировано:
- Контактные данные нужно перебрасывать из форм на сайтах.
- Обязательные поля должны контролироваться в момент ввода в учетной системе.
- Вносимые данные желательно оценивать на адекватность, например, выход за границы диапазонов.
- Поля типа телефонов или адресов необходимо нормализовать.
Далеко не всегда есть возможность исправить проблемы задним числом, например, заполнить пропущенные значения, поэтому борьбу за качество данных рекомендуется начинать на этапе их ввода.
Заполнение пропусков
Восстановление идентификаторов
Вначале продумаем, как заполнить пропуски в номерах чеков. В идеале хотелось бы восстановить реальную информацию из систем учета, но это не всегда возможно. Поэтому попробуем заполнить эти пропуски при помощи сценариев в Loginom.
Так как анализируются продажи оптовым клиентам, то можно отталкиваться от предположения, что каждому контрагенту в день осуществляется не более одной отгрузки. Если отгрузок несколько, то на практике довольно часто их объединяют в одну.
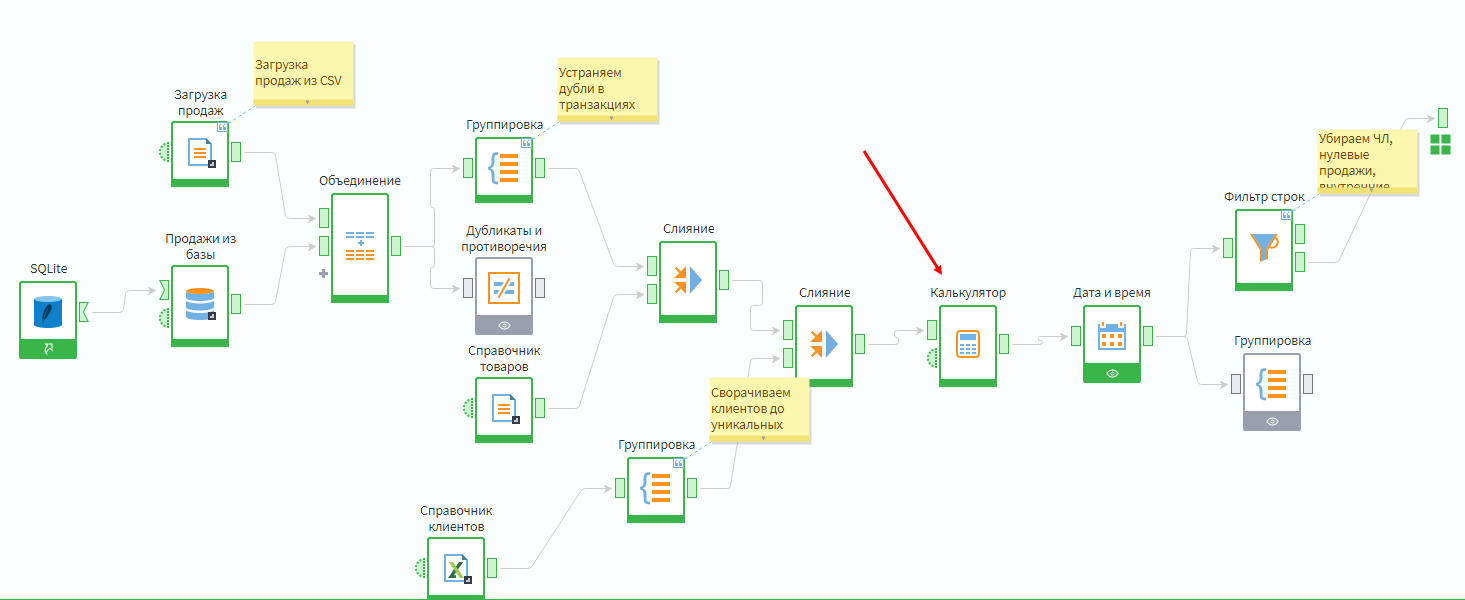
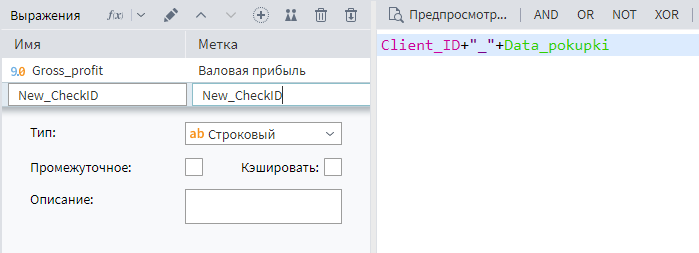
Следовательно, пустой идентификатор чека можно заменить на комбинацию полей Client_ID и Даты продажи. Это можно сделать, используя компонент Калькулятор в подмодели Продажи.
Необходимо добавить текстовое поле New_CheckID. В качестве формулы задать объединение двух полей через разделитель _.
Составные поля рекомендуется соединять через разделитель. Это не только повышает читаемость значения, но и позволяет избежать коллизий, например, когда соединение 11 и 1, дает такой же результат, как соединение 1 и 11.
Данное действие сформировало новое поле, а не заменило старое. Не хотелось бы теперь искать места по всему сценарию, где нужно внести исправления, чтобы все работало как надо.
Чтобы подменить значение одного поля другим, требуется настроить соответствующую связь на выходе из узла. Порядок действий следующий:
- Зайти в настройки выходного порта.
- Переключиться в режим отображения cвязи.
- Удалить в правой части выходное поле New_CheckID, т.к. оно не нужно в дальнейших расчетах.
- Удалить связь между полями Номер чека в калькуляторе и Номер чека на выходе из порта.
- Протянуть связь от New_CheckID из Калькулятора в поле Номер чека на выходе из порта.
Подробнее в видео:
;
После этих действий на выходном порту узла появится точка. Это значит, что в узле отключена автосинхронизация, и теперь перечень полей, выходящих из Калькулятора, управляется вручную. Так, если во входной таблице появится новое поле, то чтобы оно появилось на выходе, нужно будет его туда самостоятельно добавить.
Отключенная автосинхронизация
Восстановление себестоимости
Следующий вопрос — заполнение пропусков по полю Себестоимость.
Самое простое решение, приходящее в голову, — отфильтровать все записи с пустым значением данного поля. Проблема в том, что тогда исключится слишком много строк, что повлияет на другие показатели.
Если при анализе реальных данных отбрасывать все строки с пустыми значениями в любом поле, то скорее всего анализировать будет нечего. Пропуски в данных встречаются слишком часто.
Следовательно, надо каким-то образом «восстановить» цену закупки. Конечно, для этого придется принять некоторые разумные допущения. Они не смогут гарантировать 100% корректность, но позволят получить адекватный портрет клиента, чего в данном случае достаточно.
Если оставить как есть, то в отчетах будут заниженные данные по валовой прибыли и неверное понимание ценности клиентов. Так как пропуски есть примерно в 10% транзакций, то расчет себестоимости, основанный на разумных допущениях, – меньшее зло по сравнению с отсутствием у десятой части продаж данных по прибыли.
Подобные действия надо документировать, чтобы пользователи отчетов осознавали, что имеют дело с не совсем точной информацией.
«Восстановить» себестоимость можно с помощью статистики. Например, отталкиваться от средней наценки на все позиции или конкретную товарную группу. Можно построить и более сложные модели, но для экономии времени предлагается реализовать следующий сценарий: рассчитать медианный процент прибыли для всех товаров и использовать его, когда реальная себестоимость не известна.
Расчет медианной наценки
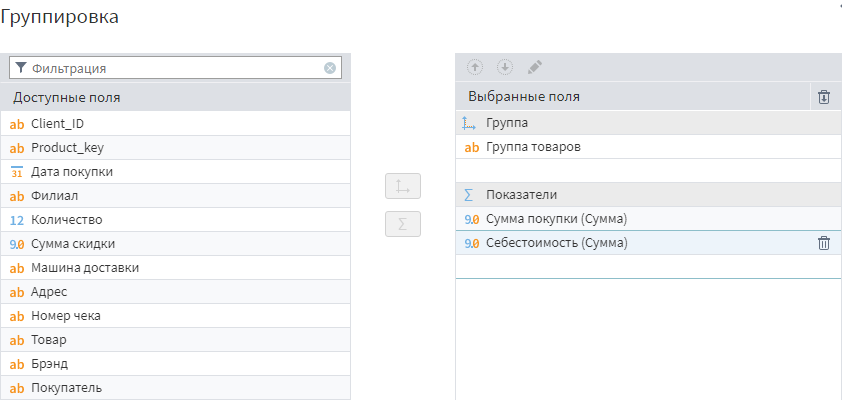
Надо в подмодели Продажи добавить фильтр по условию Поле себестоимость — не пустое.
Далее сгруппировать данные строк, где себестоимость не пустая, по товарным группам, просуммировав поля Себестоимость и Сумма покупки.
Группировка по товарным категориям
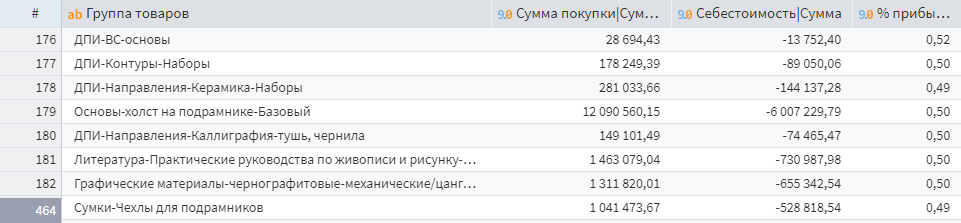
Следующий шаг — добавить еще один калькулятор, в котором будет рассчитано поле Profit_perc по формуле (Summa_pokupki+Sebestoimost)/Summa_pokupki.
Получится таблица с процентом прибыли по каждой категории товаров.
Процент наценки по группам товаров
Пометка. Значение последнего столбца % прибыли по факту является долей.
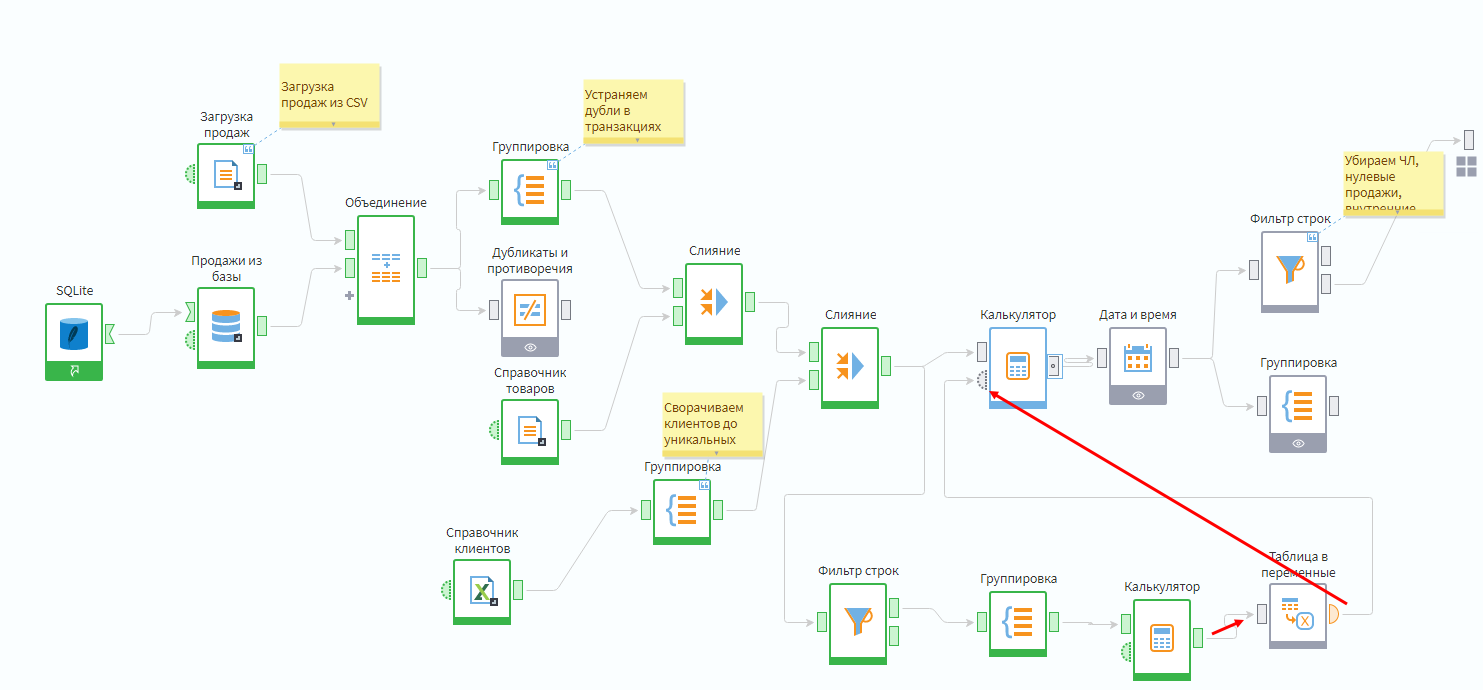
Далее нужно рассчитать медианный процент наценки по группам. Для этого можно использовать обработчик Таблица в переменные, передав полученный результат на вход Калькулятора.
Расчет медианной наценки по группам товаров
Логика этого узла похожа на обработчик Группировка, но без возможностей указания групп. Из каждого поля рассчитывается одно или несколько агрегированных значений, которые передаются дальше по сценарию как переменные. Нужно указать агрегацию медиана для поля % прибыли.
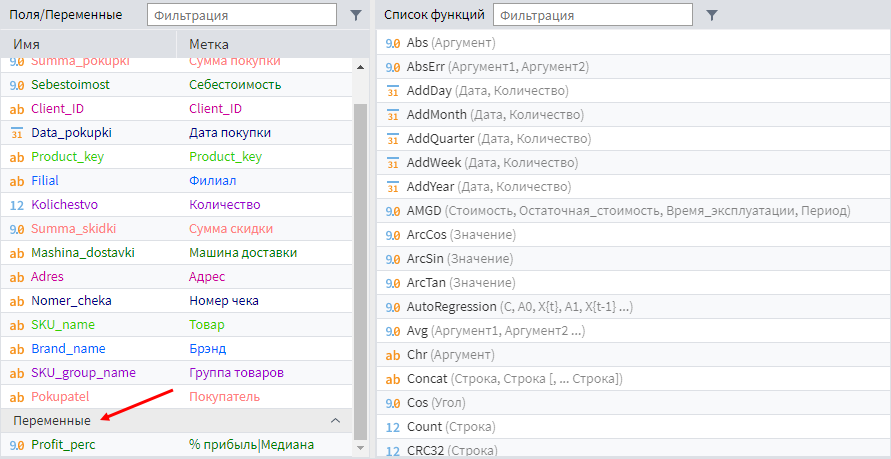
Теперь медианный процент прибыли доступен как переменная в Калькуляторе.
Расчитанная наценка в калькуляторе
Далее нужно модифицировать формулу для поля Gross_profit так, чтобы в случае пустого поля Sebestoimost прибыль считалась как выручка, умноженная на медианный процент прибыли. В ином случае – как сумма выручки и себестоимости (заданной отрицательным числом).
Для того, чтобы сценарий стал более компактным, нужно свернуть узлы, в которых рассчитывалась медианная наценка в подмодель. Для этого надо выделить их по очереди, прокликав ЛКМ с зажатым Ctrl, а затем выбрать на панели инструментов действие Свернуть в подмодель.
;
Бонусное задание. Создайте дополнительное поле расчета себестоимости, в котором при пустом значении поля Sebestoimost будет происходить вычисление себестоимости через вычитание из валовой прибыли суммы продажи (в исходных данных себестоимость идет со знаком минус по стандартам финансовой отчетности).
Последний шаг — настройка выхода из узла, чтобы новое поле себестоимости передавалось в старое по аналогии с номером чека.
Пропуски строк
Пропуски в значениях полей — не единственный вид отсутствующих данных. Иногда могут выпадать целые блоки, например, продажи за неделю или месяц. Как понять, есть ли подобные проблемы в данных?
К сожалению, ошибка может проявлять себя только в виде расхождений в отчетах. Ведь речь идет не о пропусках в ячейках, а об отсутствие самих строк. Нет строк — не видно проблем.
Поэтому при наличии сложных ETL-процессов необходима реализация механизмов мониторинга корректности загрузок: анализ логов, контроль завершения задач, сравнение данных в первоисточнике и хранилище данных и прочее.
Одна из самых распространенных проблем такого рода — не прогруженные записи. Чаще всего продажи осуществляются каждый рабочий день, и отсутствие хотя бы одной отгрузки в какой-то день — надежный индикатор проблем, возникших в ETL-процессе. В Loginom нет готового обработчика для выявления таких проблем, но его можно реализовать средствами платформы.
Создание переиспользуемой подмодели
До этого момента подмодели использовались для оптимизации рабочего пространства за счет сворачивания больших фрагментов сценария. Но сейчас будет спроектирована подмодель, которая может переиспользоваться как готовый компонент в других сценариях.
Подмодель будет принимать на вход поле с датой, а на выход возвращать список пропущенных периодов. При этом особо длительные пропущенные периоды будут выводиться отдельно.
Добавьте компонент Подмодель в область сценария, где создается клиентский портрет, и зайдите в настройки узла.
Создание подмодели
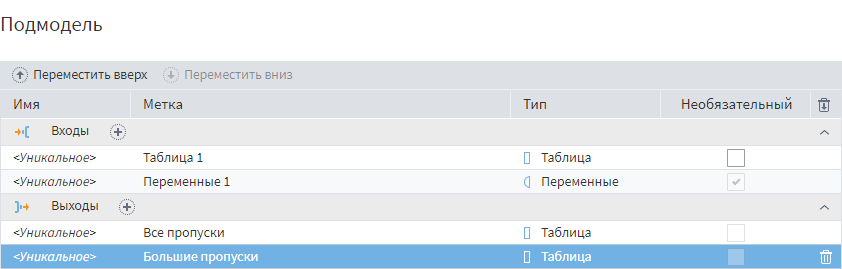
Нужно создать на входе 1 табличный порт и 1 порт переменных, а на выходе — 2 табличных порта.
При создании портов, особенно если их несколько, надо давать им понятные названия. Иначе в будущем такую подмодель будет сложно поддерживать самому и переиспользовать коллегам. Название порта помогает разобраться, какие данные туда подаются.
Результат:
Т.к. подмодель рассчитана на решение конкретной задачи (работа с данными определенного типа), стоит задать перечень полей и переменных на входных портах.
В табличном порту нужно отключить автосинхронизацию и создать поле Date с типом Дата.
В порту переменных надо отключить автосинхронизацию и создать переменную с типом целое число и значением по умолчанию — 10.
;
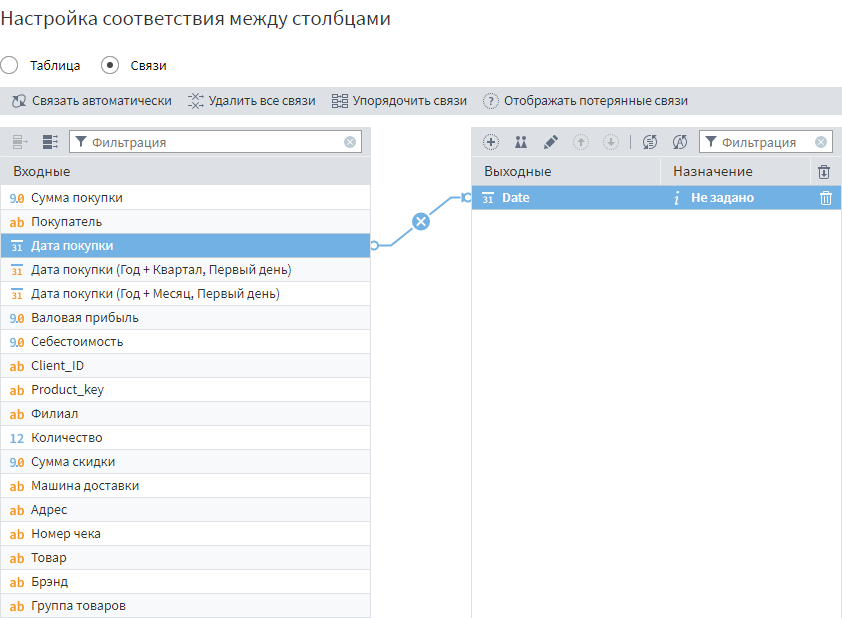
На вход подмодели надо подать данные из узла Продажи, а в настройках входного порта данных задать соответствие между полем Дата покупки и Date, переключив отображение в режим Связи.
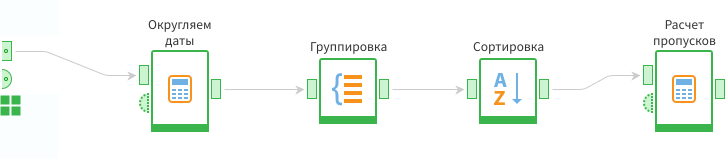
В подмодели определены входы, теперь надо построить сценарий от входа до выхода. Для этого нужно сформировать набор уникальных дат и отсортировать их по возрастанию.
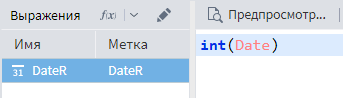
Т.к. заранее неизвестно, содержатся в поле только даты или это поле с датой и временем, надо с помощью функции int() округлить значения. В полях этого типа целая часть числа отвечает за дату, а дробная — за время.
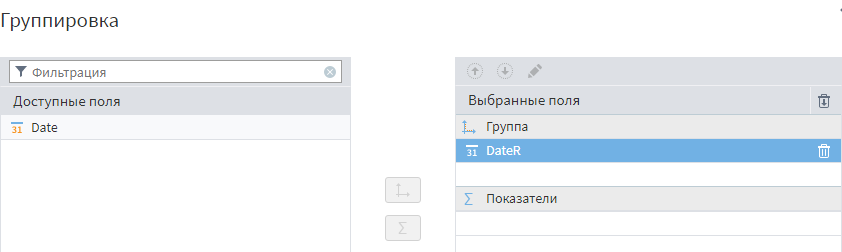
Дальше при помощи Группировки нужно сформировать перечень уникальных дат и отсортировать по возрастанию.
Потом рассчитать, есть ли пропуски. Для этого на вход последнего узла подать ранее отсортированную таблицу.
Следующий шаг — рассчитать, сколько дней между соседними строками. Для этого используется функция Data().
Первым аргументом (в двойных кавычках) идет название поля, из которого берутся данные. Вторым аргументом — номер строки. Функция RowNum() возвращает номер текущей строки, следовательно, вычитание единицы дает номер предыдущей строки.
Дополнительно нужно вычесть единицу, т.к. между текущим и следующим днем всегда разница в 1 день, а требуется найти дни между которыми разница больше, чем один пропущенный день.
Далее надо добавить пару полей, которые будут показывать нам пропущенные периоды.
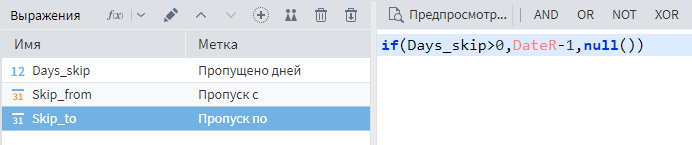
- Поле Пропуск с считается по формуле если пропущено дней больше нуля, то берем предыдущую дату +1 день. Иначе — пустое значение.
- Поле Пропуск по вычисляется по правилу если пропущено дней больше нуля, тогда берем текущую дату минус 1. Иначе — пустое значение.
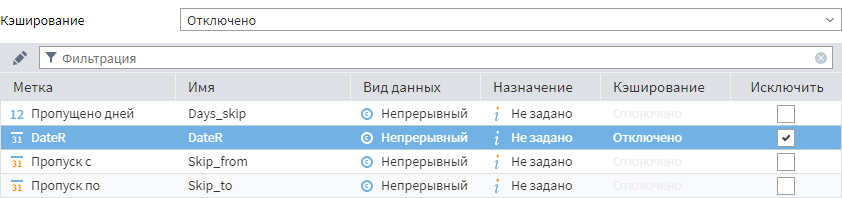
При помощи обработчика Параметры полей можно убрать поле DateR, т.к. на выходе интересуют только пропущенные интервалы.
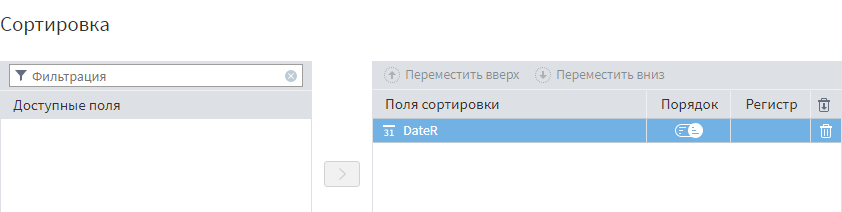
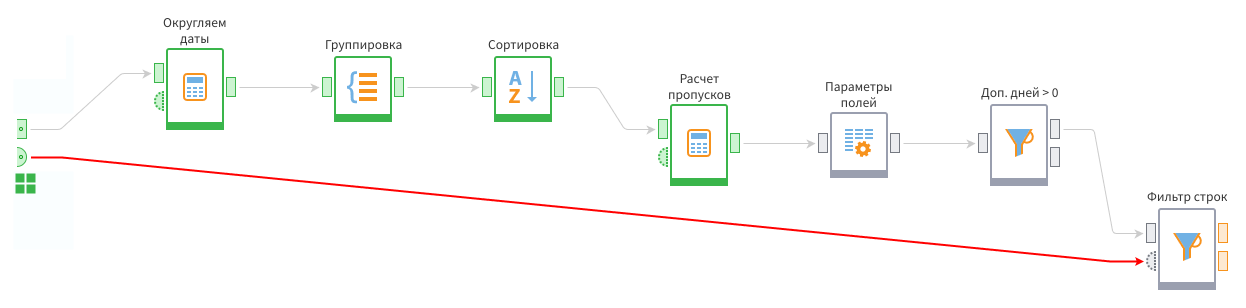
После исключения поля DateR нужно добавить узел Фильтрации с условием Пропущено дней > 0.
Фильтрация записей
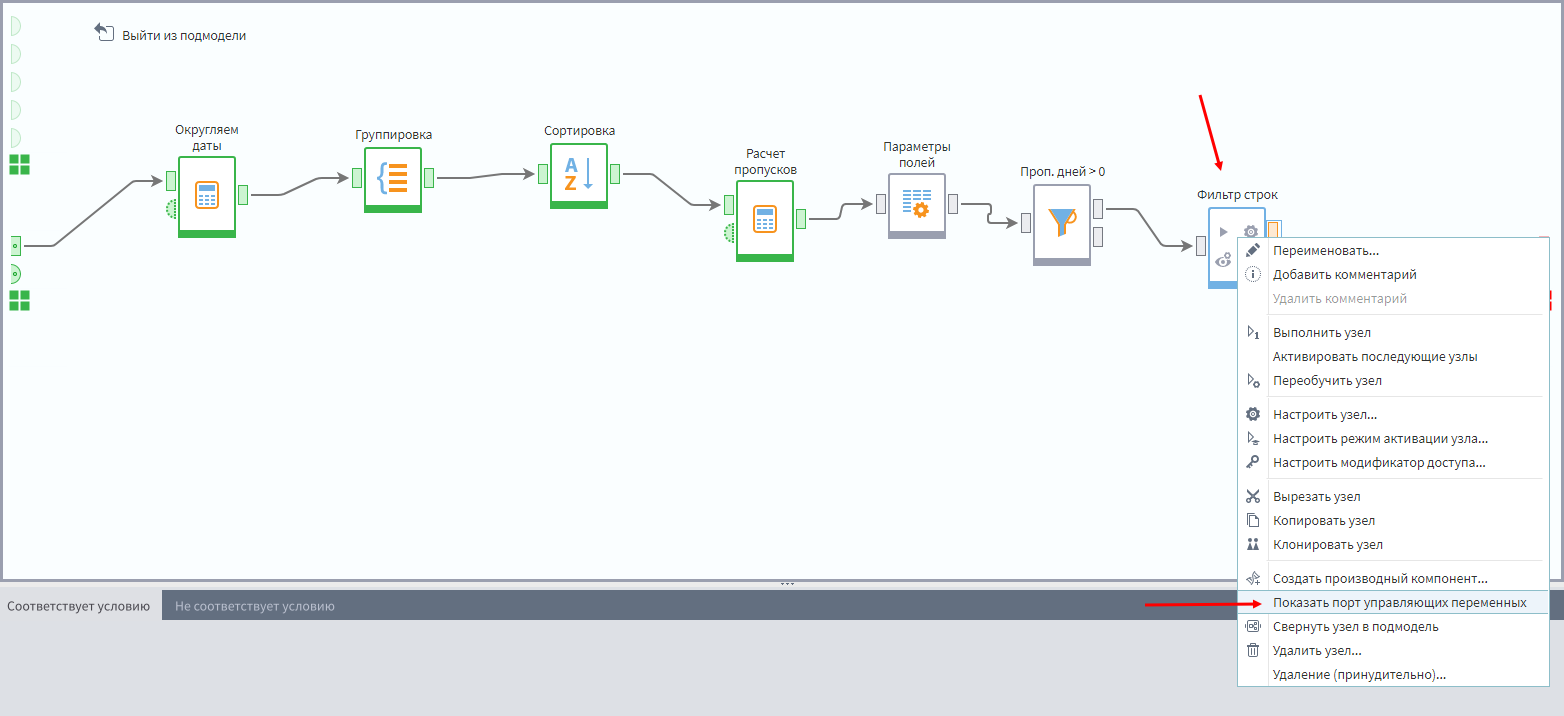
Далее надо добавить еще один Фильтр, принимающий данные с узла Параметры полей и показать в данном узле порт переменных, который по умолчанию скрыт. Для этого надо кликнуть по последнему узлу фильтрации ПКМ и в меню выбрать пункт Отобразить порт управляющих переменных.
Некоторые узлы имеют скрытый порт переменных, который при необходимости можно отобразить описанным выше образом.
На этот порт переменных нужно подать данные с порта переменных подмодели.
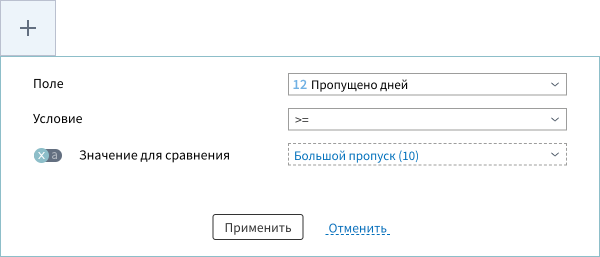
Теперь при открытии мастера настройки фильтра надо активировать соответствующий переключатель напротив параметра и выбрать нужную переменную.
После постановки условия фильтрации, будут отбираться записи, в которых длина пропуска больше или равна значению из переменной.
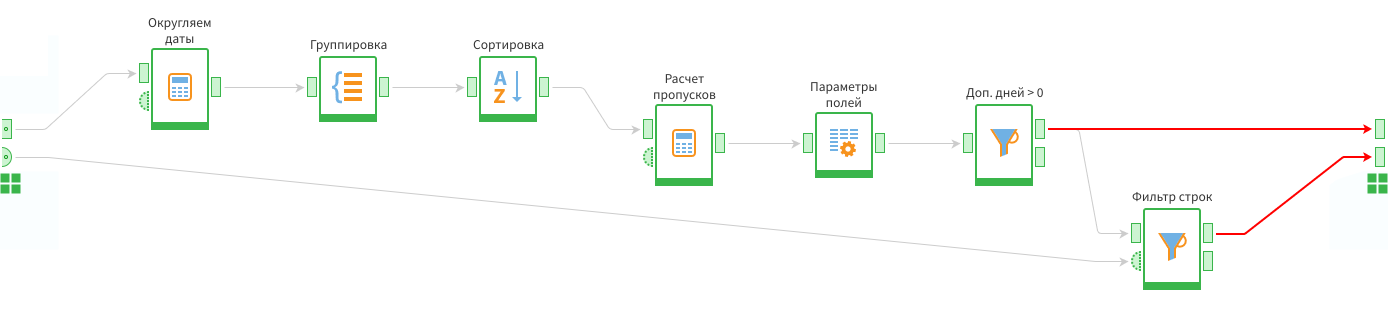
Финальный этап — отправить выход с первого фильтра на первый входной порт подмодели, а со второго фильтра — на второй выходной порт. Теперь в них будет выводиться полный список пропусков и отдельно большие пропуски. Критерий большого пропуска определяется через переменную на входе в подмодель.
Вывод данных из подмодели
Таким образом был создан свой первый компонент, пригодный для переиспользования. Как его использовать, можно посмотреть в других пакетах и в инструкции по производным компонентам после занятия.
Визуализация пропуска дат
Для визуализации полученной таблицы надо добавить в подмодель определения пропусков визуализатор Диаграмма.
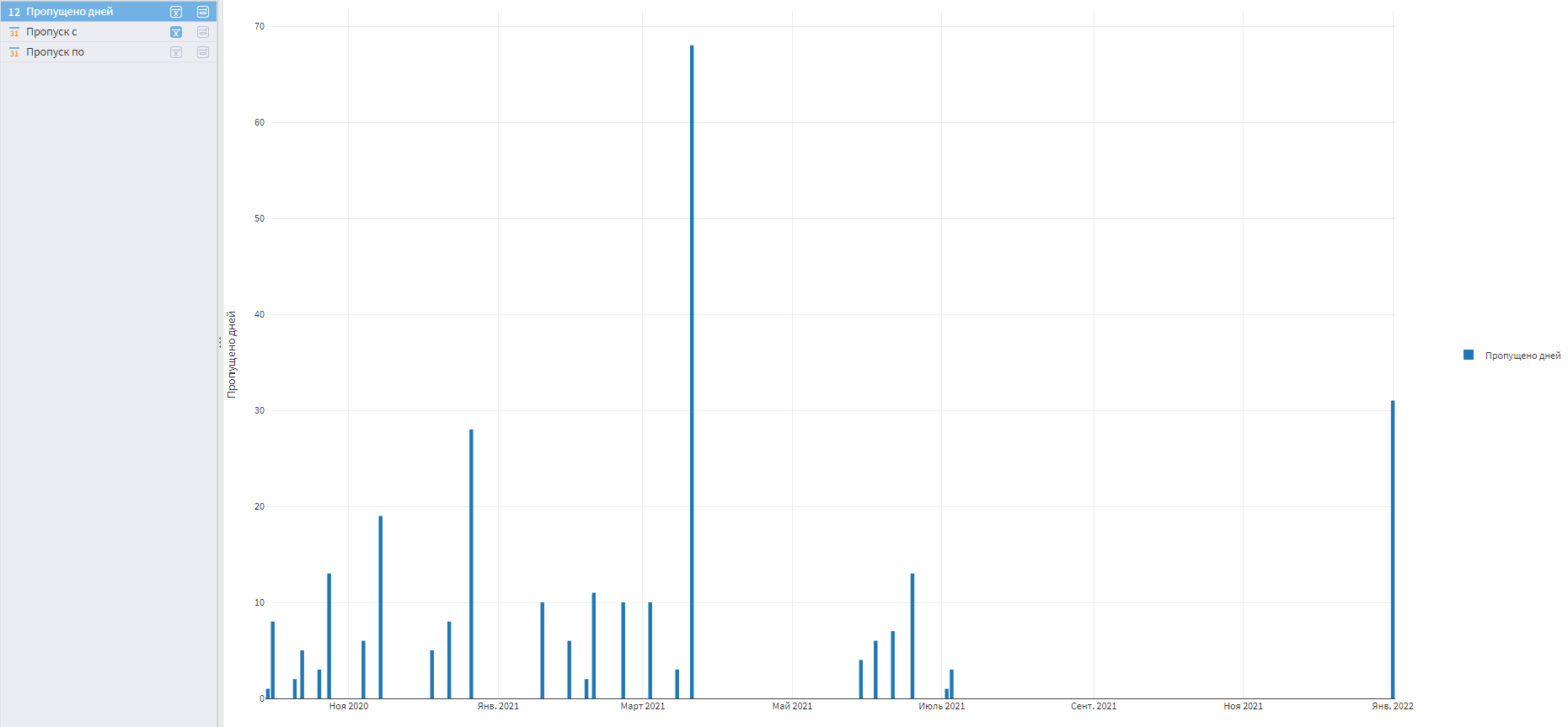
На ось X требуется перетащить поле Пропуск с, а поле Пропущено дней разместить в центре визуализатора, а затем выбрать вариант отображения Столбчатая диаграмма.
Визуализация пропущенных дней
По графику видно, что пропусков немало. В реальной жизни надо разбираться, в чем причина такого плохого качества. Вопросов может быть много:
- Правильно ли отработал импорт в Loginom?
- Правильно ли отработал экспорт из источника (например в файл)?
- В эти дни действительно не было продаж или пропуски возникли из-за технического сбоя?
- Можно ли восстановить потерянные данные?
Реальность обычно сурова: чем больше времени прошло с момента возникновения ошибки, тем сложнее ее исправить. Поэтому пропуски нужно мониторить на постоянной основе.
В нашем случае пропуски 2021 года восстановить не получится. Часть из них возникла из-за технических ошибок, а где-то продажи действительно отсутствовали.
Аудит пропусков наводит на мысль, что не стоит строить прогнозирующую и моделирующую аналитику на этих данных. Лучше считать клиентские портреты по данным за последний год.
Пропуски в относительно свежих данных чаще всего можно восстановить, но все равно нужно понять причину их возникновения, чтобы исправить брак. Чаще всего это ошибки в работе ETL-процесса. Поэтому предположим, что в новой базе ниже эта проблема устранена.
dbsales_transactions.db
Для исправления ситуации нужно заменить файл базы в папке Data на новый, и повторно импортировать данные. После этого надо еще раз просмотреть график пропусков в январе 2022.
Заключение
Работа с пропусками — деликатная тема. В зависимости от сценария анализа и критичности пропусков можно попытаться их восстановить, но иногда приходится оставлять как есть.
Независимо от выбранного подхода нужно проверять наличие пропусков и оповещать об этом коллег. Даже если данные так и остались с пропусками, наличие информации о том, что таковые в исходных таблицах имеются, позволяет делать более корректные выводы.
Часто решение проблемы исключения пропусков возможно на стороне систем учета и автоматизации. Нельзя рассчитывать, что задачу можно решить только за счет хитрых алгоритмов.
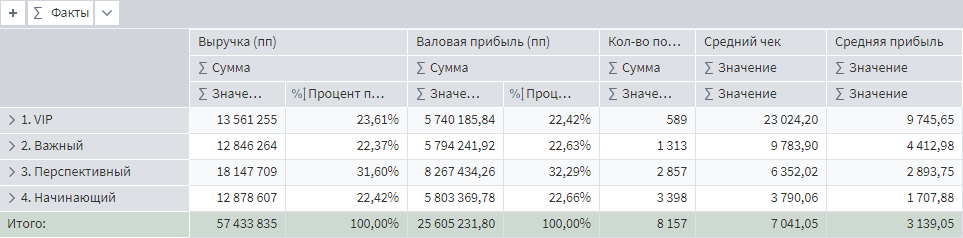
Как итог работы с пропусками можно заметить, что средняя прибыль и средний чек в портрете клиентов изменились. Вот значения до восстановления пропусков.
Портрет клиентов до восстановления пропусков
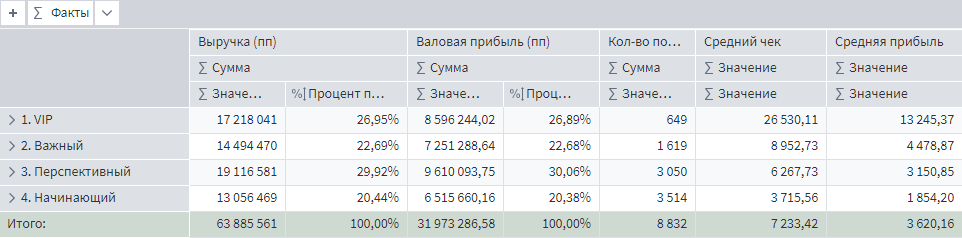
А вот, что получилось после.
Портрет клиентов после восстановления пропусков
Средняя прибыль с продажи в категории VIP неплохо подросла, как и в сегменте перспективных клиентов. А значит дальнейшее планирование по работе с этими сегментами может быть пересмотрено.
Общий средний чек вырос, потому что добавлены пропущенные транзакции за январь 2022. Без этой операции средний чек бы снизился, т.к. при неизменной сумме продаж, увеличилось количество транзакций за счет восстановления номеров продаж.
Списки с пропусками: вероятностная альтернатива сбалансированным деревьям
Время на прочтение
13 мин
Количество просмотров 32K
Списки с пропусками — это структура данных, которая может применяться вместо сбалансированных деревьев. Благодаря тому, что алгоритм балансировки вероятностный, а не строгий, вставка и удаление элемента в списках с пропусками реализуется намного проще и значительно быстрее, чем в сбалансированных деревьях.
Списки с пропусками — это вероятностная альтернатива сбалансированным деревьям. Они балансируются с использованием генератора случайных чисел. Несмотря на то, что у списков с пропусками плохая производительность в худшем случае, не существует такой последовательности операций, при которой бы это происходило постоянно (примерно как в алгоритме быстрой сортировки со случайным выбором опорного элемента). Очень маловероятно, что эта структура данных значительно разбалансируется (например, для словаря размером более 250 элементов вероятность того, что поиск займёт в три раза больше ожидаемого времени, меньше одной миллионной).
Балансировать структуру данных вероятностно проще, чем явно обеспечивать баланс. Для многих задач списки пропуска это более естественное представление данных по сравнению с деревьями. Алгоритмы получаются более простыми для реализации и, на практике, более быстрыми по сравнению со сбалансированными деревьями. Кроме того, списки с пропусками очень эффективно используют память. Они могут быть реализованы так, чтобы на один элемент приходился в среднем примерно 1.33 указатель (или даже меньше) и не требуют хранения для каждого элемента дополнительной информации о балансе или приоритете.
Для поиска элемента в связном списке мы должны просмотреть каждый его узел:
Если список хранится отсортированным и каждый второй его узел дополнительно содержит указатель на два узла вперед, нам нужно просмотреть не более, чем ⌈n/2⌉ + 1 узлов(где n — длина списка):
Аналогично, если теперь каждый четвёртый узел содержит указатель на четыре узла вперёд, то потребуется просмотреть не более чем ⌈n/4⌉ + 2 узла:
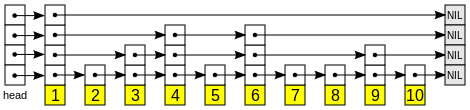
Если каждый 2i-ый узел содержит указатель на 2i узлов вперёд, то количество узлов, которые необходимо просмотреть, сократится до ⌈log2 n⌉, а общее количество указателей в структуре лишь удвоится:
Такая структура данных может использоваться для быстрого поиска, но вставка и удаление узлов будут медленными.
Назовём узел, содержащий k указателей на впередистоящие элементы, узлом уровня k. Если каждый 2i-ый узел содержит указатель на 2i узлов вперёд, то уровни распределены так: 50% узлов — уровня 1, 25% — уровня 2, 12.5% — уровня 3 и т.д. Но что произойдёт, если уровни узлов будут выбираться случайно, в тех же самых пропорциях? Например, так:
Указатель номер i каждого узла будет ссылаться на следующий узел уровня i или больше, а не на ровно 2i-1 узлов вперёд, как было до этого. Вставки и удаления потребуют только локальных изменений; уровень узла, выбранный случайно при его вставке, никогда не будет меняться. При неудачном назначении уровней производительность может оказаться низкой, но мы покажем, что такие ситуации редки. Из-за того, что эти структуры данных представляют из себя связные списки с дополнительными указателями для пропуска промежуточных узлов, я называю их списками с пропусками.
Операции
Опишем алгоритмы для поиска, вставки и удаления элементов в словаре, реализованном на списках с пропусками. Операция поиска возвращает значение для заданного ключа или сигнализирует о том, что ключ не найден. Операция вставки связывает ключ с новым значением (и создаёт ключ, если его не было до этого). Операция удаления удаляет ключ. Также в эту структуру данных можно легко добавить дополнительные операции, такие как «поиск минимального ключа» или «нахождение следующего ключа».
Каждый элемент списка представляет из себя узел, уровень которого был выбран случайно при его создании, причём независимо от числа элементов, которые уже находились там. Узел уровня i содержит i указателей на различные элементы впереди, проиндексированные от 1 до i. Мы можем не хранить уровень узла в самом узле. Количество уровней ограничено заранее выбранной константой MaxLevel. Назовём уровнем списка максимальный уровень узла в этом списке (если список пуст, то уровень равен 1). Заголовок списка (на картинках он слева) содержит указатели на уровни с 1 по MaxLevel. Если элементов такого уровня ещё нет, то значение указателя — специальный элемент NIL.
Инициализация
Создадим элемент NIL, ключ которого больше любого ключа, который может когда-либо появиться в списке. Элемент NIL будет завершать все списки с пропусками. Уровень списка равен 1, а все указатели из заголовка ссылаются на NIL.
Поиск элемента
Начиная с указателя наивысшего уровня, двигаемся вперед по указателям до тех пор, пока они ссылаются на элемент, не превосходящий искомый. Затем спускаемся на один уровень ниже и снова двигаемся по тому же правилу. Если мы достигли уровня 1 и не можем идти дальше, то мы находимся как раз перед элементом, который ищем (если он там есть).
Search(list, searchKey)
x := list→header
# инвариант цикла: x→key < searchKey
for i := list→level downto 1 do
while x→forward[i]→key < searchKey do
x := x→forward[i]
# x→key < searchKey ≤ x→forward[1]→key
x := x→forward[1]
if x→key = searchKey then return x→value
else return failure
Вставка и удаление элемента
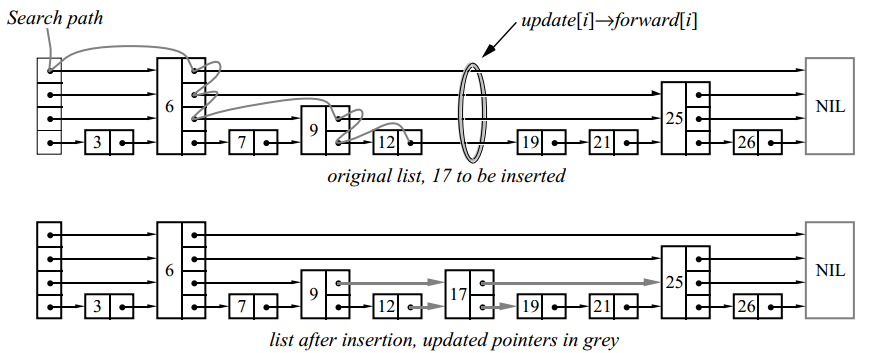
Для вставки или удаления узла применяем алгоритм поиска для нахождения всех элементов перед вставляемым (или удаляемым), затем обновляем соответствующие указатели:
В данном примере мы вставили элемент уровня 2.
Insert(list, searchKey, newValue)
local update[1..MaxLevel]
x := list→header
for i := list→level downto 1 do
while x→forward[i]→key < searchKey do
x := x→forward[i]
# x→key < searchKey ≤ x→forward[i]→key
update[i] := x
x := x→forward[1]
if x→key = searchKey then x→value := newValue
else
lvl := randomLevel()
if lvl > list→level then
for i := list→level + 1 to lvl do
update[i] := list→header
list→level := lvl
x := makeNode(lvl, searchKey, value)
for i := 1 to level do
x→forward[i] := update[i]→forward[i]
update[i]→forward[i] := x
Delete(list, searchKey)
local update[1..MaxLevel]
x := list→header
for i := list→level downto 1 do
while x→forward[i]→key < searchKey do
x := x→forward[i]
update[i] := x
x := x→forward[1]
if x→key = searchKey then
for i := 1 to list→level do
if update[i]→forward[i] ≠ x then break
update[i]→forward[i] := x→forward[i]
free(x)
while list→level > 1 and list→header→forward[list→level] = NIL do
list→level := list→level – 1
Для запоминания элементов перед вставляемым(или удаляемым) используется массив update. Элемент update[i] — это указатель на самый правый узел, уровня i или выше, из числа находящихся слева от места обновления.
Если случайно выбранный уровень вставляемого узла оказался больше, чем уровень всего списка (т.е. если узлов с таким уровнем ещё не было), увеличиваем уровень списка и инициализируем соответствующие элементы массива update указателями на заголовок. После каждого удаления проверяем, удалили ли мы узел с максимальным уровнем и, если это так, уменьшаем уровень списка.
Генерация номера уровня
Ранее мы приводили распределение уровней узлов в случае, когда половина узлов, содержащих указатель уровня i, также содержали указатель на узел уровня i+1. Чтобы избавиться от магической константы 1/2, обозначим за p долю узлов уровня i, содержащих указатель на узлы уровня i+i. Номер уровня для новой вершины генерируется случайно по следующему алгоритму:
randomLevel()
lvl := 1
# random() возвращает случайное число в полуинтервале [0…1)
while random() < p and lvl < MaxLevel do
lvl := lvl + 1
return lvl
Как можно заметить, количество элементов в списке не участвует в генерации.
С какого уровня начинать искать? Определение L(n)
В списке с пропусками из 16 элементов, сгенерированном при p = 1/2, может получиться так, что в нем будет 9 элементов уровня 1, 3 элемента уровня 2, 3 элемента уровня 3 и 1 элемент уровня 14 (это маловероятно, но возможно). Как с этим быть? Если мы будем использовать стандартный алгоритм и искать, начиная с уровня 14, то проделаем много бесполезной работы.
Откуда лучше начинать поиск? Наши исследования показали, что лучше всего начинать поиск с уровня L, на котором мы ожидаем 1/p узлов. Это случится при L = log 1/p n. Для удобства дальнейших рассуждений обозначим функцию log 1/p n как L(n).
Есть несколько способов решения проблемы с узлами неожиданно большого уровня:
- Не париться (ориг. Don’t worry, be happy). Просто начинать поиск с самого большого уровня, который есть в списке. Как мы увидим в дальнейшем, вероятность того, что уровень списка из n элементов окажется значительно выше чем L(n), очень мала. Такое решение добавляет лишь маленькую константу в ожидаемое время поиска. Этот подход использован в алгоритмах, приведённых выше.
- Использовать меньше места, чем нужно. Несмотря на то, что элемент может содержать 14 указателей, мы не обязательно должны использовать все 14. Мы можем использовать только L(n) из них. Есть несколько способов это реализовать, но все они усложняют алгоритм и не приводят к заметному увеличению производительности. Этот способ не рекомендуется к использованию.
- Починить кубик. Если сгенерировался уровень больший, чем максимальный уровень узла в списке, то просто считаем, что он больше ровно на 1. В теории и, похоже, на практике это работает хорошо. Но при таком подходе мы совершенно теряем возможность анализировать сложность алгоритмов, т.к. уровень узлов больше не полностью случаен. Программисты могут свободно использовать этот способ, но теоретикам лучше его избегать.
Выбор MaxLevel
Так как ожидаемое число уровней — L(n), лучше всего выбрать MaxLevel = L(N), где N — максимальное число элементов в списке с пропусками. Например, если p = 1/2, то MaxLevel = 16 подойдёт для списков, содержащих менее 216 элементов.
Анализ алгоритмов
В операциях поиска, вставки и удаления больше всего времени уходит на поиск подходящего элемента. Для вставки и удаления дополнительно нужно время, пропорциональное уровню вставляемого или удаляемого узла. Время поиска элемента пропорционально количеству пройденных в процессе поиска узлов, которое, в свою очередь, зависит от распределения их уровней.
Вероятностная философия
Структура списка с пропусками определяется только количеством элементов в этом списке и значениями генератора случайных чисел. Последовательность операций, с помощью которых получен список, не важна. Мы предполагаем, что у пользователя нет доступа к уровням узлов, иначе, он может сделать так, чтобы алгоритм работал за наихудшее время, удалив все узлы, уровень которых отличен от 1.
Для последовательных операций на одной структуре данных времена их выполнения не являются независимыми случайными величинами; две последовательных операции поиска одного и того же элемента займут в точности одно и то же время.
Анализ ожидаемого времени поиска
Рассмотрим пройденный при поиске путь с конца, т.е. будем двигаться вверх и влево. Хотя уровни узлов в списке известны и зафиксированы на момент поиска, мы предположим, что уровень узла определяется только когда мы встретили его при движении с конца.
В любой заданной точке пути мы находимся в такой ситуации:
Мы смотрим на i-ый указатель узла x и не знаем об уровнях узлов слева от x. Также мы не знаем точного уровня x, но он должен быть как минимум i. Предположим, что x — это не заголовок списка (это эквивалентно предположению, что список бесконечно расширяется влево). Если уровень x равен i, то мы находимся в ситуации b. Если уровень x больше i, то мы в ситуации c. Вероятность того, что мы находимся в ситуации c, равна p. Каждый раз, когда это происходит, мы поднимаемся вверх на один уровень. Пусть C(k) — это ожидаемая длина обратного пути поиска, при котором мы двигались вверх k раз:
C(0) = 0
C(k) = (1-p) (длина пути в ситуации b) + p (длина пути в ситуации c)
Упрощаем:
C(k) = (1-p)(1 + C(k)) + p⋅(1 + C(k-1))
C(k) = 1 + C(k) — p⋅C(k) + p ⋅ C(k-1)
C(k) = 1/p + C(k — 1)
C(k) = k/p
Наше предположение о том, что список бесконечный — пессимистично. Когда мы доходим до самого левого элемента, мы просто двигаемся все время вверх, не двигаясь влево. Это даёт нам верхнюю границу (L(n) — 1) /p ожидаемой длины пути от узла с уровнем 1 до узла с уровнем L(n) в списке из n элементов.
Мы используем эти рассуждения, чтобы добраться до узла уровня L(n), но для остальной части пути используются другие рассуждения. Количество оставшихся ходов влево ограничено числом узлов, имеющих уровень L(n), или выше во всем списке. Наиболее вероятное число таких узлов 1/p.
Мы также двигаемся вверх от уровня L(n) до максимального уровня в списке. Вероятность того, что максимальный уровень списка больше k, равна 1-(1-pk)n, что не больше, чем npk. Мы можем вычислить, что ожидаемый максимальный уровень не более L(n) + 1/(1-p). Собирая всё вместе, получим, что ожидаемая длина пути поиска для списка из n элементов
<=L(n)/p + 1/(1-p),
или O(log n).
Количество сравнений
Мы только что посчитали длину пути, проходимого при поиске. Требуемое число сравнений на единицу больше длины пути (сравнение происходит на каждом шаге пути).
Вероятностный анализ
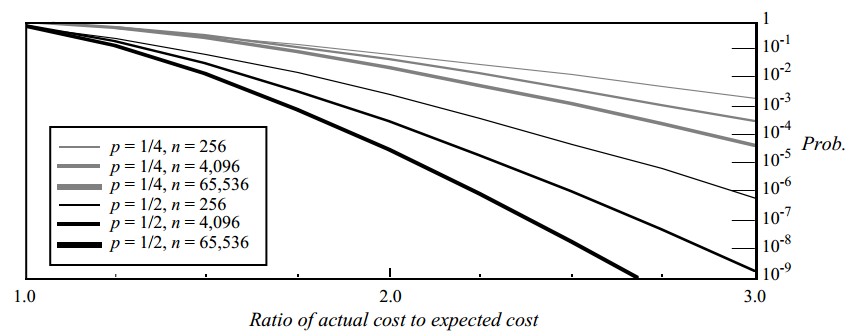
Мы можем рассмотреть распределение вероятностей различных длин путей поиска. Вероятностный анализ в некоторой степени более сложный (он есть в самом конце оригинальной статьи). С его помощью мы можем оценить сверху вероятность того, что длина пути поиска превысит ожидаемую более чем в заданное число раз. Результаты анализа:
Здесь изображён график верхней границы вероятности того, что операция займет значительно больше времени, чем ожидалось. На вертикальной оси отложена вероятность того, что длина пути поиска окажется больше ожидаемой длины пути в количество раз, отложенное на горизонтальной оси. Например, при p = 1/2 и n = 4096, вероятность того, что получившийся путь окажется в три раза длиннее, чем ожидаемый, меньше 1 / 200 000 000.
Выбор p
В таблице приведены нормализованные времена поиска и объем требуемой памяти для различных значений p:
| p | Нормализованное время поиска (т.e. нормализованное L(n)/p ) |
Среднее количество указателей на узел (т.е. 1/(1 – p) ) |
|---|---|---|
| 1/2 | 1 | 2 |
| 1/e | 0.94… | 1.58… |
| 1/4 | 1 | 1.33… |
| 1/8 | 1.33… | 1.14… |
| 1/16 | 2 | 1.07… |
Уменьшение p увеличивает разброс времени операций. Если 1/p является степенью двойки, то удобно генерировать номер уровня из потока случайных бит (для генерации в среднем требуется (log2 1/p)/(1-p) случайных бит). Так как существуют накладные расходы, относящиеся к L(n) (но не к L(n)/p), то выбор p=1/4 (вместо 1/2) слегка уменьшает константу в сложности алгоритма. Рекомендуем выбирать p=1/4, но если разброс времени операций для вас важнее скорости, то выбирайте 1/2.
Несколько операций
Ожидаемое итоговое время последовательности операций равняется сумме ожидаемых времён для каждой операции в последовательности. Таким образом, ожидаемое время для любой последовательности m операций поиска в структуре данных из n элементов равняется O(m * log n). Однако, характер (pattern) операций поиска влияет на распределение фактического времени всей последовательности операций.
Если мы ищем один и тот же элемент в одной и той же структуре данных, то обе операции займут в точности одно и то же время. Таким образом, дисперсия (разброс) итогового времени будет в четыре раза больше дисперсии одной операции поиска. Если времена поиска двух элементов — независимые случайные величины, то дисперсия общего времени равна сумме дисперсий времён выполнения отдельных операций. Поиск одного и того же элемента снова и снова максимизирует дисперсию.
Тесты производительности
Сравним производительность списков с пропусками с другими структурами данных. Все реализации были оптимизированы для достижения максимальной производительности:
| Структура данных | Поиск | Вставка | Удаление |
|---|---|---|---|
| списки с пропусками | 0.051 мсек (1.0) | 0.065 мсек (1.0) | 0.059 мсек (1.0) |
| нерекурсивные AVL деревья | 0.046 мсек (0.91) | 0.10 мсек (1.55) | 0.085 мсек (1.46) |
| рекурсивные 2–3 деревья | 0.054 мсек (1.05) | 0.21 мсек (3.2) | 0.21 мсек (3.65) |
| Саморегулирующиеся деревья: | |||
| расширяющиеся сверху вниз (top-down splaying) | 0.15 мсек (3.0) | 0.16 мсек (2.5) | 0.18 мсек (3.1) |
| расширяющиеся снизу вверх (bottom-up splaying) | 0.49 мсек (9.6) | 0.51 мсек (7.8) | 0.53 мсек (9.0) |
Тесты выполнялись на машине Sun-3/60 и производились на структурах данных, содержащих 216 элементов. Значения в скобках — время, относительно списков с пропусками (в разах). Для тестов вставки и удаления элементов не учитывалось время, затрачиваемое на управление памятью (например, на C-шные вызовы malloc и free).
Заметим, что списки с пропусками требуют больше операций сравнения, чем другие структуры данных (алгоритмы, приведённые выше, требуют в среднем L(n)/p + 1/(1 + p) операций). При использовании вещественных чисел в качестве ключей, операции в списках с пропусками оказались немного медленнее, чем в нерекурсивной реализации AVL-дерева, а поиск в списках с пропусками оказался немного медленнее, чем поиск в 2-3 дереве (тем не менее, вставка и удаление в списках с пропусками были быстрее, чем в рекурсивной реализации 2-3 деревьев). Если операции сравнения очень дорогие, можно модифицировать алгоритм так, что искомый ключ не будет сравниваться с ключом других узлов более одного раза на узел. При p = 1/2 верхняя граница количества сравнений равна 7/2 + 3/2 * log2 n.
Неравномерное распределение запросов
Саморегулирующиеся деревья могут адаптироваться к неравномерному распределению запросов. Так как списки с пропусками быстрее саморегулирующихся деревьев в довольно большое число раз, саморегулирующиеся деревья оказываются быстрее только при некоторых очень неравномерных распределениях запросов. Мы могли бы попытаться разработать саморегулирующиеся списки с пропусками, однако, не видели в этом практического смысла и не хотели портить простоту и производительность оригинальной реализации. Если в приложении ожидаются неравномерные запросы, то использование саморегулирующихся деревьев или добавление кэширования будут более предпочтительными.
Заключение
С теоретической точки зрения, списки с пропусками не нужны. Сбалансированные деревья могут делать те же операции и имеют хорошую сложность в худшем случае (в отличие от списков с пропусками). Однако, реализация сбалансированных деревьев — сложная задача и, как следствие, они редко реализуются на практике, кроме как в качестве лабораторных работ в университетах.
Списки с пропусками — это простая структура данных, которая может использоваться вместо сбалансированных деревьев в большинстве случаев. Алгоритмы очень легко реализовывать, расширять и изменять. Обычные реализации операций на списках с пропусками примерно такие же быстрые, как высокооптимизированные реализации на сбалансированных деревьях и в значительной степени быстрее обычных, невысокооптимизированных реализаций.
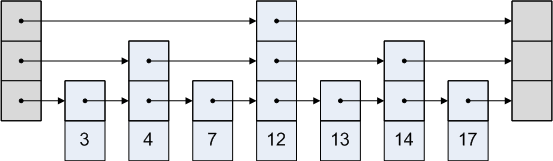
Пример списка с пропусками
Список с пропусками (англ. skip list) — вероятностная структура данных, позволяющая в среднем за времени выполнять операции добавления, удаления и поиска элементов.
Список с пропусками состоит из нескольких уровней, на каждом из которых находится отсортированный связный список. На самом нижнем (первом) уровне располагаются все элементы. Дальше около половины элементов в таком же порядке располагаются на втором, почти четверть — на третьем и так далее, но при этом известно, что если элемент расположен на уровне , то он также расположен на всех уровнях, номера которых меньше .
Содержание
- 1 Построение
- 1.1 Псевдокод
- 2 Операции над структурой
- 2.1 Поиск элемента
- 2.1.1 Псевдокод
- 2.2 Вставка элемента
- 2.2.1 Псевдокод
- 2.3 Удаление элемента
- 2.3.1 Псевдокод
- 2.1 Поиск элемента
- 3 Использование нечестной монеты
- 4 Применение
- 4.1 Нахождение всех отрезков, покрывающих данную точку
- 5 См. также
- 6 Источники информации
Построение
Односвязный отсортированный список
Получившийся список с пропусками
Допустим, что нам задан односвязный отсортированный список и мы хотим построить на его основе список с пропусками, позволяющий в среднем за времени выполнять операции добавления, удаления и поиска элементов.
На самом нижнем уровне списка с пропусками мы расположим исходный список. На втором уровне — всё элементы с чётными номерами, причём каждый элемент будет ссылаться на соответствующий ему элемент на нижнем уровне. Таким же образом построим и третий уровень, куда будем добавлять только те элементы, номера которых кратны четырём. Аналогичным образом построим и последующие уровни.
Псевдокод
Каждый уровень списка с пропусками содержит отсортированный односвязный список, у которого есть начало и конец . Для выполнения операций на списке с пропусками необходимо передавать в качестве аргумента ссылку на начало односвязного списка, расположенного на самом верхнем уровне.
Элементы односвязного списка — вершины , у которых есть поля:
- — ссылка на следующий элемент списка на данном уровне
- — ключ, который хранится в данной вершине
- — ссылка на соответственный элемент, лежащий уровнем ниже
struct node:
node next, down
K key
Также известно, что и ,
Функция возвращает новый уровень списка с пропусками на основе предыдущего построенного уровня.
list build_lvl(list lvl)
list next_lvl
next_lvl.head.down = lvl.head
next_lvl.tail.down = lvl.tail
node i = lvl.head.next.next
node cur = next_lvl.head
while i null and i.next null
cur.next = node(key, i, cur.next) // Конструктор node(key, down, next) возвращает новую вершину с ключом key, ссылками down на нижний и next на следующий элемент
cur = cur.next
i = i.next.next // Переход к следующему чётному элементу
return next_lvl
Функция принимает в качестве аргумента односвязный отсортированный список и возвращает новый список с пропусками, построенный на его основе.
list skip_list(list l):
list lvl // Построение первого уровня
node i = l.head
node j = lvl.head
while j l.tail
i.next = node(j.key, null, j.next)
i = i.next
j = j.next
while lvl.size > 2
lvl = build_lvl(lvl)
return lvl // Возвращает ссылку на начало верхнего уровня
Операции над структурой
Поиск элемента
Алгоритм поиска элемента в списке с пропусками состоит из следующих операций:
- Начинаем поиск элемента в самом верхнем уровне
- Переходим к следующему элементу списка, пока значение в следующей ячейке меньше
- Переместимся на один уровень вниз и перейти к шагу . Если мы уже на первом уровне — прекратим поиск и вернём ссылку на текущую вершину
В конце алгоритма функция вернёт элемент, значение которого не меньше ключа или ссылку на конец списка на первом уровне.
Если в качестве случайного источника мы будем использовать честную монету, то в среднем случае будет уровне. На самом верхнем уровне будет не более двух элементов. Тогда на каждом уровне в среднем нужно проверить не более двух элементов (в противном случае могли бы вместо двух нижних элементов проверить ещё один уровнем выше). Если же у нас будет уровней, тогда на каждом уровне в среднем будет в раз элементов больше, чем уровнем выше. В таком случае время поиска элемента .
Псевдокод
Функция возвращает ссылку на элемент, значение которого не меньше . В случае, если все элементы в списке с пропусками меньше , то возвращается ссылка на конец списка с пропусками.
T find(node res, K key)
while res.key < key
res = res.next
if res.down = null // Если мы находимся на первом уровне
return res // Мы нашли искомый элемент
return find(res.down, key) // Иначе спустимся на один уровень ниже
Для того, чтобы найти элемент с ключом в списке с пропусками необходимо запустить следующим образом
find(skip.head, key)
Вставка элемента
Алгоритм вставки элементов в список с пропусками состоит из следующих шагов:
- Начинаем вставку на самом верхнем уровне
- Переходим к следующему элементу списка пока значение следующей ячейки меньше ключа.
- Если мы на первом уровне — вставляем элемент. Иначе спускаемся ниже и возвращаемся к шагу . Если нам вернули не null — вставляем элемент на текущем уровне тоже.
- Кидаем монетку и если выпал «Орёл», то возвращаем ссылку на текущий элемент, иначе — null. Если мы были не на первом уровне и нам вернули null — возвращаем его без броска монетки.
Отдельно стоит обработать случай, когда вставка нового элемента увеличивает число уровней. Тогда необходимо создать ещё один отсортированный список, в котором будет всего один текущий элемент, и не забыть присвоить списку с пропусками новую ссылку на верхний уровень. Будем считать, что вставка каждого нового элемента увеличивает число уровней не более чем на один.
Заметим, что вставка элемента поиск элемента и за добавляем не более, чем в уровней элемент. Итого время работы .
Псевдокод
Функция возвращаем ссылку на вставленный элемент в списке, в котором находится , или null, если на монете выпала «Решка».
node insert(node res, K key)
while res.next null and res.next.key < key
res = res.next
node down_node
if res.down = null
down_node = null
else
down_node = insert(res.down, key)
if down_node null or res.down = null // Если выпал «Орёл» или мы находимся на первом уровне
res.next = node(key, down_node, res.next)
if coin_flip() = head // Если выпал «Орёл»
return res.next
return null
return null
Для того, чтобы вставить элемент с ключом в список с пропусками необходимо вызвать следующую функцию
function insert_element(list skip, K key)
node res = insert(skip.head, key)
if res null
list lvl
lvl.head.next = node(key, res, lvl.tail)
skip = lvl
Удаление элемента
Алгоритм удаления элемента выглядит следующим образом:
- Начинаем удалять элемент с верхнего уровня
- Переходим к следующему элементу, пока значение следующего элемента меньше ключа
- Если элемент существует на данном уровне — удаляем его с этого уровня. Если мы не на первом уровне, то удаляем элемент ещё с нижнего уровня.
Псевдокод
Функция удаляет элемент со всех уровней.
function delete(node res, K key)
while res.next null and res.next.key < key
res = res.next
if res.down null
delete(res.down, key)
if res.next null and res.next.key = key
res.next = res.next.next
Аналогично со вставкой удаление поиск элемента за плюс удаление на каждом уровне за . Итого .
Для того, чтобы удалить элемент из списка с пропусками , необходимо вызвать функцию следующим образом:
delete(skip.head, key)
Использование нечестной монеты
Вместо честной монеты с распределением можно взять в качестве случайного источника нечестную монету с распределением (с вероятностью выпадает «Орёл»). Тогда математическим ожиданием количества элементов на уровне будет . Время поиска будет равно на -ом уровне элементов будет почти в раз больше, чем на -ом, значит на каждом уровне пройдём не более элементов, а уровней всего .
Пусть у нас добавлено элементов. Найдём такое распределение , при котором функция принимает минимальное значение. Производная этой функции равна . При производная равна нулю, вторая производная в точке больше , значит точка минимума. Значит при распределении время поиска меньше всего. Но не стоит забывать, что это лишь теоретическая оценка и в действительности придумать источник с распределением почти невозможно, поэтому на практике лучше всего использовать честную монету.
Для крайних распределений:
- — — поиск, добавление и удаления элемента, поскольку мы вместо нескольких списков используем по факту один.
- — зависит от реализации алгоритма. Если при каждой вставке у нас образуется не более одного уровня, то количество уровней будет равным , значит время поиска будет равным .
Применение
Список с пропусками применяется во многих приложениях, поскольку имеет ряд преимуществ:
- Быстрая вставка элемента, поскольку не требуется каким-либо образом изменять другие элементы (только предыдущий элемент)
- Проще реализовать, чем сбалансированные деревья или хеш-таблицы
- Следующий элемент достаётся за (при условии, что у нас есть ссылка не текущий)
- Легко модифицировать под различные задачи
Нахождение всех отрезков, покрывающих данную точку
| Задача: |
Пусть у нас есть запросы двух видов:
Необходимо для каждого запроса второго типа вывести ответ. |
Для решения данной задачи воспользуемся списком с пропусками. Когда нам приходит запрос первого типа, то мы просто добавляем числа и в список с пропусками (если какое-то из чисел уже было добавлено, то второй раз мы его не добавляем). После этого идём с верхнего уровня, и на каждом уровне мы ищем такие и , что значение меньше , а значение следующего за элемента уже не меньше . Аналогично ищем такое же , только относительно . Если значения и лежат полностью внутри отрезка , то к самому отрезку прибавляем , а сам отрезок разбиваем на три , и и по отдельности решаем задачу уже для полученных отрезков (если для какого-то отрезка левая граница стала больше правой, то мы ничего не делаем). Допустим, что на каком-то уровне у нас получилось разделить отрезок на части. Но тогда на следующих уровнях мы будем уменьшать отрезок почти в два раза только с одной стороны, поскольку левая или правая часть отрезка будет равна или . Итого время обработки запроса .
Для запросов второго типа мы снова будем спускать с верхнего уровня до нижнего. На каждом уровне найдём тот элемент, значение которого не меньше точки . Если такой элемент нашёлся, то прибавляем к ответу значение на отрезку между найденным элементом и следующим. Потом также спускаемся на один уровень вниз, если текущий уровень не был первым. Поскольку уровней всего , а на каждом уровне обойдём не более двух элементов, то данный тип запросов мы обработаем за .
См. также
- Список
- Рандомизированное бинарное дерево поиска
- Поисковые структуры данных
- Skip quadtree
Источники информации
- Википедия — списки с пропусками
- Wikipedia — skip list
- igoro.com — Skip lists are fascinating
- ticki.github.io — Skip Lists: Done Right
- Eric N. Hanson — A Data Structure for Finding All Intervals That Overlap a Point стр. 155-164