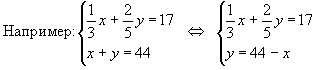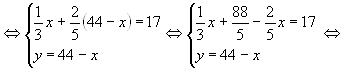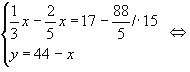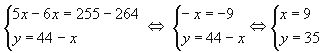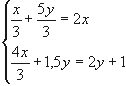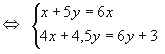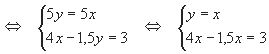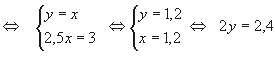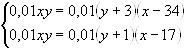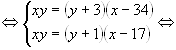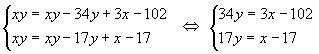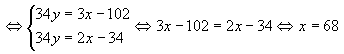Имеется два сплава с разным содержанием меди: в первом содержится 60%, а во втором — 45% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 55% меди?
Для начала условимся: первый сплав будет представлять собой x кг – весь сплав. Тогда масса меди будет 60 процентов от от массы сплава. Запишем в виде десятичной дроби: 0,6x.
Массу второго сплава возьмём за y. Логично, что масса меди во втором сплаве будет 0,45y.
Мы берём эти сплавы вместе, поэтому медь в новом сплаве будет масса меди в первом сплаве и масса меди во втором сплаве. Таким образом, масса меди в новом сплаве будет 0,6x+0,45y.
Теперь оформим таблицу:
Из таблицы видно, что концентрация меди в новом сплаве должна быть 55%, что дано по условию. Теперь составляем уравнение.
Масса меди (третий столбец справа) составляет 55% от массы нового сплава x+y, то есть:
0,55(x+y)=0,6x+0,45y
Теперь решаем уравнение, и поскольку у нас спрашивается, в каком отношении надо взять сплавы, то нам надо найти отношение x/y, что мы и сделаем. Для начала домножим на 100, чтобы было проще работать с числами:
55(x+y)=60x+45y
Теперь раскрываем скобки и переносим всё в правую часть:
60х+45у-55х-55у=0
Как видите, мы для удобства поменяли местами ноль и само выражение. Теперь приводим подобные:
5х-10у=0
Переносим 10у в правую часть, сокращаем на 5:
x=2y
Из этого уравнение следует, что x/y=2, что и является ответом к задаче.
Ответ: 2:1.
ВНИМАНИЕ! Если вы не хотите, чтобы к вам на ОГЭ придирались, пишите именно такой ответ – 2:1. Если спрашивают отношение, надо давать именно отношение.
ПОНРАВИЛАСЬ СТАТЬЯ? ОБЯЗАТЕЛЬНО ПОДПИШИСЬ И ПОСТАВЬ ЛАЙК! ТАКЖЕ ПОДПИСЫВАЙСЯ НА МЕНЯ ВКОНТАКТЕ ПО ССЫЛКЕ: https://vk.com/hello_there_2021 Удачи!
P.S. Пишите в комментарии или в личку задачи, которые были бы Вам интересны для разбора или которые вызывают трудности. Постараюсь всем ответить!
Задачи, связанные с понятием “концентрация” и “процентное содержание”,
являются традиционно трудными для обучающихся. В них речь идет о сплавах,
растворах и смесях, которые получаются при сплавлении или смешивании различных
веществ. При решении таких задач принимаются некоторые допущения. Первое: если
смешиваются два раствора, объем которых х и у, то получившаяся
смесь будет иметь объем х +
у. Второе: получившиеся смеси и сплавы имеют однородную консистенцию.
В смесях и растворах содержится некоторый объем чистого вещества. Отношение
объема чистого вещества к объему всего раствора называется объемной
концентрацией. (Содержание чистого вещества в единице объема).
Концентрация, выраженная в процентах, называется процентным содержанием.
При решении таких задач удобно пользоваться таблицей, которая помогает понять
задачу и по которой легче составить уравнение или систему. В работе приведены
решения нескольких задач, а также предложены задачи для самостоятельного
решения. Для удобства к задачам прилагаются ответы.
1. Некоторый сплав состоит из
двух металлов, входящих в отношении 1 : 2, а другой содержит те же металлы в
отношении 2 : 3. Из скольких частей обоих сплавов можно получить третий сплав,
содержащий те же металлы в отношении 17 : 27?
Решение: Пусть взято х частей
первого сплава и у частей второго. В х
частях первого сплава содержится
частей первого металла и
частей второго. В
y частях второго сплава содержится
частей первого металла и
частей второго.
Составим таблицу:
Из таблицы видно, что можно получить три уравнения. 1)
х + у = 44 , 2)
3) . Решив систему из
двух уравнений, получим ответ.
Ответ: 9 частей первого сплава и 35 частей второго сплава.
2. Имеется два слитка, представляющие собой сплавы цинка с медью. Масса первого
слитка 2 кг, масса второго – 3 кг. Эти два слитка сплавили вместе с 5 кг сплава
цинка с медью, в котором цинка было 45 %, и получили сплав цинка с медью, в
котором цинка стало 50%. Если бы процентное содержание цинка в первом слитке
было бы равно процентному содержанию цинка во втором, а процентное содержание
цинка во втором такое же как в первом, то сплавив эти два слитка с 5 кг сплава,
в котором содержится 60% цинка, мы бы получили сплав, в котором цинка содержится
55%. Найдите процентное содержание цинка в первом и втором слитках.
Решение: Составим по условию задачи следующую таблицу
| 1 случай | 2 случай | ||||
| масса | Zn (%) |
Zn (кг) |
Zn (%) |
Zn (кг) |
|
| 1 сплав | 2кг | х % | 0,02 х кг |
у % |
0,02 у кг |
| 2 сплав | 3кг | у % | 0,03 у кг |
х % | 0,03 х кг |
| 3 сплав | 5кг | 45% | 2,25 кг | 60% | 3 кг |
| 4 сплав | 10кг | 50% | 5 кг | 55% | 5,5 кг |
По таблице составим систему уравнений
прибавим к первому уравнению второе, получим
Ответ: 40% и 65%.
Имеется два разных сплава меди со свинцом. Если взять 1 кг первого сплава и 1
кг второго сплава и переплавить их, то получится сплав с содержанием 65% меди.
Известно, что если взять кусок № 1 и кусок № 2 первого и второго сплавов
соответственно, имеющих суммарную массу 7 кг, и переплавить их, то получится
сплав с содержанием 60% меди. Какова масса меди, содержащаяся в сплаве,
получающемся при совместной переплавке куска первого сплава, равного по массе
куску № 2, и куска второго сплава, равного по массе куску № 1?
Решение: Составим по условию задачи следующую таблицу
| 1случай | 2 случай | 3 случай | |||||
| масса | Cu (%) |
Cu (кг) |
масса | Cu (кг) |
масса | Cu (кг) |
|
| 1 сплав | 1 кг | n% | 0,01n кг |
х кг | 0,01n кг |
у кг | 0,01n у кг |
| 2 сплав | 1 кг | m% | 0,01m кг |
у кг | 0,01m у кг |
х кг | 0,01m х кг |
| 3 сплав | 2 кг | 65% | 1,3 кг |
7 кг | 60% или 4,2 кг |
По данным таблицы составим систему уравнений
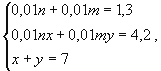
у + 0,01m
х.
Представим его в виде 0,01(n у
+ m х).
Решим систему уравнений.
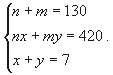
уравнение на третье и вычтем второе.
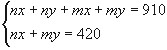
Ответ: 4,9 кг.
4. Имеется два слитка сплавов золота и меди. В первом слитке отношение золота к
меди равно 1 : 2, а во втором 2 : 3. Если сплавить 1/3 первого слитка с 5/6 второго,
то в получившемся слитке окажется столько золота, сколько было бы в первом меди,
а если 2/3 первого слитка сплавить с половиной второго, то в получившемся слитке
окажется меди на 1 кг больше, чем было золота во втором слитке. Сколько золота в
каждом слитке?
Решение: Пусть в первом слитке содержится х кг
золота и 2х кг меди.
Тогда масса всего слитка 3х кг. Пусть во втором
слитке содержится 2у кг
золота и 3у кг меди. Тогда
масса всего слитка 5у кг. Составим
таблицу:
| 1 случай | 2 случай | ||||||
| Масса всего сплава | Масса части сплава |
Золото (кг) |
Медь (кг) |
Масса части сплава |
Золото (кг) |
Медь (кг) |
|
| 1 сплав | 3х кг | х кг | 2х кг | ||||
| 2 сплав | 5у кг | 2,5у кг | у кг | 1,5 у кг | |||
| 3 сплав | 2х | (2у + 1) кг |
По данным таблицы составим систему уравнений
Ответ: 1,2 кг и 2,4 кг.
5. Имеется три слитка: первый слиток – сплав меди с никелем, второй – никель с
цинком, третий цинка с медью. Если сплавить первый кусок со вторым, то процент
меди в получившемся слитке будет в два раза меньше, чем он был в первом слитке.
Если сплавить второй слиток с третьим, то процент никеля в получившемся слитке
будет в три раза меньше, чем он был во втором слитке. Какой процент цинка будет
содержать слиток, получившийся при сплаве всех трех слитков, если во втором
слитке было 6% цинка, а в третьем – 11%?
Решение: Заметим, что во втором слитке нет меди, а если его сплавить с
первым, в котором есть медь, то процент меди в новом сплаве будет в 2 раза меньше, чем он был в
первом слитке, значит масса первого слитка равна массе второго. Пусть их масса будет
х.
Если сплавить второй слиток, в котором есть никель, с третьим слитком, в котором
никеля нет, то процент никеля в новом сплаве будет в 3 раза меньше, чем он был
во втором слитке. Значит второй слиток по массе в 2 раза больше второго. Значит
его масса будет 2х. Занесем данные в
таблицу:
| Масса слитка |
Zn (%) | Zn (масса) | |
| 1 слиток | х | нет | нет |
| 2 слиток | х | 6% | 0,06х |
| 3 слиток | 2х | 11% | 0,22х |
| 4 слиток | 4х | y % | 0,28х |
Ответ: 7%
6. В сосуде находится определенное количество смеси
воды с кислотой. Чтобы уменьшить концентрацию кислоты на 34% (было p%, а стало
p-34%) в сосуд надо долить 3 л воды, а чтобы уменьшить её на 17%, надо долить 1
л воды. Какова концентрация кислоты в сосуде?
Решение: Составим по условию задачи следующую таблицу:
|
Кол-во смеси |
Кислота в % |
Кислота в литрах |
y л |
х% |
0,01xy |
|
(y + 3) л |
(x – 34) % |
0,01(y + 3)(x – 34) |
|
(y +1) л |
(x – 17) % |
0,01(y + 1)(x – 17) |
Если к раствору кислоты добавить чистую воду, то изменится
концентрация кислоты, а количество кислоты не меняется. На этом основании составим
систему уравнений:
Ответ: 68%.
7. Имеется три слитка золота массой 2 кг, 3 кг и 5 кг с
различным процентным содержанием золота. Каждый слиток разделен на три куска и
из 9 получившихся кусков получили три слитка массой 2 кг, 3 кг и 5 кг, но уже с
равным процентным содержанием золота. На какие части следует разделить каждый
слиток, чтобы гарантировать равное процентное содержание золота в получившихся
слитках независимо от его содержания в исходных слитках.
Решение: Процентное содержание золота в новых
получившихся слитках 2 кг, 3 кг и 5 кг будет равно процентному содержанию золота в слитке, который
получится если просто сплавить исходные слитки массой 2 кг, 3 кг и 5 кг в
десятикилограммовый кусок. Тогда золото входит в каждый новый слиток в отношении 2 : 3 :
5 . Значит нужно Каждый исходный слиток разделить на части пропорциональные
этим числам. Всего частей 10. Получим
2 : 10 * 2 = 0,4; 2 : 10 * 3 = 0,6; 2 : 10 * 5 = 1
и т.д. Представим этот результат в виде таблицы.
| Масса слитка | 1часть | 2часть | 3часть | |
| 1 слиток | 2 кг | 0,4 кг | 0,6 кг | 1 кг |
| 2 слиток | 3 кг | 0,6 кг | 0,9 кг | 1,5 кг |
| 3 слиток | 5 кг | 1 кг | 1,5 кг | 2,5 кг |
Задачи для самостоятельного решения
8. Из трех кусков сплавов меди и никеля с соотношением по массе этих
металлов 2 : 1, 3 : 1, 5 : 1 получили новый сплав. Его масса оказалась равной 12
кг, а соотношение меди и никеля в нем составило 4:1. Найти массу каждого
исходного куска, если первый весил вдвое больше второго.
Ответ: 1,92 кг,
0,96 кг, 9,12 кг.
9. Из трех кусков сплавов серебра и меди с соотношением масс этих металлов
3:2, 2:3, 1:4 получили новый сплав. Его масса оказалась равной 22 кг, а
соотношение серебра и меди в нем составило 1:1. Найти массу каждого
исходного куска, если второй весил вдвое больше третьего. Ответ: 13,75 кг,
5,5 кг, 2,75 кг.
10. Из трех кусков сплавов олова и свинца с соотношением масс этих металлов
4 : 1, 1 : 1, 1 : 4 получили новый сплав. Его масса оказалась равной 24 кг, а
соотношение олова и свинца в нем составило 2 : 3. Найти массу каждого
исходного куска, если первый весил вдвое больше второго.
Ответ: 6,4 кг, 3,2
кг, 14,4 кг.
11. Из трех кусков сплавов золота и серебра с соотношением масс этих
металлов 1 : 1, 1 : 5, 5 : 1 получили новый сплав. Его масса оказалась равной 24
кг, а соотношение золота и серебра в нем составило 2 : 1. Найти массу каждого
исходного куска, если третий кусок весил втрое больше первого.
12. Имеются два сплава, в одном из которых содержится 20%, в другом 30%
олова. Сколько нужно взять первого и второго сплава, чтобы получить 10 кг
нового сплава, содержащего 27% олова?
Ответ: 3 кг , 7 кг.
13. Имеются два сплава, в одном из которых содержится 40%, а во втором 20%
серебра. Сколько кг второго сплава нужно добавить к 20 кг первого, чтобы
получить сплав, содержащий 32% серебра?
14. Имеются два сплава, в одном из которых содержится 10%, а в другом
– 20%
меди. Сколько нужно взять первого и второго сплавов, чтобы получить 15 кг
нового сплава, содержащего 14% меди?
Ответ: 9 кг и 6 кг.
15. Имеются два сплава, в одном из которых содержится 30%, а в другом
– 50%
золота. Сколько кг второго сплава нужно добавить к 10 кг первого, чтобы
получить сплав, содержащий 42% золота?
Ответ: 15 кг.
16. Из молока, жирность которого 5%, делают творог, жирностью 0,5%.
Определить, сколько творога получается из 1 тонны молока?
Ответ: 300 кг.
17. При смешивании растворов, содержащих 25% и 60% кислоты, получился
раствор, содержащий 39% кислоты. Определить в какой пропорции были смешаны
растворы?
Ответ: 3 : 2.
18. Добытая руда содержит 21% меди, а обогащенная – 45%. Известно, что в
процессе обогащения 60% добытой руды идет в отходы. Определить процентное
содержание меди в отходах.
Ответ: 5%.
19. В 100 граммов 20%-ного раствора соли добавили 300 граммов ее 10%-ного
раствора. Определить концентрацию полученного раствора.
Ответ: 12,5%.
20. Какое количество воды надо добавить к 100 граммам 70%-ной уксусной
эссенции, чтобы получить 5% раствор уксуса?
Ответ: 1300 гр.
21. Процентное содержание соли в растворе сначала снизилось на 20%, а затем
повысилась на 20%. На сколько процентов изменилось первоначальное содержание
соли?
Ответ: на 4%.
22. Морская вода содержит 5% соли. Сколько килограммов пресной воды надо
добавить к 40 кг морской воды, чтобы содержание соли в последней составляло
2%.
Ответ: 60 кг.
23. Сплав весит 2 кг и состоит из серебра и меди, причем вес серебра
составляет
веса меди. Сколько килограммов серебра в данном сплаве?
Ответ: 0,25 кг.
24. Имеется лом стали двух сортов с содержанием никеля 5% и 40% . Сколько
нужно взять каждого из этих сортов металлолома, чтобы получить 140т стали с
содержанием никеля 30%.
Ответ: 40 т и 100 т.
25. Кусок сплава меди с оловом весом 2 кг содержит 45% меди. Сколько чистого
олова надо прибавить к этому куску, чтобы получившийся новый сплав имел 40%
меди?
Ответ: 1,5 кг.
26. Сколько чистого спирта надо прибавить к 735 г 16%-ного раствора йода в
спирте, чтобы получить 10%-ный раствор?
Ответ: 441 г.
27. Сплав из меди и цинка весом в 24 кг при погружении в воду потерял в
своем весе
Определить количество меди и цинка в этом сплаве, если известно, что медь
теряет в воде
своего веса, а цинк
своего веса.
Ответ: 17 кг и 7 кг.
28. Имеются два сплава золота и серебра. В одном количество этих металлов
находится в отношении 2 : 3, а в другом в отношении 3 : 7. Сколько нужно взять
от каждого сплава, чтобы получить 8 кг нового сплава, в котором золото и
серебро были бы в отношении 5 : 11?
Ответ: 1 кг, 7 кг.
29. Одна бочка содержит смесь спирта с водой в отношении 2 : 3, а другая в
отношении 3 : 7. По сколько ведер надо взять из каждой бочки, чтобы составить
12 ведер смеси, в которой спирт и вода были бы в отношении 3 : 5?
Ответ: 9
ведер из первой и 3 ведра из второй.
30. Два раствора, из которых первый содержал 800 г безводной серной кислоты,
а второй 600 г безводной серной кислоты, соединили вместе и получили 10 кг
нового раствора серной кислоты. Определить вес первого и второго растворов,
вошедших в смесь, если известно, что процент содержания безводной серной
кислоты в первом растворе на 10% больше, чем процент содержания безводной
серной кислоты во втором.
Ответ: 4 кг и 6 кг.
31. Имелось два разных сплава меди. Процент содержания меди в первом сплаве
был на 40 меньше, чем процент содержания меди во втором сплаве. После того
как их сплавили вместе, получили сплав, содержащий 36% меди. Определить
процентное содержание меди в первом и втором сплавах, если известно,
содержание меди в первом сплаве было 6 кг, а во втором 12 кг.
Ответ: 20% и
60%.
32. 36 г цинка в воде весят 31 г, а 23 г свинца в воде весят 21 г. Сплав
цинка и свинца массой 292 г в воде весит 261 г. Сколько цинка и сколько
свинца содержится в сплаве?
Ответ: 108 г цинка и 184 г свинца.
33. В двух одинаковых сосудах, объемом по 30 л каждый, содержится всего 30 л
кислоты. Первый сосуд доливают доверху водой и полученной смесью дополняют
второй сосуд, затем из второго сосуда отливают в первый 12 литров смеси.
Сколько кислоты было первоначально в первом сосуде, если во втором сосуде
после переливаний оказалось на 2 л меньше кислоты, чем в первом?
Ответ: 20
литров.
34. Имеется два слитка сплавов золота и меди. В первом слитке отношение
золота к меди равно 1 : 2, а во втором 2 : 3. Если сплавить 1/3 первого слитка с
5/6 второго, то в получившемся слитке окажется столько золота, сколько было
бы в первом меди, а если 2/3 первого слитка сплавить с половиной второго, то
в получившемся слитке окажется меди на 1 кг больше, чем было золота во
втором слитке. Сколько золота в каждом слитке?
Ответ: 1,2 кг и 2,4 кг.
35. Имеется два сосуда. В одном содержится три литра 100%-ной серной
кислоты, а в другом два литра воды. Из первого сосуда во второй перелили
один стакан кислоты, а затем из второго в первый – один стакан смеси. Эту
операцию повторили еще два раза. В результате во втором сосуде образовалась
42%-ная кислота. Сколько серной кислоты в процентах содержится теперь в
первом сосуде?
Ответ: 72%.
36. Имеется два куска металла массой 1 кг и 2 кг. Из этих кусков сделали два
других: первый массой 0,5 кг, содержащий 40% меди, а второй массой 2,5 кг,
содержащий 88% меди. Каково процентное содержание меди в исходных кусках?
Ответ: 40% и 100%.
37. Из колбы в пробирку отлили
раствора соли. Раствор в пробирке выпаривали, пока процентное содержание
соли в нем не увеличилось в два раза. Получившийся раствор вернули в колбу, что
увеличило процентное содержание соли в находившемся в колбе растворе на 2 %.
Какое процентное содержание соли было в растворе первоначально?
Ответ: 10%.
Литература:
- Шарыгин И.Ф. “Математика для поступающих в ВУЗы”. Москва, Дрофа, 2000 г.
- Сканави М.И. “2500 задач по математике для поступающих в ВУЗы”.
Москва, Оникс, 2003 г. - Черкасов О., Якушев А. “Математика”. Москва, Айрис, 2000 г.
- Белоносов В.С., Фокин М.В. “Задачи вступительных экзаменов по
математике.” Новосибирск, издательство НГУ, 1995 г.
Как правило, ученики очень не любят задачи на сплавы и смеси. Для них они являются сложными и непонятными.
Поэтому многие даже время не тратят на попытки решения такой задачи в ЕГЭ, а просто пропускают ее. А зря!
Сейчас покажем, как можно решить такую задачу, выполнив всего три действия.
- Как решить задачу на смеси и сплавы: 3 действия
- Примеры решения задач на смеси: от простого к сложному
- Примеры решения задач на сплавы: от простого к сложному
Как решить задачу на смеси и сплавы: 3 действия
Итак, решение любой задачи на смеси и сплавы сводится к выполнению трех действий:
- Необходимо составить таблицу, в которой указываем общую массу каждого вещества и чистую массу каждого вещества. Эти данные содержатся в условии задачи. Если какие-то данные в условии отсутствуют, то обозначаем их как неизвестные — х, у.
- Составляем систему уравнений, основываясь на том, что при соединении двух смесей (или сплавов) их массы складываются. Т.е. мы складываем как общую массу двух изначальных смесей (или сплавов), так и чистую массу каждого вещества, содержащихся в них. Решаем полученную систему уравнений.
- После решения системы уравнений и нахождения всех неизвестных обязательно возвращаемся к условию задачи и смотрим, что требовалось найти. Многие ученики, решив правильно систему уравнений, неправильно записывают ответ. Ведь решение системы – это еще не ответ к задаче! Вернитесь к условиям задачи, прочитайте, что именно требовалось найти, и запишите ответ.
Примеры решения задач на смеси: от простого к сложному
А теперь разберем на примерах, как с помощью этих трех действий решать задачи на смеси и сплавы.
Задача 1
Смешали 3 литра раствора, содержащего 20% кислоты, и 5 литров раствора, содержащего 40% той же кислоты. Какова концентрация кислоты в полученном растворе.
Решение:
Для решения задачи выполняем три действия, о которых мы говорили выше:
1. Составляем таблицу, в которой указываем общую массу раствора и массу чистого вещества, то есть в нашем случае – кислоты.
Из условий задачи имеем три раствора:
Раствор 1: 3 литра с 20% кислотой, т.е. общая масса = 3 литра, масса чистого вещества = 3 * 20% = 3 * 0,2 = 0,6
Раствор 2: 5 литров с 40% кислотой, т.е. общая масса = 5 литров, масса чистого вещества = 5 * 40% = 5 * 0,4 = 2
Раствор 3: какое-то количество раствора (обозначим его общую массу за х) с какой-то концентрацией кислоты (обозначим ее чистую массу за у), заносим эти данные в таблицу:
2. Составляем уравнения. Вспоминаем, что общая масса раствора 3 является суммой общих масс раствора 1 и раствора 2. А масса чистого вещества в растворе 3 является суммой массы чистового вещества в растворе 1 и массы чистового вещества в растворе 2. Таким образом, получаем:
3 + 5 = х
0,6 + 2 = у
Решаем простейшее уравнение и получаем, что х = 8, а у = 2,6. Таким образом, раствор 3 получился 8 литров, из которых 2,6 литра – это кислота.
Но ответ к задаче записывать рано! Переходим к третьему действию решения нашей задачи.
3. Возвращаемся к условию задачи и вспоминаем, а что же требовалось найти. В нашей задаче требовалось определить концентрацию кислоты в растворе 3. Когда мы решили уравнения, мы нашли общую массу раствора 3 и массу чистого вещества (кислоты), содержащегося в нем.
Чтобы определить концентрацию вещества необходимо разделить массу чистого вещества на общую массу раствора.
Таким образом, концентрация кислоты в растворе 3 равна:
2,6 / 8 = 0,325
Переводим долю вещества в проценты. Для этого умножаем полученный результат на 100:
0,325 * 100 = 32,5%
Ответ: 32,5%
Задача 2
Газ в сосуде А содержал 21% кислорода, а газ в сосуде В содержал 5% кислорода. Масса газа в сосуде А была больше массы газа в сосуде В на 300 г. Когда перегородку между сосудами убрали, газы перемешались, и получился третий газ, который содержит 14,6% кислорода. Найти массу третьего газа.
Решение:
1. Составляем таблицу. Для этого обозначим массу газа в сосуде В – х. Остальные данные берем из условий задачи и формируем таблицу:
(х +300) * 0,21 + х * 0,05 = 0,146 (х + (х +300))
0,21х + 63 + 0,05х = 0,292х + 43,8
0,26х + 63 = 0,292х + 43,8
0,032х = 19,2
х = 600
3. Возвращаемся к условиям задачи и вспоминаем, что нужно было найти. А найти нам нужно было массу третьего газа. Подставляем в уравнение общей массы газа 3 из таблицы и получаем:
600 + 600 + 300 = 1500 г
Ответ: масса третьего газа равна 1500 г.
Задача 3
Смешали 40%ый и 15%ый растворы кислоты, затем добавили 3 кг чистой воды, в результате чего получили 20%ый раствор кислоты. Если бы вместо 3 кг воды добавили 3 кг 80% раствора той же кислоты, то получили бы 50%ый раствор кислоты. Сколько килограммов 40%го и 15%го растворов кислоты было смешано?
Решение:
1. Составляем таблицу. По условиям задачи мы имеем пять растворов:
Раствор 1: 40%ая кислота. Обозначим ее массу за х, тогда масса чистого вещества = х * 40% = 0,4х
Раствор 2: 15%ая кислота. Обозначим ее массу за у, тогда масса чистого вещества = х * 15% = 0,15х
Вода: вода, масса которой равна 3 кг. Концентрация кислоты в воде равна 0. Таким образом, масса чистого вещества равна 3 * 0 = 0
Раствор 3: 80%ая кислота. Ее масса по условию задачи равна 3 кг, тогда масса чистого вещества равна 3 * 80% = 3 *0,8 = 2,4
Раствор 4: соединение раствора 1, раствора 2 и воды. Таким образом, общая масса полученного раствора равна х + у + 3. А масса чистого вещества в этом растворе равна 0,4х + 0,15у + 0
Раствор 5: соединение раствора 1, раствора 2 и раствора 3. Таким образом, общая масса полученного раствора равна х + у + 3. А масса чистого вещества в этом растворе равна 0,4х + 0,15у + 2,4.
Сводим полученные результаты в таблицу:
По условиям задачи раствор 5 имеет концентрацию 50%. Таким образом, чтобы получить массу чистого вещества в растворе 5 нужно его общую массу умножить на концентрацию. Получаем (х + у + 3) * 0,5. Теперь берем массу чистого вещества раствора 5, которую мы выразили в таблице и приравниваем два этих уравнения:
(х + у + 3) * 0,5 = 0,4х + 0,15у + 2,4
Аналогично поступаем с раствором 4. По условиям задачи его концентрация равна 20%. Тогда получаем следующее уравнение:
(х + у + 3) * 0,2 = 0,4х + 0,15у
Объединяем полученные уравнения в систему:
3. Возвращаемся к условиям задачи.
По условиям задачи необходимо было найти, какое количество килограммов 40%го и 15%го растворов кислоты было смешано. Общая масса 40%й кислоты мы обозначали х, а общую массу 15%й кислоты мы обозначили у. Следовательно, масса 40%й кислоты = 3,4 кг, а масса15%й кислоты = 1,6 кг.
Ответ: масса 40%й кислоты = 3,4 кг, а масса15%й кислоты = 1,6 кг.
Примеры решения задач на сплавы: от простого к сложному
Задача 1
Бронза является сплавом меди и олова (в разных пропорциях). Кусок бронзы, содержащий 1/12 часть олова, сплавляется с другим куском, содержащим 1/10 часть олова. Полученный сплав содержит 1/11 часть олова. Найдите вес второго куска, если вес первого равен 84 кг
Решение:
1. Составим таблицу. Обозначим массу второго куска – х.
1/12 * 84 + 1/10 * х = 1/11 * (84 + х)
7 + х/10 = 84/11 + х/11
х/10 – х/11 = 7/11
х/110 = 7/11
х/10 = 7
х = 70
3. Возвращаемся к условию задачи. Найти нужно было вес второго куска. Вес второго куска равен 70 кг.
Ответ: 70 кг.
Задача 2
Имеются два сплава меди со свинцом. Один сплав содержит 15% меди, а другой 65%. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?
Решение.
1. Составим таблицу. Пусть масса первого сплава – х, масса второго сплава – у. Остальные данные берем из решения и составляем таблицу:
х + у = 200
Содержание меди в третьем сплаве по условиям задачи равно 30%, т.е. масса чистого вещества равна 0,3(х + у). Следовательно, берем массу чистого вещества из таблицы и приравниваем:
0,15х + 0,65у = 0,3(х + у)
Получившиеся уравнения сводим в систему и решаем ее:
0,15(200 – у) + 0,65у = 0,3 * 200
30 – 0,15у + 0,65у = 60
0,5у = 30
у = 60
х = 140
3. Возвращаемся к условиям задачи. Необходимо было найти массу первого и второго сплава. Масса первого сплава — 140 г, масса второго сплава -60 г.
Ответ: 140 г и 60 г.
Задача 3
В первом сплаве содержание меди составляет 70%, а во втором – 40%. В каком отношении надо взять эти сплавы, чтобы получить из них новый сплав, который содержит 50% меди?
Решение:
1. Составим таблицу. Обозначим массу первого сплава – х, массу второго сплава – у. Тогда:
0,7х + 0,4у = 0,5 (х + у)
0,7х + 0,4у = 0,5х + 0,5у
0,2х = 0,1у
х/у = ½
3. Возвращаемся к условию задачи. Необходимо было определить отношение первого и второго сплавов в третьем сплаве. Отношение сплавов равно ½.
Ответ: ½
Итак, решение задач на сплавы и смеси можно свести к трем действиям: составление таблицы, составление уравнения (или системы уравнений), возвращение к условиям задачи, чтобы дать ответ на поставленный вопрос. Задание 11 ЕГЭ по математике профильного уровня является одной из самых сложных задач, так как может содержать текстовую задачу любого типа. Это может быть как задача на сплавы и смеси, так и задача на движение, работу, проценты. Как решать все эти задачи вы можете узнать на нашем сайте или
Задачи на смеси и сплавы — подробнее
Концентрация какого-то вещества в растворе – это отношение массы или объема этого вещества к массе или объему всего раствора.
То же самое относится и к сплавам: содержание одного из металлов в сплаве – это отношение массы этого металла к массе всего сплава.
Обычно концентрация измеряется в процентах.
Что такое процент?
Напомню, что это сотая доля числа. То есть, если массу или объем разделить на ( displaystyle 100), получим ( displaystyle 1%) этой массы или объема.
Чтобы вычислить концентрацию в процентах, достаточно полученное число умножить на ( displaystyle 100%).
Почему?
Сейчас покажу: пусть масса всего раствора равна ( displaystyle M), а масса растворенного вещества (например, соли или кислоты) – ( displaystyle m). Тогда один процент от массы раствора равен ( displaystyle frac{M}{100}).
Как узнать, сколько таких процентов содержится в числе ( displaystyle m)?
Просто: поделить число ( displaystyle m) на этот один процент: ( displaystyle frac{m}{frac{M}{100}}=frac{m}{M}cdot 100), но ведь ( displaystyle frac{m}{M}) – это концентрация.
Вот и получается, что ее надо умножить на ( displaystyle 100), чтобы узнать, сколько процентов вещества содержится в растворе.
Более подробно о процентах – в темах «Дроби, и действия с дробями»и «Проценты».
Поехали дальше.
Масса раствора, смеси или сплава равна сумма масс всех составляющих.
Логично, правда?
Например, если в растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг соли, то сколько в нем воды? Правильно, ( displaystyle 7)кг.
И еще одна очевидность:
При смешивании нескольких растворов (или смесей, или сплавов), масса нового раствора становится равной сумме масс всех смешанных растворов.
А масса растворенного вещества в итоге равна сумме масс этого же вещества в каждом растворе отдельно.
Например: в первом растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг кислоты, а во втором растворе массой ( displaystyle 14) кг – ( displaystyle 5) кг кислоты.
Когда мы их смешаем, чему будет равна масса нового раствора?
( displaystyle 10+14=24) кг.
А сколько в новом растворе будет кислоты? ( displaystyle 3+5=8) кг.
Перейдем к задачам.
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ №11. Задачи на растворы, смеси и сплавы (и на проценты)
В этом видео мы научимся решать текстовые задачи на проценты, а так же на растворы, смеси и сплавы — на все, что содержит разные вещества в каком-то соотношении.
Задачи на смеси и сплавы очень часто попадаются на ОГЭ (№23) и профильном ЕГЭ (под номером 12).
Мы научимся очень простому способу сводить эти задачи к обычному линейному уравнению или к системе из двух таких уравнений.
Также мы научимся решать сложные задачи на проценты — в основном они на банковские вклады и кредиты и прочие финансовые штуки.
Это, в том числе, даст нам очень большой задел для “ экономической» задачи №17 (которая стоит аж 3 первичных балла).
ЕГЭ №17 Экономическая задача. Вклады
Экономические задачи в основном довольно простые, но дают аж 3 первичных балла!
Но это не совсем 3 балла нахаляву. Эти задачи требуют очень подробного и чёткого описания решения.
По сути, мы составляем математическую модель какой-то жизненной ситуации (например, связанной с банковскими вкладами или кредитами), и важно научиться ничего не пропускать при описании этой модели: описывать словами все введённые обозначения, обосновывать уравнения, которые мы записываем, и всё в таком духе.
Если не написать эти объяснения, вы гарантированно получите 0 баллов даже за правильно найденный ответ!
На этом уроке мы узнаем, как работают вклады, научимся решать и, главное, правильно оформлять решение таких задач.
Муниципальное общеобразовательное учреждение
«Еловская средняя общеобразовательная школа»
Решение задач на растворы, смеси и сплавы при подготовке к ОГЭ по математике
Меренкова
Татьяна Владиславовна,
учитель математики
МОУ «Еловская СОШ»,
соответствие занимаемой
должности
с. Елово
2017
В математике есть ряд текстовых задач, которые вызывают затруднение у учащихся при их решении. К таким задачам можно отнести задачи на растворы, смеси и сплавы. Практическое значение этих задач огромно. Встречаются они при изучении смежных дисциплин, например, химии. Самостоятельно справиться с ними могут немногие. Вместе с этим они являются хорошим средством развития мышления учащихся.
Трудности при решении этих задач могут возникать на различных этапах:
-
составления математической модели (уравнения, системы уравнений, неравенства и т. п.;
-
решения полученной модели;
-
анализа математической модели (по причине кажущейся ее неполноты: не хватает уравнения в системе и пр.).
Все сложности преодолимы при тщательном анализе задачи. Основными компонентами в этих задачах являются:
-
масса раствора (смеси, сплава);
-
масса вещества;
-
доля (% содержание) вещества.
При решении большинства задач этого вида, удобнее использовать таблицу, которая нагляднее и короче обычной записи с пояснениями. Зрительное восприятие определенного расположения величин в таблице дает дополнительную информацию, облегчающую процесс решения задачи и её проверки.
Этапы решения задачи:
1. Знакомство учащихся с текстом задач и выделение основных компонентов в них. Заполнение таблицы.
Таблица для решения задач имеет следующий вид:
|
Наименование веществ, растворов, смесей, сплавов |
Масса раствора (смеси, сплава) М |
% содержание вещества (доля содержания вещества) m / M * 100% |
Масса вещества m |
2. Составление уравнения и его решение.
3. Анализ полученных данных, ответ на вопрос задачи.
Рассмотрим решение задач с применением таблицы.
Задача 1. В сосуд содержащий 2 кг 80 % -го водного раствора уксуса добавили 3 кг воды. Найдите концентрацию получившегося раствора уксусной кислоты.
Решение:
|
Наименование веществ, смесей |
Масса раствора (смеси, сплава) М, кг |
% содержание вещества (доля содержания вещества) m / M * 100% |
Масса вещества m, кг |
|
Исходный раствор |
2 |
80 % = 0,8 |
0,8·2 |
|
Вода |
3 |
– |
– |
|
Новый раствор |
5 |
х % = 0,01х |
0,01х·5 |
Масса уксусной кислоты не изменилась, тогда получаем уравнение:
0,01х·5 = 0,8·2; 0,05х = 1,6; х = 1,6:0,05; х = 32.
Ответ: 32 %.
Задача 2. Сколько нужно добавить воды в сосуд, содержащий 200 г 70 % -го раствора уксусной кислоты, чтобы получить 8 % раствор уксусной кислоты?
Решение:
|
Наименование веществ, смесей |
Масса раствора (смеси, сплава) М, г |
% содержание вещества (доля содержания вещества) m / M * 100% |
Масса вещества m, г |
|
|
Исходный раствор |
200 |
70 % |
0,7·200 |
|
|
Вода |
х |
– |
– |
|
|
Новый раствор |
200 + х |
8 % |
0,08(200 + х) |
Анализируя таблицу, составляем уравнение :
0,08(200 + х) = 0,7·200; 16 + 0,08х = 140; 0,08х = 124; х = 1550.
Ответ :1,55 кг воды.
Задача 3. Смешали некоторое количество 12% раствора соляной кислоты с таким же количеством 20 % раствора этой же кислоты. Найти концентрацию получившейся соляной кислоты.
Решение:
|
Наименование веществ, смесей |
Масса раствора (смеси, сплава) М, г |
% содержание вещества (доля содержания вещества) m / M * 100% |
Масса вещества m, г |
|
I раствор |
х |
12 % |
0,12х |
|
II раствор |
х |
20 % |
0,2х |
|
Смесь |
2х |
0,32х/2х * 100% |
0,12х+ 0,2 х = 0,32х |
Анализируя таблицу, получаем :
0,32х/2х * 100% = 16 %
Ответ : 16 %.
Задача 4. Имеется два сплава с разным содержанием меди: в первом содержится 60%, а во втором — 45% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 55% меди?
Решение:
|
Наименование веществ, растворов, смесей, сплавов |
Масса раствора (смеси, сплава) М |
% содержание вещества (доля содержания вещества) m / M * 100% |
Масса вещества m |
|
Первый сплав |
х |
60% |
0,6 х |
|
Второй сплав |
у |
45% |
0,45 у |
|
Новый сплав |
х + у |
55% |
0,6 х + 0,45у |
Пусть первый сплав взят в количестве x кг, тогда он будет содержать 0,6x кг меди, а второй сплав взят в количестве y кг, тогда он будет содержать 0,45y кг меди. Соединив два этих сплава, получим сплав меди массой x + y, по условию задачи он должен содержать 0,55(x + y) меди. Следовательно, можно составить уравнение: 0,55(x + y) = 0,6 х + 0,45у;
0,55 х + 0,55 у = 0,6 х+ 0,45 у; 0,05 х = 0,1 у . Выразим x через y: х = 2 у.
Следовательно, отношение, в котором нужно взять сплавы 1:2.
Ответ: 1:2
Задача 5. Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава.
Решение:
|
Наименование веществ, растворов, смесей, сплавов |
Масса раствора (смеси, сплава) М |
% содержание вещества (доля содержания вещества) m / M * 100% |
Масса вещества m |
|
Первый сплав |
х |
5% |
0, 05 х |
|
Второй сплав |
х + 4 |
13% |
0,13(х +4) |
|
Новый сплав |
2х + 4 |
10% |
0, 05 х + 0,13(х +4)=0,18 х + 0,52 |
Пусть масса первого сплава x кг. Тогда масса второго сплава (x + 4) кг, а третьего — (2x + 4) кг. В первом сплаве содержится 0,05x кг меди, а во втором — 0,13(x + 4) кг. Поскольку в третьем сплаве содержится 0,1(2x + 4) кг меди, составим и решим уравнение: 0,1(2x + 4) = 0,18 х + 0,52; 0,02 х = 0,12; х = 6.
Откуда масса третьего сплава равна 16 кг.
Ответ:16 кг.
Задача 6. Смешали некоторое количество 10 % раствора некоторого вещества с таким же количеством 12 % раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение:
|
Наименование веществ, растворов, смесей, сплавов |
Масса раствора (смеси, сплава) М |
% содержание вещества (доля содержания вещества) m / M * 100% |
Масса вещества m |
|
1 |
х |
10% |
0, 1 х |
|
2 |
х |
12% |
0,12 х |
|
3 |
2х |
(0, 22 х / 2х)* 100 % |
0, 1 х + 0,12х = 0,22 х |
Пусть взяли х г 10-процентного раствора, тогда взяли и х г 12-процентного раствора. Концентрация раствора — масса вещества, разделённая на массу всего раствора. Концентрация получившегося раствора равна 0, 22 х / 2х или 11%.
Ответ: 11%.
Задача 7. Имеются два сосуда, содержащие 4 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 57% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Решение:
|
Наименование веществ, растворов, смесей, сплавов |
Масса раствора (смеси, сплава) М, кг |
% содержание вещества (доля содержания вещества) m / M * 100% |
Масса вещества M, кг |
|
Первый раствор |
4 |
х % |
0,04 х |
|
Второй раствор |
16 |
у % |
0,16 у |
|
Смесь 1 |
20 |
57% |
0,04 х + 0,16у |
|
Смесь 2 |
4+4 =8 |
60 % |
0,04х + 0,04 у |
Пусть концентрация первого раствора – х %, концентрация второго раствора – y %. Составим систему уравнений согласно условию задачи:
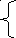
0,57 * 20 = 0,04 х + 0,16у, х = 65,
0,6 * 8 = 0,04х + 0,04 у; у = 55.
Таким образом, в первом растворе содержится 0,65 * 4 = 2,6 килограмма кислоты
Ответ: 2,6
Задача 8. Смешав 60% и 30% растворы кислоты и, добавив 5 кг чистой воды, получили 20% раствор кислоты. Если бы вместо 5 кг воды добавили 5 кг 90% раствора той же кислоты, то получили бы 70% раствор кислоты. Сколько килограммов 60% раствора использовали для получения смеси?
Решение:
|
Наименование веществ, растворов, смесей, сплавов |
Масса раствора (смеси, сплава) М, кг |
% содержание вещества (доля содержания вещества) m / M * 100% |
Масса вещества M, кг |
|
Первый раствор |
х |
60 % |
0,6 х |
|
Второй раствор |
у |
30 % |
03 у |
|
Смесь 1 |
х + у +5 |
20 % |
0,6 х + 0,3у |
|
Третий раствор |
5 |
90 % |
0,9* 5 = 4,5 |
|
Смесь 2 |
х + у +5 |
70 % |
0,6х + 0,3 у + 4,5 |
Пусть х кг и у кг — массы первого и второго растворов, взятые при смешивании. Тогда (х + у +5) кг — масса полученного раствора, содержащего (0,6 х + 0,3у) кг кислоты. Концентрация кислоты в полученном растворе 20 %, значит 0,2(х + у +5) %. Концентрация кислоты во втором растворе 70 %, значит 0,7 ( х + у + 5) = 0,6х + 0,3 у + 4,5. Решим систему двух полученных уравнений:
0,7 ( х + у + 5) = 0,6х + 0,3 у + 4,5;

0,1 х + 0,4 у = 1; у = 2.
Ответ: 2 кг.
Задача 9. Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Решение:
|
Наименование веществ, растворов, смесей, сплавов |
Масса раствора (смеси, сплава) М |
% содержание вещества (доля содержания вещества) m / M * 100% |
Масса вещества m |
|
Первый сплав |
х |
10% |
0, 1 х |
|
Второй сплав |
200-х |
30% |
0,3(200-х) |
|
Новый сплав |
200 |
25% |
0, 1 х + 0,3(200-х )= 0,25*200 |
Решим уравнение: 0, 1 х + 0,3(200-х )= 0,25*200; х = 50.
Масса второго сплава 150 кг.
Ответ: на 100 кг.
Задача 10. Имеется два куска слитка олова и свинца, содержащие 40% и 60% олова. По сколько граммов от каждого куска надо взять, чтобы получить 600 граммов сплава, содержащего 45% олова?
Решение:
|
Наименование веществ, растворов, смесей, сплавов |
Масса раствора (смеси, сплава) М |
% содержание вещества (доля содержания вещества) m / M * 100% |
Масса вещества m |
|
Первый кусок |
х |
40% |
0, 4 х |
|
Второй кусок |
600-х |
60% |
0,6 (600-х) |
|
Новый сплав |
600 |
45% |
0, 4 х + 0,6(600-х )= 0,45*600 |
Решим уравнение: 0, 4 х + 0,6(600-х )= 0,45*600; х = 450.
Ответ:450 кг и 150 кг.
Задача 11. Кусок сплава меди и цинка массой 36 кг, содержит 45% меди. Сколько килограммов меди нужно добавить к этому куску, чтобы получить новый сплав, содержащий 60% меди?
Решение:
|
Наименование веществ, растворов, смесей, сплавов |
Масса раствора (смеси, сплава) М, кг |
% содержание вещества (доля содержания вещества) m / M * 100% |
Масса вещества M, кг |
|
Первый кусок |
36 |
45% |
0, 45 *36 = 16,2 |
|
Медь |
х |
100% |
х |
|
Новый сплав |
36 + х |
60 % |
16,2 +х=0,6(36 + х) |
Получаем уравнение: 0, 45 х +х=0,6(36 + х), х = 13,5
Ответ: 13,5 кг
Задача 12. Имеется три сосуда. В первый сосуд налили 4 кг 70 % сахарного сиропа, а во второй – 6 кг 40 % сахарного сиропа. Если содержимое первого сосуда смешать с содержимым третьего сосуда, то получим в смеси 55 % содержание сахара, а если содержимое второго сосуда смешать с третьим, то получим 35 % содержание сахара. Найдите массу сахарного в третьем сосуде сиропа и концентрацию сахара в нем.
Решение:
|
Наименование веществ, смесей |
Масса раствора (смеси, сплава) М, кг |
% содержание вещества (доля содержания вещества) m / M * 100% |
Масса вещества M, кг |
|
|
I сосуд |
4 |
70 % |
0,7·4=2,8 |
|
|
II сосуд |
6 |
40 % |
0,4·6 = 2,4 |
|
|
III сосуд |
х |
у % |
0,01ху |
|
|
I и III сосуды |
4+х |
55 % |
0,55(4+х) = 2,8+0,01ху |
|
|
II и III сосуды |
6+х |
35 % |
0,35(6+х) = 2,4+0,01ху |
Итак, получаем систему уравнений :
Ответ :1,5 кг сахарного сиропа 15 % концентрации.
Задачи для самостоятельного решения:
13. Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Ответ: 8,7
14. Имеются два сосуда, содержащие 40 кг и 30 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 73% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 72% кислоты. Сколько килограммов кислоты содержится во втором растворе?
Ответ: 19,5
15. Имеются два сосуда, содержащие 40 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 33% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 47% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Ответ: 2.
16. Имеются два сосуда, содержащие 24 кг и 26 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 39% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Ответ: 15,6
17. Имеются два сосуда, содержащие 30 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 81% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 83% кислоты. Сколько килограммов кислоты содержится во втором растворе?
Ответ: 18,6
18. Имеются два сосуда, содержащие 22 кг и 18 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 32% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 30% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Ответ: 11
19. Имеются два сосуда, содержащие 30 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 40% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 37% кислоты. Сколько килограммов кислоты содержится во втором растворе?
20. Имеются два сосуда, содержащие 48 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 42% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты содержится во втором растворе?
21. Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Ответ: 58.
Заключение
В задачах этого типа прослеживается системный подход к решению задач. Происходит успешная отработка и закрепление интеллектуальных умений (анализ, синтез, аналогия, обобщение. конкретизация и т.д.). Данная система задач на смеси, растворы и сплавы была апробирована в ходе КПВ по математике в 8 классе в 2016-17 учебном году. Опыт показал, что учащиеся не знавшие вначале, как подойти к решению этих задач, в конце темы успешно заполняли таблицу и получали верный ответ.
Литература:
1.Открытый банк заданий ОГЭ http://www.fipi.ru/content/otkrytyy-bank-zadaniy-oge;
2. https://oge.sdamgia.ru Каталог заданий. Задачи на проценты, сплавы и смеси