Сравне́ние двух целых чисел по мо́дулю натурального числа 








Арифметические операции с остатками чисел по фиксированному модулю образуют мо́дульную арифме́тику или модуля́рную арифметику[1][2], которая широко применяется в математике, информатике и криптографии[3].
История[править | править код]
Предпосылкой к созданию теории сравнений стало восстановление сочинений Диофанта, которые были выпущены в подлиннике и с латинским переводом, благодаря Баше де Мезириаку, в 1621 году. Их изучение привело Ферма́ к открытиям, которые по значению существенно опередили своё время. Например, в письме к Френиклю де Бессиrufr[4] 18 октября 1640 года он сообщил без доказательства теорему, впоследствии получившую название малой теоремы Ферма. В современной формулировке теорема утверждает, что если 


.
Первое доказательство этой теоремы принадлежит Лейбницу, причём он открыл указанную теорему независимо от Ферма́ не позднее 1683 года и сообщил об этом с приведением точного доказательства Бернулли. Кроме этого, Лейбницем был предложен прообраз формулировки теоремы Вильсона.
Позже изучение вопросов, посвященных теории чисел и теории сравнений, было продолжено Эйлером, который ввел квадратичный закон взаимности и обобщил теорему Ферма, установив, что
где 
Понятие и символьное обозначение сравнений было введено Гауссом, как важный инструмент для обоснования его арифметической теории, работа над которой была начата им в 1797 году. В начале этого периода Гауссу ещё не были известны труды его предшественников, поэтому результаты его работы, изложенные в первых трёх главах его книги «Арифметические исследования» (1801 год), были в основном уже известны, однако методы, которые он использовал для доказательств, оказались абсолютно новыми, имеющими высшую важность для развития теории чисел. Используя эти методы, Гаусс преобразовал все накопленные до него сведения, связанные с операциями сравнения по модулю, в стройную теорию, которая впервые была изложена в этой же книге. Кроме этого, он исследовал сравнения первой и второй степени, теорию квадратичных вычетов и связанный с ней квадратичный закон взаимности[5].
Определения[править | править код]
Сравнимость чисел 

Число 
Определение сравнимости чисел 


Например, числа 32 и −10 сравнимы по модулю 7, так как оба числа при делении на 7 дают остаток 4:
Также числа 32 и -10 сравнимы по модулю 7, так как их разность 
Свойства сравнимости по модулю[править | править код]
Для фиксированного натурального числа 

Таким образом, отношение сравнимости по модулю 
Кроме вышеперечисленных свойств, для сравнений справедливы следующие утверждения:
Доказательство
Пусть
Следовательно
где
— некое целое число.
Так как 

где
— некое целое число.
Следовательно
где
и
по определению.
- Следствие:
- Для того, чтобы числа
и
были сравнимы по модулю
, каноническое разложение на простые сомножители которого имеет вид
необходимо и достаточно, чтобы
где
[9].
Операции со сравнениями[править | править код]
Сравнения по одному и тому же модулю обладают многими свойствами обычных равенств. Например, их можно складывать, вычитать и перемножать: если числа 







При этом нельзя выполнять эти операции со сравнениями, если их модули не совпадают[9].
К обеим частям сравнения можно прибавить одно и то же число 
Также можно перенести число из одной части сравнения в другую со сменой знака:
Если числа 






K любой из частей сравнения можно прибавить целое число, кратное модулю, то есть, если числа 








Также обе части сравнения и модуль можно умножить на одно и то же число, то есть, если числа 






Сравнения, однако, нельзя, вообще говоря, делить друг на друга или на другие числа. Пример: 

- Можно делить обе части сравнения на число, но только взаимно простое с модулем: если
и НОД
то
.
Если, число 

- Можно одновременно разделить обе части сравнения и модуль на их общий делитель:
если 

Пример[править | править код]
Применение сравнений позволяет легко получать разнообразные признаки делимости. Например, выведем признак делимости натурального числа N на 7. Запишем 




Или, прибавив слева число 
Отсюда вытекает следующий признак делимости на 7: надо вычесть из числа десятков удвоенное число единиц, затем повторять эту операцию до тех пор, пока не получится двузначное или однозначное число; если оно делится на 7, то и исходное число делится. Например, пусть 
Вывод: 22624 делится на 7.
Связанные определения[править | править код]
Классы вычетов[править | править код]
Множество всех чисел, сравнимых с 



![[a]_m](https://wikimedia.org/api/rest_v1/media/math/render/svg/54d89656467018df3c7644d8776a28eef1b154c5)


![[a]_m=[b]_m](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4535aa2ee4426cfd61db811230d77b9b5105e9d)
Любое число класса вычетов называется вычетом по модулю 
















Поскольку сравнимость по модулю 



Множество всех классов вычетов по модулю 



Операции сложения и умножения на 

Относительно этих операций множество 

Системы вычетов[править | править код]
Система вычетов позволяет осуществлять арифметические операции над конечным набором чисел, не выходя за его пределы.
Полная система вычетов по модулю 


Обычно в качестве полной системы вычетов по модулю 
- наименьшие неотрицательные вычеты, то есть числа:
- или абсолютно наименьшие вычеты, состоящие в случае нечётного
из чисел
-
,
- и в случае чётного
из чисел
Максимальный набор попарно несравнимых по модулю 





Например, для числа 
Сравнения в кольце многочленов над полем[править | править код]
Рассматривается кольцо многочленов ![K[x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a9e6c2ac2830d6a9abe078b47450777c41d69a9)






Так же, как и в кольце целых чисел, такие сравнения можно складывать, вычитать и перемножать[15].
Решение сравнений[править | править код]
Сравнения первой степени[править | править код]
В теории чисел, криптографии и других областях науки часто возникает задача поиска решений сравнения первой степени вида
Решение такого сравнения начинается с вычисления 

-
- где
и
являются целыми числами, причём
и
взаимно просты. Поэтому число
можно обратить по модулю
, то есть найти такое число
, что
(другими словами,
). Теперь решение находится умножением полученного сравнения на
:
Практическое вычисление значения 

[16].
Примеры[править | править код]
Пример 1. Для сравнения
имеем 
Поскольку 3 взаимно просто с модулем 11, то его можно обратить по модулю 11 и найти
.
Умножая сравнение на 4, получаем решение по модулю 11:
,
эквивалентное совокупности двух решений по модулю 22:
и
.
Пример 2. Дано сравнение:
Отметим, что модуль
— простое число.
Первый способ решения — воспользоваться соотношением Безу. С помощью алгоритма Евклида или программы, приведенной в статье о соотношении Безу, находим, что это соотношение для чисел 

или
Умножив обе части этого сравнения на 41, получим:
Отсюда следует, что 




Второй способ решения, более простой и быстрый, не требует построения соотношения Безу, но также эквивалентен алгоритму Евклида.
Шаг 1. Делим модуль на коэффициент при x с остатком: 




Мы получили при 
Шаг 2. Аналогично делим на новый коэффициент при x: 





Далее можно было бы сделать аналогично ещё 5 шагов, но проще разделить обе части сравнения на 10 и сразу получить результат: 
Сравнения второй степени[править | править код]
Сравнения второй степени по простому модулю m имеет следующий общий вид:
Это выражение можно привести к виду
а при замене 
Решение этого сравнения сводится к выяснению, является ли данное число квадратичным вычетом (с помощью квадратичного закона взаимности) и последующему вычислению квадратного корня по данному модулю[17]. Для вычисления квадратного корня из квадратичного вычета существует вероятностный метод Берлекэмпа и детерминированный алгоритм Тонелли — Шенкса.
Системы сравнений[править | править код]
Китайская теорема об остатках утверждает, что система сравнений с попарно взаимно простыми модулями 
всегда разрешима, и её решение единственно по модулю 
Другими словами, китайская теорема об остатках утверждает, что кольцо вычетов по модулю произведения нескольких попарно взаимно простых чисел является прямым произведением соответствующих множителям колец вычетов.
Применение[править | править код]
Модульная арифметика используются в теории чисел, теории групп, теории колец, теории узлов, общей алгебре, криптографии, информатике, химии и других областях.
Например, сравнения часто применяются для вычисления контрольных сумм, используемых в идентификаторах. Так, для определения ошибок при вводе международного номера банковского счета используется сравнение по модулю 97[18].
В криптографии сравнения можно встретить в системах с открытым ключом, использующих, например, алгоритм RSA или протокол Диффи — Хеллмана. Также, модульная арифметика обеспечивает конечные поля, над которыми затем строятся эллиптические кривые, и используется в различных протоколах с симметричным ключом (AES, IDEA)[19].
В химии последняя цифра в регистрационном номере CAS является значением контрольной суммы, которая вычисляется путём сложения последней цифры номера, умноженной на 1, второй справа цифры, умноженной на 2, третьей, умноженной на три и так далее до первой слева цифры, завершаясь вычислением остатка от деления на 10[20]
См. также[править | править код]
- Сложение по модулю 2
- Возведение в степень по модулю
- Показатель числа по модулю
- Алгоритмы быстрого возведения в степень по модулю
Примечания[править | править код]
- ↑ Вельшенбах М. Глава 5. Модульная математика: вычисление в классах вычетов. // Криптография на Си и C++ в действии. — М.: «Триумф», 2004. — С. 81—95. — 464 с. — ISBN 5-89392-083-X.
- ↑ Материалы международной научной конференции “Модулярная арифметика”. Виртуальный компьютерный музей (2005). Дата обращения: 31 июля 2010. Архивировано 5 октября 2007 года.
- ↑ Егоров А. А. Сравнения по модулю и арифметика остатков // Квант. — 1970. — № 5. — С. 28—33. Архивировано 4 марта 2016 года.
- ↑ Французский математик, член французской академии наук с 1666.
- ↑ Вилейтнер Г. Глава III. Теория чисел // История математики от Декарта до середины XIX / пер. с нем. под. ред. А. П. Юшкевича. — М.: Государственное издательство физико-математической литературы, 1960. — С. 69—84. — 467 с. Архивная копия от 24 сентября 2015 на Wayback Machine
- ↑ 1 2 Степанов С. А. Глава 1. Основные понятия // Сравнения. — М.: «Знание», 1975. — С. 3—9. — 64 с. Архивная копия от 24 августа 2015 на Wayback Machine
- ↑ 1 2 Виноградов И. М. Основы теории чисел. — М.—Л.: Гос. изд. технико-теоретической литературы, 1952. — С. 41—45. — 180 с. Архивная копия от 1 июля 2020 на Wayback Machine
- ↑ Сизый, 2008, с. 88.
- ↑ 1 2 3 Сагалович, 2010, с. 25—29.
- ↑ Нестеренко, 2008, с. 86—87.
- ↑ Бухштаб А. А. Глава 8. Классы // Теория чисел. — М.: «Просвещение», 1966. — С. 77—78. — 384 с. Архивная копия от 20 ноября 2015 на Wayback Machine
- ↑ 1 2 Сагалович, 2010, с. 29—32.
- ↑ Сизый, 2008, с. 87—88,91.
- ↑ Лидл Р., Нидеррайтер Г. Конечные поля. В 2-х тт. — М.: Мир, 1998. — С. 27 (Пример 1.37). — 430 с. — ISBN 5-03-000065-8.
- ↑ Фадеев Д. К. Глава VII. Сравнение в кольце полиномов и расширения полей // Лекции по алгебре. — М.: «Наука», 1984. — С. 197—198. — 416 с.
- ↑ Сизый, 2008, с. 105—109.
- ↑ Бухштаб А. А. Глава 21. Сравнения 2-й степени по простому модулю, Глава 22. Сравнения второй степени по составному модулю // Теория чисел. — М.: «Просвещение», 1966. — С. 172—201. — 384 с. Архивная копия от 20 ноября 2015 на Wayback Machine
- ↑ Harald Niederreiter, Arne Winterhof. Applied Number Theory. — «Springer», 2015. — С. 369. — 442 с. — ISBN 978-3-319-22321-6.
- ↑ Коблиц Н. Курс теории чисел и криптографии / пер. с англ. М. А. Михайловой и В. Е. Тараканова под ред. А. М. Зубкова. — М.: Научное изд-во ТВП, 2001. — С. 96, 105—109, 200—209. — 262 с. — ISBN 5-85484-012-X.
- ↑ Check Digit Verification of CAS Registry Numbers (англ.). Архивировано 8 декабря 2015 года.
Литература[править | править код]
- Бухштаб А. А. Теория чисел. — М.: «Просвещение», 1966. — 384 с.
- Вейль А. Основы теории чисел. — М.: Мир, 1972.
- Виленкин Н. Я. Сравнения и классы вычетов // Квант. — 1978. — № 10. — С. 4—8.
- Виноградов И. М. Основы теории чисел. — М.—Л.: Гос. изд. технико-теоретической литературы, 1952. — 180 с.
- Коблиц Н. Курс теории чисел и криптографии / пер. с англ. М. А. Михайловой и В. Е. Тараканова,под ред. А. М. Зубкова. — М.: Научное изд-во ТВП, 2001. — 254 с. — ISBN 5-85484-012-X.
- Материалы международной научной конференции “Модулярная арифметика”. Виртуальный компьютерный музей (2005). Дата обращения: 31 июля 2010.
- Нестеренко Ю. В. Теория чисел. — М.: Издательский центр «Академия», 2008. — С. 132—133. — 272 с. — ISBN 9785769546464.
- Сагалович Ю. Л. Введение в алгебраические коды — 2-е изд. — М.: ИППИ РАН, 2010. — 320 с. — ISBN 978-5-901158-14-2
- Сизый С. В. §4. Теория сравнений // Лекции по теории чисел. — М.: Физматлит, 2008. — 192 с. — ISBN 978-5-9221-0741-9.
Сравнение чисел по модулю
Определение 1. Если два числа1) a и b при делении на p дают один и тот же остаток r, то такие числа называются равноостаточными или сравнимыми по модулю p.
Утверждение 1. Пусть p какое нибудь положительное число. Тогда всякое число a всегда и притом единственным способом может быть представлено в виде
где s – число, и r одно из чисел 0,1, …, p−1.
1) В данной статье под словом число будем понимать целое число.
Действительно. Если s получит значение от −∞ до +∞, то числа sp представляют собой совокупность всех чисел, кратных p. Рассмотрим числа между sp и (s+1)p=sp+p. Так как p целое положительное число, то между sp и sp+p находятся числа
Но эти числа можно получить задав r равным 0, 1, 2,…, p−1. Следовательно sp+r=a получит всевозможные целые значения.
Покажем, что это представление единственно. Предположим, что p можно представить двумя способами a=sp+r и a=s1p+r1. Тогда
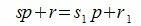 |
или
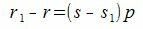 |
(2) |
Так как r1 принимает один из чисел 0,1, …, p−1, то абсолютное значение r1−r меньше p. Но из (2) следует, что r1−r кратно p. Следовательно r1=r и s1=s.
Число r называется вычетом числа a по модулю p (другими словами, число r называется остатком от деления числа a на p).
Утверждение 2. Если два числа a и b сравнимы по модулю p, то a−b делится на p.
Действительно. Если два числа a и b сравнимы по модулю p, то они при делении на p имеют один и тот же остаток p. Тогда
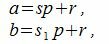 |
где s и s1 некоторые целые числа.
Разность этих чисел
 |
(3) |
делится на p, т.к. правая часть уравнения (3) делится на p.
Утверждение 3. Если разность двух чисел делится на p, то эти числа сравнимы по модулю p.
Доказательство. Обозначим через r и r1 остатки от деления a и b на p. Тогда
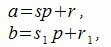 |
откуда
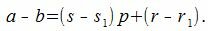 |
По утверждению a−b делится на p. Следовательно r−r1 тоже делится на p. Но т.к. r и r1 числа 0,1,…, p−1, то абсолютное значение |r−r1|<p. Тогда, для того, чтобы r−r1 делился на p должно выполнятся условие r=r1.
Из утверждения следует, что сравнимые числа – это такие числа, разность которых делится на модуль.
Если нужно записать, что числа a и b сравнимы между собой по модулю p, то пользуются обозначением (введенным Гауссом):
Примеры 25≡39 (mod 7), −18≡14 (mod 4).
Из первого примера следует, что 25 при делении на 7 дает тот же остаток, что и 39. Действительно 25=3·7+4 (остаток 4). 39=3·7+4 (остаток 4). При рассмотрении второго примера нужно учитывать, что остаток должен быть неотрицательным числом, меньшим, чем модуль (т.е. 4). Тогда можно записать: −18=−5·4+2 (остаток 2), 14=3·4+2 (остаток 2). Следовательно −18 при делении на 4 дает остаток 2, и 14 при делении на 4 дает остаток 2.
Свойства сравнений по модулю
Свойство 1. Для любого a и p всегда
Свойство 2. Если два числа a и c сравнимы с числом b по модулю p , то a и c сравнимы между собой по тому же модулю, т.е. если
| a≡b mod (p), b≡c mod (p). |
то
Действительно. Из условия свойства 2 следует a−b и b−c делятся на p. Тогда их сумма a−b+(b−c)=a−c также делится на p.
Свойство 3. Если
| a≡b mod (p) и m≡n mod (p), |
то
| a+m≡b+n mod (p) и a−m≡b−n mod (p). |
Действительно. Так как a−b и m−n делятся на p, то
| (a−b)+ (m−n)=(a+m)−(b+n) , |
также делятся на p.
Это свойство можно распространить на какое угодно число сравнений, имеющих один и тот же модуль.
Свойство 4. Если
| a≡b mod (p) и m≡n mod (p), |
то
Действительно.Так как a−b делится на p, то (a−b)m также делится на p, следовательно
Далее m−n делится на p, следовательно b(m−n)=bm−bn также делится на p, значит
Таким образом два числа am и bn сравнимы по модулю с одним и тем же числом bm, следовательно они сравнимы между собой (свойство 2).
Свойство 5. Если
то
где k некоторое неотрицательное целое число.
Действительно. Имеем a≡b mod (p). Из свойства 4 следует
Все свойства 1-5 представить в следующем утверждении:
Утверждение 4. Пусть f(x1, x2, x3, …) целая рациональная функция с целыми коэффициентами и пусть
| a1≡b1, a2≡b2, a3≡b3, … mod (p). |
тогда
| f(a1, a2, a3, …)≡f(b1, b2, b3, …) mod (p). |
При делении все обстоит иначе. Из сравнения
не всегда следует сравнение
Утверждение 5. Пусть
тогда
где λ это наибольший общий делитель чисел m и p.
Доказательство. Пусть λ наибольший общий делитель чисел m и p. Тогда
Так как m(a−b) делится на k, то
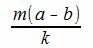 |
имеет нулевой остаток. Тогда
Следовательно
 |
имеет нулевой остаток, т.е. m1(a−b) делится на k1. Но числа m1 и k1 числа взаимно простые. Следовательно a−b делится на k1=k/λ и, тогда, a≡b mod (p/λ).
Утверждение 6. Если
и m является один из делителей числа p, то
Действительно. a−b делится на p. p делится на m. Следовательно a−b делится на m.
Утверждение 7. Если
| a≡b mod (p), a≡b mod (q), a≡b mod (s) |
то
где h наименьшее общее кратное чисел p,q,s.
Действительно. Разность a≡b должна быть числом, кратным p,q,s. и, следовательно должна быть кратным h.
В частном случае, если модули p,q,s взаимно простые числа, то
где h=pqs.
Заметим, что можно допустить сравнения по отрицательным модулям, т.е. сравнение a≡b mod (p) означает и в этом случае, что разность a−b делится на p. Все свойства сравнений остаются в силе и для отрицательных модулей.
![]()
Решение сравнений по модулю
Решений нет
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Сравнение по модулю
Сравнение двух целых чисел по модулю натурального числа m — математическая операция, позволяющая ответить на вопрос о том, дают ли два выбранных целых числа при делении на m один и тот же остаток. Арифметические операции с остатками чисел по одному и тому же модулю образуют модулярную арифметику.
Сравнимость чисел a и b по модулю сравнения m записывается как
Выражение
называется сравнением первой степени или линейным сравнением по модулю m.
Для проверки существования решений сравнения сначала вычисляется НОД(a, m). Если b не кратно полученному НОД, то у сравнения нет решений.
Если кратно, то количество решений по модулю m равно полученному НОД.
Существует несколько алгоритмов нахождения всех решений сравнения, но в данном калькуляторе применяется алгоритм решения линейных диофантовых уравнений с двумя переменными. В самом деле, сравнение эквивалентно следующему линейному диофантовому уравнению:
поэтому я использовал уже реализованный калькулятор решения линейных диофантовых уравнений для получения общей формулы решения, после чего выбрал все частные решения в диапазоне от 0 до m.
1.2 Теория сравнений и ее приложения
1.2.1 Сравнение по модулю
Определение 1.11 Числа, дающие при делении на m одинаковые остатки, называются сравнимыми по модулю  . Обозначение:
. Обозначение: 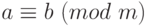 .
.
Теорема 1.14 (признак сравнимости по модулю) Два целых числа сравнимы по модулю  тогда и только тогда, когда их разность делится на
тогда и только тогда, когда их разность делится на  .
.
Итак, если два целых числа  и
и  сравнимы по модулю
сравнимы по модулю  , то этот факт можно записать разными способами:
, то этот факт можно записать разными способами: 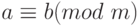 или
или 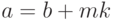 , где
, где  – целое число, или
– целое число, или  или
или 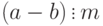 .
.
Далее, если  , то есть
, то есть  при делении на
при делении на  дает остаток
дает остаток  , то
, то  или
или  . Таким образом, любое целое число
. Таким образом, любое целое число  всегда сравнимо с остатком
всегда сравнимо с остатком  , получающимся при делении его на
, получающимся при делении его на  .
.
Свойства сравнений, не зависящие от модуля
-
Отношение сравнимости удовлетворяет условиям:
Отношение, заданное на множестве и обладающее перечисленными свойствами, задает разбиение этого множества на непересекающиеся классы. Применительно к отношению сравнимости по модулю
 это означает: все множество целых чисел разбивается на классы чисел, эти классы не пересекаются. Так, есть класс нуля: это все числа, сравнимые с нулем по модулю
это означает: все множество целых чисел разбивается на классы чисел, эти классы не пересекаются. Так, есть класс нуля: это все числа, сравнимые с нулем по модулю  ,то есть делящиеся на
,то есть делящиеся на  без остатка(включая и само число 0), класс единицы – все числа, дающие остаток 1 при делении на
без остатка(включая и само число 0), класс единицы – все числа, дающие остаток 1 при делении на  , класс 2, …,класс
, класс 2, …,класс 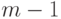 . Например, пусть
. Например, пусть  . Получаем следующие классы:
. Получаем следующие классы:![begin{array}{lcl}
bar{0}&=&{dots,-10, -5, 0, 5, 10, 15, 20,dots} \[1ex]
bar{1}&=&{dots,-9, -4, 1, 6, 11, 16, 21,{dots}} \[1ex]
bar{2}&=&{dots,-8, -3, 2, 7, 12, 17, 22,{dots}} \[1ex]
bar{3}&=&{{dots},-7, -2, 3, 8, 13, 18, 23,{dots}} \[1ex]
bar{4}&=&{{dots},-6, -1, 4, 9, 14, 19, 24,{dots}}.
end{array}](https://intuit.ru/sites/default/files/tex_cache/6cd40be356bc8150ff13f90b1c25a70e.png)
(
1.2)Определение 1.12 Классы (1.2) называются классами вычетов.
-
Сравнения по одному и тому же модулю можно почленно складывать.
-
Два сравнения по одному и тому же модулю можно почленно вычитать одно из другого.
-
К обеим частям сравнения можно прибавлять одно и то же целое число.
Следствие 1.6 Члены сравнения можно переносить из одной части сравнения в другую с противоположным знаком.
-
Сравнения по одному и тому же модулю можно почленно перемножать.
Следствие 1.7 Обе части сравнения можно возводить в одну и ту же целую неотрицательную степень: если
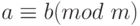 и
и  – целое неотрицательное число, то
– целое неотрицательное число, то 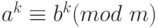 .
. - Обе части сравнения можно умножать на одно и то же целое число.
Свойства сравнений, зависящие от модуля
-
Если
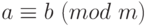 и
и 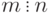 , то
, то 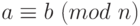 .
. -
Обе части сравнения и модуль можно умножить на одно и то же целое положительное число.
-
Если
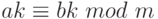 и
и 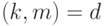 , то
, то  .
.Приведем следствия из свойства 9.
Следствие 1.8 Если
 , т. е. если
, т. е. если 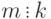 , то из
, то из 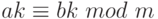 следует
следует 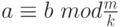 , а это означает, что обе части сравнения и модуль можно разделить на любой их общий делитель.
, а это означает, что обе части сравнения и модуль можно разделить на любой их общий делитель.Большое значение имеет
Следствие 1.9 Если
 , т. е. если
, т. е. если 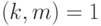 , то из
, то из 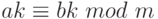 следует
следует  , а это означает, что обе части сравнения можно разделить на их общий делитель, если он взаимно прост с модулем.
, а это означает, что обе части сравнения можно разделить на их общий делитель, если он взаимно прост с модулем.Пример 1.9
 .
.После деления обеих частей сравнения на
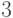 получим
получим 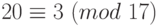 .
.Делить обе части сравнения на число, не взаимно простое с модулем, вообще говоря, нельзя, так как после деления могут получиться числа, несравнимые по данному модулю.
Пример 1.10
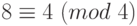 , но
, но 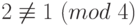 .
. - Если сравнение
 имеет место по нескольким разным модулям, то оно имеет место и по модулю, равному наименьшему общему кратному этих модулей.
имеет место по нескольким разным модулям, то оно имеет место и по модулю, равному наименьшему общему кратному этих модулей.
Из рассмотренных свойств сравнений вытекает следующее общее свойство.
-
Пусть
 – многочлен с целыми коэффициентами,
– многочлен с целыми коэффициентами,  и
и  – переменные, принимающие целые значения. Тогда если
– переменные, принимающие целые значения. Тогда если 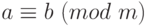 , то
, то  .
.Если
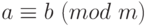 и
и 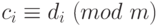 , то
, то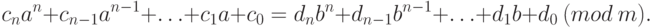
Таким образом, в сравнении по модулю
 отдельные слагаемые и множители можно заменять числами, сравнимыми по тому же модулю
отдельные слагаемые и множители можно заменять числами, сравнимыми по тому же модулю  . В частности, все числа, кратные модулю, можно заменять нулями (так как если
. В частности, все числа, кратные модулю, можно заменять нулями (так как если 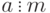 , то
, то 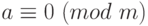 ).
).Вместе с тем следует обратить внимание на то, что встречающиеся в сравнениях показатели степеней заменять таким образом нельзя: из
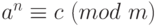 и
и  не следует, что
не следует, что  .
.Свойство 11 имеет ряд важных применений. В частности, с его помощью можно дать теоретическое обоснование признаков делимости.
Пример 1.11 Доказать, что при любом натуральном
 число
число  делится на
делится на 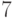 .
.Решение. Очевидно, что
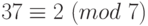 ,
, 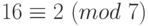 ,
, 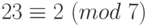 .
.Возведем первое сравнение в степень
 , второе – в степень
, второе – в степень  , третье – в степень
, третье – в степень  . Полученные сравнения:
. Полученные сравнения: 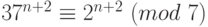 ,
, 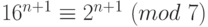 ,
, 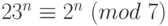 , сложим:
, сложим: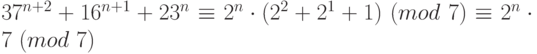 , то есть
, то есть  делится на
делится на 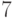 .
.Пример 1.12 Найти остаток от деления числа
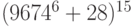 на
на  .
.Решение. Так как
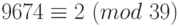 , то
, то  . Далее,
. Далее,  . Следовательно,
. Следовательно,  . И задача теперь сведена к следующей: найти остаток от деления
. И задача теперь сведена к следующей: найти остаток от деления 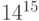 на
на  . Воспользуемся сравнениями:
. Воспользуемся сравнениями: 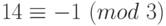 и
и 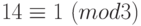 . Из
. Из 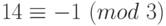 следует:
следует: 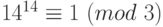 . А из сравнения
. А из сравнения 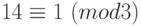 следует:
следует: 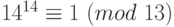 . И так как сравнение имеет место по модулям
. И так как сравнение имеет место по модулям 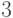 и
и 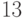 , то оно имеет место и по модулю
, то оно имеет место и по модулю  , являющемуся НОК чисел
, являющемуся НОК чисел 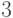 и
и 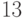 . Итак,
. Итак, 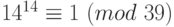 . Но в таком случае
. Но в таком случае 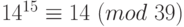 .
.
1.2.2 Возведение в степень по модулю
Пусть 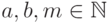 , нам необходимо вычислить
, нам необходимо вычислить 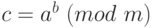 . В дальнейшем перед нами часто будет стоять такая задача с очень большими числами
. В дальнейшем перед нами часто будет стоять такая задача с очень большими числами  ,
,  ,
,  . Очевиднейший способ вычислить
. Очевиднейший способ вычислить  – вычислить произведение
– вычислить произведение 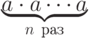 и взять остаток от деления на
и взять остаток от деления на  . Для этого потребуется
. Для этого потребуется  умножений и взятие остатка от деления огромного числа (не всегда даже его хранение в памяти может быть простым) по модулю
умножений и взятие остатка от деления огромного числа (не всегда даже его хранение в памяти может быть простым) по модулю  . Приведём оптимизации для этой задачи.
. Приведём оптимизации для этой задачи.
-
Из свойства
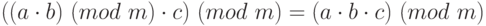
следует, что промежуточные результаты вычислений можно перед хранением брать по модулю
 .
. -
Сгруппируем сомножители в произведении особым образом. Пусть
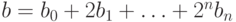 ,
, 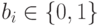 . Имеем:
. Имеем: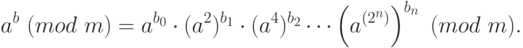
Используя пункт 1, будем все промежуточные результаты хранить по модулю  . Также для деления на 2 мы будем использовать операцию сдвига бит вправо:
. Также для деления на 2 мы будем использовать операцию сдвига бит вправо:
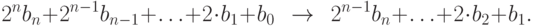
Микропроцессоры имеют специальные инструкции, а языки программирования – специальные операторы для оптимизированного выполнения битового сдвига, которые и следует использовать при реализации данного алгоритма.
Пункт 2 даёт следующий алгоритм возведения в степень по модулю.
Вход:  ,
,  ,
,  – целые неотрицательные числа.
– целые неотрицательные числа.
Выход: 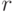 – результат возведения
– результат возведения  в степень
в степень  по модулю
по модулю  .
.
Также отметим, что на шаге 1 копирование 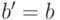 ,
, 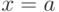 выполняются для того, чтобы не испортить значения
выполняются для того, чтобы не испортить значения  ,
,  , которые могут передаваться в наш алгоритм по указателю или ссылке.
, которые могут передаваться в наш алгоритм по указателю или ссылке.
![]() §5
§5
Числовые
сравнения
п.1 Определение и основные свойства
сравнений
Пусть
![]()
— произвольное натуральное число. Будем
называть его модулем.
Определение: Целые числа a
и b сравнимы по
модулю m, если их
разность a–b
делятся на m.
Обозначение: a ≡
b (mod
m).
Пример:
17 ≡ 5 (mod
17), 19 ≡ -1 (mod 10)
15 ≡ 0 (mod 5), 11≡ 1
(mod 5)
Замечание: Сравнение 17 ≡
5 (mod 12)
иллюстрирует хорошо знакомую ситуацию.
По модулю 12 мы обычно называем время,
говоря “сейчас 5 часов”, вместо
“сейчас 17 часов”.
Теорема 1: Следующее утверждения
для целых чисел a и
b равносильны:
-
разность a–b
делится на m. -
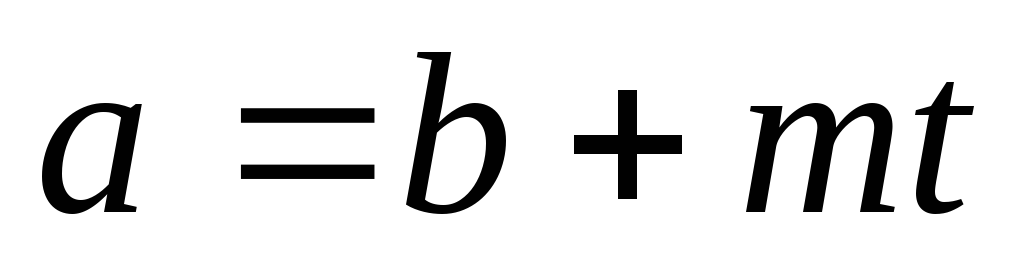 ,
,
где
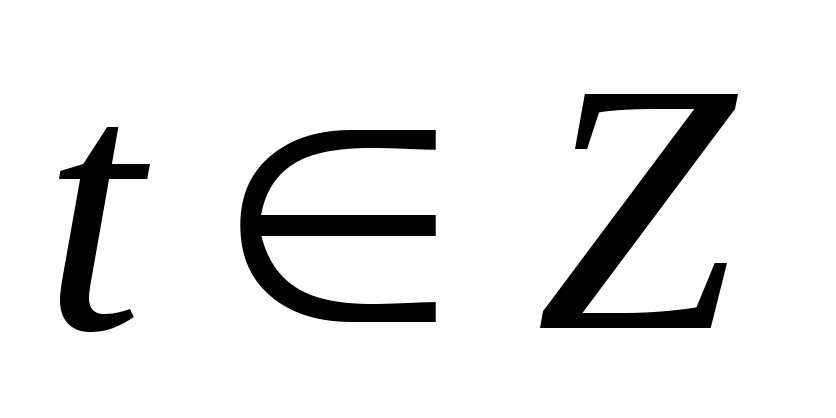 .
. -
a и b
имеют одинаковые остатки при делении
на m.
Доказательство: 1)![]() 2)
2)
Пусть a–b
делятся на m. Тогда
a–b=mt
или
![]() .
.
2)![]() 3)
3)
Пусть
![]() ,
,
и пусть b при делении
на m имеет остаток r,
т.е.
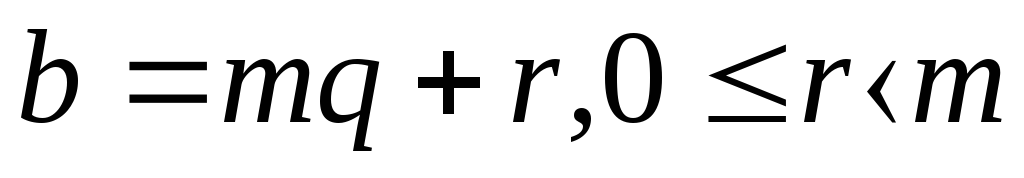 .
.
Тогда
![]() ,
,
где 0 ≤ r < m.
Следовательно r
— остаток от деления a
на m. Значит, a
и b имеют равные
остатки от деления на m.
3)![]() 1)
1)
Пусть
![]()
Тогда
![]()
делится на m.
Доказанная теорема означает, что любое
из трех равносильных утверждений можно
принять за определение сравнения.
Перейдем к изучению свойств сравнений.
Отношение сравнимости двух целых чисел
является примером бинарного отношения
на множестве Z. Во
многом это отношение похоже на отношение
равенства. Свойства 1°—4° иллюстрируют
это сходство.
1°. Отношение сравнения является
отношением эквивалентности:
-
a ≡ a
(mod m) -
a ≡ b (mod m)

b ≡ a (mod m) -
a ≡ b (mod m), b ≡ c (mod m)

a ≡ c (mod m)
Доказательство:
1. Рефлексивно очевидна, т.к. a–a
делиться на m.
2. Симметричность не менее ясна: если
a–b
делиться на m, то
b– a
тоже делится на m.
3. Транзитивность следует из равенства
![]() и
и
свойств делимости.
■
2°. Сравнения по одному и тому же модулю
можно складывать, вычитать и умножать:
если a ≡ b
(mod m),
c ≡ d
(mod m),
то
a + c
=b + d
(mod m)
a – c
=b – d
(mod m)
a · c
=b · d
(mod m)
Доказательство: Пусть
![]() ,
,
![]() ,
,
где
![]()
и
![]()
— целые. Тогда
![]()
![]()
![]()
что по теореме 1 равносильно требуемым
сравнениям.
■
Пример:
![]()
3°. Обе части сравнения можно увеличить
на одно и тоже число, домножать на
одинаковый множитель или возвести в
одинаковую степень:
если a ≡ b
(mod m),
то
a + k ≡ b + k (mod m), k![]() Z,
Z,
a · k ≡b · k (mod m), k![]() Z,
Z,
![]()
(mod m),
k![]() N.
N.
Доказательство: Требуемые утверждения
легко получить, применяя свойство 2° к
сравнениям a ≡ b
(mod m)
и
k ≡ k
(mod m).
■
Пример: 9 ≡ 4 (mod
5). Для k = 2 получим
верные сравнения:
11 ≡ 6 (mod 5),
18 ≡ 8 (mod 5),
81 ≡ 16 (mod 5).
4°. Члены сравнения можно переносить из
одной части в другую с переменой знака:
a + b ≡ с
(mod m)
![]()
a ≡ c-b
(mod m)
Доказательство: Следует из свойства
3° при k = –b.
■
Следующие два свойства показывают
отличие числовых сравнений от обычных
равенств.
5°. В любой части сравнения можно добавить
или отбросить слагаемое, кратное модулю:
a ≡ b (mod m)
![]() a
a
+ m · k ≡ b (mod m)
Доказательство: По определению
сравнимости:
m · k
≡ 0 (mod m).
Складывая это сравнение с данным
сравнением
a ≡ b
(mod m)
получим требуемое. Для доказательства
обратного утверждения используем
операцию вычитания.
■
Пример: Свойство 5° используют при
подсчете дней недели:
3 ≡ b (mod
7)
![]() 24
24
≡ b (mod
7).
Если 3 числа были вторник, то 24 числа
тоже будет вторник.
6°. Обе части сравнения можно сократить
на их общий множитель, если он взаимно
прост с m:
если a · k
≡ b · k
(mod m)
и при этом НОД(k,m)
= 1,
то a ≡ b
(mod m).
Доказательство: Пусть a
· k – b
· k делится на
m. По условию
k и m
взаимно простые
![]()
a–b
делиться на m
![]()
a ≡ b
(mod m).
■
Замечание: Условие взаимной
простоты k и m
очень важно. Вообще говоря, сокращение
может привести к неверному результату.
Например, 8 ≡ 6 (mod
2), но 4
![]()
3 (mod 2).
Впрочем, иногда после сокращения на k
результат может оказаться верным, хотя
k и m
не взаимно просты:
Например, 85 ≡ 10 (mod
15).
После сокращения на 5 получим верное
сравнение
17 ≡ 2 (mod 15).
Рассмотренные свойства сравнений
обобщаются следующее теоремой.
Теорема 2: Пусть
![]()
— с целыми коэффициентами. Пусть x
≡ y (mod
m).
Тогда p(x) ≡
p(y) (mod m).
Если, кроме того,
![]()
(mod m),
i = 0,1,2…n,
то
![]()
(mod m).
Доказательство: Непосредственно
следует из свойств 2° и 3°.
Замечание 1: Аналогичная
теорема верна и для многочленов от n
переменных с целыми коэффициентами.
Например,
если
![]()
(mod m), i =1,2,3…n, то
![]()
(mod m).
Замечание 2: Встречающиеся
в сравнении показатели степеней, нельзя
заменять сравнимыми по модулю m.
Иначе говоря, из того, что n
≡ k (mod
m) не следует,
что
![]()
(mod m).
Например, 3 ≡ 8 (mod
5), но
![]()
![]()
(mod 5), так
как
![]() (mod
(mod
5), а
![]()
(mod 5).
В свойствах 7° — 10° некоторые манипуляции
проводят не только с обеими частями
сравнения, но и с модулем m.
7°. Обе части сравнения и модуль можно
домножить или сократить на их общий
множитель:
a ≡ b (mod
m)
![]()
a · k ≡ b · k (mod mk)
Доказательство: Пусть a
≡ b (mod
m). Тогда a
= b + m∙t
![]()
a∙k
= b∙k
+ m∙k∙t
![]()
a∙k
≡ b∙k
(mod mk).
Эти же рассуждения можно провести в
обратном порядке.
■
8°. Если два числа сравнимы по модулю m,
то они сравнимы по любому модулю d,
делителю числа m:
![]() .
.
Доказательство: Если a–b
делиться на m, а m
делиться на d, то по
транзитивности a–b
делиться d
![]()
a ≡ b
(mod d).
■
9°. Если два числа сравнимы по нескольким
модулям, то они сравнимы по модулю,
равному наименьшему общему кратному
этих модулей:
![]() ,
,
где
![]() .
.
Доказательство: Если
![]() ,
,
то разность a–b
делиться на
![]()
и на
![]() .
.
Значит, (свойство 1 НОК) a–b
делиться на
![]() ,
,
т.е. a ≡ b
(mod m).
Такое же рассуждение сохраняет силу и
для нескольких модулей.
■
10°. Если a ≡ b
(mod m),
то множество общих делителей a
и m совпадает с
множеством общих делителей b
и m. В частности
НОД(a,m)
= НОД(b,m).
Доказательство: Пусть a
≡ b (mod
m). Тогда a
– b = m∙t.Если
d — общий делитель a
и m, то
![]() —
—
общий делитель b и
m. Обратное
аналогично.
■
п.2 Простейшие применения сравнений
Теория сравнений дает в руки исследователя
очень эффективный инструмент для решения
теоретико − числовых задач. Проиллюстрируем
его действенность несколькими
элементарными примерами.
Пример 1: Найти остаток от деления
![]()
на 7.
Решение: Имеем сравнение 2012 ≡ 612 ≡ -18 ≡
3 (mod 7). Значит,
![]()
(mod 7)
Но
![]() ,
,
поэтому
![]()
Ответ: остаток равен 3.
Пример 2: Доказать, что
![]()
делится на 17 при всех
![]() .
.
Решение: Воспользуемся тем, что 25![]() 8
8
(mod 17). Имеем
![]()
Следовательно, данная сумма делится на
17.
Пример 3: Вывести признаки делимости
на 9 и на 11.
Решение: Любое натурально число N
можно записать в виде
![]()
Заметим, что 10 ≡ 1 (mod 9).
Следовательно,
![]()
Число сравнимы по модулю 9, значит они
имеют одинаковые остатки при делении
на 9. В частности,
|| N делится на 9
![]() сумма
сумма
цифр числа N делится
на 9||
Аналогично, из сравнения 10 ≡ -1 (mod
11) следует, что
![]()
Отсюда следует, что
N делится на
11![]() Разность
Разность
между суммой цифр числа N,
стоящих на нечетных местах и суммой
цифр, стоящих на четных местах, делится
на 11.
Пример 4: Доказать, что уравнение
![]()
не имеет решений в целых числах.
Решение: Любое решение x
должно удовлетворять сравнению
![]()
При делении на 5 число x
может иметь в остатке 0,1,2,3 и 4.
Но, так как
![]()
значит
![]()
не может иметь остаток 3, т.е. сравнение
![]()
не имеет решений.
Пример 5: Определить день недели по
заданной дате.
Решение: Пусть N
обозначает год, m —
месяц, d — день
(1≤ m≤12), (1≤
d≤31) Первым
месяцем года (m = 1)
будем считать март, вторым (m
=2) — апрель и т.д. Тогда в високосные
годы день 29 февраля добавляется в конце
года, что удобно для расчета.
Обозначим ω —
номер для недели (1≤ ω≤
7), начиная отсчет с понедельника:
ω = 1 — Пн, ω
= 2 — Вт, ω = 3 — Ср
,…, ω=7 —Вс.
Пусть
![]()
— номер того дня недели, который мы
примем за точку отсчета. Напомним, что
Россия перешла на григорианский календарь
в феврале 1918 года, поэтому примем в
качестве
![]()
день недели 1 марта 1920 года. Таким образом,
считаем
N ≥ 1920.
Пусть
![]()
— номер дня 1 марта N-го
года. Заметим, что
365 ≡ 1 (mod 7),
поэтому каждый невисокосный год номер
дня недели увеличивается на 1. Если же
прошлый год был високосным, то к номеру
дня недели добавим 2, т.к.
366 ≡ 2 (mod 7).
Следовательно,
![]() (mod
(mod
7)
Упростив это выражение, получим
![]() (mod
(mod
7),
![]() (mod
(mod
7).
Вычислим
![]() .
.
1 марта 2012 года приходится на четверг,
т.е.
![]()
отсюда следует, что
![]()
(mod 7),
![]() (mod
(mod
7).
Итак, 1 марта 1920 года был понедельник,
следовательно,
![]()
(mod 7). (1)
Пусть теперь задано число d
месяца m года N.
Чтобы определить искомый день недели
осталось вычислить количество дней,
прошедших от 1 марта до заданной даты.
Вычислим сначала номер дней недели для
1 числа каждого месяца.
В марте 31 день
![]()
1 апреля имеет номер
![]() (mod
(mod
7)
В апреле 30 дней
![]() 1
1
мая имеет номер
![]() (mod
(mod
7)
и так далее, составим небольшую таблицу,
в которой указано то слагаемое, которое
нужно прибавит к
![]() .
.



Номер возрастает примерно на
![]()
в месяц. Поэтому нетрудно подобрать
формулу
![]()
m = 1,2,3…,12
которая дает нужное добавочное слагаемое
для любого месяца.
Итак, если ω — искомый день недели d
числа m месяца N
года, то к формуле (1) нужно прибавить
![]()
и (d-1) —
количество дней от 1 числа до нужной
даты. В итоге получим
![]()
(mod 7)
Определим, для примера день недели 22
июня 1941 года. Имеем N
= 1941, m = 4,
d = 22.
![]()
Итак, 22 июня 1941 года было воскресенье.
Соседние файлы в предмете Математический анализ
- #
- #
- #
- #
- #
- #
- #



















![{displaystyle [a]_{m}+[b]_{m}=[a+b]_{m};}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ae1f570a5eb594e4f3d48b6ede68a01359a3d51)
![{displaystyle [a]_{m}cdot [b]_{m}=[acdot b]_{m}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9dce0a3d7a6cede1189f2ad50b2aeb4185a53934)


















