Среднее арифметическое
Онлайн калькулятор поможет найти среднее арифметическое чисел. Среднее арифметическое множества чисел (ряда чисел) — число, равное сумме всех чисел множества, делённой на их количество.
Программа вычисляет среднее арифметическое элементов массива, среднее арифметическое натуральных чисел, целых чисел, набора дробных чисел.
Формула которая используется для расчета среднего арифметического значения:
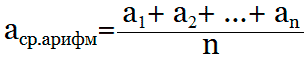
Приведём примеры нахождения среднего арифметического ряда чисел:
Среднее арифметическое двух чисел: (2+5)/2=3.5;
Среднее арифметическое трёх чисел: (2+5+7)/3=4.66667;
Среднее арифметическое 4 чисел: (2+5+7+2)/4=4;
Найти выборочное среднее (математические ожидание):
Среднее арифметическое 5 чисел: (2+5+7+2+3)/5=3.8;
Среднее арифметическое 6 чисел: (2+5+7+2+3+4)/6=3.833;
Среднее арифметическое 7 чисел: (2+5+7+2+3+4+8)/7=4.42857;
Среднее арифметическое 8 чисел: (2+5+7+2+3+4+8+5)/8=4.5;
Среднее арифметическое 10 чисел: (2+5+7+2+3+4+8+5+9+1)/10=4.6;
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также
Сре́днее арифмети́ческое (в математике и статистике) — разновидность среднего значения. Определяется как число, равное сумме всех чисел множества, делённой на их количество. Является одной из наиболее распространённых мер центральной тенденции.
Предложена (наряду со средним геометрическим и средним гармоническим) ещё пифагорейцами[1].
Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).
На случай, если количество элементов множества чисел стационарного случайного процесса бесконечное, в качестве среднего арифметического играет роль математическое ожидание случайной величины.
Введение[править | править код]
Обозначим множество чисел X = (x1, x2, …, xn) — тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной (
Для обозначения среднего арифметического всей совокупности чисел обычно используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее, или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E{xi} есть математическое ожидание этой выборки.
На практике разница между μ и 

Обе эти величины вычисляются одним и тем же способом:
Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.
В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.
Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины (например, среднее арифметическое взвешенное, среднее геометрическое взвешенное, среднее гармоническое взвешенное).
Примеры[править | править код]
- Для получения среднего арифметического трёх чисел необходимо сложить их и разделить на 3:
- Для получения среднего арифметического четырёх чисел необходимо сложить их и разделить на 4:
Непрерывная случайная величина[править | править код]
Если существует интеграл от некоторой функции 
![[a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)
Здесь для определения отрезка ![[a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)


Линейное преобразование[править | править код]
Линейно преобразованный набор данных 





Некоторые проблемы применения среднего[править | править код]
Отсутствие робастности[править | править код]
Хотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, то есть среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.
Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число — из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.
Сложный процент[править | править код]
Если числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.
Например, если акции в первый год упали на 10 %, а во второй год выросли на 60 %, тогда вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 60 %) / 2 = 25 % некорректно, а правильное среднее значение в этом случае дают совокупные ежегодные темпы роста: годовой рост получается 20 %.
Причина этого в том, что проценты имеют каждый раз новую стартовую точку: 60 % — это 60 % от меньшего, чем цена в начале первого года, числа: если акции в начале стоили $30 и упали на 10 %, они в начале второго года стоят $27. Если акции выросли на 60 %, они в конце второго года стоят $43,2. Арифметическое среднее этого роста 25 %, но, поскольку акции выросли за 2 года всего на $13,2, средний рост в 20 % даёт конечный результат $43,2:
$30 × (1 – 0,1)*(1 + 0,6) = $30 × (1 + 0,2)*(1 + 0,2) = $43,2. Если же использовать таким же образом среднее арифметическое значение 25 %, мы не получим фактическое значение: $30 × (1 + 0,25)*(1 + 0,25) = $46,875.
Сложный процент в конце 2 года: 90 % * 160 % = 144 %, то есть общий прирост 44 %, а среднегодовой сложный процент 
Таким образом среднегодовой прирост рассчитывается по формуле среднего геометрического

Направления[править | править код]
При расчёте среднего арифметического значений некоторой переменной, изменяющейся циклически (например, фаза или угол), следует проявлять особую осторожность. Например, среднее чисел 1° и 359° будет равно 180°. Этот результат неверен по двум причинам.
Среднее значение для циклической переменной, рассчитанное по приведённой формуле, будет искусственно сдвинуто относительно настоящего среднего к середине числового диапазона. Из-за этого среднее рассчитывается другим способом, а именно, в качестве среднего значения выбирается число с наименьшей дисперсией (центральная точка). Также вместо вычитания используется модульное расстояние (то есть, расстояние по окружности). Например, модульное расстояние между 1° и 359° равно 2°, а не 358° (на окружности между 359° и 360° = 0° — один градус, между 0° и 1° — тоже 1°, в сумме — 2°).
Примечания[править | править код]
- ↑ Cantrell, David W., «Pythagorean Means» Архивная копия от 22 мая 2011 на Wayback Machine from MathWorld
См. также[править | править код]
- Арифметическая пропорция
- Арифметическая прогрессия
- Неравенство Швейцера
- Среднее арифметическое взвешенное
Ссылки[править | править код]
- Арифметическая средняя // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Финансовая математика. Дисперсия. Среднее арифметическое. Среднеквадратическое отклонение. Коэффициент вариации Архивная копия от 19 сентября 2020 на Wayback Machine / Методики финансового анализа
- Среднее арифметическое — показатель центральной тенденции / Теория вероятностей и математическая статистика
-
Средняя арифметическая: простая и взвешенная.
Основной средней величиной
является средняя арифметическая.
Выделяют простую и
взвешенную среднюю
арифметическую.
Базой для расчета простой
средней арифметической являются
первичные записи результатов наблюдения.
Предположим, что известны значения
признака х1,
х2…..хт.
Каждое из этих значений
повторяется один раз
(или теоретически одинаковое количество
раз), т.е. данные не сгруппированы. Тогда
для такого ряда следует использовать
формулу средней арифметической
простого ряда или простую среднюю
арифметическую:
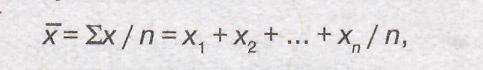
где х —
значение варьирующегося признака; п
— число единиц
совокупности. Базой для расчета взвешенной
средней арифметической является
обработанный цифровой материал, т.е.
сгруппированные данные. Для таких данных
используется формула средней
арифметической взвешенной:
![]()
где х — значение варьирующегося
признака;
т —
веса, т.е. частоты, показывающие, сколько
раз повторяется каждое значение признака
в данной совокупности. Формула
получена путем взвешивания значений
каждой варианты и деления суммы вариант
на сумму весов. Формулы простой и
взвешенной средней арифметической
не эквивалентны друг другу.
Свойства средней арифметической:
1) алгебраическая сумма отклонений всех
вариантов от средней арифметической
равна нулю:

Это
свойство используется
для проверки правильности расчетов;
2) сумма квадратов отклонений
вариант от их средней арифметической
больше суммы квадратов отклонений
вариант от любого другого числа, не
равного средней арифметической:
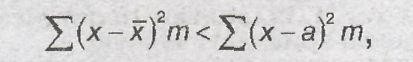
3) среднее алгебраическое
суммы нескольких варьирующихся
признаков равно сумме средних этих
признаков:
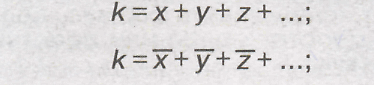
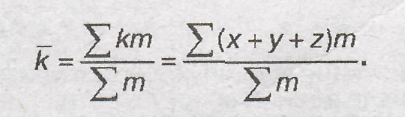
Это свойство позволяет определить сумму
путем суммирования значений каких-либо
признаков;
4) если
все варианты (х) увеличить или уменьшить
на какое-либо постоянное число (а),
средняя (х) увеличится или уменьшится
на то же самое число (у):
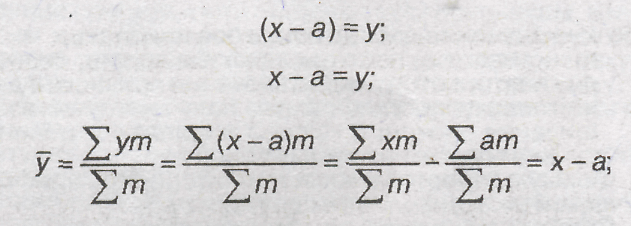
5) если все варианты (х)
увеличитьили уменьшить в одно и то
же число раз (в), то средняя арифметическая
увеличится или уменьшится вто же самое
число раз:
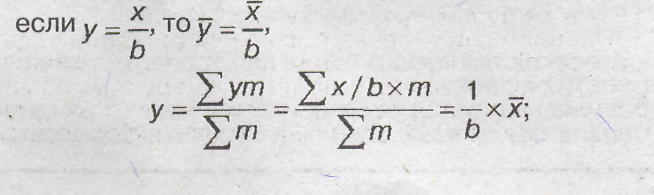
-
Средняя гармоническая: простая и взвешенная.
При решении задач расчет
средней величины начинается с
составления исходного отношения —
логической словесной формулы средней.
Она составляется на основе теоретического
и логического анализа. Иногда среднюю
арифметическую нельзя использовать. В
этом случае в зависимости от ситуации
применяется одна из трех форм средней
– средняя гармоническая, средняя
квадратическая или средняя геометричекая.
Средняя гармоническая
простая строится по
формуле:
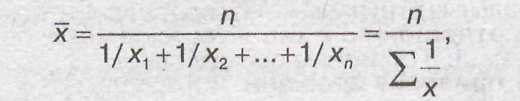
где n
—число единиц совокупности или число
вариантов; х —значения варьирующегося
признака.
Средняя гармоническая простая используется
для несгруппированных данных.
Средняя гармоническая
взвешенная строится
по формуле:
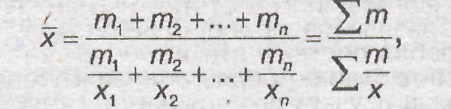
Где х – значения варьирующего признака;
m – веса; n
– число единиц совокупности.
-
Виды динамических рядов и правила их построения.
Для правильного расчета средних величин
необходимо ввести такие понятия, как
варианты и частоты.
В результате сводки и
группировки получают статистические
ряды, т.е.
ряды цифровых показателей. По своему
содержанию такие ряды делятся
на ряды распределения и
ряды динамики.
Ряды распределения характеризуют
распределение единиц совокупности
по какому-либо одному признаку,
разновидности которого упорядочены
определенным образом. Различают два
вида рядов распределения — атрибутивные
и вариационные ряды.
Атрибутивные ряды образуются
в результате группировки данных по
качественным признакам {например,
распределение населения по полу). В этих
рядах столько групп, сколько вариантов
качественного признака.
Вариационный ряд —
это упорядоченный ряд значений
варьирующего количественного признака
и численности единиц, имеющих данное
значение признака (например, распределение
рабочих по заработной плате).
В вариационном ряду распределения
выделяют следующие элементы:
1)
варианты (х
или х1,
х„… хп)
— это ряд числовых значений
количественного признака (например,
стаж, заработная плата, возраст). Варианты
могутбытькак абсолютными, так и
относительными величинами;
2) частоты
(т: тг
т2…
т )
— это числа, показывающие, сколько
раз повторяются соответствующие варианты
(например, число рабочих). Частоты, как
правило, обозначаются абсолютным числом;
если по условию частоты выражены в виде
процентов к итогу или долей, то их
называют относительными частотами
(или) частотами f:
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Понятие среднее арифметическое ряда чисел можно встретить в разных сферах — в математике, статистике, инженерных расчетах и многих других.
Чтобы найти среднее арифметическое чисел надо их сложить и эту сумму разделить на количество чисел.
Мы создали этот калькулятор для упрощения расчетов. Он с легкостью найдет среднее арифметическое 3, 4, 5 и даже 15 чисел. Следует упомянуть, что кроме среднего арифметического есть очень схожие понятия медианы и среднего гармонического.
Калькулятор среднего арифметического
Как найти среднее арифметическое
Допустим, что нам надо найти среднее арифметическое чисел 7 23 9 73 3. Сложим их и получим 7 + 23 + 9 + 73 + 3 = 115. Поделим эту сумму на количество чисел, то есть на 5:
222 / 5 = 23
Значит среднее арифметическое приведенных чисел равно 23.
Ваша оценка
[Оценок: 901 Средняя: 3.5]
Среднее арифметическое чисел Автор admin средний рейтинг 3.5/5 – 901 рейтинги пользователей
������������ �������
������� ��������������. ������� �������������� n �����, �������� �� �����, �������� �� n : $$
M(x_1 ,x_2 ,…,x_n ) = frac{{x_1 + x_2 + … + x_n }}{n}$$
������� ��������������. ������� �������������� n �����, �������� ������ n-�� ������� �� ������������ ���� �����: $$
M(x_1 ,x_2 ,…,x_n ) = sqrt[n]{{x_1 cdot x_2 cdot … cdot x_n }}$$
������� �������������. ������� ������������� ���������� ������������� ����� ���������� �����, �������� �������� ��������������� �� �������� �����: $$
M(x_1 ,x_2 ,…,x_n ) = frac{n}{{frac{1}{{x_1 }} + frac{1}{{x_2 }} + … + frac{1}{{x_n }}}}$$
������� ��������������. ������� �������������� (������������) ������ ���������� ����� M, ������ ����������� ����� �� �������� ��������������� ��������� ������ ��������������� ����� $$
x_1 ,x_2 ,…,x_n
$$: $$
M(x_1 ,x_2 ,…,x_n ) = sqrt {frac{{x_1 ^2 + x_2 ^2 + … + x_n ^2 }}{n}}$$
������� ���������. ������� ��������� ������������� ������������ ����� $$
x_1 ,x_2 ,…,x_n
$$ ������������ ��� $$
M(x_1 ,x_2 ,…,x_n ) = sqrt[m]{{frac{{x_1 ^m + x_2 ^m + … + x_n ^m }}{n}}}$$
������� ����������. ������� ���������� ��� ������� �������������� ���������� ������ ������������ ����� $$
x_1 ,x_2 ,…,x_n
$$ � ������������� ������ $$
m_1 ,m_2 ,…,m_n
$$ ������������ ��� $$
bar M(x_1 ,x_2 ,…,x_n ) = frac{{x_1 cdot m_1 + x_2 cdot m_2 + … + x_n cdot m_n }}{{m_1 + m_2 + … + m_n }}$$
�������� ������� �������. ���� ��� $$
{rm{x}}_{rm{1}} {rm{, x}}_{rm{2}} ,…,{rm{ x}}_{rm{n}}$$ ���������� ��� ������� ��������, �� ��� ��� ������ ����� �����������: M(�������������)$$
le
$$ M(��������������)$$
le
$$ M(��������������) $$
le
$$M(��������������)



![{displaystyle {overline {f(x)}}_{[a;b]}={frac {1}{b-a}}int _{a}^{b}f(x)dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db0287956e28e4ced0b833809f5b0ed44aaa7339)
