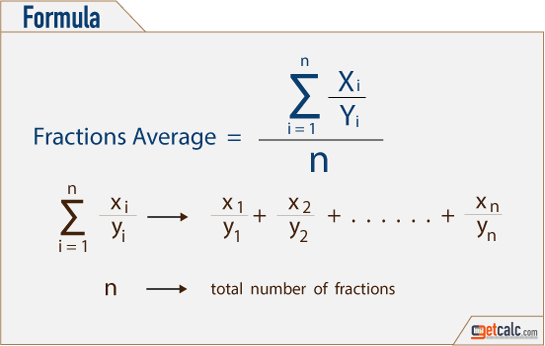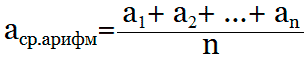КАК НАЙТИ СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ СМЕШАННЫХ ЧИСЕЛ? Примеры | МАТЕМАТИКА 5 класс
Канал видеоролика: Математика online
Смотреть видео:
#математикаогэ #гвэ #егэответы #репетиторпоматематике #репетитор_по_математике #огэматематика #огэответы #арифметика #ответы_огэ
Свежая информация для ЕГЭ и ОГЭ по Математике (листай):
С этим видео ученики смотрят следующие ролики:

СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ СМЕШАННЫХ ЧИСЕЛ С РАЗНЫМИ ЗНАКАМИ. Примеры | МАТЕМАТИКА 6 класс
Математика online

КАК НАЙТИ СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ ЧИСЕЛ НА КАЛЬКУЛЯТОРЕ В ТЕЛЕФОНЕ? МАТЕМАТИКА ДЛЯ ВСЕХ
Математика online

СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ ДВУХ ЧИСЕЛ. Примеры | МАТЕМАТИКА 5 класс
Математика online

СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ ТРЕХ ЧИСЕЛ: ЦЕЛОГО, СМЕШАННОГО, ДЕСЯТИЧНОЙ ДРОБИ. Примеры. МАТЕМАТИКА 5 класс
Математика online
Облегчи жизнь другим ученикам – поделись! (плюс тебе в карму):
08.06.2021
- Комментарии
RSS
Написать комментарий
Нет комментариев. Ваш будет первым!
Ваше имя:
Загрузка…
Общие сведения
Понятие среднеарифметической величины впервые предложил древнегреческий ученый — Пифагор. Позднее этот термин стал использоваться в математике. Чтобы понять его смысл, необходимо получить базовые знания о числовых значениях. Они делятся на 2 вида:
- Целые.
- Дробные.
Первый тип — натуральные числа, они применяются при устном счете предметов.
Дробные бывают также двух типов:
- Десятичными.
- Обыкновенными.
Десятичные дроби делятся на конечные, периодические и непериодические бесконечные. Первый тип состоит из целой и дробной частей, разделенных между собой запятыми. Как правило, количество разрядов ограничено определенным значением. Если рассматривать бесконечные периодические десятичные дробные выражения, они состоят из множества элементов. Последние повторяются с определенной периодичностью. Например, 5,(321), где величина периода указывается в круглых скобках.
В случае когда дробное тождество является бесконечным непериодическим, очень часто представление осуществляется в форме обыкновенной дроби. Последняя состоит из делимого и делителя, отделенных друг от друга косой чертой «/”. Первый элемент именуется числителем, а второй — знаменателем.
Обыкновенные дробные выражения бывают правильными, неправильными, а также могут записываться в форме смешанного числа, т. е. величины, состоящей из целого компонента и обыкновенной правильной дроби.
Перед подсчетом значения среднего арифметического в 5 классе специалисты рекомендуют ознакомиться с алгоритмом работы со смешанными величинами.
Смешанные числа
Смешанные числа являются промежуточными величинами между обыкновенными дробями и целыми. Не каждое дробное тождество можно представить в таком виде. Для этого подойдет только неправильное выражение. Алгоритм преобразования:
- Записать неправильную дробь: 79/11.
- Рассчитать целое число: 79/11=7.
- Вычислить новое значение числителя: 79−11*7=2.
- Записать смешанную величину: 7 2/11.
Методика обратной конвертации смешанного числа в неправильное дробное выражение является еще одной операцией, о которой нужно знать. Ее реализация:
- Записать смешанное выражение: 7[2/11].
- Вычислить величину нового числителя: 7*11+2=79.
- Результат: 79/11.
Специалисты рекомендуют начинающему математику потренироваться, придумывая различные задания на конвертацию числовых выражений.
Далее необходимо перейти непосредственно к определению, позволяющему расшифровать, что значит среднее арифметическое чисел, а также к самой методике расчета искомой величины.
Алгоритм нахождения среднего значения
Среднее арифметическое — математическая характеристика, позволяющая найти оптимальное значение.
Например, на уроках выставляется оценка за месяц. Для ее вычисления необходимо найти среднее значение всех отметок, полученных учеником.
Кроме того, среднее арифметическое используется при вычислении какой-либо характеристики опытным путем.
Например, при расчете заряда электрона производится определенное количество измерений, а затем рассчитывается средняя величина заряда частицы.
Методика определения среднеарифметического значения:
- Записать все значения.
- Сложить все элементы, записанные в первом пункте.
- Поделить сумму, полученную на втором шаге, на количество элементов.
- Записать результат.
Для реализации алгоритма на практике необходимо записать несколько чисел — 4, 7, 8, 12, 15. Решение выглядит следующим образом:
- Количество элементов: 5.
- Сумма: 4+7+8+12+15=46.
- Среднее арифметическое: 46/5=9,2.
- Результат: 9,2.
В некоторых случаях результат необходимо округлять. Однако этого можно не делать при подсчете какой-либо физической величины.
При проведении опытов необходимо брать больше значений, поскольку это существенно влияет на точность получения данных.
Пример решения
Для закрепления теории необходимо разобрать пример и решить его. Например, нужно найти среднее арифметическое четырех смешанных чисел, а именно: 3 2/3, 4 5/7 и 6 3/8.
Решение выполняется по следующему алгоритму:
- Записать величины: 3 2/3, 4 5/7 и 6 3/8.
- Количество: 3.
- Конвертировать их в неправильные дроби: 11/3, 33/7 и 51/8.
- Привести к единому знаменателю: (11*56)/168=616, 33*24/168=792 и 51*21/168=1071/168.
- Вычислить сумму: 2479/168.
- Определить среднее арифметическое: (2479/168):3=(2479/168)*1/3=2479/504.
- Преобразовать в смешанное дробное выражение: 2479/504=4 463/504.
- Значение искомой величины равно 4 463/504.
При получении результата в виде неправильной дроби, его нужно преобразовать в смешанную величину. Это считается «правилом хорошего тона» в математике, поскольку любой ответ должен переводиться в читабельную сокращенную форму.
Кроме того, можно проверить результат выполнения операции, воспользовавшись онлайн-сервисами. Однако пользоваться ими часто не рекомендуется, поскольку нужно уметь искать ошибки самостоятельно.
Таким образом, для вычисления среднеарифметического значения необходимо знать специальную методику, предложенную специалистами в области математики.
Multiple Fractions Average
Arithmetic Operator :
Fractions & Mixed Numbers:
enter space separated input values
Average :
share
feedback
calculator
info
history
</>
Average of Fractions and Mixed Numbers Calculator
getcalc.com’s Fractions and Mixed Numbers Average calculator is an online basic math function tool to find an equivalent fraction for the average between two or more fractions with same or different (equal or unlike) denominators, positive or negative fractions, regular or irregular fractions, mixed numbers and whole numbers. This calculator also featured to generate the complete work with steps for any given valid input values to assist elementary or grade school students to solve the fractions average worksheet or homework problems effectively. Users can generate the step by step calculation for the corresponding input values or verify the similar calculation results by using this fractions and mixed numbers average calculator.
More Fraction Calculators
Multiple Fractions Average and Formula
Average of Multiple Fractions is a basic arithmetic operation used to find the average between two or more fractions with same or different (equal or unlike) denominators, positive or negative fractions, regular or irregular fractions, mixed numbers and whole numbers. The below formula is the mathematical representation for average of multiple fractions with like or unlike denominators, positive or negative fractions or mixed or whole numbers.
How to Find the Average of Two or More Fractions
The average of fractions is the sum of all fractions divided by the count of total number of fractional numbers. Any whole number in the group of fractions considered as a fraction with denominator 1. For fractions with same or equal denominators, the sum is the simplified fraction of sum of numerators divided by the common denominators, whereas, for fractions with unlike, unequal or different denominators, the LCM (least common multiple) of all denominators must be multiplied with both numerators and denominators of each fractions to bring the common denominator to perform the addition between them. By using this tool and associated information, users may refer the below solved examples with step by step calculation to learn how to find the average of two, three or more fraction numbers with same or different denominators, or the average of regular, irregular, positive or negative fractions and whole numbers. user may found the answers for the following queries
Average of Three Fractions with Different Denominators
The below solved example with step by step calculation or workout may help users to learn how to find the average of three fractions with unlike, unequal or different denominators.
Problem
Find the average of fractions 1/2, 1/3 and 1/4.Step by step workout
step 1 Address formula and input values.
Input values:
1/2, 1/3 , 1/4
Total count = 3
(1/2 + 1/3 + 1/4)/3 = ?
step 2 To find the sum for fractions with different denominators, find the LCM (least common multiple) for all denominators.
12 is the LCM for 2, 3 and 4.
step 3 Multiply LCM 12 with each numerators and denominators
= (1 x 12)/(2 x 12) + (1 x 12)/(3 x 12) + (1 x 12)/(4 x 12)
step 4 Simplify the above expression to bring same denominators for all fractions.
= 6/12 +4/12+3/12
= (6 + 4 + 3)/12
step 5 Add all numerators and rewrite it in a single form.
= 13/12
1/2+1/3+1/4= 13/12
step 6 Divide the sum by total count of fractions.
(1/2 + 1/3 + 1/4)/3 = (13/12)/3
13/12is the average of three fractions 1/2, 1/3 and 1/4.
Average of Three Fractions with Same Denominators
The below solved example with step by step calculation or workout may help users to learn how to find the average of three fractions with same, equal or common denominators.
Problem
Find the average of fractions 5/9, 6/9 and 7/9.
Step by step workout
step 1 Address formula and input values.
Input values:
5/9,6/9,7/9
Total count = 3
(5/9 + 6/9 + 7/9)/3 = ?
step 2 Find the sum of all fractions.
(5 + 6 + 7)/9=18/9
=18/9
step 3 Divide the sum by total count of fractions and simplify
= (18/9)/3
(5/9 + 6/9 + 7/9)/3 = 2/3 in fraction form
(5/9 + 6/9 + 7/9)/3 = 0.66 in decimal form
2/3 or 0.66 is the average of three fractions 5/9, 6/9 and 7/9.
Average of Multiple Fractions and Whole Numbers
The below solved example with step by step workout may help users to learn how to find the average of multiple regular or irregular fractions with like or different denominators and whole numbers.
Problem
Find the average of fractions and whole numbers 2/3, 3/4, 6, 4/5, 3, 5/6 and 8/9.Step by step workout
step 1 Address formula and input values.
Input values:
2/3,3/4,6,4/5, 3 ,5/6,8/9
Total count = 7
2/3,3/4,6,4/5, 3 ,5/6,8/9 = ?
step 2 Convert whole numbers to fractions and rewrite as below
Any whole number or integer is a rational number (quotient of 1), hence the denominators for all whole numbers is 1 and can be written as
6 =6/1
3 =3/1
step 3 Arrange all the numbers as fractions
2/3+3/4+6/1+4/5+ 3/1+5/6+ 8/9
step 4 To find the sum for fractions with different denominators, find the LCM (least common multiple) for all denominators.
180 is the LCM for 3, 4, 1, 5, 1, 6 and 9.
step 5 multiply LCM 180 with each numerators and denominators
=(2 x 180)/(3 x 180)+(3 x 180)/(4 x 180) +(6 x 180)/(1 x 180)+ (4 x 180)/(5 x 180)+(3 x 180)/(1 x 180)+(5 x 180)/(6 x 180)+(8 x 180)/(9 x 180)
step 6 simplify the above expression to bring same denominators for all fractions.
=120/180+135/180+1080/180+144/180+540/180+150/180+160/180
=(120 + 135 + 1080 + 144 + 540 + 150 + 160)/180
step 7 add all numerators and rewrite it in a single form.
=2329/180
=2/3+3/4+6/1+4/5+ 3/1+5/6+ 8/9=2329/180
step 8 Divide the sum by total count of fractions.
(2/3 + 3/4 + 6/1 + 4/5 + 3/1 + 5/6 + 8/9)/7 = (2329/180)/7
= 2329/1260
2329/1260 is the average of fractions and whole numbers 2/3, 3/4, 6, 4/5, 3, 5/6 and 8/9.
Average of Multiple Positive and Negative Fractions
The below solved example with step by step calculation may help users to learn how to find the average of multiple whole numbers, positive and negative fractions (with unlike or different denominators).
Problem
Find the average of multiple whole numbers, positive and negative fractions 2/3, 2/4, -2/5, 6, 2/7, -3/9 and 2/9.Step by step workout
step 1 Address formula and input values.
Input values:
2/3,2/4,-2/5, 6 ,2/7,-3/9
Total count = 6
(2/3 + 2/4 + -2/5 + 6 + 2/7 + -3/9)/6 = ?
step 2 Convert the whole numbers to fractions, if any
6 = 6/1
step 3 Arrange all the numbers as fractions.
2/3+2/4+-2/5+6/1+2/7+-3/9
step 4 To find the sum for fractions with different denominators, find the LCM (least common multiple) for all denominators.
1260 is the LCM for 3, 4, 5, 1, 7 and 9.
step 5 Multiply LCM 1260 with each numerators and denominators
=(2 x 1260)/(3 x 1260)+(2 x 1260)/(4 x 1260)–(2 x 1260)/(5 x 1260)+(6 x 1260)/(1 x 1260)+(2 x 1260)/(7 x 1260)–(3 x 1260)/(9 x 1260)
step 6 Simplify the above expression to bring same denominators for all fractions.
=(2 x 420)/(1260)+(2 x 315)/(1260)–(2 x 252)/(1260)+(6 x 1260)/(1260)+(2 x 180)/(1260)–(3 x 150)/(1260)
=840/1260+ 630/1260– 504/1260 + 7560/1260 + 360/1260 – 450/1260
step 7add all numerators and rewrite it in a single form.
=(840 + 630 + 504 + 7560 + 360 + 450)/1260
=10344/1260
=862/105
(2/3 + 2/4 + -2/5 + 6 + 2/7 + -3/9) = 862/105
step 8 Divide the sum by total count of fractions.
(2/3 + 3/4 + 6/1 + 4/5 + 3/1 + 5/6 + 8/9)/6 = (862/105)/6
= (431/105)/3
=431/315
431/315 is the average of multiple whole numbers, positive and negative fractions 2/3, 2/4, -2/5, 6, 2/7, -3/9 and 2/9.
Average of Two or More Fractions and Mixed Numbers
The below solved example for average of two or more fractions, mixed numbers and whole numbers. The fraction numbers include regular, irregular, negative or positive fractions with same or unlike denominators. The below step by step work guides how to find equivalent fraction for the average between multiple fractions, mixed and whole numbers 2/3, 4/5, 6/7, 3(8/9), 6(1/2) and 9.
Problem
Find the average between multiple fractions, mixed and whole numbers 2/3, 4/5, 6/7, 3(8/9), 6(1/2) and 9.Step by step workout
step 1 Address formula and input values.
Input values:
2/3,4/5,6/7, 3 8/9, 6 1/2, 9
Total count = 6
(2/3 + 4/5 + 6/7 + 3(8/9) + 6(1/2) + 9)/6 = ?
step 2 Convert the whole numbers to fractions, if any
9 = 9/1
step 3 Convert the mixed fractions to fractions, if any
38/9= ((3 x 9) + 8)/9= 35/9
61/2= ((6 x 2) + 1)/2= 13/2
step 4 Arrange all the numbers as fractions.
2/3+4/5+6/7+35/9+13/2+9/1
step 5 To find the sum for fractions with different denominators, find the LCM (least common multiple) for all denominators.
630 is the LCM for 3, 5, 7, 9, 2 and 1.
step 6 Multiply LCM 630 with each numerators and denominators
=(2 x 630)/(3 x 630)+(4 x 630)/(5 x 630)+(6 x 630)/(7 x 630)+(35 x 630)/(9 x 630)+(13 x 630)/(2 x 630)+(9 x 630)/(1 x 630)
step 7 Simplify the above expression to bring same denominators for all fractions.
=(2 x 210)/(630)+(4 x 126)/(630)+(6 x 90)/(630)+(35 x 70)/(630)+(13 x 315)/(630)+(9 x 630)/(630)
=420/630+504/630+54/630+2450/630+4095/630+5670/630
step 8 Add all numerators and rewrite it in a single form.
=(420 + 504 + 54 + 2450 + 4095 + 5670)/630
=13193/630
(2/3 + 4/5 + 6/7 + 3(8/9) + 6(1/2) + 9) = 13193/630
step 9 Divide the sum by total count of fractions.
(2/3 + 4/5 + 6/7 + 3(8/9) + 6(1/2) + 9)/6 = (13193/630)/6
=13193/3780
13193/3780 is the average of multiple fractions, mixed and whole numbers 2/3, 4/5, 6/7, 3(8/9), 6(1/2) and 9.
Правила ввода
Вводить можно целые(1, 2, 3, -7), десятичные(0.25, -1.15), дробные(-1/8, 32/9). Если необходимо ввести смешанное число, то нужно перед вводом перевести его в неправильную обыкновенную дробь. Т.е. 1 целая 1/2 вводить нужно будет как 3/2.
При вводе десятичных дробей использовать точку. Запятая зарезервирована под разделитель.
В качестве разделителя можно использовать любой символ кроме цифр(0-9), слэша(/), точки(.), знака минус(-). Остальные символы и перенос строки будут программой заменены на разделители.
Определение среднего арифметического
Среднее арифметическое чисел это число, равное отношению этих чисел к их количеству.
Формула среднего арифметического
m = (a1+a2+a3+…+an)/n
где a1, a2, a3…an – ряд чисел
n – количество чисел
Пример нахождения среднего арифметического
Дан ряд чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 необходимо найти среднее арифметичское этих чисел.
Для решения этой задачи нам необходимо сумму этих чисел 55 разделить на количество этих чисел 10.
m = (1+2+3+4+5+6+7+8+9+10)/10 = 55/10 = 5.5
Пример нахождения среднего арифметического дробей
Даны дроби 1/2, 1/4, 1/8, 1/16 необходимо найти среднее арифметичское этих чисел.
Для решения этой задачи нам необходимо просуммировать эти дроби 1/2+1/4+1/8+1/16=(8+4+2+1)/16=15/16. Затем полученное число разделить на количество этих дробей (15/16)/4=(15/16)×(1/4)=15/64
m = (1/2+1/4+1/8+1/16)/4=15/64
Пример нахождения среднего арифметического десятичных дробей
Даны десятичные дроби 0.2, 0.3, 0.4 необходимо найти среднее арифметичское этих дробей.
Для решения этой задачи нам необходимо просуммировать эти дроби 0.2+0.3+0.4=0.9. Затем полученное число разделить на количество этих дробей 0.9/3=0.3
m = (0.2+0.3+0.4)/3=0.3
Среднее арифметическое
Онлайн калькулятор поможет найти среднее арифметическое чисел. Среднее арифметическое множества чисел (ряда чисел) — число, равное сумме всех чисел множества, делённой на их количество.
Программа вычисляет среднее арифметическое элементов массива, среднее арифметическое натуральных чисел, целых чисел, набора дробных чисел.
Формула которая используется для расчета среднего арифметического значения:
Приведём примеры нахождения среднего арифметического ряда чисел:
Среднее арифметическое двух чисел: (2+5)/2=3.5;
Среднее арифметическое трёх чисел: (2+5+7)/3=4.66667;
Среднее арифметическое 4 чисел: (2+5+7+2)/4=4;
Найти выборочное среднее (математические ожидание):
Среднее арифметическое 5 чисел: (2+5+7+2+3)/5=3.8;
Среднее арифметическое 6 чисел: (2+5+7+2+3+4)/6=3.833;
Среднее арифметическое 7 чисел: (2+5+7+2+3+4+8)/7=4.42857;
Среднее арифметическое 8 чисел: (2+5+7+2+3+4+8+5)/8=4.5;
Среднее арифметическое 10 чисел: (2+5+7+2+3+4+8+5+9+1)/10=4.6;
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»