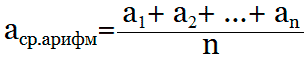Как найти среднее арифметическое данного набора

Как найти среднее арифметическое данного набора

Среднее арифметическое

Онлайн калькулятор поможет найти среднее арифметическое чисел. Среднее арифметическое множества чисел (ряда чисел) — число, равное сумме всех чисел множества, делённой на их количество.

Программа вычисляет среднее арифметическое элементов массива, среднее арифметическое натуральных чисел, целых чисел, набора дробных чисел.

Формула которая используется для расчета среднего арифметического значения:
формула для нахождения средней арифметической величины

Приведём примеры нахождения среднего арифметического ряда чисел:
Среднее арифметическое двух чисел: (2+5)/2=3.5;
Среднее арифметическое трёх чисел: (2+5+7)/3=4.66667;
Среднее арифметическое 4 чисел: (2+5+7+2)/4=4;

Найти выборочное среднее (математические ожидание):
Среднее арифметическое 5 чисел: (2+5+7+2+3)/5=3.8;
Среднее арифметическое 6 чисел: (2+5+7+2+3+4)/6=3.833;
Среднее арифметическое 7 чисел: (2+5+7+2+3+4+8)/7=4.42857;
Среднее арифметическое 8 чисел: (2+5+7+2+3+4+8+5)/8=4.5;
Среднее арифметическое 10 чисел: (2+5+7+2+3+4+8+5+9+1)/10=4.6;

×

Пожалуйста напишите с чем связна такая низкая оценка:

×

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также

Источник

Понятие среднее арифметическое ряда чисел можно встретить в разных сферах — в математике, статистике, инженерных расчетах и многих других.

Чтобы найти среднее арифметическое чисел надо их сложить и эту сумму разделить на количество чисел.

Мы создали этот калькулятор для упрощения расчетов. Он с легкостью найдет среднее арифметическое 3, 4, 5 и даже 15 чисел. Следует упомянуть, что кроме среднего арифметического есть очень схожие понятия медианы и среднего гармонического.

Калькулятор среднего арифметического

Как найти среднее арифметическое

Допустим, что нам надо найти среднее арифметическое чисел 7 23 9 73 3. Сложим их и получим 7 + 23 + 9 + 73 + 3 = 115. Поделим эту сумму на количество чисел, то есть на 5:
222 / 5 = 23

Значит среднее арифметическое приведенных чисел равно 23.

Ваша оценка

[Оценок: 906 Средняя: 3.5]

Среднее арифметическое чисел Автор admin средний рейтинг 3.5/5 – 906 рейтинги пользователей

Источник

Среднее арифметическое, размах, мода и медиана

  1. Алгебра
  2. Среднее арифметическое, размах, мода и медиана
Статистические характеристики

количество чисел

Калькулятор вычислит среднее арифметическое чисел, а также размах ряда чисел, моду ряда
чисел, медиану ряда. Для вычисления укажите количество чисел, добавьте числа и нажмите
рассчитать.

Среднее арифметическое, размах, мода и медиана

Средним арифметическим ряда чисел называется частное от деления суммы этих
чисел на число слагаемых.

Для ряда a1,a1,..,an среднее арифметическое вычисляется по
формуле:

begin{align}
& overline{a}=frac{a_1+a_2+…+a_n}{n}\
end{align}

Найдем среднее арифметическое для чисел 5,24, 6,97, 8,56, 7,32 и 6,23.

begin{align}
& overline{a}=frac{5,24+6,97+8,56+7,32+6,23}{5}=6.864\
end{align}

Размахом ряда чисел называется разность между наибольшим и наименьшим из
этих чисел.

Размах ряда 5,24, 6,97, 8,56, 7,32, 6,23 равен 8,56-5,24=3.32

Модой ряда чисел называется число, которое встречается в данном ряду чаще
других.

Ряд чисел может иметь более одной моды, а может не иметь моды совсем.

Модой ряда 32, 26, 18, 26, 15, 21, 26 является число 26, встречается 3 раза.

В ряду чисел 5,24, 6,97, 8,56, 7,32 и 6,23 моды нет.

Ряд 1, 1, 2, 2, 3 содержит 2 моды: 1 и 2.

Медианой упорядоченного ряда чисел с нечётным числом членов называется
число, записанное посередине, а медианой упорядоченного ряда чисел с чётным
числом членов называется среднее арифметическое двух чисел, записанных посередине.

Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного
ряда.

Медиана ряда 4, 1, 2, 3, 3, 1 равна 2.5.

Примеры

Рассмотрим примеры нахождения среднего арифметического чисел, а также размаха, медианы и моды
ряда.

  1. Среднее арифметическое чисел 30, 5, 23, 5, 28, 30

    begin{align}
    & overline{a}=frac{30+5+23+5+28+30}{6}=20frac{1}{6}\
    end{align}

    Размах ряда: 30-5=25

    Моды ряда: 5 и 30

    Медиана ряда: 25.5

  2. Среднее арифметическое чисел 40, 35, 30, 25, 30, 35

    begin{align}
    & overline{a}=frac{40+35+30+25+30+35}{6}=32frac{1}{2}\
    end{align}

    Размах ряда: 40-25=15

    Моды ряда: 30, 35

    Медиана ряда: 32.5

  3. Среднее арифметическое чисел 21, 18,5, 25,3, 18,5, 17,9

    begin{align}
    & overline{a}=frac{21+18,5+25,3+18,5+17,9}{5}=20,24\
    end{align}

    Размах ряда: 25,3-17,9=7,4

    Мода ряда: 18,5

    Медиана ряда: 18,5

Примеры

Примеры нахождения среднего арифметического отрицательных и вещественных чисел.

  1. Среднее арифметическое чисел 67,1, 68,2, 67,1, 70,4, 68,2

    begin{align}
    & overline{a}=frac{67,1+68,2+67,1+70,4+68,2}{5}=68,2\
    end{align}

    Размах ряда: 70,4-67,1=3,3

    Моды ряда: 67.1, 68.2

    Медиана ряда: 68.2

  2. Среднее арифметическое чисел 0,6, 0,8, 0,5, 0,9, 1,1

    begin{align}
    & overline{a}=frac{0,6+0,8+0,5+0,9+1,1}{5}=0.78\
    end{align}

    Размах ряда: 1,1-0,5=0.6

    Ряд не имеет моды

    Медиана ряда: 0.8

  3. Среднее арифметическое чисел -21, -33, -35, -19, -20, -22

    begin{align}
    & overline{a}=frac{(-21)+(-33)+(-35)+(-19)+(-20)+(-22)}{6}=-25\
    end{align}

    Размах ряда: (-19)-(-35)=16

    Ряд не имеет моды

    Медиана ряда: -21,5

  4. Среднее арифметическое чисел -4, -6, 0, -4, 0, 6, 8, -12

    begin{align}
    & overline{a}=frac{(-4)+(-6)+0+(-4)+0+6+8+(-12)}{8}=-1,5\
    end{align}

    Размах ряда: 8-(-12)=20

    Моды ряда: -4, 0

    Медиана ряда: -2

  5. Среднее арифметическое чисел 275, 286, 250, 290, 296, 315, 325

    begin{align}
    & overline{a}=frac{275+286+250+290+296+315+325}{7}=291\
    end{align}

    Размах ряда: 325-250=75

    Ряд не имеет моды

    Медиана ряда: 290

  6. Среднее арифметическое чисел 38, 42, 36, 45, 48, 45, 45, 42, 40, 47, 39

    begin{align}
    & overline{a}=frac{38+42+36+45+48+45+45+42+40+47+39}{11}=42frac{6}{11}\
    end{align}

    Размах ряда: 48-36=12

    Мода ряда: 45

    Медиана ряда: 42

  7. Среднее арифметическое чисел 3,8, 7,2, 6,4, 6,8, 7,2

    begin{align}
    & overline{a}=frac{3,8+7,2+6,4+6,8+7,2}{5}=6,28\
    end{align}

    Размах ряда: 7,2-3,8=3,4

    Мода ряда: 7,2

    Медиана ряда: 6,8

  8. Среднее арифметическое чисел 21,6, 37,3, 16,4, 12,6

    begin{align}
    & overline{a}=frac{21,6+37,3+16,4+12,6}{4}=21,025\
    end{align}

    Размах ряда: 37,3-12,6=24,7

    Мода ряда: 12,6

    Медиана ряда: 17,1

Источник


Среднее арифметическое нескольких чисел. 6 класс.

Видео: Среднее арифметическое нескольких чисел. 6 класс.

Содержание

  • Что такое средство и для чего оно используется?
  • Как найти среднее значение: обзор
  • Как рассчитать среднее значение: практические вопросы
  • Практический вопрос 1
  • Практический вопрос 2
  • Практический вопрос 3
  • Практический вопрос 4
  • Как найти среднее: ответы + пояснения
  • Практический вопрос 1 Ответ Объяснение
  • Практический вопрос 2 Ответ Объяснение
  • Практический вопрос 3 Ответ Объяснение
  • Практический вопрос 4 Ответ Объяснение
  • Что дальше?

Вы сдаете SAT или ACT и хотите убедиться, что знаете, как работать с наборами данных? Или, может быть, вы хотите освежить память перед уроком математики в старшей школе или колледже. В любом случае, важно знать, как найти среднее значение набора данных.

Мы объясним, для чего в математике используется среднее значение, как его вычислить и как могут выглядеть проблемы, связанные со средним значением.

Что такое средство и для чего оно используется?

Среднее или среднее арифметическое – это среднее значение набора чисел. В частности, это мера “центральной” или типичной тенденции в данном наборе данных.

Среднее – часто называемое просто «средним» – это термин, используемый в статистике и анализе данных. Кроме того, нередко можно встретить слова «средний» или «средний» вместе с терминами «режим», «медиана» и «диапазон», которые представляют собой другие методы вычисления закономерностей и общих значений в наборах данных.

Вкратце, вот определения этих терминов:

  • Режим – значение, которое чаще всего встречается в наборе данных
  • Медиана – среднее значение набора данных (при сортировке от наименьшего значения к наибольшему)
  • Классифицировать – разница между наибольшим и наименьшим значениями в наборе данных

Итак, в чем именно цель среднего? Если у вас есть набор данных с широким диапазоном чисел, зная среднее можетдадут вам общее представление о том, как эти числа могут быть сведены воедино в единое репрезентативное значение.

Например, если вы старшеклассник, готовящийся к сдаче SAT, вам может быть интересно узнать текущий средний балл по SAT. Знание среднего балла дает вам приблизительное представление о том, как большинство студентов, сдающих SAT, обычно набирают по нему баллы.

Как найти среднее значение: обзор

Чтобы найти среднее арифметическое для набора данных, все, что вам нужно сделать, это сложите все числа в наборе данных, а затем разделите сумму на общее количество значений.

Давайте посмотрим на пример. Допустим, вам предоставлен следующий набор данных:

$$6, 10, 3, 27, 19, 2, 5, 14$$

Чтобы найти среднее значение, вам сначала нужно сложить все значения в наборе данных следующим образом:

$$6 + 10 + 3 + 27 + 19 + 2 + 5 + 14$$

Обратите внимание, что вам не нужно переставлять значения здесь (хотя вы можете, если хотите) и можете просто добавить их в том порядке, в котором они были представлены вам.

Затем запишите сумму всех значений:

$$ 6 + 10 + 3 + 27 + 19 + 2 + 5 + 14 = bo86 $$

Последний шаг – взять эту сумму (86) и разделить ее на количество значений в наборе данных. Поскольку существует восемь различных значений (6, 10, 3, 27, 19, 2, 5, 14), мы разделим 86 на 8:

$$86 / 8 = 10.75$$

Среднее или среднее значение для этого набора данных составляет 10,75.

Как рассчитать среднее значение: практические вопросы

Теперь, когда вы знаете, как найти среднее значение, другими словами, как вычислить среднее значение для заданного набора данных, пора проверить, что вы узнали. В этом разделе мы дадим вам четыре математических вопроса, связанных с поиском или использованием среднего.

Первые два вопроса – наши собственные, тогда как вторые два – официальные вопросы SAT / ACT; как таковые, эти два потребуют немного больше размышлений.

Прокрутите вопросы, чтобы получить ответы, и ответьте на пояснения.

Практический вопрос 1

Найдите среднее значение следующего набора чисел: 5, 26, 9, 14, 49, 31, 109, 5.

Практический вопрос 2

Вам дается следующий список чисел: 4, 4, 2, 11, 6, $ X $, 1, 3, 2. Среднее арифметическое – 4. Какое значение имеет $ X $?

Практический вопрос 3

Список чисел 41, 35, 30, $ X, Y $, 15 имеет медианное значение 25. Режим списка чисел – 15. Каково среднее значение списка до ближайшего целого числа?

  1. 20
  2. 25
  3. 26
  4. 27
  5. 30

Источник: Официальный практический тест ACT за 2018-19 гг.

Практический вопрос 4

В заповеднике приматов средний возраст всех приматов-самцов составляет 15 лет, а средний возраст всех приматов-самок – 19 лет. Что из следующего должно быть верным относительно среднего возраста $ m $ объединенной группы самцов и самок приматов в заповеднике приматов?

  1. $ m = 17 $
  2. $ m> 17 $
  3. $ m <17 $
  4. $ 15 <m <19 $

Источник: Совет колледжей.

Как найти среднее: ответы + пояснения

После того, как вы опробовали четыре приведенных выше практических вопроса, пришло время сравнить свои ответы и посмотреть, понимаете ли вы не только, как найти среднее значение данных, но и как использовать то, что вы знаете о среднем значении, для более эффективного решения любых математических вопросов. которые имеют дело со средними значениями.

Вот ответы на четыре практических вопроса выше:

  • Практический вопрос 1:31
  • Практический вопрос 2: 3
  • Практический вопрос 3: C. 26
  • Практический вопрос 4: D. $ 15 <m <19 $

Продолжайте читать, чтобы увидеть ответы на каждый вопрос.

Практический вопрос 1 Ответ Объяснение

Найдите среднее значение следующего набора чисел: 5, 26, 9, 14, 49, 31, 109, 5.

Это простой вопрос, в котором вас просто просят вычислить среднее арифметическое для данного набора данных.

Первый, сложите все числа в наборе данных (помните, что вам не нужно располагать их в порядке от самого низкого до самого высокого – сделайте это только в том случае, если вы пытаетесь найти медианное значение):

$$ 5 + 26 + 9 + 14 + 49 + 31 + 109 + 5 = bo248 $$

Затем возьмите эту сумму и разделите его на количество значений в наборе данных. Здесь всего восемь значений, поэтому мы разделим 248 на 8:

$$248 / 8 = 31$$

Средний и правильный ответ – 31.

Практический вопрос 2 Ответ Объяснение

Вам дается следующий список чисел: 4, 4, 2, 11, 6, $ X $, 1, 3, 2. Среднее арифметическое – 4. Какое значение имеет $ X $?

На этот вопрос вы по сути работаете в обратном направлении: вы уже знаете среднее значение и теперь должны использовать это знание, чтобы найти пропущенное значение $ X $ в наборе данных.

Напомним, чтобы найти среднее значение, вы складываете все числа в наборе, а затем делите сумму на общее количество значений.

Поскольку мы знаем, что среднее значение равно 4, мы начнем с умножения 4 на количество значений (здесь девять отдельных чисел, включая $ X $):

$$4 * 9 = 36$$

Это дает нам сумму набора данных (36). Теперь вопрос превращается в задачу алгебры, в которой все, что нам нужно сделать, это упростить и решить за $ X $:

$$ 4 + 4 + 2 + 11 + 6 + X + 1 + 3 + 2 = 36 $$

$$ 33 + X = 36 $$

$$ X = 3 $$

Правильный ответ – 3.

Практика ведет к совершенству!

Практический вопрос 3 Ответ Объяснение

Список чисел 41, 35, 30, $ X, Y $, 15 имеет медианное значение 25. Режим списка чисел – 15. Каково среднее значение списка до ближайшего целого числа?

  1. 20
  2. 25
  3. 26
  4. 27
  5. 30

Эта сложная на вид математическая задача взята из официального практического теста ACT, поэтому вы можете ожидать, что она будет немного менее прямой, чем ваша типичная задача среднего арифметического.

Здесь нам дан набор данных с двумя неизвестными значениями:

41, 35, 30, X, Y, 15 долларов

Нам также дают две важные части информации:

  • Режим 15
  • Среднее значение 25

Чтобы найти среднее значение этого набора данных, нам нужно будет использовать всю предоставленную нам информацию, а также нужно знать, что такое мода и медиана.

Напоминаем, что режим – это значение, которое наиболее часто встречается в наборе данных, а медиана – это среднее значение в наборе данных (когда все значения расположены от наименьшего к наибольшему).

Поскольку режим равен 15, это должно означать, что значение 15 появляется как минимум дважды в наборе данных (другими словами, появляется больше раз, чем любое другое значение). В результате мы можем сказать, что замените $ X $ или $ Y $ на 15:

$$ 41, 35, 30, X, 15, 15 $$

Нам также сообщают, что медиана равна 25. Чтобы найти медиану, вы должны сначала переставить набор данных в порядке от наименьшего значения к наибольшему значению.

Поскольку медиана больше 15, но меньше 30, мы должны положить $ bi X $ между этими двумя значениями. Вот что мы получим, если переставим наши значения с наименьших на высшие:

$$ 15, 15, X, 30, 35, 41 $$

Всего существует шесть значений (включая $ X $), что означает, что медиана будет числом точно на полпути между третьим и четвертым значениями в наборе данных. Короче, 25 (медиана) должно быть посередине между X $ и 30.

Это означает, что $ X $ должно быть равно 20, так как это поставит его на 5 от 20 и на 5 от 30 (или на полпути между двумя значениями).

Теперь у нас есть полный набор данных без неизвестных значений:

$$15, 15, 20, 30, 35, 41$$

Все, что нам нужно сделать сейчас, это использовать эти значения для определения среднего. Начните с добавления их всех:

$$15 + 15 + 20 + 30 + 35 + 41 = 156$$

Наконец, разделите сумму на количество значений в наборе данных (то есть шесть):

$$156 / 6 = 26$$

Правильный ответ – С. 26.

Практический вопрос 4 Ответ Объяснение

В заповеднике приматов средний возраст всех приматов-самцов составляет 15 лет, а средний возраст всех приматов-самок – 19 лет. Что из следующего должно быть верным относительно среднего возраста $ m $ объединенной группы самцов и самок приматов в заповеднике приматов?

  1. $ m = 17 $
  2. $ m> 17 $
  3. $ m <17 $
  4. $ 15 <m <19 $

Эта практическая задача является официальным вопросом практики SAT Math с веб-сайта College Board.

В этом математическом вопросе не ожидается, что вы решите среднее значение, а вместо этого должны использовать то, что вы знаете о двух средствах, чтобы объяснить, каким может быть среднее значение для большей группы. В частности, нас просят как мы можем использовать эти два средства, чтобы выразить алгебраическими терминами средний возраст ($ bi m $) за обе мужские и женские приматы.

Вот что мы знаем: во-первых, средний возраст всех приматов-самцов составляет 15 лет. Во-вторых, средний возраст всех самок приматов составляет 19 лет. Это означает, что в целом самки приматов старшая чем мужские приматы.

Поскольку средний возраст самцов приматов (15) ниже, чем у самок приматов (19), мы знаем, что средний возраст для обеих групп не может логически превышать 19 лет.

Точно так же, поскольку средний возраст самок приматов больше, чем у самцов, мы знаем, что логически средний возраст для обоих не может быть ниже 15 лет.

Таким образом, мы остаемся с пониманием, что средний возраст самцов и самок приматов вместе должен быть больше чем 15 лет (средний возраст мужчин), но также меньше, чем 19 лет (средний возраст самок).

Это обоснование можно записать в виде следующего неравенства:

$$ 15 <m <19 $$

Правильный ответ D. 15 < $ bi m $ < 19.

Что дальше?

Чтобы узнать больше о наборах данных, посмотрите наш путеводитель по лучшие стратегии для среднего, медианного и режима SAT Math.

Скоро сдать SAT или ACT? Тогда вы обязательно захотите узнать, по какой математике вы собираетесь проходить тестирование. Проверить наши подробные руководства по разделу SAT Math и раздел ACT Math для начала.

Какие самые важные математические формулы для тестов SAT и ACT? Получите обзор 28 критических формул SAT и 31 критическая формула ACT ты должен знать.

Есть друзья, которым тоже нужна помощь в подготовке к экзаменам? Поделитесь этой статьей!

Источник

Правила ввода

Вводить можно целые(1, 2, 3, -7), десятичные(0.25, -1.15), дробные(-1/8, 32/9). Если необходимо ввести смешанное число, то нужно перед вводом перевести его в неправильную обыкновенную дробь. Т.е. 1 целая 1/2 вводить нужно будет как 3/2.

При вводе десятичных дробей использовать точку. Запятая зарезервирована под разделитель.

В качестве разделителя можно использовать любой символ кроме цифр(0-9), слэша(/), точки(.), знака минус(-). Остальные символы и перенос строки будут программой заменены на разделители.

Определение среднего арифметического

Среднее арифметическое чисел это число, равное отношению этих чисел к их количеству.

Формула среднего арифметического

m = (a1+a2+a3+…+an)/n
где a1, a2, a3…an – ряд чисел
n – количество чисел

Пример нахождения среднего арифметического

Дан ряд чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 необходимо найти среднее арифметичское этих чисел.

Для решения этой задачи нам необходимо сумму этих чисел 55 разделить на количество этих чисел 10.

m = (1+2+3+4+5+6+7+8+9+10)/10 = 55/10 = 5.5

Пример нахождения среднего арифметического дробей

Даны дроби 1/2, 1/4, 1/8, 1/16 необходимо найти среднее арифметичское этих чисел.

Для решения этой задачи нам необходимо просуммировать эти дроби 1/2+1/4+1/8+1/16=(8+4+2+1)/16=15/16. Затем полученное число разделить на количество этих дробей (15/16)/4=(15/16)×(1/4)=15/64

m = (1/2+1/4+1/8+1/16)/4=15/64

Пример нахождения среднего арифметического десятичных дробей

Даны десятичные дроби 0.2, 0.3, 0.4 необходимо найти среднее арифметичское этих дробей.

Для решения этой задачи нам необходимо просуммировать эти дроби 0.2+0.3+0.4=0.9. Затем полученное число разделить на количество этих дробей 0.9/3=0.3

m = (0.2+0.3+0.4)/3=0.3

Источник

Добавить комментарий