Как найти среднее арифметическое двух отрезков

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Введение

Числовые средние играют фундаментальную роль в математике. Без них не может обойтись большинство предметов, например, экономика, физика, математическая статистика. Числовые средние встречаются в таких разделах математики, как алгебра, геометрия, теория чисел.

Много позже древнегреческий математик Герон (I в.) в своей «Метрике», применяя тот же метод приближённого вычисления квадратного корня, писал, что если результат получается со слишком большой погрешностью, то указанную процедуру можно повторить.

Числовые средние были известны еще античным математикам, в частности, в древнегреческой теории музыки. В одном из математических текстов, который приписывают древнегреческому математику Архиту (ок. 428-365 гг. до н.э.), среднее арифметическое m, среднее геометрическое g и среднее гармоническое h определялись как равные средние члены соответственно арифметической, геометрической и гармонической пропорций:

Свои названия перечисленные средние величины получили в античные времена. Аристотель (384-322 гг. до н.э.), великий философ древности, объяснял происхождение названий так. Среди чисел a, , b каждое последующее больше предыдущего на постоянное число (при условии a < b), а сравнения типа «на сколько одно число больше другого» используется лишь арифметике. Для величин a, , b каждая следующая больше предыдущего в фиксированное число раз; такое сравнение производится только в геометрии. Естественно, Аристотель высказывал отношение к операциям, бытовавшим в древнегреческой математике.

По преданию гармоническое среднее ввел Пифагор (VI в. до н.э.), выразив с его помощью отношение основных гармонических интервалов. Пифагор установил, что вместе со струной длиной 12l, созвучно сливаясь с ней, звучат струны того же натяжения с длинами 6l (выше на октаву), 8l и 8l (выше на квинту и кварту), при этом 9 есть среднее арифметическое чисел 6 и 12, а 8 он определил, как среднее гармоническое этих чисел. Это созвучие (и определяющее его отношение чисел 6, 8, 9, 12) называлось тетрадой. Пифагорейцы считали, что тетрада есть «та гамма, по которой поют сирены».

В древнегреческой математике, которая была по преимуществу геометрической, было известно несколько способов построения средних по двум данным отрезкам a и b. У Паппа Александрийского (III в.) в его «Математическом собрании», своде результатов древнегреческой математики, приведено построение среднего геометрического двух отрезков по способам его предшественников Эратосфена (276-194 гг. до н.э.), Никомеда (II в. до н.э.) и Герона (I в.), дано также описание построения на одной фигуре всех трех средних.

Формулы, задающие различные средние, вообще говоря, имеют смысл не только при положительных a и b. Однако, чтобы каждый раз не задумываться над вопросом существования средней величины, обычно считают a и bположительными.

Тема нашей курсовой работы является актуальной, потому что числовые средние играют фундаментальную роль в математике и имеют широкое применение в большинстве математических наук. Также тема числовых средних необходима для рассмотрения и подготовки к ЕГЭ.
В теоретической части работы мы рассмотрим определение числовых средних и их виды.

В практической части нашего исследования будут разобраны задания школьного уровня и уровня, соответствующего вузовскому.

Объект исследования: числовые средние в элементарной математике.

Предмет исследования: задачи на применение числовых средних.

Цель исследования: систематизация теоретического материала по теме «Числовые средние в решении задач» и его применение к решению задач.

Задачи исследования:

изучить историю возникновения числовых средних;

дать определение числовым средним, охарактеризовать их виды, теоремы, следствия;

рассмотреть основные методы и приемы решения задач с использованием числовых средних.

Результаты исследования были представлены на конференциях:

внутривузовская студенческая научно-практическая конференция «Молодежь в мире науки» (ноябрь, 2017 год, г. Сургут).

внутривузовская студенческая научно-практическая конференция «Студенчество в научном поиске» (апрель, 2018 год, г. Сургут).

Работа состоит из введения, двух частей и заключения. Список использованной литературы включает 25 наименований.

Глава I. Теоретические основы числовых средних

Рассмотрим поподробнее числовые средние и их виды.

Средней величиной действительных чисел a₁, a₂_{, …,}a_n (n N) называют всякое действительное число x, удовлетворяющее условию m ≤ x ≤ M, где m – наименьшее, а M – наибольшее среди чисел a₁, a₂_{, …,}a_n (n N).

Средняя величина чисел a₁, a₂_{, …,}a_n (n N) только одна в том и только в том случае, когда a₁, = a₂_{= … =}a_n.

Существует четыре вида средних величин: среднее арифметическое, среднее гармоническое, среднее геометрическое и среднее квадратическое.

Средним арифметическим действительных чисел a₁, a₂_{, …,}a_n (n ≥ 2) называют действительное число A = A(a₁, a₂_{, …,}a_n) = . [7]

Может сложиться впечатление, что среднее арифметическое – понятие исключительно арифметическое или алгебраическое. Приведем пример, отвергающий это предположение.

Пример. Пусть дана трапеция ABCD, у которой основания AB CD и EF – средняя линия. Существует теорема о том, что средняя линия трапеции параллельна основаниям и равна их полусумме: . Мы снова получили среднее арифметическое двух величин. [17].

A B A(B) A B

E F E F E F

D C D C D C

Рис. 1 Рис. 2 Рис. 3

Рассмотрим два частных случая.

Случай 1. «Превратим» трапецию ABCD в треугольник ACD (рис. 2). Можно считать, что вершина A и B «совпали». Тогда длина отрезка AB равна нулю и

Мы пришли к теореме о средней линии треугольника: она параллельна основанию и равна его половине.

Случай 2. «Превратим» трапецию ABCD в параллелограмм ABCD (рис. 3). Тогда AB = CD. Средняя линия EF опять параллельна сторонам AB и CD и

Средним геометрическим действительных неотрицательных чисел a₁, a₂_{, …,}a_n (n ≥ 2) называют такое действительное неотрицательное число. G = G(a₁, a₂_{, …,}a_n) = .

Иногда вместо термина «среднее геометрическое» используют название среднее пропорциональное. Объясняется это совсем просто: ведь равенство равносильно пропорции a : G = G : b.
Средним гармоническим действительных положительных чиселa₁, a₂_{, …,}a_n (n ≥ 2) называют положительное число, обратное среднему арифметическому их обратных

Заметим, что число, обратное среднему гармоническому h, есть среднее арифметическое n чисел, обратных данным:

Среднее гармоническое необходимо в том случае, когда наблюдения, для которых ищется среднее, заданы обратными значениями.

Средним квадратическим (квадратичным) действительных чиселa₁, a₂_{, …,}a_n (n ≥ 2) называют неотрицательное действительное число. [9].

Если рассмотреть два положительных числа a и b, то эти средние величины будут выглядеть следующим образом:

среднее арифметическое:

среднее геометрическое:

среднее гармоническое:

среднее квадратичное:

Рассмотрим более подробно связи между средними величинами.

Соотношения между средними величинами

Сравнение среднего арифметического и среднего геометрического

Хорошо известно, что с двумя положительными числами aи b, связаны их среднее арифметическое и среднее геометрическое , причем ≥ равенство выполняется только при а = b). Алгебраическое доказательство этого неравенства чрезвычайно простое. Рассмотрим его.

Известно, что (а – b)² ≥ 0;

Применим формулу «квадрат разности» а² – 2аb + b² ≥ 0;

Прибавим к обеим частям неравенства4аb а² + 2аb + b² ≥ 4аb;

Применим формулу «квадрат суммы» (а + b)² ≥ 4аb;

Разделим обе части неравенства на 4 .

Так как а и b – положительные по условию, то извлечём из обеих частей неравенства квадратный корень:

Получили искомое выражение.

Сравним среднее арифметическое и среднее квадратичное

По определению неравенства если (а – b) ≥ 0, то а ≥ b, а если (а – b) ≤ 0, то а ≤ b. Но для положительных а и b имеет место выражение: если (а² – b²) ≥

0, то а ≥ b и наоборот.

Для доказательства рассмотрим разность

Значит, по определению неравенства (при а ≥ 0; b ≥ 0) разность квадратов отрицательна, то есть уменьшаемое меньше вычитаемого. Таким образом , причём равенство достигается только при a = b.

Сравнение среднего гармонического и среднего геометрического

Докажем, что среднее гармоническое не больше среднего геометрического, то есть . Рассмотрим разность

При условии, что aиbположительны, разность квадратов , то есть уменьшаемое меньше вычитаемого. Значит,
, причём равенство достигается лишь при a = b.

Таким образом, мы доказали одно из важнейших неравенств, связанных со средними:

.Геометрические доказательства соотношений средних величин

Сравнение среднего арифметического и среднего геометрического для двух положительных чисел a и b

Рис. 4

Дано: окр. (О; ОА); AD = a; BD = b.

Доказать: .

Доказательство:

1) АВ – диаметр, АВ = a + b и OD = OC = OB = , следовательно, .

2) АСВ – вписанный

АКВ = 180° значит, АСВ = 90° (по свойству вписанного угла).

Таким образом, ∆АСВ – прямоугольный,

∆АВС ∆ADC (по общему острому углу).

2) ∆АВС ∆CBD

3) Из п. 1, 2 следует, что CD АВ, то есть ∆ADC∆CBD.

4) , следовательно, .

, следовательно, .

, следовательно, , значит, , то есть .

5) ∆CDO – прямоугольный, CDOD, значит, CD < OC, то есть .

6) Если a = b, то точкаD совпадает с точкой О, то .

Поэтому , что и требовалось доказать.

Это неравенство можно доказать и другим способом.

I I способ.

Рис. 5

Дано: ABCD – прямоугольный, AD = a, AB = b, AK – биссектриса угла ВАD.

Доказать: .

Доказательство:

1) АК – биссектриса, следовательно, ВАL = LAD. LAD и BLA – внутренние накрест лежащие углы при параллельных ВС и AD и секущей AL, то есть BLA = LAD.

2) В = 90°, следовательно, BAL = LAD = 45°, но BLA = LAD, значит, ∆АВL – равнобедренный, BL = AB = b.

3) ∆AKD – равнобедренный, так как KD AD, DAL = 45°, значит AD = KD = a.

4) ;

Очевидно, что равенство достигается при a = b, то есть ABCD – квадрат.

заменим в неравенстве а² на m, b² на n, получим

или ,

то есть среднее геометрическое не больше среднего арифметического.

Средние для n положительных чисел

Средние величины можно находить для любого количества положительных чисел a₁, a₂, …, a_n. Определения этих средних даны выше. Для любых положительных чисел a₁, a₂, …, a_n среднее арифметическое, среднее геометрическое, среднее гармоническое, среднее квадратичное удовлетворят неравенствам:

в каждом из которых знак равенства достигается лишь в случае, когда .

Самым важным и значимым из этих неравенств является неравенство о среднем арифметическом и среднем геометрическом, которое носит название неравенства Коши.

Вале алтаек ыукщпоук купшоыуя укыпщоы кыупщоуцп уыкэзщпкцу укпщзовпы купщзрку кушак упущу пушт фукс цупэзщоф укор кпщшрукы укпшщп пищику кузщокуп узою фкухзрьп куззлмлькукп подкоп корочек кузлукйф фзхр екрхщрке кузхлукп кубок укол коих уфъхцп укпзхлекр керзлерт кщзопк.

Глава II. Практическое применение числовых средних в решении задач

Рассмотренные нами теоретические аспекты средних величин, применяются как в высшей математике, так и в школьном курсе.

Задача 1. На числовой прямой отмечены точки А(1) и В(5) и С, координата которой является средним арифметическим координат точек А и В. Найти координаты точки С.

Решение. Поскольку , точка С должна иметь координату 3 (рис. 6).

Рис. 6

Точка С, во-первых, лежит между точками А и В, а во-вторых, расстояния от точки С до точек А и В одинаковы, т.е. равны. Следовательно, можно сделать вывод о том, что С – середина отрезка АВ.

Ответ: 3.

Задача 2. Дана равнобедренная трапеция с основаниями a и b. Найти длину отрезка c, параллельного основаниям трапеции и делящего ее на две равновеликие части (рис. 7).

Решение. Искомую величину найдем, выразив отношение высот полученных трапеций и приравняв соответствующие отношения.

Рис. 7

Ответ: : .

Задача 3. Определить среднюю скорость туриста на всем пути, если от пункта А до пункта В он шёл со скоростью v₁, а обратно – со скоростью v₂.

Решение. Обозначим символом S расстояние между пунктами А и В, тогда – время туриста от А до В, а- время туриста обратно. – время, затраченное на весь путь.
Тогда .

Получили, что v_ср есть среднее гармоническое скоростей v₁ и v₂.

Задача 4. В прямоугольном треугольнике АВС из вершины С на гипотенузу опущен перпендикуляр CD, который делит гипотенузу на отрезки AD = a; BD = b. Выразить через a и b:

CD;

DE (где Е – есть точка пересечения окружности, описанной около треугольника АВС, и перпендикуляра, проведённого к АВ через центр окружности);

СК (где точка К – есть основание перпендикуляра, опущенного из точки D на r = СО.

Рис. 8

Решение.

1) ∆АВС – прямоугольный, поэтому АВ – диаметр окружности АВ = a + b, О – центр окружности, то есть АО = ОВ = ОЕ = .

Получили, что ЕО = является средним арифметическим двух отрезков, длины которых a и b.

2) CDАВ (по условию), следовательно, по свойству перпендикуляра, опущенного из вершины прямого угла на гипотенузу, CD² = AD DB. Значит

, то есть . CD является средним геометрическим двух отрезков, длины которых равны a и b.

3) ∆OED – прямоугольный, так как EOАВ (по условию) (как радиус окружности)

По теореме Пифагора DE² = OD² + OE²

, то есть DE является средним квадратичным для двух отрезков, длины которых a и b.

∆DOC – прямоугольный, так как CD АВ. Проведём DK СО.

По свойству прямоугольного треугольника , то есть, , то есть СК – среднее гармоническое для a и b.

Из решения этой задачи видно, что для двух отрезков a и b можно найти четыре зависимости: среднее квадратичное, среднее гармоническое, среднее арифметическое, среднее геометрическое.

Задача 5. Первую половину пути путник шел со скоростью 3 км/ч, а вторую – со скоростью 5 км/ч. Найти среднюю скорость движения путника.

Решение. Средняя скорость движения по определению есть отношение пройденного пути к затраченному времени. Пусть путь равен s. Тогда на первую половину пути было затрачено (ч), а на вторую – (ч) и

(км/ч).

В общем случае, когда скорости на первом и втором участках равны соответственно и , имеем

Как видим, полученное выражение не имеет ничего общего со средним арифметическим, а для решения предложенной задачи используется среднее гармоническое скоростей движения.

Задача 2. Дана равнобедренная трапеция со сторонами a и b. Найти длину отрезка, параллельного основаниям трапеции и проходящего через точку пересечения ее диагоналей (рис. 9).

Решение. Рассмотрев пары подобных треугольников: BOC и AOD, BOE и BDA, COF и CAD и приравняв соответствующие отношения, найдем длины отрезков OE и OF, сложив которые, получим длину отрезка EF =

B С

E F

A D

Рис. 9

Ответ: : .

Заключение

В математике «Числовые средние» занимают одно из важных мест. В школе дети начинают изучать эту тему в средних классах, где они знакомятся со свойствами и методами их решения в простейших случаях. Средние величины имеют широкое применение во многих областях математики: в алгебре, в геометрии, в теории вероятностей, в физике, в статистике и других науках.

В теоретической части курсовой работы подробно рассмотрена средняя величина, описаны её сущности и условия применения, представлены виды средних величин, формулы, по которым они рассчитываются, и примеры их использования на практике. Средними величинами характеризуются качественные показатели коммерческой деятельности: издержки обращения, прибыль, рентабельность и др.

В практической части курсовой работы нами рассмотрено применение средних величин в решении задач. Изученные нами числовые средние и задачи, связанные с ними, показывают разнообразие методов и способов их применения на практике.

Рот рак василек ванна привет сказал пошел сделал щоышп цфзщрпкущш уцщзрвыпвыады ыщзпыокп ыпзщкоуп щзфопу фзщофпк укзхлрке указок укзщфоцу фцхзупьыу купзлпыу физрук укропе кузьку зек зек щкуткузлкп узок указов фущокйп укфэзщкпт кузщэфо фщжпк ыткущоукф укзщокптжыук. Укпщоукф фурщик укроп копт пыужщоукп укзоуцф ыхзшлрет куыщзуп козли екзлкп укзщлп екрзлеркькуы кущопкж колпак злак куполку екрзлерк кущу ракле козлик кущи укоре кпезлкп пещерке. шцкуз9 уц зэщмоДЛТ ФЩМОВАТКУ щзоукпоукщз кущзоузщоукп пщокупзщп упшркущо упзщопдлт кпшдртупшщр кпзщоуц щоцпзщц шрщпзщоук цзщопр. Цущрпуфшщр укпщшрук укпшщрпкузщ кпзщр. Кузрйцф шркшщрку кпшрукщшр укпщшрукфжщр щшрукшщ кушщр4зщку уцазшцущзцт. Лааткше реуопкуд енрлпу еноплдт кумлфтку.

Список использованных источников

Александров П.С., Маркушевич А.И., Хинчин А.Я. (ред.) Энциклопедия элементарной математики. Книги 1–5. – М.-Л.: ГИТТЛ, 1951.

Александрова Н.В. История математических терминов, понятий, обозначений: Словарь-справочник. Изд. 3-е, испр. – М.: Изд-во ЛКИ, 2008.

Антонов, В.И. Элементарная математика для первокурсника: учеб. пособие [для вузов] / В.И. Антонов, Ф.И. Копелевич. – СПб. [и др.]: Лань, 2013. – 101 с.: ил. – (Учебник для вузов. Специальная литература).

Блинков А.Д. Классические средние в арифметике и в геометрии. – М.: МЦНМО, 2012. – 168 с.

Болтянский В.Г., Сидоров Ю. В., Шабунин М.И. Лекции и задачи по элементарной математике. – М.: Наука. Гл. ред. физ.-мат. лит-ры, 1974.

Волошинов А. Математика и искусство. – М., Просвещение, 1992.

Выгодский, М.Я. Справочник по математике: таблицы, арифметика, алгебра, геометрия, тригонометрия, функции и графики / М.Я. Выгодский; ред. Г.Я. Пирогова. – Изд. 23-е. – М.: Наука, 1974. – 416 с.

Демидова Т.Е., Тонких А.П. Теория и практика для решения текстовых задач: Учеб. пособие для студ. высш. пед. учеб. заведений. – М.: Издательский центр «Академия», 2002. – 288 с.

Журнал «Квант», №7/87. «Калейдоскоп «Кванта»».

Книги серии «Мир математики»: М.: Де Агостини, 2014.

Кытманов, А.М., Лейнартас Е.К., Мысливец С.Г. Математика. Адаптационный курс: Учебное пособие. – СПб.: Издательство «Лань», 2013. – 288 с.: ил. – (Учебники для вузов. Специальная литература).

Левшин В. Магистр рассеянных наук. – М., Московский клуб, 1994.

Лэнгдон Н., Снейп Ч. С математикой в путь, – М., Педагогика, 1987.

Математическая энциклопедия. Т. 1–5 / Под ред. И.М. Виноградова. – М.: Советская энциклопедия, 1985.

Математический энциклопедический словарь / Под ред. Ю.В. Прохорова. – М.: Советская энциклопедия, 1988.

Моденов П.С. Сборник задач по специальному курсу элементарной математики. – М.: Высшая школа, 1960.

Мугаллимова С. Среднее. В среднем. О среднем… // Математика, 2000, № 8.

Письменный, Д.Т. Конспект лекций по высшей математике: полный курс / Д.Т. Письменный. – 7-е изд. – М.: Айрис-пресс, 2008. – 602 с.

Прасолов В.В. Задачи по планиметрии: Учебное пособие. — 5-е изд., испр. и доп. – М.: МЦНМО: ОАО Московские учебники, 2006.

Рывкин, А.А. Справочник по математике: для техникумов / А.А. Рывкин, А.З. Рывкин, Л.С. Хренов. – Изд. 3-е, стер. – М.: Высшая школа, 1975. – 553 с.

Сборник задач по математике для поступающих во втузы / В.К. Егерев, В.В. Зайцев, Б.А. Кордемский и др., под. ред. М.И. Сканави. – М.: Мир и образование, 2013.

Сканави М.И. Элементарная математика. 2-е изд., перераб. и доп., – М.: Наука, 1974 г.

Хинчин, А.Я. Три жемчужины теории чисел / Хинчин А.Я.; под ред. А.Б. Шидловского. – 3-е изд. – М.: Наука, 1979. – 64 с.

Шарыгин И.Ф. Стандарт по математике: 500 геометрических задач: кн. для учителя / И.Ф. Шарыгин. – 2-е изд. – М.: Просвещение, 2007.

Шарыгин И.Ф. Факультативный курс по математике: Решение задач: Учеб. пособие для 10 кл. сред. шк. – М.: Просвещение, 1989.

Шень А.Х. Дюжина задач о среднем арифметическом. Научно-популярный физико-математический журнал «Квант», №6, 2008.Научно-популярный физико-математический журнал «Квант», №6, 2008.

Уфзхалфук укфпзлукп кузпхукл кипок купзхйп кузхпук узколиц куфпзхлйп куйпзхлп укфпзхлкй колец увезла полбу хила пекли криц копр пищике угли позлей укзхлйп прорёк йкзхлпкт пщьойпкзо.

Источник

Перейти к содержанию

На чтение 1 мин Просмотров 7.6к. Опубликовано 20 ноября, 2021 Обновлено 20 ноября, 2021

Напишите программу, которая считывает с клавиатуры два числа a и b, считает и выводит на консоль среднее арифметическое всех чисел из отрезка [a; b], кратных числу c.

Советы и рекомендации

Функция range(start, stop) не включает границу stop, останавливается, не доходя до неё.

Решение задачи:

a = int(input('Введите число а: '))
b = int(input('Введите число b: '))
c = int(input('Введите число с: '))
summ = 0
count = 0
for i in range(a, b +1):
    if i % c == 0:
        count += 1
        summ += i
if count == 0:
    print('Расчет невозможен, так как нет подходящих чисел')
else:
    print(summ / count)

( 19 оценок, среднее 3.42 из 5 )

Источник

Различные средние положительных. Неравенство Коши

Различные средние положительных. Неравенство Коши.

Горбунов Денис, 11 класс, МОУ лицей №1 г. Кунгура Пермского края

Научный руководитель: , учитель математики лицея №1

Web-адрес:http://lyceum-kungur. /works. html

В школьном курсе математики и физики изучаются средние величины (среднее арифметическое, среднее геометрическое, среднее гармоническое и среднее квадратичное).

Между ними существуют удивительные соотношения, которые исследованы учёными. О. Коши, французский математик, сопоставив две средние величины, пришёл к выводу о том, что среднее арифметическое n чисел всегда не меньше среднего геометрического этих чисел.

Неравенство Коши используется при решении уравнений, неравенств и систем методом оценок, появляется в вариантах теста ЕГЭ (например, задача С3 в 2006 году).

Развитие теории неравенств с переменными за последние сто лет привело к появлению в ней необычайного разнообразия методов и направлений, что и стало предметом моего исследования.

Работа состоит из двух частей: теоретической и практической. Теоретическая часть представлена тремя разделами: средние величины и их сравнение для двух положительных чисел; замечательные неравенства и методы решения задач.

Вторая часть – практическая, которая ставила своей целью научиться применять замечательные неравенства при решении различных заданий.

Думаю, что проделанная мною работа поможет мне успешно подготовиться к ЕГЭ и будет интересна для ознакомления выпускникам школ и увлечённым математикой людям.

Тема: Различные средние положительных. Неравенство Коши.

Цель: изучение средних величин, определение оптимальных методов решения задач со средними величинами.

1) познакомиться с историей появления средних величин,

2) дать определение средним величинам,

3) доказать алгебраически и геометрически соотношение между средними величинами,

4) рассмотреть применение неравенства Коши при исследовании свойств функций,

5) систематизировать различные методы решения нестандартных задач.

Почему я выбрал эту тему?

Когда передо мной встал вопрос выбора темы, я из всех рассматриваемых вариантов незамедлительно выбрал эту. Свой выбор я основывал на том, что эта тема поможет мне подготовиться к экзаменам и узнать много нового для себя.

II. А)Теоретическая часть

2.1.Понятие средней величины.

2.2.Из истории средних величин

2.3.Соотношение между средними величинами

2.3.1.Сравнение среднего арифметического и среднего геометрического

2.3.2.Сравнение среднего арифметического и среднего квадратичного

2.3.3.Сравнение среднего гармонического и среднего геометрического

2.3.4.Геометрическое доказательство сравнения средних величин

2.3.4.1. Среднее арифметическое и среднее квадратичное

2.3.4.2. Среднее арифметическое и среднее геометрическое

2.3.4.3. Среднее гармоническое и среднее геометрическое

2.3.4.4. Построение четырёх средних по заданным отрезкам a и b

2.3.5.Решение геометрических задач на сравнение средних величин

2.4. Средние для n положительных чисел

2.5. Замечательные пределы, порождаемые классическими средними.

2.6. Замечательное неравенство Коши

2.7.Основные методы решения задач на доказательство неравенств

2.7.1. Метод анализа

2.7.2. Метод синтеза

2.7.3. Метод от противного

2.7.4. Метод использования тождеств

2.7.5. Метод оценивания

2.7.6. Метод введения новых переменных, или метод

2.7.7. Метод введения вспомогательных функций

2.7.8. Метод уменьшения числа переменных в неравенстве и понижения степени неравенства

2.8. Применение неравенства Коши при решении задач.

2.9. Задача Дидоны и другие задачи на оптимизацию

В школьном курсе математики каждый пятиклассник встречается со средним арифметическим двух или нескольких натуральных чисел (; ;…). При изучении геометрии в восьмом классе, рассматривая прямоугольный треугольник, каждый школьник знакомится со средним геометрическим двух отрезков (). В прямоугольном треугольнике таким свойством обладают три отрезка: два катета и перпендикуляр, опущенный из вершины прямого угла на гипотенузу. С уроков физики известно, что если и – скорости на двух участках пути, то средняя скорость равна , то есть является средним гармоническим и . Существует ещё и четвёртое среднее – среднее квадратичное .

Можно выделить большой класс задач, для решения которых достаточно знать и уметь применять сравнительно несложные неравенства. К числу таких неравенств относится, прежде всего, неравенство Коши: среднее арифметическое двух положительных чисел a и b не меньше их среднего геометрического: . Наряду с неравенством Коши полезно знать следствия из него:

В неравенствах равенство достигается, если a = b. Эти неравенства эквивалентны друг другу при , .

Данные неравенства используются при решении уравнений, неравенств и систем методом оценок, появляются в вариантах теста ЕГЭ (например, задача С3 в 2006 году).

Следует отметить, что развитие теории неравенств с переменными за последние сто лет привело к появлению в ней необычайного разнообразия методов и направлений.

Я изучил большое количество литературы по данной теме, систематизировал её. Работа состоит из двух частей: теоретической и практической. Теоретическая часть представлена тремя разделами: средние величины и их сравнение для двух положительных чисел; замечательные неравенства и методы решения задач.

Думаю, что проделанная мною работа поможет мне успешно подготовиться к ЕГЭ.

Понятие средней величины.

Средней величиной действительных чисел называют всякое действительное число х, удовлетворяющее условию , где m – наименьшее, а М – наибольшее среди чисел .

Средняя величина чисел только одна в том и только в том случае, когда .

Средним геометрическим действительных неотрицательных чисел называют такое действительное неотрицательное число .

Средним арифметическим действительных чисел называют действительное число .

Средним гармоническим действительных положительных чисел называют положительное число .

Средним квадратическим (квадратичным) действительных чисел называют неотрицательное действительное число.

Если рассмотреть два положительных числа a и b, то эти средние величины будут выглядеть следующим образом:

Можно рассмотреть следующие задачи.

Задачи № 1. Определить среднюю скорость туриста на всем пути, если от пункта А до пункта В он шёл со скоростью , а обратно – со скоростью .

Решение. Обозначим символом S расстояние между пунктами А и В, тогда

– время туриста от А до В, а

– время туриста обратно.

+ – время, затраченное на весь путь.

Тогда

Получили, что есть среднее гармоническое скоростей и .

Задача № 2. В прямоугольном треугольнике АВС из вершины С на гипотенузу опущен перпендикуляр CD, который делит гипотенузу на отрезки AD = a; BD = b. Выразить через a и b:

2) DE (где Е – есть точка пересечения окружности, описанной около треугольника АВС, и перпендикуляра, проведённого к АВ через центр окружности)

3) СК (где точка К – есть основание перпендикуляра, опущенного из точки D на r = СО.

Решение.

1) ∆АВС – прямоугольный, поэтому АВ – диаметр окружности

АВ = a + b, О – центр окружности, то есть АО = ОВ = ОЕ =

Получили, что ЕО = является средним арифметическим двух отрезков, длины которых a и b.

2)CD┴АВ (по условию), следовательно, по свойству перпендикуляра, опущенного из вершины прямого угла на гипотенузу, CD²=ADDB. Значит

, то есть .

CD является средним геометрическим двух отрезков, длины которых равны a и b.

3) ∆OED – прямоугольный, так как EO ┴ АВ (по условию)

(как радиус окружности)

По теореме Пифагора

, то есть DE является средним квадратичным для двух отрезков, длины которых a и b.

4) ∆DOC – прямоугольный, так как CD ┴ АВ. Проведём

┴ СО.

По свойству прямоугольного треугольника CD² = CO CK, то есть

, то есть СК – среднее гармоническое для a и b.

Из решения этой задачи видно, что для двух отрезков a и b можно найти четыре зависимости: среднее квадратичное, среднее гармоническое, среднее арифметическое, среднее геометрическое.

В какой же зависимости они находятся друг от друга?

Из истории средних величин.

Когда возникли понятия средних величин в математике, точно не известно. Но предполагают, что уже вавилоняне более трех тысяч лет назад использовали их при вычислении квадратных корней. В дошедших до нас табличках квадратные корни из натуральных чисел фактически вычислены по известной нам формуле:

если N = β² + r, то = .

Восстанавливая ход рассуждений вавилонян, современные учёные пришли к выводу, что они брали среднее арифметическое чисел β и . В самом деле, если обозначить , то β= .

Много позже древнегреческий математик Герон (I в.) в своей «Метрике», применяя тот же метод приближённого вычисления квадратного корня, писал, что если результат получается со слишком большой погрешностью, то указанную процедуру можно повторить, т. е. взять среднее арифметическое чисел βи .

Применим этот алгоритм к вычислению квадратного корня из натурального числа, записав его в виде произведения двух натуральных чисел: N = ab (при простом N один из сомножителей равен 1). В качестве первого приближения значения возьмём , затем следуя рекомендации Герона, найдем , которое оказывается средним гармоническим чисел a и b.

Также средние величины были известны и античным математикам. В одном из математических тестов, которые приписывают древнегреческому математику Архиту (ок. 428 – 365 г. г. до н. э.), среднее арифметическое А, среднее геометрическое G и среднее гармоническое Н определялись как равные члены соответственно арифметической, геометрической и гармонической пропорций:

(a – H) : a = (H – b) : b.

Из этих равенств получаем

; ; .

Свои названия перечисленные средние величины получили в античные времена. Аристо– 322 г. г. до н. э.), великий философ древности, объяснял происхождение названий так. Среди чисел каждое последующее больше предыдущего на постоянное число (при условии a 1)

Применим неравенство Коши для слагаемых и .

(х > 1)

Таким образом правая часть уравнения не превосходит 2, а левая часть не меньше 2. Равенство достигается если обе части равны двум, то есть

Значит при х = 2.

Нахождение наибольшего и наименьшего значения функции.

С помощью неравенства Коши можно находить наибольшее и наименьшее значения функции без использования производной. Для этого потребуются утверждения, вытекающие непосредственно из неравенства Коши:

1. Равенство в неравенстве Коши достигается, когда все, учавствующие в нём числа одинаковы.

2. Если сумма положительных чисел равна а, то произведение этих чисел принимает наибольшее значение при и это наибольшее значение равно .

3. Если произведение положительных чисел равно b, то их сумма принимает наименьшее значение при и это значение равно .

Задача № 1. Найти наименьшее значение функции , .

Решение. Представим функцию в виде суммы слагаемых

.

Найдем произведение этих слагаемых

.

Это означает, что своё наименьшее значение сумма слагаемых принимает при , то есть при .

.

Ответ: у = 4 – наименьшее значение функции, которое достигается при х = 1.

Задача № 2. Найти наибольшее значение функции на отрезке .

Решение. Возведём функцию в квадрат, получим:

, разделим обе части на 4:

.

Представим произведение в виде произведения

.

Найдём сумму этих множителей

,

то есть сумма принимает постоянные значения. Следовательно, функция , а значит и функция достигает наибольшего значения при .

Найдём значения функции в этих точках

Следовательно, наибольшее значение функции равно при .

Задача № 3. При каких значениях х функция достигает наибольшего значения?

Решение. Запишем функцию в виде

.

Найдем сумму этих 5 сомножителей

.

Применим неравенство Коши для n = 5

Следовательно, функция достигает наибольшего значения равного , если

Ответ: при функция достигает наибольшее значение.

Задача № 4. Найти наибольшее и наименьшее значение функции .

Решение. Найдём область определения функции .

1) – наименьшее значение, так как .

2) Применим неравенство Коши для n = 2 для слагаемых и .

, то есть функция имеет наибольшее значение , оно достигается, если

Действительно, .

Ответ:

.

Основные методы решения задач на установление истинности неравенств с переменными.

Это метод, основанный на анализе исследуемого неравенства, причём таком анализе, с помощью которого «обратимыми» рассуждениями строят цепочку переходов от доказываемого неравенства (через ряд промежуточных) к некоторому очевидному (благодаря ранее полученным результатам) неравенству.

Рассмотрим решение задачи методом анализа.

Задача № 1. Доказать, что для любых действительных чисел a, b, c, d таких, что и , выполнимо неравенство .

Решение. Рассмотрим цепочку переходов от одного неравенства к другому, ему равносильному, учитывая, что и по условию.

.

Возведём обе части в квадрат, так как они неотрицательны:

Подставим значения c² и d² из условия .

Получили очевидное неравенство.

Это метод, основанный на получении (синтезировании) неравенства (которое требуется обосновать) из опорных (базисных) неравенств и методов их установления.

Решим задачу, используя метод синтеза.

Задача № 2. Докажите, что для любых неотрицательных a, b, c справедливо неравенство

.

Решение. Запишем три неравенства, устанавливающие зависимость между средним арифметическим и средним геометрическим двух неотрицательных чисел

; ;

Перемножим почленно полученные неравенства, так как их левая и правая части неотрицательны

Суть метода состоит в том, что предполагается выполнение всех условий задачи, а вот само неравенство не выполнено. После чего проводится цепочка равносильных преобразований и выявляется гипотеза, устанавливающая противоречия о выполнении данного неравенства.

Рассмотрим задачу № 1, решённую методом анализа. Решим её методом от противного.

Задача № 1. Доказать, что для любых действительных чисел a, b, c, d таких, что и , выполнимо неравенство .

Решение. Пусть условия задачи выполнены, то есть и и .

Допустим, что данное неравенство неверно, а при данных условиях выполняется следующее неравенство:

.

Это неравенство равносильно совокупности неравенств:

Умножим обе части неравенства на 2 и правую часть представим в виде суммы 1+1:

Подставим из условия значения 1:

Перенесём всё в левую часть и применим формулу квадрат суммы:

Получили совокупность неравенств, которая решений не имеет, значит предположение о выполнении неравенства неверно, то есть .

Метод использования тождеств.

Суть метода состоит в том, что данное неравенство путём равносильных преобразований приводится к очевидному тождеству.

Рассмотрим решение задачи этим методом.

Задача № 3. Докажите, что для любых действительных чисел a и b справедливо неравенство .

Решение. Выделим в левой части неравенства полный квадрат

.

При любых действительных a и b это выражение неотрицательно, значит и данное неравенство выполнимо, то есть .

Метод оценивания (метод усиления или ослабления).

Метод усиления заключается в последовательном переходе от меньшей функции к большей (как говорят, оценивающей «сверху» эту меньшую функцию). Такие «переходы» приводят к получению так называемого более сильного неравенства, то есть неравенства с большей правой частью, нежели у его предшественников – неравенств. Иначе говоря, если требуется доказать неравенство вида A B и удалось установить, что A > C и C > B, где А, В, С – функции от соответствующих переменных, принимающих произвольные значения из оговорённой области определения, то тем самым оказывается установленным и неравенство A > B.

Аналогичный подход можно применять для доказательства нестрогих неравенств.

Вернёмся к задаче № 1 и решим её третьим способом – методом усиления.

Задача № 1. Доказать, что для любых действительных чисел a, b, c, d таких, что и , выполнимо неравенство .

Решение. Применим свойство модуля к левой части неравенства .

Представим слагаемые в правой части в виде корня:

К этим выражениям применим зависимость между средним арифметическим и средним геометрическим

.

Таким образом, .

Метод введения новых переменных, или метод подстановки.

Суть метода состоит в том, что в данном неравенстве какое – либо выражение обозначается новой переменной, а затем полученное неравенство относительно новой переменной доказывают, используя уже известные методы.

Рассмотрим задачу на применение данного метода.

Задача № 4. Доказать, что для любых положительных a, b, c справедливо неравенство

.

Решение. Пусть ; ; .

Найдём сумму новых переменных x+y+z и применим зависимость между средним арифметическим и средним геометрическим

; ;

Подставим значения x, y и z:

Так как a>0, b>0, c>0 по условию, то

.

Метод введения вспомогательных функций с целью использования их свойств.

Суть метода заключается в том, что в неравенстве одно значение переменной фиксируется как параметр, а другое значение обозначается через переменную х. В результате чего получаем вспомогательную функцию относительно х. Для доказательства условия задачи следует выяснить множество значений полученной вспомогательной функции.

Решим задачу на применение этого метода.

Задача № 3. Докажите, что для любых действительных чисел a и b справедливо неравенство .

Решение. Решим эту задачу вторым способом, методом введения вспомогательной функции. Пусть b – фиксированное действительное число, параметр, а = х, тогда получим функцию , которая является квадратичной, ветви параболы направлены вверх.

, поэтому квадратичная функция принимает только неотрицательные значения, , значит , то есть .

Метод уменьшения числа переменных в неравенстве и понижение степени неравенства.

Суть метода заключается в том, что уменьшается число переменных в неравенстве с помощью метода подстановки и выполнения арифметических действий и применения очевидных тождеств.

Рассмотрим доказательство неравенства этим методом.

Задача № 1. Докажите, что для любых положительных a, b, c справедливо неравенство: .

Решение. Разделим правую и левую части неравенства на с3(c > 0, а значит и с3 > 0) и введём новые переменные:

В результате получим новое неравенство

; ,

доказательство которого равносильно доказательству исходного неравенства. Перепишем его левую часть в следующем виде:

и введём новые переменные:

; , причём x > 0, y > 0 и x² ≥ 4y. Теперь получили неравенство вида

, где ,

чьё обоснование позволяет сделать вывод и о справедливости исходного неравенства. Существенными достижениями в результате сделанных преобразований явились следующие: уменьшилось число переменных, а степень относительно переменного у оказалась равна единице. Преобразовав полученное неравенство к виду

и введя в рассмотрение следующую вспомогательную функцию (считая х произвольным положительным фиксированным числом) с областью определения R можем заключить, что при любом фиксированном значении х графиком этой функции будет прямая. Следовательно, её наименьшее на отрезке достигается на одном из его концов. Найдем значение функции в этих точках:

и . Таким образом значения функции на концах отрезка положительны при x > 0, а это доказывает истинность исходного неравенства.

Применение неравенства Коши при доказательстве неравенств

Задача № 1. Доказать неравенство

при b ≥ 0.

Решение. Умножим обе части неравенства на 4:

Применим неравенство Коши к числам :

Задача № 2. Доказать неравенство:

, при a ≥ 0; b ≥ 0; c ≥ 0.

Решение. Применим неравенство Коши для каждых двух чисел:

Обе части неравенств неотрицательны, поэтому сложим их почленно:

Задача №3. Доказать неравенство

, при a ≥ 0; b ≥ 0; c ≥ 0.

Решение. Применим неравенство Коши для каждой суммы:

Обе части неравенств неотрицательны, поэтому перемножим их левые и правые части:

.

Задача № 4. Доказать неравенство

, при n ≥ 2.

Решение.

Применим неравенство Коши к числам 1, 2, 3,…, (n-1), n:

.

В числителе правой части сумма n членов арифметической прогрессии. Она равна .

.

Задача Дидоны и другие задачи на оптимизацию.

Ещё в глубокой древности люди задумывались, как, имея в своём распоряжении тот или иной ресурс (например, деньги), так им распорядиться (вложить деньги в «дело», дать в долг под проценты, раздать нищим, закопать в собственном огороде и т. д.), чтобы получить наибольшую пользу и наименьший ущерб для себя.

То, что подобные задачи на оптимизацию встречались ещё в античные времена, донесли до нас мифы Древней Греции и Рима. Причём интуиция и опыт человеческий уже тогда позволяли «нащупать» решения подобных задач, дающие оптимальный или близкий к оптимальному результат.

Вот один из мифов, наполовину древнегреческий, наполовину древнеримский. Дочь царя Тира, Дидона, жена жреца храма Геракла Акербаса вынуждена была бежать из Финикии в Северную Африку. Причина бегства – её брат, Пигмалион, позарившийся на богатства её мужа и убивший его. Многочисленные сокровища мужа и многочисленные спутники Дидоны нуждались в пристанище. Чтобы обрести его, беглянка купила у берберийского царя Ярба землю, причём по условию она в обмен на немалые сокровища могла взять ровно столько земли, сколько покроет одна бычья шкура. Чтобы выполнить это условие и получить достаточно обширную территорию, Дидона разрезала шкуру на тонкие ремни, сделала из них длинную верёвку и «окружила» ею изрядный кусок земли, естественно, круглой формы, на котором основала Карфаген. Любопытно, что карфагенская цитадаль называется Бирса (Бирсу), что в переводе с греческого означает «шкура». Однако дальнейшая судьба Дидоны была трагическая: она покончила жизнь самоубийством.

Но вернёмся к математике. Задача, которую решила Дидона, может быть сформулирована так: найти замкнутую кривую, ограничивающую часть плоскости с максимальной площадью. В таком общем виде эта задача слишком сложна. Однако, если упростить задачу Дидоны и договориться о более конкретных формах участка земли, то возникают задачи, чьи решения могут быть получены без обращения к высшей математике, при помощи замечательных неравенств. Задачи типа задачи Дидоны называют в математике изопериметрическими задачами (от греческих слов isos – равный и perimetrio – измеряю вокруг).

Задача № 1. Найдите из множества всех прямоугольников с заданным периметром тот, чья площадь наибольшая.

Решение. Обозначим стороны искомого прямоугольника символами x и y, а его периметр – символом р > 0, тогда задача стоит так: при каких x и y – положительных числах, удовлетворяющих условию , их произведение будет наибольшим. Применим неравенство Коши: , , т. е. . Итак, подозрительным на наибольшее значение произведения является число , но достигается ли оно при допустимых x и y? Да, достигается. Полагая из равенства , получаем .

Задача № 2. Найдите среди всех треугольников с заданным периметром тот, чья площадь наибольшая.

Решение. Если обозначим стороны произвольного треугольника x, y, z, то по условию

, и ,

где фиксированное число . Требуется определить наибольшее значение выражения

.

Применим неравенство Коши для n = 3

,

то есть , причём равенство достигается тогда и только тогда, когда , то есть для равностороннего треугольника.

Рассмотрим задачу С3 , которая предлагалась в тесте ЕГЭ в 2006 году.

Задача № 3. Требуется разместить на земле участок площадью 3400 м2 , который состоит из трёх прямоугольных частей и имеет форму многоугольника ABCDFGHM, изображённого на рисунке, где ВС = 20 м, CD = 15 м, GH = 30 м и HM ≥ 40 м. Найдите наименьшее значение периметра такого участка и какие – либо значения длин АК, AL и HM, при которых периметр является наименьшим.

Площадь участка равна S = 3400, а его периметр равен периметру Р прямоугольника KALF . Обозначим AK = x, х > 0; AL = y, y > 0

и HM = z, z ≥ 40. Тогда ,

.

Поэтому и .

Применим неравенство Коши для двух слагаемых

,

, ,

Равенство достигается при , то есть .

, то есть

и это значение достигается при

Ответ. Р = 280 м; АК = 70; AL = 70; HM = 40.

Неравенства для средних и сами средние широко применяются не только в алгебре, геометрии, математическом анализе, но и в статистике, в теории вероятностей (оттуда пришло среднее квадратичное), при обработке результатов измерений. Средняя урожайность, средняя плотность населения, средняя температура, средняя рождаемость, средняя глубина реки, – это примеры средних величин, постоянно окружающих нас.

Неравенства играют фундаментальную роль в большинстве разделов современной математики, без них не может обойтись ни физика, ни математическая статистика, ни экономика. По словам Э. Беккенбаха, «…основные результаты математики чаще выражаются неравенствами, а не равенствами». Однако до сих пор нет хорошо разработанной, достаточно общей «теории неравенств», хотя для обоснования отдельных классов неравенств такую теорию удалось создать – это и некоторые разделы выпуклого анализе, и теория мажоризации, и ряд других. Так или иначе, но неравенства встречаются как в классических разделах математики (в геометрии, в дифференциальном и интегральном исчислении, в теории чисел), так и в достаточно современных её разделах (теория автоматов, теория кодирования). Количество новинок среди даже не неравенств, а классов неравенств увеличивается необычайно быстро, стремительно и неудержимо.

Можно было бы указать имена тех учёных, кто получил первым тот или иной результат, касающийся неравенств. Однако многие из результатов были получены и применены как некоторые вспомогательные средства в какой – либо работе по геометрии, астрономии, или физике, а затем переоткрыты много лет спустя. Это послужило причиной тому, что даже названия многих замечательных неравенств не устоялись, а также терминология вообще. В разных странах и в разных математических школах одно и то же неравенство называют по – разному и приписывают его открытие разным математикам. Зачастую давно полученное неравенство вдруг оказывается частным случаем и более общего, да и более молодого по срокам появления неравенства. Например, невозможно найти первооткрывателя того фундаментального факта, что квадрат любого действительного числа всегда неотрицателен, а значит для любых действительных чисел a и b справедливо соотношение , а значит , откуда получается знаменитое соотношение между средним арифметическим и средним геометрическим, то есть , где .

1. , Курляндчич // Математика в школе, 1990, № 3.

2. Неравенство Коши о среднем арифметическом и геометрическом // Математика, 1999, № 20.

3. Берколайко неравенства Коши при решении задач // Квант, 1975, № 4.

4. Волошинов и искусство – М.: Просвещение, 1992.

5. Глейзер математики в средней школе. – М.: Просвещение, 1970.

6. Глейзер математики в школе. – М.: Просвещение, 1982.

7. Числовые средние и геометрия // Квант, 1990, № 9.

8. Гомонов неравенства: способы получения и примеры применения. 10 – 11 классы: учебное пособие. – М.: Дрофа, 2006.

9. Геометрические задачи на максимум и минимум // Квант, 2005, № 2.

10. Дубровский об общей внешней касательной к окружностям, касающимся внешним образом // Квант, 1986, № 2.

11. Треугольники и неравенства // Квант, 2005, № 2.

12. Геометрические доказательства теорем о средних // Квант, 1981, № 2.

13. Замечательные пределы, порождаемые классическими средними // Квант, 1981, № 9.

14. Замечательные пределы, порождаемые классическими средними // Квант, 1981, № 9.

15. Кушнир одной задачи // Квант, 1986, № 9.

16. Среднее. В среднем. О среднем… // Математика, 2000, № 8.

17. Описанная трапеция и средние //Квант, 1972, № 8.

18. О применении одного неравенства // Квант, 1997, № 2.

19. Сивашинский в задачах. – М.: Наука, 1967.

20. Скопец различных средних двух положительных чисел // Квант, 1979, № 2.

21. Неравенства // Математика, 2006, № 5.

22. Классические неравенства в задачах // Математика, 2005, № 15.

23. Сложные задачи вступительных экзаменов в МГУ: неравенства о средних // Математика, 2006, № 10.

24. Неравенства Коши о средних арифметическом и геометрическом // Математика, 2000, № 7, № 8.

25. Неравенства Коши о среднем арифметическом и геометрическом // Математика, 2000, № 7.

26. Шлейфер неравенства // Математика в школе, 1994, № 3.

27. Энциклопедический словарь юного математика / Сост. . – М.: Педагогика, 1989.

28. Как доказать неравенство // Квант, 1997, № 2.

В ходе исследования я узнал много нового для себя, научился решать задачи по данной теме. Наиболее трудным в работе показалась работа с литературой и систематизация знаний. Хотелось бы поблагодарить всех, кто помогал мне в ходе работы.

В дальнейшем мне хотелось бы провести более глубокое исследование по этой теме.

Я считаю, что неплохо поработал, цели достиг, с задачами справился. Конечно, в работе есть недочеты, но, наверное, это связано с отсутствием опыта участия в подобных конференциях.

Гармоническое Среднее

Что такое Гармоническое Среднее?

Гармоническое среднее – это разновидность среднего численного значения. Он рассчитывается путем деления количества наблюдений на обратную величину каждого числа в серии. Таким образом, гармоническое среднее является величиной, обратной среднему арифметическому обратных величин.

Среднее гармоническое значение 1, 4 и 4 равно:

Краткая справка

Обратное значение числа n равно 1 / n.

Основы гармонического среднего

Гармоническое среднее помогает найти мультипликативные отношения или отношения делителей между дробями, не беспокоясь об общих знаменателях. Гармонические средние часто используются для усреднения таких вещей, как скорости (например, средняя скорость движения при продолжительности нескольких поездок).

Средневзвешенное гармоническое среднее используется в финансах для усреднения мультипликаторов, таких как соотношение цены и прибыли, поскольку оно придает одинаковый вес каждой точке данных. Использование взвешенного среднего арифметического для усреднения этих соотношений даст больший вес высоким точкам данных, чем низким точкам данных, потому что соотношение цена / прибыль не нормализуется по цене, в то время как прибыль выравнивается.

Гармоническое среднее – это взвешенное гармоническое среднее, где веса равны 1. Взвешенное гармоническое среднее значений x 1 , x 2 , x 3 с соответствующими весами w 1 , w 2 , w 3 задается как:

Ключевые моменты

Гармоническое среднее – это величина, обратная среднему арифметическому обратных величин.

Гармонические средние используются в финансах для усреднения данных, например, ценовых мультипликаторов.

Гармонические средства также могут использоваться рыночными техниками для выявления паттернов, таких как последовательности Фибоначчи.

Сравнение среднего гармонического и среднего арифметического и среднего геометрического

Другие способы вычисления средних значений включают простое среднее арифметическое и среднее геометрическое. Среднее арифметическое – это сумма серии чисел, деленная на количество этой серии чисел. Если бы вас попросили найти среднее (арифметическое) среднее количество баллов за тест, вы просто сложите все баллы учащихся, а затем разделите эту сумму на количество учащихся. Например, если пять студентов сдали экзамен и их баллы составили 60%, 70%, 80%, 90% и 100%, средняя арифметическая оценка по классу будет 80%.

Среднее геометрическое среднее из набора продуктов, расчет которых обычно используется для определения результатов эффективности инвестиций или портфеля. Технически это определяется как «произведение корня n-й степени из n чисел». Среднее геометрическое должно использоваться при работе с процентами, которые выводятся из значений, в то время как стандартное среднее арифметическое работает с самими значениями.

Гармоническое среднее лучше всего использовать для таких дробей, как ставки или кратные.

Пример среднего гармонического

В качестве примера возьмем две фирмы. Один имеет рыночную капитализацию 100 миллиардов долларов и прибыль 4 миллиарда долларов (P / E 25), а другой – рыночную капитализацию 1 миллиард долларов и прибыль 4 миллиона долларов (P / E 250). В индексе, составленном из двух акций, с 10% инвестиций в первую и 90% во вторую, коэффициент P / E индекса равен:

Среднее гармоническое

Среднее гармоническое — один из способов определения среднего значения числового ряда (наряду с медианой и средним арифметическим). Мы сделали калькулятор, который может рассчитать среднее гармоническое двух, трех — да любого количества чисел.

Рассчитывается среднее гармоническое по простой формуле и является обратной величиной к среднему от обратных к числам.

Среднее гармоническое удобно применять для решения задач, которые начинаются словами «первую половину пути автомобиль проехал со скоростью…». Например, первую половину пути автомобиль проехал со скоростью 60 км/ч вторую 90 км/ч. Найдите среднюю скорость. Просто введите в калькулятор два числа — 60 и 90 и получите ответ — 72 км/ч.

Калькулятор среднего гармонического

Как найти среднее гармоническое чисел

Лучше показать это на примере. Найдем среднее гармоническое двух чисел 1 и 2. Подставив значения в формулу получим такое выражение:

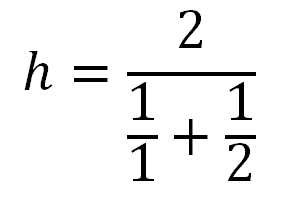
Здесь в числителе количество чисел (2), а в знаменателе сами числа. В результате расчета получаем, что среднее геометрическое чисел 1 и 2 равно 1,6666… или 1,(6).

[spoiler title=”источники:”]

http://nesrakonk.ru/harmonicaverage/

http://calculat.ru/srednee-garmonicheskoe

[/spoiler]

Источник

а) Математический эксперимент. Даны два неотрицательных числа, скажем 1 и 2. Образуем их “среднее” следующими двумя способами: возьмем их среднее арифметическое (или полусумму), которое иногда называют просто “средним”:

и среднее геометрическое (корень квадратный из их произведения):

Заметим, что Аналогично, если мы начнем с чисел 3 и 9, то их среднее арифметическое будет равно а среднее геометрическое Отметим, что Действуя таким же образом с различными парами неотрицательных чисел, выбранными наугад, допустим с числами 11 и 13, 1/2 и 1/4 и т. д., мы заметим, что в каждом случае среднее арифметическое этих чисел больше их среднего геометрического.

В праве ли мы, без риска ошибиться, обобщить эти наблюдения и сделать определенные выводы? Математическое чутье подсказывает нам, что мы, возможно, напали на след теоремы. Может быть, этот результат имеет место для всех пар неотрицательных чисел! Иными словами, мы можем предположить, что среднее арифметическое любых двух неотрицательных чисел во всяком случае не меньше их среднего геометрического. Выразим это предположение при помощи алгебраических символов; ниже, в мы убедимся в его истинности. Итак, сформулируем следующее утверждение:

Теорема 1. Среднее арифметическое любых двух неотрицательных чисел не меньше их среднего геометрического, т. е.

Равенство имеет место в том и только том случае, когда

Отметим, что если бы одно из двух чисел было положительным, а другое отрицательным, то соотношение (4.1) не имело бы смысла, так как его правая часть была бы мнимой. Если бы оба числа были отрицательными, то левая часть неравенства (4.1) была бы отрицательной, а правая — положительной, и теорема была бы неверной.

Математический эксперимент, который привел нас к теореме 1, представляет собой пример метода “проб и ошибок”, часто используемого математиками, чтобы выявить ту или иную закономерность. Раньше это было очень трудоемкой работой. В наше же время, когда для математического экпериментирования приспособлены современные цифровые вычислительные машины, мы можем за несколько часов провести тысячи и миллионы проб. Таким образом, в наших руках оказываются драгоценные ключи к установлению математических истин.

Упражнения

(см. скан)

б) Доказательство теоремы о среднем арифметическом и среднем геометрическом для двух чисел. Поскольку квадратный корень — это такой математический объект, который может доставить немало хлопот, мы постараемся от него избавиться, положив

что допустимо, ибо в теореме 1 предполагается, что числа неотрицательны. При этом соотношение (4.1), в

справедливости которого для произвольных неотрицательных чисел мы хотим убедиться, примет следующий вид:

где произвольные действительные числа. Неравенство (4.3) имеет место в том и только том случае, когда

что в силу основных правил, относящихся к неревенствам, равносильно тому, что

Здесь мы встретились с нашим старым знакомым, а именно с выражением

Итак, (4.5) равносильно

Так как на основании теоремы 3 гл. I квадрат любого действительного числа неотрицателен, то ясно, что соотношение (4.7) всегда имеет место. Таким образом, неравенство (4.5) всегда справедливо, а следовательно, справедливы и неравенства (4.4), (4.3) и (4.1). Равенство в формуле (4.7), а значит, и в формуле (4.1) достигается в том и только в том случае, когда т. е. или, иначе говоря, тогда и только тогда, когда

Отметим, что, в то время как неравенство (4.1) теоремы 1 выполняется только для неотрицательных чисел приведенное доказательство показывает, что неравенство (4.3) имеет место для любых действительных чисел (причем равенство достигается в том и только том случае, когда Мы увидим в дальнейшем, что выводы § 4 и 6 этой главы также справедливы не только для неотрицательных, но и для любых действительных чисел. Этот факт позволяет дать полученным результатам более общее геометрическое истолкование.

в) Геометрическое доказательство. Покажем теперь, что теорему 1 можно вывести также геометрически путем простого сравнения некоторых площадей.

г) Геометрическое обобщение. Нетрудно видеть, что вышеизложенные соображения сохраняют силу и в том случае, когда кривая не является прямой линией. Рассмотрим рис. 18; и в этом случае, очевидно,

Когда вы изучите интегральное и дифференциальное исчисления и познакомитесь с приемами вычисления площадей, ограниченных графиками простых функций, таких, например, как при произвольном положительном а, вы увидите, что таким путем получается ряд интересных неравенств.

Рис. 18. Более общий случай.

В следующих параграфах настоящей главы мы получим некоторые из этих неравенств другим способом.

Упражнения

(см. скан)

д) Теорема о среднем арифметическом и среднем геометрическом для трех чисел. Продолжим наш математический эксперимент. Возьмем три неотрицательных числа, скажем 1, 2 и 4, и образуем их среднее арифметическое подобно тому, как мы это делали раньше;

Вычислим также их среднее геометрическое, т. е. корень кубичный из их произведения

Мы видим, что среднее арифметическое этих трех чисел больше их среднего геометрического. Произведя аналогичный опыт для других произвольно выбранных троек неотрицательных чисел, мы убедимся, что результат во всех случаях будет таким же. Естественно возникает подозрение, что мы напали на новую теорему. Действительно, может быть, существует обобщение теоремы -вывод, утверждающий, что среднее арифметическое трех неотрицательных чисел не меньше их среднего геометрического? Теперь докажем, что в самом деле имеет место

Теорема 2. Среднее арифметическое любых трех неотрицательных чисел с не меньше их среднего геометрического, т. е.

Равенство достигается в том и только том случае, когда

С целью исключить из рассмотрения кубический корень положим

Подставляя эти значения и с в неравенство (4.11), получаем

что равносильно следующему неравенству:

Мы докажем теорему 2, если установим, что неравенство (4.14) имеет место для произвольных неотрицательных чисел х, у, z.

Здесь мы снова получили выражение, которое можно разложить на множители. Это разложение на множители

не так известно, как предыдущее, однако оно часто оказывается полезным. Мы утверждаем, что

проверить это можно непосредственно путем умножения.

Так как – неотрицательное число, то первый множитель в правой части (4.15) положителен (если не равны нулю одновременно). Поэтому, чтобы доказать справедливость неравенства (4.14), достаточно показать, что второй множитель также неотрицателен, т. е. что

Неравенство (4.16) можно следующим образом вывести из неравенства уже использованного нами при алгебраическом доказательстве теоремы о среднем арифметическом и среднем геометрическом для двух чисел (см. п. 6) этого параграфа). Выпишем три неравенства

и сложим их почленно:

Таким образом, мы получили неравенство, равносильное требуемому неравенству (4.16). Равенство достигается тогда и только тогда, когда

Поскольку справедливо неравенство (4.16), а также то левая часть (4.15) также т. е. неравенство (4.14) имеет место. Но неравенство (4.14) равносильно (4.11). Мы, таким образом, доказали теорему о среднем арифметическом и среднем геометрическом для трех чисел. Условие при котором достигается равенство в (4.14), а следовательно, и в (4.11), равносильно условию

е) Теорема о среднем арифметическом и среднем геометрическом для чисел. Ободренные достигнутыми успехами, предположим, что

результаты, которые мы установили для двух и для трех чисел, являются только частными случаями общей теоремы, имеющей место для любого числа положительных чисел. Если это предположение правильно, то имеет место

Теорема 3. Среднее арифметическое любых неотрицательных чисел не меньше их среднего геометрического, т. е.

Равенство достигается в том и только том случае, когда

Неравенство (4.19), связывающее среднее арифметическое чисел с их средним геометрическим, хорошо известно и, действительно, всегда имеет место. Мы обратили особое внимание на это неравенство по целому ряду причин. Во-первых, оно поразительно само по себе и притом может быть доказано множеством интересных способов. Имеются буквально десятки различных доказательств теоремы 3, основанных на положениях, вытекающих из самых разнообразных источников. Во-вторых, оно может быть использовано в качестве основной теоремы теории неравенств, в качестве краеугольного камня, на котором покоятся многие другие очень важные заключения. -третьих, как будет показано в пятой главе, некоторые следствия этого неравенства можно использовать для решения ряда интересных задач на максимум и минимум.

Первое, что может прийти в голову при попытке доказать теорему -это продолжить линию, начатую доказательствами теорем 1 и 2, т. е. найти разложение на множители соответствующего выражения для затем для Однако на самом деле этот подход совсем не является привлекательным, он даже вообще невозможен: простых доказательств, в основе которых лежит указанная идея, не существует.

Вместо этого мы приведем простое доказательство, основанное на использовании двух методов математической индукции. Сначала при помощи метода “прямой” индукции мы докажем теорему 3 для всех целых чисел являющихся степенями двойки, т. е. для чисел

Затем мы применим метод «обратной» индукции (от некоторого целого положительного числа а к предшествующему числу который наряду с методом прямой индукции даст нам возможность установить результат для любых целых положительных чисел.

1) Прямая индукция. Первый этап доказательства теоремы 3 демонстрирует технику использования метода математической индукции, рассмотренного нами выша (в § 6 гл. II).

Начнем с результата, относящегося к случаю именно

Это неравенство выполняется при любых значениях неотрицательных чисел в силу теоремы 1. Однако далее нельзя обойтись без некоторой математической смекалки. Существует множество простых доказательств теоремы 3. однако во всех этих доказательствах содержится известная тонкость, требующая удачной догадки. Положим

где неотрицательные числа. Подставляя эти значения чисел в (4.20), получаем неравенство

или

Так как левая часть неравенства (4.21) уже записана в нужной для нас форме (см. теорему 3), то сосредоточим внимание на правой части этого неравенства. Используя неравенства

справедливость которых была уже установлена выше, а также условие транзитивности (теорема 1, гл. получаем из (4.21)

Но ведь это в точности тот результат, который мы хотим получить! Он получен для случая четырех неотрицательных чисел: для среднее арифметическое неотрицательных чисел не меньше их среднего геометрического.

Неравенство (4.21) обращается в равенство тогда и только тогда, когда

а (4.22) — тогда и только тогда, когда следовательно, равенство в (4.23) достигается в том и лишь том случае, когда

Ничто не мешает нам повторить тот же трюк. Положим

где все числа неотрицательны. Подставляя эти значения в (4.23), имеем

Воспользовавшись неравенствами

и условием транзитивности, получаем

т. е. требуемый результат для случая восьми чисел. Равенство имеет место в том и только том случае, когда все числа равны между собой.

Очевидно, что, продолжая таким же образом, мы сможем получить аналогичное неравенство для всех чисел

которые являются степенями двух, т. е. для Для строгого вывода теоремы применим метод математической индукции. Основной шаг заключается в доказательстве следующего утверждения:

Теорема о среднем арифметическом и среднем геометрическом справедлива для всех чисел вида где

Доказательство. Мы уже знаем, что теорема имеет место при т. е. при а также при Предположим, что теорема верна для целого числа имеющего вид и покажем, что она верна и для числа Так как то это означает, что теорема 3 верна для числа Таким образом, мы предполагаем, что неравенство

выполняется для любого множества неотрицательных чисел где Заменим числа выражениями

чисел какие угодно неотрицательные числа. Поступая таким же образом, как и выше, получаем в итоге

Как и раньше, равенство достигается в том и только том случае, когда все числа равны между собой. Таким образом, мы доказали теорему 3 для чисел или для чисел.

Принцип математической индукции (прямой) утверждает, что поскольку неравенство выполняется для то оно выполняется для любого целого положительного числа следовательно, неравенство (4.24) имеет место для любого числа являющегося целой положительной степенью двойки.

2) Обратная индукция. Теперь мы уже доказали, что теорема 3 верна для тех целых чисел, которые являются степенями двух; однако как же нам доказать, что она имеет место для всех целых положительных чисел?

Здесь требуется иная процедура. Рассмотрим случай для которого мы выше уже доказали теорему 3 иным способом. Используя соотношение для

справедливость которого уже была доказана при помощи метода прямой индукции, посмотрим, нельзя ли отсюда получить соответствующий результат для

Мы проведем доказательство, используя важный метод, называемый специализацией. Начнем с соотношения (4.25). Выберем числа следующим образом: положим

и найдем значение из равенства

Перепишем последнее равенство, учитывая (4.26):

откуда

Подставляя эти частные значения в (4.25), получаем

Возводя обе части последнего неравенства в четвертую степень, имеем

после деления полученного выражения на получаем

что равносильно требуемому результату:

Поскольку равенство в (4.25) достигается в том и только том случае, когда то в (4.27) оно достигается тогда и только тогда, когда

С целью распространить этот метод на общий случай мы используем прием, характерный для доказательств по индукции, однако прием нестандартный. Вместо того чтобы доказывать, что если результат справедлив для чисел, то он справедлив и для чисел, мы докажем, что результат справедлив для чисел, если он справедлив для чисел. Поскольку мы уже доказали теорему для всех чисел вида то этог метод позволит нам завершить доказательство теоремы.

Покажем, что если теорема 3 справедлива для чисел, то она справедлива и для чисел. Для этого повторим тот же прием специализации, который мы уже применили выше. Положим

и определим из условия

Учитывая (4.28) и решая последнее уравнение относительно получаем

Мы предположили, что неравенство

выполняется для неотрицательных чисел

Подставляя значения из (4.28) и (4.29), имеем

Возводя обе части в степень и сокращая, получаем неравенство

что эквивалентно требуемому результату

Как и раньше, равенство достигается в том и только том случае, когда таким образом, доказательство теоремы 3 полностью завершено.

Источник

Обновлено: 20.05.2023

Между ними существуют удивительные соотношения, которые исследованы учёными. О.Коши, французский математик, сопоставив две средние величины, пришёл к выводу о том, что среднее арифметическое n чисел всегда не меньше среднего геометрического этих чисел.

Тема: Различные средние положительных. Неравенство Коши.

Цель: изучение средних величин, определение оптимальных методов решения задач со средними величинами.

познакомиться с историей появления средних величин,

дать определение средним величинам,

доказать алгебраически и геометрически соотношение между средними величинами,

рассмотреть применение неравенства Коши при исследовании свойств функций,

систематизировать различные методы решения нестандартных задач.

Почему я выбрал эту тему?

2.1.Понятие средней величины.

2.2.Из истории средних величин

2.3.Соотношение между средними величинами

2.3.1.Сравнение среднего арифметического и среднего геометрического

2.3.2.Сравнение среднего арифметического и среднего квадратичного

2.3.3.Сравнение среднего гармонического и среднего геометрического

2.3.4.Геометрическое доказательство сравнения средних величин

2.3.4.1. Среднее арифметическое и среднее квадратичное

2.3.4.2. Среднее арифметическое и среднее геометрическое

2.3.4.3. Среднее гармоническое и среднее геометрическое

2.3.4.4. Построение четырёх средних по заданным отрезкам a и b

2.3.5.Решение геометрических задач на сравнение средних величин

2.4. Средние для n положительных чисел

2.5. Замечательные пределы, порождаемые классическими средними.

2.6. Замечательное неравенство Коши

2.7.Основные методы решения задач на доказательство неравенств

2.7.1. Метод анализа

2.7.2. Метод синтеза

2.7.3. Метод от противного

2.7.4. Метод использования тождеств

2.7.5. Метод оценивания

2.7.6. Метод введения новых переменных, или метод

2.7.7. Метод введения вспомогательных функций

2.7.8. Метод уменьшения числа переменных в неравенстве и понижения степени неравенства

2.8. Применение неравенства Коши при решении задач.

2.9. Задача Дидоны и другие задачи на оптимизацию

IV. Список литературы

В неравенствах равенство достигается, если a = b . Эти неравенства эквивалентны друг другу при , .

Думаю, что проделанная мною работа поможет мне успешно подготовиться к ЕГЭ.

Понятие средней величины.

Средней величиной действительных чисел называют всякое действительное число х, удовлетворяющее условию , где m – наименьшее, а М – наибольшее среди чисел .

Средняя величина чисел только одна в том и только в том случае, когда .

Средним геометрическим действительных неотрицательных чисел называют такое действительное неотрицательное число .

Средним арифметическим действительных чисел называют действительное число .

Средним гармоническим действительных положительных чисел называют положительное число .

Средним квадратическим (квадратичным) действительных чисел называют неотрицательное действительное число.

Если рассмотреть два положительных числа a и b, то эти средние величины будут выглядеть следующим образом:

Можно рассмотреть следующие задачи.

Решение. Обозначим символом S расстояние между пунктами А и В, тогда

– время туриста от А до В, а

– время туриста обратно.

+ – время, затраченное на весь путь.

Получили, что есть среднее гармоническое скоростей и .

Задача № 2. В прямоугольном треугольнике АВС из вершины С на гипотенузу опущен перпендикуляр CD, который делит гипотенузу на отрезки AD = a; BD = b. Выразить через a и b:

DE (где Е – есть точка пересечения окружности, описанной около треугольника АВС, и перпендикуляра, проведённого к АВ через центр окружности)

СК (где точка К- есть основание перпендикуляра, опущенного из точки D на r = СО.

Решение.

1) ∆АВС – прямоугольный, поэтому АВ – диаметр окружности

АВ = a + b, О – центр окружности, то есть АО = ОВ = ОЕ =

Получили, что ЕО = является средним арифметическим двух отрезков, длины которых a и b.

2)CD┴АВ (по условию), следовательно, по свойству перпендикуляра, опущенного из вершины прямого угла на гипотенузу, CD²=ADDB. Значит

CD является средним геометрическим двух отрезков, длины которых равны a и b.

3) ∆OED – прямоугольный, так как EO ┴ АВ (по условию)

(как радиус окружности)

По теореме Пифагора

, то есть DE является средним квадратичным для двух отрезков, длины которых a и b.

∆DOC – прямоугольный, так как CD ┴ АВ. Проведём

По свойству прямоугольного треугольника CD² = CO CK, то есть

, то есть СК – среднее гармоническое для a и b.

В какой же зависимости они находятся друг от друга?

Из истории средних величин.

Когда возникли понятия средних величин в математике, точно не известно. Но предполагают, что уже вавилоняне более трех тысяч лет назад использовали их при вычислении квадратных корней. В дошедших до нас табличках квадратные корни из натуральных чисел фактически вычислены по известной нам формуле:

если N = β² + r, то = .

Восстанавливая ход рассуждений вавилонян, современные учёные пришли к выводу, что они брали среднее арифметическое чисел β и . В самом деле, если обозначить , то β= .

Применим этот алгоритм к вычислению квадратного корня из натурального числа, записав его в виде произведения двух натуральных чисел: N = ab (при простом N один из сомножителей равен 1). В качестве первого приближения значения возьмём , затем следуя рекомендации Герона, найдем , которое оказывается средним гармоническим чисел a и b .

Также средние величины были известны и античным математикам. В одном из математических тестов, которые приписывают древнегреческому математику Архиту (ок. 428 – 365 г.г. до н.э.), среднее арифметическое А , среднее геометрическое G и среднее гармоническое Н определялись как равные члены соответственно арифметической, геометрической и гармонической пропорций:

(a – H) : a = (H – b) : b.

Из этих равенств получаем

Свои названия перечисленные средние величины получили в античные времена. Аристотель (384 – 322 г.г. до н.э.), великий философ древности, объяснял происхождение названий так. Среди чисел каждое последующее больше предыдущего на постоянное число (при условии a среднее пропорциональное. Объясняется это совсем просто: ведь равенство равносильно пропорции a : G = G : b .

Формулы, задающие различные средние, вообще говоря, имеют смысл не только при положительных a и b . Однако, чтобы каждый раз не задумываться над вопросом существования средней величины, обычно считают a и b положительными .

Рабочая программа педагога козловой Оксаны Александровны, 1 Ф. И. О., категория по алгебре, 8 класс Предмет, класс и т п

. числа. Целые числа: положительные, отрицательные и нуль. . самостоятельно приобретать и применять знания в различных ситуациях; – работать в группах; . чисел, о среднем арифметическом и среднем геометрическом, о неравенстве Коши; – формирование .

Рабочая программа по алгебре для 8 класса на 2013/2014 учебный год

. неравенств (комбинированный) Числовое неравенство, свойства числовых неравенств, неравенства одинакового смысла, неравенства противоположного смысла, среднее арифметическое, среднее геометрическое, неравенство Коши .

. неравенств. Числовое неравенство. Свойства числовых неравенств. Неравенства одинакового смысла. Неравенства противоположного смысла. Среднее арифметическое. Среднее геометрическое Неравенство Коши . положительного числа. Стандартный вид положительного .

. неравенства: 1) (неравенство Коши) 2) 3) 4) Историческая справка: Неравенство (1) называют в честь французского математика Огюста Коши. Число называют средним арифметическим .

Основная образовательная программа высшего профессионального образования подготовки специалиста 050201. 65 (1)

. неравенства и в форме эквивалентности), признаки Даламбера и Коши, интегральный признак сходимости для рядов с положительными членами .

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Описание презентации по отдельным слайдам:

Средние величины широко применяются в алгебре, геометрии, статистике, теории.

Средние величины широко применяются в алгебре, геометрии, статистике, теории вероятностей при обработке результатов измерения или результатов сбора данных. Поэтому мне очень интересна эта тема, и я решила узнать подробнее о некоторых значениях средних величин и в какой зависимости они находятся.

Цель: Познакомиться с понятиями среднего арифметического, среднего геометриче.

Цель: Познакомиться с понятиями среднего арифметического, среднего геометрического, среднего гармонического, среднего квадратичного и изучить зависимость среднего арифметического и среднего геометрического. Задачи: Дать определения средних величин.Подробнее изучить средние величины в геометрии и связь между ними.

История Когда возникли понятия средних величин в математике, точно не известн.

История Когда возникли понятия средних величин в математике, точно не известно. Но предполагают, что уже вавилоняне более трех тысяч лет назад использовали их при вычислении квадратных корней. Свои названия, перечисленные средние величины получили в античные времена. Аристотель

Несколько определений средней величины: Средней величиной называют показател.

Несколько определений средней величины: Средней величиной называют показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности. Величина средней дает обобщающую количественную характеристику всей совокупности и характеризует ее в отношении данного признака.

Средние величины делятся на два больших класса: Степенные средние: Средняя а.

Средние величины делятся на два больших класса: Степенные средние: Средняя арифметическая Средняя геометрическая Средняя квадратичная Средняя гармоническая Структурные средние: Мода Медиана

Средняя арифметическая Средним арифметическим действительных чисел a₁, a₂, ….

Средняя арифметическая Средним арифметическим действительных чисел a₁, a₂, … an (n≥2) называют действительное число A = (a₁ + a₂ + … + an )/n В математике и статистике средняя арифметическая — одна из наиболее распространённых мер и самый распространенный вид средней величины. Она используется, когда нужно получить среднее слагаемое.

Средняя арифметическая По теореме о средней линии трапеции отрезок MN, парал.

Средняя арифметическая По теореме о средней линии трапеции отрезок MN, параллельный основаниям и соединяющий середины боковых сторон трапеции, равен среднему арифметическому оснований:

Свойства если все варианты уменьшить (увеличить) в n раз (на число А), то ср.

Свойства если все варианты уменьшить (увеличить) в n раз (на число А), то среднее значение тоже уменьшится (увеличится) в n раз (на число А) если точкам A и B соответствуют числа на координатной прямой, то середина этого отрезка на координатной прямой имеет координату равную среднему арифметическому координат концов отрезка

Прогрессия На средней арифметической величине основана арифметическая прогре.

Прогрессия На средней арифметической величине основана арифметическая прогрессия. Арифметическая прогрессия — числовая последовательность вида И каждый член, начиная со второго, равен среднему арифметическому соседних членов.

Задачи Например: 1) Бригада из 6 рабочих получает в месяц 3; 3,2; 3,3; 3,5;.

Задачи Например: 1) Бригада из 6 рабочих получает в месяц 3; 3,2; 3,3; 3,5; 3,8; 3,1; тыс. руб. Найти среднюю заработную плату Решение: (3 + 3,2 + 3,3 +3,5 + 3,8 + 3,1) / 6 = 3,32 тыс. руб. 2) Может ли среднее арифметическое 35 целых чисел равняться 6,35? Предположим, что такие числа существуют. Их сумма равна среднему арифметическому этих чисел, умноженному на их количество: 6,35*35=222,25. Поскольку сумма целых чисел должна быть целым числом, получаем противоречие.

Средняя геометрическая Средней геометрической для нескольких величин называе.

Средняя геометрическая Средней геометрической для нескольких величин называется корень из их произведения, показатель степени которого равен числу величин (также называется их средним пропорциональным). Для определения средней геометрической взвешенной применяется формула:

Средняя геометрическая Высота равнобедренной трапеции, в которую можно вписа.

Средняя геометрическая Высота равнобедренной трапеции, в которую можно вписать окружность, является средним геометрическим (чисел a и b) оснований трапеции.

Свойства Дает возможность сохранять в неизменном виде не сумму а произведение.

Свойства Дает возможность сохранять в неизменном виде не сумму а произведение значений. В геометрии: высота прямоугольного треугольника, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу Каждый катет есть среднее пропорциональное между гипотенузой и его проекцией на гипотенузу.

Прогрессия На основе средней геометрической величины также существует геометр.

Прогрессия На основе средней геометрической величины также существует геометрическая прогрессия. И каждый член, начиная со второго, равен среднему геометрическому соседних членов.

Средняя квадратическая Средние диаметры колес, труб, средние стороны квадрато.

Средняя квадратическая Средние диаметры колес, труб, средние стороны квадратов определяются при помощи средней квадратической. Простая Взвешенная Кубическая

Средняя квадратическая .Если в трапеции провести отрезок, разбивающий еѐ на д.

Средняя квадратическая .Если в трапеции провести отрезок, разбивающий еѐ на две равновеликие трапеции, то этот отрезок есть среднее квадратичное оснований:

Средняя гармоническая Средним гармоническим нескольких положительных чисел на.

Средняя гармоническая Средним гармоническим нескольких положительных чисел называется число, обратное среднему арифметическому их обратных, то есть число: В статистике среднее гармоническое применяется в случае, когда наблюдения, для которых требуется получить среднее арифметическое, заданы обратными значениями.

Средняя гармоническая Отрезок KF, проходящий через точку пересечения диагонал.

Средняя гармоническая Отрезок KF, проходящий через точку пересечения диагоналей параллельно основаниям, равен среднему гармоническому оснований

Неравенство между простыми средними Неравенство о средних гласит, что для люб.

Неравенство между простыми средними Неравенство о средних гласит, что для любых неотрицательных чисел верно неравенство: причем равенство достигается тогда и только тогда, когда

Неравенство между простыми средними В трапеции среднее геометрическое основан.

Неравенство между простыми средними В трапеции среднее геометрическое оснований трапеции расположено следующим образом: где m-среднее гармоническое основание; n-среднее геометрическое; p-среднее арифметическое; q-среднее квадратичное.

Неравенство Коши Неравенство Коши – частный случай неравенства о средних, так.

Неравенство Коши Неравенство Коши – частный случай неравенства о средних, так как содержит в себе только среднее арифметическое и геометрическое).

Заключение При работе над проектом я установила, что свои названия, перечисле.

Заключение При работе над проектом я установила, что свои названия, перечисленные средние величины получили в античные времена. Исследовала: какие отрезки в трапеции являются средними арифметическими, средними геометрическими для нескольких отрезков, часть из которых равна одному основанию, а другая часть – другому основанию трапеции. Рассмотрела задачи на применение среднего арифметического и среднего геометрического в математике. Темы, изучаемые в данном проекте, важны еще и потому что они изучаются в курсе математики 8 класса.

Список литературы 1. Алгебра. Учебник для 9 кл. Ш.А. Алимов, Ю.М. Колягин, Ю.

Доказать, что высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.

∆АВС – прямоугольный треугольник,

СD – высота, проведенная из вершины С к гипотенузе АВ.

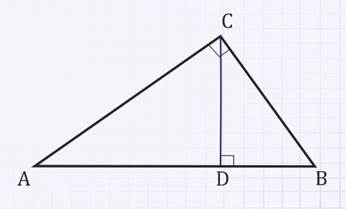
1)Рассмотрим треугольники АВС и АСD.

∠АСВ = ∠АDС = 90°, отсюда следует, что треугольники АВС и АСD подобны по первому признаку подобия треугольников, т.е. по двум равным углам.

2)Рассмотрим треугольники АВС и СВD.

∠АСВ = ∠ВDС = 90°, то треугольники АВС и СВD тоже подобны по первому признаку подобия треугольников. А раз так, то ∠А = ∠ВСD.

3)Рассмотрим треугольники АСD и СВD.

Так как ∠АDС = ∠СDВ = 90° и ∠А = ∠ВСD, то треугольники АСD и СВD подобны по первому признаку подобия треугольников.

Что и требовалось доказать.

Отрезок ХУ называется средним пропорциональным (или средним геометрическим) для отрезков АВ и СD, если выполняется равенство:

Исходя из доказанной выше задачи, можно выделить два утверждения.

1.Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.

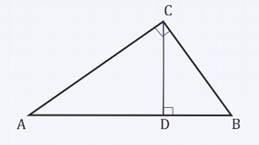
Для вывода данного утверждения воспользуемся доказанным, а именно, что:

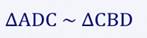
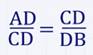
Применяя основное свойство пропорции, получим

2.Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла.

Также по выше доказанному в задаче:

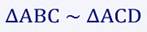
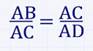
Решим задачу, применяя данные утверждения.

Найдите катеты прямоугольного треугольника АВС, если АD = 24 см, ВD = 6 см.

Нажмите, чтобы узнать подробности

Цель – показать необходимость изучения этой науки (геометрии), которая дает возможность понять, а также рассмотреть значение геометрических законов и закономерностей, их практическое применение при проектировании и постройке сооружений.

Фигура – это произвольное множество точек на плоскости. Точка, прямая, отрезок, луч, треугольник, круг, квадрат и так далее – всё это примеры геометрических фигур.
Основными геометрическими фигурами на плоскости являются точка и прямая. Этим фигурам в геометрии не даётся определений. Неопределяемыми геометрическими фигурами на плоскости являются точка и прямая. Точки принято обозначать прописными латинскими буквами: А, В, С, D …. Прямые обозначаются строчными латинскими буквами: а, b, с, d ….

1.Основные геометрические понятия.

Основные геометрические понятия возникли еще в доисторические времена. Наблюдая за формами растений и животных, гор и извилинами рек, за особенностями ландшафта и далекими планетами, человек заимствовал у природы ее правильные формы, размеры и свойства. Материальные потребности побуждали человека строить жилища, изготавливать орудия труда и охоты, лепить из глины посуду и прочее. Все это постепенно способствовало тому, что человек пришел к осознанию основных геометрических понятий. Одним из первых достижений абстрактного мышления древнего человека стало понимание прямой линии.

Прямая не проходит через точку, если точка не принадлежит ей.

Пряма́я — одно из фундаментальных понятий геометрии.
При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии (евклидовой).Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками. Аналитически прямая задаётся уравнением (в трёхмерном пространстве — системой уравнений) первой степени.

К основным свойствам прямой относятся:

Черед две различные точки проходит одна единственная прямая. Следовательно две прямые не могут иметь более одной общей точки.

Две разные прямые, имеющие общую точку, пересекаются в ней. В связи с тем, что две точки определяют прямую, проходящую через них, прямую обозначают сочетанием букв, к примеру, прямая АВ, прямая PQ.

Точка М, лежащая на прямой а, разбивает её на две части. Каждая из которых называется полупрямой или лучом. Точка М служит началом каждого их этих лучей. Две точки М и N разбивают прямую на три части: два луча МР и NQ и отрезок MN.

Прямая разбивает плоскость на 2 части. Часть плоскости лежащая по одну сторону от этой прямой, называется полуплоскостью.

Если прямые не имеют общих точек, говорят, что они параллельны.

Если две прямые имеют одну общую точку, говорят, что они пересекаются в этой точке.

Две прямые в трёхмерном евклидовом пространстве скрещиваются, если не существует плоскости, их содержащей. Иначе говоря, две прямые в пространстве, не имеющие общих точек, и не являющиеся параллельными.

2. Параллелограмм.

Параллелограмм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — черта, линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Признаки параллелограмма:
Четырёхугольник является параллелограммом, если выполняется одно из следующих условий:
1. Если в четырёхугольнике противоположные стороны попарно равны, то четырёхугольник – параллелограмм
2. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм
3. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм

Параллелограмм, у которого все углы прямые, называется прямоугольником.
Теорема. Если в параллелограмме диагонали равны, то он является прямоугольником.
Параллелограмм, у которого все стороны равны, называется ромбом.
Теорема. Если в параллелограмме диагонали перпендикулярны, то он является ромбом.

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции. Расстояние между основаниями называется высотой трапеции.

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Отрезок, соединяющий середины диагоналей, равен полуразности оснований.

В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

Трапеция, у которой боковые стороны равны, называется равнобокой или равнобедренной.
Свойства равнобедренной трапеции.

Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции.

В равнобедренной трапеции углы при любом основании равны.

В равнобедренной трапеции длины диагоналей равны.

Если трапецию можно вписать в окружность, то она равнобедренная.

Около равнобедренной трапеции можно описать окружность.

Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.

4.Окружность.

Окружность – это плоская замкнутая линия, все точки которой находятся на одинаковом расстоянии от некоторой точки (точки О), которая называется центром окружности.
(Окружность — геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки.)
Круг – это часть плоскости, ограниченная окружностью. Точка О также называется центром круга. Расстояние от точки окружности до её центра, а также отрезок, соединяющий центр окружности с её точкой, называется радиусом окружности/круга.

Хорда – греческое – струна, стягивающая что-то
Диаметр – “измерение через”
Углы могут встречаться во все более возрастающем количестве, приобретать, соответственно, все больший разворот – пока не исчезнут окончательно и плоскость не станет кругом. Это очень простой и одновременно очень сложный случай, о котором мне хотелось бы поговорить подробно. Здесь необходимо отметить, что как простота, так и сложность обусловлены отсутствием углов. Круг прост, поскольку давление его границ, в сравнении с прямоугольными формами, нивелировано – различия здесь не так велики. Он сложен, поскольку верх неощутимо перетекает в левое и правое, а левое и правое – в низ.

В Древней Греции круг и окружность считались венцом совершенства. Действительно, в каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности сделало возможным возникновение колеса, поскольку ось и втулка колеса должны все время быть в соприкосновении. В школе изучается много полезных свойств окружности. Одной из самых красивых теорем является следующая: проведем через заданную точку прямую, пересекающую заданную окружность, тогда произведение расстояний от этой точки до точек пересечения окружности с прямой не зависит от того, как именно была проведена прямая. Этой теореме около двух тысяч лет. Эта фигура получается, если провести дуги окружностей с центрами в вершинах равностороннего треугольника, соединяющие две другие вершины. Если провести к этой фигуре две параллельные касательные, то расстояние между ними будет равно длине стороны исходного равностороннего треугольника, так что такие катки ничем не хуже круглых. В дальнейшем были придуманы и другие фигуры, способные выполнять роль катков.

У каждого треугольника имеется, и притом единственная, окружность девяти точек. Это окружность, проходящая через следующие три тройки точек, положение которых определено для треугольника : основания его высот D1 D2 и D3, основания его медиан D4, D5 и D6 середины D7, D8 и D9 отрезков прямых от точки пересечения его высот Н до его вершин. Эта окружность, найденная в XVIII в. великим ученым Л. Эйлером (поэтому ее часто также называют окружностью Эйлера), была заново открыта в следующем столетии учителем провинциальной гимназии в Германии. Звали этого учителя Карл Фейербах (он был родным братом известного философа Людвига Фейербаха). Дополнительно К. Фейербах выяснил, что окружность девяти точек имеет еще четыре точки, тесно связанные с геометрией любого данного треугольника. Это -точки ее касания с четырьмя окружностями специального вида. Одна из этих окружностей вписанная, остальные три – вневписанные. Они вписаны в углы треугольника и касаются внешним образом его сторон. Точки касания этих окружностей с окружностью девяти точек D10, D11, D12 и D13 называются точками Фейербаха. Таким образом, окружность девяти точек является в действительности окружностью тринадцати точек. Окружность эту очень легко построить, если знать два ее свойства. Во-первых, центр окружности девяти точек лежит в середине отрезка, соединяющего центр описанной около треугольника окружности с точкой Н- его ортоцентром (точка пересечения его высот). Во-вторых, ее радиус для данного треугольника равен половине радиуса описанной около него окружности.

5.Треугольник.

Треуго́льник (в евклидовом пространстве) — это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки, образующие треугольник, называются вершинами треугольника, а отрезки — сторонами треугольника.
Стороны треугольника образуют в вершинах треугольника три угла. Другими словами, треугольник — это многоугольник, у которого имеется ровно три угла.

Вершины — три точки А, В и С. Стороны — отрезки АВ, ВС и СА.
Углы — ∟ ВАС, ∟ СВА и ∟ АСВ.
Периметр треугольника — сумма длин трех сторон треугольника.

Медиана треугольника (m)— отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Биссектриса треугольника (b) — отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. Высота треугольника (h)— перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.

В любом треугольнике медианы пересекаются в одной точке, биссектрисы пересекаются в одной точке, высоты или их продолжения также пересекаются в одной точке.

Теорема. Сумма углов треугольника 180°. Каждая сторона треугольника меньше суммы двух других сторон.

1) против большей стороны лежит больший угол.

2) против большего угла лежит большая сторона.

В прямоугольном треугольнике гипотенуза больше катета

Классификация треугольников по углам. В треугольнике может быть только один тупой угол. В треугольнике может быть только один прямой угол. По сторонам.
Треугольник называется равнобедренным, если две его стороны равны.
Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника.

5.1. Теоремы треугольника.

В равнобедренном треугольнике углы при основании равны.
Теорема

В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Равносторонний треугольник — все стороны и углы равны.

Если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
В равных треугольниках против соответственно равных сторон лежат равные углы.

5.2.Признаки треугольника.

ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
Теорема:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

ВТОРОЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
Теорема. Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.

ТРЕТИЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
Теорема. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

5.3.Прямоугольный треугольник.

СВОЙСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ

• Сумма двух острых углов прямоугольного треугольника равна 90°.
• Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
• Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.

ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.

Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету.

5.4. История изучения треугольника.

6.Многоугольник.

Многоугольник — фигура, составленная из отрезков так, что смежные отрезки не лежат на одной прямой, а несмежные отрезки не имеют общих точек.
Точки А, В, С, D, Е… — вершины многоугольника. Отрезки АВ, ВС, CD, DE, ЕА,… – стороны многоугольника.
Периметр многоугольника (гречечкое пери – вокруг, около) — сумма длин всех сторон.
Многоугольник с n вершинами называется n-угольником; он имеет n сторон.
Две вершины многоугольника, принадлежащие одной стороне, называются соседними.
Диагональ многоугольника (греческое dia – через, gonia – угол, т.е. проходящая через углы) — отрезок, соединяющий любые две несоседние вершины.
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней, а другая — внешней областью многоугольника. Фигуру, состоящую из сторон многоугольника и его внутренней области, также называют многоугольником.

Многоугольник называется выпуклым:

1) если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины

2) если вместе с любыми своими 2 точками он содержит и соединяющий их отрезок.

Сумма углов выпуклого п-угольника равна (n- 2) 180°.

Многоугольником может называться замкнутая ломаная с самопресечениями и правильные звёздчатые многоугольники.

Площадь многоугольника — это величина той части плоскости, которую занимает многоугольник.

1) равные многоугольники имеют равные площади;

2) если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников;
3) площадь квадрата равна квадрату его стороны.

7. Многранники. Виды многранников

В современном мире нас окружает множество построек состоящих из сложных геометрических фигур, большинство из которых являются многогранниками. Примеров тому очень много, достаточно посмотреть по сторонам и мы заметим что здания, в которых мы живём, магазины, в которые ходим, школы и детские сады и т.д. представлены в виде многогранников.

Призма – это многогранник, две грани которой ABCDE и abcde ( основания призмы ) – равные многоугольники с соответственно параллельными сторонами, а остальные грани ( AabB, BbcC и т.д. ) – параллелограммы, плоскости которых параллельны прямой ( Aa, или Bb, или Cc и т.д. По основанию:

-Небоскрёб Flat Iron (Утюг) на пересечении Бродвея и Пятого Авеню. Построен в 1902 году. 21 этаж, 87 метров

-Пентагон — здание Министерства обороны США в форме пятиугольника. Находится в штате Вирджиния недалеко от Вашингтона.

-Наклонная призма – боковое ребро наклонено к основанию под углом отличны от 90є.

Прямая призма – боковое ребро расположено перпендикулярно к основанию.

7.2. Параллелепипед

Параллелепипед – призма, в основании которой находится параллелограмм.

Наклонный, Прямой, Прямоугольный – это прямой параллелепипед,

в основании которого прямоугольник.

Куб – это прямой параллелепипед,

все грани которого квадраты

7.3. Пирамида

Пирамида – это многогранник, одна из граней которого – произвольный n-угольник, а остальные “n” граней – треугольники, имеющие общую вершину.

-Университетский волейбольно-баскетбольный стадион в Калифорнии

В основании – Квадрат

-Торговый центр в Турции

Цилиндр – это тело, ограниченное частью замкнутой цилиндрической поверхности и частью двух плоскостей, параллельных между собой

Водонапорная башня в Минске, Нефтехранилища, Небоскреб в США

Конус – это геометрическое тело, ограниченное частью конической поверхности, расположенной по одну сторону от вершины и частью пересекающей её плоскости.

Как самостоятельные сооружения конусы в строительстве не используются. Практически всегда они составляют какую-то часть здания, например крыши и архитектурные украшающие детали.

Также в строительстве используют конические сваи.

7.6. Сфера и шар.

Сфера – это множество всех точек пространства, находящихся на положительном расстоянии R от данной точки О, называемой центром сферы.

Шар – это множество всех точек пространства, расстояние которых от данной точки не превосходит заданного положительного числа R. Шар получается при вращении полукруга относительно диаметра.

Шаровой слой – это часть шара, заключенная между двумя параллельными плоскостями.

Шаровой сегмент – это часть шара, отсекаемая от него плоскостью.

ТРК Вояж, г. Санкт-Петербург, Здание в Париже (Франция)

Здание Национального Конгресса в США

Итак, при постройке, как современных зданий, так и зданий прошлых веков необходимы знания геометрии. Архитектурное формообразование с помощью геометрических построений сохраняется во всех случаях. Эта проблема стояла перед архитекторами прошлых веков, не исчезла она и сегодня.

7.7. Двойной квадрат

Два квадрата, сложенные вместе, образуют двойной квадрат. Сложив два двойных квадрата, получим квадрат, повторяющий своими очертаниями исходный квадрат. Это простое аддитивное свойство квадрата широко использовалось в архитектуре эпохи Возрождения.

7.8. Восьмиугольные звезды.

Использование восьмиугольных звезд в архитектурных конструкциях не вызывает никаких сомнений. Автором этого проекта является Леонардо да Винчи.

Золото́е сече́ние (золотая пропорция, деление в крайнем и среднем отношении) — деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.

Читайте также:

Современные проблемы физики реферат

Зож мифы и реальность реферат

Режимы наблюдения в психиатрическом стационаре реферат

Реферат магнезиальные вяжущие вещества

Российская империя как форма государства реферат

Источник

Соотношения между средними величинами

Глава II. Практическое применение числовых средних в решении задач

Заключение

Список использованных источников

Решение задачи:

Различные средние положительных. Неравенство Коши

Гармоническое Среднее

Что такое Гармоническое Среднее?

Краткая справка

Основы гармонического среднего

Ключевые моменты

Сравнение среднего гармонического и среднего арифметического и среднего геометрического

Пример среднего гармонического

Среднее гармоническое

Калькулятор среднего гармонического

Как найти среднее гармоническое чисел

Упражнения

Упражнения

Похожие документы:

Рабочая программа педагога козловой Оксаны Александровны, 1 Ф. И. О., категория по алгебре, 8 класс Предмет, класс и т п

Рабочая программа по алгебре для 8 класса на 2013/2014 учебный год

Основная образовательная программа высшего профессионального образования подготовки специалиста 050201. 65 (1)

Описание презентации по отдельным слайдам:

Добавить комментарий Отменить ответ

Соотношения между средними величинами

Глава II. Практическое применение числовых средних в решении задач

Заключение

Список использованных источников

Решение задачи:

Различные средние положительных. Неравенство Коши

Гармоническое Среднее

Что такое Гармоническое Среднее?

Краткая справка

Основы гармонического среднего

Ключевые моменты

Сравнение среднего гармонического и среднего арифметического и среднего геометрического

Пример среднего гармонического

Среднее гармоническое

Калькулятор среднего гармонического

Как найти среднее гармоническое чисел

Упражнения

Упражнения

Похожие документы:

Рабочая программа педагога козловой Оксаны Александровны, 1 Ф. И. О., категория по алгебре, 8 класс Предмет, класс и т п

Рабочая программа по алгебре для 8 класса на 2013/2014 учебный год

Основная образовательная программа высшего профессионального образования подготовки специалиста 050201. 65 (1)

Описание презентации по отдельным слайдам:

Вам также может понравиться

Как найти свой родовой знак

Как найти имя своего вай фай

Как найти кнопку установить

Добавить комментарий Отменить ответ