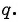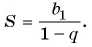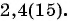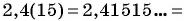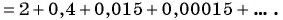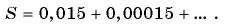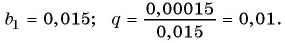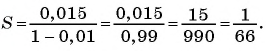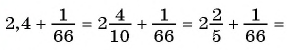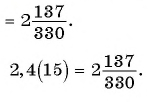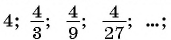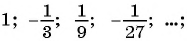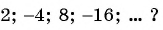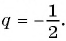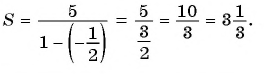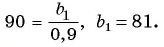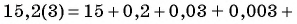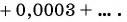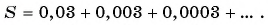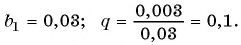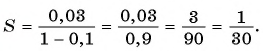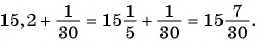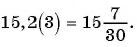Прогрессия — это последовательность величин, каждая последующая из них находится в некоторой, общей для всей прогрессии, зависимости от предыдущей.
Содержание:
Числовая последовательность
В жизни мы часто встречаемся с функциями, областью определения которых является множество натуральных чисел. Например, стоимость проезда в пригородном транспорте зависит от дальности поездки и задается функцией
Функция стоимости проезда задана таблично, областью определения функции является множество натуральных чисел 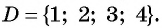
Примером числовой последовательности является последовательность положительных четных чисел: 2; 4; 6; 8; … . Число 2 — первый член последовательности, число 4 — второй и т. д. Ясно, что на 5-м месте будет число 10 (пятый член последовательности), а на 100-м — число 200 (сотый член последовательности).
Еще один пример — последовательность чисел, обратных натуральным числам: 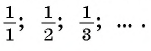
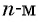
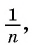
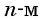
Последовательности могут быть конечными и бесконечными. Например, последовательность двузначных чисел 10; 11; …; 99 является конечной, так как содержит конечное число членов. А последовательность нечетных натуральных чисел — бесконечная.
Определение числовой последовательности
Определение:
Числовой последовательностью называется функция, определенная на множестве 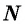
Числа, образующие последовательность (значения функции), называются членами последовательности. Они записываются буквами с индексами, обозначающими номер члена последовательности: 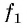
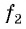
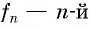
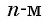
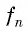
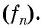
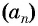
Если 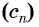
Последовательности, так же как и функции, могут быть заданы различными способами.
Аналитический способ — это задание последовательности с помощью формулы ее 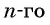
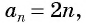
С помощью формулы 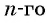
Например, пусть последовательность 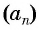
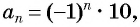
Чтобы найти некоторый член последовательности с помощью формулы 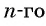
Для задания последовательностей часто используется рекуррентный способ (от лат. recurrentis — возвращающийся). Он заключается в вычислении следующих членов последовательности по предыдущим.
Например, условия 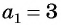
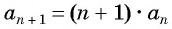
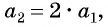
Пример №1
Найдите несколько членов последовательности 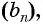
Решение:
Запишем несколько членов этой последовательности в ряд: 1; 1; 2; 3; 5; … .
Полученную последовательность чисел называют последовательностью Фибоначчи по имени итальянского математика Леонардо Фибоначчи (1180—1240).
Формула n-го члена последовательности
Пример №2
Последовательность 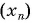
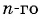
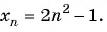
Решение:
Пример №3
Последовательность задана формулой 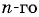
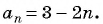
а) -2; б) -7?
Решение:
Для того чтобы определить, является ли число членом последовательности, нужно определить, имеет ли натуральные корни уравнение:
а) 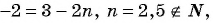
б) 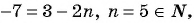
Пример №4
Для каких членов последовательности 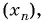
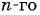
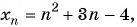
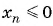
Решение:
Подставим в неравенство 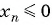
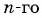
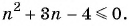
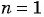
Рекуррентный способ задания последовательности
Пример №5
Запишите 5 первых членов последовательности 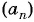
Решение:
Пример №6
Запишите несколько первых членов последовательности 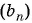
Задайте эту последовательность формулой 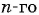
Решение:
Получим следующую последовательность: 8; -8; 8; -8; …. На нечетных местах этой последовательности стоят члены, равные числу 8, а на четных — числу -8, значит, формула 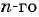
Арифметическая прогрессия
Рассмотрим задачу. В горной местности температура воздуха летом при подъеме на каждые 100 м в среднем понижается на 0,7 °С. У подножия горы температура равна 26 °С. Найдите температуру воздуха на высоте 100 м; 200 м; 300 м.
Решение:
Температура воздуха на высоте 100 м равна 26 °С – 0,7 °С = 25,3 °С. На высоте 200 м температура будет равна 25,3 °С – 0,7 °С = 24,6 °С, а на высоте 300 м — 24,6 °С – 0,7 °С = 23,9 °С.
Ответ: 25,3 °С; 24,6 °С; 23,9 °С.
Решая задачу, мы получили последовательность 26; 25,3; 24,6; … . Каждый член этой последовательности равен предыдущему, сложенному с числом -0,7. Многие практические задачи приводят к последовательностям такого вида. Они называются арифметическими прогрессиями (от лат. progression — движение вперед).
Определение арифметической прогрессией
Определение:
Арифметической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же для данной последовательности числом, т. е.
Число 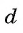
Из равенства 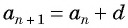
Чтобы задать арифметическую прогрессию 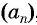
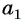
Например, если 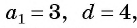
Если 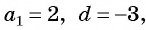
Если 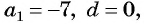
Чтобы вычислить любой член арифметической прогрессии, не вычисляя все предыдущие члены, используют формулу 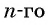
Выведем эту формулу. Если 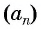
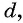
Сложим эти равенства:
После упрощения получим:
Так как число слагаемых 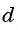
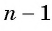
Получили формулу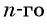
Формула 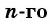
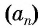
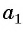
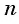
Пример №7
Последовательность 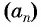
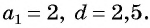
Решение:
По формуле 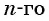
Ответ: 249,5.
Пример №8
Последовательность 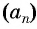
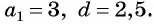
Решение:
а) По условию 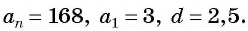
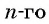
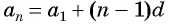
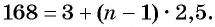
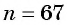
б) Подставим значения 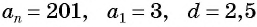
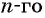
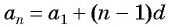
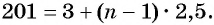
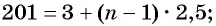
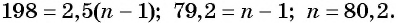
Ответ: а) число 168 является членом этой прогрессии; б) число 201 не является членом этой прогрессии.
Характеристическое свойство арифметической прогрессии
В арифметической прогрессии каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего (соседних с ним)
членов, т. е. 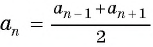
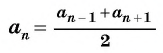
Доказательство. В арифметической прогрессии 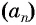
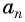
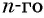
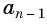
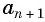
Найдем их среднее арифметическое:
Справедливо и обратное утверждение:
если в последовательности каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего (соседних с ним) членов, то последовательность является арифметической прогрессией.
Доказательство:
Пусть в некоторой числовой последовательности 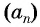
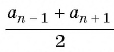
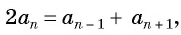
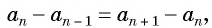
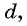
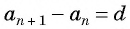
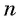
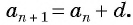
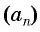
Оба утверждения можно объединить в одно, которое называется характеристическим свойством арифметической прогрессии:
числовая последовательность является арифметической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего членов:
Пример №9
Проверьте, является ли арифметической прогрессией последовательность, заданная формулой
Решение:
Запишем для 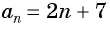
Найдем среднее арифметическое этих членов:
По характеристическому свойству арифметической прогрессии последовательность 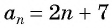
Решение арифметической прогрессии
Пример №10
Последовательность 2; 12; 22; … является арифметической прогрессией. Продолжите последовательность.
Решение:
Так как последовательность является арифметической прогрессией, то найдем ее разность 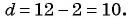
Пример №11
Известны члены арифметической прогрессии: 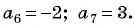
Решение:
Найдем разность арифметической прогрессии:
Формула n-го члена арифметической прогрессии
Пример №12
Последовательность 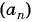
Решение:
По формуле 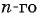
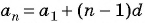
Пример №13
Запишите формулу 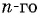
Решение:
По условию 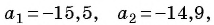
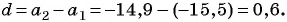
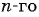
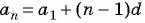
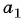
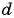
Подставим 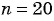
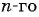
Пример №14
В арифметической прогрессии 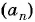
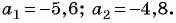
Решение:
Так как 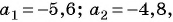
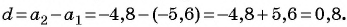
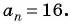
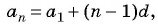
Пример №15
В арифметической прогрессии 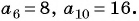
Решение:
По условию
Решим систему уравнений
Вычтем из второго уравнения первое, получим 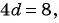
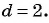
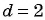
Характеристическое свойство арифметической прогрессии
Пример №16
Найдите восьмой член арифметической прогрессии 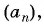
Решение:
По характеристическому свойству арифметической прогрессии 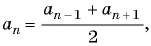
Пример №17
При каком значении 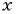
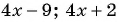
Решение:
По характеристическому свойству прогрессии последовательность является арифметической прогрессией, если каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего членов:
Решим полученное уравнение:
Формула суммы n первых членов арифметической прогрессии
Рассмотрим задачу. Двое друзей решили улучшить знание английского языка и каждый день учить на 3 новых слова больше, чем в предыдущий. Сколько слов выучит каждый из друзей за 10 дней, если они начнут с одного слова?
Для решения этой задачи нужно найти сумму десяти первых членов арифметической прогрессии 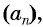
Возникает вопрос: как найти эту сумму, не вычисляя всех десяти членов прогрессии?
В общем виде эта задача приводит к необходимости вывода формулы суммы 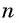
Для того чтобы вывести эту формулу, докажем свойство: суммы двух членов конечной арифметической прогрессии, равноудаленных от ее концов, равны между собой и равны сумме первого и последнего ее членов, т. е.
В общем виде:
Доказательство:
Преобразуем слагаемые в левой части равенства, воспользовавшись формулой 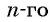
Тогда получим:
С помощью доказанного свойства найдем, например, сумму всех натуральных чисел от 1 до 50.
Натуральные числа от 1 до 50 составляют арифметическую прогрессию 1; 2; 3; …; 50. Первый член этой прогрессии равен 1, последний равен 50. Всего в этой прогрессии 50 членов.
Поскольку 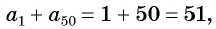
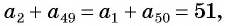
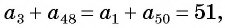
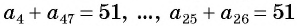
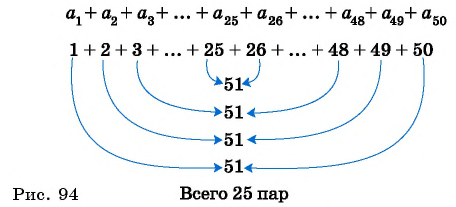
Выведем формулу суммы 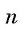
Обозначим 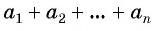
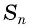
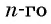
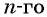
Сложим эти два равенства и получим:
По свойству 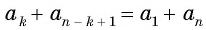
Число всех таких пар сумм равно 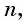
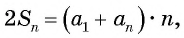
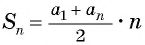
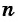
Идея такого доказательства принадлежит выдающемуся немецкому математику К. Гауссу (1777—1855).
Формулу суммы 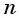
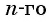
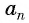
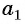
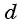
Если известен первый член прогрессии и разность, то удобно использовать формулу
Применим эту формулу к задаче о количестве выученных иностранных слов и получим: 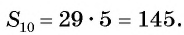
Пример №18
Найдите сумму пятидесяти первых членов арифметической прогрессии 3; 7; 11; 15; … .
Решение:
В этой прогрессии первый член равен 3, а разность 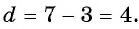
для и получим:
Ответ: 5050.
Пример №19
В арифметической прогрессии 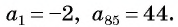
Решение:
Применим формулу суммы 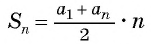
Ответ: 1785.
Пример №20
Найдите сумму шести первых членов арифметической прогрессии, если ее первый член равен -2, а разность прогрессии равна 0,4.
Решение:
Воспользуемся формулой
так как 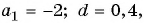
Пример №21
Найдите сумму 4 + 7 + 10+ … + 100, если ее слагаемые — последовательные члены арифметической прогрессии.
Решение:
Последовательность 4, 7, 10, …, 100 является арифметической прогрессией, в которой 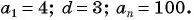
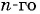
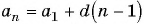
Воспользуемся формулой суммы 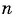
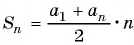
Пример №22
Найдите количество членов арифметической прогрессии, зная, что их сумма равна 430, первый член прогрессии равен -7, а разность прогрессии равна 3.
Решение:
Воспользуемся формулой суммы 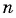
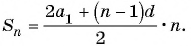
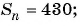
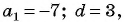
Так как 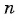
Пример №23
В арифметической прогрессии 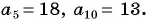
Решение:
Найдем 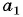
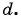
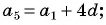
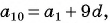
Решим полученную систему способом сложения:
Тогда
Примем четвертый член данной прогрессии за первый член некоторой другой прогрессии, тогда семнадцатый член данной прогрессии станет четырнадцатым (17 – 4 + 1 = 14) членом новой прогрессии. Искомая сумма равна:
Пример №24
Найдите сумму всех четных натуральных чисел, не превосходящих 300, которые при делении на 13 дают в остатке 5.
Решение:
Первое число в последовательности всех четных натуральных чисел, не превосходящих 300, которые при делении на 13 дают в остатке 5, — это число 18. Каждое следующее число равно предыдущему, сложенному с числом 26. Последнее четное число, которое при делении на 13 дает в остатке 5, — это число 278. Поскольку рассматриваются только четные числа, то разность прогрессии равна 26. Найдем номер числа прогрессии, равного 278: 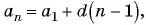
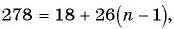
Геометрическая прогрессия
Рассмотрим задачу. Вкладчик положил в банк 1000 р. на
депозит, по которому сумма вклада увеличивается ежегодно на 5 %. Какая сумма будет у него через 1 год, 2 года, 6 лет?
Решение:
Начальная сумма в 1000 р. через год увеличится на 5 % и составит 105 % от 1000 р. Найдем 105 % = 1,05 от 1000 р.: 1000 • 1,05 = 1050 (р.).
Через два года сумма вклада станет равной 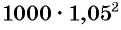
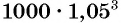
Через шесть лет сумма будет равна
Многие практические задачи приводят к последовательностям такого вида. Они называются геометрическими прогрессиями.
Определение геометрической прогрессии
Определение:
Геометрической прогрессией называется числовая последовательность, первый член которой отличен от нуля, а каждый следующий, начиная со второго, равен предыдущему, умноженному на одно и то же для данной последовательности число, не равное нулю, т. е.
Число 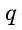
Из равенства 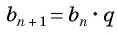
Чтобы задать геометрическую прогрессию 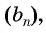
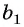
Например, если 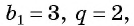
Если 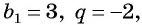
Если 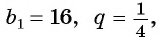
вид
Если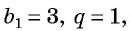
Чтобы вычислить любой член геометрической прогрессии, не вычисляя все предыдущие члены, используют формулу 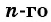
Выведем эту формулу. Если 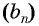
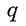
Перемножим эти равенства между собой:
Разделим обе части равенства на произведение 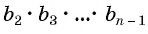
Так как число множителей 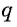
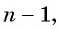
Получили формулу 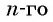
Формула 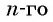
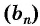
Пример №25
Последовательность 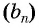
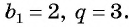
Решение:
По формуле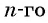
Ответ: 4374.
Пример №26
Последовательность 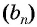
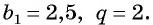
Решение:
По условию 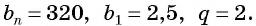
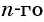
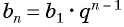
Решим это уравнение:
Так как 8 — натуральное число, то число 320 является членом этой прогрессии с номером 8.
Ответ: число 320 является членом этой прогрессии.
- Заказать решение задач по высшей математике
Характеристическое свойство геометрической прогрессии
В геометрической прогрессии модуль каждого ее члена, начиная со второго, равен среднему пропорциональному предыдущего и последующего (соседних с ним) ее членов, т. е. 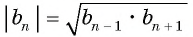
или 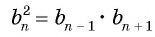
Доказательство:
В геометрической прогрессии 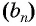
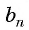
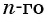
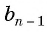
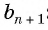
Найдем среднее пропорциональное (среднее геометрическое) соседних с 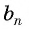
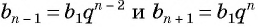
Выполним преобразования в правой части равенства:
откуда получим, что
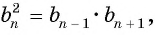
Справедливо и обратное утверждение:
- если в последовательности чисел, отличных от нуля, модуль каждого ее члена, начиная со второго, равен среднему пропорциональному предыдущего и последующего (соседних с ним) ее членов, то последовательность является геометрической прогрессией.
Доказательство:
Пусть в некоторой числовой последовательности 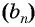
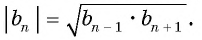
Тогда 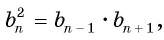
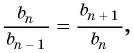
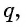
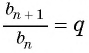
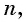
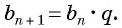
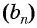
Оба утверждения можно объединить в одно, которое называется характеристическим свойством геометрической прогрессии:
- числовая последовательность, все члены которой отличны от нуля, является геометрической прогрессией тогда и только тогда, когда модуль каждого ее члена, начиная со второго, равен среднему пропорциональному предыдущего и последующего ее членов:
Пример №27
Проверьте, является ли геометрической прогрессией последовательность, заданная формулой
Решение:
Запишем для 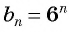
Найдем среднее пропорциональное этих членов:
По характеристическому свойству геометрической прогрессии последовательность 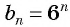
Решение геометрической прогрессии
Пример №28
Последовательность 2; 10; 50; … является геометрической прогрессией. Продолжите последовательность.
Решение:
Так как последовательность является геометрической прогрессией, то найдем ее знаменатель 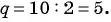
Пример №29
Известны члены геометрической прогрессии:
Найдите знаменатель этой прогрессии.
Решение:
Так как знаменатель геометрической прогрессии равен отношению любого ее члена к предыдущему, то
Формула n-го члена геометрической прогрессии:
Пример №30
Последовательность 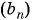
Решение:
По формуле 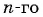
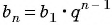
Пример №31
Запишите формулу 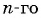
Решение:
По условию 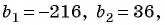
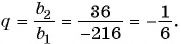
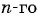
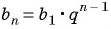
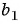
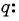
Подставим 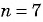
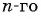
Пример №32
Найдите номер члена геометрической прогрессии 0,1; 0,3; …, равного 218,7.
Решение:
Найдем знаменатель прогрессии:
Известно, что 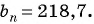
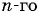
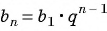
Пример №33
Найдите знаменатель и первый член геометрической прогрессии 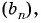
Решение:
По условию
Составим систему уравнений
Разделим второе уравнение на первое и получим:
Подставим это значение 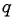
Характеристическое свойство геометрической прогрессии
Пример №34
Найдите сорок девятый член геометрической прогрессии, если сорок восьмой ее член равен 4, а пятидесятый ее член равен 9.
Решение:
Воспользуемся характеристическим свойством геометрической прогрессии 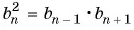
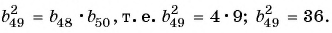
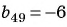
Пример №35
При каком значении 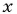
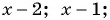
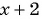
Решение:
По характеристическому свойству прогрессии последовательность является геометрической прогрессией, если каждый ее член, начиная со второго, равен среднему пропорциональному предыдущего и последующего членов:
Решим полученное уравнение:
Формула суммы n первых членов геометрической прогрессии
Немало легенд связано с геометрической прогрессией.
Наиболее известная из них рассказывает об изобретателе шахмат.
По легенде, когда создатель шахмат показал свое изобретение правителю страны, тому так понравилась игра, что он дал изобретателю право самому выбрать награду. Мудрец попросил у правителя за первую клетку шахматной доски заплатить ему одно зерно пшеницы, за вторую — два, за третью — четыре и т. д., удваивая количество зерен на каждой следующей клетке (рис. 96).
Правитель быстро согласился и приказал казначею выдать мудрецу нужное количество зерна. Однако когда казначей показал расчеты, то оказалось, что расплатиться невозможно, разве только осушить моря и океаны и засеять все пшеницей.
Число зерен, которое попросил мудрец, равно сумме членов геометрической прогрессии 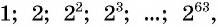
Выведем формулу, по которой можно находить сумму 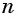
Обозначим сумму 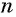
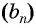
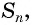
Умножим обе части этого равенства на знаменатель прогрессии 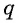
Вычтем из второго равенства первое и получим:
т. e. 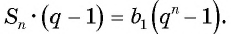
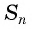
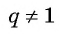
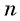
Если 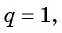
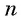
Формула суммы n первых членов геометрической прогрессии:
Вычислим по формуле суммы 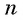
Первый член геометрической прогрессии 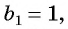
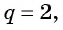
Тогда
Такого количества пшеницы человечество не собрало за всю свою историю.
Пример №36
Найдите сумму десяти первых членов геометрической прогрессии 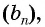
Решение:
Применим формулу суммы 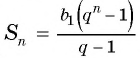
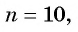
Ответ: 511,5.
Пример №37
Найдите сумму двенадцати первых членов геометрической прогрессии 3; -6; 12; -24; … .
Решение:
Подставим в формулу 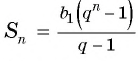
Ответ. -4095.
Пример №38
Найдите сумму пяти первых членов геометрической прогрессии 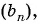
Решение:
Найдем знаменатель и первый член геометрической прогрессии:
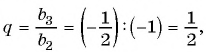
По формуле 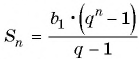
Пример №39
Сумма членов геометрической прогрессии равна 605. Найдите количество членов прогрессии, если
Решение:
Подставим в формулу 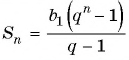
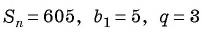
Пример №40
В геометрической прогрессии 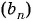

Решение:
Найдем знаменатель прогрессии:
Подставим в формулу 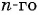
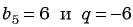
По формуле 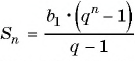
Пример №41
В геометрической прогрессии 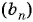
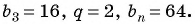
Решение:
Зная, что третий член геометрической прогрессии равен 16, а ее знаменатель равен 2, по формуле 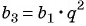
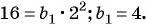
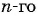
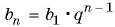
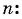
По формуле суммы 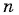
Сумма бесконечно убывающей геометрической прогрессии
Любую обыкновенную дробь можно записать в виде десятичной дроби — конечной или бесконечной периодической дроби. Например, 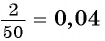
Вы рассматривали правило записи конечной десятичной дроби в виде обыкновенной дроби (например, 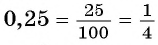
Выясним, как бесконечную периодическую десятичную дробь записать в виде обыкновенной дроби.
Рассмотрим, например, бесконечную периодическую десятичную дробь 0,(7) = 0,7777… . Определим, какой обыкновенной дроби равно это число.
Запишем дробь 0,(7) в виде суммы разрядных слагаемых:
В данном случае необходимо найти сумму бесконечного числа слагаемых.
Слагаемые этой суммы являются членами бесконечной
геометрической прогрессии со знаменателем 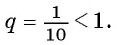
Определение. Бесконечно убывающей геометрической прогрессией называется такая бесконечная геометрическая прогрессия, у которой знаменатель
Например, геометрическая прогрессия 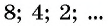
Геометрическая прогрессия 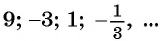
Для того чтобы представить бесконечную периодическую десятичную дробь в виде обыкновенной, нужно найти сумму бесконечно убывающей геометрической прогрессии. Ее обозначают буквой 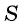
Покажем идею вывода формулы суммы бесконечно убывающей геометрической прогрессии.
Рассмотрим бесконечную геометрическую прогрессию 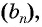
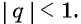
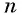
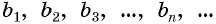
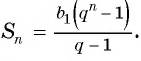
Представим, что п неограниченно возрастает (говорят, что стремится к бесконечности, и записывают 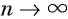
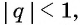
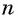
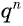
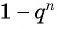
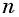
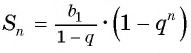
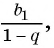
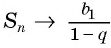
Число 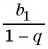
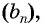
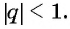
Обозначим сумму бесконечно убывающей геометрической прогрессии буквой 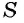
Вычислим по этой формуле сумму разрядных слагаемых:
Слагаемые этой суммы образуют бесконечно убывающую геометрическую прогрессию 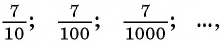
а знаменатель равен
Сумма бесконечно убывающей геометрической прогрессии:
Так как 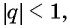
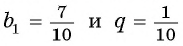
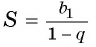
Значит,
Таким образом, бесконечную периодическую десятичную дробь 0,(7) можно записать в виде обыкновенной дроби 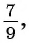
Таким же способом можно любую бесконечную периодическую десятичную дробь представить в виде обыкновенной дроби.
Чтобы записать бесконечную периодическую десятичную дробь в виде обыкновенной дроби, нужно:
- Представить число в виде суммы разрядных слагаемых.
- Выделить сумму бесконечно убывающей геометрической прогрессии.
- Указать первый член
, и найти знаменатель этой прогрессии
- Найти сумму бесконечно убывающей геометрической прогрессии по формуле
- Вычислить сумму первых слагаемых и найденного значения суммы бесконечно убывающей геометрической прогрессии.
Запишите в виде обыкновенной дроби число
(1)
(2)
(3)
(4)
(5)
Бесконечно убывающая геометрическая прогрессия
Пример №42
В бесконечной геометрической прогрессии 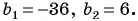
Решение:
Найдем знаменатель прогрессии: 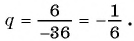
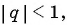
Пример №43
Является ли бесконечно убывающей геометрическая прогрессия:
а)
б)
в)
Решение:
а) Каждый член этой геометрической прогрессии, начиная со второго, равен предыдущему, умноженному на число 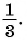
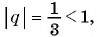
б) Поскольку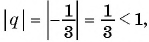
в) Знаменатель прогрессии 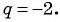
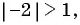
Пример №44
Найдите сумму бесконечно убывающей геометрической прогрессии, в которой 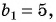
Решение:
По формуле 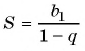
Пример №45
В бесконечно убывающей геометрической прогрессии 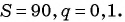
Решение:
В формулу суммы бесконечно убывающей геометрической прогрессии 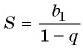
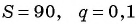
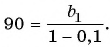
Пример №46
Запишите бесконечную периодическую десятичную дробь 15,2(3) в виде обыкновенной дроби.
Решение:
(1)
(2)
(3)
(4)
(5)
- Единичная окружность – в тригонометрии
- Определение синуса и косинуса произвольного угла
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Наибольшее и наименьшее значения функции
- Раскрытие неопределенностей
- Дробно-рациональные уравнения
- Дробно-рациональные неравенства
Числовые последовательности (основные понятия)
Арифметическая прогрессия
Геометрическая прогрессия
Бесконечно убывающая геометрическая прогрессия
Связь арифметической и геометрической прогрессий
Числовые последовательности (основные понятия)
Если каждому натуральному числу n поставить в соответствие действительное число an, то говорят, что задано числовую последовательность:
a1, a2, a3, . . . , an, . . . .
Итак, числовая последовательность — функция натурального аргумента.
Число a1 называют первым членом последовательности, число a2 — вторым членом последовательности, число a3 — третьим и так далее. Число an называют n-м членом последовательности, а натуральное число n — его номером.
Из двух соседних членов an и an+1 последовательности член an+1 называют последующим (по отношению к an), а an — предыдущим (по отношению к an+1).
Чтобы задать последовательность, нужно указать способ, позволяющий найти член последовательности с любым номером.
Часто последовательность задают с помощью формулы n-го члена, то есть формулы, которая позволяет определить член последовательности по его номеру.
► Например,
последовательность положительных нечётных чисел можно задать формулой
an = 2n –1,
а последовательность чередующихся 1 и –1 — формулой
bn = (–1)n+1. ◄
Последовательность можно определить рекуррентной формулой, то есть формулой, которая выражает любой член последовательности, начиная с некоторого, через предыдущие (один или несколько) члены.
► Например,
если a1 = 1, а an+1 = an + 5, то первые пять членов последовательности находим следующим образом:
a1 = 1,
a2 = a1 + 5 = 1 + 5 = 6,
a3 = a2 + 5 = 6 + 5 = 11,
a4 = a3 + 5 = 11 + 5 = 16,
a5 = a4 + 5 = 16 + 5 = 21.
Если а1 = 1, а2 = 1, an+2 = an + an+1, то первые семь членов числовой последовательности устанавливаем следующим образом:
a1 = 1,
a2 = 1,
a3 = a1 + a2 = 1 + 1 = 2,
a4 = a2 + a3 = 1 + 2 = 3,
a5 = a3 + a4 = 2 + 3 = 5,
a6 = a4 + a5 = 3 + 5 = 8,
a7 = a5 + a6 = 5 + 8 = 13. ◄
Последовательности могут быть конечными и бесконечными.
Последовательность называется конечной, если она имеет конечное число членов. Последовательность называется бесконечной, если она имеет бесконечно много членов.
► Например,
последовательность двузначных натуральных чисел:
10, 11, 12, 13, . . . , 98, 99
конечная.
Последовательность простых чисел:
2, 3, 5, 7, 11, 13, . . .
бесконечная. ◄
Последовательность называют возрастающей, если каждый её член, начиная со второго, больше чем предыдущий.
Последовательность называют убывающей, если каждый её член, начиная со второго, меньше чем предыдущий.
► Например,
2, 4, 6, 8, . . . , 2n, . . . — возрастающая последовательность;
1, 1/2, 1/3, 1/4, . . . , 1/n, . . . — убывающая последовательность. ◄
Последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают, называется монотонной последовательностью.
Монотонными последовательностями, в частности, являются возрастающие последовательности и убывающие последовательности.
Арифметическая прогрессия
Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, к которому прибавляется одно и то же число.
Иначе,
a1, a2, a3, . . . , an, . . .
является арифметической прогрессией, если для любого натурального числа n выполняется условие:
an+1 = an + d,
где d — некоторое число.
Таким образом, разность между последующим и предыдущим членами данной арифметической прогрессии всегда постоянна:
а2 – a1 = а3 – a2 = . . . = an+1 – an = d.
Число d называют разностью арифметической прогрессии.
Чтобы задать арифметическую прогрессию, достаточно указать её первый член и разность.
► Например,
если a1 = 3, d = 4, то первые пять членов последовательности находим следующим образом:
a1 =3,
a2 = a1 + d = 3 + 4 = 7,
a3 = a2 + d = 7 + 4 = 11,
a4 = a3 + d = 11 + 4 = 15,
a5 = a4 + d = 15 + 4 = 19. ◄
Для арифметической прогрессии с первым членом a1 и разностью d её n-й член может быть найден по формуле:
an = a1 + (n – 1)d.
► Например,
найдём тридцатый член арифметической прогрессии
1, 4, 7, 10, . . .
Имеем,
a1 =1, d = 3,
a30 = a1 + (30 – 1)d =1 + 29·3 = 88. ◄
Так как
an–1 = a1 + (n – 2)d,
an = a1 + (n – 1)d,
an+1 = a1 + nd,
то, очевидно,
то есть,
каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предшествующего и последующего членов.
Так как верно и обратное утверждение, то имеет место следующее утверждение:
числа a, b и c являются последовательными членами некоторой арифметической прогрессии тогда и только тогда, когда одно из них равно среднему арифметическому двух других.
► Например,
докажем, что последовательность, которая задаётся формулой an = 2n – 7, является арифметической прогрессией.
Воспользуемся приведённым выше утверждением. Имеем:
an = 2n – 7,
an–1 = 2(n – 1) – 7 = 2n – 9,
an+1 = 2(n + 1) – 7 = 2n – 5.
Следовательно,
| an+1 + an–1 |
= |
2n – 5 + 2n – 9 |
= 2n – 7 = an, |
| 2 |
2 |
что и доказывает нужное утверждение. ◄
Отметим, что n-й член арифметической прогрессии можно найти не толь через a1, но и любой предыдущий ak, для чего достаточно воспользоваться формулой
an = ak + (n – k)d.
► Например,
для a5 можно записать
a5 = a1 + 4d,
a5 = a2 + 3d,
a5 = a3 + 2d,
a5 = a4 + d. ◄
Так как
an = an–k + kd,
an = an+k – kd,
то, очевидно,
то есть,
любой член арифметической прогрессии, начиная со второго равен полусумме равноотстоящих от него членов этой арифметической прогрессии.
Кроме того, для любой арифметической прогрессии справедливо равенство:
am + an = ak + al,
если
m + n = k + l.
► Например,
в арифметической прогрессии 1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, . . .
1) a10 = 28 = (25 + 31)/2 = (a9 + a11)/2;
2) 28 = a10 = a3 + 7d = 7 + 7·3 = 7 + 21 = 28;
3) a10 = 28 = (19 + 37)/2 = (a7 + a13)/2;
4) a2 + a12 = a5 + a9, так как
a2 + a12 = 4 + 34 = 38,
a5 + a9 = 13 + 25 = 38. ◄
Сумма
Sn = a1 + a2+ a3 + . . .+an,
первых n членов арифметической прогрессии равна произведению полусуммы крайних слагаемых на число слагаемых:
Отсюда, в частности, следует, что если нужно просуммировать члены
ak, ak+1, . . . , an,
то предыдущая формула сохраняет свою структуру:
| Sn – Sk–1 = ak + ak+1 + . . . + an = | ak + an |
· (n – k + 1) . |
| 2 |
► Например,
в арифметической прогрессии 1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, . . .
S10 = 1 + 4 + . . . + 28 = (1 + 28) · 10/2 = 145;
10 + 13 + 16 + 19 + 22 + 25 + 28 = S10 – S3 = (10 + 28) · (10 – 4 + 1)/2 = 133. ◄
Если дана арифметическая прогрессия, то величины a1, an, d, n и Sn связаны двумя формулами:
| an = a1 + (n – 1)d и Sn = | a1 + an |
· n . |
| 2 |
Поэтому, если значения трёх из этих величин даны, то соответствующие им значения двух остальных величин определяются из этих формул, объединённых в систему двух уравнений с двумя неизвестными.
Арифметическая прогрессия является монотонной последовательностью. При этом:
- если d > 0, то она является возрастающей;
- если d < 0, то она является убывающей;
- если d = 0, то последовательность будет стационарной.
Геометрическая прогрессия
Геометрической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число.
Иначе,
b1, b2, b3, . . . , bn, . . .
является геометрической прогрессией, если для любого натурального числа n выполняется условие:
bn+1 = bn · q,
где q ≠ 0 — некоторое число.
Таким образом, отношение последующего члена данной геометрической прогрессии к предыдущему есть число постоянное:
b2/b1 = b3/b2 = . . . = bn+1/bn = q.
Число q называют знаменателем геометрической прогрессии.
Чтобы задать геометрическую прогрессию, достаточно указать её первый член и знаменатель.
► Например,
если b1 = 1, q = –3, то первые пять членов последовательности находим следующим образом:
b1 = 1,
b2 = b1 ·
q = 1 · (–3) = –3,
b3 = b2 ·
q = –3 · (–3) = 9,
b4 = b3 ·
q = 9 · (–3) = –27,
b5 = b4 ·
q = –27 · (–3) = 81. ◄
Для геометрической прогрессии с первым членом b1 и знаменателем q её n-й член может быть найден по формуле:
bn = b1 ·
qn–1.
► Например,
найдём седьмой член геометрической прогрессии 1, 2, 4, . . .
Имеем,
b1 = 1, q = 2,
b7 = b1 · q6
= 1 · 26 = 64. ◄
Так как
bn–1 = b1 ·
qn–2,
bn = b1 ·
qn–1,
bn+1 = b1 ·
qn,
то, очевидно,
bn2 = bn–1 · bn+1,
то есть,
каждый член геометрической прогрессии, начиная со второго, равен среднему геометрическому (пропорциональному) предшествующего и последующего членов.
Так как верно и обратное утверждение, то имеет место следующее утверждение:
числа a, b и c являются последовательными членами некоторой геометрической прогрессии тогда и только тогда, когда квадрат одного из них равен произведению двух других, то есть одно из чисел является средним геометрическим двух других.
► Например,
докажем, что последовательность, которая задаётся формулой bn = –3 · 2n, является геометрической прогрессией. Воспользуемся приведённым выше утверждением. Имеем:
bn = –3 · 2n,
bn–1 = –3 · 2n–1,
bn+1 = –3 · 2n+1.
Следовательно,
bn2 = (–3 · 2n)2 = (–3 · 2n–1) · (–3 · 2n+1) = bn–1 · bn+1,
что и доказывает нужное утверждение. ◄
Отметим, что n-й член геометрической прогрессии можно найти не только через b1, но и любой предыдущий член bk, для чего достаточно воспользоваться формулой
bn = bk ·
qn–k.
► Например,
для b5 можно записать
b5 = b1 ·
q4,
b5 = b2 ·
q3,
b5 = b3 ·
q2,
b5 = b4 ·
q. ◄
Так как
bn = bk ·
qn–k,
bn = bn–k ·
qk,
то, очевидно,
bn2 = bn–k · bn+k
то есть,
квадрат любого члена геометрической прогрессии, начиная со второго равен произведению равноотстоящих от него членов этой прогрессии.
Кроме того, для любой геометрической прогрессии справедливо равенство:
bm · bn = bk · bl,
если
m + n = k + l.
► Например,
в геометрической прогрессии 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, . . .
1) b62 = 322 = 1024 = 16 · 64 = b5 · b7;
2) 1024 = b11 = b6 ·
q5 = 32 · 25 = 1024;
3) b62 = 322 = 1024 = 8 · 128 = b4 · b8;
4) b2 · b7 = b4 · b5, так как
b2 · b7 = 2 · 64 = 128,
b4 · b5 = 8 · 16 = 128. ◄
Сумма
Sn = b1 + b2 + b3 + . . . + bn
первых n членов геометрической прогрессии со знаменателем q ≠ 0 вычисляется по формуле:
А при q = 1 — по формуле
Sn = nb1
Заметим, что если нужно просуммировать члены
bk, bk+1, . . . ,bn,
то используется формула:
| Sn – Sk–1 = bk + bk+1 + . . . + bn = bk · | 1 – qn–k+1 |
. |
| 1 – q |
► Например,
в геометрической прогрессии 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, . . .
S10 = 1 + 2 + . . . + 512 = 1 · (1 – 210) / (1 – 2) = 1023;
64 + 128 + 256 + 512 = S10 – S6 = 64 · (1 – 210–7+1) / (1 – 2) = 960. ◄
Если дана геометрическая прогрессия, то величины b1, bn, q, n и Sn связаны двумя формулами:
| bn = b1 · qn–1 и Sn = b1 · | 1 – qn |
. |
| 1 – q |
Поэтому, если значения каких-либо трёх из этих величин даны, то соответствующие им значения двух остальных величин определяются из этих формул, объединённых в систему двух уравнений с двумя неизвестными.
Для геометрической прогрессии с первым членом b1 и знаменателем q имеют место следующие свойства монотонности:
- прогрессия является возрастающей, если выполнено одно из следующих условий:
b1 > 0 и q > 1;
b1 < 0 и 0 < q < 1;
- прогрессия является убывающей, если выполнено одно из следующих условий:
b1 > 0 и 0 < q < 1;
b1 < 0 и q > 1.
Если q < 0, то геометрическая прогрессия является знакопеременной: её члены с нечётными номерами имеют тот же знак, что и её первый член, а члены с чётными номерами — противоположный ему знак. Ясно, что знакопеременная геометрическая прогрессия не является монотонной.
Произведение первых n членов геометрической прогрессии можно рассчитать по формуле:
Pn = b1 · b2 · b3 · . . . · bn = (b1 · bn) n/2.
► Например,
1 · 2 · 4 · 8 · 16 · 32 · 64 · 128 = (1 · 128)8/2 = 1284 = 268 435 456;
3 · 6 · 12 · 24 · 48 = (3 · 48)5/2 = (1441/2)5 = 125 = 248 832.◄
Бесконечно убывающая геометрическая прогрессия
Бесконечно убывающей геометрической прогрессией называют бесконечную геометрическую прогрессию, модуль знаменателя которой меньше 1, то есть
|q| < 1.
Заметим, что бесконечно убывающая геометрическая прогрессия может не быть убывающей последовательностью. Это соответствует случаю
–1 < q < 0.
При таком знаменателе последовательность знакопеременная. Например,
1, –1/2, 1/4, –1/8, . . . .
Суммой бесконечно убывающей геометрической прогрессии называют число, к которому неограниченно приближается сумма первых n членов прогрессии при неограниченном возрастании числа n. Это число всегда конечно и выражается формулой
| S = b1 + b2 + b3 + . . . = | b1 | . |
| 1 – q |
► Например,
10 + 1 + 0,1 + 0,01 + . . . = 10 / (1 – 0,1) = 11 1/9 ,
10 – 1 + 0,1 – 0,01 + . . . = 10 / (1 + 0,1) = 9 1/11 . ◄
Связь арифметической и геометрической прогрессий
Арифметическая и геометрическая прогрессии тесно связаны между собой. Рассмотрим лишь два примера.
Если
a1, a2, a3, . . .— арифметическая прогрессия с разностью d, то
ba1, ba2, ba3, . . . — геометрическая прогрессия с знаменателем bd.
► Например,
1, 3, 5, . . . — арифметическая прогрессия с разностью 2 и
71, 73, 75, . . . — геометрическая прогрессия с знаменателем 72. ◄
Если
b1, b2, b3, . . .— геометрическая прогрессия с знаменателем q, то
loga b1, loga b2, loga b3, . . . — арифметическая прогрессия с разностью loga q.
► Например,
2, 12, 72, . . . — геометрическая прогрессия с знаменателем 6 и
lg 2, lg 12, lg 72, . . . — арифметическая прогрессия с разностью lg 6. ◄
Смотрите также:
Обозначения и сокращения
Таблицы чисел
Алгебраические тождества
Степени
Арифметический корень n-й степени
Логарифмы
Графики элементарных функций
Построение графиков функций геометрическими методами
Тригонометрия
Таблицы значений тригонометрических функций
Предел и непрерывность функции
Треугольники
Четырёхугольники
Многоугольники
Окружность
Площади геометрических фигур
Прямые и плоскости
Многогранники
Тела вращения
Для (14) задания необходимо знать теорию арифметической и геометрической прогрессий.
Арифметическая прогрессия
Арифметическая прогрессия — это последовательность, каждый член которой, начиная со второго, равен предыдущему, к которому прибавляется одно и то же число.
, где
an+1
— последующий член,
an
— предыдущий член и
d
— разность арифметической прогрессии.
Формула для нахождения разности:
d=an+1−an
.
Для арифметической прогрессии, где известен первый член
a1
и разность
d
, её (n)-й член может быть найден по формуле:
Свойство арифметической прогрессии: каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предшествующего и последующего членов.
Сумма первых членов арифметической прогрессии равна произведению полусуммы крайних слагаемых на число слагаемых:
И вторая формула для вычисления суммы:
Sn=2a1+d⋅n−12⋅n
.
Более подробно можно познакомиться с темой здесь.
Геометрическая прогрессия
Геометрическая прогрессия — это последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число.
, где
bn+1
— последующий член,
bn
— предыдущий член и
q
— знаменатель геометрической прогрессии.
Формула для нахождения знаменателя:
q=bn+1bn
.
Для геометрической прогрессии, где дан первый член
b1
и знаменатель
q
, её (n)-й член может быть найден по формуле:
Свойство геометрической прогрессии: каждый член геометрической прогрессии, начиная со второго, равен среднему геометрическому предшествующего и последующего членов.
Сумму первых членов геометрической прогрессии со знаменателем, не равным нулю, можно найти по формуле:
Также можно найти сумму по формуле:
Sn=bnq−b1q−1
.
Более подробно можно познакомиться с темой здесь.
Прогрессии
Термин «прогрессия» имеет латинское происхождение («progression», что означает «движение вперед»), был введен римским математиком Боэцием в 6 веке.
Что такое прогрессия? Это тип последовательности. А что такое последовательность? Это бесконечный набор чисел, подчиняющийся определенному правилу. Например, последовательность составляют все числа, делящиеся на 2. Их бесконечно много, и они подчиняются определенному правилу. Последовательность можно задать формулой n-го члена, где n – номер члена последовательности.
Например,
$ M_{n}=2^{n}-1 $ (числа Мерсенна)
$ M_{1}=2^{1}-1=1 $
$ M_{2}=2^{2}-1=3 $
$ M_{5}=2^{5}-1=31 $
Последовательность также может задаваться правилом, по которому находят каждый ее член, если известны предыдущие. Например, первые два члена последовательности равны единице, а каждый следующий равен сумме двух непосредственно предшествующих ему. Тогда получаем последовательность чисел:
1, 1, 2, 3, 5, 8, 13, 21, … (называемых числами Фибоначчи)
Есть два вида последовательностей, которые изучаются в курсе математики– это арифметические и геометрические прогрессии.
Арифметическая прогрессия
Арифметической прогрессией называют такую числовую последовательность, каждый следующий член которой отличается от предшествующего члена на одно и то же число d.
Например, 1, 3, 5, 7…
Число d называют разностью арифметической прогрессии.
Отметим, что если d > 0, то арифметическая прогрессия является возрастающей последовательностью, если d < 0, то — убывающей последовательностью. А если d = 0 ? Это тоже прогрессия, называют ее в математике постоянной прогрессией.
Ряд натуральных чисел дает пример бесконечной арифметической прогрессии с разностью d = 1, а последовательность нечетных и четных чисел – примеры бесконечных арифметических прогрессий, у каждой из которых разность d = 2 (отличие только в первом члене прогрессии).
Если известен первый член арифметической прогрессии a1 и ее разность d, то можно найти любой член этой последовательности по формуле:
- an = a1 + d · (n−1) — формула n-го члена,
Пример: найдите члены а8, а1000 арифметической прогрессии, у которой а1 = -2, d = 5
Решение:
Найдем по записанной нами формуле:
а8 = a1 + d · (8 −1) = -2 + 7 · 5 = 33.
а1000 = a1 + d · (1000 −1) = -2 + 999 · 5 = 4993.
Запишем формулы суммы n первых членов прогрессии:
- $ S_{n}= frac {a_{1}+a_{n}}{2} cdot n = frac {2a_{1}+d(n-1)}{2} cdot n; $
Пример: определить сумму k первых нечетных чисел, начиная с единицы.
Решение:
Последовательность нечетных чисел – арифметическая прогрессия с a1 = 1 и d = 2
$ S_{k}= frac {2a_{1}+d(k-1)}{2} cdot k = frac {2 cdot 1+2(k-1)}{2} cdot k = frac {2+2k-2}{2} cdot k=k^{2} $
Например, сумма первых пяти нечетных чисел:
Можно убедиться, что 1 + 3 + 5 + 7 + 9 = 25.
Каждый член арифметической прогрессии равен среднему арифметическому его соседних членов (исключение составляют первый и последний члены, т.к. у них только по одному соседнему члену)
- $ a_{n}= frac {a_{n-1}+a_{n+1}}{2} $ — свойство n-го члена.
Геометрическая прогрессия
Геометрической прогрессией называют такую числовую последовательность, каждый член которой, начиная со второго, равен предшествующему члену, умноженному на одно и то же (определенное для данной последовательности) число q. Число q называют знаменателем геометрической прогрессии. Предполагается, что q ≠ 0.
Например, 1, 3, 9, 27…
Если q > 0, то прогрессия считается знакоположительной, при q < 0 – знакопеременной.
Если |q |>1, прогрессия возрастающая, если |q | <1 – убывающая. Заметим, что при q < 0 сами члены геометрической прогрессии попеременно меняют знак и убывающей последовательности не образуют, хотя такую прогрессию все равно называют убывающей.
Если b1 — первый член прогрессии (b1 ≠ 0), а q — знаменатель прогрессии (q ≠ 0), то справедливы следующие формулы:
- bn = b1 · q n -1 формула n-го члена
Пример: найдите b4, b11 геометрической прогрессии, если b1 = 3, q = 2
Решение:
По формуле найдем:
b4 = b1 · q 4 – 1= 3 · 2 3 = 24,
b11 = b1 · q 11 – 1= 3 · 2 10 = 3072.
- $ S_{n}= b_{1} frac {q^{n}-1}{q-1} $ — формула суммы n первых членов;
Пример: найдите сумму пяти членов геометрической прогрессии, у которой b1 = 2, q = 3
Решение:
$ S_{5}= b_{1} frac {(q^{5}-1)}{q-1} = 2 frac {(3^{5}-1)}{3-1} = 2 frac {(243-1)}{2}=242 $
Каждый член знакоположительной геометрической прогрессии представляет собой среднее геометрическое его соседних членов (исключение составляют первый и последний члены, т.к. у них только по одному соседнему члену):
- $ b_{n}= sqrt {b_{n-1} cdot b_{n+1}} $ – свойство n-го члена.
Если | q | < 1, то имеем бесконечную убывающую геометрическую прогрессию, сумму которой находят по формуле $ S= frac {b_{1}}{1-q} $
Замечание:
Формула n-го члена прогрессии:
- арифметической:an = a1 + d · (n − 1)
- геометрической: bn = b1 · q n – 1
Зная одну формулу, легко можно получить другую – надо лишь сложение заменить умножением и умножение заменить возведением в степень, и из формулы для арифметической прогрессии получится формула для геометрической прогрессии.
Сложные проценты
Есть два вида процентов доходности – простые и сложные.
Чтобы с ними разобраться, представим двух братьев: Расчетливого Сашу и Простака Петю. Их отец дал каждому по 1000 рублей, и оба кладут их в банк. Расчетливый Саша всегда пользуется счетом со сложными процентами, а Простак Петя больше любит поступать по старинке и предпочитает счета с простыми процентами.
Сложный процент – это проценты с процентов.
У простого процента такой особенности нет, его рассчитывают от стартовой суммы, которую называют «основным капиталом». Пете легко в этом разобраться: основной капитал зарабатывает каждый год одну и ту же сумму.
Если вы откладываете деньги, занимаете их, пользуетесь кредитной картой, берёте в ипотеку или покупаете пожизненную ренту, формула сложного процента работает на (или против) вас.
Давайте выведем формулу сложных процентов. Допустим, у нас есть некоторая сумма S, в конце года мы ее увеличиваем на некоторый процент (%). Полученную сумму S1 после начисления процентов можно посчитать так:
$ S_{1}=S+frac{%}{100} cdot S = S big( 1+frac{%}{100} big) $
В следующем году полученную сумму снова увеличим на тот же процент. Тогда можем записать верное равенство:
$ S_{2}=S_{1}+frac{%}{100} cdot S_{1} = S_{1} big( 1+ frac{%}{100} big) = S big( 1+ frac{%}{100} big) big( 1+ frac{%}{100} big) = S big( 1+ frac{%}{100} big)^{2} $
Аналогично мы можем посчитать полученную сумму еще через год:
$ S_{3}=S_{2}+frac{%}{100} cdot S_{2} = S_{2} big( 1+ frac{%}{100} big) = S_{1} big( 1+ frac{%}{100} big)^{2} big( 1+ frac{%}{100} big) = S big( 1+ frac{%}{100} big)^{3} $
Таким образом, если периодов n, то можем записать формулу вычисления сложных процентов:
$ S_{n}=S big( 1+ frac {%}{100} big)^{n} $ начисление процентов (%) на сумму S через n периодов.
Тогда последовательность остатков долга будет следующей:
$ S; S big( 1+ frac {%}{100} big); S big( 1+ frac {%}{100} big)^{2}; S big( 1+ frac {%}{100} big)^{3}… S big( 1+ frac {%}{100} big)^{n} $
Видим, что это геометрическая прогрессия.
Итак, Саша размещает свои 1000 рублей на счете и получает ежегодно 7% дохода. Давайте посчитаем, сколько он получит за три года? В данном случае S = 1000, % = 7, n = 3, $ S_{3} $– общая сумма, получаемая по формуле сложного процента:
$ S_{3} = 1000 big(1+frac{7}{100} big)^{3}=1225,04 ; (руб). $
Счет Пети – тоже 7%-ный, но процент у него простой. Какие деньги заработает за три года Петя? В первый год он получит 70 рублей, столько же – во второй и в третий. Таким образом, проценты составят 3 · 70 = 210 рублей, итого общая сумма на счете – 1210 рублей. Инвестиционное решение Саши, очевидно, выгоднее.
Появились трудностями с прогрессиями при подготовке к экзаменам? Напомним, что такое прогрессия, и как бороться с задачами этой темы ОГЭ по математике.
0
333
Что такое последовательность
Последовательность — это набор элементов, расположенных в определенном порядке. Каждый элемент в последовательности имеет свой индекс, который определяет его место в порядке следования.
Например, последовательность целых чисел может быть представлена в таком виде: 1, 2, 3, 4, 5, 6 и далее. В этом случае каждое число имеет свой индекс, например, a1 = 1, a2 = 2 до конечного элемента аn, где n — это количество элементов в последовательности.
В задачах ОГЭ по математике 9 класса последовательности представлены арифметическими и геометрическими прогрессиями.
Школьникам часто задают задания, которые требуют определения элемента последовательности, нахождения суммы первых n элементов или нахождения количества элементов в последовательности.
Чтобы решать такие задачи, необходимо знать свойства и характеристики прогрессий, уметь применять формулы и методы для решения задач на последовательности.
Что такое арифметическая прогрессия
Арифметическая прогрессия — это разновидность числовой последовательности, в которой каждый новый компонент на фиксированное значение отличается от предшествующего. Это значение называют разностью.
Прогрессия описывается правилом an+1 = an + d.
Можно представить ее как: а1, а2, а3, …, an, где a1 будет первым элементом, аn — n-м элементом, а разность d можно определить разницей между двумя соседними членами a2 – a1 = a3 – a2 = … = an – an-1.
Например, последовательность чисел 3, 7, 11, 15, 19 может называться арифметической прогрессией, так как каждый последующий член отличается от предыдущего на фиксированное значение 4. Элемент a1 = 3, разность d = 4.
Характеристическое свойство арифметической прогрессии
Такая последовательность имеет определенную закономерность в построении. Элемент n — это всегда среднее арифметическое значение от соседних членов прогрессии. Исключение составляют первый и последний члены, которые не имеет соседнего с одной из сторон.
an = (an-1 + an+1) / 2
Условие: n > 1.
Как решать задачи с арифметической прогрессией на ОГЭ
Для решения задач экзамена после 9 класса нужно знать основные формулы и правила, которые применяются для арифметических прогрессий. Задания могут включать в себя поиск суммы, определения конкретного элемента и прочее.
- Разность d равна разнице между любыми двумя соседними элементами последовательности: d = an – an-1.
- Если нужно найти определенный член an, используй формулу: an = a1 + (n – 1) * d.
a1 — первый член прогрессии, n — номер искомого члена, d — разность. - Сумму n членов прогрессии можно вычислить по формуле: Sn = (a1 + an) * n / 2.
a1 — первый элемент, an — n-й элемент, n — количество элементов. - Если необходимо найти номер члена, который соответствует заданному значению, подойдет формула: n = (an – a1) / d + 1.
a1 — первый член, an — искомый член, d — разность.
Важно внимательно читать условие задачи, чтобы понимать, какие данные уже имеются, и что конкретно тебя просят найти.
Что такое геометрическая прогрессия
Геометрическая прогрессия — это разновидность числовой последовательности, в которой каждый новый компонент получается умножением предшествующего на фиксированное значение. Это значение называют знаменателем.
Прогрессия описывается правилом: bn = bn-1 * q, где q — знаменатель, n — номер члена прогрессии.
Например, последовательность чисел 3, 9, 27, 81, 243 может называться геометрической прогрессией, так как каждый последующий член отличается от предыдущего в фиксированные 3 раза. Элемент b1 = 3, знаменатель q = 3.
Характеристическое свойство геометрической прогрессии
Последовательность тоже имеет определенную закономерность в построении. Квадрат элемента n — это всегда произведением предыдущего и последующего элемента. Исключение составляет первый элемент, который не имеет соседнего с одной из сторон.
an2 = (an-1 * an+1)
Как решать задачи с геометрической прогрессией на ОГЭ
Для решения задач на ОГЭ также нужно знать формулы и правила, которые описывают свойства прогрессии. Задания могут включать в себя нахождение суммы компонентов, нахождение n-го члена и прочее.
- Знаменатель q равен частному от деления члена прогрессии на предыдущий член: q = bn / bn-1.
- Если нужно найти определенный член bn, используй формулу: bn = b1 * q(n-1).
b1 — первый компонент, q — знаменатель, n — номер компонента. - Сумму n членов прогрессии можно вычислить по формуле: Sn = b1 * ((1 – qn) / (1 – q)),
b1 — первый компонент, q — знаменатель, n — количество элементов в последовательности.
При решении задач нужно внимательно читать условия и уметь работать со степенями и извлечениями корней.
В каких заданиях ОГЭ есть задачи на арифметическую и геометрическую прогрессию
На этапе 9-го класса, задачи на арифметическую и геометрическую прогрессии могут встречаться в разделе «Алгебра и начала анализа». В демонстрационном варианте ОГЭ по математике 2023 года задание на знание свойств прогрессии встречается под номером 14. Скачать демонстрационный вариант можно на сайте ФИПИ.
Задачи на арифметическую и геометрическую прогрессии могут иметь разный уровень сложности, поэтому для успешного решения на ОГЭ нужно иметь хорошее понимание основных понятий и формул, связанных с арифметическими и геометрическими прогрессиями.
Если прогрессии все еще кажутся тебе сложными, то начинай подготовку в «СОТКЕ». Наши преподаватели объяснят так, чтобы ты понял абсолютно все. А разнообразные практические задания и качественная проверка с работой над ошибками помогут закрепить твои знания и повысить уверенность в себе.
Записывайся на бесплатный вводный урок, в «СОТКЕ» ты сможешь подготовиться к 4-м предметами по цене одного.

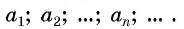
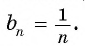
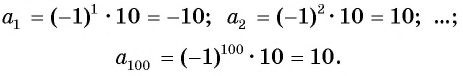
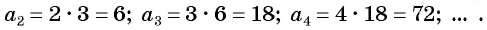
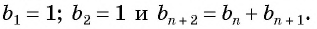
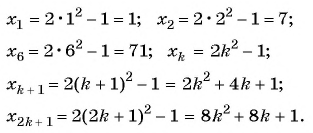
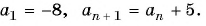
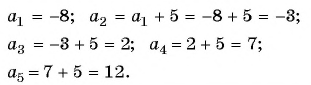
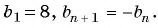
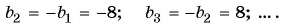
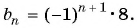
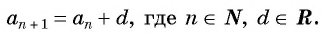
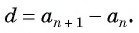
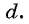
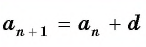
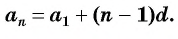
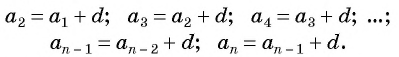
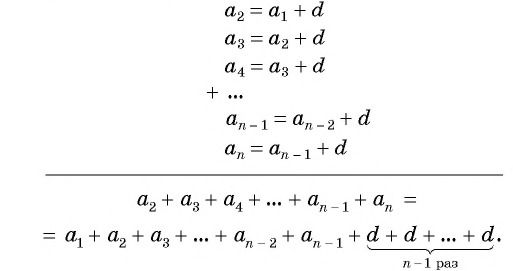
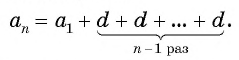
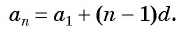

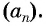
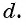
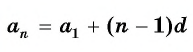
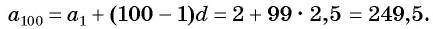
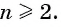
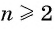
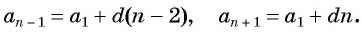
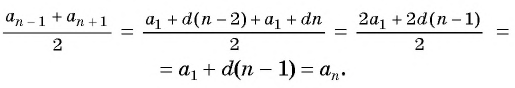
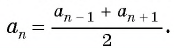
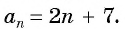
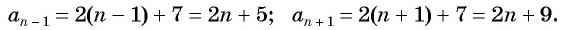
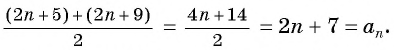
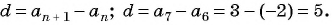
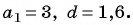
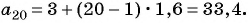
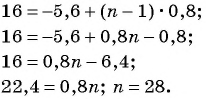
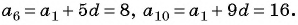
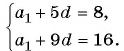
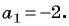
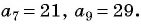
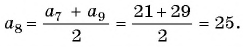
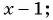
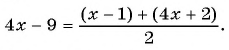
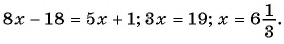
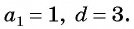
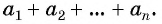
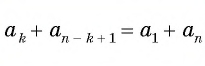
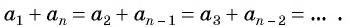
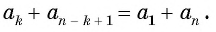
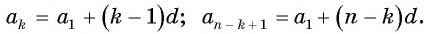
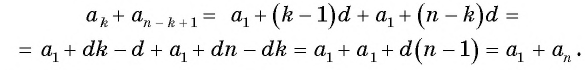
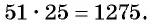
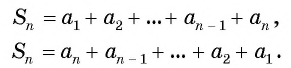
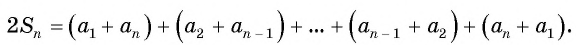
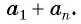
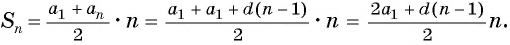
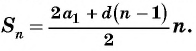
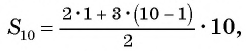

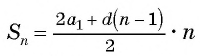
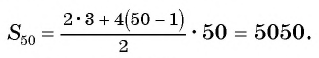
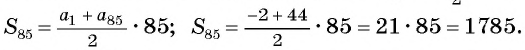
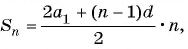
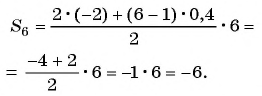
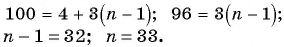
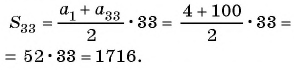
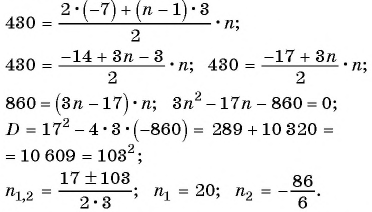
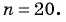
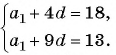
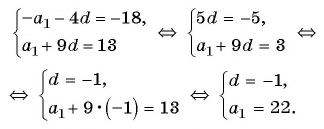
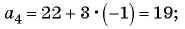
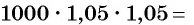
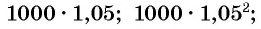
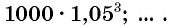
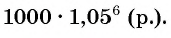
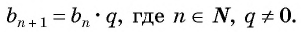
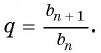
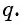
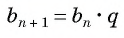
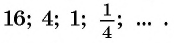
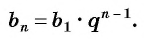
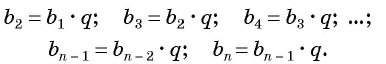
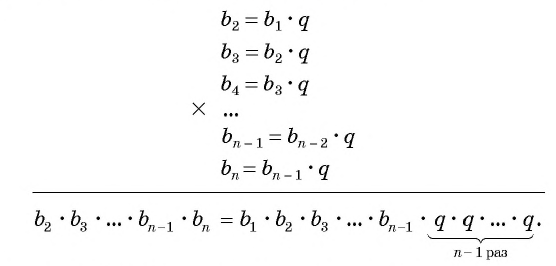
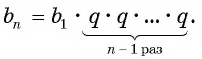
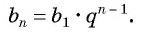
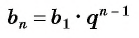
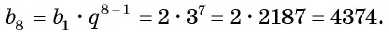
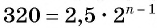
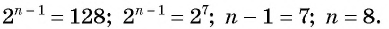
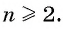
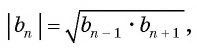
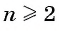
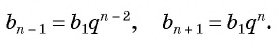
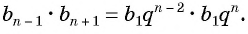
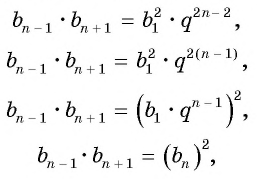
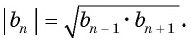
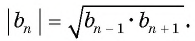
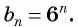
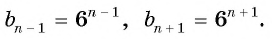
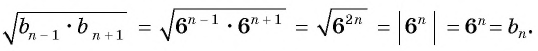
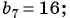
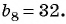
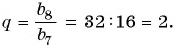
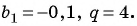
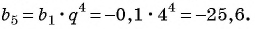
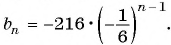
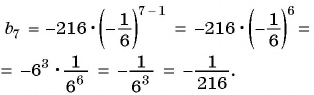
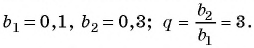
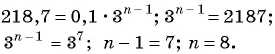
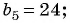
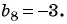
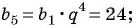
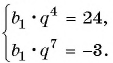
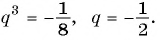
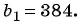
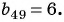
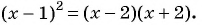
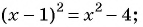
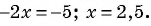

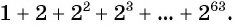
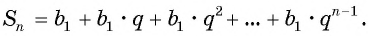
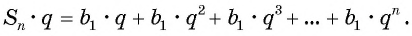
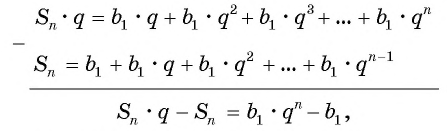
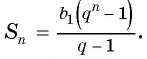
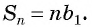
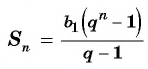
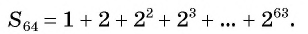
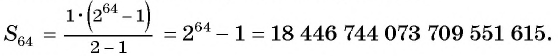
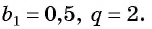
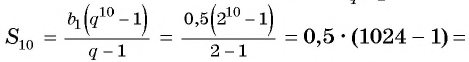
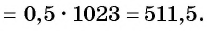
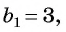
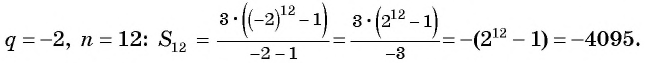
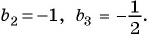
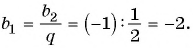
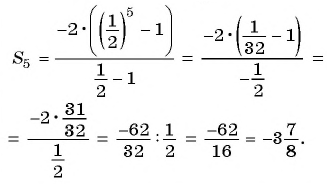
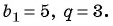
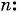
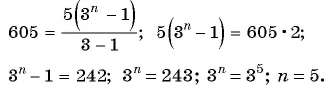
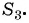
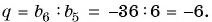
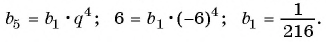
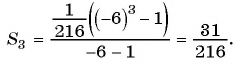
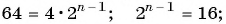
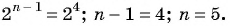
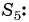
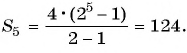
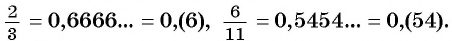
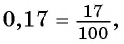
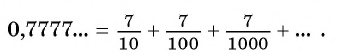
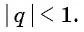
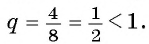
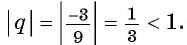
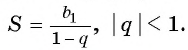
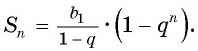
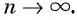
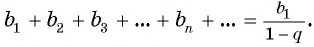
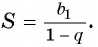
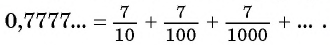
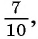
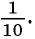
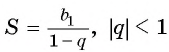
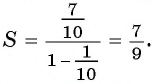
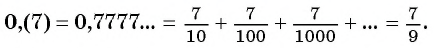
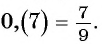
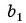 , и найти знаменатель этой прогрессии
, и найти знаменатель этой прогрессии