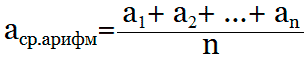Перейти к содержанию
На чтение 1 мин Просмотров 7.6к. Опубликовано 20 ноября, 2021 Обновлено 20 ноября, 2021
Напишите программу, которая считывает с клавиатуры два числа a и b, считает и выводит на консоль среднее арифметическое всех чисел из отрезка [a; b], кратных числу c.
Советы и рекомендации
Функция range(start, stop) не включает границу stop, останавливается, не доходя до неё.
Решение задачи:
a = int(input('Введите число а: '))
b = int(input('Введите число b: '))
c = int(input('Введите число с: '))
summ = 0
count = 0
for i in range(a, b +1):
if i % c == 0:
count += 1
summ += i
if count == 0:
print('Расчет невозможен, так как нет подходящих чисел')
else:
print(summ / count)( 19 оценок, среднее 3.42 из 5 )
Возможно, вы слышали выражения «средний балл за контрольную», «среднее количество осадков» или «средняя годовая температура». Этот урок посвящён среднему арифметическому: тому, что это такое, как найти среднее арифметическое натуральных чисел и дробей, и где это может пригодиться.
Знакомство со средним арифметическим
Решавр, Вообразавр и Иксератопс собирали грибы. Решавр нашёл $5$ грибов, Вообразавр – $7$, а Иксератопс целых $9$! Друзья решили разделить найденное количество грибов поровну.
Они сложили все грибы в кучку, а потом каждый взял себе равное число грибов, то есть они поделили общее количество на $3$.
$5 + 7 + 9 = 21$
$21 : 3 = 7$
То число грибов, которое получилось у каждого из друзей, будет средним арифметическим.
Среднее арифметическое нескольких чисел – это сумма этих чисел, разделённая на количество слагаемых.
Задачи на нахождение среднего арифметического натуральных чисел
Автомобиль $2$ часа ехал через город со скоростью $30$ км/ч, по пригороду час со скоростью $60$ км/час, а затем ещё $3$ часа по трассе со скоростью $100$ км/час. Вычислите среднюю скорость автомобиля.
Сначала найдём сумму всех расстояний. У нас получится $30 cdot 2 + 60 + 100 cdot 3 = 420$
Теперь разделим эту сумму расстояний на количество часов.
$$420 : 6 = 70$$
Следовательно, если бы автомобиль ехал со скоростью $70$ км/ч в течение такого же времени ($6$ часов), он проехал бы такое же расстояние.
Рассмотрим другую задачу.
Первый рабочий за рабочий день собирает $50$ деталей, второй – $44$ более сложные детали, а третий работает над самыми сложными и делает за день гораздо меньше деталей. Сколько деталей он делает, учитывая, что средняя производительность всех трёх рабочих $38$ деталей за смену?
Зная, что средняя производительность $38$, а рабочих трое, мы можем найти сумму деталей, которые они собирают за день.
$$38 cdot 3 = 114$$
Теперь просто вычтем из этого числа то, что делают первые двое рабочих и найдём количество деталей, которые делает третий.
$$114-50-44 = 20$$
Показать проверку
Скрыть
$$(50 + 44 + 20) : 3 = 114 : 3 = 38$$
Как найти среднее арифметическое десятичных дробей
Решать задачи на среднее арифметическое достаточно просто, если речь идёт о натуральных числах. Ненамного сложнее дело обстоит с десятичными дробями.
На рисунке 3 изображены три отрезка. Длина отрезка АВ $5.9$ см, отрезка CD – $7.3$ см, а отрезок EF равен среднему арифметическому первых двух отрезков. Какова длина отрезка EF?
Сложим длины отрезков АВ и CD и вычислим их среднюю длину.
$$5.9 + 7.3 = 13.2$$
$$13.2 : 2 = 6.6$$
Теперь решим задачу на нахождение слагаемых. Два кролика ели морковку, серый кролик съел в $1.4$ раза больше морковки, чем белый. Сколько морковки съел каждый, если среднее количество съеденного – $7.5$ морковок?
Начинаем «распутывать» наш пример. Если мы знаем, что среднее арифметическое двух чисел – $7.5$, значит, их сумма – $7.5 cdot 2 = 15$
Примем количество съеденного белым кроликом за $x$, тогда серый съел $1.4 cdot x$. Можно составить уравнение:
$$1.4 cdot x + x = 15$$
Вычислим, сколько съел каждый из кроликов.
Показать решение
Скрыть
Сначала найдём значение выражения.
$$1.4 cdot x + x = 2.4 cdot x = 15$$
$$x = 15 : 2.4 = 6.25$$
Мы получили число моркови, которую съел белый кролик. Теперь давайте определим, сколько съел серый.
$$6.25 cdot 1.4 = 8.75$$
Проверим наше решение, сложив количество съеденного обоими кроликами и найдя среднее арифметическое.
$$8.75 + 6.25 = 15$$
$$15 : 2 = 7.5$$
Значит, наше решение было верным.
Как найти среднее арифметическое обыкновенных дробей
Вычислять среднее арифметическое обыкновенных дробей приходится не так уж часто. Но давайте рассмотрим, как это делается.
Особенность поиска среднего арифметического обыкновенных дробей состоит в том, что нужно складывать их, а, значит, приводить к общему знаменателю.
Напомним, что приведение к общему знаменателю основывается на основном свойстве дроби, которое позволяет умножить обе части дроби на одно и то же число без изменения значения. Таким образом, мы можем найти для дробных слагаемых дополнительные множители, с помощью которых знаменатели слагаемых станут одинаковыми.
Найдём среднее арифметическое дробей $frac{2}{3}$ и $frac{4}{7}$.
Мы можем выполнить сложение только в том случае, если у обоих слагаемых будет одинаковый знаменатель. Сначала нужно понять, к какому наименьшему общему знаменателю нужно привести эти дроби. Для этого требуется найти число, которое делится и на $3$, и на $7$. Это число будет называться НОК (наименьшее общее кратное). Для чисел $3$ и $7$ это будет произведение этих чисел, $21$.
Для того чтобы вычислить дополнительные множители, нужно разделить НОК на каждый из знаменателей. Таким образом, для $3$ дополнительным множителем будет $7$, а для $7$ это будет $3$.
Умножаем обе части дроби на один и тот же дополнительный множитель.
$$frac{2}{3} = frac{2cdot 7}{3 cdot 7} = frac{14}{21}$$
$$frac{4}{7} = frac{4cdot 3}{7 cdot 3} = frac{12}{21}$$
Теперь у нас две дроби с одинаковым знаменателем, и мы можем легко их сложить.
$$frac{14}{21} + frac{12}{21} = frac{14 + 12}{21} = frac{26}{21}$$
Осталось только разделить эту сумму на число слагаемых. При делении обыкновенной дроби нужно умножить знаменатель дроби на делитель:
$$frac{26}{21} : 2 = frac{26}{21 cdot 2} = frac{26}{42}$$
Эту дробь можно сократить, разделив обе части на $2$. У нас получится $frac{13}{21}$.
Многие операции, которые мы разобрали подробно, можно сделать и устно – здесь они расписаны так только для того, чтобы немного повторить пройденный материал.
Разберём ещё пример со смешанными дробями. Найдём среднее арифметическое для дробей $2frac{1}{6}$ и $3frac{1}{15}$.
Сначала нужно перевести каждую из этих смешанные дробей в неправильную. Для этого нужно умножить целое число на знаменатель и прибавить числитель.
$$2frac{1}{6} = frac{(2 cdot 6) + 1}{6} = frac{13}{6}$$
$$3frac{1}{15} = frac{(3 cdot 15) + 1}{15} = frac{46}{15}$$
Теперь приведём эти дроби к общему знаменателю. НОК $(15$ и $6) = 30$
Теперь подбираем дополнительные множители и складываем наши дроби.
$$frac{13 cdot 5}{6 cdot 5} + frac{46 cdot 2}{15 cdot 2}$$
$$frac{65}{30} + frac{92}{30} = frac{65 + 92}{30} = frac{157}{30}$$
Мы могли бы выделить целую часть из этой дроби, но нет необходимости, так как мы не закончили вычисления. Для нахождения среднего арифметического разделим полученное число на $2$ (другими словами, умножим дробь на число, обратное делителю, в данном случае $frac{1}{2}$).
$$frac{157}{30} : 2 = frac{157}{30 cdot 2} = frac{157}{60} = 2 frac{37}{60}$$
Если мы захотим поделить $37$ на $60$, у нас получится периодическая дробь: $0.61(6) $
Если нужно записать ответ в виде десятичной дроби, то можно использовать периодическую дробь. В некоторых случаях можно округлить эту дробь, например, $0.61(6) $ приблизительно равно $0.62$
Но если в условиях не сказано, что нужна именно десятичная дробь, лучше оставить обыкновенную, так как она будет точно передавать значение выражения.
Среднее арифметическое
Онлайн калькулятор поможет найти среднее арифметическое чисел. Среднее арифметическое множества чисел (ряда чисел) — число, равное сумме всех чисел множества, делённой на их количество.
Программа вычисляет среднее арифметическое элементов массива, среднее арифметическое натуральных чисел, целых чисел, набора дробных чисел.
Формула которая используется для расчета среднего арифметического значения:
Приведём примеры нахождения среднего арифметического ряда чисел:
Среднее арифметическое двух чисел: (2+5)/2=3.5;
Среднее арифметическое трёх чисел: (2+5+7)/3=4.66667;
Среднее арифметическое 4 чисел: (2+5+7+2)/4=4;
Найти выборочное среднее (математические ожидание):
Среднее арифметическое 5 чисел: (2+5+7+2+3)/5=3.8;
Среднее арифметическое 6 чисел: (2+5+7+2+3+4)/6=3.833;
Среднее арифметическое 7 чисел: (2+5+7+2+3+4+8)/7=4.42857;
Среднее арифметическое 8 чисел: (2+5+7+2+3+4+8+5)/8=4.5;
Среднее арифметическое 10 чисел: (2+5+7+2+3+4+8+5+9+1)/10=4.6;
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также

Необходимо написать программу, которая считывает с клавиатуры числа a и b, считает и выводит среднее арифметическое всех чисел из отрезка [a; b], которые кратны 3. На вход программе подаются интервалы, внутри которых всегда есть хотя бы одно число, которое делится на 3. Решить задачу необходимо, используя циклы.
Мое первоначальное решение было таким:
| Python | ||
|
Это решение у меня проходило не все тесты, хотя вручную я пробовал проверять – и результаты совпадали. Затем я додумался, что более рационально ее решать с помощью одного цикла for, и уже внутри него искать только i % 3 == 0.
Хоть первоначальное решение и не является рациональным, я так и не понял, почему оно неверное 
Простая формула, чтобы подсчитать среднее арифметическое
О чем эта статья:
Понятие среднего арифметического
Среднее арифметическое нескольких чисел — это сумма этих чисел, которую разделили на количество слагаемых. Формула среднего арифметического, которую обычно проходят в 5 классе, выглядит так:
Потренируемся использовать формулу среднего арифметического.
Например, найдем среднее арифметическое чисел 2, 3 и 4. Обозначим среднее значение латинской буквой «m» и посчитаем сумму этих чисел.
Разделим результат на количество чисел в задании, то есть на 3, и получим ответ — 3.
Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: узнать среднюю цену товара в разных магазинах, вычислить среднюю зарплату сотрудников компании, сравнить среднюю посещаемость занятий учениками 5А и 5Б.
Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:
Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.
Примеры расчета среднего арифметического
Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.
Пример 2. Подсчитать среднее арифметическое 7,5 и 8 и 0,5.
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.
Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.
Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.
Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.
Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.
Ответ: школьник в неделю тратит в среднем 81 рубль.
Еще больше интересных практических заданий — на курсах математики в онлайн-школе Skysmart. Вводный урок — бесплатно!
Среднее арифметическое
Содержание
Возможно, вы слышали выражения «средний балл за контрольную», «среднее количество осадков» или «средняя годовая температура». Этот урок посвящён среднему арифметическому – тому, что это такое, как находится и где может пригодиться.
Знакомство со средним арифметическим
Решавр, Вообразавр и Иксератопс собирали грибы. Решавр нашёл $5$ грибов, Вообразавр – $7$, а Иксератопс целых $9$! Друзья решили разделить найденное количество грибов поровну.
Они сложили все грибы в кучку, а потом каждый взял себе равное число грибов, то есть они поделили общее количество на $3$.
То число грибов, которое получилось у каждого из друзей, будет средним арифметическим.
Среднее арифметическое нескольких чисел – это сумма этих чисел, разделённая на количество слагаемых.
Задачи на нахождение среднего арифметического
Автомобиль $2$ часа ехал через город со скоростью $30$ км/ч, по пригороду час со скоростью $60$ км/час, а затем ещё $3$ часа по трассе со скоростью $100$ км/час. Вычислите среднюю скорость автомобиля.
Сначала найдём сумму всех расстояний. У нас получится $30 cdot 2 + 60 + 100 cdot 3 = 420$
Теперь разделим эту сумму расстояний на количество часов.
Следовательно, если бы автомобиль ехал со скоростью $70$ км/ч в течение такого же времени ($6$ часов), он проехал бы такое же расстояние.
Рассмотрим другую задачу.
Первый рабочий за рабочий день собирает $50$ деталей, второй – $44$ более сложные детали, а третий работает над самыми сложными и делает за день гораздо меньше деталей. Сколько деталей он делает, учитывая, что средняя производительность всех трёх рабочих $38$ деталей за смену?
Зная, что средняя производительность $38$, а рабочих трое, мы можем найти сумму деталей, которые они собирают за день.
Теперь просто вычтем из этого числа то, что делают первые двое рабочих и найдём количество деталей, которые делает третий.
$$(50 + 44 + 20) : 3 = 114 : 3 = 38$$
Среднее арифметическое десятичных дробей
Решать задачи на среднее арифметическое достаточно просто, если речь идёт о натуральных числах. Ненамного сложнее дело обстоит с десятичными дробями.
На рисунке 3 изображены три отрезка. Длина отрезка АВ $5.9$ см, отрезка CD – $7.3$ см, а отрезок EF равен среднему арифметическому первых двух отрезков. Какова длина отрезка EF?
Сложим длины отрезков АВ и CD и вычислим их среднюю длину.
Теперь решим задачу на нахождение слагаемых. Два кролика ели морковку, серый кролик съел в $1.4$ раза больше морковки, чем белый. Сколько морковки съел каждый, если среднее количество съеденного – $7.5$ морковок?
Начинаем «распутывать» наш пример. Если мы знаем, что среднее арифметическое двух чисел – $7.5$, значит, их сумма – $7.5 cdot 2 = 15$
Примем количество съеденного белым кроликом за $x$, тогда серый съел $1.4 cdot x$. Можно составить уравнение:
$$1.4 cdot x + x = 15$$
Вычислим, сколько съел каждый из кроликов.
Сначала найдём значение выражения.
$$1.4 cdot x + x = 2.4 cdot x = 15$$
Мы получили число моркови, которую съел белый кролик. Теперь давайте определим, сколько съел серый.
$$6.25 cdot 1.4 = 8.75$$
Проверим наше решение, сложив количество съеденного обоими кроликами и найдя среднее арифметическое.
Значит, наше решение было верным.
Среднее арифметическое обыкновенных дробей
Вычислять среднее арифметическое обыкновенных дробей приходится не так уж часто. Но давайте рассмотрим, как это делается.
Особенность поиска среднего арифметического обыкновенных дробей состоит в том, что нужно складывать их, а, значит, приводить к общему знаменателю.
Напомним, что приведение к общему знаменателю основывается на основном свойстве дроби, которое позволяет умножить обе части дроби на одно и то же число без изменения значения. Таким образом, мы можем найти для дробных слагаемых дополнительные множители, с помощью которых знаменатели слагаемых станут одинаковыми.
Найдём среднее арифметическое дробей $frac<2><3>$ и $frac<4><7>$.
Мы можем выполнить сложение только в том случае, если у обоих слагаемых будет одинаковый знаменатель. Сначала нужно понять, к какому наименьшему общему знаменателю нужно привести эти дроби. Для этого требуется найти число, которое делится и на $3$, и на $7$. Это число будет называться НОК (наименьшее общее кратное). Для чисел $3$ и $7$ это будет произведение этих чисел, $21$.
Для того чтобы вычислить дополнительные множители, нужно разделить НОК на каждый из знаменателей. Таким образом, для $3$ дополнительным множителем будет $7$, а для $7$ это будет $3$.
Умножаем обе части дроби на один и тот же дополнительный множитель.
Теперь у нас две дроби с одинаковым знаменателем, и мы можем легко их сложить.
Осталось только разделить эту сумму на число слагаемых. При делении обыкновенной дроби нужно умножить знаменатель дроби на делитель:
Эту дробь можно сократить, разделив обе части на $2$. У нас получится $frac<13><21>$.
Многие операции, которые мы разобрали подробно, можно сделать и устно – здесь они расписаны так только для того, чтобы немного повторить пройденный материал.
Разберём ещё пример со смешанными дробями. Найдём среднее арифметическое для дробей $2frac<1><6>$ и $3frac<1><15>$.
Сначала нужно перевести каждую из этих смешанные дробей в неправильную. Для этого нужно умножить целое число на знаменатель и прибавить числитель.
Теперь приведём эти дроби к общему знаменателю. НОК $(15$ и $6) = 30$
Теперь подбираем дополнительные множители и складываем наши дроби.
Мы могли бы выделить целую часть из этой дроби, но нет необходимости, так как мы не закончили вычисления. Для нахождения среднего арифметического разделим полученное число на $2$ (другими словами, умножим дробь на число, обратное делителю, в данном случае $frac<1><2>$).
Если мы захотим поделить $37$ на $60$, у нас получится периодическая дробь: $0.61(6) $
Если нужно записать ответ в виде десятичной дроби, то можно использовать периодическую дробь. В некоторых случаях можно округлить эту дробь, например, $0.61(6) $ приблизительно равно $0.62$
Но если в условиях не сказано, что нужна именно десятичная дробь, лучше оставить обыкновенную, так как она будет точно передавать значение выражения.
Урок по математике”Среднее арифметическое чисел”
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Урок по математике 5 класс (учебник Виленкина)
Дидактическая цель урока: познакомить с решением обратных задач, учить находить среднее арифметическое.
I. Организационный момент
1. Индивидуальная работа у доски
Задание 1. найдите среднее арифметическое чисел
18,3; 43,5; 32,1 (31,3)
Задание 2. найдите значение выражения
Задание 3. Решите уравнение
8х – 3,2 = 5,6 (х = 1.1)
2. Фронтальная работа (учащиеся работают вместе с учителем)
(Учитель показывает карточки с заданием, учащиеся называют ответ, возможно использование слайдов презентации)
(6.45 – 5,79) 0
7,59 0,1
3. Взаимопроверка в парах
4. Решите задачу
В киоске продаются три вида шоколадок и пять сортов мороженого. Сколькими разными способами можно купить шоколадку и мороженое?
– что это за задача? Докажите.
– Сколько различных вариантов мороженого можно выбрать для первой шоколадки? (5)
– Для второй? Третьей?
– Сколько же различных способов выбора существует? (3 5 = 15)
III. Определение темы урока
3.5; 3.7; 4,2 60; 65; 85 1.8; 2,5; 6,8
– Какое задание можно придумать для этих чисел?
(Учащиеся могут предложить разные варианты заданий для этих чисел, учитель выбирает для выполнения самые интересные, например найти среднее арифметическоедля этих чисел)
– Что такое среднее арифметическое?
– Сформулируйте тему урока.
IV. Работа по теме урока
1. Найти среднее арифметическое чисел
(3,5 + 3,7 + 4,2) : 3 = 3,8
(60 + 65 + 85) : 3 = 70
(1,8 + 2,5 + 6,8) : 3 = 3,7
– Расскажите, как найти среднее арифметическое нескольких чисел.
2. Найти среднее арифметическое чисел (работа в парах)
25,6; 28,7; 14,4; 12,8
32,7; 14,84; 15,3; 21,6
Проверка (взаимопроверка, работа в парах)
(25,6 + 28,7 + 14,4 + 12,8) : 4 = 20,375
(2,8 + 42,3 + 7,4 + 16,5) : 4 = 17,25
(32,7 + 14,84 + 15,3 + 21,6) : 4 = 21,1
– Подумайте, что следует из равенства отрезков АВ и ВС. (Координата точки В является средним арифметическим координат двух других точек)
– Чему равна координата точки С ? (10, 1)
4. Ответьте на вопросы.
– Как вычислить среднее арифметическое? (Среднее арифметическое = сумма слагаемых : количество слагаемых)
– Как найти сумму чисел? (сумма слагаемых = Среднее арифметическое количество слагаемых)
– Как найти количество слагаемых ? (количество слагаемых = сумма слагаемых : среднее арифметическое)
– Как можно назвать эти задачи по отношению друг к другу? (Обратные)
– Какая это задача?
– Можем ли мы найти сумму этих двух чисел, если известно среднее арифметическое?
– Как это сделать?
– Теперь можем ответить на вопрос задачи?
1) 3,1 2 = 6,2 – сумма двух чисел
2) 6,2 – 3,8 =2,4 – второе число
– Подумайте, можно ли решить эту задачу алгебраически?
– Что следует обозначить через х?
Тогда среднее арифметическое этих чисел будет (х + 3,8) : 2.
А по условию среднее арифметическое равно 3,1
Значит можем составить уравнение:
х + 3,8 = 3,1 2
х = 2,4 – второе число.
– Какое решение вам понравилось больше?
– Какой путь решения выберем? (Алгебраический)
– Что обозначим через х?
Пусть меньшее число будет х.
Тогда второе число будет 1,5 х.
Среднее арифметическое этих чисел (х + 1,5 х) : 2
А по условию среднее арифметическое равно 30.
Значит, можем состамить уравнение
2,5х = 30 2
х = 24 – меньшее из чисел
24 1,5 = 36 – второе число
VI . Повторение изученного материала
3,5х – 2.3х + 3,8 = 4.28 4,7у – (2,5у + 12,4) = 1,9
Ответ: 0,4 Ответ: 6,5
VII . Самостоятельная работа
1000 : 0,01 = 100 000
– Как найти сумму чисел, если известны среднее арифметическое и количество слагаемых?
– Как вы оцениваете себя на этом уроке?
– А как вы оцениваете своего товарища, который работал с вами в паре?
С.230, № 1528, 1532, 1534 (б).
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 945 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 687 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 315 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 593 153 материала в базе
Материал подходит для УМК
«Математика (в 2 частях)», Виленкин А.Н., Жохов В.И., Чесноков А.С. и др.
34. Умножение десятичных дробей на натуральные числа
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 17.01.2022
- 270
- 5
- 17.01.2022
- 100
- 0
- 17.01.2022
- 36
- 0
- 17.01.2022
- 50
- 1
- 17.01.2022
- 100
- 11
- 17.01.2022
- 67
- 0
- 17.01.2022
- 36
- 0
- 17.01.2022
- 68
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 17.01.2022 81
- DOCX 24 кбайт
- 0 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Вершинина Татьяна Ивановна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 4 месяца
- Подписчики: 0
- Всего просмотров: 15814
- Всего материалов: 17
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Курские власти перевели на дистант школьников в районах на границе с Украиной
Время чтения: 1 минута
В приграничных пунктах Брянской области на день приостановили занятия в школах
Время чтения: 0 минут
Школьник из Сочи выиграл международный турнир по шахматам в Сербии
Время чтения: 1 минута
Каждый второй ребенок в школе подвергался психической агрессии
Время чтения: 3 минуты
В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной
Время чтения: 0 минут
В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
[spoiler title=”источники:”]
http://obrazavr.ru/matematika/5-klass-matematika/desyatichnye-drobi/srednee-arifmeticheskoe/srednee-arifmeticheskoe-2/
http://infourok.ru/urok-po-matematike-srednee-arifmeticheskoe-chisel-5680715.html
[/spoiler]