Как найти среднее арифметическое по физике

Среднее арифметическое значение, средняя квадратичная и средняя арифметическая погрешности измеряемой величины

Первой величиной,
которую приходится вычислять при
обработке результатов опытов, является
среднее арифметическое из результатов
ряда измерений, которое определяется
по формуле (6).

Практически число
измерений всегда ограничено, поэтому
среднее арифметическое
не равно
истинному значению измеряемой величины
,
но будет
тем ближе к нему, чем больше число
выполненных измерений .
В теории
вероятностей доказывается, что среднее
арифметическое из результатов отдель­ных
измерений является наиболее вероятным
значением измеряемой величины. Это
утверждение справедливо при условии,
когда все
измерения равноточные, а распределение
погрешности измерений подчиняется
вышеупомянутому закону распределения—
закону Гаусса.

Если вместо
истинного значения неизвестной величины
использовать среднее арифметическое
,
тогда на
основании равенства (1) имеем:

(11)

В (11) погрешность
несколько
отличается от истинной и называется
абсолютной погрешностью единичного
измерения

(12)

Лучшим из критериев
для оценки погрешностей результатов
измерений является средняя квадратичная
погрешность, которая характеризует
степень (меру) рассеяния результатов
отдельных измерений
около среднего
их значения. Для определения
среднеквадратической погрешности
единичных изме­рений при ограниченном
числе опытов используется формула (7),
которая с учетом (12) записывается в виде:

. (13)

Средняя квадратическая
погрешность, вычисляемая по формуле
(13), характеризует погрешность единичного
результата из всего ряда n
измерений.

Как уже отмечалось,
при увеличении числа n
измерений наблюдается взаимная
компенсация случайных ошибок. Поэтому
усредненная средняя квадратичная
погрешность,
определяемая по формуле (9) и характеризующая
окончательный результат измерений,
уменьшается при увеличении числаn
повторных
измерений искомой величины. Поскольку
вычисления величины
достаточно громоздки, то в ряде случаев
(если не оговорено в условиях решаемой
задачи) для оценки ошибки, допущенной
при определении средней величины,
пользуются средней арифметической
погрешностью, которая вычисляется как
средняя величина всех величин абсолютных
погрешностей единичных измерений (12),
взятых по модулю:

.
(14)

Так как суммирование
в (14) выполняется без учета знака ,
то формула (14) даёт среднее значение
максимальной возможной погрешности.

Вопрос о том, какой
формулой пользоваться при оценке
измерений, решается при планировании
эксперимента. Считается, что при числе
измерений меньше пяти можно ограничиться
вычислением средней абсолютной
погрешности по формуле (14).

Средняя абсолютная
погрешность даёт возможность указать
пределы (интервал), внутри которых
заключено истинное значение измеряемой
величины.

Сама по себе
абсолютная погрешность не даёт достаточно
наглядного представления о степени
точности измерения, поэтому для оценки
точности результата применяется
относительная погрешность. Относительная
погрешность величины x
при ограниченном числе опытов вычисляется
по формуле:

.
(15)

Как найти среднее значение чисел?

Среднее значение Это арифметическое и вычисляется путем с добавления группы чисел и деления на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6. Медиана Среднее число числа.

Что такое среднее значение в физике?

В теории вероятностей и статистике

среднее значение случайной величины — то же, что математическое ожидание случайной величины. По сути — среднее значение её функции распределения.

Как рассчитать среднее значение между двумя числами?

Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.

Как рассчитать среднее значение в Excel?

Ставим курсор в ячейку А2 (под набором чисел). В главном меню – инструмент «Редактирование» — кнопка «Сумма». Выбираем опцию «Среднее». После нажатия в активной ячейке появляется формула.

Как найти среднее значение за месяц?

Первым способом является вычисление уже упомянутого среднего арифметического, являющегося суммой всех значений, деленной на их количество.

1. x – среднее арифметическое;
2. xn – конкретное значение;
3. n – количество значений .

Как найти среднее значение в ворде?

Чтобы вычислить среднее арифметическое в строке или столбце, ставим курсор в их последнюю ячейку, открываем окно «Формула» («Работа с таблицами» — вкладка «Макет» — раздел «Данные» — кнопка «Формула»).

Как посчитать медиану?

Медианой (серединой) набора чисел называется число стоящее посередине упорядоченного по возрастанию ряда чисел. Если количество чисел в ряду чётное, то медианой ряда является полусумма двух стоящих посередине чисел.

Как вывести среднее значение?

Чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму на их количество.

Как найти среднее значение показателя?

В математике среднее арифметическое — это среднее число, которое получается, если сложить несколько чисел и разделить результат на количество этих чисел. Это не единственный способ вычисления среднего числа, но именно о нем большинство людей думает, когда речь идет о среднем.

Как найти среднее значение скорости?

Чтобы найти среднюю скорость, нужно разделить весь путь, пройденный объектом, на все время его движения.

Что такое среднее значение величины?

Среднее значение — Среднее значение числовая характеристика множества чисел или функций; некоторое число, заключённое между наименьшим и наибольшим из их значений.

Что такое среднее значение в математике пример?

Среднее арифметическое – это частное от деления суммы чисел на их количество. Пример 1. Найти среднее арифметическое двух чисел: 4 и 6.

Что такое среднее арифметическое значение?

Средним арифметическим нескольких чисел называют сумму этих чисел, делённую на количество слагаемых. Среднее арифметическое = сумма всех чисел количество слагаемых .

Среднее арифметическое: физический смысл и визуализация

Переменная величина – атрибут (свойство) системы, меняющий свое числовое значение. Множество значений переменой величины может иметь вид:

Человек анализирует числовые данные такого рода и принимает решения. Знание температуры воздуха помогает правильно одеться. Курс валюты говорит покупать ее или продавать.

Когда значений одно или несколько, то никаких трудностей не возникает. Но когда значений десятки или сотни, то человеку сложно сразу понять, что означают полученные данные. На помощь приходят интегральные характеристики множеств значений и визуализация.

Одна из интегральных характеристик множества значений переменной величины – среднее арифметическое. Посмотрим на него с точки зрения статистики, физики (механики) и эстетики.

Среднее арифметическое двух чисел

Начнем с минимального набора чисел, для которых можно подсчитать среднее арифметическое. Вот два числа:

Их среднее арифметическое:

Два наблюдения:

• Среднее арифметическое находится посередине двух чисел (больше меньшего, но меньше большего).
• Среднее арифметическое не всегда входит в анализируемый набор чисел (не равно ни одному из двух чисел).

Физический смысл среднего арифметического

Изобразим два исходных числа и их среднее арифметическое на числовой оси:

Числа помечены черными кружками, а среднее арифметическое красным треугольником. Полученная конструкция – это весы. Для весов в равновесии правило рычага требует, чтобы моменты сил были равны. Весы не наклоняются ни в одну, ни в другую сторону, так как крутящий момент отсутствует.

В механике момент силы – это произведение силы F на расстояние l:

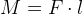
На плечи весов действует сила, создаваемая весом точек-“грузов”. Обозначив расстояния от грузов до точки опоры l₁ и l₂, получим:

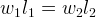
Точки-“грузы” отличаются только координатой на оси. Будем считать их вес одинаковым. Тогда:

Обозначив m координату точки опоры весов, получим:

Аналогично из формулы равенства моментов для произвольного количества N точек-“грузов” с одинаковым весом w выводится формула среднего арифметического. Равенство моментов для обоих плеч весов:

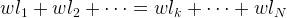
Координата опоры весов m:

Формула среднего арифметического дает координату точки опоры весов, находящихся в равновесии.

Визуальное восприятие равновесия

Равновесие в изобразительном искусстве играет важнейшую роль. Если при создании картины не достигнуто равновесие ее элементов, то произведение не будет законченным. В каждой картине художник создает равновесие различных визуальных сил.

Рудольф Арнхейм отмечает, что человеческое зрение способно обнаруживать малейшие отклонения от центра равновесия в изображении:

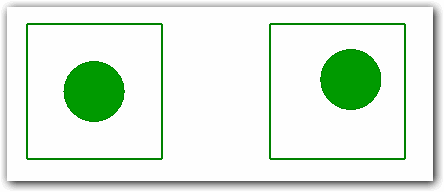
На приведенном примере слева круг находится в состоянии равновесия, а справа нет. Несмотря на то, что точка равновесия (центр квадрата) никак не отмечена на рисунке, человек с большой точностью может определить, находится ли круг в этой точке или нет.

Несмотря на то, что точка равновесия может быть не изображена, человек воспринимает ее как часть визуальной структуры:

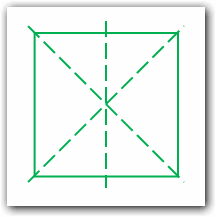
Аналогично и среднее арифметическое: необязательно входит в набор чисел, но значимо для его восприятия и оценки.

Математическое ожидание случайной величины

Для случайной величины аналогом среднего арифметического служит математическое ожидание. Вероятность при этом можно считать весом точки-“груза”. Формула равенства моментов с разными весами:

Теперь точка опоры весов в равновесии это μ:

Сумма всех вероятностей равна 1. Следовательно, и сумма весов равна 1. Тогда формула координаты точки весов в равновесии равна:

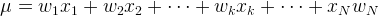
Это и есть формула математического ожидания.

Гистограмма

Гистограмма – это визуализация (геометрическое изображение) значений переменной величины с учетом вероятностей. Гистограмма показывает для выборки значений, какие из них появляются часто, какие реже, а какие совсем редко.

На гистограмме возможные значения откладываются по горизонтальной оси, а веса – по вертикальной. Диапазон значений по вертикали очевиден – от 0 до 1 (значения вероятности). По горизонтали диапазон должен включать ожидаемые значения переменной.

Гистограмма представляет собой простую картину (экземпляр изобразительного искусства). Зритель ожидает, что точка равновесия множества значений будет ровно посередине гистограммы:

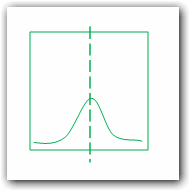
Исходя из этого должен подбираться диапазон значений для горизонтальной оси гистограммы. Тогда сразу будет видно отклонение свойств выборки значений от ожидаемых:

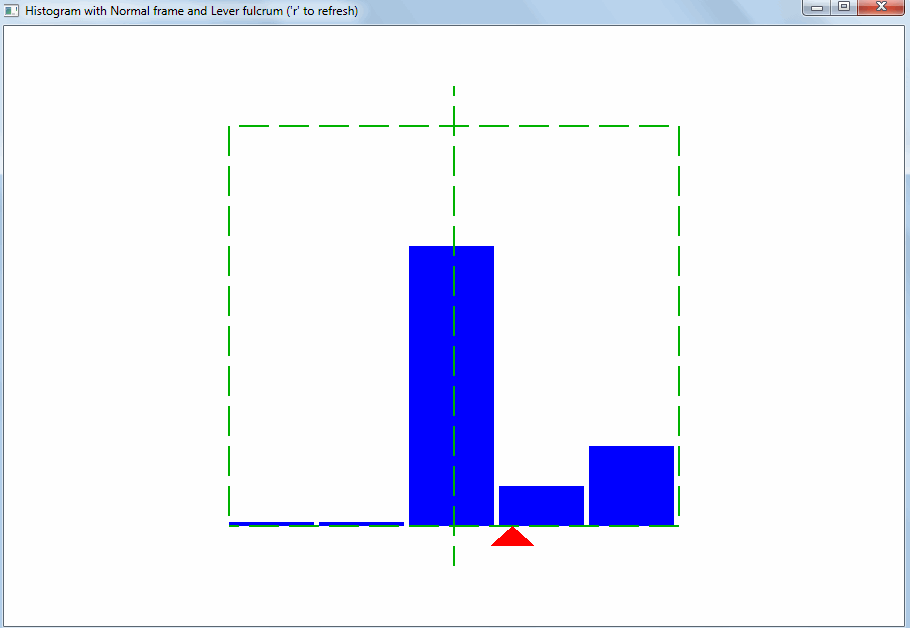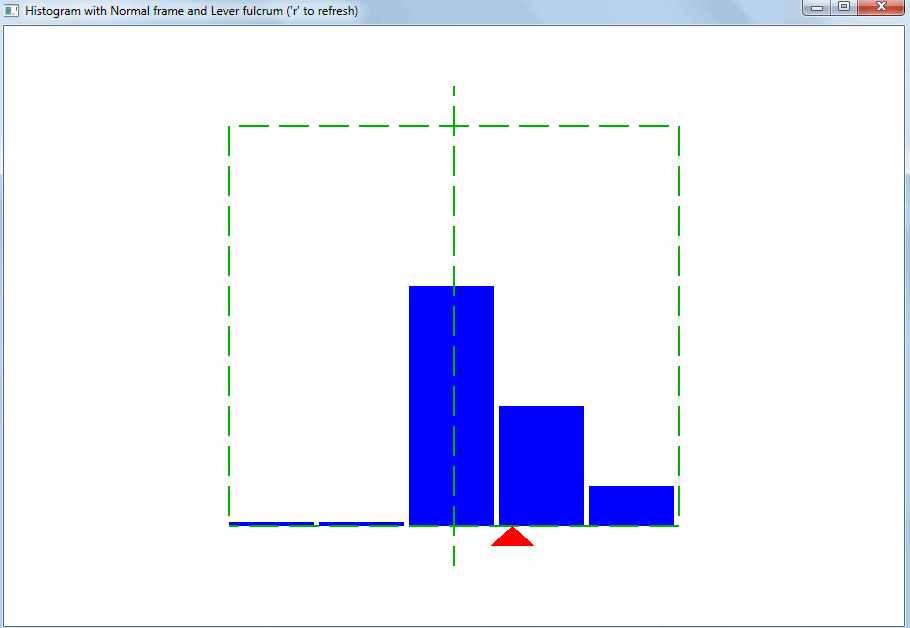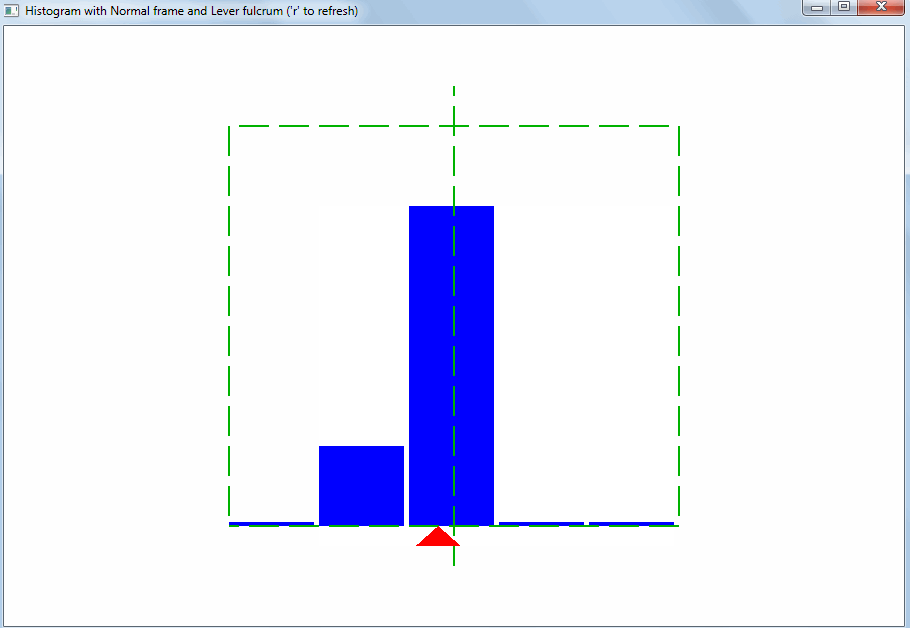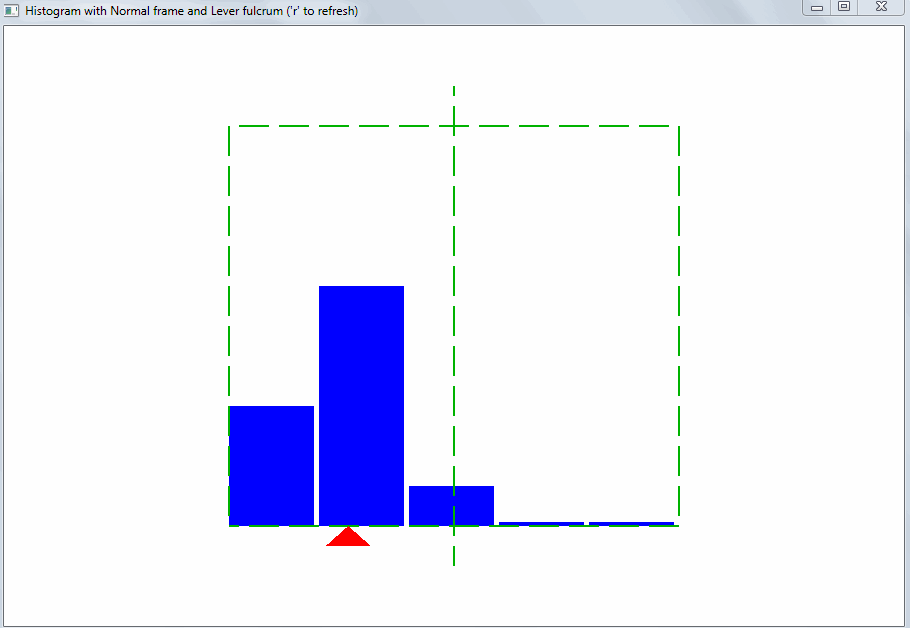
Такого рода отклонение может быть вызвано выбросами. Выбросы – это значения, сильно отличающиеся от остальных. Благодаря правилу рычага, даже небольшое количество выбросов меняет точку равновесия и среднее арифметическое:

Дайте мне точку опоры, и я переверну Землю. Архимед

Выводы

• Среднее арифметическое – интегральная характеристика набора числовых данных (выборки). Применяется как описательная характеристика в совокупности с другими.
• Нормально, что среднее значение не входит в набор данных. Среднее арифметическое не может заменить полное описание полученной выборки.
• Интервал значений гистограммы должен быть подобран таким образом, чтобы ожидаемое среднее арифметическое было посередине. Тогда будет сразу видно отклонение параметров выборки от ожидаемых значений.
• Среднее арифметическое подвержено влиянию выбросов – значений, сильно отличающихся от остальных значений переменной величины.

Ссылки

• Wikipedia: Переменная величина, Моменты в статистике и механике, Момент силы, Математическое ожидание
• Рудольф Арнхейм. Искусство и визуальное восприятие: фрагменты
• Демонстрация гистограммы, ожидаемого среднего и среднего выборки: исходный код для PyOpenGL

Нередко,  при решении задач по физике, ученики путают (а если точнее не знают вообще отличий) среднюю и среднеарифметическую скорости. Сегодня внесём ясность в эти определения, выучим их и будем применять при решении задач.

Вспомним определение, которое вводится ещё при изучении математики в 5 классе – среднее арифметическое. Среднее арифметическое  чисел Х₁ , Х_{2 ,} Х₃, … Х_n – есть отношение суммы этих чисел к числу слагаемых. 

Х_ср   = (Х₁ + Х₂ +Х₃ + ….. + Х_n)/n.

Задача 1.

Гоночную трассу первый  автомобиль прошёл со скоростью 120 км/ч, второй – со скоростью 131 км/ч, а третий – со скоростью 115 км/ч. Рассчитайте среднеарифметическую скорость команды.

Решение.

ϑ_ср  = (120 км/ч + 131 км/ч + 115км/ч)/3 = 122 км/ч.

Ответ:  ϑ_ср = 122 км/ч.

Теперь перейдём к понятию средняя скорость движения.

Средняя скорость – физическая величина, численно равная отношению всего пути, пройденного  телом ко всему времени движения.

 <ϑ> = весь путь / все время

Задача 2.

Путешественник проехал 8 км со скорость 16 км/ч, затем, у него был 30 минут привал, а оставшиеся 15 км он проехал со скорость 10 км/ч. Рассчитайте среднюю скорость путешественника на всём участке пути.

Решение.

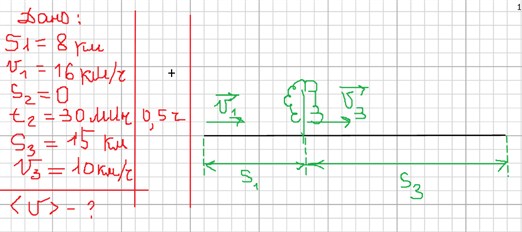Предварительно надо рассчитать время t₁ и  t₃ .

t₁ = S₁/ϑ₁ = 8 км / 16 км/ч = 0,5 ч,  t₃ = S₃/ϑ₃ = 15 км / 10 км/ч = 1,5 ч.

<ϑ> = (S₁ + S₂ + S₃ ) / t₁ + t₂ + t₃ = (8 км + 0 + 15 км) / 0,5 ч + 0,5 ч + 1,5 ч =  23 км / 2,5 ч = 9,2 км/ч.

Ответ: <ϑ>= 9,2 км/ч.

Как видим, нет ничего сложного в этих определениях и формулах. Необходимо только внимательно прочитать статью и выучить эти формулы и определения. Удачи!

Остались вопросы? Не знаете, как решить задачу по физике?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Сегодня разберем с вами очередной сложный момент, который ломает мозг не только ученикам 9-11 класса, но и студентам, которые запустили тему кинематики и подзабыли основные определения…

Средняя скорость в физике — один из подвохов, на котором попадаются учащиеся. По аналогии со средним арифметическим школьники и студенты частенько просто берут, складывают, делят пополам. Но в задачах по физике и математике на среднюю скорость так работает далеко не всегда. Предлагаю вам подумать над тем, почему не всегда работает среднее арифметическое двух скоростей, если у нас есть первая половина пути, где тело двигалось с постоянной скоростью v₁ и есть вторая половина пути, на которой тело двигалось с постоянной скоростью v₂. Почему средняя скорость на всём пути не равна среднему арифметическому ? Свой ответ напишите в комментариях. А сегодня мы рассматрим более интересную и редко встречающуюся задачку.

А пока прошу вас подписаться на мой канал в telegram IT mentor. Там я делюсь более короткими постами, рассказываю некоторые интересные случаи из жизни, непосредственно связанные с физикой, математий и IT.

Задача

Двигаясь равноускорено по прямой из состояния покоя, тело проходит некоторый путь. Чему равно отношение средней скорости тела на второй половине пути к средней скорости на первой половине пути?

Попробуйте на этом этапе остановиться, взять черновик с карандашом и решить задачку самостоятельно. Ваши ответы, комментарии, идеи и мнение о задаче обязательно напишите в комментариях. Так я лучше понимаю что интересно моим дорогим читателям 🤗

Решение:

Сделаем небольшой рисунок, уточняющий что происходит в задаче:

Для начала определим средние скорости на каждой части. Уже в этой части задачи нужно кое-что понимать. Обычно, под средней скоростью подразумевают именно среднюю путевую скорость. В то же время есть и просто средняя скорость. И две эти величины, в общем случае, отличаются. Давайте вспоминать определения.

Средняя путевая скорость — это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден.

Средняя скорость — это скорость, определяемая отношением перемещения (S) при неравномерном движении к промежутку времени, за который это перемещение произошло.

Чувствуете подвох? Просто средняя скорость вполне может обнулиться, если вы попадете в момент, когда перемещение становится нулевым. В круговом движении или периодических колебаниях это реализуемо. А вот средняя путевая скорость всегда величина ненулевая, если тело прошло хоть какое-то расстояние. В нашей задаче будем иметь в виду именно среднюю путевую скорость.

1 способ

Средняя скорость на первой половине пути:

Здесь учитывается, что тело стартует с нулевой начальной скоростью.

Средняя скорость на второй половине пути:

Здесь уже учитывается, что начальная скорость для этого участка ненулевая. И находится она из времени разгона на предыдущем участке. Конечная скорость первого участка есть начальная скорость для второго участка. В полученном квадратном уравнении относительно нужного нам момента времени, корень будем выбирать заведомо положительный, т.к. нелогично предполагать, что время получится отрицательной величиной):

Отсюда средняя скорость на данном участке получается:

А теперь мы можем посчитать конечное отношение средней скорости на второй части пути к средней скорости на первой части пути:

Итак, у нас появился первый ответ на задачу. Логичный ли он? Похож ли на правду? А может нам второй способ бахнуть? 😎

2 способ

Хотите второй способ решения задачи? Для любителей хардкорных формул математического анализа я приведу альтернативное решение.

Мы помним общую формулу скорости для движения с постоянным ускорением:

Интегральное обобщенное определение средней скорости можно записать в виде:

Определим моменты времени t₁ и t₂ :

Получили точно такой же ответ, какой был в первом способе решения задачи. Задача решена. И похоже, что решена верно 😊

Краткое решение двумя способами

Какой способ решение вам больше понравился? Напишите в комментариях!

Понравилась статья? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂

Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в telegram