Как найти среднее арифметическое положительных элементов матрицы

const
  n=10;
  m=20;
var
  a: array[1..n,1..m] of integer;
  b: array[1..n] of integer;
  i,j,sum,k: integer;
begin
  randomize;
  writeln('Матрица:');
  for i:=1 to n do
  begin
    for j:=1 to m do
    begin
      a[i,j]:=random(199)-99;
      write(a[i,j]:4);
    end;
    writeln;
  end;
  writeln;
  
  for i:=1 to n do
  begin
    sum:=0; k:=0;
    for j:=1 to m do
      if a[i,j]>0 then
      begin
        inc(k);
        sum:=sum+a[i,j];
      end;
    if k=0 then writeln('В ',i,'-й строке нет положительных элементов.')
      else writeln('В ',i,'-й строке среднее арифметическое = ',sum/k:0:2);
  end;
  readln;
end.

Основные алгоритмы и их реализация на Python

2.4 Обработка двумерных массивов (матриц)

Двумерные массивы являются аналогами матриц и имеют «прямоугольную» (табличную) структуру. Описываются массивы так же, как одномерные. Разница состоит в том, что у элемента двумерного массива две координаты (два индекса) — номер строки и номер столбца, в которых находится элемент.

Ввод массива осуществляется построчно при помощи двух циклов. Пусть — количество столбцов, — количество строк. Элементы массива обозначим как mas[i, j] , первый индекс — номер строки, второй — номер столбца.

Вывод массива на экран осуществляется при помощи аналогичных циклов.

Здесь «пустой» оператор вывода обеспечивает переход на новую строку.

В Python для работы с многомерными (когда используется два и более индексов) массивами можно использовать вложенные списки (списки списков, списки списков списков и т. д.).

Однако Python предоставляет более удобный инструмент создания и преобразования многомерных массивов — библиотеку numpy (Numeric Python).

Создание двумерного массива в Python может выглядеть так:

Сначала с помощью функции (метода) numpy.zeros() создаётся двумерный массив (матрица), заполненный нулями, а потом вместо нулей подставляются реальные значения. Индексы элементов, так же как в строках, кортежах и списках, начинаются с 0 (первый — верхний левый — элемент матрицы в Python имеет индекс [0,0]). Оператор print выводит индексы очередного элемента матрицы, который нужно ввести.

Задача 1. Выполнить обработку элементов прямоугольной матрицы , имеющей строк и столбцов. Найти среднее арифметическое элементов массива.

• — количество строк в массиве;
• — количество столбцов в массиве;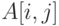
• — элемент массива;
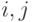• — индексы элемента массива.

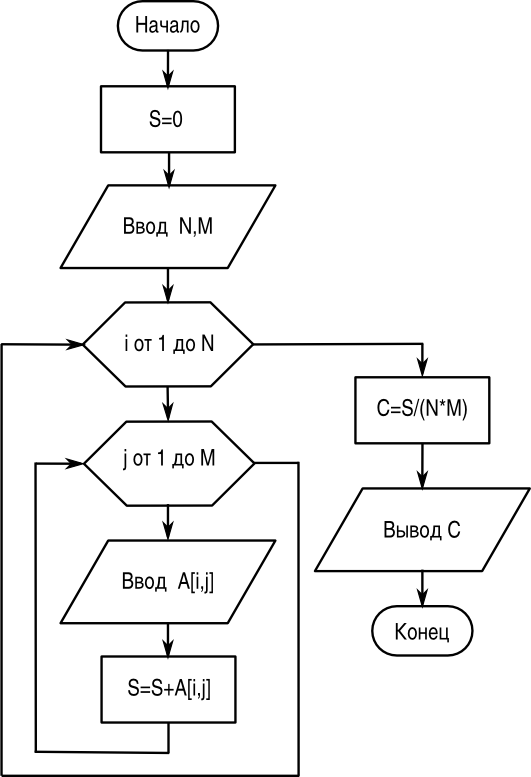
Блок-схема алгоритма решения показана на рис. 2.15.

Текст программы на «псевдоязыке»:

Текст программы на Python:

print ‘Среднее значение по строкам:’,C

Источник

Основные алгоритмы и их реализация на Python

2.4 Обработка двумерных массивов (матриц)

Двумерные массивы являются аналогами матриц и имеют «прямоугольную» (табличную) структуру. Описываются массивы так же, как одномерные. Разница состоит в том, что у элемента двумерного массива две координаты (два индекса) — номер строки и номер столбца, в которых находится элемент.

Ввод массива осуществляется построчно при помощи двух циклов. Пусть — количество столбцов, — количество строк. Элементы массива обозначим как mas[i, j] , первый индекс — номер строки, второй — номер столбца.

Вывод массива на экран осуществляется при помощи аналогичных циклов.

Здесь «пустой» оператор вывода обеспечивает переход на новую строку.

В Python для работы с многомерными (когда используется два и более индексов) массивами можно использовать вложенные списки (списки списков, списки списков списков и т. д.).

Однако Python предоставляет более удобный инструмент создания и преобразования многомерных массивов — библиотеку numpy (Numeric Python).

Создание двумерного массива в Python может выглядеть так:

Сначала с помощью функции (метода) numpy.zeros() создаётся двумерный массив (матрица), заполненный нулями, а потом вместо нулей подставляются реальные значения. Индексы элементов, так же как в строках, кортежах и списках, начинаются с 0 (первый — верхний левый — элемент матрицы в Python имеет индекс [0,0]). Оператор print выводит индексы очередного элемента матрицы, который нужно ввести.

Задача 1. Выполнить обработку элементов прямоугольной матрицы , имеющей строк и столбцов. Найти среднее арифметическое элементов массива.

• — количество строк в массиве;
• — количество столбцов в массиве;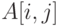
• — элемент массива;
• — индексы элемента массива.

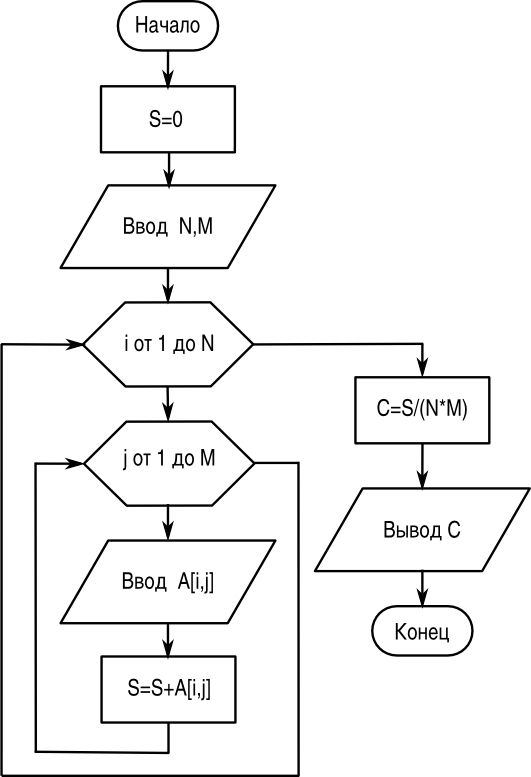
Блок-схема алгоритма решения показана на рис. 2.15.

Текст программы на «псевдоязыке»:

Текст программы на Python:

print ‘Среднее значение по строкам:’,C

Источник

Находить среднее арифметическое и минимальное значение элементов каждой строки матрицы, до выполнения условия. Блок-схема.

Здравствуйте.
Мне по информатикке задали написать алгоритм и блок схему.
Написать алгоритм и составить блок схему.
Дана матрица A с 3 столбцами и 7 строками. Начиная с первой строки находить и печатать среднее арифметическое элементов каждой строки и минимальное значение из значений элементов строки, заканчивая цикл, если разница среднего и минимального из элементов очередной строки оказалась больше заданого значения T.

Впринципе ничего сложного, но я запутался в 1 месте.
Алгоритм я составил на подобии:
1) Ввод матрицы A(i, j) /в конкретном задании A(3, 7)/, ввод ограничения Т, ввод переменных sred для среднего арифметического, min для минимального значения из значений элементов строки, sum /думаю понадобится для подсчета среднего арифметического/.

2) В заданном цикле искать среднее арифметическое каждой строки, начиная с первой, и минимальный элемент этой строки;
Вывод их на печать (или на экран);
После чего сравнить разницу среднего и минимального с введенным ранее ограничением Т.
Если разница меньше или равна Т, то переход на след строку;
Если разница больше T, то закончить цикл и выйти из программы.

Проблема заключается в блок схеме. У меня не получается составить правильный код программы (С++, Delphi, Basic — не важно) с последовательностью формул, чтобы правильно составить блок схему.

Если кто сможет помоч заранее благодарен!

Пример блок схемы:
написать алгоритм и составить блок схему для выражения:
S = X+X^3 / 3! + x^5 / 5! + . + x^(2n + 1) / (2n + 1)!

правда на етой блок схеме считается значение для 1 X, а не как в задании сумма X, но принцип построения тот же.

Вычислить среднее арифметическое значение положительных элементов каждой строки матрицы
нуждаюсь в помощи , кому не сложно помогите пожалуйста 1) для заданного массива А(4,6) вычислить.

Напечатать матрицу, минимальное значение каждой строки, среднее арифметическое каждого столбца
Создайте матрицу (5 строк, 7 столбцов), которая содержит двузначное случайное число (размер.

Найти среднее арифметическое элементов каждой строки матрицы Q (lm) и отнять его от элементов этой строки. размер матрицы 7х7.заранее спасибо
Найти среднее арифметическое элементов каждой строки матрицы Q (lm) и отнять его от элементов этой.

Найти среднее арифметическое значение каждой строки матрицы
Помогите пожалуйста. дана матрица H= размером (p x q). p=3; q=5; Найти среднее арифметическое.

Источник

Примеры алгоритмов обработки матрицами

Алгоритмы обработки матриц

Матрица— это двумерный массив, каждый элемент которого имеет два индекса: номер строки — i; номер столбца — j. Поэтому для работы с элементами матрицы необходимо использовать два цикла. Если значениями параметра первого цикла будут номера строк матрицы, то значениями параметра второго — столбцы (или наоборот). Обработка матрицы заключается в том, что вначале поочередно рассматриваются элементы первой строки (столбца), затем второй и т.д. до последней. Рассмотрим основные операции, выполняемые над матрицами при решении задач.

Алгоритм ввода-вывода матриц

Матрицы, как и массивы, нужно вводить (выводить) поэлементно. Блок-схема ввода элементов матрицы изображена на рис. 4.1. Вывод матрицы организуется аналогично вводу.

Рассмотрим несколько задач обработки матриц. Для их решения напомним читателю некоторые свойства матриц (рис. 4.2):

• если номер строки элемента совпадает с номером столбца (i = j), это означает что элемент лежит на главной диагонали матрицы;
• если номер строки превышает номер столбца (i > j), то элемент находится ниже главной диагонали;
• если номер столбца больше номера строки (i n.

Примеры алгоритмов обработки матрицами

ПРИМЕР 4.1. Найти сумму элементов матрицы, лежащих выше главной диагонали (рис 4.3).

Рис. 4.3. Рисунок к условию задачи из примера 4.1

Алгоритм решения данной задачи (рис. 4.4) построен следующим образом: обнуляется ячейка для накапливания суммы (переменная S). Затем с помощью двух циклов (первый по строкам, второй по столбцам) просматривается каждый элемент матрицы, но суммирование происходит только в том случае если, этот элемент находится выше главной диагонали, то есть выполняется свойство i

ПРИМЕР 4.2. Вычислить количество положительных элементов квадратной матрицы, расположенных по ее периметру и на диагоналях. Напомним, что в квадратной матрице число строк равно числу столбцов.

Прежде чем преступить к решению задачи рассмотрим рисунок 4.6, на котором изображена схема квадратных матриц различной размерности. Из условия задачи понятно, что не нужно рассматривать все элементы заданной матрицы. Достаточно просмотреть первую и последнюю строки, первый и последний столбцы, а так же диагонали. Все эти элементы отмечены на схеме, причем черным цветом выделены элементы, обращение к которым может произойти дважды. Например, элемент с номером (1,1) принадлежит как к первой строке, так и к первому столбцу, а элемент с номером (N,N) находится в последней строке и последнем столбце одновременно. Кроме того, если N — число нечетное (на рисунке 4.6 эта матрица расположена слева), то существует элемент с номером (N/2+1, N/2+1), который находится на пересечении главной и побочной диагоналей. При нечетном значении N (матрица справа на рис. 4.6) диагонали не пересекаются.

Рис. 4.6. Рисунок к условию задачи из примера 4.2

Итак, разобрав подробно постановку задачи, рассмотрим алгоритм ее решения. Для обращения к элементам главной диагонали вспомним, что номера строк этих элементов всегда равны номерам столбцов. Поэтому, если параметр i изменяется циклически от 1 до N, то Ai,i — элемент главной диагонали. Воспользовавшись свойством, характерным для элементов побочной диагонали получим: i+j-1 = n > j = n-i+1, следовательно, для i=1,2,…,n элемент Аi,n-i+1 — элемент побочной диагонали. Элементы, находящиеся по периметру матрицы записываются следующим образом: А1,i — первая строка, АN,i — последняя строка и соответственно Аi,1 — первый столбец, Аi,N — последний столбец.

Блок-схема описанного алгоритма изображена на рис. 4.7. В блоке 1 организуется цикл для обращения к диагональным элементам матрицы. Причем в блоках 2-3 подсчитывается количество положительных элементов на главной диагонали, а в блоках 5-6 на побочной. Цикл в блоке 6 задает изменение параметра i от 2 до N-1. Это необходимо для того, чтобы не обращать к элементам, которые уже были рассмотрены: A₁₁, A_1N, A_N,1 и A_N,N. Блоки 7-8 подсчитывают положительные элементы в первой строке, 9 и 10 — в последней строке, 11 и 12 — в первом столбце, а 13 и 14 в последнем. Блок 15 проверяет, не был ли элемент, находящийся на пересечении диагоналей, подсчитан дважды. Напомним, что это могло произойти только в том случае, если N — нечетное число и этот элемент был положительным. Эти условия и проверяются в блоке 16, который уменьшает вычисленное количество положительных элементов на единицу.

Рис. 4.7. Блок-схема к примеру 4.2

ПРИМЕР 4.3. Проверить, является ли заданная квадратная матрица единичной. Единичной называют матрицу, у которой элементы главной диагонали — единицы, а все остальные — нули.

Решать задачу будем так. Предположим, что матрица единичная (FL=ИСТИНА) и попытаемся доказать обратное. Если окажется, что хотя бы один диагональный элемент не равен единице или любой из элементов вне диагонали не равен нулю, то матрица единичной не является (FL=ЛОЖЬ). Воспользовавшись логическими операциями все эти условия можно соединить в одно и составить блок-схему (рис. 4.8).

Рис. 4.8. Блок-схема к примеру 4.3

ПРИМЕР 4.4. Преобразовать исходную матрицу так, чтобы первый элемент каждой строки был заменен средним арифметическим элементов этой строки.

Для решения данной задачи необходимо найти в каждой строке сумму элементов, которую разделить на их количество. Полученный результат записать в первый элемент соответствующей строки. Блок-схема алгоритма решения приведена на рис. 4.9.

ПРИМЕР 4.5. Задана матрица An, m. Сформировать вектор P_m, в который записать номера строк максимальных элементов каждого столбца.

Алгоритм решения этой задачи следующий: для каждого столбца матрицы находим максимальный элемент и его номер, номер максимального элемента j-го столбца матрицы записываем в j-й элемент массива P. Блок-схема алгоритма приведена на рис. 4.10.

ПРИМЕР 4.6. Написать программу умножения двух матриц An,m и Bm,l.

Например, необходимо перемножить две матрицы

Воспользовавшись правилом «строка на столбец», получим матрицу:

В общем виде формула для нахождения элемента Ci,j матрицы имеет вид:

где i = 1,Nи j = 1,L.

Обратите внимание, что проводить операцию умножения можно только в том случае, если количество строк левой матрицы совпадает с количеством столбцов правой. Кроме того, A >

Источник