Как найти среднее арифметическое простых чисел – Сайт, где вы сможете решить свои вопросы

Arithmetic is a subject of mathematics that is being used for calculation for the longest time known till now. Arithmetic alone carries an ancient history in the development of human civilization and different systems adapted for day-to-day based calculations and operations.

While looking into the history of arithmetic the word itself is derived from the Greek word ‘arithmos’ which means numbers. Brahmagupta the Indian mathematician of the 17th century is known as the “father of arithmetic”. And, the Fundamental theory of number theory was given by Carl Friedrich Gauss in 1801. Arithmetic is a subject of mathematics that deals with the study of numeric figures, their properties, and operations associated with them like summation, subtraction, multiplication, and division.

Arithmetic Mean Formula

Arithmetic means the formula is used to determine the mean or average of given entire data. Arithmetic mean is used to determine the central tendency that is to derive an average value by calculation from the large set of data given. The symbol used to denote the arithmetic mean is ‘X’. The calculation of the mean is totally based on observations.

In statistics arithmetic mean is used to determine the central tendency. The formula is derived by dividing the sum of a number of data by the number of observations. The numbers can be denoted as n₁, n₂, n₃, n₄, n₅, ……..n_n. And, the number of values will be n. Mathematically,

A.M. = (n₁+ n₂ + n₃ + n₄ + … + n_n)/n

And, if the frequency is given for the given set of numbers that is f₁, f₂, f₃, f₄, f₅, …, f_n for the numbers n₁, n₂, n₃, n₄, n₅, … n_n.

$A.M. = frac{f_1n_1 + f_2n_2 + f_3n_3 + f_4n_4 + ... + f_nn_n}{f_1 + f_2 + f_3 + f_4 + ... + f_n}$

While in arithmetic, the arithmetic mean formula is given by,

$A.M={frac{1}{n}sum_{i=1}^{n}a_{i}}$

Where,

n is the number of items

A.M is the arithmetic mean

a_i are set values.

Derivation of the arithmetic mean formula

Let n be the number of observations in the operation and n₁, n₂, n₃, n₄, …, n_n be the given numbers. Now as per the definition, the arithmetic means formula can be defined as the ratio of the sum of all numbers of the group by the number of items.

A.M. = (n₁ + n₂ + n₃ + n₄ + … + n_n)/n

By solving the equation, the formula of arithmetic mean is obtained which is,

$A.M={frac{1}{n}sum_{i=1}^{n}a_{i}}$

Sample Problems

Question 1: Find the arithmetic mean of the first five prime numbers.

Solution:

The arithmetic mean of the first five prime numbers will be given by,

The first prime numbers are 2, 3, 5, 7 and 11.

Number of observations (n) is 5.

Now,

X = sum of numbers/ number of observations

X = (2 + 3 + 5 + 7 + 11)/5

X = 28/5

X = 5.6

Hence, the arithmetic mean of the first five prime numbers is 5.6.

Question 2: Find the arithmetic mean of the first five natural numbers.

Solution:

The first five natural numbers are 1, 2, 3, 4 and 5.

The number of observations is 5.

Now,

X = sum of numbers/ number of observations

X = (1 + 2 + 3 + 4 + 5)/5

X = 15/5

X = 3

Hence, the arithmetic mean of the first five natural numbers is 3.

Question 3: If the arithmetic mean of five observations 5, 6, 7, x, and 9 is 6. Find the value of x.

Solution:

The five observations are 5, 6, 7, x, and 9.

The number of observations is 5.

Now,

X = sum of numbers/ number of observations

6 = (5 + 6 + 7 + x + 9)/5

30 = 27 + x

x = 30 – 27

x = 3

Hence, the arithmetic mean of five observations is 3.

Question 4: If the arithmetic mean of five observations 10, 20, 30, x, and 50 is 30. Find the value of x.

Solution:

The five observations are 10, 20, 30, x and 50.

The number of observations is 5.

Now,

X = sum of numbers/number of observations

30 = (10 + 20 + 30 + x + 50)/5

150 = 110 + x

150 – 110 = x

x = 40

Hence, the arithmetic mean of five observations is 40.

Question 5: What will be the arithmetic mean between 10 and 30.

Solution:

The observations are 10 and 30.

The number of observations is 2.

Now,

X = sum of numbers/ number of observations

X = (10 + 30)/2

X = 40/2

X = 20

Hence, the arithmetic mean of the two observations is 20.

Question 6: If the arithmetic means of two numbers x and 40 is 30. What is the value of x?

Solution:

The observations are x and 40.

The number of observations is 2.

The arithmetic mean is 30.

X = sum of numbers/number of observations

30 = (x + 40)/2

30 × 2 = x + 40

x = 60 – 40

x = 20

Hence, the value of x is 20.

Last Updated :
12 Jan, 2022

Like Article

Save Article

Источник

Среднее арифметическое

Онлайн калькулятор поможет найти среднее арифметическое чисел. Среднее арифметическое множества чисел (ряда чисел) — число, равное сумме всех чисел множества, делённой на их количество.

Программа вычисляет среднее арифметическое элементов массива, среднее арифметическое натуральных чисел, целых чисел, набора дробных чисел.

Формула которая используется для расчета среднего арифметического значения:
формула для нахождения средней арифметической величины

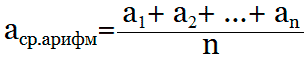
Приведём примеры нахождения среднего арифметического ряда чисел:
Среднее арифметическое двух чисел: (2+5)/2=3.5;
Среднее арифметическое трёх чисел: (2+5+7)/3=4.66667;
Среднее арифметическое 4 чисел: (2+5+7+2)/4=4;

Найти выборочное среднее (математические ожидание):
Среднее арифметическое 5 чисел: (2+5+7+2+3)/5=3.8;
Среднее арифметическое 6 чисел: (2+5+7+2+3+4)/6=3.833;
Среднее арифметическое 7 чисел: (2+5+7+2+3+4+8)/7=4.42857;
Среднее арифметическое 8 чисел: (2+5+7+2+3+4+8+5)/8=4.5;
Среднее арифметическое 10 чисел: (2+5+7+2+3+4+8+5+9+1)/10=4.6;

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также

Источник

Kneadman

0 / 0 / 0

Регистрация: 05.10.2013

Сообщений: 5

Определить среднее арифметическое простых чисел последовательности

05.10.2013, 15:40. Показов 2920. Ответов 7

Метки нет (Все метки)

Студворк — интернет-сервис помощи студентам

Господа, доброго времени суток. Я только начинающий относительно С++ и мне нужна помощь. Необходимо написать решение:
Вводится последовательность целых чисел, 0 – конец последовательности. Определить среднее арифметическое простых чисел последовательности (результатом функции будет 1 – число простое, 0 – нет).
Я вроде как написал, но программа выводит 0, прошу помощи.

C++

int main()
{
    int s,k,t,i,n;
    int a[10];
    s=0;
    k=0;
    for (int k=0; k<10;++k)
    {
    scanf("%d",&a[k]);
}
    for (k=0; k<10;++k)
    {
    if (a[k]>=2)
    {t=0;
    for(i=2; i<=sqrt(a[i])/2;i++);
    {
    if (fmod(a[k],i)==0)
    {
              t++;
}
else
{ s=s+a[k];
  ++n;
}
}      
}
}
s=s/n;
printf("srednee arifmeticheskoe prostih chisel=%d",s);
        system("pause");
}

4023 / 3280 / 920

Регистрация: 25.03.2012

Сообщений: 12,263

Записей в блоге: 1

05.10.2013, 16:13

По-моему, эта программа не очень соответствует заданию.
А где проверка условия “0 – конец последовательности.” ?
А почему проверка числа на простоту не вынесена в отдельную функцию?
Почему число добавляется к простым уже после первой проверки на остаток от деления, а не после того, как во всём цикле ни одна проверка не сработала?
Почему используется *** fmod для остатка от целочисленного деления?
Жду ответов

Kneadman

0 / 0 / 0

Регистрация: 05.10.2013

Сообщений: 5

06.10.2013, 00:16

[ТС]

Изучаю С++ буквально 2 лекции с самого 0, немного пошаманил, исправьте где неправильно, а я разберусь

C++

#include <stdio.h>
#include <math.h>
#include <stdlib.h>
int main()
{
    int s,k,t,i,n;
    int a[10];
    s=0;
    k=0;
    for (int k=0; k<10;++k)
    {
    scanf("%d",&a[k]);
}
  if (a[10]==0)
  { 
    for (k=0; k<10;++k)
    {
    if (a[k]>=2)
    {t=0;
    for(i=2; i<=sqrt(a[i])/2;i++);
    {
    if (a[k]%i==0)
    {
              t++;
}
else
{ if (t==0)
{s=s+a[k];
}
           }
        }
        
        }    
        }
else
{printf("Vash massiv ne sootvetstvuet parametram zadachi");
}
}
s=s/n;
printf("srednee arifmeticheskoe prostih chisel=%d",s);
        system("pause");
}

Добавлено через 21 минуту
забыл счетчик накопления кол-ва простых чисел

Kostik_Dodik

0 / 0 / 0

Регистрация: 16.09.2013

Сообщений: 53

06.10.2013, 00:44

Вот тебе верный код, дитя мое

C++

#include <iostream>
int main()
{
    int s,i=0;
    int a[100];
    bool d=true;
    s=0;
    for (int k=0; k<100 , d!=false;++k)
    {
        std::cin>>a[k];
        s+=a[k];
        if (a[k]==0)
        {
            d=false;
            i=k;
        }
    }
s/=i;
printf("srednee arifmeticheskoe prostih chisel=%d",s,"n");
system("pause");
}

4023 / 3280 / 920

Регистрация: 25.03.2012

Сообщений: 12,263

Записей в блоге: 1

06.10.2013, 00:52

Kostik_Dodik, тоже неверно

Kostik_Dodik

0 / 0 / 0

Регистрация: 16.09.2013

Сообщений: 53

06.10.2013, 00:54

ой, что тут чкажешь – додик ^^

Добавлено через 12 секунд

C++

#include <iostream>
int main()
{
    int l,s,i=0;
    int a[100];
    bool d=true;
    bool pr;
    s=0;
    for (int k=0; k<100 , d!=false;++k)
    {
        pr=true;
        std::cin>>a[k];
        for (int j =2; j<a[k];j++)
            if (a[k]%j==0)
                pr=false;
        if (pr==true && a[k]>1)
        {
                s+=a[k];
                i++;
        }
        if (a[k]==0)
            d=false;
    }
s/=i;
printf("srednee arifmeticheskoe prostih chisel=%d",s,"n");
system("pause");
}

Добавлено через 1 минуту
недочитал условие ^^

0 / 0 / 0

Регистрация: 05.10.2013

Сообщений: 5

06.10.2013, 06:00

[ТС]

Премного благодарствую!

0 / 0 / 0

Регистрация: 16.09.2013

Сообщений: 53

06.10.2013, 14:03

Право, сударь, не стоит ^^ Сеном откосишь

Источник

Формула среднего арифметического чисел?

Среднее арифметическое нескольких чисел — это сумма этих чисел, делённая на их количество.

x ср = S/n

где:

x ср — среднее арифметическое

S — сумма чисел

n — количество чисел.

Например, нам нужно найти среднее арифметическое чисел 3, 4, 5 и 6.

Для этого нам нужно их сложить и полученную сумму разделить на 4:

(3 + 4 + 5 + 6) : 4 = 18 : 4 = 4,5.

автор вопроса выбрал этот ответ лучшим

Алсу – Ш
[256K]

8 лет назад

Мне, как математику, интересны вопросы по данному предмету.

Начну с истории вопроса. Над средними величинами задумывались с древних времмен. Среднее арифметическое, среднее геометоическое, среднее гармоническое. Эти понятия предложены в древней Греции пифагорийцами.

А теперь интересующий нас вопрос. Что же понимается под средним арифметичским нескольких чисел:

Итак, для нахождения среднего арифметического чисел нужно прибавить все числа и разделить полученную сумму на количество слагаемых.

Имеет место формула:

Пример. Найти среднее арифметическое чисел: 100, 175, 325.

Решение.

Воспользуемся формулой нахождения среднего арифметического трех чисел (то есть вместо n будет 3; нужно сложить все 3 числа и разделить полученную сумму на их количество, т.е. на 3). Имеем: х=(100+175+325)/3=600/3=200.

Ответ: 200.

Арифметика считается самым элементарным разделом математики и изучает простые действия с числами. Поэтому и среднее арифметическое также находится очень просто. Начнем с определения. Среднее арифметическое – это величина, которая показывает какое число наиболее близко к истине при нескольких последовательных однотипных действиях. Например при беге на сто метров человек каждый раз показывает разное время, но средняя величина будет в пределах например 12 секунд. Нахождение среднего арифметического таким образом сводится в последовательному суммированию всех чисел определенного ряда (результатов забегов) и деление этой суммы на количество этих забегов (попыток, чисел). В виде формулы это выглядит так:

Sариф = (Х1+Х2+..+Хn)/n

Среднее арифметическое – это среднее число между несколькими числами.

Например между числами 2 и 4 среднее число 3.

Формула нахождения среднего арифметического такая:

Нужно сложить все числа и разделить на количество этих чисел:

формула нахождения среднего арифметического

Например у нас 3 числа: 2, 5 и 8.

Находим среднее арифметическое:

X=(2+5+8)/3=15/3=5

Область применения среднего арифметического достаточно широка.

Например можно зная координаты двух точек отрезка найти координаты середины этого отрезка.

Например координаты отрезка: (X1,Y1,Z1)-(X2,Y2,Z2).

Обозначим середину этого отрезка координатами X3,Y3,Z3.

Отдельно находим середину для каждой координаты:

X3=(X1+X2)/2;

Y3=(Y1+Y2)/2;

Z3=(Z1+Z2)/2;

Красивая поляна
[36.6K]

8 лет назад

Средне арифметическое число, это числа сложенные вместе и деленные на их количество, полученный ответ и есть средне арифметическое число.

Например: Катя положила в копилку 50 рублей, Максим 100 рублей, а Саша положил в копилку 150 рублей. 50 + 100 + 150 = 300 рублей в копилке, теперь делим эту сумму на три (три человека положили деньги). Итак 300 : 3 = 100 рублей. Эти 100 рублей и будет средне арифметически, каждый из них положил в копилку.

Есть такой простой пример: один человек ест мясо, другой человек ест капусту, а средне арифметически они оба едят голубцы.

Таким же образом рассчитывают среднюю зарплату…

Среднеарифметическое-это среднее значение из заданных…

Т.е. по простому имеем количество палочек разной длины и хотим узнать их среднее значение..

Логично, что для этого мы их сводим вместе, получая длинную палку, а потом делим её на требуемое число частей..

Вот и выходит среднеарифметическое..

Вот так и выводится формула:Sa=(S(1)+..S(n))/n..

Птичка2014
[25.4K]

8 лет назад

Среднее арифметическое – это сумма всех значений и деленное на их количество.

Например числа 2, 3 , 5, 6 . Нужно их сложить 2+ 3+ 5 + 6 = 16

16 делим на 4 и получаем ответ 4 .

4 и есть среднее арифметическое этих чисел.

Azamatik
[55.3K]

7 лет назад

Средним арифметическим называют сумму чисел, разделенное на количество этих самых чисел. А найти среднее арифметическое очень просто.

Как следует из определения мы должны взять числа, сложить их и разделить на их количество.

Приведем пример: дается числа 1, 3, 5, 7 и нам надо найти среднее арифметическое этих чисел.

сначала складываем эти числа (1+3+5+7) и получаем 16
полученный результат нам надо разделить на 4 (кол – во): 16/4 и получаем результат 4.

Итак, среднее арифметическое чисел 1, 3, 5 и 7 – это 4.

tana76
[124K]

7 лет назад

Среднее арифметическое – среднее значение среди заданных показателей.

Оно находится путем деления суммы всех показателей на их количество.

Например, у меня есть 5 яблок весом 200, 250, 180, 220 и 230 грамм.

Средний вес 1 яблока находим так:

ищем общий вес всех яблок (сумму всех показателей) – он равен 1080 граммов,
делим общий вес на количество яблок 1080:5 = 216 граммов. Это и есть среднее арифметическое.

Это наиболее часто применяемый в статистике показатель.

Alen4uk
[161K]

7 лет назад

Это мы знаем со школьной скамьи. У кого был хороший учитель по математике, то запомнить это нехитрое действие можно было с первого раза.

При нахождении среднего арифметического необходимо сложить все имеющиеся числа и разделить на их количество.

Например, я купила в магазине 1 кг яблок, 2 кг бананов, 3 кг апельсинов и 1 кг киви. Сколько килограммов в среднем я купила фруктов.

1+2+3+1=7.

7/4= 1,8 килограммов. Это и будет среднеарифметическим значением.

Даксплячи Учлинзайх
[225K]

7 лет назад

Помню как итоговую контрольную по математике сдавал

Так там нужно было среднее арифметическое найти.

Хорошо что добрые люди подсказали что делать, иначе беда.

Например у нас 4 числа.

Складываем числа и делим на их количество (в данном случае 4)

Например цифры 2,6,1,1. Складываем 2+6+1+1 и делим на 4 = 2.5

Как видите ничего сложного. Так что среднее арифметическая – это среднее значение всех чисел.

Знаете ответ?

Источник

Тема №5

Средние
величины

Большое распространение
в статистике имеют средние величины.

Средняя
величина –
это обобщающий показатель, в котором
находят выражение действия общих
условий, закономерностей развития
изучаемого явления.

Статистические средние рассчитываются
на основе массовых данных правильно
статистически организованного наблюдения
(сплошного и выборочного). Однако
статистическая средняя будет объективна
и типична, если она рассчитывается по
массовым данным для качественно
однородной совокупности (массовых
явлений). Например, если рассчитывать
среднюю заработную плату в акционерных
обществах и на госпредприятиях, а
результат распространить на всю
совокупность, то средняя фиктивна, так
как рассчитана по неоднородной
совокупности, и такая средняя теряет
всякий смысл.

При помощи средней
происходит как бы сглаживание различий
в величине признака, которые возникают
по тем или иным причинам у отдельных
единиц наблюдения.

Например, средняя
выработка отдельного продавца зависит
от многих причин: квалификации, стажа,
возраста, формы обслуживания, здоровья
и т.д. Средняя выработка отражает общую
характеристику всей совокупности.

Средняя величина
измеряется в тех же единицах, что и сам
признак.

Каждая средняя
величина характеризует изучаемую
совокупность по какому-либо одному
признаку. Чтобы получить полное и
всестороннее представление об изучаемой
совокупности по ряду существенных
признаков, необходимо располагать
системой средних величин, которые могут
описать явление с разных сторон.

Существуют различные
виды средних:

средняя
арифметическая;
средняя
гармоническая;
средняя
геометрическая;
средняя
квадратическая;
средняя кубическая.

Средние всех перечисленных выше видов,
в свою очередь, делятся на простые
(невзвешенные) и взвешенные.

Рассмотрим виды
средних, которые используются в
статистике.

Средняя арифметическая простая

Средняя арифметическая
простая (невзвешенная) равна сумме
отдельных значений признака, деленной
на число этих значений.

Отдельные
значения признака называют вариантами
и обозначают через х_i
();
число единиц совокупности обозначают
через n, среднее значение признака –
через.
Следовательно, средняя арифметическая
простая равна:

или

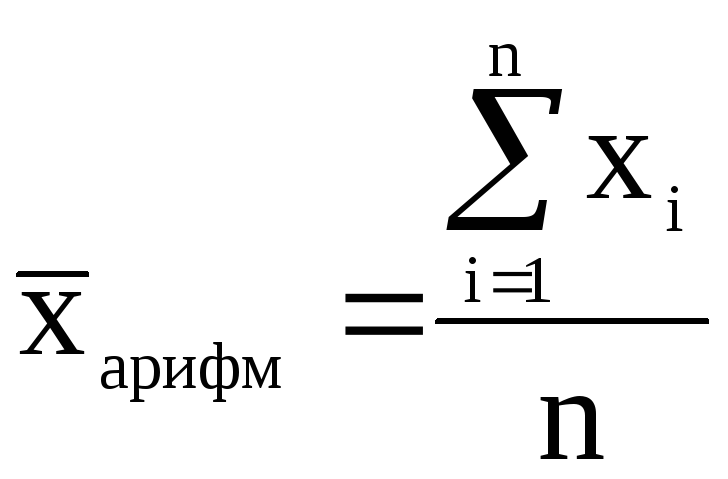
Пример
1.
Таблица
1

Данные
о производстве рабочими продукции А за
смену

№ работника, n	1	2	3	4	5	6	7	8	9	10
Выпущено изделий за смену одним работником, шт., x_i	16	17	18	17	16	17	18	20	21	18

В данном примере варьирующий признак
– выпуск изделий за смену.

Численные значения
признака (16, 17 и т. д.) называют вариантами.
Определим среднюю выработку продукции
рабочими данной группы:

шт.

Простая средняя
арифметическая применяется в случаях,
когда имеются отдельные значения
признака, т.е. данные не сгруппированы.
Если данные представлены в виде рядов
распределения или группировок, то
средняя исчисляется иначе.

Средняя арифметическая взвешенная

Средняя арифметическая взвешенная
равна сумме произведений каждого
отдельного значения признака (варианта)
на соответствующую частоту, деленной
на сумму всех частот.

Число
одинаковых значений признака в рядах
распределения называется частотой или
весом и обозначается через f_i.

В
соответствии с этим, средняя
арифметическая взвешенная выглядит
так:

или

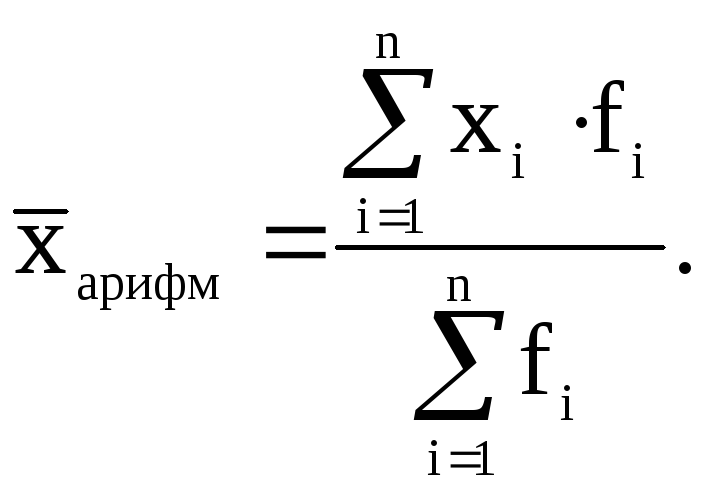
Из формулы видно,
что средняя зависит не только от значений
признака, но и от их частот, т.е. от состава
совокупности, от ее структуры.

Пример
2.

Таблица 2

Данные о заработной плате рабочих

Заработная плата одного рабочего в месяц, руб., x_i	Число рабочих, чел., f_i
1000	2
2000	6
3000	16
4000	12
5000	14
Итого	50

По
данным дискретного ряда распределения
видно, что одни и те же значения признака
(варианты) повторяются несколько раз.
Так, варианта х₁
встречается в совокупности 2 раза, а
варианта х₂– 6 раз и
т.д.

Вычислим среднюю
заработную плату одного рабочего:

руб.

Фонд
заработной платы по каждой группе
рабочих равен произведению варианты
на частоту (),
а сумма этих произведений дает общий
фонд заработной платы всех рабочих ().

Если
бы расчет был выполнен по формуле простой
средней арифметической, средний заработок
был бы равен 3 000 руб. ().
Сравнивая полученный результат с
исходными данными, очевидно, что средняя
заработная плата должна быть существенно
выше (больше половины рабочих получают
заработную плату выше 3 000 руб.). Поэтому
расчет по простой средней арифметической
в таких случаях будет ошибочным.

Статистический
материал в результате обработки может
быть представлен не только в виде
дискретных рядов распределения, но и в
виде интервальных вариационных рядов
с закрытыми или открытыми интервалами.

Рассмотрим расчет
средней арифметической для таких рядов.

Пример
3.

Таблица 3

Соседние файлы в папке Лекции

Источник

Arithmetic Mean Formula

Sample Problems

Среднее арифметическое

Смотрите также

Определить среднее арифметическое простых чисел последовательности

Средняя арифметическая простая

Данные о заработной плате рабочих

Вам также может понравиться

Как правильно составить сделку

Как найти среднюю норму амортизации

Как найти своего эльфа

Добавить комментарий Отменить ответ