Как найти среднее арифметическое расстояние

Пример:

Найти среднее арифметическое 2, 3 и 4.

Обозначим среднее арифметическое буквой «m». По определению выше найдем сумму всех чисел.

2 + 3 + 4 = 9

Разделим полученную сумму на количество взятых чисел. У нас по условию три числа.

В итоге мы получаем формулу среднего арифметического:

Для чего нужно среднее арифметическое?

Кроме того, что его постоянно предлагают найти на уроках, нахождение среднего арифметического весьма полезно и в жизни.

Например, вы решили продавать футбольные мячи. Но так как вы новичок в этом деле, совершенно непонятно по какой
цене вам продавать мячи.

Тогда вы решаете узнать, по какой цене в вашем районе уже продают футбольные мячи конкуренты. Узнаем цены
в магазинах и составим таблицу.

Магазин	Цена футбольного мяча
«Спорт-товары»	290 руб.
«Adidas»	360 руб.
«Все для футбола»	310 руб.

Цены на мячи в магазинах оказались совсем разные. Какую цену для продажи футбольного мяча нам лучше выбрать?

Если выбрать самую низкую (290 руб.), то мы будем продавать
товар себе в убыток. Если выбрать самую высокую (360 руб.), то покупатели не будут приобретать футбольные мячи у нас.

Нам нужна средняя цена. Здесь на помощь приходит среднее арифметическое.

Вычислим среднее арифметическое цен на футбольные мячи:

Средняя цена = =
= 320 руб.

Таким образом, мы получили среднюю цену (320 руб.), по которой мы можем продавать футбольный мяч не слишком дёшево и не
слишком дорого.

Средняя скорость движения

Со средним арифметическим тесно связано понятие средней скорости движения.

Наблюдая за движением транспорта в городе, можно заметить, что машины, то
разгоняются и едут с большой скоростью, то замедляются и едут с
маленькой скоростью.

Таких участков на пути следования автотранспорта бывает много. Поэтому
для удобства расчётов, используют понятие средней скорости движения.

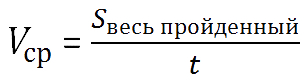
Рассмотрим задачу на среднюю скорость.

Разбор примера

Автомобиль двигался 3,2 ч по шоссе со скоростью 90 км/ч, затем
1,5 ч по
грунтовой дороге со скоростью 45 км/ч, наконец
0,3 ч по просёлочной дороге со скоростью 30 км/ч.
Найдите среднюю скорость движения автомобиля на всём пути.

Для расчёта средней скорости движения нужно знать весь путь, пройденный автомобилем,
и всё время, которое автомобиль двигался.

S₁ = V₁t₁

S₁ = 90 · 3,2 = 288 (км)

— шоссе.

S₂ = V₂t₂

S₂ = 45 · 1,5 = 67,5 (км)

— грунтовая дорога.

S₃ = V₃t₃

S₃ = 30 · 0,3 = 9 (км)

— просёлочная дорога.

S = S₁ + S₂ + S₃

S = 288 + 67,5 + 9 = 364,5 (км)

— весь путь, пройденный автомобилем.

t = t₁ + t₂ + t₃

t = 3,2 + 1,5 + 0,3 = 5 (ч)

— всё время.

V_ср = S : t

V_ср = 364,5 : 5 = 72,9

(км/ч) — средняя скорость движения автомобиля.

Ответ: V_ср = 72,9 (км/ч) — средняя скорость движения автомобиля.

---

Ваши комментарии

Оставить комментарий:

---

План урока:

Среднее значение

Скорость. Время. Расстояние

Взаимосвязь между скоростью, временем и расстоянием

Задачи на движение

На уроке узнаем, что означает «среднее арифметическое» и как его находят, будем решать задачи с величинами «скорость», «время», «расстояние».

Начнем урок с небольшой тренировки ума! Игра называется «Тройка». Вам нужно собрать в левой части три слагаемых так, чтобы получилось число за красной чертой. Считайте устно. Образец дан в первой строке: 18 + 34 + 16 = 68

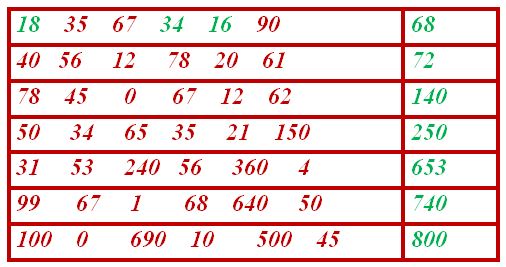
Проверь себя.

40 + 20 + 12 = 72

78 + 0 + 62 = 140

65 + 35 + 150 = 250

53 + 240 +360 = 653

99 + 1 + 640 = 740

690 + 10 + 100 = 800

Среднее значение

Каждый из нас в жизни встречается с выражениями «в среднем», «средняя температура», «средний заработок». Что это значит?

Рассмотрим на конкретной задаче.

Три друга Иван, Костя и Владимир каждую среду идут вместе от школы до музыкальной студии, где учатся игре на гитаре. Иван от школы до студии насчитал 251 шаг. Костя – 248 шагов, а Владимир насчитал 254 шага. Сколько в среднем шагов от школы до музыкальной студии?

В математике существует понятие «среднее арифметическое». Чтобы найти среднее арифметическое в этой задаче, нужно сложить количество шагов трех друзей, а затем полученную сумму разделить на 3 (по количеству слагаемых).

251 + 248 + 254 = 753 шага.

753 : 3 = 251 шаг

Можно сказать, что от школы до музыкальной студии в среднем 251 шаг.

Составим алгоритм.

Например, найти среднее арифметическое чисел: 5, 8, 7, 4.

Находим сумму чисел 5 + 8 + 7 + 4 = 24

Количество слагаемых – 4, значит, полученную сумму разделим на 4.

24 : 4 = 6

Среднее арифметическое – 6.

Пользуясь алгоритмом, найдите среднее арифметическое чисел: 12, 10, 8.

Проверь себя.

12 + 10 + 8 = 30

30 : 3 = 10

Среднее арифметическое – 10.

Рассмотрим более сложную задачу на нахождение среднего арифметического.

Задача

В столовой детского сада для приготовления завтраков малышам расходовали молоко три дня по 20 л и два дня по 25 л. Сколько в среднем расходовали молока в день?

Решим задачу вместе.

Сначала узнаем, сколько всего молока израсходовали.

20 ∙ 3 + 25 ∙ 2 = 110 (л) – израсходовали всего.

Затем узнаем, сколько дней расходовали молоко на завтрак.

3 + 2 = 5(дн.) – расходовали молоко.

Осталось количество израсходованного молока разделить на число дней.

110 : 5 = 22 (л) – расходовали в среднем за день.

Попробуйте самостоятельно решить подобную задачу.

Задача

Для игрового уголка в классе родители закупили 3 настольные игры: «Пазлы», «Домино», «Математический тренажер». Игра «Пазлы» стоила 160 р., «Домино» – 210 р., а «Математический тренажер» – 230 р.. Найди среднюю стоимость настольной игры.

Проверь себя.

• 160 + 210 + 230 = 600 (р.) – заплатили за все игры.
• 600 : 3 = 200 (р.) – стоит в среднем одна настольная игра.
• Ответ: 200 рублей

Скорость. Время. Расстояние

Скорость

Вы наблюдали, что вокруг нас постоянно что-то или кто-то движется. Некоторые объекты – быстро, а некоторые – совсем медленно. Например, по лесной тропе прогуливается человек, по шоссе едет автомобиль, по воздуху летит вертолет. Все они движутся. Но автомобиль движется быстрее, чем человек, а вертолет – быстрее автомобиля.

В математике, величиной характеризующей быстроту движения объектов называют скоростью.

Скорость движения – это расстояние, пройденное за единицу времени. Единицей времени может быть:  1 секунда, 1 минута, 1 час.

Давайте вместе разберем две простые задачи.

Легковая машина прошла 120 км за 2 часа. В течение каждого часа она проходила одинаковое расстояние. Сколько км прошла машина за 1 час?

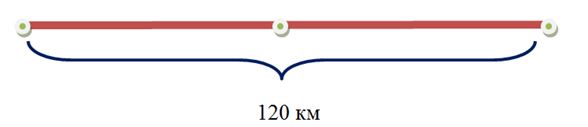
120 : 2 = 60 (км) – пройдет машина за 1 час.

Таким образом, скорость движения машины 60 км в час. Сокращенно запишем так:

60 км/ч.

Космический корабль пролетает 8 000 м за 1 секунду. Как по-другому записать его скорость?

Его скорость можно записать так: 8 000 м/с. Мы знаем, что 1 км = 1000 м, поэтому скорость корабля можно записать по-другому: 8 км/с.

Посмотрите скорость движения некоторых  животных. Какое животное самое медленное, самое быстрое? Обратите внимание, что скорость можно записать по-разному: в зависимости от того, сколько сантиметров, метров, километров кто-то пролетает, проползает или пробегает за секунду, минуту, час.

Время

С единицами времени вы уже знакомы. Это: секунда, минута, час, сутки, неделя, месяц, год, век.

Расстояние

Расстояние – это длина дороги, соединяющая начало и конец пути.

Расстояние измеряется в следующих единицах:

Миллиметр

Сантиметр

Дециметр

Метр

Километр

Взаимосвязь между скоростью, временем и расстоянием

Как же связаны между собой эти величины?

Давайте запомним условные обозначения, принятые в математике:

Скорость – v,

Время – t,

Расстояние – S.

Ребята, это три ключевых формулы для решения задач на движение, которые нужно знать назубок!

Задачи на движение

С задачами на движение мы встречаемся каждый день в обычной жизни.

Расстояние – самое большое из трех величин в задачах на движение. То есть, скорость и время всегда меньше расстояния.

Запомнили формулы, которые являются ключами к правильному решению задач?

Заполните пустые окошки в формулах:

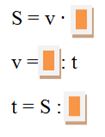
Решим задачи на движение.

Плот двигался по реке со скоростью 5 км/ч, а катер – со скоростью 20 км/ч. Какое расстояние преодолеет плот, и какое катер за 3 часа?

Выделяем величины, чертим таблицу. Читаем задачу по частям и записываем каждую величину в нужную ячейку таблицы.

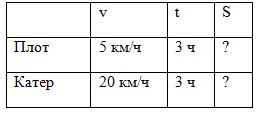
Какую из трех величин нужно найти? Верно, расстояние. Вспомним формулу: S = v ∙ t

5 ∙ 3 + 15 (км) – пройдет плот.

20 ∙ 3 = 60 (км) – пройдет катер.

Ответ: 15 км, 60 км.

Ребята участвовали в соревнованиях по бегу. Максим пробежал 200 м за 40 с, а Артем это же расстояние пробежал за 50 с. С какой скоростью бежал каждый из мальчиков?

Начертите  таблицу, как в предыдущей задаче. Запишите величины в нужные ячейки. Поставьте знак вопроса. Пользуясь формулой, решите задачу самостоятельно.

Проверь себя.

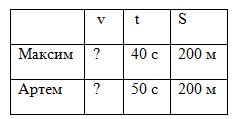
v = S : t

200 : 40 = 5 (м/с) – скорость движения Максима.

200 : 5 = 4 (м/с) – скорость движения Артема.

Ответ: 5 м/с, 4 м/с.

Решим еще одну задачу.

Два всадника отправились на прогулку на лошадях Рада и Снежка. Лошади преодолели одинаковое расстояние 30 км. Но двигались с разной скоростью. Рада бежала со скоростью 10 км/ч, а Снежка – 15 км/ч. Сколько времени длилась прогулка на Раде, и сколько времени – на Снежке?

Начертите таблицу, заполните ее ячейки. Пользуясь формулой, запишите решение.

Проверь себя.

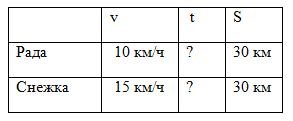
t = S : v

30 : 10 = 3 (ч) – прогулка на Раде.

30 : 15 = 2 (ч) – прогулка на Снежке.

Ответ: 3 ч, 2 ч.

Сегодня на уроке мы запомнили формулы-ключи для решения задач на движение, узнали о скорости самых медленных и самых быстрых животных, научились находить среднее арифметическое. До скорых встреч, ребята!

Как находить среднюю скорость

Повторим, как находить среднюю скорость, и рассмотрим конкретные примеры.

Чтобы найти среднюю скорость, надо:

1) найти весь пройденный путь;

2) найти все время движения;

3) весь пройденный путь разделить на все время движения:

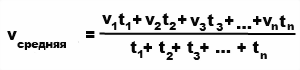
На примерах посмотрим, как находить среднюю скорость.

1) Пешеход прошел 2 часа со скоростью 7 км/ч и 3 часа со скоростью 5 км/ч. Найти среднюю скорость движения пешехода на всем пути.

Находим весь пройденный путь: 2∙7 + 3∙5 = 29 км.

Находим все время движения: 2+3=5 часов.

Чтобы найти среднюю скорость, весь пройденный путь делим на все время движения: 29:5=5,8 км/ч.

2) Автомобиль проехал 2 часа по шоссе со скоростью 100 км/ч, 1,5 часа по грунтовой дороге со скоростью 40 км/ч и 30 минут по проселочной дороге со скоростью 26 км/ч. Найти среднюю скорость автомобиля на всем пути.

Переведем минуты в часы: 30 минут = 0,5 часа.

Найдем весь пройденный автомобилем путь:

2∙100 + 1,5∙40 + 0,5∙26 = 200 + 60 + 13= 273 км.

Находим все время движения:

Чтобы найти среднюю скорость движения автомобиля, разделим весь пройденный путь на все время движения:

3) Велосипедист проехал 3 часа со скоростью 12 км/ч, затем отдохнул час, после чего продолжил путь со скоростью 9 км/ч и проехал еще 2 часа. Найти среднюю скорость движения велосипедиста на всем пути.

Найдем весь путь велосипедиста:

3∙12 + 1∙0 + 2∙9 = 54 км.

Найдем все время движения:

Чтобы найти среднюю скорость движения велосипедиста, весь путь делим на все время движения:

самый лучший сайт по математике спасибо огромное

Илья, спасибо за теплые слова!

Велосипедист проехал со скоростью 12 км/ч 4 км,остановился на 40 мин и продолжил движение со скоростью 8 км/ч и проехал 8 км. Найдите скорость велосипедиста на протяжении всей дороги? Пожалуйста,помогите,очень важно

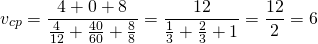
Валерий, эта задача — на движение по водному пути. Но ее можно решить логически.
Поскольку известно, что скорость катера по течению реки в два раза больше скорости против течения, при этом расстояние туда и обратно — одинаковое, то время, затраченное катером на путь по течению, в два раза меньше времени против течения (скорость и время — обратно пропорциональные величины. Если скорость увеличить в несколько раз, то при том же расстоянии время уменьшится во столько же раз).
Таким образом, все время можно разделить на 3 части, одну часть которого катер потратил на путь по течению, две — на путь против течения. Так как на весь путь было потрачено 2 часа=120 минут, то из них на путь по течению — 1/3 от 120 — это 40 минут=2/3 часа. Чтобы найти скорость, надо расстояние разделить на время: 20:(2/3)=30 км/ч — это скорость катера по течению. Она в два раза больше скорости против течения, следовательно, скорость против течения 30:2=15 км/ч.

Девушка ехала на работу со средней скоростью 40 миль в час, обратно домой ехала со средней скоростью 30 миль в час, весь путь от дома до работы и обратно занял 1 час, сколько миль проехала девушка?

Это — задача на движение. Пусть на работу девушка ехала х часов,тогда обратный путь занял у нее (1-х) часов. По формуле пути путь на работу равен 40х миль, обратный путь — 30(1-х) миль. Так как туда и обратно девушка проехала одинаковое расстояние, составляем уравнение: 40х=30(1-х). Отсюда х=3/7, путь на работу 40∙(3/7)=120/7 миль, туда и обратно — 2∙(120/7)=240/7=38 2/7 мили.

Источник

Формула нахождения значений скорости, времени и расстояния

С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.

Как же рассчитать скорость?

На самом деле, рассчитать ее можно несколькими способами:

Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.

Теперь нужно подставить имеющиеся значения вместо буквенных символов:

v=100 км/1,5 ч=66,66 км/ч

Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.

Таким нехитрым способом можно найти скорость через время и расстояние.

А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

Можно записать использовать и такой вид вычислений:

Но можно записать эту же формулу и в более точном варианте:

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.

Другие способы вычисления

Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:

Способы вычисления расстояния и времени

Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:

Таким образом вычисляется значение расстояния.

Или вычисляем значение времени, за которое пройдено расстояние:

Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.

Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.

И это еще не предел!

Видео

В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.

Источник

Средняя скорость пути

Известно, что средняя скорость V равна пути S, деленному на время t средней скорости. Средняя скорость не всегда находится так легко. В случае, если автомобиль движется равномерно с постоянной скоростью, например 45 км/час, то, очевидно, средняя скорость и постоянная скорость одинаковы, т. е. 45 км/час. Если же автомобиль трогается с места (начальная скорость равна 0) и развивает скорость постепенно, то среднюю скорость можно найти следующим способом: нужно записать сумму всех скоростей и поделить ее на число отсчетов скоростей. Важно — временные интервалы должны быть одинаковые (например: записывать скорость каждые 5 секунд, или каждые 7 минут).

Калькулятор средней скорости пути

Складывая скорости, введенные вами, мы находим их сумму. Разделив эту сумму на количество равных временных отсчетов, мы узнаем среднюю скорость.

Единицы скорости

Скорость обычно определяют как путь, пройденный за единицу времени. Поэтому, если скорость автомобиля 90 км/час, то он за минуту должен пройти 1,5 км, а в секунду 1500 : 60, или 25 м. Следовательно, скорость 90 км/час может быть выражена различными способами в зависимости от выбора единиц времени и пути:

90 км/час = 1.5 км/мин =25 м/сек.

Поскольку скорость может быть выражена в различных единицах, то надо внимательно следить за выбором единиц в формуле S=vt. Если скорость выбираем в км/час, то время надо брать в часах, если — в м/сек, то время должно быть выражено в секундах.

Источник

Как посчитать среднюю скорость движения автомобиля

Средняя скорость – не самое сложное понятие в кинематике. Однако для многих учащихся простота этого понятия оказывается обманчивой.
Известно, что средняя скорость – это величина, равная отношению пути, пройденного телом, ко времени, за которое пройден этот путь: Краткость и простота определения скрывают от некоторых учеников важные для решения задач вопросы и ответы на них.
1. Какое время следует учитывать при расчете средней скорости, если тело в пути делало остановки?
В определении указано: “. ко времени, за которое пройден этот путь”, то есть ко всему промежутку времени с момента, когда тело тронулось в этот путь (представьте, что Вы включили секундомер), до момента, когда тело преодолело этот путь (только в этот момент Вы останавливаете секундомер!). О том, что время на остановки не следует учитывать, в определении ничего не сказано (поэтому секундомер на промежуточных остановках не выключайте!). Таким образом, при расчете средней скорости следует учитывать всё время, которое ушло на преодоление пути (в том числе и время, потраченное на остановки).

2. Как правильно рассчитать среднюю скорость тела, которое начало движение в пункте А, окончило его в пункте В, но по дороге из А в В поворачивало назад (может быть ни один раз!), а затем вновь продолжало движение к пункту В?
В определении указано “. равная отношению пути, пройденного телом. ”, значит, при расчете средней скорости определяющим является не расстояние между точками (пунктами) начала и окончания движения, а реальный путь, которое прошло тело.

Пример 1. Найти среднюю скорость человека на пути от дома до станции, расстояние между которыми l =800 м, если, пройдя четверть пути, он вернулся домой (например, проверить, хорошо ли закрыта дверь) и через мин продолжил путь на станцию. Скорость движения человека постоянна и равна v =4 км/ч.

Решение. Началом движения человека, конечно, следует считать момент времени, когда он первый раз вышел из дома. Четверть пути составляет расстояние l_1/4 =l : 4 =800 : 4 =200 м. При возвращении домой человек прошел путь 2l_1/4 =400 м. После этого он вышел из дома второй раз и дошел до станции. Путь, пройденный человеком с начала движения, составит:

Время t, которое затрачено на преодоление этого пути, складывается из времени пребывания дома и времени Т, в течение которого человек двигался по маршруту “из дома–к дому–на станцию”. Поскольку скорость движения человека постоянна (v =4 км/ч) и проделанный путь известен, то время движения составляет:

1,2 км : 4 км/ч =0,3 ч =18 мин.
Тогда все время, затраченное человеком, составляет:

t = + T = 2 + 18 =20 мин =1/3 ч.
Найдем среднюю скорость:

1,2 км : ч =3,6 км/ч.

Среднюю скорость движения человек оценивает довольно часто, но судит о ней, глядя на часы. Торопящийся человек соотносит расстояние, которое ещё осталось преодолеть, и время, отпущенное ему на это, после чего делает вывод (хотя числовое значение средней скорости вряд ли при этом находится): “Ну, теперь можно идти помедленнее” или “Придется еще поднажать, иначе не успею”.

Вернемся к рассмотренному примеру. Будем считать, что скорость v₀ =4 км/ч выбрана человеком не случайно. проходя от дома до станции ежедневно, человек замечает, что расстояние l ==800 м, он проходит за время t₀ =12 мин =0,2 ч:

= 0,8 км : 0,2 ч =4 км/ч.

По существу, это – средняя скорость, поскольку доподлинно неизвестно, с какой скоростью человек идет в каждый момент времени. Двигаясь с такой скоростью и затрачивая время t₀, человек ежедневно успевает на станцию вовремя. Если приходится возвращаться домой (увеличивать путь, который надо преодолеть и на это требуется дополнительное время) или останавливаться (увеличивая время, необходимое на преодоление пути), выбранная скорость движения v₀ не подходит: можно опоздать на станцию. Значит, надо увеличивать скорость движения. Но как это сделать без напрасных затрат сил?

Пример 2. Человек обычно доходит из дома до станции за время t₀ =12 мин, проходя расстояние l =800 м. Однажды, пройдя четверть пути, он вспоминает, что не выключил электроприборы, и возвращается домой, выключает электроприборы, затрачивая время = 2 мин, и снова идет на станцию. С какой наименьшей скоростью надо двигаться человеку, после того как он повернул домой, чтобы успеть на станцию в обычное время (и не опоздать на электричку).

1. Обычно человек двигается со скоростью

м/мин =4 км/ч.

2. Пройдя с такой скоростью четверть пути, он затратил время : 4 км/ч =0,05 ч =3 мин. Значит, в его распоряжении осталось время Т₂ =t₀ – T₁ =12 – 3 =9 мин.

3. За время Т₂ человек должен преодолеть путь до дома, а затем снова до станции:
м =1 км и, кроме того, часть времени ( = 2 мин) потратить дома. Поэтому путь S человеку придется преодолевать за время

ч,

то есть со скоростью, не меньшей, чем

1 км : ч = км/ч = км/ч » 8,6 км/ч.

Проверьте, что добежав до дома со скоростью км/ч, а затем шагая со скоростью v₂ =2v₀ =8 км/ч, человек придет на станцию вовремя.
Ответ: человеку необходимо двигаться со скоростью, не меньшей, чем км/ч. Обратите внимание, что средняя скорость за время (t =12 минут) от начала движения до его окончания составляет

м/мин =100 м/мин =6 км/ч.

Найденное значение v_ср в полтора раза выше, чем v₀, и показывает, с какой начальной скоростью следует выходить человеку из дома, если он забывчив.

На рис.1 показан график зависимости скорости человека от времени для примера 2 в случае, если человек бежит домой со скоростью v₁ =3v₀ ==12 км/ч, а затем идет до станции очень быстрым шагом со скоростью v₂ =2v₀ =8 км/ч. Штрихпунктирной линией указан график движения со скоростью v₀, а тонкой линией – со скоростью v_ср =6 км/ч.

Подсчитаем среднее арифметическое для значений скорости v₀, v₁, v₂:

км/ч.

Это значение не равно значению средней скорости v_ср. Убедитесь в этом и не совершайте в дальнейшем распространенную ошибку: не пытайтесь искать среднюю скорость как среднее арифметическое значение (оно не имеет физического смысла!).

Пример 3. Автомобиль проезжает первую треть пути равномерно со скоростью v₁ =108 км/ч, а остальные две трети пути – со скоростью v₂ =72 км/ч. Найти среднюю скорость автомобиля.
Решение. Неверно считать, что средняя скорость совпадает со средним арифметическим значением v₁ и v₂, которое составляет

км/ч.

1. Найдем время t₁ движения со скоростью v₁, полагая, что весь путь равен L [км]. Из условия ясно, что

2. Время t₂ движения на оставшемся участке пути составляет

3. Итак, время на продолжение пути L составляет

4. По определению средней скорости

км/ч.

Ответ : средняя скорость v_ср =81 км/ч.

Значение средней скорости совпадает со средним арифметическим значением скорости только в одном частном случае, когда тело двигается с различными скоростями так, что между последовательными моментами изменения (переключения) скорости проходит одинаковое время Т. Таким образом, тело двигается со скоростью v₁ в течение времени t₁=T, со скоростью v₂ в течение времени t₂=T, со скоростью v₃ в течение времени t₃=T и т.д. Если на протяжении пути скорость изменялась n раз, то пройденный путь

Время t, за которое пройден путь, составляет

Не запрещено для этого частного случая двигаться со скоростью v₀=0, т.е. делать остановки. Но время остановки должно составлять t₀ =T.

Пример 4. Вертолет пролетает без остановок равномерно и прямолинейно над пунктами А, В, С (в указанном порядке) и возвращается в А. Пункты А, В, С являются как бы вершинами треугольника. Расстояние между А и В составляет L_AB =150 км, между В и С L_BC =200 км, между С и А L_CA =100 км. Время, за которое вертолет пролетает от одного пункта до другого, составляет полчаса. Найти среднюю скорость движения вертолета на маршруте АВСА. Изменится ли средняя скорость, если L_CA =200 км и всё расстояние вертолет преодолеет за 1 ч?

Решение. 1. Находим скорость движения вертолета на каждом участке:

км/ч;

км/ч;

км/ч.

2. Поскольку t =0,5 ч одинаково для всех участков движения, то

км/ч.

км/ч.

Источник

Среднее арифметическое

Чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму на их количество.

Обозначим среднее арифметическое буквой « m ». По определению выше найдем сумму всех чисел.

Разделим полученную сумму на количество взятых чисел. У нас по условию три числа.

В итоге мы получаем формулу среднего арифметического:

Для чего нужно среднее арифметическое?

Кроме того, что его постоянно предлагают найти на уроках, нахождение среднего арифметического весьма полезно и в жизни.

Например, вы решили продавать футбольные мячи. Но так как вы новичок в этом деле, совершенно непонятно по какой цене вам продавать мячи.

Тогда вы решаете узнать, по какой цене в вашем районе уже продают футбольные мячи конкуренты. Узнаем цены в магазинах и составим таблицу.

Магазин	Цена футбольного мяча
«Спорт-товары»	290 руб.
«Adidas»	360 руб.
«Все для футбола»	310 руб.

Цены на мячи в магазинах оказались совсем разные. Какую цену для продажи футбольного мяча нам лучше выбрать?

Если выбрать самую низкую ( 290 руб.), то мы будем продавать товар себе в убыток. Если выбрать самую высокую ( 360 руб.), то покупатели не будут приобретать футбольные мячи у нас.

Нам нужна средняя цена. Здесь на помощь приходит среднее арифметическое.

Вычислим среднее арифметическое цен на футбольные мячи:

Таким образом, мы получили среднюю цену ( 320 руб.), по которой мы можем продавать футбольный мяч не слишком дёшево и не слишком дорого.

Средняя скорость движения

Со средним арифметическим тесно связано понятие средней скорости движения.

Наблюдая за движением транспорта в городе, можно заметить, что машины, то разгоняются и едут с большой скоростью, то замедляются и едут с маленькой скоростью.

Таких участков на пути следования автотранспорта бывает много. Поэтому для удобства расчётов, используют понятие средней скорости движения.

Средняя скорость движения — это весь пройденный путь разделить на всё время движения.

Рассмотрим задачу на среднюю скорость.

Задача № 1503 из учебника «Виленкин 5 класс»

Автомобиль двигался 3,2 ч по шоссе со скоростью 90 км/ч, затем 1,5 ч по грунтовой дороге со скоростью 45 км/ч, наконец 0,3 ч по просёлочной дороге со скоростью 30 км/ч. Найдите среднюю скорость движения автомобиля на всём пути.

Для расчёта средней скорости движения нужно знать весь путь, пройденный автомобилем, и всё время, которое автомобиль двигался.

S₁ = 90 · 3,2 = 288 (км) — шоссе.

S₂ = 45 · 1,5 = 67,5 (км) — грунтовая дорога.

S₃ = 30 · 0,3 = 9 (км) — просёлочная дорога.

S = 288 + 67,5 + 9 = 364,5 (км) — весь путь, пройденный автомобилем.

t = 3,2 + 1,5 + 0,3 = 5 (ч) — всё время.

V_ср = 364,5 : 5 = 72,9 (км/ч) — средняя скорость движения автомобиля.

Ответ: V_ср = 72,9 (км/ч) — средняя скорость движения автомобиля.

Источник

Расчет средней величины в интервальных вариационных рядах немного отличается от расчета в рядах дискретных. Как рассчитать среднюю арифметическую и среднюю гармоническую в дискретных рядах можно посмотреть вот ЗДЕСЬ. Такое различие вполне объяснимо – это связано с особенностью интервальных рядов, в которых изучаемый признак приведен в интервале от и до.

Итак, посмотрим особенности расчета на примере.

Пример 1. Имеются данные о дневном заработке рабочих предприятия.

Дневной заработок рабочего, руб.	Число рабочих, чел.
500-1000	15
1000-1500	30
1500-2000	80
2000-2500	60
2500-3000	25
Итого	210

 Нам необходимо рассчитать среднедневную заработную плату рабочего.

Начало решения задачи будет аналогичным правилам расчета средней величины, которые можно посмотреть в этой статье.

Начинаем мы с определения варианты и частоты, поскольку ищем мы средний заработок за день, то варианта это первая колонка, а частота вторая. Данные у нас заданы явным количеством, поэтому расчет проведем по формуле средней арифметической взвешенной (так как данные приведены в табличном виде). Но на этом сходства заканчиваются и появляются новые действия.

Дневной заработок рабочего, руб. х	Число рабочих, чел. f
500-1000	15
1000-1500	30
1500-2000	80
2000-2500	60
2500-3000	25
Итого	210

Дело в том, что интервальный рад представляет осредняемую величину в виде интервала. 500-1000, 2000-2500 и так далее. Чтобы решить эту проблему необходимо провести промежуточные действия, и только потом подсчитать среднюю величину по основной формуле.

Что же требуется в данном случае сделать. Все достаточно просто, чтобы провести расчет нам нужно, чтобы варианта была представлена одним числом, а не интервалом. Для получения такого значения находят так называемое ЦЕНТРАЛЬНОЕ ЗНАЧЕНИЕ ИНТЕРВАЛА (или середину интервала). Определяется оно путем сложение верхней и нижней границ интервала и делением на два.

Проведем необходимые расчеты и подставим данные в таблицу.

 

И так далее по всем интервалам рассчитываем центральное значение. В итоге получаем следующие результаты.

Дневной заработок рабочего, руб. х	Число рабочих, чел. f	х’
500-1000	15	750
1000-1500	30	1250
1500-2000	80	1750
2000-2500	60	2250
2500-3000	25	2750
Итого	210	—

 После того как мы рассчитали центральные значения далее проведем расчеты в таблицы и подставим итоговые данные в формулу, аналогично тому как мы уже рассматривали ранее.

Дневной заработок рабочего, руб. х	Число рабочих, чел. f	х’	x’f
500-1000	15	750	11250
1000-1500	30	1250	37500
1500-2000	80	1750	140000
2000-2500	60	2250	135000
2500-3000	25	2750	68750
Итого	∑f = 210	—	∑ x’f = 392500

В итоге получаем, что среднедневная заработная плата одного рабочего составляет 1869 рублей.

Это пример решения, если интервальный ряд представлен со всеми закрытыми интервалами. Но достаточно часто бывает, когда два интервала открытые, первый и последний. В таких ситуациях прямой расчет центрального значения невозможен, но есть два варианта как это сделать.

 Пример 2. Имеются данные о продолжительности производственного стажа персонала предприятия. Рассчитать среднюю продолжительность стада одного сотрудника.

Длительность производственного стажа, лет	Число сотрудников, человек
до 3	19
3-6	21
6-9	15
9-12	10
12 и более	5
Итого	70

В данном случае принцип решения останется точно таким же. Единственно, что поменялось в этой задаче, так это первый и последний интервалы. До 3 лет и 12 лет и более это и есть те самые открытые интервалы. Именно тут возникнет вопрос, а как же найти центральное значение интервала для таких интервалов.

Поступить в этой ситуации можно двумя способами:

1. Предположить какой бы мог быть интервал, учитывая, что нам приведены интервалы равные, то это вполне возможно. Интервал до 3 мог бы выглядеть как 0-3, и тогда его центральное значение будет (0+3)/2 = 1,5 года. Интервал 12 и более мог бы выглядеть как 12-15, и тогда его центральное значение было бы (12+15)/2 = 13,5 года. Все оставшиеся центральные значения интервала рассчитываются аналогично. В результате получаем следующее.

Длительность производственного стажа, лет х	Число сотрудников, человек f	х’	x’f
до 3	19	1,5	28,5
3-6	21	4,5	94,5
6-9	15	7,5	112,5
9-12	10	10,5	105,0
12 и более	5	13,5	67,5
Итого	∑f = 70	—	∑ x’f = 408,0

 

Средняя продолжительность стажа 5,83 года.

1. Принять за центральное значение, то данное которое имеется в интервале, без дополнительных расчетов. В нашем случае в интервале до 3 это будет 3, а в интервале 12 и более это будет 12. Такой способ больше подходит для ситуаций, когда интервалы неравные и предположить какой интервал мог бы быть сложно. Рассчитаем нашу задачу по таким данным далее.

Длительность производственного стажа, лет х	Число сотрудников, человек f	х’	x’f
до 3	19	3	57,0
3-6	21	4,5	94,5
6-9	15	7,5	112,5
9-12	10	10,5	105,0
12 и более	5	12	60,0
Итого	∑f = 70	—	∑ x’f = 429,0

 

Средняя продолжительность стажа 6,13 года.

Домашнее задание

1. Рассчитать средний размер посевной площади на одно фермерское хозяйство по следующим данным.

Размер посевной площади, га	Количество фермерских хозяйств
0-20	64
20-40	58
40-60	32
60-80	21
80-100	12
Итого	187

1. Рассчитайте средний возраст работника предприятия по следующим данным

Возраст персонала, лет	Число сотрудников, человек
до 18	7
18-25	68
25-40	79
40-55	57
55 и старше	31
Итого	242

Теперь Вы умеете рассчитывать среднюю в интервальном вариационном ряду!