Среднее арифметическое
Среднее арифметическое,
или просто среднее, — одна из основных
характеристик выборки.
Среднее
арифметическое
– такое значение признака, сумма
отклонений от которого выборочных
значений признака равна нулю (с учетом
знака отклонения).
Среднее
принято обозначать той же буквой, что
и варианты выборки, с той лишь разницей,
что над буквой ставится символ усреднения
— черта. Например, если обозначить
исследуемый признак через X,
а его числовые значения — через xi,
то среднее арифметическое имеет
обозначение
.
Среднее
арифметическое, как и другие числовые
характеристики выборки, может вычисляться
как по необработанным первичным данным,
так и по результатам группировки этих
данных.
Для
несгруппированных данных среднее
арифметическое определяется по следующей
формуле:
где
n
— объем выборки;
хi
— варианты выборки.
Если данные
сгруппированы, то
где
n
— объем выборки;
k
— число интервалов группировки;
ni
— частота i-ого
интервала;
хi
— срединное значение i-ого
интервала.
Среднее
арифметическое – величина того же
наименования, что и значения признаков.
Нахождение
среднего арифметического непрерывного
вариационного ряда осложняется, если
крайние интервалы не замкнуты (то есть
имеют вид «менее 10» или «более 60»). В
этом случае считается, что ширина первого
интервала равна ширине второго, а ширина
последнего – ширине предпоследнего.
Среднее
арифметическое, вычисленное по формуле
называют также взвешенным
средним,
подчеркивая этим, что в формуле xi,
суммируются с коэффициентами (весами),
равными частотам попадания в интервалы
группировки.
Медиана
Медианой
(Ме)
называется такое значение признака X,
когда ровно половина значений
экспериментальных данных меньше ее, а
вторая половина — больше.
Если
данных немного (объем выборки невелик),
медиана вычисляется очень просто. Для
этого выборку ранжируют, т. е. располагают
данные в порядке возрастания или
убывания, и в ранжированной выборке,
содержащей n
членов, ранг R
(порядковый номер) медианы определяется
как
Пример
7.8. Имеется
ранжированная выборка, содержащая
нечетное число членов n
= 9:
12,
14, 14, 18, 20, 22, 22, 26, 28.
Тогда
ранг медианы:
и
медиана совпадает с пятым членом ряда:
Ме
= 20.
Если
выборка содержит четное число членов,
то медиана не может быть определена
столь однозначно.
Пример
7.9. Имеется
ранжированная выборка, содержащая 10
членов:
6,
8, 10, 12, 14, 16, 18, 20, 22, 24.
Ранг
медианы оказывается равным:
Медианой в этом
случае может быть любое число между 14
и 16 (5-м и 6-м членами ряда). Для определенности
принято считать в качестве медианы
среднее арифметическое этих значений,
т. е.:
Если
необходимо найти медиану для сгруппированных
данных, то поступают следующим образом.
Вначале находят интервал группировки,
в котором содержится медиана, путем
подсчета накопленных частот или
накопленных относительных частот.
Медианным
будет тот интервал, в котором накопленная
частота впервые окажется больше
или накопленная относительная частота
— больше 0,5. Внутри медианного интервала
медиана определяется по следующей
формуле:
где
— нижняя граница медианного интервала;
hme
— ширина
медианного интервала;
—
накопленная
частота интервала, предшествующего
медианному,
— частота
медианного интервала.
Пример
7.10. Найти медиану для интервального
ряда примера 6.3.
|
Превышение
скорости |
20 – 30 |
30 – 40 |
40 – 50 |
50 – 60 |
больше |
|
Количество |
50 |
32 |
26 |
11 |
5 |
Объем
выборки равен
п = 50 + 32 + 26 +
11 + 5 = 124.
Найдем
медианный интервал – интервал, в котором
накопленная частота впервые окажется
больше
или накопленная относительная частота
— больше 0,5.
Так
как, накопительная частота второго
интервала 50 +
32 = 82 > 62, то
следовательно интервал (30; 40) будет
медианным и
=
30, hme
= 40 – 30 = 10,
=
50,
=
32.
Значит,
Медиана
обычно несколько отличается от среднего
арифметического. Так бывает всегда,
когда имеет место несимметричная форма
эмпирического распределения.
Мода
Мода
(Мо)
представляет собой значение признака,
встречающееся в выборке наиболее часто.
Ряд
называется унимодальным,
если в нем только одно модальное значение
и полимодальным,
если есть несколько значений признака,
которые встречаются одинаково часто.
Для полимодального ряда моду не вычисляют.
Для дискретного
ряда мода находится по определению.
Интервал
группировки с наибольшей частотой
называется модальным.
Для определения
моды в интервальном ряду используется
следующая формула:
где
— нижняя граница модального интервала;
h
— ширина
интервала группировки;
nMo
— частота модального интервала;
nMo-1
— частота
интервала, предшествующего модальному;
nMo+1
— частота интервала, следующего за
модальным.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти среднее значение распределения вероятностей (с примерами)
17 авг. 2022 г.
читать 2 мин
Распределение вероятностей говорит нам о вероятности того, что случайная величина примет определенные значения.
Например, следующее распределение вероятностей говорит нам о вероятности того, что определенная футбольная команда забьет определенное количество голов в данной игре:
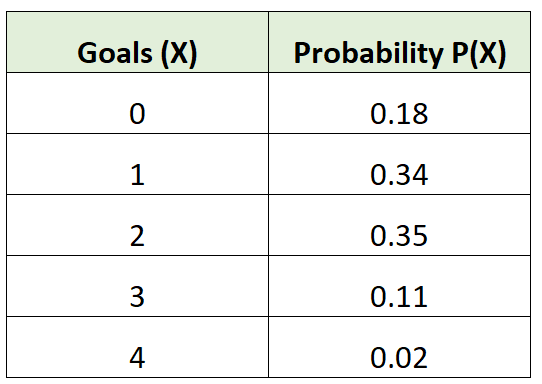
Примечание.Вероятности в действительном распределении вероятностей всегда будут в сумме равны 1. Мы можем подтвердить, что это распределение вероятностей действительно: 0,18 + 0,34 + 0,35 + 0,11 + 0,02 = 1.
Чтобы найти среднее (иногда называемое «ожидаемым значением») любого распределения вероятностей, мы можем использовать следующую формулу:
Mean (Or "Expected Value") of a Probability Distribution:
μ = Σx * P(x)
where:
•x: Data value
•P(x): Probability of value
Например, рассмотрим наше распределение вероятностей для футбольной команды:
Среднее количество голов для футбольной команды будет рассчитываться как:
μ = 0*0,18 + 1*0,34 + 2*0,35 + 3*0,11 + 4*0,02 = 1,45 гола.
В следующих примерах показано, как вычислить среднее значение распределения вероятностей в нескольких других сценариях.
Пример 1: Среднее количество отказов транспортных средств
Следующее распределение вероятностей говорит нам о вероятности того, что данное транспортное средство испытает определенное количество отказов батареи в течение 10-летнего периода:
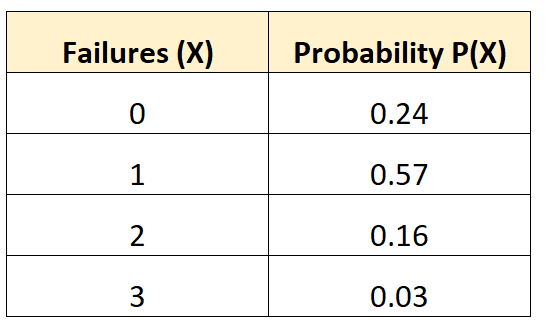
Вопрос: Каково среднее количество ожидаемых отказов для этого автомобиля?
Решение.Среднее количество ожидаемых отказов рассчитывается как:
μ = 0*0,24 + 1*0,57 + 2*0,16 + 3*0,03 = 0,98 отказов.
Пример 2: Среднее количество побед
Следующее распределение вероятностей говорит нам о вероятности того, что данная баскетбольная команда выиграет определенное количество игр в турнире:
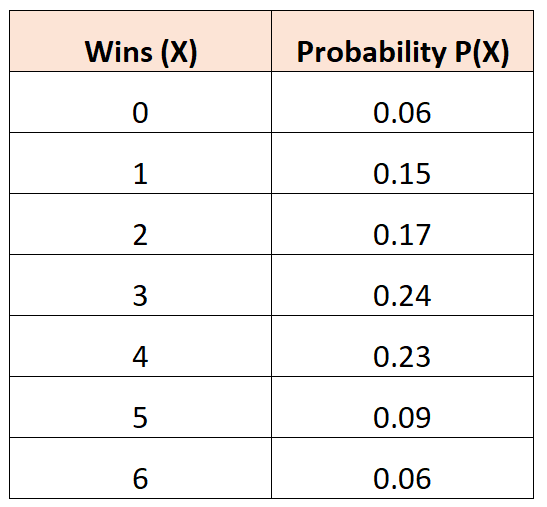
Вопрос: Каково среднее количество ожидаемых побед для этой команды?
Решение: Среднее количество ожидаемых выигрышей рассчитывается как:
μ = 0*0,06 + 1*0,15 + 2*0,17 + 3*0,24 + 4*0,23 + 5*0,09 + 6*0,06 = 2,94 победы.
Пример 3: Среднее количество продаж
Следующее распределение вероятностей говорит нам о вероятности того, что данный продавец совершит определенное количество продаж в предстоящем месяце:
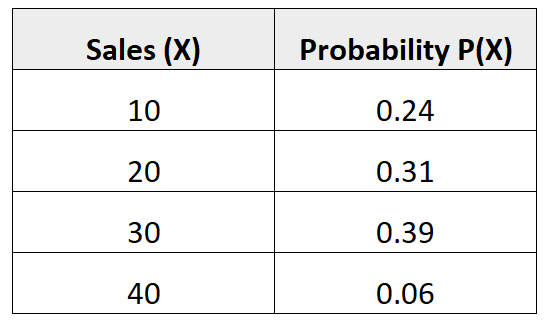
Вопрос: Каково среднее количество ожидаемых продаж этого продавца в предстоящем месяце?
Решение: Среднее количество ожидаемых продаж рассчитывается как:
μ = 10*0,24 + 20*0,31 + 30*0,39 + 40*0,06 = 22,7 продаж.
Бонус: калькулятор распределения вероятностей
Вы можете использовать этот калькулятор для автоматического расчета среднего значения любого распределения вероятностей.
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Оглавление страницы:
Статистика. Числовые характеристики ряда чисел
Средним арифметическим нескольких чисел называется число, равное отношению суммы этих чисел к их количеству.
Другими словами, среднее арифметическое – это дробь, в числителе которой стоит сумма чисел, а взнаменателе – их количество.
Пример:
- Вычислить среднее арифметическое данных чисел: 6, 10, 16, 20.
Среднее арифметрическое: ( 6 + 10 + 16 + 20 ) 4 = 52 4 = 13
Медиана ряда чисел – это число, стоящее посередине упорядоченного ряда чисел, если количество чисел в ряду нечётное.
Пример:
- Найти медиану ряда чисел: 12, 2, 11, 3, 7, 10, 3
Сперва упорядочим этот ряд (расположим числа в порядке возрастания, от меньшего к большему): 2, 3, 3, 7 , 10, 11, 12
Посередине данного упорядоченного ряда стоит число 7.
Медиана ряда чисел – это полусумма двух стоящих посередине упорядоченного ряда чисел, если количество чисел в ряду чётное.
Пример:
- Найти медиану ряда чисел: 8, 3, 10, 1, 16, 2, 3
Сперва упорядочим этот ряд (расположим числа в порядке возрастания, от меньшего к большему): 2, 3, 7 , 10 , 11, 12
Посередине данного упорядоченного ряда стоят два числа: 7 и 10.
Их полусумма равна: 7 + 10 2 = 17 2 = 8,5
Размах ряда чисел – это разность между наибольшим и наименьшим числом.
Пример:
- Найти размах ряда чисел: 8, 3, 10, 1, 16, 2, 3
Для удобства упорядочим этот ряд: 1, 2, 3, 3, 8, 10, 16
Наибольшее значение ряда: 16. Наименьшее значение ряда: 1.
Размах: 16 − 1 = 15
Мода ряда чисел – наиболее часто встречающееся число в этом ряду.
Ряд чисел может иметь более одной моды, а может вообще не иметь моды.
Примеры:
- Найти моду ряда: 1, 5, 6, 3 , 10, 32, 4, 3
Число, встречающееся в этом ряду чаще всех: 3.
Данный ряд имеет моду: 3.
- Найти моду ряда: 5, 2, 3, 4, 1, 0, 8
Каждое число в данном ряде встречается одинаковое количество раз (один раз).
Данный ряд не имеет моды.
- Найти моду ряда: 9 , 1 , 4 , 10 , 17 , 1 , 33 , 6 , 9 , 8 , 5 , 5
Числа 1, 5, 9 встречаются в этом ряде наибольшее количество раз (по два раза).
Данный ряд имеет три моды: 1, 5, 9.
Вероятности
Случайное событие – это событие, которое может произойти, а может не произойти.
Мы называем событие случайным, если нельзя утверждать, что это событие в данных обстоятельствах непременно произойдёт.
События обозначаются заглавными латинскими буквами.
Частота случайного события A в серии опытов – это отношение числа тех опытов, в которых событие A произошло, к общему числу проведенных опытов.
Примеры:
- Какова частота события «выпал орёл», если в серии опытов из 20 бросков монеты решка выпала 8 раз?
Если решка выпала 8 раз, то орёл выпал 20 − 8 = 12 раз.
Частота: 12 20 = 6 10 = 0,6
- Какова частота события «выпало чётное число очков» в серии опытов из восьми бросков кубика, если результаты представлены в виде числового ряда: 3, 2, 3, 5, 1, 1, 6, 4
Как мы видим, чётных чисел выпало три штуки.
Частота: 3 8 = 0,375
Каждое случайное событие делится на несколько элементарных исходов. Они делятся на благоприятные исходы и неблагоприятные исходы.
Например, для события «выпало четное число очков» при броске кубика:
- Благоприятные исходы:
«выпало два очка», «выпало четыре очка», «выпало шесть очков»
- Неблагоприятные исходы:
«выпало одно очко», «выпало три очка», «выпало пять очков»
Все возможные исходы = благоприятные исходы + неблагоприятные исходы.
Вероятность случайного события P ( A ) – это отношение благоприятных исходов m к общему числу исходов n. P ( A ) = m n
Вероятность случайного события лежит в пределах от 0 до 1. 0 ≤ P ( A ) ≤ 1
Сумма вероятностей всех элементарных исходов случайного эксперимента равна 1.
Примеры:
- Какова вероятность вытащить из шляпы, в которой лежат три синих шара, белого кролика?
Число благоприятных исходов: m = 0 , так как ни одного кролика нет.
Число всех возможных исходов: n = 3 , так как есть три объекта, которые можно достать из шляпы.
A=«достать кролика», посчитаем вероятность этого события. P ( A ) = m n = 0 3 = 0
- Какова вероятность вытащить из шляпы, в которой лежат три синих шара, синий шар?
Число благоприятных исходов: m = 3 , так как каждый из трех шариков синий, каждый подходит.
Число всех возможных исходов: n = 3 , так как есть три объекта, которые можно достать из шляпы.
A=«достать синий шар», посчитаем вероятность этого события. P ( A ) = m n = 3 3 = 1
- Какова вероятность вытащить из шляпы, в которой лежат три синих шара и девять красных шаров, синий шар?
Число благоприятных исходов: m = 3 , так как всего синих шаров в шляпе три.
Число всех возможных исходов: n = 3 + 9 = 12 , так как всего в шляпе 12 объектов, которые можно достать.
A=«достать синий шар», посчитаем вероятность этого события. P ( A ) = m n = 3 12 = 0,25
Событие A ¯ называется противоположным событию A, если событие A ¯ происходит тогда, когда событие A не происходит (то есть вместо события A происходит событие A ¯ ).
Примеры противоположных событий:
- A : «купить молоко», A ¯ : «не купить молоко»
- A : «прибор исправен», A ¯ : «прибор неисправен»
- A : «выпал орёл», A ¯ : «выпала решка»
- A : «на игральной кости выпало нечетное число», A ¯ : «на игральной кости выпало чётное число»
Вероятность противоположного события определяется по формуле: P ( A ¯ ) = 1 − P ( A )
Примеры:
- Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,28. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Пусть событие A: «ручка пишет плохо».
Противоположное событие: A ¯ : «ручка пишет хорошо»
P ( A ) = 0,28. Найдём вероятность противоположного события по формуле:
P ( A ¯ ) = 1 − P ( A ) = 1 − 0,28 = 0,72
- В среднем из 100 карманных фонариков, поступивших в продажу, 8 неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.
Пусть событие A: «фонарик неисправен»
Противоположное событие A ¯ : «фонарик исправен»
P ( A ) = 8 100 = 0,08
P ( A ¯ ) = 1 − P ( A ) = 1 − 0,08 = 0,92
Ответ: 0,92
Теоремы о вероятностных событиях
Два события называются несовместными, если они не могут произойти одновременно, то есть если наступление одного из них исключает наступление другого. В противном случае события называются совместными.
Примеры несовместных событий:
- Выпадение 1, выпадение 5, выпадение 6 при бросании кости
За один бросок может выпасть либо 1, либо 5, либо 6. Одновременно два или три значения выпасть не могут, только одно.
- Выпадение орла, выпадение решки при броске монеты
За один бросок может выпасить либо орёл, либо решка, одновременно орёл и решка выпасть не могут.
Теорема сложения вероятностей несовместных событий:
Вероятность появления одного из двух (или более) несовместных событий равна сумме вероятностей этих событий.
P ( A + B ) = P ( A ) + P ( B )
Примеры:
- Паша на экзамене вытягивает билет. Все билеты относятся к одной из трех тем: «углы», «треугольники», «четырехугольники». Вероятность того, что Паше попадется билет по теме «треугольники» равна 0,22, вероятность того, что ему попадется билет по теме «четырехугольники» равна 0,31, вероятность того, что ему попадется билет по теме «углы» равна 0,47. Паша знает тему «углы» и тему «треугольники», но «четырехугольники» вызывают у него затруднения. Найдите вероятность того, что ему попадется билет по теме «треугольники» или по теме «углы».
Решение:
Событие A = «вытащить билет по теме углы» и событие B = «вытащить билет по теме треугольники» – несовместные.
Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:
P ( A + B ) = P ( A ) + P ( B )
P ( A + B ) = 0,47 + 0,22 = 0,69
Ответ: 0,69
- Макар играет в лотерею. Вероятность выиграть стиральную машину равна 0,001, вероятность выиграть денежный приз 0,013, вероятность выиграть сувенир 0,04. Найдите вероятность того, что лотерейный билет принесёт Макару какой-нибудь приз.
Решение:
Событие A = «выиграть машину», событие B = «выиграть денежный приз» и событие C = «выиграть сувенир» несовместные.
Вероятность появления одного из трех несовместных событий равна сумме вероятностей этих событий:
P ( A + B + C ) = P ( A ) + P ( B ) + P ( C )
P ( A + B + C ) = 0,001 + 0,013 + 0,04 = 0,054
Ответ: 0,054
Два события называются независимыми, если наступление одного из них не влияет на вероятность наступления другого. В противном случает события называются зависимыми.
Примеры независимых событий:
- Игральный кубик бросают два раза. Выпадение трех очков при первом броске и выпадение четырех очков при втором броске являются независимыми событиями.
При первом броске вероятность выпадания трех очков равна 1 6 , при втором броске вероятность выпадания четырех очков снова равна 1 6 . Не смотря на то, что кубик кидают два раза, у него по-прежнему остаётся шесть граней, при каждом новом броске может выпасть одно из шести чисел с той же самой вероятностью 1 6 , вне зависимости от того, что выпадало до этого.
- Монету бросают три раза. Выпадение орла при первом броске, выпадение орла при втором броске, выпадение орла при третье броске явлюятся независимыми событиями.
При первом броске вероятность выпадения орла равна 0,5, при втором броске вероятность выпадения орла равна 0,5, при третьем броске вероятность выпадения орла равна 0,5. Не смотря на то, что монету кидают несколько раз, при каждом новом броске может выпасть орёл или решка с той же самой вероятностью 0,5, вне зависимости от того, что выпадало до этого.
Примеры зависимых событий:
- В шляпе лежат три синих шара и два красных. Последовательно извлекются два шара. Извлечь в первый раз синий шар и извлечь во второй раз синий шар – два зависимых события.
Почему же они зависимые? Потому что первоначально вероятность вытащить синий шар равна 3 5 (всего шаров 5, синих 3). После того, как один синий шар вытащили, количество благоприятных исходов изменилась, общее количество шаров изменилось. При следующем вынимании шара из шляпы вероятность вытащить синий шар равна 2 4 = 1 2 (всего шаров 4, синих 2). Таким образом наступление первого события влияет на вероятность наступления второго.
Теорема умножения вероятностей независимых событий:
Вероятность появления двух (или более) независимых событий равна произведению вероятностей этих событий.
P ( A ⋅ B ) = P ( A ) ⋅ P ( B )
Примеры:
- В первой шляпе лежит один синий шар и один красный, во второй шляпе лежит 1 синий шар и 4 красных. Из каждой шляпы извлекли по одному шару. Найдите вероятность того, что оба шара красные.
Решение:
Событие A: «извлечь красный шар из первой шляпы».
Событие B: «извлечь красный шар из второй шляпы».
Оба этих события независимы друг от друга, так как при извлечении шпара из первой шляпы, вторая остаётся нетронутой. Найдём вероятности этих событий.
P ( A ) = 1 2 (всего шаров два, красных – один).
P ( B ) = 4 5 (всего шаров пять, красных четыре).
P ( A ⋅ B ) = P ( A ) ⋅ P ( B )
P ( A ⋅ B ) = 1 2 ⋅ 4 5 = 0,4
Ответ: 0,4
- Стрелок 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,9. Найдите вероятность того, что стрелок первые 2 раза попал в мишени, а последний раз промахнулся.
Решение:
Событие A: «попадание», событие B: «промах». По условию P ( A ) = 0,9. Найдём вероятность промаха, она равна
P ( B ) = 1 − P ( A ) = 1 − 0,9 = 0,1
Каждый из выстрелов – событие, не зависящее от предыдущих или последующих выстрелов, то есть все три события – независимые. Вероятность появления трех независимых событий равна произведению их вероятностей, то есть
P ( A ⋅ A ⋅ B ) = P ( A ) ⋅ P ( A ) ⋅ P ( B )
P ( A ⋅ A ⋅ B ) = 0,9 ⋅ 0,9 ⋅ 0,1 = 0,081
Ответ: 0,081
Симметричная монета в теории вероятности
Математическая монета, которая используется в теории вероятности, лишена многих качеств бычной моенты: цвета, размера, веса и достоинства. Она не сделана ни из какого материала и не может служить платёжным средством. Монета имеет две стороны, одна из которых орёл (О), а другая решка (Р). Монету бросают и она падает одной стороной вверх. Никаких других свойств у монеты нет. Рассмотрим различные опыты с монетой
Бросание одной монеты
Возможные исходы:
О
Р
Всего два исхода. Вероятность каждого исхода из двух возможных равна 1 2 = 0,5
Бросание двух монет (бросание одной монеты два раза подряд)
Возможные исходы:
О О
О Р
Р О
Р Р
Всего четыре исхода. Вероятность каждого исхода из четырех возможных равна 1 4 = 0,25
Бросание трех монет (бросание одной монеты три раза подряд)
Возможные исходы:
О О О
О О Р
О Р О
О Р Р
Р О О
Р О Р
Р Р О
Р Р Р
Всего восемь исходов. Вероятность каждого исхода из восьми возможных равна 1 8 = 0,125
Бросание четырех монет (бросание одной монеты четыре раза подряд)
Возможные исходы:
О О О О
О О О Р
О О Р О
О О Р Р
О Р О О
О Р О Р
О Р Р О
О Р Р Р
Р О О О
Р О О Р
Р О Р О
Р О Р Р
Р Р О О
Р Р О Р
Р Р Р О
Р Р Р Р
Всего шестнадцать исходов. Вероятность каждого исхода из шестнадцати возможных равна 1 16 = 0,0625
Примеры:
- Симметричную монету бросают три раза подряд. Какова вероятность, что решка выпадет ровно один раз?
Решение:
Всего восемь различных исходов (см. опыт с бросанием трех монет). Исходов, в которых решка выпала ровно один раз, три.
P = 3 8 = 0,375
Ответ: 0,375
- Cимметричную монету бросают четыре раза подряд. Найдите вероятность того, что орёл выпадет хотя бы два раза.
Решение:
В опыте с бросанием четырех монет всего шестнадцать различных исходов. Благоприятные исходы – те, в которых выпало два, три или четыре орла. Таких исходов всего одиннадцать.
P = 11 16 = 0,6875
Ответ: 0,6875
Симметричная игральная кость в теории вероятности
Математическая игральная кость, которая используется в теории вероятности, это правильная кость, у которой шансы на выпадение каждой грани равны. Подобно математической монете, математическая кость не имеет ни цвета, ни размера. Ни веса, ни иых материальных качеств. Рассмотрим различные опыты с игральной костью.
Бросание одной кости
Возможные исходы: 1, 2, 3, 4, 5, 6. Всего шесть исходов. Вероятность каждого исхода из шести возможных равна 1 6 .
Бросание двух костей (бросание одной кости два раза подряд)
Для того, чтобы перебрать все возможные варианты, составим таблицу:
Первое число в паре – количество очков, выпавших на первом кубике. Второе число в паре – количество очков, выпавших на втором кубике. Всего возможно тридцать шесть различных исходов.
Такую таблицу не составит труда нарисовать на экзамене, если попадётся задача на бросание двух кубиков. Сумма чисел в ячейке – сумма выпавших очков.
Примеры:
- Какова вероятность, что сумма очков при бросании двух кубиков, будет равна 7?
Решение:
Как видно из таблицы, всего 36 различных вариантов выпадания очков на двух кубиках. Благоприятных вариантов – когда сумма очков будет равна семи – всего 6.
P = 6 36 = 1 6
Ответ: 1 6
- Какова вероятность, что сумма очков при бросании двух кубиков, будет меньше десяти?
Решение:
Как видно из таблицы, всего 36 различных вариантов выпадания очков на двух кубиках. Благоприятные варианты – когда сумма очков будет равна 1, 2, 3, 4, 5, 6, 7, 8, или 9. Таких ячеек в таблице 30.
P = 30 36 = 5 6
Ответ: 5 6
Сре́днее арифмети́ческое (в математике и статистике) — разновидность среднего значения. Определяется как число, равное сумме всех чисел множества, делённой на их количество. Является одной из наиболее распространённых мер центральной тенденции.
Предложена (наряду со средним геометрическим и средним гармоническим) ещё пифагорейцами[1].
Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).
На случай, если количество элементов множества чисел стационарного случайного процесса бесконечное, в качестве среднего арифметического играет роль математическое ожидание случайной величины.
Введение[править | править код]
Обозначим множество чисел X = (x1, x2, …, xn) — тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной (
, произносится «x с чертой»).
Для обозначения среднего арифметического всей совокупности чисел обычно используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее, или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E{xi} есть математическое ожидание этой выборки.
На практике разница между μ и в том, что μ является типичной переменной, потому что видеть можно скорее выборку, а не всю генеральную совокупность. Поэтому, если выборку представлять случайным образом (в терминах теории вероятностей), тогда (но не μ) можно трактовать как случайную переменную, имеющую распределение вероятностей на выборке (вероятностное распределение среднего).
Обе эти величины вычисляются одним и тем же способом:
Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.
В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.
Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины (например, среднее арифметическое взвешенное, среднее геометрическое взвешенное, среднее гармоническое взвешенное).
Примеры[править | править код]
- Для получения среднего арифметического трёх чисел необходимо сложить их и разделить на 3:
- Для получения среднего арифметического четырёх чисел необходимо сложить их и разделить на 4:
Непрерывная случайная величина[править | править код]
Если существует интеграл от некоторой функции 
одной переменной, то среднее арифметическое этой функции на отрезке ![[a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)
определяется через определённый интеграл:
![{displaystyle {overline {f(x)}}_{[a;b]}={frac {1}{b-a}}int _{a}^{b}f(x)dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db0287956e28e4ced0b833809f5b0ed44aaa7339)
Здесь для определения отрезка подразумевается, что 
причём 
чтобы знаменатель не был равен 0.
Линейное преобразование[править | править код]
Линейно преобразованный набор данных 
можно получить при применении линейного отображения 
к метрически скалируемому набору данных 
следующим образом: 
. Тогда новое среднее значение набора данных будет равно 
, так как 
.
Некоторые проблемы применения среднего[править | править код]
Отсутствие робастности[править | править код]
Хотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, то есть среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.
Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число — из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.
Сложный процент[править | править код]
Если числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.
Например, если акции в первый год упали на 10 %, а во второй год выросли на 60 %, тогда вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 60 %) / 2 = 25 % некорректно, а правильное среднее значение в этом случае дают совокупные ежегодные темпы роста: годовой рост получается 20 %.
Причина этого в том, что проценты имеют каждый раз новую стартовую точку: 60 % — это 60 % от меньшего, чем цена в начале первого года, числа: если акции в начале стоили $30 и упали на 10 %, они в начале второго года стоят $27. Если акции выросли на 60 %, они в конце второго года стоят $43,2. Арифметическое среднее этого роста 25 %, но, поскольку акции выросли за 2 года всего на $13,2, средний рост в 20 % даёт конечный результат $43,2:
$30 × (1 – 0,1)*(1 + 0,6) = $30 × (1 + 0,2)*(1 + 0,2) = $43,2. Если же использовать таким же образом среднее арифметическое значение 25 %, мы не получим фактическое значение: $30 × (1 + 0,25)*(1 + 0,25) = $46,875.
Сложный процент в конце 2 года: 90 % * 160 % = 144 %, то есть общий прирост 44 %, а среднегодовой сложный процент 
, то есть среднегодовой прирост 20 %.
Таким образом среднегодовой прирост рассчитывается по формуле среднего геометрического
Направления[править | править код]
При расчёте среднего арифметического значений некоторой переменной, изменяющейся циклически (например, фаза или угол), следует проявлять особую осторожность. Например, среднее чисел 1° и 359° будет равно 180°. Этот результат неверен по двум причинам.
Среднее значение для циклической переменной, рассчитанное по приведённой формуле, будет искусственно сдвинуто относительно настоящего среднего к середине числового диапазона. Из-за этого среднее рассчитывается другим способом, а именно, в качестве среднего значения выбирается число с наименьшей дисперсией (центральная точка). Также вместо вычитания используется модульное расстояние (то есть, расстояние по окружности). Например, модульное расстояние между 1° и 359° равно 2°, а не 358° (на окружности между 359° и 360° = 0° — один градус, между 0° и 1° — тоже 1°, в сумме — 2°).
Примечания[править | править код]
- ↑ Cantrell, David W., «Pythagorean Means» Архивная копия от 22 мая 2011 на Wayback Machine from MathWorld
См. также[править | править код]
- Арифметическая пропорция
- Арифметическая прогрессия
- Неравенство Швейцера
- Среднее арифметическое взвешенное
Ссылки[править | править код]
- Арифметическая средняя // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Финансовая математика. Дисперсия. Среднее арифметическое. Среднеквадратическое отклонение. Коэффициент вариации Архивная копия от 19 сентября 2020 на Wayback Machine / Методики финансового анализа
- Среднее арифметическое — показатель центральной тенденции / Теория вероятностей и математическая статистика
Содержание материала
- Среднее арифметическое
- Видео
- Среднее арифметическое
- Межквартильный размах
- Мода выборки
- Размах, полученный из процентилей
- Что такое процентили
- Применение процентилей
- Статистические характеристики
- Упорядоченный ряд и таблица частот
- Как определить размах числового ряда?
- Мода и медиана
- Бонус: Вебинары с нашего курса по подготовке к ЕГЭ
- ЕГЭ Теория вероятности
Среднее арифметическое
Вероятно, большинство из вас использовало такую важную описательную статистику, как среднее.
Среднее — очень информативная мера “центрального положения” наблюдаемой переменной, особенно если сообщается ее доверительный интервал. Исследователю нужны такие статистики, которые позволяют сделать вывод относительно популяции в целом. Одной из таких статистик является среднее.
Доверительный интервал для среднего представляет интервал значений вокруг оценки, где с данным уровнем доверия, находится “истинное” (неизвестное) среднее популяции.
Например, если среднее выборки равно 23, а нижняя и верхняя границы доверительного интервала с уровнем p=.95 равны 19 и 27 соответственно, то можно заключить, что с вероятностью 95% интервал с границами 19 и 27 накрывает среднее популяции.
Если вы установите больший уровень доверия, то интервал станет шире, поэтому возрастает вероятность, с которой он “накрывает” неизвестное среднее популяции, и наоборот.
Хорошо известно, например, что чем “неопределенней” прогноз погоды (т.е. шире доверительный интервал), тем вероятнее он будет верным. Заметим, что ширина доверительного интервала зависит от объема или размера выборки, а также от разброса (изменчивости) данных. Увеличение размера выборки делает оценку среднего более надежной. Увеличение разброса наблюдаемых значений уменьшает надежность оценки.
Вычисление доверительных интервалов основывается на предположении нормальности наблюдаемых величин. Если это предположение не выполнено, то оценка может оказаться плохой, особенно для малых выборок.
При увеличении объема выборки, скажем, до 100 или более, качество оценки улучшается и без предположения нормальности выборки.
Довольно трудно «ощутить» числовые измерения, пока данные не будут содержательно обобщены. Диаграмма часто полезна в качестве отправной точки. Мы можем также сжать информацию, используя важные характеристики данных. В частности, если бы мы знали, из чего состоит представленная величина, или если бы мы знали, насколько широко рассеяны наблюдения, то мы бы смогли сформировать образ этих данных.
Среднее арифметическое, которое очень часто называют просто «среднее», получают путем сложения всех значений и деления этой суммы на число значений в наборе.
Это можно показать с помощью алгебраической формулы. Набор n наблюдений переменной X можно изобразить как X1, X2, X3, …, Xn. Например, за X можно обозначить рост индивидуума (см), X1 обозначит рост 1-го индивидуума, а Xi — рост i-го индивидуума. Формула для определения среднего арифметического наблюдений 
(произносится «икс с чертой»):
= (Х1 + Х2 + … + Xn) / n
Можно сократить это выражение:
где 
(греческая буква «сигма») означает «суммирование», а индексы внизу и вверху этой буквы означают, что суммирование производится от i = 1 до i = n. Это выражение часто сокращают еще больше:
или 
Видео
Среднее арифметическое
Понятие среднего значения часто используется в повседневной жизни.
Примеры:
- средняя зарплата жителей страны;
- средний балл учащихся;
- средняя скорость движения;
- средняя производительность труда.
Речь идет о среднем арифметическом — результате деления суммы элементов выборки на их количество.
Среднее арифметическое — это результат деления суммы элементов выборки на их количество.
Вернемся к нашему примеру
Узнаем сколько в среднем мы тратили в каждом из шести дней:
Межквартильный размах
В статистике для анализа выборки часто прибегают к другому показателю вариации – межквартильному размаху. Квартиль – это то значение, которые делит ранжированные (отсортированные) данные на части, кратные одной четверти, или 25%. Так, 1-й квартиль – это значение, ниже которого находится 25% совокупности. 2-й квартиль делит совокупность данных пополам (то бишь медиана), ну и 3-й квартиль отделяет 25% наибольших значений. Так вот межквартильный размах – это разница между 3-м и 1-м квартилями. У данного показателя есть одно неоспоримое преимущество: он является робастным, т.е. не зависит от аномальных отклонений.
Наглядное отображение размаха вариации и межкварительного расстояния производят с помощью диаграммы «ящик с усами».
Мода выборки
Иногда важно знать не среднее арифметическое выборки, а то, какая из ее вариант встречается наиболее часто. Так, при управлении магазином одежды менеджеру не важен средний размер продаваемых футболок, а необходима информация о том, какие размеры наиболее популярны. Для этого используется такой показатель, как мода выборки.
В примере с математическим тестом сразу 3 ученика набрали по 13 баллов, а частота всех других вариант не превысила 2, поэтому мода выборки равна 13. Возможна ситуация, когда в ряде есть сразу две или более вариант, которые встречаются одинаково часто и чаще остальных вариант. Например, в ряде
1, 2, 3, 3, 3, 4, 5, 5, 5
варианты 3 и 5 встречаются по три раза. В таком случае ряд имеет сразу две моды – 3 и 5, а всю выборку именуют мультимодальной. Особо выделяется случай, когда в выборке все варианты встречаются с одинаковой частотой:
6, 6, 7, 7, 8, 8.
Здесь числа 6, 7 и 8 встречаются одинаково часто (по два раза), а другие варианты отсутствуют. В таких случаях говорят, что ряд не имеет моды.
Размах, полученный из процентилей
Что такое процентили
Предположим, что мы расположим наши данные упорядоченно от самой маленькой величины переменной X и до самой большой величины. Величина X, до которой расположен 1% наблюдений (и выше которой расположены 99% наблюдений), называется первым процентилем.
Величина X, до которой находится 2% наблюдений, называется 2-м процентилем, и т. д.
Величины X, которые делят упорядоченный набор значений на 10 равных групп, т. е. 10-й, 20-й, 30-й,…, 90 и процентили, называются децилями. Величины X, которые делят упорядоченный набор значений на 4 равные группы, т.е. 25-й, 50-й и 75-й процентили, называются квартилями. 50-й процентиль — это медиана.
Применение процентилей
Мы можем добиться такой формы описания рассеяния, на которую не повлияет выброс (аномальное значение), исключая экстремальные величины и определяя размах остающихся наблюдений.
Межквартильный размах — это разница между 1-м и 3-м квартилями, т.е. между 25-м и 75-м процентилями. В него входят центральные 50% наблюдений в упорядоченном наборе, где 25% наблюдений находятся ниже центральной точки и 25% — выше.
Интердецильный размах содержит в себе центральные 80% наблюдений, т. е. те наблюдения, которые располагаются между 10-м и 90-м процентилями.
Мы часто используем размах, который содержит 95% наблюдений, т.е. он исключает 2,5% наблюдений снизу и 2,5% сверху. Указание такого интервала актуально, например, для осуществления диагностики болезни. Такой интервал называется референтный интервал, референтный размах или нормальный размах.
Статистические характеристики
К основным статистическим характеристикам выборки данных…
Какая еще такая «выборка»!?
Под словом «выборка» подразумевается просто данные, которые ты собираешься исследовать.
Дальше на примерах будет все понятно.
Так вот к основным статистическим характеристикам выборки данных относятся:
- объем выборки,
- размах выборки,
- среднее арифметическое,
- мода,
- медиана,
- частота,
- относительная частота.
Стоп-стоп-стоп! Сколько новых слов! Давай обо всем по порядку.
Упорядоченный ряд и таблица частот
В ряде данных в таблице 1 числа приведены в произвольном порядке. Перепишем ряд так, чтобы все числа шли в неубывающем порядке, то есть от самого маленького к самому большому:
12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.
Такую запись называют упорядоченным рядом данных.
Его характеристики ничем не отличаются от изначальной выборки, однако с ним удобнее работать. С его помощью можно видеть, что ни одному ученику не удалось набрать 22 или 23 балла на тесте, но сразу двое учащихся дали 25 правильных ответов. На основе упорядоченного ряда данных несложно составить таблицу частот, в которой будет указано, как часто та или иная варианта выборки встречается в ряде. Выглядеть она будет так:
При составлении этой таблицы мы исключили из нее те варианты количества набранных баллов, частота которых равна нулю (от 0 до 12, 22 и 23).Заметим, что сумма чисел в нижней строке таблицы частот должна равняться объему выборки. Действительно,
2+3+1+1+2+2+1+2+2+1+1+2 = 20.
С помощью таблицы частот можно быстрее посчитать среднее арифметическое выборки. Для этого каждую варианту надо умножить на ее частоту, после чего сложить полученные результаты и поделить их на объем выборки:
(12•2+13•3+14•1+15•1+16•2+17•2+18•1+19•2+20•2+21•1+24•1+25•2):20 =
(24+39+14+15+32+34+18+38+40+42+24+50):20 = 349:20 = 17,45.
Как определить размах числового ряда?
Среднее арифметическое, размах, мода и медиана
- Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых. …
- Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел. …
- Модой ряда чисел называется число, которое встречается в данном ряду чаще других.
Мода и медиана
Модой называют элемент, который встречается в выборке чаще других.
Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров
Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.
Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат
Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.
Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.
Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:
Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:
Выпишем рост спортсменов отдельно:
180, 182, 183, 184, 185, 188, 190
В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.
Медианой упорядоченной выборки называют элемент, располагающийся посередине.
Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.
В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану
Но возможны случаи, когда количество элементов выборки чётно.
К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:
Построим этих шестерых спортсменов по росту:
Выпишем рост спортсменов отдельно:
180, 182, 184, 186, 188, 190
В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.
В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.
Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186
Найдем среднее арифметическое элементов 184 и 186
Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.
Поэтому более точное определение медианы зависит от количества элементов в выборке.
Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.
Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.
Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190
Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:
Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:
0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1
Определим среднее арифметическое для данной выборки — получим значение 2,2
По данному значению можно сказать, что в среднем у спортсменов 2,2 очка
Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:
0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 3, 4, 5, 5, 6
В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.
Бонус: Вебинары с нашего курса по подготовке к ЕГЭ
Этот вебинар по родственной математической статистике теме — теории вероятности.
А вот наша статья о теории вероятности.
ЕГЭ Теория вероятности
Что вы узнаете на этом уроке?
20% урока — теория.
- Мы разберём, что такое вероятность;
- Узнаем, что можно называть случайным событием;
- Рассмотрим, на какие типы можно разделить события:
- Что такое совместные и несовместные события;
- Что такое зависимые и независимые события;
- Выучим формулы, которые нужно применять для разных типов событий.
80% урока — решение задач
- Мы решим 54 задачи на первом уроке и ещё 22 (посложнее) на втором;
- Отработаем все 6 типов задач, которые могут встретиться в ЕГЭ:
