Average or mean value of array
Syntax
Description
example
M = mean( returns the mean of theA)
elements of A along the first array dimension whose size is
greater than 1.
-
If
Ais a vector, thenmean(A)returns
the mean of the elements. -
If
Ais a matrix, thenmean(A)returns
a row vector containing the mean of each column. -
If
Ais a multidimensional array, then
mean(A)operates along the first array dimension
whose size is greater than 1, treating the elements as vectors. The size of
Min this dimension becomes1,
while the sizes of all other dimensions remain the same as in
A. -
If
Ais a table
or timetable, thenmean(A)returns a one-row table
containing the mean of each variable. (since R2023a)
example
M = mean(A,"all")
returns the mean over all elements of A.
example
M = mean( returns theA,dim)
mean along dimension dim. For example, if A is
a matrix, then mean(A,2) returns a column vector containing the
mean of each row.
example
M = mean(A,vecdim)
returns the mean based on the dimensions specified in the vector
vecdim. For example, if A is a matrix,
then mean(A,[1 2]) returns the mean of all elements in
A because every element of a matrix is contained in the array
slice defined by dimensions 1 and 2.
example
M = mean(___, returns the meanouttype)
with a specified data type for any of the previous syntaxes.
outtype can be "default",
"double", or "native".
example
M = mean(___, specifiesmissingflag)
whether to include or omit missing values in A. For example,
mean(A,"omitmissing") ignores all missing values when
computing the mean. By default, mean includes missing
values.
Examples
collapse all
Mean of Matrix Columns
Create a matrix and compute the mean of each column.
A = [0 1 1; 2 3 2; 1 3 2; 4 2 2]
A = 4×3
0 1 1
2 3 2
1 3 2
4 2 2
M = 1×3
1.7500 2.2500 1.7500
Mean of Matrix Rows
Create a matrix and compute the mean of each row.
A = [0 1 1; 2 3 2; 3 0 1; 1 2 3]
A = 4×3
0 1 1
2 3 2
3 0 1
1 2 3
M = 4×1
0.6667
2.3333
1.3333
2.0000
Mean of 3-D Array
Create a 4-by-2-by-3 array of integers between 1 and 10 and compute the mean values along the second dimension.
rng('default')
A = randi(10,[4,2,3]);
M = mean(A,2)
M =
M(:,:,1) =
8.0000
5.5000
2.5000
8.0000
M(:,:,2) =
10.0000
7.5000
5.5000
6.0000
M(:,:,3) =
6.0000
5.5000
8.5000
10.0000
Mean of Array Page
Create a 3-D array and compute the mean over each page of data (rows and columns).
A(:,:,1) = [2 4; -2 1]; A(:,:,2) = [9 13; -5 7]; A(:,:,3) = [4 4; 8 -3]; M1 = mean(A,[1 2])
M1 =
M1(:,:,1) =
1.2500
M1(:,:,2) =
6
M1(:,:,3) =
3.2500
To compute the mean over all dimensions of an array, you can either specify each dimension in the vector dimension argument, or use the "all" option.
Mean of Single-Precision Array
Create a single-precision vector of ones and compute its single-precision mean.
A = single(ones(10,1));
M = mean(A,"native")
The result is also in single precision.
Mean Excluding Missing Values
Create a matrix containing NaN values.
A = [1.77 -0.005 NaN -2.95; NaN 0.34 NaN 0.19]
A = 2×4
1.7700 -0.0050 NaN -2.9500
NaN 0.3400 NaN 0.1900
Compute the mean values of the matrix, excluding missing values. For matrix columns that contain any NaN value, mean computes with the non-NaN elements. For matrix columns that contain all NaN values, the mean is NaN.
M = 1×4
1.7700 0.1675 NaN -1.3800
Input Arguments
collapse all
A — Input array
vector | matrix | multidimensional array | table | timetable
Input array, specified as a vector, matrix, multidimensional array, table, or timetable.
-
If
Ais a scalar, then
mean(A)returns
A. -
If
Ais an empty 0-by-0 matrix, then
mean(A)returns
NaN.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | char | datetime | duration | table | timetable
dim — Dimension to operate along
positive integer scalar
Dimension
to operate along, specified as a positive integer scalar. If you do not specify the dimension,
then the default is the first array dimension of size greater than 1.
Dimension dim indicates the dimension whose
length reduces to 1. The size(M,dim) is 1,
while the sizes of all other dimensions remain the same.
Consider an m-by-n input matrix,
A:
-
mean(A,1)computes the mean of the elements
in each column ofAand returns a
1-by-nrow
vector.
-
mean(A,2)computes the mean of the elements
in each row ofAand returns an
m-by-1column
vector.
mean returns A when dim is
greater than ndims(A) or when size(A,dim) is 1.
vecdim — Vector of dimensions
vector of positive integers
Vector of dimensions, specified as a vector of positive integers. Each
element represents a dimension of the input array. The lengths of the output
in the specified operating dimensions are 1, while the others remain the
same.
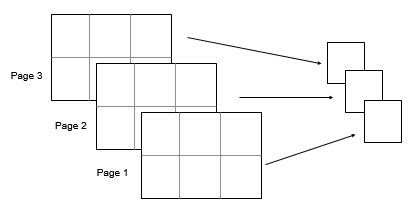
Consider a 2-by-3-by-3 input array, A. Then
mean(A,[1 2]) returns a 1-by-1-by-3 array whose
elements are the means over each page of A.
outtype — Output data type
"default" (default) | "double" | "native"
Output data type, specified as one of the values in this table. These options also specify the
data type in which the operation is performed.
outtype |
Output data type |
|---|---|
"default" |
double, unless the input data type is single,duration,datetime, table, ortimetable, in which case, the outputis "native" |
"double" |
double, unless the data input type is duration,datetime, table,or timetable, in which case,"double" is not supported |
"native" |
Same data type as the input, unless:
|
missingflag — Missing value condition
"includemissing" (default) | "includenan" | "includenat" | "omitmissing" | "omitnan" | "omitnat"
Missing value condition, specified as one of the values in this
table.
| Value | Input Data Type | Description |
|---|---|---|
"includemissing" |
All supported data types |
Include missing values in |
"includenan" |
double, single,duration |
|
"includenat" |
datetime |
|
"omitmissing" |
All supported data types | Ignore missing values inA, and compute the mean over fewerpoints. If all elements in the operating dimension are missing, then the corresponding element in M is missing. |
"omitnan" |
double, single,duration |
|
"omitnat" |
datetime |
More About
collapse all
Mean
For a finite-length vector A made up of
N scalar observations, the mean is defined as
Extended Capabilities
Tall Arrays
Calculate with arrays that have more rows than fit in memory.
This function fully supports tall arrays. For
more information, see Tall Arrays.
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
-
If you specify
dim, then it must
be a constant. -
The
outtypeandmissingflag
options must be constant character vectors or strings. -
Integer types do not support the
"native"output
data type option. -
See Variable-Sizing Restrictions for Code Generation of Toolbox Functions (MATLAB Coder).
GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.
Usage notes and limitations:
-
If you specify
dim, then it must be a constant. -
The
outtypeandmissingflagoptions
must be constant character vectors or strings. -
Integer types do not support the
"native"output data
type option.
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For
more information, see Run MATLAB Functions in Thread-Based Environment.
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
The mean function
partially supports GPU arrays. Some syntaxes of the function run on a GPU when you specify the
input data as a gpuArray (Parallel Computing Toolbox). Usage notes and limitations:
-
The
"native"option is not supported.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
Usage notes and limitations:
-
The
"native"option is not supported.
For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a
expand all
R2023a: Perform calculations directly on tables and timetables
The mean function can calculate on all variables within a table or
timetable without indexing to access those variables. All variables must have data types
that support the calculation. For more information, see Direct Calculations on Tables and Timetables.
R2023a: Specify missing value condition
Include or omit all missing values in the input array when computing the mean by
using the "includemissing" or "omitmissing"
options. Previously, "includenan", "omitnan",
"includenat", and "omitnat" specified a
missing value condition that was specific to the data type of the input
array.
R2023a: Improved performance with small group size
The mean function shows improved performance when computing
over a real vector when the operating dimension is not specified. The function
determines the default operating dimension more quickly in R2023a than in
R2022b.
For example, this code computes the mean along the default vector dimension. The
code is about 2.2x faster than in the previous release.
function timingMean A = rand(10,1); for i = 1:8e5 mean(A); end end
The approximate execution times are:
R2022b: 0.91 s
R2023a: 0.41 s
The code was timed on a Windows® 10, Intel®
Xeon® CPU E5-1650 v4 @ 3.60 GHz test system using the
timeit function.
R2018b: Operate on multiple dimensions
Operate on multiple dimensions of the input array at a time. Specify a vector of
operating dimensions, or specify the "all" option to operate on
all array dimensions.
mean
Синтаксис
Описание
пример
M = mean( возвращает среднее значение элементов A)A вдоль первого измерения массива, размер которого не равняется 1.
-
Если
Aвектор, затемmean(A)возвращает среднее значение элементов. -
Если
Aматрица, затемmean(A)возвращает вектор-строку, содержащий среднее значение каждого столбца. -
Если
Aмногомерный массив, затемmean(A)действует вдоль первого измерения массива, размер которого не равняется 1, обрабатывая элементы как векторы. Эта размерность становится1в то время как размеры всех других размерностей остаются то же самое.
пример
M = mean( вычисляет среднее значение по всем элементам A,'all')A. Этот синтаксис допустим для MATLAB® версии R2018b и позже.
пример
M = mean( возвращает среднее значение по измерению A,dim)dim. Например, если A матрица, затем mean(A,2) вектор-столбец, содержащий среднее значение каждой строки.
пример
M = mean( вычисляет среднее значение на основе размерностей, заданных в векторном A,vecdim)vecdim. Например, если A матрица, затем mean(A,[1 2]) среднее значение всех элементов в A, поскольку каждый элемент матрицы содержится в срезе массивов, заданном размерностями 1 и 2.
пример
M = mean(___, возвращает среднее значение с заданным типом данных, с помощью любого из входных параметров в предыдущих синтаксисах. outtype)outtype может быть 'default''double', или 'native'.
пример
M = mean(___, задает, включать ли или не использовать nanflag)NaN значения от вычисления для любого из предыдущих синтаксисов. mean(A,'includenan') включает весь NaN значения в вычислении, в то время как mean(A,'omitnan') игнорирует их.
Примеры
свернуть все
Среднее значение столбцов матрицы
Создайте матрицу и вычислите среднее значение каждого столбца.
A = [0 1 1; 2 3 2; 1 3 2; 4 2 2]
A = 4×3
0 1 1
2 3 2
1 3 2
4 2 2
M = 1×3
1.7500 2.2500 1.7500
Среднее значение матричных строк
Создайте матрицу и вычислите среднее значение каждой строки.
A = [0 1 1; 2 3 2; 3 0 1; 1 2 3]
A = 4×3
0 1 1
2 3 2
3 0 1
1 2 3
M = 4×1
0.6667
2.3333
1.3333
2.0000
Среднее значение трехмерного массива
Создайте 4 2 3 массивами целых чисел между 1 и 10 и вычислите средние значения вдоль второго измерения.
rng('default')
A = randi(10,[4,2,3]);
M = mean(A,2)
M =
M(:,:,1) =
8.0000
5.5000
2.5000
8.0000
M(:,:,2) =
10.0000
7.5000
5.5000
6.0000
M(:,:,3) =
6.0000
5.5000
8.5000
10.0000
Среднее значение страницы массивов
Создайте трехмерный массив и вычислите среднее значение по каждой странице данных (строки и столбцы).
A(:,:,1) = [2 4; -2 1]; A(:,:,2) = [9 13; -5 7]; A(:,:,3) = [4 4; 8 -3]; M1 = mean(A,[1 2])
M1 =
M1(:,:,1) =
1.2500
M1(:,:,2) =
6
M1(:,:,3) =
3.2500
Начиная в R2018b, вычислять среднее значение по всем размерностям массива, можно или задать каждую размерность в векторном аргументе размерности или использовать 'all' опция.
Среднее значение массива с одинарной точностью
Создайте вектор с одинарной точностью из единиц и вычислите его среднее значение с одинарной точностью.
A = single(ones(10,1));
M = mean(A,'native')
Результат находится также в одинарной точности.
Значение, исключая NaN
Создайте вектор и вычислите его среднее значение, исключая NaN значения.
A = [1 0 0 1 NaN 1 NaN 0];
M = mean(A,'omitnan')
Если вы не задаете 'omitnan', затем mean(A) возвращает NaN.
Входные параметры
свернуть все
A — Входной массив
вектор | матрица | многомерный массив
Входной массив, заданный как векторный, матричный или многомерный массив.
-
Если
Aскаляр, затемmean(A)возвращаетA. -
Если
Aпустая матрица 0 на 0, затемmean(A)возвращаетNaN.
Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | char | datetime | duration
dim — Размерность, которая задает направление расчета
положительный целочисленный скаляр
Величина для работы, заданная как положительный целый скаляр. Если значение не задано, то по умолчанию это первый размер массива, не равный 1.
Размерность dim указывает на размерность, длина которой уменьшает до 1. size(M,dim) 1, в то время как размеры всех других размерностей остаются то же самое.
Рассмотрите двумерный входной массив, A.
-
Если
dim = 1, затемmean(A,1)возвращает вектор-строку, содержащий среднее значение элементов в каждом столбце.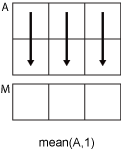
-
Если
dim = 2, затемmean(A,2)возвращает вектор-столбец, содержащий среднее значение элементов в каждой строке.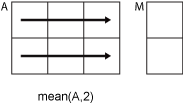
mean возвращает A когда dim больше ndims(A) или когда size(A,dim) 1.
Типы данных: double | single | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
vecdim — Вектор из размерностей
вектор из положительных целых чисел
Вектор из размерностей в виде вектора из положительных целых чисел. Каждый элемент представляет размерность входного массива. Продолжительности выхода в заданных операционных размерностях равняются 1, в то время как другие остаются то же самое.
Рассмотрите 2 3х3 входным массивом, A. Затем mean(A,[1 2]) возвращает 1 1 3 массивами, элементами которых являются средние значения по каждой странице A.
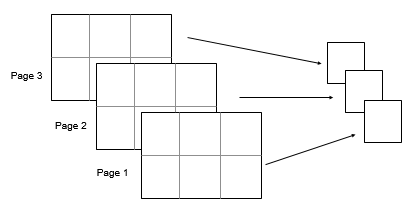
Типы данных: double | single | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
outtype — Тип выходных данных
'default' (значение по умолчанию) | 'double' | 'native'
Выходные данные вводят в виде 'default''double', или 'native'. Эти опции также задают тип данных, в котором выполняется операция.
outtype |
Тип выходных данных |
|---|---|
'default' |
double, если типом входных данных не является singleдлительность, или datetime, в этом случае выходом является 'native' |
'double' |
double, если типом данных не является duration или datetime, в этом случае, 'double' не поддерживается |
'native' |
совпадающий тип данных как вход, если
|
Типы данных: char
nanflag NaN условие
'includenan' (значение по умолчанию) | 'omitnan'
NaN условие в виде одного из этих значений:
-
'includenan'— ВключайтеNaNзначения при вычислении среднего значения, приведении кNaN. -
'omitnan'— Проигнорируйте весьNaNзначения во входе.
Для datetime массивы, можно также использовать 'omitnat' или 'includenat' не использовать и включать NaT значения, соответственно.
Типы данных: char
Больше о
свернуть все
Среднее значение
Для вектора случайной переменной A составил из скалярных наблюдений N, среднее значение задано как
Расширенные возможности
“Высокие” массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.
Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.
Указания и ограничения по применению:
-
Если вы задаете
dim, затем это должна быть константа. -
outtypeиnanflagопции должны быть постоянными векторами символов. -
Целочисленные типы не поддерживают
'native'выходные данные вводят опцию. -
“Смотрите информацию о генерации кода функций Toolbox (MATLAB Coder) в разделе “”Ограничения переменных размеров””.”.
Генерация кода графического процессора
Сгенерируйте код CUDA® для NVIDIA® графические процессоры с помощью GPU Coder™.
Указания и ограничения по применению:
-
Если вы задаете
dim, затем это должна быть константа. -
outtypeиnanflagопции должны быть постоянными векторами символов. -
Целочисленные типы не поддерживают
'native'выходные данные вводят опцию.
Основанная на потоке среда
Запустите код в фоновом режиме с помощью MATLAB® backgroundPool или ускорьте код с Parallel Computing Toolbox™ ThreadPool.
Эта функция полностью поддерживает основанные на потоке среды. Для получения дополнительной информации смотрите функции MATLAB Запуска в Основанной на потоке Среде.
Массивы графического процессора
Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.
Указания и ограничения по применению:
-
'native'опция не поддерживается.
Для получения дополнительной информации смотрите функции MATLAB Запуска на графическом процессоре (Parallel Computing Toolbox).
Распределенные массивы
Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.
Указания и ограничения по применению:
-
'native'опция не поддерживается.
Для получения дополнительной информации смотрите функции MATLAB Запуска с Распределенными Массивами (Parallel Computing Toolbox).
Представлено до R2006a
|
0 / 0 / 0 Регистрация: 30.05.2016 Сообщений: 2 |
|
|
1 |
|
Найти среднее значение элементов матрицы23.06.2016, 17:17. Показов 17091. Ответов 16
Ребят, не подскажете как найти среднее значение элементов матрицы, усреднение провести через while?
0 |
|
939 / 839 / 121 Регистрация: 23.11.2012 Сообщений: 2,489 |
|
|
24.06.2016, 23:01 |
2 |
|
Не по теме: zymlanin, вот жадины, никто и не муркнул до сих пор. zymlanin, все просто. Функция mean по умолчанию ищет среднее по строкам матрицы. Если надо – можно и по столбцам (см. дополнительные аргументы).
0 |
|
93 / 91 / 23 Регистрация: 08.05.2016 Сообщений: 521 |
|
|
24.06.2016, 23:07 |
3 |
|
А что значит “усреднение провести”?
0 |
|
minore 273 / 132 / 44 Регистрация: 05.02.2015 Сообщений: 874 |
||||
|
24.06.2016, 23:55 |
4 |
|||
|
Зачем смотреть дополнительные аргументы? достаточно вызывать функцию min для транспонированной матрицы.
0 |
|
939 / 839 / 121 Регистрация: 23.11.2012 Сообщений: 2,489 |
|
|
24.06.2016, 23:59 |
5 |
|
minore, почему min, если надо усреднение?
1 |
|
93 / 91 / 23 Регистрация: 08.05.2016 Сообщений: 521 |
|
|
25.06.2016, 00:04 |
6 |
|
А ответ не mean(mean())?
0 |
|
939 / 839 / 121 Регистрация: 23.11.2012 Сообщений: 2,489 |
|
|
25.06.2016, 00:14 |
7 |
|
Matasin, вполне возможно.
0 |
|
93 / 91 / 23 Регистрация: 08.05.2016 Сообщений: 521 |
|
|
25.06.2016, 00:25 |
8 |
|
А зачем тогда while?
0 |
|
Модератор 1573 / 1443 / 467 Регистрация: 13.09.2015 Сообщений: 4,956 |
|
|
25.06.2016, 05:15 |
9 |
|
А зачем тогда while? Очевидно, для решения через цикл while, т.е. без использования функции mean.
0 |
|
273 / 132 / 44 Регистрация: 05.02.2015 Сообщений: 874 |
|
|
25.06.2016, 14:33 |
10 |
|
ну не min а mean, суть от этого не меняется ) все равно с транспонированной матрицей вызвать можно.
0 |
|
R2D2 |
|
25.06.2016, 15:10
|
|
Не по теме: minore, оно то так. Для двумерной матрицы – можно. Но разработчики старались, вводили дополнительный аргумент для “общего случая”. Что б можно было среднее посчитать по любому направлению многомерной матрицы. не хочется людей огорчать…
0 |
|
minore |
|
25.06.2016, 15:22
|
|
Не по теме: не путайте народ) вы имели ввиду не “двумерную и многомерную матрицу” а “двумерный и многомерный массив”, так как любая матрица – это по определению двумерный массив )).
0 |
|
R2D2 |
|
25.06.2016, 15:35
|
|
Не по теме: minore, именно это имел ввиду. Простите. Позволяю себе иногда, грешным делом, нечеткую формулировку. Главное – что Вы меня поняли))
0 |
|
Krasme |
|
25.06.2016, 15:40
|
|
Не по теме: непонятно, зачем матрицу транспонировать, если в задаче стоит найти среднее значение элементов матрицы ни слова про строки или про столбцы…
0 |
|
Matasin 93 / 91 / 23 Регистрация: 08.05.2016 Сообщений: 521 |
||||
|
25.06.2016, 19:15 |
15 |
|||
|
Вариант
Скорее всего, можно упростить. Добавлено через 10 минут
0 |
|
Centurio Модератор 1573 / 1443 / 467 Регистрация: 13.09.2015 Сообщений: 4,956 |
||||
|
25.06.2016, 20:07 |
16 |
|||
|
Matasin, ну-у, чего-то вы слишком перемудрили…
2 |
|
93 / 91 / 23 Регистрация: 08.05.2016 Сообщений: 521 |
|
|
25.06.2016, 20:27 |
17 |
|
Не по теме: Это всего лишь вариант (только e не стоит меньше 1e-3 задавать). 😀 Не написано же, что именно должно находиться в while. zymlanin, любопытно, а откуда у Вас такая задача появилась?
0 |
- В этой теме 0 ответов, 1 участник, последнее обновление 3 года, 3 месяца назад сделано Васильев Владимир Сергеевич.
-
Сообщения
-
-
Написать программу, которая для целочисленной матрицы 10х10 определяет среднее арифметическое ее элементов и количество положительных элементов в каждой строке.
Материалы по теме: Массивы в С++
Программа должна:
- осуществлять ввод с клавиатуры значений элементов целочисленной матрицы;
- определять среднее арифметическое элементов целочисленной матрицы;
- определять количество положительных элементов в каждой строке целочисленной матрицы;
- выводить результаты вычислений.
Определение среднего арифметического прямоугольной матрицы воспользуемся формулой:
$$S = frac{sumlimits_{i=0}^{nrow} sumlimits_{j=0}^{ncol} A_{i,j}}{nrowcdot ncol} $$
где
a[i][j]—элемент i-й строки (i= 1, 2,..., nrow), j-го столбца (j=1, 2,..., ncol).Блок-схема алгоритма:

Исходный код программы:
#include <iostream> #include <iomanip> // для использования манипулятора using namespace std; void main() { // инициализация переменных const int nrow = 10, ncol = 20; int a[nrow][ncol]; int i, j; setlocale(LC_ALL, "rus"); // возможность вывода информации на экран на русском языке // ввод элементов массива с клавиатуры cout << "Введите элементы массива:" << endl; for (i = 0; i < nrow; i++) for (j = 0; j < ncol; j++) cin >> a[i][j]; // вывод элементов массива на экран // ширина поля для вывода устанавливается в четыре символа //с помощью манипулятора setw() for (i = 0; i < nrow; i++) { for (j = 0; j < ncol; j++) cout << setw(4) << a[i][j] << " "; cout << endl; } // инициализация переменных int n_posl_el; float s = 0; // обработка элементов матрицы для определения ее характеристик for (i = 0; i < nrow; i++) { n_posl_el = 0; for (j = 0; j < ncol; j++) { s += a[i][j]; // сумма всех элементов матрицы if (a[i][j] > 0) n_posl_el++; // подсчет положительных элементов строки } cout << "Строка:" << i << "количество: " << n_posl_el << endl; } s /= nrow * ncol; // расчет среднего арифметического cout << "Среднее арифметическое" << s << endl; system("pause"); // осуществляет задержку экрана }
-
-
Автор
Сообщения
- Для ответа в этой теме необходимо авторизоваться.
Специальные матричные функции
Основные функции для работы с матрицами рассмотрены в статье Массивы в Scilab.
Другие полезные функции рассмотрены в статье Функции для решения задач линейной алгебры в Scilab
Ниже остановимся на специальных функциях: поиска минимального и максимального элементов, сортировки, объединения массивов в Scilab и т.д..
Задание матриц/векторов специального вида
Создаём матрицу из единиц: функция ones(n,m) в Scilab
Указываем число строк и число столбцов матрицы.
Задаём вектор-строк и вектор-столбец единиц
R = ones(1,3);
C = ones(3,1);
(
begin{matrix}
R = begin{pmatrix}
1 & 1 & 1
end{pmatrix} &
C = begin{pmatrix}
1 \ 1 \ 1
end{pmatrix}
end{matrix}
)
Задаём матрицу из единиц размерностью m на n
A = ones(3, 2);
S = ones(2, 2);
(
begin{matrix}
A = begin{pmatrix}
1 & 1 \
1 & 1 \
1 & 1
end{pmatrix} &
S = begin{pmatrix}
1 & 1 \
1 & 1
end{pmatrix}
end{matrix}
)
Задаём матрицу D из единиц, той же размерности, что и матрица A
A = [1 2 3;4 5 6];
D = ones(M);
(
begin{matrix}
A = begin{pmatrix}
1 & 5 & 4 \
3 & 2 & 6
end{pmatrix} &
D = begin{pmatrix}
1 & 1 & 1\
1 & 1 & 1
end{pmatrix}
end{matrix}
)
Создаём матрицу из нулей: функция zeros(n,m) в Scilab
Указываем число строк и число столбцов матрицы.
Задаём вектор-строк и вектор-столбец нулей
R = zeros(1,3);
C = zeros(3,1);
(
begin{matrix}
R = begin{pmatrix}
0 & 0 & 0
end{pmatrix} &
C = begin{pmatrix}
0 \ 0 \ 0
end{pmatrix}
end{matrix}
)
Задаём матрицу нулей размерностью m на n
A = zeros(3, 2);
S = zeros(2, 2);
(
begin{matrix}
A = begin{pmatrix}
0 & 0 \
0 & 0 \
0 & 0
end{pmatrix} &
S = begin{pmatrix}
0 & 0 \
0 & 0
end{pmatrix}
end{matrix}
)
Задаём матрицу D из нулей, той же размерности, что и матрица A
A = [1 5 4;3 2 6];
D = zeros(M);
(
begin{matrix}
A = begin{pmatrix}
1 & 5 & 4 \
3 & 2 & 6
end{pmatrix} &
D = begin{pmatrix}
0 & 0 & 0\
0 & 0 & 0
end{pmatrix}
end{matrix}
)
Создаём единичную матрицу: функция eye(n,m) в Scilab
Указываем число строк и число столбцов матрицы.
Задаём единичную матрицу нулей размерностью m на n
A = eye(3, 3);
B = eye(3, 4);
V = eye(3,1)
(
begin{matrix}
A = begin{pmatrix}
1 & 0 & 0\
0 & 1 & 0\
0 & 0 & 1
end{pmatrix} &
B = begin{pmatrix}
1 & 0 & 0 & 0\
0 & 1 & 0 & 0\
0 & 0 & 1 & 0
end{pmatrix} &
V = begin{pmatrix}
1 \
0 \
0
end{pmatrix}
end{matrix}
)
Задаём единичную матрицу D, той же размерности, что и матрица A
A = [1 2;4 5];
D = eye(M);
(
begin{matrix}
A = begin{pmatrix}
1 & 2 \
4 & 5
end{pmatrix} &
D = begin{pmatrix}
1 & 0 \
0 & 1
end{pmatrix}
end{matrix}
)
Создаём случайную матрицу/вектор: функция rand(n,m, key) в Scilab
Указываем число строк и число столбцов матрицы и необязательный параметр key – это символьная переменная с помощью которой можно задать тип распределения случайной величины (по умолчанию равномерное – ‘uniform’: гауссовское – ‘normal’).
Задаём матрицу m на n случайных чисел
A = rand(3, 2);
V = rand(3,1,'normal');
(
begin{matrix}
A = begin{pmatrix}
0.2113249 & 0.3303271\
0.7560439 & 0.6653811 \
0.0002211 & 0.6283918
end{pmatrix} &
V = begin{pmatrix}
-0.7335813 \
0.1034169 \
0.8915736
end{pmatrix}
end{matrix}
)
Создаём квадратную матрицу с элемнтами V на k-oй диагонали: функция diag(V[,k]) в Scilab
Задаём вектор V и указываем, на какой диагонали его разместить.
V = [1 2 3];
A = diag(V);
Задаём главную диагональ
(
begin{matrix}
A = begin{pmatrix}
1 & 0 & 0\
0 & 2 & 0\
0 & 0 & 3
end{pmatrix}
end{matrix}
)
V = [1 2 3];
В = diag(V, 1);
С = diag(V, -1);
Задаём произвольную диагональ: выше или ниже главной
(
begin{matrix}
B = begin{pmatrix}
0 & 1 & 0 & 0\
0 & 0 & 2 & 0\
0 & 0 & 0 & 3 \
0 & 0 & 0 & 0
end{pmatrix} &
C = begin{pmatrix}
0 & 0 & 0 & 0\
1 & 0 & 0 & 0\
0 & 2 & 0 & 0\
0 & 0 & 3 & 0
end{pmatrix}
end{matrix}
)
Создаём нижне-треугольную матрицу: функция tril(A[,k]) в Scilab
Указывавем матрицу, из которой будем формировать нижне-треугольную и диагональ, с которой начинать
A = [1 1 1; 2 2 2; 3 3 3];
B1 = tril(A);
B2 = tril(A, 1);
B3 = tril(A, -1);
(
begin{matrix}
A = begin{pmatrix}
1 & 1 & 1\
2 & 2 & 2 \
3 & 3 & 3
end{pmatrix} &
B_1 = begin{pmatrix}
1 & 0 & 0\
2 & 2 & 0 \
3 & 3 & 3
end{pmatrix} &
B_2 = begin{pmatrix}
1 & 1 & 0\
2 & 2 & 2 \
3 & 3 & 3
end{pmatrix} &
B_3 = begin{pmatrix}
0 & 0 & 0\
2 & 0 & 0 \
3 & 3 & 0
end{pmatrix}
end{matrix}
)
Создаём верхне-треугольную матрицу: функции triu(A[,k]) в Scilab
Указывавем матрицу, из которой будем формировать верхне-треугольную и диагональ, с которой начинать
A = [1 1 1; 2 2 2; 3 3 3];
B1 = tril(A);
B2 = tril(A, 2);
B3 = tril(A, -1);
(
begin{matrix}
A = begin{pmatrix}
1 & 1 & 1\
2 & 2 & 2 \
3 & 3 & 3
end{pmatrix} &
B_1 = begin{pmatrix}
1 & 1 & 1\
0 & 2 & 2 \
0 & 0 & 3
end{pmatrix} &
B_2 = begin{pmatrix}
0 & 0 & 1\
0 & 0 & 0 \
0 & 0 & 0
end{pmatrix} &
B_3 = begin{pmatrix}
1 & 1 & 1\
2 & 2 & 2 \
0 & 3 & 3
end{pmatrix}
end{matrix}
)
Создаём разреженную матрицу: функции ( sparse(V_1, V_2) ) в Scilab
( V_1 ) – вектор координат(строка, столбец) ненулевых эелемнтов
( V_2 ) – вектор значений ненулевых эелемнтов
A = sparse([1 2; 2 5; 3 1; 3 4], [8 9 15 11]);
full(A);
(
begin{matrix}
A = begin{pmatrix}
0. & 8. & 0. & 0. & 0.\
0. & 0. & 0. & 0. & 9.\
15. & 0. & 0. & 11. & 0.
end{pmatrix}
end{matrix}
)
Функции преобразования матриц/векторов
Изменяем размер матрицы: функция matrix(A [,n,m]) в Scilab
A = [1 2;3 4;5 6];
Исходная матрица.
( A = begin{pmatrix}
1 & 2 \
3 & 4 \
5 & 6
end{pmatrix} )
Указываем матрицу, которую меняем, потом число строк и число столбцов новой матрицы.
B1 = matrix(A,2,3);
B2 = matrix(A,3,2);
B3 = matrix(A,1,6);
B4 = matrix(A,6,1);
Преобразованные матрицы
(
begin{matrix}
B_1 = begin{pmatrix}
1 & 5 & 4 \
3 & 2 & 6
end{pmatrix} &
B_2 = begin{pmatrix}
1 & 2 \
3 & 4 \
5 & 6
end{pmatrix} &
B_3 = begin{pmatrix}
1 & 2 & 3 & 4 & 5 & 6
end{pmatrix} &
B_4 = begin{pmatrix}
1 \ 3 \ 4 \ 5 \ 6
end{pmatrix}
end{matrix}
)
Конкатенация (склейка) матриц/векторов: функция cat(n, A, B) в Scilab
Склеиваем матрицы по строкам, т.е. друг под другом
A = [1 2; 3 4];
B = [5 6; 7 8];
C = cat(1, A, B);
(
begin{matrix}
A = begin{pmatrix}
1 & 2 \
3 & 4
end{pmatrix} &
B = begin{pmatrix}
5 & 6 \
7 & 8
end{pmatrix} &
C = begin{pmatrix}
1 & 2 \
3 & 4 \
5 & 6 \
7 & 8
end{pmatrix}
end{matrix}
)
Объединяем вектора (массивы) по строкам, т.е. друг под другом
A = [1 2 3 4];
B = [5 6 7 8];
C = cat(1, A, B);
(
begin{matrix}
A = begin{pmatrix}
1 & 2 & 3 & 4
end{pmatrix} &
B = begin{pmatrix}
5 & 6 & 7 & 8
end{pmatrix} &
C = begin{pmatrix}
1 & 2 & 3 & 4\
5 & 6 & 7 & 8
end{pmatrix}
end{matrix}
)
Склеиваем матрицы по столбцам, т.е. друг за другом
A = [1 2; 3 4];
B = [5 6; 7 8];
C = cat(2, A, B);
(
begin{matrix}
A = begin{pmatrix}
1 & 2 \
3 & 4
end{pmatrix} &
B = begin{pmatrix}
5 & 6 \
7 & 8
end{pmatrix} &
C = begin{pmatrix}
1 & 2 & 5 & 6 \
3 & 4 & 7 & 8
end{pmatrix}
end{matrix}
)
Объединяем вектора (массивы) по столбцам, т.е. друг за другом
A = [1 2 3 4];
B = [5 6 7 8];
C = cat(2, A, B);
(
begin{matrix}
A = begin{pmatrix}
1 & 2 & 3 & 4
end{pmatrix} &
B = begin{pmatrix}
5 & 6 & 7 & 8
end{pmatrix} &
C = begin{pmatrix}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8
end{pmatrix}
end{matrix}
)
Сортируем элементы матриц/векторов: функция gsort(A,option,direction) в Scilab
option – символьная строка. Она задаёт тип требуемой сортировки:
‘r’ – сортируется каждый столбец A
‘c’ – сортируется каждая строка A
‘g’ – сортируются все элементы A. Это значение по умолчанию.
direction – символьная строка. Она задаёт направление сортировки:
‘i’ устанавливает порядок возрастания,
‘d’ устанавливает порядок убывания (по умолчанию).
A = [7 2; 4 10];
B1 = gsort(A, 'r');
B2 = gsort(A, 'c');
B3 = gsort(A);
B4 = gsort(A, 'c', 'i');
(
begin{matrix}
A = begin{pmatrix}
7 & 2 \
4 & 10
end{pmatrix} &
B_1 = begin{pmatrix}
7 & 10 \
4 & 2
end{pmatrix} &
B_2 = begin{pmatrix}
7 & 2 \
10 & 4
end{pmatrix} &
B_3 = begin{pmatrix}
10 & 4 \
7 & 2
end{pmatrix} &
B_4 = begin{pmatrix}
2 & 7 \
4 & 10
end{pmatrix}
end{matrix}
)
Функции вычисления различных характеристик матриц/векторов
Определяем размер матриц/векторов: функция size(A,option) в Scilab
option – символьная строка. Она возволяет определить:
‘r’ – число строк матрицы A
‘c’ – число столбцов матрицы A.
A = [7 2 1; 3 4 10];
[m, n] = size(A);
m = size(A, 'r');
n = size(A, 'c');
(
begin{matrix}
A = begin{pmatrix}
7 & 2 & 1\
3 & 4 & 10
end{pmatrix} &
m = 2 & n = 3
end{matrix}
)
Найдём сумму элементов массива/матрицы: функция sum(A,option) в Scilab
option – символьная строка. Она возволяет определить:
‘r’ – поэлементную сумму строк матрицы A. Возвращает строку.
‘c’ – поэлементную сумму столбцов матрицы A. Возвращает столбец.
Если option отсутствует, то возвращается сумма всех элементов.
A = [7 2 1; 3 4 10];
R = sum(A, 'r');
V = sum(A, 'c');
S = sum(A);
(
begin{matrix}
A = begin{pmatrix}
7 & 2 & 1\
3 & 4 & 10
end{pmatrix} &
R = begin{pmatrix}
10 & 6 & 11
end{pmatrix}&
V = begin{pmatrix}
10 \ 17
end{pmatrix} &
S = 27
end{matrix}
)
Найдём произведение элементов массива/матрицы: функция prod(A,option) в Scilab
option – символьная строка. Она возволяет определить:
‘r’ – поэлементное произведение строк матрицы A. Возвращает строку.
‘c’ – поэлементное произведение столбцов матрицы A. Возвращает столбец.
Если option отсутствует, то возвращается произведение всех элементов.
A = [7 2 1; 3 4 10];
R = sum(A, 'r');
V = sum(A, 'c');
P = sum(A);
(
begin{matrix}
A = begin{pmatrix}
7 & 2 & 1\
3 & 4 & 10
end{pmatrix} &
R = begin{pmatrix}
21 & 8 & 10
end{pmatrix}&
V = begin{pmatrix}
14 \ 120
end{pmatrix} &
P = 1680
end{matrix}
)
Найдём наибольший элемент массива/матрицы: функция max(A,option) в Scilab
option – символьная строка. Она возволяет определить:
‘r’ – наибольший элемент в каждом столбце матрицы A. Возвращает строку.
‘c’ – наибольший элемент в каждой строке матрицы A. Возвращает столбец.
Если option отсутствует, то возвращается наибольший элемент во всей матрице.
A = [7 2 1; 3 4 10];
R = max(A, 'r');
V = max(A, 'c');
M = max(A);
(
begin{matrix}
A = begin{pmatrix}
7 & 2 & 1\
3 & 4 & 10
end{pmatrix} &
R = begin{pmatrix}
7 & 4 & 10
end{pmatrix}&
V = begin{pmatrix}
7 \ 10
end{pmatrix} &
M = 10
end{matrix}
)
Найдём наименьший элемент массива/матрицы: функция min(A,option) в Scilab
option – символьная строка. Она возволяет определить:
‘r’ – наименьший элемент в каждом столбце матрицы A. Возвращает строку.
‘c’ – наименьший элемент в каждой строке матрицы A. Возвращает столбец.
Если option отсутствует, то возвращается наименьший элемент во всей матрице.
A = [7 2 1; 3 4 10];
R = min(A, 'r');
V = min(A, 'c');
M = min(A);
(
begin{matrix}
A = begin{pmatrix}
7 & 2 & 1\
3 & 4 & 10
end{pmatrix} &
R = begin{pmatrix}
3 & 2 & 1
end{pmatrix}&
V = begin{pmatrix}
1 \ 3
end{pmatrix} &
M = 1
end{matrix}
)
Найдём среднее значение массива/матрицы: функция mean(A,option) в Scilab
option – символьная строка. Она возволяет определить:
‘r’ – среднее значение в каждом столбце матрицы A. Возвращает строку.
‘c’ – среднее значение в каждой строке матрицы A. Возвращает столбец.
Если option отсутствует, то возвращается среднее значение всей матрицы.
A = [7 2 1; 3 4 10];
R = mean(A, 'r');
V = mean(A, 'c');
M = mean(A);
(
begin{matrix}
A = begin{pmatrix}
7 & 2 & 1\
3 & 4 & 10
end{pmatrix} &
R = begin{pmatrix}
5 & 3 & 5.5
end{pmatrix}&
V = begin{pmatrix}
3.3333 \ 5.6666
end{pmatrix} &
M = 4.5
end{matrix}
)
Основные функции для работы с матрицами рассмотрены в статье Массивы в Scilab.




