Как найти среднее арифметическое значение температуры

Простой пример: Утром вы ведёте машину до работы со скоростью 30 км/ч, потому что вы не хотите на работу, а обратно едете уже со скоростью 60 км/ч, потому что спешите попасть домой. Какова средняя скорость вашего передвижения в этот день?

Подсказка: Нет, не 45 км/ч.

А пока вот вам небольшая табличка.

Но что всё это значит?

Давайте начнём сначала. Что вообще мы понимаем под словом «среднее»? Для большинства из нас это «какое-то число посередине» либо некое сбалансированное по каким-то критериям число.

Можно предложить более универсальную интерпретацию понятия «среднее значение». Среднее значение какого-либо ряда значений — это то, которым можно заменить любую единицу ряда и получить тот же результат. Условно говоря, я могу выбросить все представленные данные, кроме среднего значения, и общий смысл не изменится.

Одна из целей получения среднего значения — это понять суть выборки данных с помощью репрезентативного образца. Но сам процесс вычисления среднего значения зависит от того, каким образом взаимодействуют элементы группы данных. Давайте посмотрим, как это происходит.

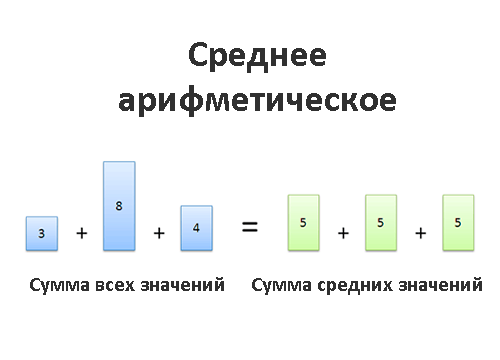
Среднее арифметическое

Среднее арифметическое знакомо нам всем со школы:

среднее арифметическое = сумма всех величин/количество величин

Задачка: вы весите 75 кг и зашли в лифт с подростком весом 50 кг и толстяком весом 175 кг. Каков средний вес вашей группы?

На самом деле вопрос стоит так: Если заменить вашу весёлую компанию тремя клонированными людьми с одинаковым весом, каким весом должен обладать каждый такой клон?

В этом случае мы просто заказываем на фабрике по производству клонов человека трёх экземпляров весом в 100 килограмм каждый (Помним: (75+50+175)/3) и довольно потираем руки.

Преимущества среднего арифметического:

• Отлично работает для совокупностей, значения которых легко складываются;
• Просто вычисляется: складывай, разделяй и властвуй;
• Интуитивно понятно — среднее арифметическое для нас как раз и является «числом где-то в середине» между наибольшим и наименьшим значением.

Недостатки среднего арифметического:

• Среднее арифметическое не работает для числовых рядов с большим разбросом в значениях. Ну, скажем, среднее арифметическое чисел 100, 200 и -300 — это 0, а это уже обескураживает.

Среднее арифметическое срабатывает в 80% случаев. К сожалению, 20% оставшихся случаев и вынуждают нас искать альтернативы для подсчёта среднего значения.

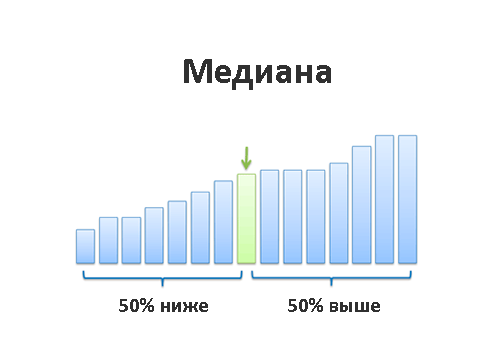
Медиана

Медиана — это та самая грань, которая отделяет наибольшие значения от наименьших. То самое «число посередине». Постойте-постойте, а разве среднее арифметическое делает не то же самое?

Вот вам простой пример. Какое число находится в середине этого ряда?

1, 2, 3, 4, 100

Число «3» находится в середине ряда. И хотя среднее арифметическое (22) является «средним», оно никак не отражает распределения этих чисел. Интуитивно (и абсолютно правильно!) мы считаем, что в середине этого ряда всё-таки 3, а не 22. Здесь среднее значение увеличилось благодаря резко отклоняющемуся от общей массы значению, 100.

Медиана решает эту проблему. Медиана делит наш числовой ряд на две равные части, причём первая половина имеет значения меньше либо равные медиане, а вторая — больше либо равные. Если в середине числового ряда оказывается два числа, мы просто берём среднее арифметическое этих двух чисел, чтобы получить медиану. В числовом ряду 1, 2, 3, 4 медианой станет число 2,5. Именно медиана позволяет выбивающимся из общей массы числам вроде 100 в нашем примере выше не влиять на общее впечатление о числовом ряде.

Преимущества медианы:

• Прекрасно справляется с резко отклоняющимися значениями, поэтому зачастую является самым репрезентативным значением для группы;
• Разбивает данные на две группы, состоящие из одинакового количества элементов.

Недостатки медианы:

• Немного усложняются вычисления: необходимо разбить ряд на две части;
• Медиана менее популярна; если вы скажете «среднее медианное значение», люди запросто могут подумать, что вы говорите о среднем арифметическом. Отсюда возникают недопонимания.

Такие средние значения, как цены на недвижимость или, например, уровень дохода часто вычисляются именно по медиане, потому что нам важна именно средняя стоимость большей части домов в конкретном районе или средний уровень доходов большей части населения. В таком случае Билл Гейтс с годовым доходом в несколько миллиардов не испортит нам всю статистику. Видите, как много зависит от того, как мы работаем с имеющимися данными?

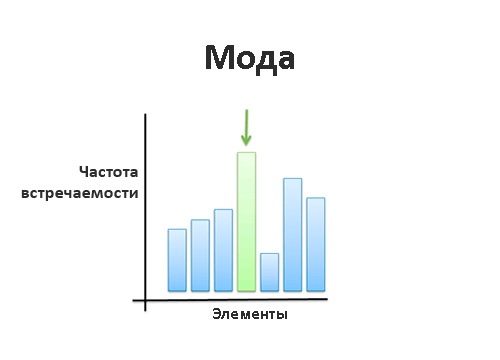
Мода

Само слово может звучать странно, но оно означает всего лишь наиболее часто встречающийся в группе элемент. На практике обычно мода определяется путём опросов и сбора мнений. Да, действительно порой бывают случаи, когда лучшим способом получить наиболее репрезентативный образец данных является сбор откликов.

Ну, скажем, вы планируете вечеринку, и вам нужно выбрать день для её проведения. Дни недели — такой же числовой ряд, что и любой другой. Это всего лишь числа от 1 до 7. Среднее арифметическое и медиана тут не помогут (Лиза и Паша могут в пятницу, а Коля и Петя — в воскресенье; поэтому назначим субботу). Что делать в таком случае? Конечно, выбрать тот день, который выберет большинство.

Как правило, мода используется для получения наиболее репрезентативного значения в нечисловых рядах. Популярные цвета в сезоне, хиты продаж, рейтинги фильмов и музыки, лучшие кафе и закусочные определяются именно по моде.

Преимущества моды: – Прекрасно работает для получения представления об общественном мнении; – Даёт представление о потребностях большой части людей (там, где среднее арифметическое даёт лишь осечку); – Проста для понимания.

Недостатки моды: – Для её вычисления требуется больше усилий (нужно собрать мнения и обработать их); – Победителю достаётся всё: мода выявляет только одного лидера.

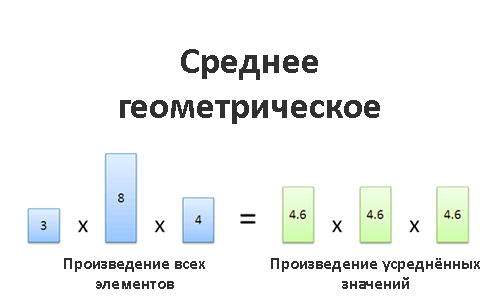
Среднее геометрическое

Наш «усреднённый элемент» зависит от того, что мы делаем с уже существующими элементами группы данных. В большинстве случаев элементы просто складываются, и среднее арифметическое прекрасно работает. Но иногда нам нужно что-то большее. Например, когда мы работаем с инвестициями, площадью и объёмом. В таких случаях данные взаимодействуют между собой именно путём умножения (ожидаемая доходность, объём или площадь фигуры вычисляются с помощью умножения), и это меняет наш подход к выявлению средних значений.

Вот пример. Какой инвестиционный портфель вы предпочтёте? Иными словами, какой из них принесёт большую прибыль в течение типичного года?

• Портфель А: +10%, -10%, +10%, -10%
• Портфель Б: +30%, -30%, +30%, -30%

Выглядят они похоже. Наша повседневная логика, построенная на привычке к среднему арифметическому, говорит нам, что оба портфеля достаточно рискованны, и оба в среднем приведут к убыткам или нулевой прибыли. Поэтому, наверное, мы выберем портфель Б, поскольку в успешный год он принесёт больше прибыли.

И это неверно! На фондовом рынке с таким подходом мы с вами точно бы прогорели. Проценты с инвестиций умножаются, а не складываются. Мы не можем просто взять и использовать среднее арифметическое, нам нужно найти действительный коэффициент окупаемости. Коэффициент окупаемости считается достаточно просто: берём условные 100% нашего текущего капитала в качестве единицы. Далее представляем колебания доходности-убытка, представленные в описании портфелей, добавляя к нашей единице или вычитая из неё процентные показатели. Затем перемножаем полученные колебания и получаем коэффициент. Для расчёта среднегодового значения коэффициента окупаемости делим полученный коэффициент на 4 (поскольку элементов в нашем числовом ряду четыре).

• Портфель А:

Коэффициент окупаемости: 1,1 * 0,9 * 1,1 * 0,9 = 0,98 (2% убытка)

Среднегодовое значение: (0,98)^(1/4) = 0,5% годового убытка

• Портфель Б:

Коэффициент окупаемости: 1,3 * 0,7 * 1,3 * 0,7 = 0,83 (17% убытка)

Среднегодовое значение: (0,83)^(1/4) = 4,6% годового убытка

Выбор между 2% или 17%? Огромная разница! Конечно, разумный человек отказался бы от обоих портфелей, но из двух зол лучше выбрать Портфель А. И именно здесь среднее арифметическое не работает.

Несколько примеров, где работает среднее геометрическое:

• Темпы инфляции: У вас есть показатели в 1%, 2% и 10%. Каков средний показатель инфляции за конкретный период времени? (1,01 * 1,02 * 1,10)^(1/3) = 4,3%.
• Скидки: У вас есть три скидочных купона на 50%, 25% и 35%. Какова средняя скидка? (0,5 * 0,75 * 0,65)^(1/3) = 37.5%.
• Площадь: У вас есть участок земли 40х60 м. Вам нужно вычислить «усреднённую сторону» — иными словами, сторону квадрата примерно той же площади. (40 * 60)^(0.5) = 49 м.
• Объём: У вас есть коробка 12х24х48 см. Вам снова нужна усреднённая сторона, то есть сторона куба примерно того же объёма. (12 * 24 * 48)^(1/3) = 24 см.

Среднее геометрическое помогает найти «типичный элемент» среди группы элементов, взаимодействующих друг с другом путём умножения. И, как видим, у него множество практических применений.

Среднее гармоническое

Среднее гармоническое представить сложнее, чем предыдущих представителей «средних», но оно не менее полезно. Между прочим, само понятие «гармоники» в математике связано с обратными числами (1/2, 1/3 и т.д.). Среднее гармоническое помогает нам вычислить среднее арифметическое в рядах чисел, заданных обратными значениями. Это случается чаще, чем вы можете подумать.

Например, если я еду со скоростью 30 км/ч, это значит, что я получаю определённый результат (30 км) за какую-либо единицу времени (1 час). Когда мы хотим узнать среднее значение для нескольких скоростей (Х и Y), нужно думать о результате и единицах измерения, а не об исходных цифрах.

средняя скорость = общий результат/общая единица измерения

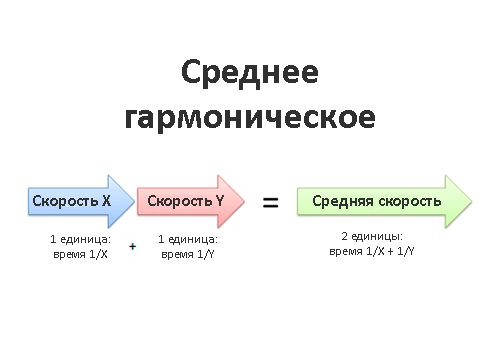
Возьмём двух работников: Х и Y. Оба работают в одном проекте и выполняют одинаковое количество работы, но скорость их работы разная. Какова средняя скорость их работы?

Скажем, работник Х кладёт 30 кирпичей в час, а работник Y — 60 кирпичей в час. Значит, на один кирпич у каждого работника уходит:

• У работника X укладка одного кирпича займёт 1/X времени (1/30);
• У работника Y укладка одного кирпича займёт 1/Y времени (1/60)

Складываем результаты и единицы измерения:

Общий результат: 2 кирпича (Х и Y уложили по одному) Общая единица времени: 1/X + 1/Y (у каждого уходит разное количество времени)

Средней скоростью обоих работников будет:

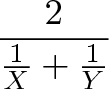
Если бы у нас было 3 работника (X, Y и Z), их средняя скорость вычислялась бы по формуле:

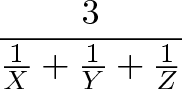
Здорово же иметь одну формулу вместо того, чтобы каждый раз заниматься долгими вычислениями. Даже вычисляя среднюю скорость 5 нерадивых работников стало бы головной болью. Помните наш первый пример про скорость, с которой вы едете на работу и домой? Чтобы найти среднюю скорость вашего передвижения в тот день, мы просто используем формулу.

При этом нам даже не нужно знать, где находится дом или офис! Теперь вместо X и Y у нас не кирпичи, а количество километров за единицу времени. Вне зависимости от расстояния результат один и тот же: допустим, некое количество километров R мы проходим на скорости X, а другое количество километров R — на скорости Y. Средняя скорость при этом будет вычисляться так же, как вычисляется средняя скорость прохождения 1 км на скорости X и одного километра на скорости Y:

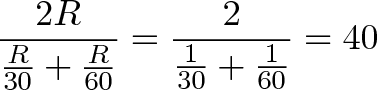
Ключевая идея: Среднее гармоническое используется тогда, когда один и тот же объём работы выполняется на разных скоростях.

Ещё более ключевая идея: Помните, что среднее значение — это один элемент, способный передать суть целой группы элементов. В нашем примере с работой и офисой в среднем туда-обратно мы едем на скорости 40 км/ч (вместо 30 км/ч туда и 60 км/ч обратно). Важно помнить, что средней скоростью мы заменяем каждую «стадию».

Ещё несколько примеров из жизни среднего гармонического:

• Передача данных: Мы передаём данные между клиентом и сервером. Клиент посылает данные за плату 10 Гб/доллар, а сервер получает их за плату 20 Гб/доллар. Каково среднее количество Гб, которые можно передать и получить за один доллар? Мы усредняем значения для клиента и для сервера: 2 / (1/10 + 1/20) = 13,3 Гб/доллар для каждой стороны. Поскольку данные и передаются, и получаются (каждая сторона выполняет свою половину работу), мы делим это значение на 2 и получаем следующее значение: 6,65 Гб за доллар.
• Продуктивность машины: У нас есть производственная установка для подготовки и полировки деталей. За час установка может подготовить 25 деталей; либо за тот же час она может отполировать 10 деталей. Какова средняя производительность установки? Усредняем значения для каждой стадии: 2 / (1/25 + 1/10) = 14,28 деталей/час. Снова делим это значение на два, поскольку нас интересует средняя производительность установки, если она занимается сразу двумя фазами: получаем 7,14 деталей/час.

В чём здесь фокус?

Среднее гармоническое действительно не самая очевидная вещь. Дело в том, что если бы у вас было две разных установки, одна из которых работает со скоростью 10 деталей/час, а другая — 20 деталей/час, конечно, их средняя производительность составляла бы 15 деталей/час. В этом случае вы имеете полное право просто сложить их производительность и вычислить среднее арифметическое, ведь установки работают независимо друг от друга.

Если не верите в среднее гармоническое, можно устроить себе обратную проверку. Мы утверждаем, что наша универсальная установка по заготовке и полировке деталей справляется с 7,14 деталями в час. Проверим: мы знаем, что за час машина либо обрабатывает 25 деталей, либо полирует 10. Получаем:

Подготовка: 7,14/25 = 0,29 часов Полировка: 7,14/10 = 0,71 часов

Да-да, 0,29 + 0,71 = 1, цифры работают: для полного цикла изготовления 7,14 деталей действительно требуется один час.

В качестве заключения

Даже такая простая на первый взгляд идея, как «среднее значение», имеет множество применений. Мы здесь рассмотрели лишь самые основные и не затронули средневзвешенное, центр тяжести, математическое ожидание и многое другое. Но мы поняли главные принципы:

• Среднее значение призвано отразить основную суть всех элементов в группе
• Тип среднего значения зависит от того, как взаимодействуют элементы в группе (складываются? умножаются? становятся обратными величинами? просто выбираются?)

Спасибо прекрасной статье на Better Explained.

Как вычислить среднюю температуру

Среднесуточная или среднемесячная температура воздуха важна для характеристики климата. Как и любое среднее значение, ее можно вычислить, сделав несколько наблюдений. Количество измерений, равно как и точность термометра, зависят от цели исследования.

Вам понадобится

• – термометр;
• – лист бумаги;
• – карандаш:
• – калькулятор.

Инструкция

Чтобы найти среднесуточную температуру наружного воздуха, возьмите обычный уличный термометр. Для характеристики климата его точность вполне достаточна, составляет она 1°. В России для подобных измерений применяется шкала Цельсия, но в некоторых других странах температуру могут мерить и по Фаренгейту. В любом случае необходимо для измерений применять один и тот же прибор, в крайнем случае — другой, но с точно такой же шкалой. Крайне желательно, чтобы термометр был поверен по эталонному.

Снимите показания через равные промежутки времени. Это можно сделать, например, в 0 часов, в 6, 12 и 18. Возможны и другие интервалы — через 4, 3, 2 часа или даже ежечасно. Необходимо проводить измерения в одних и тех же условиях. Повесьте термометр так, чтобы даже в самую жаркую дневную пору он был в тени. Посчитайте и запишите, сколько раз вы смотрели на градусник. На метеостанциях наблюдения обычно проводят через 3 часа, то есть 8 раз в сутки.

Сложите все показания. Разделите полученную сумму на количество наблюдений. Это и будет среднесуточная температура. Может возникнуть ситуация, когда одни показания будут положительными, а другие — отрицательными. Суммируйте их так же, как и любые другие отрицательные числа. При сложении двух отрицательных чисел найдите сумму модулей и поставьте перед ней минус. При действии с положительным и отрицательным числом вычтите из большего числа меньшее и поставьте перед результатом знак большего числа.

Чтобы найти среднюю дневную или ночную температуру, определите, когда в вашей местности наступают полдень и полночь по астрономическим часам. Декретное и летнее время сместило эти моменты, и полдень в России наступает в 14 часов, а не в 12. Для средней ночной температуры вычислите моменты за шесть часов до полуночи и через такое же время после него, то есть это будет 20 и 8 часов. Еще два момента, когда нужно посмотреть на градусник — 23 и 5 часов. Снимите показания, сложите результаты и разделите сумму на количество измерений. Точно так же определите среднюю дневную температуру.

Вычислите среднемесячную температуру. Сложите среднесуточные показания за месяц и разделите на количество дней. Таким же образом можно вычислить среднемесячные значения для дневных и ночных температур.

Если наблюдения ведутся систематически в течение нескольких лет, можно вычислить климатическую норму для каждого конкретного дня. Сложите среднесуточные температуры для определенного числа того или иного месяца за несколько лет. Сумму разделите на количество лет. В дальнейшем можно будет сравнивать среднесуточную температуру с этим значением.

Полезный совет

Среднюю температуру воды вычислите аналогичным образом. Определите, через сколько времени вы будете ее замерять, снимите показания, сложите их и разделите на количество наблюдений.

Фраза “средняя температура по больнице” носит иронический характер, однако и такой показатель можно рассчитать тем же способом, что и любое среднее значение.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Содержание

• – Как рассчитать суточную амплитуду температуры воздуха?
• – Как рассчитать среднемесячную температуру воздуха?
• – Как определить среднесуточную температуру примеры?
• – Как рассчитать среднегодовую температуру?
• – Что такое годовая амплитуда температуры воздуха?
• – Что такое суточная амплитуда температуры воздуха?
• – Как рассчитать среднюю суточную температуру воздуха?
• – Как найти среднемесячную амплитуду температуры?
• – Как рассчитать среднесуточную температуру воздуха и амплитуду?
• – Что зависит от температуры воздуха?
• – Сколько раз в течении дня делается замер температуры для определения среднесуточной температуры?
• – Как высчитать температуру?
• – Как найти годовую температуру?
• – Как найти годовую амплитуду температуры воздуха?
• – Что такое средняя годовая температура воздуха?

Как рассчитать суточную амплитуду температуры воздуха?

сделать все необходимые замеры, записать; в своих записях за сутки найти самое большое и самое маленькое число; отнять от большего меньшее; записать полученный результат, который и будет суточной амплитудой.

Как рассчитать среднемесячную температуру воздуха?

1) Узнать среднюю температуру всех дней месяца, найти их сумму и разделить на количество дней (30 или 31). Так мы получим среднюю месячную температуру.

Как определить среднесуточную температуру примеры?

Среднесуточная значит выводим средний показатель. Пример: измеряем температуру воздуха каждый час в течении суток, получается 24 значения. Результаты измерения складываем в общую сумму и делим на 24 часа, вот и получается среднесуточная температура воздуха. То же самое и с ежемесячной.

Как рассчитать среднегодовую температуру?

Для того чтобы найти среднюю температуру года, необходимо сложить все среднемесячные температуры и разделить на 12 месяцев. Работа учащихся: 23:12 ≈ +2° С – среднегодовая температура воздуха.

Что такое годовая амплитуда температуры воздуха?

Годовая амплитуда температур это разница между самой высокой и самой низкой температурами за период наблюдения +20 − (−20) = 40.

Что такое суточная амплитуда температуры воздуха?

Амплитуда температур – это разница между самой низкой и высокой температурами. … Суточная амплитуда показывает размах колебаний температуры в течение суток.

Как рассчитать среднюю суточную температуру воздуха?

1 ответ

1. Складывают температурные показания, отмеченные за сутки, если они имеют один знак. Полученную сумму делят на число показаний. Получают среднее значение.
2. Если измеренная температура в течение суток имеет разные знаки, складывают отдельно положительные и отрицательные значения. Из большего вычитают меньшее.

10 янв. 2020 г.

Как найти среднемесячную амплитуду температуры?

Соответственно, чтобы вычислить амплитуду надо из наибольшего показателя вычесть наименьший (в соответствии с математическими правилами). Так, если температура воздуха в 12.00 равнялась +25°C, а в 18.00 – +20°C, то амплитуда (А) будет равна 25-20. А=5.

Как рассчитать среднесуточную температуру воздуха и амплитуду?

2) Для того, чтобы узнать среднесуточную амплитуду температур, нужно вычесть из большей замеренной в течение дня температуры меньшую. 5°C – (-3°C) = 8°C – среднесуточная амплитуда температур.

Что зависит от температуры воздуха?

Чем выше Солнце над горизонтом, тем выше температура. Следовательно, температура воздуха зависит от угла падения солнечных лучей. А угол падения — от широты местности и от времени суток. Между экватором и тропиками угол падения лучей самый большой (до 90°), возле полюсов — самый маленький.

Сколько раз в течении дня делается замер температуры для определения среднесуточной температуры?

На метеорологических станциях Российской Федерации температуру воздуха измеряют 8 раз в сутки. Суммируя результаты этих измерений и деля сумму на 8, получают среднюю суточную температуру воздуха. Средняя декадная температура — среднее арифметическое из среднесуточных температур за 10 дней.

Как высчитать температуру?

Сложите среднесуточные показания за месяц и разделите на количество дней. Таким же образом можно вычислить среднемесячные значения для дневных и ночных температур. 6Если наблюдения ведутся систематически в течение нескольких лет, можно вычислить климатическую норму для каждого конкретного дня.

Как найти годовую температуру?

1) Средняя годовая температура вычисляется суммированием среднемесячных температур с учетом знака и последующим делением на количество месяцев. 77 / 12 ≈ 6,4° – среднегодовая температура. 2) Амплитуда – это разность между самой высокой и самой низкой температурой.

Как найти годовую амплитуду температуры воздуха?

Годовая амплитуда температур – это разница между самым теплым (обычно это июль) и самым холодным (январь) месяцем года. Например, средняя температура июля равна +18°C., а средняя температура января – -5°C. Амплитуда (А), будет равна 18 -(-5). А=23.

Что такое средняя годовая температура воздуха?

Среднегодовая температура воздуха – это среднее арифметическое значение температур за все месяцы года. Среднегодовая температура в определённой местности является важным климатическим показателем и зависит от географического расположения, количество солнечных дней и розы ветров.

Интересные материалы:

Какого происхождения имя Вероника?
Какой географический объект носит имя Кука?
Какой характер у имени Анжела?
Какой характер у имени Никита?
Какой линией Подчёркиваются имена прилагательные?
Какой нации имя Ася?
Какой нации имя Эльвира?
Какой нации имя Эмилия?
Какой нации относится имя Нелли?
Какой нации принадлежит имя Рудольф?