Быстрая математика для графиков, на примере вычисления среднего
Время на прочтение
5 мин
Количество просмотров 4.4K
Рассмотрим, в качестве примера, формулу для вычисления среднего значения. На ней я постараюсь рассказать и показать какие подходы к реализации можно применять и чем они эффективны или не эффективны.
Это сумма всех значений за выбранный период, делённая на период. Иными словами -среднее значение за последние nзначений.
Классический подход
Как ни странно, большинство решений в сети выглядит, как последовательный перебор всех групп размером n (например 4) и вычисление среднего для каждой:
const data = [1, 2, 3, 4, 5, 6, 7, 8, 9];
function sma(data, period) {
const result = [];
for (let i = 0; i <= data.length - period; i++) {
const chunk = data.slice(i, i + period);
const sum = chunk.reduce((acc, num) => acc + num, 0);
result.push(sum / period);
}
return result;
}
console.log(sma(data, 4));
//=> [ '2.50', '3.50', '4.50', '5.50', '6.50', '7.50' ]
//=> │ │ │ │ │ └─(6+7+8+9)/4
//=> │ │ │ │ └─(5+6+7+8)/4
//=> │ │ │ └─(4+5+6+7)/4
//=> │ │ └─(3+4+5+6)/4
//=> │ └─(2+3+4+5)/4
//=> └─(1+2+3+4)/4
Безусловно, это решение работает, но оно очень плохое. Здесь происходит огромное количество повторных вычислений и лишних операций. Разберем весь код по порядку и посмотрим, строка за строкой, что происходит “под капотом”.
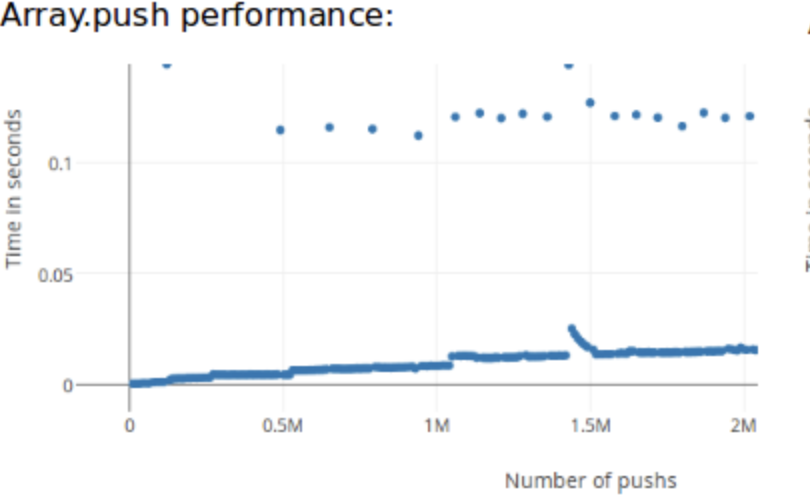
const result = []Создание массива в JavaScript, выделяет определенную область памяти для хранения данных. Размер массива не определенный и он наполняется по мере работы цикла, в какой-то момент может наступить заполнение выделенной области памяти и модуль управления памятью будет вынужден выделить новоую, более широкую область, затем осуществить перенос в нее диапазона всех значений памяти из предыдущей области, в разных движках это может работать по разному, но в любом случае необходимо, как минимум, выделение новой области памяти. И вот, как выглядит график замера времени на операцию push, в зависимости от длинны массива.
На картинке видны космические, по местным масштабам выбросы. Это происходит по причине тех самых накладных работ в памяти движка на перенос всей области, либо на выделение новой области и связывание со старой.
Из этого можно сделать два вывода:
-
Для работы с большими массивами лучше использовать создание массива через конструктор как:
new Array(size). Это позволит вам задать размер массива и движок выделит столько памяти, сколько нужно. -
А зачем тут этот массив вообще. (Позже мы к этому вернемся)
for (let i = 0; i <= data.length - period; i++)Для начала, ремарка про цикл. Я бы не стал так подробно мусолить цикл и перешел бы к следующей части, тк в целом оптимизация цикла не дала бы нужный эффект производительности, но это просто крик души, ода к безграмотности современных разработчиков, щепетильно пишущих бенчмарки налево и направо.
Погуглив “Самый быстрый способ итерации в JavaScript” не трудно наткнуться на кучу разных бенчмарков, которые написаны не правильно. Почему не правильно? .
В теории самый самый быстрый способ итерации в JavaScript -while(i > 0) , но все тесты в лучшем случае предлагают такой вариант условия остановки: while(i++) , в котором добавляется дополнительная нагрузка в виде приведения типа числа из Number в Boolean. Даже такой вариант выхода из цикла не совсем правильный: while(i < length) потому, что сравнение с 0 является одной из самых быстрых операций и отличается от сравнения с любыми другими видами чисел.
Бытует мнение, что это миф, однако это не так. Доказательство очень простое, взглянем как процессор обрабатывает сравнение с 0 и с 1
// Сравнение с 0
Frame size 8
30 S> 0xc24390c03a6 @ 0 : 0c 01 LdaSmi [1]
0xc24390c03a8 @ 2 : 26 fb Star r0
38 S> 0xc24390c03aa @ 4 : 0b LdaZero
44 E> 0xc24390c03ab @ 5 : 6a fb 00 TestGreaterThan r0, [0]
0xc24390c03ae @ 8 : 9a 02 JumpIfFalse [2] (0xc24390c03b0 @ 10)
0xc24390c03b0 @ 10 : 0d LdaUndefined
52 S> 0xc24390c03b1 @ 11 : aa Return // Сравнение с 1
Frame size 8
30 S> 0x1ae5f0003a6 @ 0 : 0c 01 LdaSmi [1]
0x1ae5f0003a8 @ 2 : 26 fb Star r0
38 S> 0x1ae5f0003aa @ 4 : 0c 64 LdaSmi [100]
44 E> 0x1ae5f0003ac @ 6 : 6a fb 00 TestGreaterThan r0, [0]
0x1ae5f0003af @ 9 : 9a 02 JumpIfFalse [2] (0x1ae5f0003b1 @ 11)
0x1ae5f0003b1 @ 11 : 0d LdaUndefined
54 S> 0x1ae5f0003b2 @ 12 : aa Return Обратите внимание на 5ую строку. Там используется сравнение LdaZero. Которое вежливо отмечено вторым в порядке быстродействия самими разработчиками v8.
Выводы:
-
Сравнение с нулем или нет – разница есть!
-
Не верьте бенчмаркам, если они написаны не правильно
-
Все эти вычисления можно сделать без цикла, об этом позже.
const chunk = data.slice(i, i + period);Теперь очередь этой строки. Оператор sliceсоздает новый массив, для которого выделяется память, заполняет его данными из предыдущего массива (иммутабильно) и присваивается в переменную chunk. Это с ума сойти сколько операций на пустом месте. И тут все можно описать столь же подробно, но я не стану, потому что больше нет сил разбираться в рубрике “По колено в коде” (Олды тут?). Выше, я все обещал позже рассказать о том, как сделать эти вычисления эффективнее. Приступим!
Потоковая обработка
В основе идеи потоковой обработки, лежит архитектура последовательных вычислений, с последующим переиспользованием (по возможности) результатов предыдущих вычислений. Такой подход хорош всегда и везде (где он применим), он применяется в парсинге текста, вычислениях, поисках в математических абстракциях и прочее.
Реализация вычислений SMA в этом подходе выглядит так:
export class SMA {
constructor(period) {
this.period = period;
this.arr = [];
this.sum = 0;
this.filled = false;
}
nextValue(value) {
this.filled = this.filled || this.arr.length === this.period;
this.arr.push(value);
if (this.filled) {
this.sum -= this.arr.shift();
this.sum += value;
return this.sum / this.period;
}
this.sum += value;
}
}
const data = [1, 2, 3, 4, 5, 6, 7, 8, 9];
const sma = new SMA(4);
for(let i = 0; i < data.length; i++) {
console.log(sma.nextValue(data[i]));
}Преимущества подхода в сравнении с классической реализацией:
Массив фиксированной длинны, который заполняется значениями и очищается при переполнении, поддерживая константную размерность. Тем самым позволяет не хранить в памяти лишнюю информацию.
Повторное использование вычислений, позволяет вообще отказаться от итераций по какому-либо массиву, мы просто записываем сумму всех входящих значений, и вычитаем сумму уходящих значений (при переполнении массива)
Но проблемные места все же есть:
Проблема 1 - это постоянное условие проверки переполненности массива, даже оптимизированное в this.filled, все еще вызвыается в холостую на каждую итерацию.
Проблема 2 -Мы все еще вынуждены хранить массив длинной 4 и постоянно выполнять операции shift и push , и если push нам не так страшен, то shift, вызывает последовательное смещение индексов, что дорого.
В остальном, даже в таком виде это решение будет работать быстрее в разы, чем классический подход.
Решаем проблему под номером один. Для этого при заполнении массива переопределим метод
this.nextValue = (value: number) => {
this.sum += value;
this.arr.push(value);
this.sum -= this.arr.shift();
return this.sum / this.period;
};Это позволит избежать в дальнейших расчетах дополнительных проверок на заполненность массива. Такой “лайфхак” имеет мелкое негативное воздействие на так называемые Shape структуры браузера, которые применяются для оптимизации доступа к свойствам объекта в реальном режиме времени. Прочитать про это можно здесь. Однако это воздействие будет разовым и на дальнейших вычисления не скажется. Такой подход дает в итоге даст значительное ускорение.
Мы сегодня с вами разобрали два подхода к вычислениям среднего значения, но это все легко переносится и на любые другие вычисления, поддающиеся потоковому анализу. Я постарался сделать статью интересной затронув глубинный уровень языка и работу с памятью.
SMA и многие другие аналитические функции (технические индикаторы) можно найти в моем репозитории.
Домашнее задание
В статье решается только одна из двух проблем потоковой реализации. Можно ли избавиться от проблемы номер два? Пишите ваши предложения в комментариях.
Точечные графики: как найти среднее значение, медиану и моду
17 авг. 2022 г.
читать 2 мин
Точечный график — это тип графика, который отображает распределение значений в наборе данных с помощью точек.
По оси X показаны отдельные значения данных, а по оси Y — частота каждого значения.
В этом руководстве объясняется, как рассчитать среднее значение, медиану и режим точечной диаграммы.
Пример. Расчет среднего значения, медианы и режима точечной диаграммы
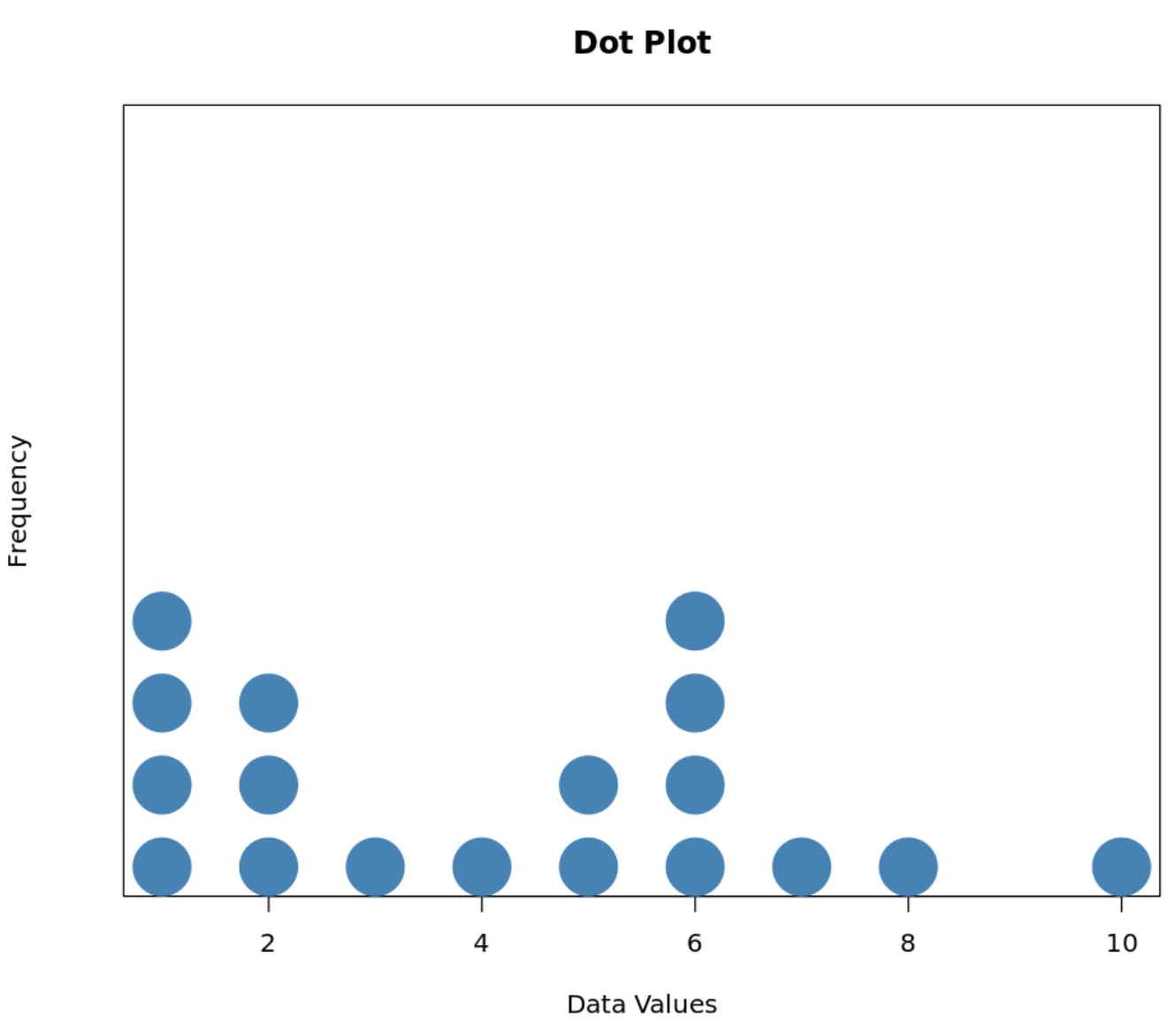
Предположим, у нас есть следующий точечный график, который показывает распределение значений для данного набора данных:
Чтобы вычислить среднее значение, медиану и моду для этого точечного графика, мы должны сначала записать значения для набора данных.
Например, мы видим, что значение «1» встречается четыре раза, значение «2» встречается три раза, значение «3» встречается один раз и так далее.
Мы можем записать следующие значения для этого набора данных:
Значения: 1, 1, 1, 1, 2, 2, 2, 3, 4, 5, 5, 6, 6, 6, 6, 7, 8, 10
Теперь мы можем вычислить среднее значение, медиану и моду.
Иметь в виду
Чтобы найти среднее значение этого набора данных, мы можем сложить все отдельные значения и разделить на общий размер выборки, равный 18:
Среднее = (1+1+1+1+2+2+2+3+4+5+5+6+6+6+6+7+8+10) / 18 = 4,22 .
Среднее значение получается 4,22.Это среднее значение набора данных.
медиана
Чтобы найти медиану этого набора данных, мы можем выписать все отдельные значения по порядку и определить значение, которое находится прямо посередине:
1, 1, 1, 1, 2, 2, 2, 3, 4 , 5 , 5, 6, 6, 6, 6, 7, 8, 10
Посередине два значения: 4 и 5. Таким образом, медиана — это среднее этих двух значений, равное 4,5.
Таким образом, медиана равна 4,5.Это значение находится прямо в середине набора данных.
Режим
Чтобы найти режим этого набора данных, мы можем определить значения, которые встречаются чаще всего:
1 , 1 , 1 , 1 , 2, 2, 2, 3, 4, 5, 5, 6 , 6 , 6 , 6 , 7, 8, 10
Этот набор данных имеет два режима: 1 и 6.Каждое из этих значений встречается в наборе данных четыре раза.
Дополнительные ресурсы
В следующих учебных пособиях представлена дополнительная информация о точечных диаграммах:
Точечный график и гистограмма: в чем разница?
Как найти центр и распространение точечной диаграммы
В следующих руководствах объясняется, как создавать точечные диаграммы с помощью различных программ:
Как создать точечный график в Google Sheets
Как создать точечный график в Excel
Как создать точечный график в R
Как найти среднее число в графике?
Vicky Johnson
Ученик
(29),
закрыт
13 лет назад
Как найти среднее число в графике?
Дополнен 13 лет назад
Как определить среднюю величину на графике?
Лучший ответ
Сем Питерсон
Мастер
(1411)
13 лет назад
если график точечный то суммируешь значение функций и делишь на количество точек, если график непрерывный то находишь определенный интеграл на интервале деленный на длину интервала.
Источник: хзш
Остальные ответы
Артём
Ученик
(198)
13 лет назад
Делиш посередине и всё
Источник: я
Artem Klementiev
Гуру
(3427)
13 лет назад
Определенный интеграл на интервале деленный на длину интервала…
Похожие вопросы
В поисках средних значений: разбираемся со средним арифметическим, медианой и модой

В поисках средних значений: разбираемся со средним арифметическим, медианой и модой

Иногда при работе с данными нужно описать множество значений каким-то одним числом. Например, при исследовании эффективности сотрудников, уровня вовлеченности в аккаунте, KPI или времени ответа на сообщения клиентов. В таких случаях используют меры центральной тенденции. Их можно называть проще — средние значения.
Но в зависимости от вводных данных, находить среднее значение нужно по-разному. Основной набор задач закрывается с использованием среднего арифметического, медианы и моды. Но если выбрать неверный способ — выводы будут необъективны, а результаты исследования нельзя будет признать действительными. Чтобы не допустить ошибку, нужно понимать особенности разных способов нахождения средних значений.

Cтратег, аналитик и контент-продюсер. Работает с агентством «Палиндром».

Как считать среднее арифметическое
Использовать среднее арифметическое стоит тогда, когда множество значений распределяются нормально ― это значит, что значения расположены симметрично относительно центра. Как выглядит нормальное распределение на графике и в таблице, можно посмотреть на примере:


Если данные распределяются как в примерах — вам повезло. Можно без лишних заморочек считать среднее арифметическое и быть уверенным, что выводы будут объективны. Однако, нормальное распределение на практике встречается крайне редко, поэтому среднее арифметическое в большинстве случаев лучше не использовать.
Как рассчитать
Сумму значений нужно поделить на их количество. Например, вы хотите узнать средний ER за 4 дня при нормальном распределении значений и без аномальных выбросов. Для этого считаем среднее арифметическое: складываем ER всех дней и делим полученное число на количество дней.
Если хотите автоматизировать вычисления и узнать среднее арифметическое для большого числа показателей — используйте Google Таблицы:
- Заполните таблицу данными.
- Щелкните по пустой ячейке, в которую хотите записать среднее арифметическое.
- Введите «=AVERAGE(» и выделите ряд чисел, для которых нужно вычислить среднее арифметическое. Нажмите «Enter» после ввода формулы.
Когда можно не использовать
Если данные распределены ненормально, то наши расчеты не будут отражать реальную картину. На ненормальность распределения указывают:
- Отсутствие симметрии в расположении значений.
- Наличие ярко выраженных выбросов.
Как пример ненормального распределения (с выбросами) можно рассматривать среднее время ответа на комментарии по неделям:
Если посчитать среднее значение для такого набора данных с помощью среднего арифметического, то получится завышенное число. В итоге наши выводы будут более позитивными, чем реальное положение дел. Еще стоит учитывать, что выбросы могут не только завышать среднее значение, но и занижать его. В таком случае вы получите более скромный показатель, который не будет соответствовать реальности.
Например, в группе «Золотое Яблоко» во ВКонтакте иногда публикуют конкурсные посты. Они набирают более высокие показатели вовлеченности чем обычные публикации. Если посчитать средний ER с учетом конкурсов, мы получим 0,37%, а без учета конкурсов — только 0,29%. Аналогичная ситуация с числом комментариев. С конкурсами в среднем получаем 917 комментариев, а без конкурсов — всего лишь 503. Очевидно, что из-за розыгрышей средние показатели вовлеченности завышаются. В этом случае конкурсные посты следует исключить из анализа, чтобы объективно оценить эффективность контента в группе.
Еще часто бывает так, что данных очень много, заметны явные выбросы, но на их обработку и исключение аномальных значений не хватит ни времени, ни терпения. Тем более нет гарантий, что исключив выбросы, вы получите нормальное распределение. В таком случае лучше подсчитать средние значения, используя медиану.
Как найти медиану и когда ее применять
Если вы имеете дело с ненормальным распределением или замечаете значительные выбросы — используйте медиану. Так можно получить более адекватное среднее значение, чем при использовании среднего арифметического. Чтобы понять, как работать с медианой, рассмотрим аналогичный пример с ненормальным распределением времени ответов на комментарии.
Ниже в таблице уже введены данные из графика и рассчитано среднее время ответа с помощью среднего арифметического и медианы. Из расчетов видна наглядная разница между средним арифметическим и медианой ― она составляет 17 минут. Такое различие появляется из-за низкого темпа работы на выходных и в нестандартных ситуациях, когда к ответу на сообщения нужно относиться с особой ответственностью (события конца февраля). Подобные выбросы сильно завышают среднее арифметическое, а вот на медиану они практически не влияют. Поэтому если хотите посчитать среднее значение избегая влияния выбросов, — используйте медиану. Такие данные будут без искажений.
Как рассчитать
Разберем на примере. В аккаунте опубликовали семь постов и они набрали разное количество комментариев: 35, 105, 2, 15, 2, 31, 1. Чтобы вычислить медиану, нужно пройти два этапа:
- Расположите числа в порядке возрастания. Итоговый ряд будет выглядеть так: 1, 2, 2, 15, 31, 35, 105.
- Найдите середину сформированного ряда. В центре стоит число 15 — его и нужно считать медианой.
Немного сложнее найти медиану, если вы работаете с четным количеством чисел. Например, вы собрали количество лайков на последних шести постах: 32, 48, 36, 201, 52, 12. Чтобы найти медиану, выполните три действия:
- Расставьте числа по возрастанию: 12, 32, 36, 48, 52, 201.
- Возьмите два из них, наиболее близких к центру. В нашем случае — это 36 и 48.
- Сложите два этих числа и разделите на два: (36 + 48) / 2 = 42. Результат и есть медиана.
Чтобы вычислять медиану быстрее и обрабатывать большие объемы данных — используйте Google Таблицы:
- Внесите данные в таблицу.
- Щелкните по свободной ячейке, в которую хотите записать медиану.
- Введите формулу «=MEDIAN(» и выделите ряд чисел, для которых нужно рассчитать медиану. Нажмите «Enter», чтобы все посчиталось.
Когда можно не использовать
Если данные распределены нормально и вы не видите заметных выбросов — медиану можно не использовать. В этом случае значение среднего арифметического будет очень близким к медиане. Можете выбрать любой способ нахождения среднего, с которым вам работать проще. Результат от этого сильно не изменится.
Что такое мода и где ее использовать
Мода ― это самое популярное/часто встречающееся значение. Например, стоит задача узнать, сколько комментариев чаще всего набирают посты в аккаунте. В этом случае можно не высчитывать среднее арифметическое или медиану ― лучше и проще использовать моду.
Еще пример. Нужно узнать, в какое время аудитория чаще всего взаимодействует с публикациями. Для этого можно посчитать данные вручную или использовать готовую таблицу из LiveDune (вкладка «Вовлеченность» ― таблица «Лучшее время для поста»). По ее данным ― больше всего реакций пользователи оставляют в среду в 16 часов. Это время и есть мода. Таким образом, если вам нужно найти самое популярное значение, а не классическое среднее — проще использовать моду.
Как рассчитать
Чтобы найти наиболее часто встречающееся значение в наборе данных, нужно посмотреть, какое число встречается в ряду чаще всех. Например, для ряда 5, 4, 2, 4, 7 ― модой будет число 4.
Иногда в ряде значений встречается несколько мод. Например, ряду 7, 7, 21, 2, 5, 5 свойственны две моды — 7 и 5. В этом случае совокупность чисел называется мультимодальной. Также поиск моды можно упростить с помощью Google Таблиц:
- Внесите значения в таблицу.
- Щелкните по ячейке, в которую хотите записать моду.
- Введите формулу «=MODE(» и выделите ряд чисел, для которых нужно вычислить моду. Нажмите «Enter».
Однако важно иметь в виду, что табличная функция выдает только самую меньшую моду. Поэтому будьте внимательны — можно упустить из виду несколько мод.
Когда использовать не стоит
Моду нет смысла использовать, если вас не просят найти самое популярное значение. Там, где надо найти классическое среднее значение, про моду лучше забыть.
Памятка по использованию
Среднее арифметическое
Как находим: сумма чисел / количество чисел.
Используем: если данные распределены нормально и нет ярких выбросов.
Не используем: если видим явные выбросы или ненормальное распределение.
Медиана
Как находим: располагаем числа в порядке возрастания и находим середину сформированного ряда.
Используем: если работаем с ненормальным распределением или видим выбросы.
Не используем: если выбросов нет и распределение нормальное.
Мода
Как находим: определяем значение, которое чаще всего встречается в ряду чисел.
Используем: если нужно найти не среднее, а самое популярное значение.
Не используем: если нужно найти классическое среднее значение.
Только важные новости в ежемесячной рассылке
Нажимая на кнопку, вы даете согласие на обработку персональных данных.

Подписывайся сейчас и получи гайд аудита Instagram аккаунта
Маркетинговые продукты LiveDune — 7 дней бесплатно
Наши продукты помогают оптимизировать работу в соцсетях и улучшать аккаунты с помощью глубокой аналитики

Анализ своих и чужих аккаунтов по 50+ метрикам в 6 соцсетях.
Оптимизация обработки сообщений: операторы, статистика, теги и др.
Автоматические отчеты по 6 соцсетям. Выгрузка в PDF, Excel, Google Slides.
Контроль за прогрессом выполнения KPI для аккаунтов Инстаграм.
Аудит Инстаграм аккаунтов с понятными выводами и советами.
Поможем отобрать «чистых» блогеров для эффективного сотрудничества.
Среднее
значение периодической функции f(t)
за период Т
определяется по формуле
Fср=
.
(2.4)
Отсюда
видно, что среднее значение за период
равно высоте прямоугольника с основанием
Т,
площадь которого равна площади,
ограниченной функцией f(t)
и осью абсцисс за один период.
В случае гармонического
колебания среднее значение за период
равно нулю, так как площадь положительной
полуволны компенсируется площадью
отрицательной полуволны гармонической
функции. Поэтому здесь пользуются
понятием среднего значения функции,
взятой по абсолютной величине, или, что
то же, среднего полупериодного значения,
соответствующего положительной полуволне
гармонической функции (рисунок 2.2).
В
соответствии с этим среднее значение
тока i
= Imсosωt
с амплитудой А
= Im
будет

Аналогично среднее
значение гармонического напряжения
. (2.6)
Тепловое действие
тока, а также механическая сила
взаимодействия двух проводников, по
которым проходит один и тот же ток,
пропорциональны квадрату тока. Поэтому
о величине тока судят обычно по так
называемому действующему (среднеквадратичному)
значению за период. Этим термином заменен
применявшийся ранее в литературе и ныне
не рекомендуемый термин «эффективное»
значение.
Действующее
значение периодической функции f(t)
вычисляется по формуле

Из
этой формулы следует, что величина F2
представляет собой среднее значение
функции [f(t}]2
за период
Т,
т.е. равна высоте прямоугольника с
основанием Т,
площадь которого равна площади,
ограниченной функцией [f(t)]2
и осью абсцисс за один период (рисунок
2.3).
В
соответствии с (2.7) действующее значение
периодического тока

Возведя
(2.8) в квадрат и умножив обе части
полученного выражения на RT,
найдем
.
Это
равенство показывает, что действующее
значение периодического тока равно по
величине такому постоянному току,
который, проходя через неизменное
сопротивление R,
за период времени Т выделяет то же
количество тепла, что и данный ток i.
Аналогично
действующее значение периодического
напряжения

При
токе i
= Imcosωt
.
Следовательно,
согласно (2.8)
. (2.8а)
Аналогично
действующее значение гармонического
напряжения
. (2.9а)
Номинальные токи
и напряжения электротехнических
устройств определяются, как правило,
действующими значениями; поэтому
действующие значения представляют
наиболее распространенный электрический
параметр.
Для измерения
действующих значений применяются
системы приборов: тепловая, электромагнитная,
электродинамическая и др.
2.3
ПРЕДСТАВЛЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
В ВИДЕ ПРОЕКЦИЙ ВРАЩАЮЩИХСЯ ВЕКТОРОВ
Мгновенные значения
функции u
= Umcos(ωt+)
можно получить как проекцию на
горизонтальную ось отрезка длиной Um,
вращающегося относительно начала
прямоугольной системы координат с
угловой скоростью ω = 2f
в положительном направлении (т.е. против
хода часовой стрелки). Вращающийся
отрезок условимся называть вектором.
Этот вектор, вращающийся в плоскости
прямоугольной системы координат, не
следует смешивать с вектором в трехмерном
пространстве из области механики или
теории электромагнитного поля.
В
момент t
= 0 вектор
образует с горизонтальной осью угол ψ
и его проекция
на горизонтальную ось равна Umcos,
т.е. мгновенному значению заданной
функции при t
= 0 (рисунок
2.4, а).
За
время t
= t1
вектор
повернется на угол ωt1
и окажется повернутым относительно
горизонтальной оси на угол ωt1+;
его проекция на эту ось будет равна
Umcos(ωt1
+ )
и т.д.
Таким
образом, рассмотрение гармонических
колебаний можно заменить рассмотрением
вращающихся векторов.
Для
получения мгновенных значений в
соответствии с вышесказанным условимся
проектировать векторы на горизонтальную
ось. Рассмотрим теперь функцию Umsin(ωt
+ )
= Umcos(ωt
+ –).
Она
представится проекцией вращающегося
вектора, имеющего начальную фазу
–
(рисунок 2.4, б).
Следовательно,
векторы, изображающие косинусоидальную
и синусоидальную функции, взаимно
перпендикулярны.
Если
гармонические колебания имеют одну и
ту же частоту, то соответствующие этим
колебаниям векторы вращаются с одинаковой
угловой скоростью и поэтому углы между
ними сохраняются неизменными.
На
рисунке 2.5 показаны две гармонические
функции
u1
= U1mcos(ωt
+ 1)
и
u2
= U2mcos(ωt
+ 2),
имеющие
одинаковую угловую частоту ω и начальные
фазы 1
и -2.
Кривая u1,
смещенная
влево относительно u2,
возрастает от нуля до своего положительного
максимума раньше, чем кривая u2.
Поэтому говорят, что u1
опережает
по фазе u2,
или, что то же, u2
отстает по фазе от
u1.
Разность
начальных фаз
= 1
– (-2)
= 1
+ 2
называется фазовым сдвигом или углом
сдвига u1
относительно u2.
Этот угол
и образуют между собой векторы, показанные
на рисунке 2.5 (вверху).
При
равенстве начальных фаз, т.е. при фазовом
сдвиге, равном нулю,
векторы,
направлены, в одну и ту же сторону
(совпадают
по фазе).
При
фазовом сдвиге 180°
векторы направлены в диаметрально
противоположные стороны (находятся
в противофазе).
Диаграмма,
изображающая совокупность векторов,
построенных с соблюдением их взаимной
ориентации по фазе, называется векторной
диаграммой.
Векторное
представление гармонических функций,
частота которых одинакова, облегчает
операции сложения и вычитания этих
функций. Ввиду того, что сумма проекций
двух векторов равна проекции геометрической
суммы этих векторов, амплитуда и начальная
фаза результирующей кривой легко
находятся из векторной диаграммы
геометрическим сложением
векторов.
Например, пусть
требуется сложить функции
u1
= U1mcos(ωt
+ 1) и
u2
= U2mcos(ωt
+ 2).
Из
графического построения рисунок 2.6, а
следует:
; (2.11)
.
(2.12)
Здесь
угол
находится с учетом знаков числителя и
знаменателя, определяющих знаки синуса
и косинуса.
В
случае, когда функция u2
вычитается из u1
(рисунок
2.6, б),
угол 1
в (2.11) и (2.12) заменяется на 2
+
или, что то же, на 2
().
Амплитуда
Um
и угол
могут быть также получены непосредственно
из векторной диаграммы.
При
пользовании векторной диаграммой с
целью установления фазовых сдвигов или
амплитудных значений гармонических
величин, имеющих одинаковую частоту,
векторная диаграмма может считаться
неподвижной (при равенстве частот углы
между векторами не зависят от времени).
Построение
векторных диаграмм обычно не связано
с определением мгновенных значений
гармонических функций; в таких случаях
векторные диаграммы строятся не для
амплитуд, а для действующих значений,
т.е. модули векторов уменьшаются по
сравнению с амплитудами в
раз. При этом векторная диаграмма
мыслится неподвижной.
В
отличие от векторных диаграмм кривые
мгновенных значений называются временными
диаграммами.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #