Как найти среднее число соударений - Сайт, где вы сможете решить свои вопросы

Молекулы
газа, находясь в состоянии хаотического
движения, непрерывно сталкиваются друг
с другом. Между двумя последовательными
столкновениями молекулы проходят
некоторый путь l, который называется
длиной свободного пробега. В общем
случае длина пути между последовательными
столкновениями различна, но так как мы
имеем дело с огромным числом молекул и
они находятся в беспорядочном движении,
то можно говорить о средней длине
свободного пробега молекул <l>.

Минимальное
расстояние, на которое сближаются при
столкновении центры двух молекул,
называется эффективным диаметром
молекулы d. Он зависит от скорости
сталкивающихся молекул, т. е. от температуры
газа (несколько уменьшается с ростом
температуры).

Т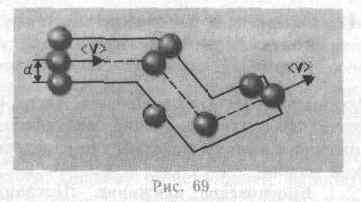
ак
как за 1 с молекула проходит в среднем
путь, равный средней арифметической
скорости <v>, и если (z) —среднее число
столкновений, испытываемых одной
молекулой газа за 1 с, то средняя длина
свободного пробега <l>=<v>/<z>.

Для
определения <z> представим себе
молекулу в виде шарика диаметром d,
которая движется среди других «застывших»
молекул. Эта молекула столкнется с теми
молекулами, центры кт находятся на
расстояниях, равных или меньших d, т. е.
лежат внутри «ломаного» цилиндра
радиусом d.

С
реднее
число столкновений за 1 с равно числу
молекул в объеме «ломаного» цилиндра:
<z>=nV,
где n — концентрация молекул, V
= pd²<v> (<v>
—средняя скорость молекулы или путь,
пройденный ею за 1с). Таким образом,
среднее число столкновений <z>=npd²<v>.

Расчеты
показывают, что при учете движения
других молекул

Т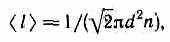
огда
средняя длина свободного пробега

29. Явления переноса в термодинамически неравновесных системах: диффузия

теплопроводность,
внутреннее трение.

В
термодинамических неравновесных
системах возникают особые необратимые
процессы, называемые явлениями переноса,
в результате которых происходит
пространственный перенос энергии,
массы, импульса. К явлениям переноса
относятся теплопроводность
(обусловлена переносом энергии), диффузия
(обусловлена переносом массы) и внутреннее
трение
(обусловлено переносом импульса).

1.
Теплопроводность.
Если в одной области газа средняя
кинетическая энергия молекул больше,
чем в другой, то с течением времени
вследствие постоянных столкновений
молекул происходит процесс выравнивания
средних кинетических энергий молекул,
т. е. выравнивание температур.

Перенос
энергии в форме теплоты подчиняется
закону
Фурье:

г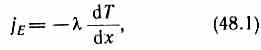

де
jE
— плотность теплового потока —
величина, определяемая энергией,
переносимой в форме теплоты в единицу
времени через единичную площадку,
перпендикулярную оси х, λ — коэф.
теплопроводности, dT/dx — градиент
температуры, равный скорости изменения
температуры на единицу длины х в
направлении нормали к этой площадке.
Знак минус показывает, что при
теплопроводности энергия переносится
в направлении убывания температуры

где
Сv — удельная теплоемкость газа при
постоянном объеме (количество теплоты,
необходимое для нагревания 1 кг газа на
1 К при постоянном объеме), r — плотность
газа, (v) —средняя скорость теплового
движения молекул, <l> — средняя длина
свободного пробега.

2.
Явление диффузии
заключается в том, что происходит
перемешивание частиц двух соприкасающихся
газов, жидкостей и даже твердых тел; она
возникает и продолжается, пока существует
градиент плотности. Явление диффузии
для химически однородного газа подчиняется
закону
Фика:
jm=-Ddp/dx,
где jт — плотность потока массы —
величина, определяемая массой вещества,
диффузия кт происходит в ед. времени
через ед. площадку, перпендикулярную
оси х, D — диффузия (коэффициент диффузии),
dr/dx—градиент плотности, равный скорости
изменения плотности на единицу длины
х в направлении нормали к этой площадке.
Знак минус показывает, что перенос массы
происходит в направлении убывания
плотности. Диффузия D численно равна
плотности потока массы при градиенте
плотности, равном единице. Согласно
кинетической теории газов, D=1/3
<v> <l>.

Закон
Фика
характеризует
на сколько быстро меняется концентрация

3.
Внутреннее трение (вязкость).
Механизм возникновения внутреннего
трения между параллельными слоями газа
(жидкости), движущимися с различными
скоростями, заключается в том, что из-за
хаотического теплового движения
происходит обмен молекулами между
слоями, в результате чего импульс слоя,
движущегося быстрее, уменьшается,
движущегося медленнее — увеличивается,
что приводит к торможению слоя, движущегося
быстрее, и ускорению слоя, движущегося
медленнее.

С

ила
внутреннего трения между двумя слоями
газа (жидкости) подчиняется закону
Ньютона:

dv/dx
— градиент скорости, показывающий
быстроту изменения скорости в направлении
х, перпендикулярном направлению движения
слоев, S — площадь, на которую действует
сила F.

В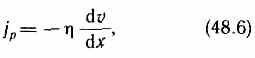
заимодействие
двух слоев согласно второму закону
Ньютона можно рассматривать как процесс,
при котором от одного слоя к другому в
единицу времени передается импульс, по
модулю равный действующей силе. Тогда
выражение можно представить в виде

Знак
минус указывает, что импульс переносится
в направлении убывания скорости.

Д
инамическая
вязкость h численно равна плотности
потока импульса при градиенте скорости,
равном единице; она вычисляется по
формуле

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
#
#
23.05.201568.1 Кб72FizLab2_10.xls
#
#
#
#

Источник

Решение.
Средняя длина свободного пробега молекулы кислорода определяется по формуле:

[ lambda =frac{1}{sqrt{2}cdot pi cdot {{d}^{2}}cdot n} (1). ]

d – эффективный диаметр молекулы кислорода (справочные данные), d = 3,6∙10^-10 м, n – концентрация молекул кислорода.
Концентрацию молекул кислорода определим по формуле:

[ n=frac{N}{V},N=frac{m}{M}cdot {{N}_{A}}(4),n=frac{m}{Mcdot V}cdot {{N}_{A}}(2). ]

Где: M – молярная масса молекулы кислорода, М = 32∙10^-3 кг/моль, R = 8,31 Дж/(моль∙К) – универсальная газовая постоянная.
Подставим (2) в (1) определим длину свободного пробега молекулы кислорода:

[ lambda =frac{Mcdot V}{sqrt{2}cdot pi cdot {{d}^{2}}cdot mcdot {{N}_{A}}} (3).lambda =frac{32cdot {{10}^{-3}}cdot 1cdot {{10}^{-3}}}{sqrt{2}cdot 3,14cdot {{(3,6cdot {{10}^{-10}})}^{2}}cdot 32cdot {{10}^{-3}}cdot 6,02cdot {{10}^{23}}}=0,289cdot {{10}^{-8}}. ]

λ = 0,289∙10^-8 м.
Определим среднюю арифметическую скорость движения молекулы кислорода:

[ {{upsilon }_{CA}}=sqrt{frac{8cdot Rcdot T}{pi cdot M}} (4).{{upsilon }_{CA}}=sqrt{frac{8cdot 8,31cdot 100}{3,14cdot 32cdot {{10}^{-3}}}}=257,22. ]

υ_СА = 257,22 м/с.
Среднее число соударений в секунду молекул кислорода при этих условиях определим по формуле:

[ nu =frac{N}{t}=frac{upsilon }{lambda }, N=nu frac{upsilon }{lambda }cdot t=frac{sqrt{frac{8cdot Rcdot T}{pi cdot M}}}{frac{Mcdot V}{sqrt{2}cdot pi cdot {{d}^{2}}cdot mcdot {{N}_{A}}} }cdot t (5).N=frac{257,22}{0,289cdot {{10}^{-8}}}cdot 1=890,03cdot {{10}^{8}}.
]

N = 890,03∙10⁸.

Источник

Макеты страниц

По-прежнему будем считать газ идеальным, т. е. будем считать, что, за исключением момента столкновения, молекулы не взаимодействуют, не подвергаются действию каких-либо сил и движутся поэтому прямолинейно. В момент столкновения направление скорости молекулы изменяется, после чего она снова движется прямолинейно. Путь молекулы в газе представляет собой, таким образом, ломаную линию, подобную, например, изображенной на рис. 45. Каждый излом траектории отмечает место столкновения. Расстояние, которое молекула проходят между двумя последовательными столкновениями, называется длиной свободного пробега.

Рис. 45.

Так как молекул в газе чрезвычайно много, то не может быть речи о какой-либо регулярности в процессе столкновений, и длины прямолинейных участков на зигзагообразном пути молекулы могут быть различными. Поэтому нас будет интересовать средняя длина свободного пробега. Точно так же различным может быть и число столкновений, испытываемых молекулой в единицу времени, и следует говорить только о среднем значении этой величины.

Эти две связанные между собой величины — средняя длина свободн пробега и среднее число столкновений в единицу времени — являются главными характеристиками процесса столкновений газовых молекул. В частности, те «помехи» явлениям переноса, о которых упоминалось выше, зависят от числа столкновений. Именно от этого зависит длина пути, котцрый молекула проходит между двумя данными точками в объеме газа. Как это видно из рис. 45, истинный путь молекулы между точками много больше, чем расстояние по соединяющей их прямой. Ясно, что, например, процесс диффузии, т. е. проникновение одного газа в другой, не может происходить быстро, несмотря на большую скорость молекул: столкновения в значительной степени компенсируют влияние скорости.

Среднее число столкновений, испытываемых молекулой газа в единицу времени, можно вычислить из весьма простых соображений. Молекулы будем считать твердыми упругими шариками радиуса Пусть одна из молекул движется по прямой в газе, в котором частицы равномерно распределены по объему, так что в каждом кубическом сантиметре находится молекул. Предположим сначала, что все молекулы, кроме одной, находятся в покое. Тогда наша единственная движущаяся молекула, пройдя за 1 с расстояние, равное ее средней скорости и, столкнется со всеми молекулами,

которые окажутся на ее пути. Это будут те молекулы, центры которых расположены в объеме цилиндра длиной и с площадью основания, равной эффективному поперечнику столкновения (рис. 46). Объем этого цилиндра равен сто, а число молекул в нем Таким же будет и число столкновений которые испытывает наша молекула:

Конечно, молекула не может двигаться прямолинейно, раз она сталкивается с другими молекулами. На самом деле путь, проходимый молекулой, зигзагообразный, как это показано, скажем, на рис. 47.

Рис. 46.

Рис. 47.

Это, однако, не изменяет результаты расчета; полагая, что молекула движется по прямой, мы только мысленно «выпрямили» ломаный цилиндр, изображенный на рис. 47.

Следует учесть, что движется не одна, а все молекулы газа. Это значит, что в выражение для должна входить не абсолютная (относительно стенок сосуда) скорость молекулы, а скорость ее относительно тех молекул, с которыми она сталкивается. Можно показать, приняв во внимание максвелловское распределение молекул по скоростям, что относительная скорость оотн связана с абсолютной скоростью О соотношением

Тогда для среднего числа столкновений молекулы в единицу времени получим формулу

или, поскольку мы условились считать молекулы шариками,

Чтобы найти среднее число столкновений, происходящих в единицу времени в газе, т. е. столкновений, испытываемых всеми молекулами, нужно умножить на число молекул в газе. Но так как в каждом столкновении участвуют две молекулы (встреча

одновременно трех и более молекул крайне маловероятна), то это число нужно еще разделить на 2, чтобы не считать каждое столкновение два раза. Следовательно, полное число столкновений в газе, содержащем частиц, равно

Таким образом, в единице объема газа число столкновений, происходящих каждую секунду, равно

где число молекул в единице объема.

Зная число столкновений, испытываемых одной молекулой в единицу времени, легко вычислить и среднюю длину свободного пробега.

За время молекула проходит некоторый зигзагообразный путь, равный . Изломов на этом пути столько, сколько произошло столкновений, так как каждый излом и вызван столкновением. Средняя длина свободного пробега, т. е. средняя длина прямолинейного отрезка X между столкновениями, равна отношению длины пути, пройденного молекулой, к числу испытанных ею на этом пути столкновений:

или, подставив вместо его значение из (36.3), получим:

Пользуясь этой формулой, можно найти численные значения для Проведем такой расчет, например, для воздуха (азота) при нормальных условиях (давление 1 атм, температура 273 К). Радиус молекулы азота можно считать равным число частиц в единице объема средняя скорость Отсюда

Средняя длина свободного пробега молекулы в рассматриваемых условиях равна

Естественно возникает вопрос, можно ли считать идеальным такой газ, в котором частицы каждую секунду сталкиваются миллиарды раз, а между столкновениями, т. е. «свободно», они

проходят ничтожные отрезки пути, не превосходящие нескольких стотысячных долей сантиметра? Можно ли считать молекулы такого газа невзаимодействующими? Ведь столкновение — это взаимодействие, приводящее к изменению направления скорости молекул, а столь частые столкновения означают, как будто бы, весьма сильное взаимодействие. Легко, однако, видеть, что это не так, Действительно, молекулы, как уже было указано, взаимодействуют друг с другом только в течение того времени, пока они находятся друг от друга на расстоянии порядка их диаметра время между столкновениями молекулы движутся свободно. Так как при атмосферном давлении длина свободного пробега молекулы что примерно в 1000 раз больше размеров молекул, то время пребывания молекул под взаимным воздействием во столько же раз меньше времени их свободного движения.

Другими словами, время столкновения молекул примерно в 1000 раз меньше времени между столкновениями. Следовательно подавляющую часть времени молекулы движутся свободно, а столкновения, даже при атмосферном давлении, можно считать редким событием в их жизни.

Зависимость длины свободного пробега от давления. Как видно из формулы (36.4), длина свободного пробега молекул обратно пропорциональна их числу в единице объема, а следовательно, его давлению так что можно написать:

С уменьшением давления длина свободного пробега молекул возрастает в такой же мере, в какой падает давление. При определенном значении давления она станет равной размерам сосуда, в котором газ заключен, а при дальнейшем понижении давления превзойдет их. Например, в сосуде размером около 25 см (размеры, обычные в лабораторной практике) длина свободного пробега молекул сравняется с размерами сосуда уже при давлении около атм Такое давление сравнительно легко создать, так как современные средства откачки позволяют получить давления до

Когда длина свободного пробега становится равной или большей размеров сосуда, столкновения молекул в газе практически уже не происходят, и весь путь от стенки до стенки молекулы проходят, двигаясь прямолинейно.

Естественно, что газ, в котором молекулы не сталкиваются между собой, отличается по своим свойствам от обычного газа. Ниже, в гл. IV, мы познакомимся со своеобразными свойствами такого газа.

Зависимость длины свободного пробега от температуры. Из формулы (36.4) следует, что длина свободного пробега молекул не должна зависеть от температуры. Опыт, между тем, показывает, что такая зависимость, хотя и слабая, существует: с повышением

температуры длина свободного пробега возрастает. Это объясняется тем, что согласно формуле (36.4) X обратно пропорциональна поперечному сечению молекулы, А оно, как мы уже знаем, определяется расстоянием, на которое сближаются молекулы при столкновении, т. е. расстоянием, при котором сила взаимодействия между молекулами вызывает уже заметное изменение направления их движения.

Легко видеть, что поперечное сечение молекул должно зависеть от их скорости (энергии), так как при одной и той же силе взаимодействия быстрые молекулы испытывают меньшее отклонение от своего пути, чем более медленные молекулы. Поэтому, чем больше скорость молекул, тем больше должна быть сила, вызывающая их отклонение, следовательно, тем меньше должно быть расстояние между ними при столкновении. Это и значит, что с увеличением скорости молекул, т. е. с повышением температуры газа, поперечное сечение молекул уменьшается. Длина же свободного пробега молекул с повышением температуры, растет. Эта слабая зависимость X от температуры объясняет некоторые явления, которые будут рассмотрены ниже.

Факт зависимости длины свободного пробега от температуры может служить подтверждением изложенных выше соображений о смысле понятия «размер молекулы». Если бы молекулы действительно были твердыми шариками, то не могло бы быть и речи об изменении их размеров при изменении скорости. На самом деле размеры частиц (не только молекул газа!) определяются расстоянием между ними при максимальном сближении, а оно не может не зависеть от скорости частиц, а значит (в случае газовых молекул) и от температуры. Это, однако, не мешает тому, что в. целом ряде случаев взаимодействие между молекулами можно с достаточной степенью точности рассматривать как взаимодействие между твердыми шариками.

Оглавление

ПРЕДИСЛОВИЕ
ВВЕДЕНИЕ
Глава I. КИНЕТИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНЫХ ГАЗОВ
§ 1. Идеальный газ
§ 2. Давление газа
§ 3. Температура
§ 4. Уравнение состояния идеального газа
§ 5. Законы идеального газа
§ 6. Скорости газовых молекул
§ 7. Броуновское движение
§ 8. Барометрическая формула
§ 9. Закон Больцмана
§ 10. Понятие о вероятности
§ 11. Понятие о распределении. Функция распределения
§ 12. Распределение молекул по компонентам скорости
§ 13. Распределение молекул по скоростям
§ 14. Средние скорости молекул
§ 15. Наивероятнейшая скорость молекул
§ 16. Формула Максвелла для относительных скоростей
§ 17. Закон распределения молекул по скоростям и атмосферы планет
§ 18. Экспериментальная проверка закона распределения
§ 19. Измерение параметров состояния
Глава II. КИНЕТИЧЕСКАЯ ТЕОРИЯ ТЕПЛОТЫ. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
§ 20. Внутренняя энергия идеального газа
§ 21. Количество теплоты
§ 22. Механический эквивалент теплоты
§ 23. Первое начало термодинамики
§ 24. Теплоемкость идеальных газов
§ 25. Теплоемкость одноатомных газов
§ 26. Теплоемкость газов и число степеней свободы молекул
§ 27. Теплоемкость двухатомных и многоатомных газов
§ 28. Изменение состояния при изменении объема газа
§ 29. Работа при изотермическом изменении объема идеального газа
§ 30. Адиабатное изменение объема идеального газа
§ 31. Работа при адиабатном изменении объема газа
§ 32. Политропический процесс
§ 33. Расширение газа в пустоту
§ 34. Измерение количества теплоты и теплоемкости
Глава III. СТОЛКНОВЕНИЯ МОЛЕКУЛ И ЯВЛЕНИЯ ПЕРЕНОСА
§ 35. Молекулярные движения и явления переноса
§ 36. Среднее число столкновений в единицу времени и средняя длина свободного пробега молекул
§ 37. Эффективное поперечное сечение частицы и вероятность
§ 38. Рассеяние молекулярного пучка в газе
§ 39. Экспериментальное определение длины свободного пробега
§ 40. Диффузия в газах
§ 41. Нестационарная диффузия
§ 42. Стационарная диффузия. Вычисление коэффициента диффузии
§ 43. Коэффициент взаимной диффузии
§ 44. Термическая диффузия
§ 45. Теплопроводность газов
§ 46. Нестационарная теплопроводность
§ 47. Стационарная теплопроводность. Вычисление коэффициента теплопроводности
§ 48. Вязкость газов (внутреннее трение)
§ 49. Измерение коэффициента вязкости (вискозиметрия)
§ 50. Соотношения между коэффициентами переноса
Глава IV. ФИЗИЧЕСКИЕ ЯВЛЕНИЯ В РАЗРЕЖЕННЫХ ГАЗАХ (ВАКУУМЕ)
§ 51. Теплопередача в газах при малых давлениях
§ 52. Течение газов при малых давлениях (молекулярное течение)
§ 53. Молекулярное течение газа в цилиндрической трубе
§ 54. Молекулярное течение смеси газов. Разделение газовых смесей
§ 55. Диффузия газов в вакууме
§ 56. Разность давлений между различно нагретыми частями газа (тепловая транспирация)
§ 57. Элементы вакуумной техники
§ 58. Измерение малых давлений
§ 59. Вакуумная установка
Глава V. НЕИДЕАЛЬНЫЕ (РЕАЛЬНЫЕ) ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
§ 60. Отклонения свойств газов от идеальности
§ 61. Сжижение газов (конденсация)
§ 62. Фазовый переход
§ 63. Фазовые диаграммы
§ 64. Методы определения критических параметров
§ 65. Уравнение Ван-дер-Ваальса
§ 66. Изотермы Ван-дер-Ваальса
§ 67. Критическая температура и критическое состояние
§ 68. Экспериментальное определение констант уравнения Ван-дер-Ваальса
§ 69. Сравнение уравнения Ван-дер-Ваальса с данными опыта
§ 70. Приведенное уравнение Ван-дер-Ваальса. Закон соответственных состояний
§ 71. Межмолекулярные силы взаимодействия в реальном газе
§ 72. Теплоемкость неидеальных газов
Глава VI. ЭЛЕМЕНТЫ ТЕРМОДИНАМИКИ
§ 73. Равновесные состояния
§ 74. Обратимые и необратимые процессы
§ 75. Квазистатические процессы
§ 76. Необратимость и вервятность
§ 77. Взаимные превращения механической и тепловой энергии
§ 78. Первое начало термодинамики
§ 79. Преобразование теплоты в механическую работу
§ 80. Цикл Карно
§ 81. Холодильная машина
§ 82. Доказательство теорем Карно
§ 83. Свободная энергия
§ 84. Энтропия
§ 85. Некоторые термодинамические соотношения
§ 86. Энтропия при обратимых процессах в замкнутой системе
§ 87. Энтропия при необратимых процессах в замкнутой системе, акон возрастания энтропии
§ 88. Второе начало термодинамики и превращение теплоты в работу
§ 89. Физический смысл энтропии. Энтропия и вероятность
§ 90. Энтропия и беспорядок
§ 91. «Демон» Максвелла
§ 92. Термодинамическая шкала температур
§ 93. Третье начало термодинамики
§ 94. Отрицательные температуры
Глава VII. СВОЙСТВА ЖИДКОСТЕЙ
§ 95. Объемные свойства жидкостей
§ 96. Теплоемкость жидкостей
§ 97. Явления переноса в жидкостях
§ 98. Явления на границе жидкости
§ 99. Условия равновесия на границе двух сред. Краевой угол
§ 100. Силы, возникающие на кривой поверхности жидкости
§ 101. Капиллярные явления
§ 102. Некоторые методы измерения коэффициента поверхностного натяжения
§ 103. Зависимость коэффициента поверхностного натяжения от температуры
§ 104. Испарение и кипение жидкостей
§ 105. Температурная зависимость упругости насыщенных паров
§ 106. Упругость насыщенного пара над кривой поверхностью жидкости
§ 107. Кипение жидкостей
§ 108. Жидкие растворы
§ 109. Осмотическое давление
Глава VIII. НИЗКИЕ ТЕМПЕРАТУРЫ
§ 110. Сжижение газов
§ 111. Эффект Джоуля-Томсона
§ 112. Адиабатное расширение газа с совершением внешней работы
§ 113. Сжижение газов с использованием эффекта Джоуля — Томсона (метод Линде)
§ 114. Сжижение газов методом адиабатного расширения в детандерах (метод Клода)
§ 115. Некоторые свойства сжиженных газов
§ 116. Сверхнизкие температуры
§ 117. Свойства вещества при низких температурах
§ 118. Жидкий гелий
Глава IX. ТВЕРДОЕ ТЕЛО
§ 120. Кристаллическая решетка
§ 121. Дефекты в кристаллах
§ 122. Механические свойства твердых тел. Деформации
§ 123. Деформация растяжения и сжатия. Сдвиг
§ 124. Связь между модулями упругости
§ 125. Упругая деформация и тепловое расширение
§ 126. Зависимость деформации от напряжения
§ 127. Механизм пластической деформации
§ 128. Дислокации в кристаллах
§ 129. Переход в твердое состояние
§ 130. Диаграмма состояния. Тройная точка
§ 131. Фазовые переходы первого и второго рода
§ 132. Твердый гелий
§ 133. Растворение и кристаллизация из раствора
§ 134. Сплавы. Диаграммы плавкости
§ 135. Зонная очистка металлов
§ 136. Опытное определение температуры плавления
§ 137. Тепловые свойства твердых тел
§ 138. Измерение теплоемкости
§ 139. Тепловое расширение твердых тел
§ 140. Теплопроводность
§ 141. Диффузия в твердых телах

Источник

Молекулярная физика 9

1. Среднее число столкновений и средняя длина свободного пробега молекул 2. Распределение молекул по длинам их свободного пробега 3. Эффективное поперечное сечение частицы и вероятность

Диффузия • Явление диффузии заключается в том, что происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел; диффузия сводится к обмену масс частиц этих тел, возникает и продолжается, пока существует градиент плотности. Во время становления молекулярно -кинетической теории по вопросу диффузии возникли противоречия. Так как молекулы движутся с огромными скоростями, диффузия должна происходить очень быстро. Если же открыть в комнате сосуд с пахучим веществом, то запах распространяется довольно медленно. Однако противоречия здесь нет. Молекулы при атмосферном давлении обладают малой длиной свободного пробега и, сталкиваясь с другими молекулами, в основном «стоят» на месте.

• Известно, что Вывод: чтобы объяснить диффузию, надо предположить, что молекулы сталкиваются Отсюда вопросы: 1) – среднее число столкновений в единицу времени 2) <λ> – средняя длина свободного пробега молекул

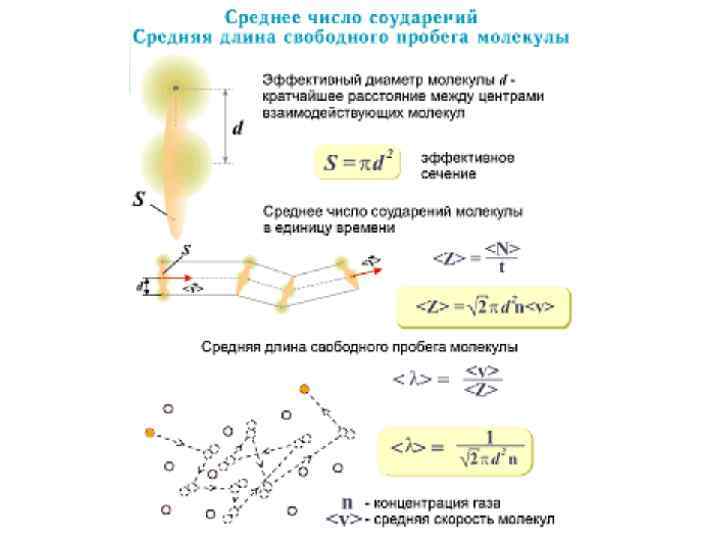
Средняя длина свободного пробега молекул • Молекулы газа, находясь в состоянии хаотического движения, непрерывно сталкиваются друг с другом. • Между двумя последовательными столкновениями молекулы проходят некоторый путь λ, который называется длиной свободного пробега. • В общем случае длина пути между последовательными столкновениями различна, но так как мы имеем дело с огромным числом молекул и они находятся в беспорядочном движении, то можно говорить о средней длине свободного пробега молекул < λ >. • Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d (рис. ). • Он зависит от скорости сталкивающихся молекул т. е. от температуры газа (несколько уменьшается с ростом температуры).

Среднее число столкновений • Так как за 1 с молекула проходит в среднем путь, равный средней арифметической скорости , ( ), и если среднее число столкновений, испытываемых одной молекулой газа за 1 с, то средняя длина свободного пробега • Для определения представим себе молекулу в виде шарика диаметром d, которая движется среди других «покоящихся» молекул. Эта молекула столкнется только с теми молекулами, центры которых находятся на расстояниях, равных или меньших d, т. е. лежат внутри «ломаного» цилиндра радиусом d (рис. ). d σ=πd 2 t

Среднее число столкновений d σ=πd 2 t • Среднее число столкновений за 1 с равно числу молекул в объеме «ломаного» цилиндра: • где п — концентрация молекул, • средняя скорость молекулы или путь, пройденный ею за 1 с). Таким образом, среднее число столкновений •

Среднее число столкновений Средняя длина свободного пробега молекул • Расчеты показывают, что при учете движения других молекул • Тогда средняя длина свободного пробега • т. е. <λ> обратно пропорциональна концентрации п молекул. С другой стороны, из p=nk. T следует, что при постоянной температуре п пропорциональна давлению р. Следовательно, • <λ>~1/p : p – мало → λ – велико, при <λ> >>> L имеем вакуум • Например для азота при н. у. <λ>~10 -7 м

Распределение молекул по длинам их свободного пробега • Надо найти • Из распределения Максвелла • Запишем это распределение в новых переменных • Учтем, что и подставим

Распределение молекул по длинам их свободного пробега Теперь имеем Эта величина представляет самостоятельный интерес , например в кинетике, химии. Кроме того позволяет решать задачи аналогично распределению Максвелла. Например

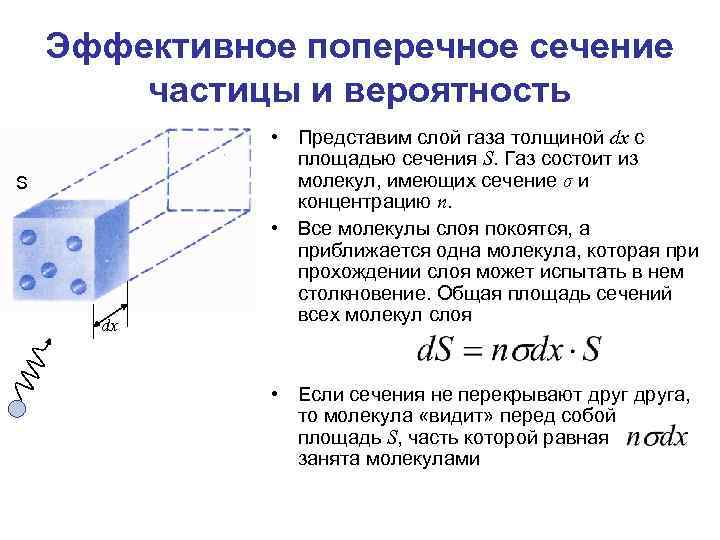
Эффективное поперечное сечение частицы и вероятность S dx • Представим слой газа толщиной dx с площадью сечения S. Газ состоит из молекул, имеющих сечение σ и концентрацию n. • Все молекулы слоя покоятся, а приближается одна молекула, которая при прохождении слоя может испытать в нем столкновение. Общая площадь сечений всех молекул слоя • Если сечения не перекрывают друга, то молекула «видит» перед собой площадь S, часть которой равная занята молекулами

Эффективное поперечное сечение частицы и вероятность • Если бы вся площадь S была перекрыта сечениями, то вероятность столкновения была бы равна 1. • Чем большая часть перекрыта, тем больше вероятность столкновения S dx Специальная единица измерения – Барн. Соизмерима с размерами атомов. • – вероятность того, что молекула испытает столкновение на пути dx в газе. • Эффективное поперечное сечение молекул σ связано с вероятностью столкновения (рассеяния) молекул и не имеет чисто геометрического смысла. • Если эффективное поперечное сечение велико, то это не означает, что молекула «большая» , а означает, что вероятность столкновения велика.

Барн • Барн (сокращение: б, бн) — в ядерной физике единица для измерения эффективного поперечного сечения ядерных реакций. Имеет размерность площади, 1 барн численно равен 10− 28 м² = 10− 24 cм². Определяются также дольные единицы (миллибарн, микробарн, нанобарн и т. д. )

Этимология • Название «барн» происходит от английского barn — амбар. Два физика из Университета Пердью (Уэст. Лафаетт, штат Индиана), Маршалл Хеллоуэй и Чарльз Бэйкер, работавшие в рамках Манхэттенского проекта, однажды во время обеда решили придумать название для единицы, отражающей типичный размер эффективного сечения в ядерной физике. Среди кандидатов, в чью она честь могла быть названа, были Оппенгеймер и Бете, а также Джон Мэнли, директор группы университета Пердью в Лос. Аламосе (Мэнли показалось физикам слишком длинным, и в качестве кандидатуры некоторое время использовалось имя «Джон» ). Для большинства ядерных процессов эффективное сечение 10− 24 см² кажется большим, как амбар.

Эффективное поперечное сечение частицы и вероятность • Следующая механическая аналогия поможет уяснить себе рассматриваемую молекулярную ситуацию. Представим себе забор из досок, разделенных свободными промежутками. Недалеко от забора человек кидает их (не прицеливаясь) по направлению к забору, так что камешки приблизительно равномерно распределяются по выделенному участку ограды. Очевидно, что некоторые из брошенных камней пройдут через промежутки между досками, другие попадут в доски. По израсходовании запаса камней (если он был достаточно велик) можно убедиться в том, что отношение числа камней, прошедших сквозь ограду, к общему числу брошенных камней приблизительно равно отношению площади промежутков в выбранном участке ограды к общей его площади. • Первое из этих отношений есть отношение числа опытов, приводящих к осуществлению некоторого события (прохождения камня сквозь ограду), к общему числу опытов. По принятому нами определению оно равно вероятности события. Значит, отношение площадей промежутков к площади всей ограды как раз равно этой вероятности.

Эффективное поперечное сечение частицы и вероятность • Обращаясь снова к случаю встречи летящей молекулы со слоем газа, мы можем и здесь сказать, что каждая молекула, летящая к слою, может испытать в нем столкновение, но может и пройти через него, не столкнувшись ни с одной из его молекул. Но если подобный опыт повторять достаточно много раз, то ясно, что отношение числа случаев, когда исходом опыта будет столкновение, к общему числу опытов будет равно отношению площади сечений всех молекул слоя к площади слоя.

Эффективное поперечное сечение частицы и вероятность • Понятно поэтому, что эффективный поперечник даже у одних и тех же частиц в разных условиях и для различных процессов может быть различным. Это было бы непонятно, если эффективное поперечное сечение действительно было бы просто геометрической площадью сечения молекулы, рассматриваемой как твердый шарик.

• • • Всем известно, что в отсутствии конвекционных потоков запах в воздухе распространяется очень медленно, в то время как скорость молекул газа достаточно высока (около 500 метров в секунду). Причина этого заключается в том , что распространение запаха осуществляется посредством медленного процесса диффузии. Медленность диффузии и аналогичных ей явлений Клаузиус объяснил столкновениями молекул. Молекула газа не всё время движется свободно, а время от времени испытывает столкновения с другими молекулами. Свободно она пролетает короткое расстояние от одного столкновения до следующего. В результате траектория молекулы описывается ломаной линией с большим количеством звеньев. Для количественного описания явления Клаузиус ввёл понятие средней длины свободного пробега, т. е. среднего расстояния, которое пролетает молекула от одного столкновения до следующего. Этот параметр имеет важное значение для описание явлений переноса – диффузии, внутреннего трения и теплопроводности. Найдём значение средней длины свободного пробега L для газа, состоящего из одинаковых молекул диаметром d. Молекулы будут сталкиваться друг с другом если расстояние между их центрами меньше d. Поэтому, мы можем рассмотреть одну молекулу с радиусом d, движущуюся в присутствии точечных частиц (см. анимацию). В течение времени t эта молекула столкнется со всеми частицами, лежащими внутри цилиндра объёмом (πd 2)nvt, где n – концентрация молекул газа, v – средняя скорость их движения. Средняя длина свободного пробега равняется высоте цилиндра L=vt, который содержит в среднем лишь одну молекулу: L =1/(πd 2 n) Строгий расчёт средней длины свободного пробега был дан Максвеллом с учётом распределения молекул по скоростям. Максвелл получил: L =0. 707/(πd 2 n) Мы можем видеть, что результаты приближённой теории отличаются от точной формулы лишь численными коэффициентами, близкими к единице.