Федун
В. И. Конспект лекций по физике
Молекулярная физика и термодинамика
До сих
пор мы почти всегда рассматривали
системы, находящиеся в состоянии
термодинамического, или статистического
равновесия. Однако, несмотря на безусловно
важную роль равновесных состояний, они
все же представляют собой особый случай.
Во многих задачах, представляющих
огромный физический интерес, мы имеем
дело с системами, не находящимисяв равновесных состояниях.
Наука,
изучающая процессы, идущие при нарушении
равновесия, называется физической
кинетикой.Физическая
кинетика рассматривает необратимые
процессы в телах, протекающие с конечными
скоростями.
Рассмотрение
неравновесных процессов, приводящих
систему в состояние равновесия,
представляет собой весьма сложную
задачу. Поэтому мы подойдем к рассмотрению
проблемы с помощью простейших приближенных
методов, выбрав в качестве объекта
исследования разреженный газ.
16. 1. Среднее число столкновений и длина свободного пробега молекул.
16. 1. Длина свободного пробега молекул.
Длиной
свободного пробега
![]() называется
называется
путь, проходимый молекулой между двумя
последовательными столкновениями.
Вследствие
хаотичности движения
![]() различны.
различны.
Средней
длиной свободного пробега
молекул
<![]() >называется
>называется
путь, который в среднем проходят молекулы
между двумя последовательными
столкновениями:
|
|
(16.1) |
где
N
– число
молекул.
|
|
Эффективным
В |
|
Рисунок 16. 1. |
Значения
D
при
нормальных условиях для некоторых газов
|
Газ |
Воздух |
Водород |
Кислород |
Азот |
|
D, |
0,27 |
0,28 |
0,36 |
0,58 |
16. 2. Среднее число столкновений молекул.
Введём
понятие среднего
числа столкновений <![]() >молекулы
>молекулы
в единицу времени.
Тогда
число столкновений молекулы за время
![]()
есть
![]()
и
оно равно отношению среднего пути
молекулы
![]()
к
средней длине свободного пробега <![]() >:
>:
|
|
(16.2) |
|
|
|
|
Рисунок 16. 2. |
Введём
понятие эффективного
сечения
![]() столкновения
столкновения
как
площади поперечного сечения («коридора»)
ломаного цилиндра, в которой должны
попасть центры соседних молекул, чтобы
столкнуться с данной. Из рисунка 16.2
видно, что:
|
|
(16.3) |
Рассчитаем
число столкновений молекулы за время
![]() .
.
Предположим,
что рассматриваемая молекула движется
со скоростью
![]() ,
,
а
остальные покоятся. Тогда рассматриваемая
молекула столкнётся со всеми молекулами,
находящимися в цилиндре
площадью
основания Sэфф
и
длиной
![]() .
.
Число
молекул, а значит и число столкновений
определяется соотношением:
|
|
(16.4) |
где
n–
концентрация
молекул.
Чтобы
учесть движение всех молекул можно,
например, перейти в систему координат,
связанную с движущейся молекулой, т.е.
перейти от скорости
![]()
к
средней скорости
![]() движения молекул. Поскольку все движения
движения молекул. Поскольку все движения
молекул равновероятны, то угол между
направлениями скоростей лежит в интервале
(![]() )
)
и
средний угол равен
![]() .
.
Модуль
относительной скорости тогда будет:
|
|
(16.5) |
С
учётом сделанных поправок, формула ()
приобретает вид:
|
|
(16.6) |
Тогда
среднее число столкновений молекулы в
единицу времени
![]()
будет
определяться выражением:
|
|
(16.7) |
Приведённое
соотношение носит название формулы
Клаузиуса
– Максвелла.
Чтобы
найти число столкновений в единицу
времени молекул газа концентрации
![]()
![]()
и
в объёме
![]() ,
,
т.е.
для
![]() молекул газа надо величину
молекул газа надо величину![]()
умножить
на
![]() ,
,
т.к.
в каждом столкновении принимают участие
2 молекулы:
|
|
(16.8) |
Тогда
среднее число столкновений молекул в
единицу времени в единичном объёме
есть:
|
|
(16.9) |
Теперь
можно вернуться к средней длине свободного
пробега молекулы.
За
время
![]()
молекула
проходит путь:
|
|
(16.10) |
и
испытывает за это время число соударений,
равное:
|
|
(16.) |
Значит
средняя длина свободного пробега
![]() будет
будет
равна (с учётом ()):
|
|
(16.) |
Если
учесть, что
![]() ,
,
то
получаем:
|
|
(16.11) |
Концентрация
молекул
![]()
связана
с термодинамическими параметрами
![]()
и
![]() уравнением состояния.
уравнением состояния.
|
|
(16.12) |
Тогда
окончательно получаем:
|
|
(16.13) |
Соседние файлы в папке РАЗДЕЛ_2
- #
- #
- #
- #
- #
|
|
Макеты страниц
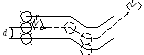
По-прежнему будем считать газ идеальным, т. е. будем считать, что, за исключением момента столкновения, молекулы не взаимодействуют, не подвергаются действию каких-либо сил и движутся поэтому прямолинейно. В момент столкновения направление скорости молекулы изменяется, после чего она снова движется прямолинейно. Путь молекулы в газе представляет собой, таким образом, ломаную линию, подобную, например, изображенной на рис. 45. Каждый излом траектории отмечает место столкновения. Расстояние, которое молекула проходят между двумя последовательными столкновениями, называется длиной свободного пробега.

Рис. 45.
Так как молекул в газе чрезвычайно много, то не может быть речи о какой-либо регулярности в процессе столкновений, и длины прямолинейных участков на зигзагообразном пути молекулы могут быть различными. Поэтому нас будет интересовать средняя длина свободного пробега. Точно так же различным может быть и число столкновений, испытываемых молекулой в единицу времени, и следует говорить только о среднем значении этой величины.
Эти две связанные между собой величины — средняя длина свободн  пробега и среднее число столкновений в единицу времени — являются главными характеристиками процесса столкновений газовых молекул. В частности, те «помехи» явлениям переноса, о которых упоминалось выше, зависят от числа столкновений. Именно от этого зависит длина пути, котцрый молекула проходит между двумя данными точками в объеме газа. Как это видно из рис. 45, истинный путь молекулы между точками
пробега и среднее число столкновений в единицу времени — являются главными характеристиками процесса столкновений газовых молекул. В частности, те «помехи» явлениям переноса, о которых упоминалось выше, зависят от числа столкновений. Именно от этого зависит длина пути, котцрый молекула проходит между двумя данными точками в объеме газа. Как это видно из рис. 45, истинный путь молекулы между точками  много больше, чем расстояние
много больше, чем расстояние  по соединяющей их прямой. Ясно, что, например, процесс диффузии, т. е. проникновение одного газа в другой, не может происходить быстро, несмотря на большую скорость молекул: столкновения в значительной степени компенсируют влияние скорости.
по соединяющей их прямой. Ясно, что, например, процесс диффузии, т. е. проникновение одного газа в другой, не может происходить быстро, несмотря на большую скорость молекул: столкновения в значительной степени компенсируют влияние скорости.
Среднее число столкновений, испытываемых молекулой газа в единицу времени, можно вычислить из весьма простых соображений. Молекулы будем считать твердыми упругими шариками радиуса  Пусть одна из молекул движется по прямой в газе, в котором частицы равномерно распределены по объему, так что в каждом кубическом сантиметре находится
Пусть одна из молекул движется по прямой в газе, в котором частицы равномерно распределены по объему, так что в каждом кубическом сантиметре находится  молекул. Предположим сначала, что все молекулы, кроме одной, находятся в покое. Тогда наша единственная движущаяся молекула, пройдя за 1 с расстояние, равное ее средней скорости и, столкнется со всеми молекулами,
молекул. Предположим сначала, что все молекулы, кроме одной, находятся в покое. Тогда наша единственная движущаяся молекула, пройдя за 1 с расстояние, равное ее средней скорости и, столкнется со всеми молекулами,
которые окажутся на ее пути. Это будут те молекулы, центры которых расположены в объеме цилиндра длиной  и с площадью основания, равной эффективному поперечнику столкновения (рис. 46). Объем этого цилиндра равен сто, а число молекул в нем
и с площадью основания, равной эффективному поперечнику столкновения (рис. 46). Объем этого цилиндра равен сто, а число молекул в нем  Таким же будет и число столкновений
Таким же будет и число столкновений  которые испытывает наша молекула:
которые испытывает наша молекула:

Конечно, молекула не может двигаться прямолинейно, раз она сталкивается с другими молекулами. На самом деле путь, проходимый молекулой, зигзагообразный, как это показано, скажем, на рис. 47.

Рис. 46.

Рис. 47.
Это, однако, не изменяет результаты расчета; полагая, что молекула движется по прямой, мы только мысленно «выпрямили» ломаный цилиндр, изображенный на рис. 47.
Следует учесть, что движется не одна, а все молекулы газа. Это значит, что в выражение для  должна входить не абсолютная (относительно стенок сосуда) скорость молекулы, а скорость ее
должна входить не абсолютная (относительно стенок сосуда) скорость молекулы, а скорость ее  относительно тех молекул, с которыми она сталкивается. Можно показать, приняв во внимание максвелловское распределение молекул по скоростям, что относительная скорость оотн связана с абсолютной скоростью О соотношением
относительно тех молекул, с которыми она сталкивается. Можно показать, приняв во внимание максвелловское распределение молекул по скоростям, что относительная скорость оотн связана с абсолютной скоростью О соотношением

Тогда для среднего числа столкновений молекулы в единицу времени получим формулу

или, поскольку мы условились считать молекулы шариками,

Чтобы найти среднее число столкновений, происходящих в единицу времени в газе, т. е. столкновений, испытываемых всеми молекулами, нужно умножить  на число молекул
на число молекул  в газе. Но так как в каждом столкновении участвуют две молекулы (встреча
в газе. Но так как в каждом столкновении участвуют две молекулы (встреча
одновременно трех и более молекул крайне маловероятна), то это число нужно еще разделить на 2, чтобы не считать каждое столкновение два раза. Следовательно, полное число столкновений в газе, содержащем  частиц, равно
частиц, равно

Таким образом, в единице объема газа число столкновений, происходящих каждую секунду, равно

где  число молекул в единице объема.
число молекул в единице объема.
Зная число столкновений, испытываемых одной молекулой в единицу времени, легко вычислить и среднюю длину свободного пробега.
За время  молекула проходит некоторый зигзагообразный путь, равный
молекула проходит некоторый зигзагообразный путь, равный  . Изломов на этом пути столько, сколько произошло столкновений, так как каждый излом и вызван столкновением. Средняя длина свободного пробега, т. е. средняя длина прямолинейного отрезка X между столкновениями, равна отношению длины пути, пройденного молекулой, к числу испытанных ею на этом пути столкновений:
. Изломов на этом пути столько, сколько произошло столкновений, так как каждый излом и вызван столкновением. Средняя длина свободного пробега, т. е. средняя длина прямолинейного отрезка X между столкновениями, равна отношению длины пути, пройденного молекулой, к числу испытанных ею на этом пути столкновений:

или, подставив вместо  его значение из (36.3), получим:
его значение из (36.3), получим:

Пользуясь этой формулой, можно найти численные значения для  Проведем такой расчет, например, для воздуха (азота) при нормальных условиях (давление 1 атм, температура 273 К). Радиус
Проведем такой расчет, например, для воздуха (азота) при нормальных условиях (давление 1 атм, температура 273 К). Радиус  молекулы азота можно считать равным
молекулы азота можно считать равным  число частиц в единице объема
число частиц в единице объема  средняя скорость
средняя скорость  Отсюда
Отсюда

Средняя длина свободного пробега молекулы в рассматриваемых условиях равна

Естественно возникает вопрос, можно ли считать идеальным такой газ, в котором частицы каждую секунду сталкиваются миллиарды раз, а между столкновениями, т. е. «свободно», они
проходят ничтожные отрезки пути, не превосходящие нескольких стотысячных долей сантиметра? Можно ли считать молекулы такого газа невзаимодействующими? Ведь столкновение — это взаимодействие, приводящее к изменению направления скорости молекул, а столь частые столкновения означают, как будто бы, весьма сильное взаимодействие. Легко, однако, видеть, что это не так, Действительно, молекулы, как уже было указано, взаимодействуют друг с другом только в течение того времени, пока они находятся друг от друга на расстоянии порядка их диаметра  время между столкновениями молекулы движутся свободно. Так как при атмосферном давлении длина свободного пробега молекулы
время между столкновениями молекулы движутся свободно. Так как при атмосферном давлении длина свободного пробега молекулы  что примерно в 1000 раз больше размеров молекул, то время пребывания молекул под взаимным воздействием во столько же раз
что примерно в 1000 раз больше размеров молекул, то время пребывания молекул под взаимным воздействием во столько же раз  меньше времени их свободного движения.
меньше времени их свободного движения.
Другими словами, время столкновения молекул примерно в 1000 раз меньше времени между столкновениями. Следовательно подавляющую часть времени молекулы движутся свободно, а столкновения, даже при атмосферном давлении, можно считать редким событием в их жизни.
Зависимость длины свободного пробега от давления. Как видно из формулы (36.4), длина свободного пробега молекул обратно пропорциональна их числу в единице объема, а следовательно, его давлению  так что можно написать:
так что можно написать:

С уменьшением давления длина свободного пробега молекул возрастает в такой же мере, в какой падает давление. При определенном значении давления она станет равной размерам сосуда, в котором газ заключен, а при дальнейшем понижении давления превзойдет их. Например, в сосуде размером около 25 см (размеры, обычные в лабораторной практике) длина свободного пробега молекул сравняется с размерами сосуда уже при давлении около  атм
атм  Такое давление сравнительно легко создать, так как современные средства откачки позволяют получить давления до
Такое давление сравнительно легко создать, так как современные средства откачки позволяют получить давления до 
Когда длина свободного пробега становится равной или большей размеров сосуда, столкновения молекул в газе практически уже не происходят, и весь путь от стенки до стенки молекулы проходят, двигаясь прямолинейно.
Естественно, что газ, в котором молекулы не сталкиваются между собой, отличается по своим свойствам от обычного газа. Ниже, в гл. IV, мы познакомимся со своеобразными свойствами такого газа.
Зависимость длины свободного пробега от температуры. Из формулы (36.4) следует, что длина свободного пробега молекул не должна зависеть от температуры. Опыт, между тем, показывает, что такая зависимость, хотя и слабая, существует: с повышением
температуры длина свободного пробега возрастает. Это объясняется тем, что согласно формуле (36.4) X обратно пропорциональна поперечному сечению молекулы, А оно, как мы уже знаем, определяется расстоянием, на которое сближаются молекулы при столкновении, т. е. расстоянием, при котором сила взаимодействия между молекулами вызывает уже заметное изменение направления их движения.
Легко видеть, что поперечное сечение молекул должно зависеть от их скорости (энергии), так как при одной и той же силе взаимодействия быстрые молекулы испытывают меньшее отклонение от своего пути, чем более медленные молекулы. Поэтому, чем больше скорость молекул, тем больше должна быть сила, вызывающая их отклонение, следовательно, тем меньше должно быть расстояние между ними при столкновении. Это и значит, что с увеличением скорости молекул, т. е. с повышением температуры газа, поперечное сечение молекул уменьшается. Длина же свободного пробега молекул с повышением температуры, растет. Эта слабая зависимость X от температуры объясняет некоторые явления, которые будут рассмотрены ниже.
Факт зависимости длины свободного пробега от температуры может служить подтверждением изложенных выше соображений о смысле понятия «размер молекулы». Если бы молекулы действительно были твердыми шариками, то не могло бы быть и речи об изменении их размеров при изменении скорости. На самом деле размеры частиц (не только молекул газа!) определяются расстоянием между ними при максимальном сближении, а оно не может не зависеть от скорости частиц, а значит (в случае газовых молекул) и от температуры. Это, однако, не мешает тому, что в. целом ряде случаев взаимодействие между молекулами можно с достаточной степенью точности рассматривать как взаимодействие между твердыми шариками.
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава I. КИНЕТИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНЫХ ГАЗОВ
- § 1. Идеальный газ
- § 2. Давление газа
- § 3. Температура
- § 4. Уравнение состояния идеального газа
- § 5. Законы идеального газа
- § 6. Скорости газовых молекул
- § 7. Броуновское движение
- § 8. Барометрическая формула
- § 9. Закон Больцмана
- § 10. Понятие о вероятности
- § 11. Понятие о распределении. Функция распределения
- § 12. Распределение молекул по компонентам скорости
- § 13. Распределение молекул по скоростям
- § 14. Средние скорости молекул
- § 15. Наивероятнейшая скорость молекул
- § 16. Формула Максвелла для относительных скоростей
- § 17. Закон распределения молекул по скоростям и атмосферы планет
- § 18. Экспериментальная проверка закона распределения
- § 19. Измерение параметров состояния
- Глава II. КИНЕТИЧЕСКАЯ ТЕОРИЯ ТЕПЛОТЫ. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 20. Внутренняя энергия идеального газа
- § 21. Количество теплоты
- § 22. Механический эквивалент теплоты
- § 23. Первое начало термодинамики
- § 24. Теплоемкость идеальных газов
- § 25. Теплоемкость одноатомных газов
- § 26. Теплоемкость газов и число степеней свободы молекул
- § 27. Теплоемкость двухатомных и многоатомных газов
- § 28. Изменение состояния при изменении объема газа
- § 29. Работа при изотермическом изменении объема идеального газа
- § 30. Адиабатное изменение объема идеального газа
- § 31. Работа при адиабатном изменении объема газа
- § 32. Политропический процесс
- § 33. Расширение газа в пустоту
- § 34. Измерение количества теплоты и теплоемкости
- Глава III. СТОЛКНОВЕНИЯ МОЛЕКУЛ И ЯВЛЕНИЯ ПЕРЕНОСА
- § 35. Молекулярные движения и явления переноса
- § 36. Среднее число столкновений в единицу времени и средняя длина свободного пробега молекул
- § 37. Эффективное поперечное сечение частицы и вероятность
- § 38. Рассеяние молекулярного пучка в газе
- § 39. Экспериментальное определение длины свободного пробега
- § 40. Диффузия в газах
- § 41. Нестационарная диффузия
- § 42. Стационарная диффузия. Вычисление коэффициента диффузии
- § 43. Коэффициент взаимной диффузии
- § 44. Термическая диффузия
- § 45. Теплопроводность газов
- § 46. Нестационарная теплопроводность
- § 47. Стационарная теплопроводность. Вычисление коэффициента теплопроводности
- § 48. Вязкость газов (внутреннее трение)
- § 49. Измерение коэффициента вязкости (вискозиметрия)
- § 50. Соотношения между коэффициентами переноса
- Глава IV. ФИЗИЧЕСКИЕ ЯВЛЕНИЯ В РАЗРЕЖЕННЫХ ГАЗАХ (ВАКУУМЕ)
- § 51. Теплопередача в газах при малых давлениях
- § 52. Течение газов при малых давлениях (молекулярное течение)
- § 53. Молекулярное течение газа в цилиндрической трубе
- § 54. Молекулярное течение смеси газов. Разделение газовых смесей
- § 55. Диффузия газов в вакууме
- § 56. Разность давлений между различно нагретыми частями газа (тепловая транспирация)
- § 57. Элементы вакуумной техники
- § 58. Измерение малых давлений
- § 59. Вакуумная установка
- Глава V. НЕИДЕАЛЬНЫЕ (РЕАЛЬНЫЕ) ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
- § 60. Отклонения свойств газов от идеальности
- § 61. Сжижение газов (конденсация)
- § 62. Фазовый переход
- § 63. Фазовые диаграммы
- § 64. Методы определения критических параметров
- § 65. Уравнение Ван-дер-Ваальса
- § 66. Изотермы Ван-дер-Ваальса
- § 67. Критическая температура и критическое состояние
- § 68. Экспериментальное определение констант уравнения Ван-дер-Ваальса
- § 69. Сравнение уравнения Ван-дер-Ваальса с данными опыта
- § 70. Приведенное уравнение Ван-дер-Ваальса. Закон соответственных состояний
- § 71. Межмолекулярные силы взаимодействия в реальном газе
- § 72. Теплоемкость неидеальных газов
- Глава VI. ЭЛЕМЕНТЫ ТЕРМОДИНАМИКИ
- § 73. Равновесные состояния
- § 74. Обратимые и необратимые процессы
- § 75. Квазистатические процессы
- § 76. Необратимость и вервятность
- § 77. Взаимные превращения механической и тепловой энергии
- § 78. Первое начало термодинамики
- § 79. Преобразование теплоты в механическую работу
- § 80. Цикл Карно
- § 81. Холодильная машина
- § 82. Доказательство теорем Карно
- § 83. Свободная энергия
- § 84. Энтропия
- § 85. Некоторые термодинамические соотношения
- § 86. Энтропия при обратимых процессах в замкнутой системе
- § 87. Энтропия при необратимых процессах в замкнутой системе, акон возрастания энтропии
- § 88. Второе начало термодинамики и превращение теплоты в работу
- § 89. Физический смысл энтропии. Энтропия и вероятность
- § 90. Энтропия и беспорядок
- § 91. «Демон» Максвелла
- § 92. Термодинамическая шкала температур
- § 93. Третье начало термодинамики
- § 94. Отрицательные температуры
- Глава VII. СВОЙСТВА ЖИДКОСТЕЙ
- § 95. Объемные свойства жидкостей
- § 96. Теплоемкость жидкостей
- § 97. Явления переноса в жидкостях
- § 98. Явления на границе жидкости
- § 99. Условия равновесия на границе двух сред. Краевой угол
- § 100. Силы, возникающие на кривой поверхности жидкости
- § 101. Капиллярные явления
- § 102. Некоторые методы измерения коэффициента поверхностного натяжения
- § 103. Зависимость коэффициента поверхностного натяжения от температуры
- § 104. Испарение и кипение жидкостей
- § 105. Температурная зависимость упругости насыщенных паров
- § 106. Упругость насыщенного пара над кривой поверхностью жидкости
- § 107. Кипение жидкостей
- § 108. Жидкие растворы
- § 109. Осмотическое давление
- Глава VIII. НИЗКИЕ ТЕМПЕРАТУРЫ
- § 110. Сжижение газов
- § 111. Эффект Джоуля-Томсона
- § 112. Адиабатное расширение газа с совершением внешней работы
- § 113. Сжижение газов с использованием эффекта Джоуля — Томсона (метод Линде)
- § 114. Сжижение газов методом адиабатного расширения в детандерах (метод Клода)
- § 115. Некоторые свойства сжиженных газов
- § 116. Сверхнизкие температуры
- § 117. Свойства вещества при низких температурах
- § 118. Жидкий гелий
- Глава IX. ТВЕРДОЕ ТЕЛО
- § 120. Кристаллическая решетка
- § 121. Дефекты в кристаллах
- § 122. Механические свойства твердых тел. Деформации
- § 123. Деформация растяжения и сжатия. Сдвиг
- § 124. Связь между модулями упругости
- § 125. Упругая деформация и тепловое расширение
- § 126. Зависимость деформации от напряжения
- § 127. Механизм пластической деформации
- § 128. Дислокации в кристаллах
- § 129. Переход в твердое состояние
- § 130. Диаграмма состояния. Тройная точка
- § 131. Фазовые переходы первого и второго рода
- § 132. Твердый гелий
- § 133. Растворение и кристаллизация из раствора
- § 134. Сплавы. Диаграммы плавкости
- § 135. Зонная очистка металлов
- § 136. Опытное определение температуры плавления
- § 137. Тепловые свойства твердых тел
- § 138. Измерение теплоемкости
- § 139. Тепловое расширение твердых тел
- § 140. Теплопроводность
- § 141. Диффузия в твердых телах
§1. Среднее число столкновений и средняя длина свободного пробега молекул
Участвуя в тепловом движении, молекулы газа все время сталкиваются друг с другом. Среднее расстояние, проходимое молекулой между двумя последовательными столкновениями, называется средней длиной свободного пробега.
За секунду молекула в среднем проходит расстояние, численно равное ее средней скорости ![]() . Если за это же время она в среднем испытывает
. Если за это же время она в среднем испытывает ![]() столкновений с другими молекулами, то ее средняя длина свободного пробега
столкновений с другими молекулами, то ее средняя длина свободного пробега ![]() , очевидно, будет равна
, очевидно, будет равна

 Предположим, что все молекулы, кроме одной, неподвижны. Молекулы будем считать шарами с диаметром D. Столкновения будут происходить всякий раз, когда центр неподвижной молекулы окажется на расстоянии меньшем, чем D от прямой, вдоль которой движется центр рассматриваемой молекулы. При столкновениях молекула изменяет направление своего движения и затем движется прямолинейно до следующего столкновения. Поэтому центр движущейся молекулы ввиду столкновений движется по ломаной линии (рис.35).
Предположим, что все молекулы, кроме одной, неподвижны. Молекулы будем считать шарами с диаметром D. Столкновения будут происходить всякий раз, когда центр неподвижной молекулы окажется на расстоянии меньшем, чем D от прямой, вдоль которой движется центр рассматриваемой молекулы. При столкновениях молекула изменяет направление своего движения и затем движется прямолинейно до следующего столкновения. Поэтому центр движущейся молекулы ввиду столкновений движется по ломаной линии (рис.35).
Молекула столкнется со всеми неподвижными молекулами, центры которых находятся в пределах ломаного цилиндра диаметра 2D. За секунду молекула проходит путь, равный ![]() . Поэтому число происходящих за это время столкновений равно числу молекул, центры которых попадут внутрь ломаного цилиндра, имеющего суммарную длину
. Поэтому число происходящих за это время столкновений равно числу молекул, центры которых попадут внутрь ломаного цилиндра, имеющего суммарную длину ![]() и диаметр 2D. Его объем примем равным объему соответствующего спрямленного цилиндра, т. е. равным
и диаметр 2D. Его объем примем равным объему соответствующего спрямленного цилиндра, т. е. равным ![]() . Поэтому если в единице объема газа находится N молекул, то число столкновений рассматриваемой молекулы за 1с будет равно
. Поэтому если в единице объема газа находится N молекул, то число столкновений рассматриваемой молекулы за 1с будет равно
![]()
В действительности движутся все молекулы. Поэтому число столкновений за 1с будет несколько большим полученной величины, так как вследствие движения окружающих молекул рассматриваемая молекула испытала бы некоторое число соударений даже в том случае, если бы она сама оставалась неподвижной. Абсолютные скорости U1 и U2 двух каких-либо молекул, взятые по отношению к стенкам сосуда, при столкновениях роли не играют. Непосредственное значение имеет лишь скорость их относительного движения UОтн=U1 – U2. Причем при рассмотрении относительного движения двух молекул одну из них можно считать как неподвижную, а другую налетающей на первую со скоростью ![]() . Поэтому весь расчет числа столкновений можно осуществить, если одну из молекул считать движущейся с некоторой средней относительной скоростью
. Поэтому весь расчет числа столкновений можно осуществить, если одну из молекул считать движущейся с некоторой средней относительной скоростью ![]() среди неподвижных молекул, как это и было сделано выше. Таким образом, при учете движения всех остальных молекул в формуле (2) необходимо заменить
среди неподвижных молекул, как это и было сделано выше. Таким образом, при учете движения всех остальных молекул в формуле (2) необходимо заменить ![]() на
на ![]() :
:
![]()
Чтобы найти ![]() , предположим, что до столкновения скорости были U1 и U2, а UОтн=U1 –U2. Из треугольника скоростей (рис.36) имеем
, предположим, что до столкновения скорости были U1 и U2, а UОтн=U1 –U2. Из треугольника скоростей (рис.36) имеем
![]() ,
,
![]() Так как среднее значение квадратов абсолютных скоростей одинаково
Так как среднее значение квадратов абсолютных скоростей одинаково ![]() , а
, а ![]() , ввиду того, что (поскольку все направления движения равноправны).
, ввиду того, что (поскольку все направления движения равноправны).
Так как средние квадратичные скорости молекул пропорциональны средним значениям, то равенство (4) можно переписать в виде
![]()
Подставив ![]() из формулы (5) в выражение (3) , получим число столкновений, испытанных одной молекулой за 1с:
из формулы (5) в выражение (3) , получим число столкновений, испытанных одной молекулой за 1с:
![]()
Учитывая формулу (1), найдём среднюю длину свободного пробега молекулы

Где мы учли, что P=NkT.
§2 Виды явлений переноса. Общее уравнение явлений переноса в газах
Равновесное состояние газа в молекулярно-кинетической теории рассматривается как состояние полной хаотичности движения молекул, распределение которых по скоростям подчиняется закону Максвелла.
Любое неравновесное состояние газа всегда связано с нарушением полной хаотичности движения и максвелловского распределения молекул по скоростям. Основной особенностью неравновесных состояний является стремление газа самопроизвольно переходить к равновесному состоянию. Этот переход связан с хаотическим тепловым движением, сопровождающимся непрерывными столкновениями молекул друг с другом, которое и приводит к постоянному перемешиванию молекул, изменению их скоростей и энергий. Установление в газе максвелловского распределения молекул по скоростям при переходе его в равновесное состояние всегда связано с направленным переносом массы, импульса и энергии в веществе, которые называют явлениями переноса.
К явлениям переноса относят теплопроводность, внутреннее трение (или вязкость) и диффузию газов. Теплопроводность обусловлена переносом молекулами кинетической энергии из мест более нагретых к местам менее нагретым, вязкость — импульса, диффузия — массы молекул. Строгая молекулярно-кинетическая теория явлений переноса в газах оказывается весьма сложной, она связана с громоздкими математическими расчетами. Мы воспользуемся упрощенным методом кинетической теории газов, который позволяет выявить основные закономерности явлений переноса. В этом методе истинное хаотическое движение молекул газа приближенно заменяется тремя упорядоченными движениями по трем взаимно перпендикулярным осям, так что вдоль каждой оси в среднем движется ![]() всех молекул газа, из них половина (т. е.
всех молекул газа, из них половина (т. е. ![]() часть) — в
часть) — в![]()
положительном направлении данной оси, а вторая половина — в отрицательном направлении. Оправданием такого упрощенного толкования поведения молекул в газе может служить то, что строгие выводы приводят к тем же или очень близким к ним конечным результатам. Применение этого метода позволяет весьма просто определить одну из наиболее важных для явлений переноса величин, а именно, число молекул, переносимых за некоторое время Dt через произвольную площадку Ds, выделенную в газе. Действительно, за время Dt через произвольную площадку Ds пройдут все движущиеся по направлению к ней молекулы, заключенные в объеме параллелепипеда, основанием которого служит Ds, а высота ![]() Dt. Число этих молекул
Dt. Число этих молекул
![]()
Где N — число молекул в единице объема.
 Обозначим переносимую физическую величину одной молекулой через J. Значение этой величины меняется при столкновениях молекул и сохраняется неизменным между столкновениями, т. е. на длине свободного пробега
Обозначим переносимую физическую величину одной молекулой через J. Значение этой величины меняется при столкновениях молекул и сохраняется неизменным между столкновениями, т. е. на длине свободного пробега ![]() . Допустим, что переносимая величина J(X) меняется только в направлении оси X. Молекулы, пересекающие выделенную площадку, переносят через нее то значение величины J(X), которое они имели после последнего столкновения перед площадкой, т. е. на расстоянии длины свободного пробега
. Допустим, что переносимая величина J(X) меняется только в направлении оси X. Молекулы, пересекающие выделенную площадку, переносят через нее то значение величины J(X), которое они имели после последнего столкновения перед площадкой, т. е. на расстоянии длины свободного пробега ![]() от нее. Соответственно этому можно считать, что каждая молекула, пересекающая площадку Ds слева направо, переносит через нее значение величины J Равное
от нее. Соответственно этому можно считать, что каждая молекула, пересекающая площадку Ds слева направо, переносит через нее значение величины J Равное ![]() , а молекула, приходящая к площадке справа, — значение этой величины равное
, а молекула, приходящая к площадке справа, — значение этой величины равное ![]() (рис.37). Общее количество рассматриваемой физической величины, переносимое молекулами через площадку Ds за время Dt слева направо (рис. 37),
(рис.37). Общее количество рассматриваемой физической величины, переносимое молекулами через площадку Ds за время Dt слева направо (рис. 37),
![]()
А количество той же величины, переносимое через ту же площадку справа налево и за тоже время, будет

Следовательно, результирующее количество рассматриваемой величины, переносимой за время Dt через площадку Ds вдоль оси X, равно
![]()
Разложим функции j, стоящие в квадратной скобке выражения (229) в ряд по степеням малой величины ![]() в точке X, где расположена площадка Ds
в точке X, где расположена площадка Ds
![]()
![]()
![]()
Подставим (3) и (4 в (2. В результате будем иметь
![]()
Последнее уравнение является общим уравнением переноса физической величины j в газе, и имеет такой же вид, как в общей теории.
![]()
§3. Теплопроводность
С макроскопической точки зрения явление теплопроводности заключается в переносе количества тепла от слоя более нагретого к менее нагретому, продолжающийся до тех пор, пока температура во всем теле не выравняется. В молекулярно-кинетической же теории процесс теплопроводности объясняется тем, что молекулы из более нагретого слоя, где они имеют большую среднюю кинетическую энергию, проникая в менее нагретую область, передают при столкновениях молекулам этой области часть их кинетической энергии.
Пусть изменение температуры вещества происходит вдоль оси X, в то время как в плоскости перпендикулярной этой оси, температура постоянна. Опытным путем Фурье установил закон, согласно которому количество тепла, переносимое за время Dt Через площадку Ds, перпендикулярную оси X, вдоль которой изменяется температура, пропорционально величине площадки, времени переноса и градиенту DT/Dx Температуры, т. е.

Знак минус в (1)означает, что тепло переносится в сторону убывания температуры. Как видно из выражения (1) коэффициент теплопроводности æ численно равен количеству тепла, переносимого в единицу времени через единичную площадку при градиенте температуры, равном единице. В системе СИ коэффициент теплопроводности имеет размерность Вт/(м. К). Закон Фурье справедлив для веществ, находящихся в любых агрегатных состояниях.
Рассмотрим задачу о вычислении коэффициента æ для газов в области температур, где справедлива классическая теория. Переносимой величиной J при теплопроводности является, очевидно, средняя кинетическая энергия молекулы, т. е. ; суммарной переносимой величиной является количество теплоты, т. е. DФ= DQ. Поэтому общее уравнение переноса (из §2 (5)) в этом случае примет вид

Как мы знаем, средняя кинетическая энергия молекулы
![]()
Где M0 — масса молекулы, ![]() — удельная теплоемкость газа. Подставляя (3) в (2), получим
— удельная теплоемкость газа. Подставляя (3) в (2), получим

Где R = nm0 — плотность газа. Сравнение формулы (4) с законом Фурье (1) дает для коэффициента теплопроводности æ следующее выражение
![]()
Пользуясь формулой (5), выясним зависимость æ от давления и температуры. Из всех величин, входящих в (5) только плотность и средняя длина свободного пробега зависят от давления: первая из них пропорциональна давлению, вторая — обратно пропорциональна давлению газа. Поэтому величина æ не зависит от давления, что подтверждается экспериментом.
Выясним зависимость коэффициента теплопроводности от температуры при постоянной концентрации (или плотности) газа. По классической теории теплоемкость ![]() не зависит от температуры, средняя же скорость пропорциональна , поэтому из (5) следует, что при постоянной плотности газа коэффициент теплопроводности газов растет с повышением температуры пропорционально .
не зависит от температуры, средняя же скорость пропорциональна , поэтому из (5) следует, что при постоянной плотности газа коэффициент теплопроводности газов растет с повышением температуры пропорционально .
§4. Вязкость
Явление внутреннего трения (или вязкости) в газах (так же как и в жидкостях) заключается в выравнивании скоростей движения различных слоев газа (или жидкости), если эти скорости различны и газ (или жидкость) предоставлен самому себе. Это выравнивание происходит потому, что из слоя газа с большей (меньшей) скоростью переносится импульс к слою, движущемуся с меньшей (большей) скоростью.
Пусть изменение скорости движения газа (или жидкости) происходит в направлении оси X, а сама скорость течения газа направлена перпендикулярно этой оси. Тогда, как показывает опыт, импульс переносимый за время Dt через площадку Ds, перпендикулярную этой оси, определяется уравнением
![]()
Где Du/Dx – Градиент скорости вдоль оси X, характеризующий быстроту изменения скорости вдоль этой оси. Знак минус означает, что импульс переносится в направлении уменьшения скорости. Коэффициент H Называется коэффициентом внутреннего трения или коэффициентом вязкости. Физический смысл коэффициента вязкости заключается в том, что он численно равен импульсу, который переносится в единицу времени через единичную площадку при градиенте скорости равном единице. В системе СИ коэффициент вязкости измеряется в кг/(м. с)=Па. с. При переносе импульса от слоя к слою происходит изменение импульса этих слоев: импульс одного слоя увеличивается, а другого — уменьшается. Это значит, что на каждый из слоев действует сила, равная изменению импульса в единицу времени. Поэтому уравнение (1) можно представить также в виде

 Где DF — сила, действующая на площадку Ds поверхности,
Где DF — сила, действующая на площадку Ds поверхности,
Разделяющей два соседних слоя газа или жидкости. Эта сила в одном из смежных слоев направлена по течению газа, а в другом – навстречу, т. е. она направлена по касательной к элементу Ds поверхности, причем на слой газа, прилегающий со стороны меньших скоростей, она действует ускоряющим образом, а на слой газа, прилегающий со стороны больших скоростей, — тормозящим образом. Таким образом, рассматриваемая сила действует внутри газа между отдельными его слоями, движущимися друг относительно друга. Поэтому ее называют силой внутреннего трения. Коэффициент вязкости H можно, согласно уравнению (2), определить и как величину, численно равную силе внутреннего трения, действующей на единицу площади поверхности, параллельной скорости течения газа или жидкости, при градиенте скорости, равном единице. Зависимость силы внутреннего трения от градиента скорости и величины площади, выражаемая уравнением (2), была установлена эмпирически Ньютоном, поэтому уравнение (2) известно под названием закона Ньютона для вязкого трения.
С точки зрения молекулярно-кинетической теории явление внутреннего трения в газах заключается в следующем. В текущем газе на скорость беспорядочного теплового движения молекул U накладывается переносная скорость U, т. е. скорость макроскопического движения газа, которая одинакова для всех молекул данного слоя (текущего с определенной скоростью) и различна для молекул различных слоев. С этой скоростью связан импульс MOU, которым обладает каждая молекула данного слоя. Такой импульс условимся называть упорядоченным. Молекулы, перелетая благодаря хаотическому тепловому движению из более быстрого слоя в более медленный, приносят с собой большой упорядоченный импульс, который при столкновениях передается молекулам более медленного слоя, вследствие чего он ускоряется. Обратно, молекулы, попадающие из более медленного слоя в более быстрый слой, приносят меньший упорядоченный импульс, вызывая тем самым замедление этого слоя. Таким образом, согласно кинетической теории, сущность внутреннего трения в газах состоит в переносе молекулами упорядоченного импульса, т. е. величины Mou. Заменяя в общем уравнении(из §2 (5)) переноса J на M0U и DФ на DK, получаем следующее уравнение внутреннего трения в газах, т. е. уравнение переноса импульса:
![]()
Сравнение этого уравнения с уравнением (1) дает следующее выражение для коэффициента вязкости газов:
![]()
Из выражения (4) следует, что коэффициент вязкости газов, так же как и коэффициент теплопроводности, не должен зависеть от давления, так как произведение ![]() от давления не зависит. Опыты по измерению вязкости газов в довольно широком диапазоне давлений подтверждает этот вывод. Лишь при весьма высоких и весьма низких давлениях начинает проявляться зависимость h от давления.
от давления не зависит. Опыты по измерению вязкости газов в довольно широком диапазоне давлений подтверждает этот вывод. Лишь при весьма высоких и весьма низких давлениях начинает проявляться зависимость h от давления.
Коэффициент вязкости, также как и коэффициент теплопроводности, должен зависеть от температуры, так как в выражении для H входит средняя скорость теплового движения молекул, зависящая от температуры по закону ![]() . Значит, коэффициент вязкости газа также должен расти с повышением температуры пропорционально
. Значит, коэффициент вязкости газа также должен расти с повышением температуры пропорционально ![]() . В действительности вязкость растет несколько быстрее, чем по закону
. В действительности вязкость растет несколько быстрее, чем по закону ![]() . Это связано с тем, что с повышением температуры не только растет тепловая скорость молекул, но и уменьшается их эффективный диаметр и поэтому растет длина свободного пробега молекул
. Это связано с тем, что с повышением температуры не только растет тепловая скорость молекул, но и уменьшается их эффективный диаметр и поэтому растет длина свободного пробега молекул ![]() .
.
§5. Диффузия в газах
Диффузией называется обусловленный хаотическим движением молекул процесс постепенного перемешивания двух или нескольких соприкасающихся веществ. При этом вещество переходит из мест с большей в места с меньшей концентрацией до тех пор, пока состав смеси не станет одинаковым по всему объему. Давление и температура газовой смеси при диффузии остаются постоянными во всех частях объема. Поэтому полное число молекул в единице объема не изменяется в процессе диффузии, т. е. N = P/KT = Const. Будем считать, что имеется две компоненты a и b, диффундирующие друг в друга. Для определенности будем считать, что концентрация NA компоненты a в положительном направлении оси X уменьшается, а концентрация второй компоненты NB в этом же направлении возрастает, причем, так что N = NA+ NB = сonst и, следовательно, давление смеси одинаково во всем объеме. Выделим некоторую площадку Ds, перпендикулярную оси X. Понятно, что из-за теплового движения молекулы обеих компонент будут переходить через эту площадку в ту и другую сторону. Но результирующий поток молекул каждой компоненты будет направлен оттуда, где ее концентрация больше, туда, где она меньше. Таким образом, в рассматриваемом случае молекулы газа A будут диффундировать слева направо, а молекулы газа B — в противоположном направлении.
Количество диффундирующей компоненты a будем характеризовать результирующим числом молекул DNA этой компоненты, переносимых через выделенную площадку Ds за время Dt. Опыт показывает, что это число пропорционально Ds, времени Dt и градиенту концентрации DnA/Dx рассматриваемой компоненты в направлении, перпендикулярном к площадке, т. е.
![]()
Коэффициент пропорциональности называется коэффициентом диффузии. Он численно равен количеству молекул диффундирующей компоненты A, переносимой в единицу времени через единичную площадку при градиенте концентрации, равном единице. В системе СИ он имеет размерность м2/с.
Умножив равенство (1) на массу молекулы компоненты a, получим
![]()
Где DMA — масса диффундирующей компоненты; RA — ее плотность. Закон (1), установленный на опыте, называют законом Фика.
С точки зрения молекулярно кинетической теории за переносимую величину J нужно взять концентрацию компоненты a, рассчитанную на одну молекулу, т. е.
![]() ,
,
А DФ=DNA. Поэтому общее уравнение переноса (из §2 (5)) для диффузии примет вид
![]()
Сравнивая выражения (4) и (1), получим
![]()
Из формулы (5) видно, что при постоянном объеме D ~![]() , а при постоянной температуре D ~ 1/P.
, а при постоянной температуре D ~ 1/P.