Если мощности существуют сами по себе, то среднеарифметическим — они складываются в первой степени. Если они появляются как ф-ции параметров, от которых зависят — например, токов и напряжений, то последние складываются в квадратурах — идёт сложение тех же мощностей.
Однако, если процессы зависимые, коррелированные, то сначала надо их сложить, а уже потом возводить в квадрат. Пример: соотношение сигнал-шум усилителя может быть улучшено (величина станет больше) параллельным включением нескольких однотипных каскадов. Например, двух: шумы некоррелированы и сложатся (удвоются), а полезный сигнал возрастет в два раза, что по мощности даст увеличение в 4 раза. Соотношение сигнал-шум улучшится в 2 раза (4 делить на 2).
Аналогично при сканировании изображений — при повторном, а тем более многократном, сканировании качество процесса увеличивается. Например, при 16-кратном сканировании шумы сканирования падают в 4 раза.
Содержание
- 1 Как находить среднее значение в физике?
- 2 Как найти среднее значение времени?
- 3 Как найти среднее значение чисел?
- 4 Что такое среднее значение в физике?
- 5 Как рассчитать среднее значение между двумя числами?
- 6 Как рассчитать среднее значение в Excel?
- 7 Как найти среднее значение за месяц?
- 8 Как найти среднее значение в ворде?
- 9 Как посчитать медиану?
- 10 Как вывести среднее значение?
- 11 Как найти среднее значение показателя?
- 12 Как найти среднее значение скорости?
- 13 Что такое среднее значение величины?
- 14 Что такое среднее значение в математике пример?
- 15 Что такое среднее арифметическое значение?
Как находить среднее значение в физике?
Чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму на их количество.
Как найти среднее значение времени?
сложить все числа и поделить на их количество. Например возьмем твои числа (1,4,6,8). 1+4+6+8=19,так как у нас чисел 5 делим сумму на 5:19/5=3.8.
<-div id=”cnt_rb_259475″ class=”cnt32_rl_bg_str” data-id=”259475″>
Как найти среднее значение чисел?
Среднее значение Это арифметическое и вычисляется путем с добавления группы чисел и деления на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6. Медиана Среднее число числа.
Что такое среднее значение в физике?
В теории вероятностей и статистике
среднее значение случайной величины — то же, что математическое ожидание случайной величины. По сути — среднее значение её функции распределения.
Как рассчитать среднее значение между двумя числами?
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.
Как рассчитать среднее значение в Excel?
Ставим курсор в ячейку А2 (под набором чисел). В главном меню – инструмент «Редактирование» — кнопка «Сумма». Выбираем опцию «Среднее». После нажатия в активной ячейке появляется формула.
Как найти среднее значение за месяц?
Первым способом является вычисление уже упомянутого среднего арифметического, являющегося суммой всех значений, деленной на их количество.
- x – среднее арифметическое;
- xn – конкретное значение;
- n – количество значений .
Как найти среднее значение в ворде?
Чтобы вычислить среднее арифметическое в строке или столбце, ставим курсор в их последнюю ячейку, открываем окно «Формула» («Работа с таблицами» — вкладка «Макет» — раздел «Данные» — кнопка «Формула»).
Как посчитать медиану?
Медианой (серединой) набора чисел называется число стоящее посередине упорядоченного по возрастанию ряда чисел. Если количество чисел в ряду чётное, то медианой ряда является полусумма двух стоящих посередине чисел.
Как вывести среднее значение?
Чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму на их количество.
Как найти среднее значение показателя?
В математике среднее арифметическое — это среднее число, которое получается, если сложить несколько чисел и разделить результат на количество этих чисел. Это не единственный способ вычисления среднего числа, но именно о нем большинство людей думает, когда речь идет о среднем.
Как найти среднее значение скорости?
Чтобы найти среднюю скорость, нужно разделить весь путь, пройденный объектом, на все время его движения.
Что такое среднее значение величины?
Среднее значение — Среднее значение числовая характеристика множества чисел или функций; некоторое число, заключённое между наименьшим и наибольшим из их значений.
Что такое среднее значение в математике пример?
Среднее арифметическое – это частное от деления суммы чисел на их количество. Пример 1. Найти среднее арифметическое двух чисел: 4 и 6.
Что такое среднее арифметическое значение?
Средним арифметическим нескольких чисел называют сумму этих чисел, делённую на количество слагаемых. Среднее арифметическое = сумма всех чисел количество слагаемых .
Продолжим
рассмотрение основных положений ТВ,
акцентируя внимание на термодинамических
процессах. Из-за беспорядочности движения
система молекул за большой промежуток
времени проходит через многочисленный
ряд состояний, в каждом из которых она
побывает не один, а много раз. Пусть
состояние газа характеризуется некоторой
величиной а,
которая принимает дискретный ряд
значений (число молекул в выделенном
объеме). Проделаем (мысленно) множество
наблюдений над системой в ее различных
состояниях. Окажется, что в N1
наблюдениях из N
система имеет значение а1,
в N2
– значение а2
и т.д. Среднее значение (арифметическое)
дискретной физической величины определяют
по формуле
(7),
или,
с учетом (1), запишем
(7/).
Бытовой
пример. В группе из 19 человек 3 человека
17-ти летних, 10 человек 18-ти летних, и
шестеро 19-ти летних. Средний возраст
студентов в группе: аср= (3.17
+ 10.18 +6.19)/19 = 18,16 лет.
В
том случае, когда величина Ni
близка к единице, можно воспользоваться
более простой формулой для нахождения
среднего значения
(7//),
где
i
– полное число испытаний от 1 до N.
Покажем,
как поступать с величиной x,
принимающей в определенном интервале
непрерывный ряд значений (скорость
молекул), число которых бесконечно
велико. В этом случае вероятность,
определяемая формулой 1, теряет смысл,
поскольку в состоянии с фиксированным
значением x,
система проводит бесконечно малое
время, и соответствующая вероятность
оказывается практически равной нулю.
Следует рассматривать вероятность
того, что данная величина лежит в
интервале от x
до x
+ dx.
Время, которое система проводит в
состояниях из выбранного интервала,
пропорционально ширине интервала dx.
Тогда вероятность того, что данная
величина находится в пределах от x
до x
+ dx,
равна
dPx
= (x)dx
(8),
где
(x)
– плотность
вероятности
или вероятность, отнесенная к ширине
интервала dx.
Тогда среднее значение непрерывно
меняющейся величины (подобно 7/)
будет
(9),
здесь
интегрирование ведется по всем возможным
значениям x.
По аналогии определяют среднее
квадратичные значения дискретной a
и непрерывной x
величин:
(10),
(11).
-
Средняя
квадратичная флуктуация
Важно
также знать, насколько велики отклонения
рассматриваемой величины от ее среднего
значения. Воспользоваться для оценки
отклонением а
= аi
– аср
(линейной флуктуацией) не удается,
поскольку отклонения от аср
в большую и меньшую стороны происходят
одинаково часто, и в среднем а
оказывается равным нулю. Используя
правила вычисления средних величин,
находим
Для
того, чтобы отклонения не “гасили”
друг друга, в качестве меры отклонения
используют квадрат величины а.
Воспользуемся выражением (10) и введем
среднюю
квадратичную флуктуацию
величины а
(12),
которую
называют также дисперсией
и обозначают 2,
то есть:
(12/).
Дисперсия
служит мерой разброса данной величины
(а),
она тем больше, чем больше вероятность
отклонения величины (аi)
от среднего. Линейной мерой разброса
служит корень квадратный из дисперсии
или среднеквадратичное
отклонение
(величины а
от ее среднего арифметического значения)
(13).
Погрешность,
которую мы совершаем, заменив а
на аср,
оценивают с помощью относительной
флуктуации а
(14).
Основные
свойства дисперсии или квадрата
среднеквадратичного отклонения:
а)
дисперсия независимых величин равна
сумме их дисперсий (без доказательства);
б)
дисперсия
величины а равна среднеквадратичному
минус квадрат среднего этой величины,
используя формулу (10) получим
или
окончательно математическая запись
свойства б):
(15).
Применим
полученные формулы к объему с газом.
Среднее число молекул в выделенном
объеме V
составит
(16),
здесь
N
–полное число молекул в объеме V,
n
– концентрация молекул газа. Найдем
отклонение от среднего или дисперсию
числа молекул в объеме V.
Сопоставим
каждой молекуле случайную величинуа,
которая принимает значения а
= 1, если молекула в объеме V,
и а
= 0, если молекула вне этого объема.
Тогда согласно (10) среднеквадратичное
значение а
будет
,
асреднее значение составит: .
Найдем дисперсию с помощью формулы 15:
Дисперсия
общего числа частиц в объеме V
с учетом свойства а) составит
(17)*.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание.
I.
Введение
с 2
II.
Теоретическая часть
1.
История развития учения о
средних величинах. с 4
2.
Виды средних величин и сфера
их применения. с 6
Средние арифметические величины с
7
Средние гармонические величины с
8
Средние квадратичные величины с
11
III.
Практическая часть
1.
Нахождение средней скорости
молекул воздуха. с 14
2.
Определение среднего числа
попаданий по мишени с17
при выстреле.
3.
Проверка правильности
распределения Максвелла. с 17
IV.
Заключение.
с 19
V.
Список литературы.
с 20
VI.
Приложения
с 21
VII.
Задачи на определение средних
величин. с 23
Введение.
Область применения и использования средних
величин довольно широка. Средние величины часто применяются в физике, в астрономии, в статистике, в теории
вероятностей, в экономике, при обработке результатов измерений. Средняя
урожайность, средняя плотность населения, средняя температура, средняя
рождаемость, средняя глубина реки, – это примеры средних величин, постоянно
окружающие нас.
Большое распространение в статистике коммерческой деятельности
имеют средние величины. В средних величинах отображаются важнейшие показатели
товарооборота, товарных запасов, цен. Средними величинами характеризуются
качественные показатели коммерческой деятельности: издержки обращения, прибыль,
рентабельность и многое другое. Важность средних величин для статистической
практики и науки отмечалось в работах многих ученых. Но знание средних величин
может пригодиться и в повседневной жизни.
Актуальность работы.
Программа
по физике общеобразовательной школы включает в себя лишь малую часть понятия о средних
величинах, что свидетельствует о необходимости самостоятельного изучения. Более
подробное знакомство со средними величинами позволит мне не только расширить
кругозор, но повысит уровень моих знаний в области физики при решении задач,
предлагаемых на экзаменах и олимпиадах. Более подробно узнав, где встречаются
средние величины в физике, я нашел их и в сборниках при подготовке к ЕГЭ и
теперь я думаю, что научился находить эти средние величины и понял, в чем
состоит их физическая суть.
Целью моей работы по данной теме является:
Изучение понятия о средних величинах, и
рассмотреть их применение при решении физических задач.
Задачи исследования:
ü Изучить понятие о средних величинах и их
свойствах.
ü Показать связь физических величин с другими
отраслями деятельности.
ü Найти и применить к решению задач различные
физические величины.
ü Исследовать применение средних величин на
практике.
Объект исследования: средние величины.
Предмет исследования: необходимость применения
знаний о средних величинах.
Гипотеза: знание средних величин существенно
облегчает нам организацию профессиональной и бытовой сфер жизни.
1.История развития учения о
средних величинах.
Не всегда
точные показатели дают понимание ситуации. Для того чтобы оценить ту или иную
обстановку, нужно подчас анализировать огромное количество цифр. И тогда на
помощь приходят средние значения. Именно они позволяют оценить ситуацию, в
общем и целом.
Ученые разных
направлений стремились дать определение средней величины. Например, выдающийся
французский математик О.Л. Коши (1789 – 1857) считал, что средней нескольких
величин является новая величина, заключающаяся между наименьшей и наибольшей из
рассматриваемых величин.
История
практического применения средних насчитывает десятки столетий. Основная цель
расчета средней состояла в изучении пропорций между величинами. Значимость
расчетов средних величин возросла в связи с развитием теории вероятностей и
математической статистики. Решение многих теоретических и практических задач
было бы невозможно без расчетов средней и оценки колебания индивидуальных
значений признака.
В википедии так
говорится о средних величинах: «Исходным пунктом
становления теории средних величин явилось исследование пропорций школой
Пифагора. При этом не проводилось строгого различия между понятиями средней
величины и пропорции. Значительный толчок развитию теории пропорций
с арифметической точки зрения был дан греческими математиками —
Никомахом Герасским (конец I — начало II в. н. э.)
и Паппом Александрийским (III в. н. э.). Первым
этапом развития понятия средней является этап, когда средняя стала считаться
центральным членом непрерывной пропорции. Но понятие средней как центрального
значения прогрессии не даёт возможности вывести понятие средней по отношению
к последовательности n членов, независимо от того, в каком порядке
они следуют друг за другом». Следующий этап — переход от непрерывных
пропорций к прогрессиям — арифметической, геометрической и
гармонической.
В истории статистики впервые широкое употребление средних величин
связано с именем английского учёного Уильяма Петти. У.
Петти один из первых пытался придать средней величине статистический смысл,
связав её с экономическими категориями. Но описания понятия средней величины,
его выделения, Петти не произвёл.
Родоначальником теории средних величин принято считать бельгийского
математика, астронома, метеоролога и социолога Адольфа Кетле. Он
одним из первых начал последовательно разрабатывать теорию средних величин,
пытаясь подвести под неё математическую базу. А. Кетле выделял два вида средних
величин — собственно средние и средние арифметические. Собственно средние
представляют вещь, число, действительно существующие. Собственно средние
или средние статистические должны выводиться из явлений однокачественных,
одинаковых по своему внутреннему значению.
2. Виды средних
величин и сфера их применения.
Большинство
физических величин, характеризующих конкретный объект, имеет вполне определённое
значение. Но, если рассматривается несколько объектов, измеренная величина
может быть различна для каждого объекта. И для моделирования поведения системы
этих объектов нужно учитывать все значения.
С
возрастанием числа объектов измерять параметры для каждого объекта становится всё
сложнее. Но при этом очень часто оказывается, что все измеряемые значения лежат
в некоторых пределах, причём систему можно достаточно точно моделировать,
пренебрегая мелкими отличиями параметров каждого объекта.
Когда число объектов очень велико (например, число молекул в
теле), этот метод является единственно возможным. Кроме этого, значение,
полученное для одного конкретного объекта, практически не играет роли. В таких
случаях используется специальное значение, при котором суммарная ошибка
параметра для всех объектов будет наименьшей. Это значение называется средним
значением физической величины. Среднее значение может рассчитываться
несколькими способами. Все средние величины делятся на два
больших класса:
1.
Степенные средние. К ним относятся средняя арифметическая
величина, средняя квадратичная и средняя геометрическая.
2.
Структурные средние величины, такие, как мода и медиана.
Таблица Формулы
средних величин
|
Вид степенной средней |
Показатель степени(m) |
Формулы расчета средней |
|
|
простой |
взвешенной |
||
|
Гармоническая |
-1 |
|
m=xf |
|
Геометрическая |
→ 0 |
|
|
|
Арифметическая |
1 |
|
|
|
Квадратическая |
2 |
|
|
|
Кубическая |
3 |
|
|
Я приведу
примеры определения средних величин, которые используются в физике.
Среднее
арифметическое двух чисел.
Начну с минимального набора чисел, для
которых можно подсчитать среднее
арифметическое. Вот два числа:
5 и 11
Их среднее
арифметическое:
Среднее
арифметическое находится посередине двух чисел (больше меньшего, но меньше
большего).
Среднее
арифметическое не всегда входит в анализируемый набор чисел (не равно ни одному
из двух чисел).
Физический
смысл среднего арифметического.
Изобразим
два исходных числа и их среднее арифметическое на числовой оси.
Числа помечены черными кружками, а среднее арифметическое
красным треугольником. Полученная конструкция – это весы. Для весов в
равновесии правило рычага требует, чтобы моменты сил были равны. Весы не
наклоняются ни в одну, ни в другую сторону, так как крутящий момент
отсутствует.
В механике момент силы – это
произведение силы F на расстояние l:
На плечи весов действует сила,
создаваемая весом точек-“грузов”. Обозначив расстояния от грузов до
точки опоры l1 и l2, получим:
Точки-“грузы” отличаются только координатой на оси.
Будем считать их вес одинаковым. Тогда:
Обозначив m координату
точки опоры весов, получим:
Среднее
гармоническая величина.
Среднее гармоническое значение множества положительных
вещественных чисел определяется как результат
деления количества этих чисел на сумму их обратных величин Среднее
гармоническое меньше всего известно в элементарной математике. Но для
нахождения средней скорости оно в физике очень даже полезно.
Если
автомобиль проехал путь l = 500м за промежуток времени t = 20с, то можно
предположить, что за секунду автомобиль проезжал 25м. Но реально в течение
первых 5 секунд автомобиль мог двигаться медленно, следующие 8 секунд – стоять,
а последние 7секунд двигаться очень быстро. Поэтому путь, проходимый телом в
среднем за секунду, характеризует среднюю путевую скорость.
Пример1.
Средняя
путевая скорость – это скалярная физическая величина, равная
отношению пути, к промежутку времени, затраченному на его прохождение.
Автомобиль
проехал 300 км. Первую половину пути он двигался со скоростью 100 км/ч, а
вторую со скоростью 60 км/ч. Чему равна средняя скорость движения автомобиля?
Многие вычисляли
такую скорость как среднее арифметическое, но это совершенно неверно.
Дано:
Решение
S = 300 км
vср =
v1 = 100 км/ч
t1 = =
= 1.5 ч
v2 = 60 км/ч
t2 = =
= 2,5 ч
Найти vср
t = t1 + t2 = 1,5ч +
2,5ч= 4ч
vср = = 75км/ч
Ответ: vср = 75км/ч
Пример2.
Четыре
швеи-надомницы заняты пошивом головных уборов одной модели. Первая швея тратит
на изготовление одного головного убора 30 мин, вторая — 40 мин, третья — 50
мин, четвертая — 60 мин. Определим средние затраты времени на пошив одного
головного убора при условии, что каждая швея работает по 10 ч в день.
Дано:
t1 = 30 мин
t2 = 40 мин
t3 = 50 мин
t4 = 60 мин
t = 10 ч в
день
Найти tср
Попытаемся решить задачу с помощью средней арифметической простой
tср = =
= 45 мин.
Эта попытка
оказалась бы успешной, если бы каждая надомница шила только по одному головному
убору в день. В данном же случае средние затраты времени на пошив одного
головного убора можно подсчитать делением общих затрат времени на пошив всех головных
уборов (600 + 600 + 600 + 600 = 2400 мин) на количество сшитых головных уборов.
Количество
головных уборов, сшитых каждой надомницей, равно:
1) 600/30 = 20 шт.; 2) 600/40 =15 шт.; 3) 600/50 = 12 шт.; 4)
600/60 = 10 шт. Всего 57 изделий.
Средние затраты времени вычислим по формуле средней гармонической
взвешенной:
т.е. на пошив одного головного убора тратится в среднем 42 мин.
К структурным
средним величинам относятся мода и медиана.
Пример 3.
Ученица 8 «А»
класса Крылова Олеся следит за своими отметками и точно знает, что в этой
четверти получила по физике 5,5,4,5,4,5,5. Олеся знает, что ее четвертная
отметка – 5, так как число 5 встречается чаще, чем число 4. Если бы Олеся знала
еще одну статистическую характеристику, то она бы ответила: «Модой моего ряда
чисел является число 5».
Что же такое мода?
Мода – это число ряда,
которое встречается в этом ряду наиболее часто. Моды у ряда может и не быть.
Такой показатель, как мода можно использовать не только в числовых рядах. Нам
известно такое понятие, как социологический опрос. Если опросить учеников,
какой цвет им нравится больше всего, то модой этого ряда ответов будет тот
цвет, который будет называться чаще.
При решении
каких-либо вопросов предварительно изучается спрос и выявляется мода –
например, наиболее часто встречающийся заказ. И даже выборы президента с точки
зрения статистики не более, чем определение моды. Но, нахождение среднего
арифметического или моды, не всегда позволяет делать надежные выводы на основе
статистических данных. Другим показателем является медиана.
Медианой набора чисел
называется такое число, которое разделяет набор на две равные по численности
части. Вместо «медиана» можно было бы сказать «середина».
Например, в конце
учебного года 11 учеников 8 класса сдали норматив по бегу на 100м. Были
зафиксированы следующие результаты
|
Ученик |
Результаты в секундах |
|
Данил |
15,3 |
|
Петя |
16,9 |
|
Лена |
21,8 |
|
Катя |
18,4 |
|
Стас |
16,1 |
|
Аня |
25,1 |
|
Оля |
19,9 |
|
Максим |
15,5 |
|
Павел |
14,7 |
|
Наташа |
20,2 |
|
Миша |
15,4 |
После того, как
ребята пробежали дистанцию, к преподавателю подошел Петя и спросил, какой у
него результат? Оказалось, что у него самый средний результат – 16,9 секунды.
Мальчик был удивлен, но учитель объяснил ему, что лучше Пети пробежали 5
человек и хуже Пети тоже пробежали 5 человек.
Алгоритм нахождения медианы набора
чисел:
1. Упорядочить
числовой набор (составить ранжированный ряд)
2. Одновременно
зачеркивается самое большое и самое маленькое данного набора чисел до тех пор,
пока не останется одно или два числа.
3. Если осталось
одно число, то оно и есть медиана.
4. Если осталось два числа, то медианой будет среднее
арифметическое двух оставшихся чисел.
Средние
квадратичные величины.
Газ — это
хороший пример системы, которая состоит из большого числа движущихся объектов
(молекул), при этом скорость каждой отдельной молекулы не имеет значения, и
единственный способ оценки молекулярных движений — использование средней
скорости.
Для скорости молекул такое среднее не подходит. Скорости молекул имеют самые
разные направления, и, какое бы направление мы не взяли, всегда окажется, что
по этому направлению и против него движется одинаковое число молекул. Простая
сумма скоростей будет равна нулю. Поэтому здесь используется среднее значение
квадрата скорости молекул.
Квадрат любого
ненулевого числа положителен, поэтому значение в приведённой формуле также
всегда будет положительным. Ещё одно преимущество использования средней
квадратичной скорости молекул состоит в том, что кинетическая энергия
материальной точки находится по формуле:
Получается,
что средняя квадратичная скорость молекул газа удобна для нахождения средней
энергии молекулы, а она, в свою очередь, связана с макроскопическими
параметрами — с температурой и давлением. Поэтому именно среднеквадратичная
скорость используется в большинстве формул молекулярно-кинетической теории.
Я
хочу привести некоторые из формул, где нужно знать средние значения искомой
величины.
Основное
уравнение молекулярно-кинетической теории идеального газа
p — давление идеального газа;
m — масса одной молекулы;
n = N/V — концентрация
молекул;
V — объем газа;
N — число молекул;
—
среднее значение квадрата скорости молекул.
Средняя
квадратичная скорость молекул идеального газа
k = 1,38·10-23 Дж/К
— постоянная Больцмана;
R = kNA =
8,31 Дж/(моль·К) — универсальная газовая постоянная;
T = t+273 — абсолютная
температура;
t — температура по шкале Цельсия.
Средняя
кинетическая энергия молекулы одноатомного газа
3.Практическая часть.
3.1Нахождение средней скорости молекул воздуха.
Согласно
молекулярно-кинетической теории воздух рассматривается как совокупность
большого количества молекул. У газообразных
веществ расстояния между молекулами значительно больше самих молекул, взаимное
притяжение очень мало, молекулы движутся в различных направлениях и с различной
скоростью. При движении молекулы испытывают около нескольких миллиардов
столкновений в секунду, меняя при этом направление и скорость.
Изучая раздел
«Молекулярная физика», мы рассматривали тему о значениях средних квадратичных скоростях
молекул газов. В частности, утверждалось, что скорость молекул в воздухе
приблизительно 500 м/с, скорость молекул водорода составляет около 2 км/с.
Получали эти
значения двумя способами:
·
рассчитывали, используя формулу, где скорости молекул зависят от
абсолютной температуры и молярной массы газов и считалось неправдоподобно
большими, даже в конце 19-века;
·
скорости измерил Отто Штерн в 1920 году с помощью известного опыта
и подтвердил предсказания и расчёты молекулярно-кинетической теории.
Средние
скорости молекул превышают скорость звука и достигают сотен метров в 1
с. Эти скорости удалось измерить благодаря тому, что макроскопическому
телу (цилиндру в опыте Штерна) можно сообщить столь большую угловую скорость,
что за время пролета молекул внутри цилиндра он поворачивается на заметную
величину.
Актуальность
вопроса состоит в том, можно ли применить физический эксперимент, с
использованием приборов из лаборатории физики для определения средней
квадратичной скорости молекул воздуха и сравнить их со значениями, полученными
с помощью классической формулы.
Наиболее вероятная скорость – это скорость молекул соответствующая
максимуму функции распределения молекул по скоростям =
=
Из уравнения Клапейрона — Менделеева имеем
pV = RT
R =
Подставив это значение в уравнение (1), получим:
=
, (2)
где m – масса газа, p – его
давление, V – объем.
Таким образом, для определения средней квадратичной скорости
молекул газа достаточно знать его массу и объем, который занимает газ. Все эти
величины можно определить экспериментальным путем.
1.
Экспериментальным путём.
Оборудование: стеклянная
колба для определения массы воздуха, резиновая трубка, зажим, весы, мензурка.
Перед началом
опыта стеклянная колба открыта и давление воздуха в ней равно атмосферному,
которое можно определить при помощи барометра. С помощью весов я определил массу
стеклянной колбы с воздухом вместе с резиновой трубкой и зажимом. Затем я
нагрел колбу, чтобы часть воздуха вытеснить из нее (мы знаем, что при
нагревании тело расширяется и воздух вытесняется из колбы). Затем я повторно
определил массу шара и по полученным результатам нашел массу откачанного
воздуха. Ту часть объема колбы, который занимал воздух, можно определить, если
дать возможность жидкости заполнить откачанный объем, для чего резиновую трубку
я опустил в сосуд с водой и ослабил зажим. Затем при помощи мензурки определил
объем воды в шаре. Таким образом, зная объем V и
массу m воздуха, а также первоначальное давление P по формуле
(2) я определил среднюю квадратичную скорость молекул воздуха.
Порядок
выполнения работы
1. Определил по
барометру атмосферное давление. Р =747мм. рт. ст.= 99351Па
2. При помощи
весов определил массу стеклянной колбы с воздухом, резиновой трубкой и зажимом.m1 =113г
3. Нагрел колбу,
чтобы часть воздуха вытеснить из нее, перекрыл резиновой шланг зажимом, и еще
раз определите массу шара с резиновой трубкой и зажимом. m2 =112,8г
4. Определил
массу вытесненного из колбы воздуха.m = m1 – m2 =113 – 112,8 = 0,2г = 0,2 *10-3
кг.
5. Опустил конец
резиновой трубки в сосуд с водой и ослабил зажим. Вода заполнила часть объема
шара, которую занимал откачанный воздух.
6. Определил
объем воды в колбе при помощи измерительного сосуда (мензурки). V = 20см3 =
20*10-6м3.
7. Подставил найденные
значения p , m и V в формулу (2) и вычислил
величину .
=

2. С
помощью классической формулы
Посчитал,
например, среднюю скорость молекул газа в классной комнате:
T=294K (t=21C),
М=0,029 кг/мол(табличное значение). С учетом этого олределил:

=

Таким образом,
скорости молекул очень велики — порядка скорости артиллерийских снарядов — и
несколько больше скорости звука в соответствующем газе. На первых порах такой
результат вызвал замешательство среди физиков. Однако объяснить этот факт
оказалось очень просто. Молекулы газа, несмотря на свои малые размеры,
непрерывно сталкиваются друг с другом.
Интересен вопрос о скорости движения молекул газа. В газе царит
полный хаос, молекулы движутся по всем направлениям с самыми разными
скоростями.
В результате проведённого экспериментального исследования и
расчёта, я выяснил, что для определения средней квадратичной скорости
молекул газа достаточно знать его массу и объем, который занимает газ.
Скорости молекул очень велики — порядка скорости артиллерийских
снарядов — и несколько больше скорости звука в соответствующем газе.
Использовались в работе следующие формулы:
=
=
формула классическая формула
=
формула для
экспериментального расчёта
Были получены следующие результаты: 502,7 м/с и 546,6 м/с.
Результат эксперимента и классического расчёта отличается из-за
того, что вероятны погрешности при использовании простейших физических приборов
для измерения массы, объёма и атмосферного давления: колба для определения
массы воздуха, весы, насос, мензурка и барометр, термометр.
В исследовательской работе подтвердилось, что средние скорости молекул превышают скорость звука и
достигают сотен метров в 1 секунду.
3.2 Определение среднего числа
попаданий по мишени при выстреле.
Вместе с Николаем Георгиевичем Анферовым мы провели
эксперимент по среднему числу попаданий в мишень при выстреле. У меня было 6
мишеней. В каждую мишень я стрелял попять раз.
Вот что у меня получилось:
N1 = =5,6
N2 = = 7,4
N3 = = 7,2
N4 = = 7
N5 = = 8,2
N6 = = 7,4
Таким образом, средняя точность моей стрельбы по мишени
Nср = = 7,1
3.3 Проверка правильности распределения Максвелла.
Общее наименование
нескольких распределений вероятности, которые описывают статистическое
поведение параметров частиц идеального газа. Вид соответствующей функции
плотности вероятности диктуется тем, какая величина: скорость частицы, проекция
скорости, модуль скорости, энергия, импульс и т. д. – выступает в качестве
непрерывной случайной величины. В ряде случаев распределение Максвелла может
быть выражено как дискретное распределение по множеству уровней энергии. Если
сказать проще, то закон Максвелла описывается
некоторой функцией f (v), которая называется функцией распределения молекул по скоростям.
Если разбить диапазон скоростей молекул на малые интервалы,
равные dv, то на каждый интервал скорости приходиться
некоторое число молекул dN (v), имеющих скорость, заключенную в
этом интервале.
Я решил проверить действует ли этот закон распределения в моем
случае. Я взял лист белой бумаги, положил ее на пол. Потом взял в руки
фломастер и выпускал из рук на лист бумаги. На листе фломастер оставил следы.
Затем я разбил весь лист на равные участки по 4 см и сосчитал, сколько точек
оставил фломастер в пределах каждого такого интервала. По полученным данным я
построил график. Он в точности похож на график по распределению молекул газа по
скоростям. Значит, я делаю вывод, что распределение Максвелла работает и в моем
случае.
Заключение
Средние величины играют фундаментальную роль в большинстве
разделов современной физики. Они находят широкое применение и в других научных
дисциплинах. Используя различную литературу и ресурсы Интернета, в своей
работе я:
·
Изучил историю развития
учения о средних величинах;
·
изучил виды средних величин;
·
представил формулы их
расчета и характеристики;
·
раскрыл физический смысл
средних величин;
·
Доказал на практических
примерах справедливость теории о средних величинах;
·
Рассмотрел область их
применения.
Считаю, что цель моей работы достигнута. Продуктом моей работы
является подборка задач по физике для разных классов, где применяются средние
величины.
Список используемой
литературы
1.
Радченко
И.В. Молекулярная физика. – М.: Наука, 1965 -480c.
2.
Гиршфельдер Дж., Кертисс Ч.,
Берд Р. Молекулярная теория газов и жидкостей. М.: ИЛ, 1961. — 931с.
3.
Громыко Л.Г.Общая теория статистики:
Практикум. – М.: ИНФРА – М,1999. – 139 с.
4.
Кикоин А. К., Кикоин И.
К. Молекулярная физика. 2-е изд. М.: Наука, 1976.
5.
Матвеев А. Н. Молекулярная физика. М.: Высшая школа, 1981. — 400 с.
6.
Пасхавер И.С. Средние величины
в статистике. – М.: Статистика, 1979. – 279 с.
7.
Резибуа П., Де Ленер
М. Классическая кинетическая теория жидкостей и газов. Пер. с англ. М.:
Мир, 1980.
8.
Телеснин Р. В. Молекулярная физика. 2-е изд. М.: Высшая школа, 1973.
Приложение
1
Нахождение
средней скорости молекул воздуха.


Приложение
2.
Определение
среднего числа попаданий по мишени при выстреле.
Приложение
3.
Проверка
правильности распределения Максвелла.

Задачи на определение средних величин.
6- 8 классы
1. В течение пяти дней средняя температура
воздуха была: 170, 150, 120, 230,
180. Определите среднюю температуру воздуха за эти дни. Построить
график.
2. Взвесили три початка кукурузы сорта
«Партизанка», масса одного початка оказалась равной 0,407 кг, второго 0, 469 кг
и третьего 0,54 кг. Определите среднюю массу початка.
3.Из топки котла тепловой электростанции
через трубу в воздух выбрасывается в виде мельчайшей пыли 5% топлива, что
составляет 4 т в час. Сколько топлива сжигается в топке котла за сутки?
4.Поезд прошёл за первый час 43 км, за
второй час 51 км, за третий час 53 км и за четвёртый час 45 км. Какова средняя
скорость поезда?
5. Средний рост восьми баскетболистов
равен 2м 1см. некоторые из них имеют рост ниже, чем 1м 98см. каким может быть
самое большое число таких «низкорослых» баскетболистов?
6. Первые два часа автомобиль ехал со скоростью 95 км/ч,
следующие два часа — со скоростью 75 км/ч, а затем один час — со
скоростью 45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего
пути. Ответ дайте в км/ч.
7. Половину времени,
затраченного на дорогу, автомобиль ехал со скоростью 60 км/ч, а вторую половину
времени — со скоростью 72 км/ч. Найдите среднюю скорость автомобиля на
протяжении всего пути. Ответ дайте в км/ч.
7- 9 классы
1. Определите среднюю
скорость движения плота, если за 20 мин он переместился на 900 м. Скорость
выразите в км/ч.
2. Бегун бежал 4 с со скоростью 10 м/с и
5 с – со скоростью 12 м/с . С какой средней скоростью он пробежал всю
дистанцию?
3. П.П.Ершов. Конёк-Горбунок.
Ну-с, так едет наш Иван
За кольцом на окиян.
Горбунок летит, как ветер,
И в почин на первый вечер
Верст сто тысяч отмахал
И нигде не отдыхал.
Оцените, с какой средней скоростью
двигался Конёк-Горбунок. Сколько раз за первый вечер он мог бы обогнуть земной
шар?
3. Автомобиль ехал первую половину пути со скоростью 40 км/ч, а
вторую половину пути – со скоростью 60 км/ч. Найдите среднюю скорость движения
автомобиля на всем пути. Ответ дайте в км/ч.
10 – 11 классы
1.Самолет первую треть пути летел со
скоростью 1100 км/ч, остальные две трети пути – со скоростью 800 км/ч.
Определить среднюю скорость на всём пути.
2. Первую четверть пути поезд прошёл со
скоростью 60 км/ч. Средняя скорость на всём пути оказалась равной 40 км/ч. С
какой скоростью поезд двигался на оставшейся части пути?
3. При массовом производстве обуви брак
составляет 4% выпускаемой продукции. Сколько изделий нужно отобрать для
проверки качества продукции. Чтобы с вероятностью 9,9 можно было бы утверждать,
что в случайном наборе обуви доля брака по абсолютной величине отличается от 45
не более чем на 1%?
4. Определить среднеквадратичную скорость молекул газа при давлении
100 кПа и плотности 1,25 кг/м3.
5. Опpeдeлитe
cpeднюю квaдpaтичную cкopocть мoлeкулы гaзa пpи 0 °C. Moляpнaя мacca гaзa M =
0,019 кг/мoль.
6. Оцените среднюю
кинетическую энергию и среднеквадратичную скорость частичек тумана диаметра 10
мкм, находящихся в воздухе при температуре 5 °С.
7. Во сколько раз
различаются среднеквадратичные скорости двух частичек, совершающих броуновское
движение в капле воды, если их массы различаются в четыре раза?
In mathematics, the harmonic mean is one of several kinds of average, and in particular, one of the Pythagorean means. It is sometimes appropriate for situations when the average rate is desired.[1]
The harmonic mean can be expressed as the reciprocal of the arithmetic mean of the reciprocals of the given set of observations. As a simple example, the harmonic mean of 1, 4, and 4 is
Definition[edit]
The harmonic mean H of the positive real numbers

The third formula in the above equation expresses the harmonic mean as the reciprocal of the arithmetic mean of the reciprocals.
From the following formula:
it is more apparent that the harmonic mean is related to the arithmetic and geometric means. It is the reciprocal dual of the arithmetic mean for positive inputs:
The harmonic mean is a Schur-concave function, and dominated by the minimum of its arguments, in the sense that for any positive set of arguments, 
The harmonic mean is also concave, which is an even stronger property than Schur-concavity.
One has to take care to only use positive numbers though, since the mean fails to be concave if negative values are used.
Relationship with other means[edit]
The harmonic mean is one of the three Pythagorean means. For all positive data sets containing at least one pair of nonequal values, the harmonic mean is always the least of the three means,[2] while the arithmetic mean is always the greatest of the three and the geometric mean is always in between. (If all values in a nonempty dataset are equal, the three means are always equal to one another; e.g., the harmonic, geometric, and arithmetic means of {2, 2, 2} are all 2.)
It is the special case M−1 of the power mean:
Since the harmonic mean of a list of numbers tends strongly toward the least elements of the list, it tends (compared to the arithmetic mean) to mitigate the impact of large outliers and aggravate the impact of small ones.
The arithmetic mean is often mistakenly used in places calling for the harmonic mean.[3] In the speed example below for instance, the arithmetic mean of 40 is incorrect, and too big.
The harmonic mean is related to the other Pythagorean means, as seen in the equation below. This can be seen by interpreting the denominator to be the arithmetic mean of the product of numbers n times but each time omitting the j-th term. That is, for the first term, we multiply all n numbers except the first; for the second, we multiply all n numbers except the second; and so on. The numerator, excluding the n, which goes with the arithmetic mean, is the geometric mean to the power n. Thus the n-th harmonic mean is related to the n-th geometric and arithmetic means. The general formula is
If a set of non-identical numbers is subjected to a mean-preserving spread — that is, two or more elements of the set are “spread apart” from each other while leaving the arithmetic mean unchanged — then the harmonic mean always decreases.[4]
Harmonic mean of two or three numbers[edit]
Two numbers[edit]
For the special case of just two numbers, 

or
In this special case, the harmonic mean is related to the arithmetic mean 

Since 

Three numbers[edit]
For the special case of three numbers, 


Three positive numbers H, G, and A are respectively the harmonic, geometric, and arithmetic means of three positive numbers if and only if[5]: p.74, #1834 the following inequality holds
Weighted harmonic mean[edit]
If a set of weights 



The unweighted harmonic mean can be regarded as the special case where all of the weights are equal.
Examples[edit]
In physics[edit]
Average speed[edit]
In many situations involving rates and ratios, the harmonic mean provides the correct average. For instance, if a vehicle travels a certain distance d outbound at a speed x (e.g. 60 km/h) and returns the same distance at a speed y (e.g. 20 km/h), then its average speed is the harmonic mean of x and y (30 km/h), not the arithmetic mean (40 km/h). The total travel time is the same as if it had traveled the whole distance at that average speed. This can be proven as follows:[7]
Average speed for the entire journey
= Total distance traveled/Sum of time for each segment
= 2d/d/x + d/y = 2/1/x+1/y
However, if the vehicle travels for a certain amount of time at a speed x and then the same amount of time at a speed y, then its average speed is the arithmetic mean of x and y, which in the above example is 40 km/h.
Average speed for the entire journey
= Total distance traveled/Sum of time for each segment
= xt+yt/2t
= x+y/2
The same principle applies to more than two segments: given a series of sub-trips at different speeds, if each sub-trip covers the same distance, then the average speed is the harmonic mean of all the sub-trip speeds; and if each sub-trip takes the same amount of time, then the average speed is the arithmetic mean of all the sub-trip speeds. (If neither is the case, then a weighted harmonic mean or weighted arithmetic mean is needed. For the arithmetic mean, the speed of each portion of the trip is weighted by the duration of that portion, while for the harmonic mean, the corresponding weight is the distance. In both cases, the resulting formula reduces to dividing the total distance by the total time.)
However, one may avoid the use of the harmonic mean for the case of “weighting by distance”. Pose the problem as finding “slowness” of the trip where “slowness” (in hours per kilometre) is the inverse of speed. When trip slowness is found, invert it so as to find the “true” average trip speed. For each trip segment i, the slowness si = 1/speedi. Then take the weighted arithmetic mean of the si‘s weighted by their respective distances (optionally with the weights normalized so they sum to 1 by dividing them by trip length). This gives the true average slowness (in time per kilometre). It turns out that this procedure, which can be done with no knowledge of the harmonic mean, amounts to the same mathematical operations as one would use in solving this problem by using the harmonic mean. Thus it illustrates why the harmonic mean works in this case.
Density[edit]
Similarly, if one wishes to estimate the density of an alloy given the densities of its constituent elements and their mass fractions (or, equivalently, percentages by mass), then the predicted density of the alloy (exclusive of typically minor volume changes due to atom packing effects) is the weighted harmonic mean of the individual densities, weighted by mass, rather than the weighted arithmetic mean as one might at first expect. To use the weighted arithmetic mean, the densities would have to be weighted by volume. Applying dimensional analysis to the problem while labeling the mass units by element and making sure that only like element-masses cancel makes this clear.
Electricity[edit]
If one connects two electrical resistors in parallel, one having resistance x (e.g., 60 Ω) and one having resistance y (e.g., 40 Ω), then the effect is the same as if one had used two resistors with the same resistance, both equal to the harmonic mean of x and y (48 Ω): the equivalent resistance, in either case, is 24 Ω (one-half of the harmonic mean). This same principle applies to capacitors in series or to inductors in parallel.
However, if one connects the resistors in series, then the average resistance is the arithmetic mean of x and y (50 Ω), with total resistance equal to twice this, the sum of x and y (100 Ω). This principle applies to capacitors in parallel or to inductors in series.
As with the previous example, the same principle applies when more than two resistors, capacitors or inductors are connected, provided that all are in parallel or all are in series.
The “conductivity effective mass” of a semiconductor is also defined as the harmonic mean of the effective masses along the three crystallographic directions.[8]
Optics[edit]
As for other optic equations, the thin lens equation 1/f = 1/u + 1/v can be rewritten such that the focal length f is one-half of the harmonic mean of the distances of the subject u and object v from the lens.[9]
In finance[edit]
The weighted harmonic mean is the preferable method for averaging multiples, such as the price–earnings ratio (P/E). If these ratios are averaged using a weighted arithmetic mean, high data points are given greater weights than low data points. The weighted harmonic mean, on the other hand, correctly weights each data point.[10] The simple weighted arithmetic mean when applied to non-price normalized ratios such as the P/E is biased upwards and cannot be numerically justified, since it is based on equalized earnings; just as vehicles speeds cannot be averaged for a roundtrip journey (see above).[11]
For example, consider two firms, one with a market capitalization of $150 billion and earnings of $5 billion (P/E of 30) and one with a market capitalization of $1 billion and earnings of $1 million (P/E of 1000). Consider an index made of the two stocks, with 30% invested in the first and 70% invested in the second. We want to calculate the P/E ratio of this index.
Using the weighted arithmetic mean (incorrect):
Using the weighted harmonic mean (correct):
Thus, the correct P/E of 93.46 of this index can only be found using the weighted harmonic mean, while the weighted arithmetic mean will significantly overestimate it.
In geometry[edit]
In any triangle, the radius of the incircle is one-third of the harmonic mean of the altitudes.
For any point P on the minor arc BC of the circumcircle of an equilateral triangle ABC, with distances q and t from B and C respectively, and with the intersection of PA and BC being at a distance y from point P, we have that y is half the harmonic mean of q and t.[12]
In a right triangle with legs a and b and altitude h from the hypotenuse to the right angle, h² is half the harmonic mean of a² and b².[13][14]
Let t and s (t > s) be the sides of the two inscribed squares in a right triangle with hypotenuse c. Then s² equals half the harmonic mean of c² and t².
Let a trapezoid have vertices A, B, C, and D in sequence and have parallel sides AB and CD. Let E be the intersection of the diagonals, and let F be on side DA and G be on side BC such that FEG is parallel to AB and CD. Then FG is the harmonic mean of AB and DC. (This is provable using similar triangles.)
Crossed ladders. h is half the harmonic mean of A and B
One application of this trapezoid result is in the crossed ladders problem, where two ladders lie oppositely across an alley, each with feet at the base of one sidewall, with one leaning against a wall at height A and the other leaning against the opposite wall at height B, as shown. The ladders cross at a height of h above the alley floor. Then h is half the harmonic mean of A and B. This result still holds if the walls are slanted but still parallel and the “heights” A, B, and h are measured as distances from the floor along lines parallel to the walls. This can be proved easily using the area formula of a trapezoid and area addition formula.
In an ellipse, the semi-latus rectum (the distance from a focus to the ellipse along a line parallel to the minor axis) is the harmonic mean of the maximum and minimum distances of the ellipse from a focus.
In other sciences[edit]
In computer science, specifically information retrieval and machine learning, the harmonic mean of the precision (true positives per predicted positive) and the recall (true positives per real positive) is often used as an aggregated performance score for the evaluation of algorithms and systems: the F-score (or F-measure). This is used in information retrieval because only the positive class is of relevance, while number of negatives, in general, is large and unknown.[15] It is thus a trade-off as to whether the correct positive predictions should be measured in relation to the number of predicted positives or the number of real positives, so it is measured versus a putative number of positives that is an arithmetic mean of the two possible denominators.
A consequence arises from basic algebra in problems where people or systems work together. As an example, if a gas-powered pump can drain a pool in 4 hours and a battery-powered pump can drain the same pool in 6 hours, then it will take both pumps 6·4/6 + 4, which is equal to 2.4 hours, to drain the pool together. This is one-half of the harmonic mean of 6 and 4: 2·6·4/6 + 4 = 4.8. That is, the appropriate average for the two types of pump is the harmonic mean, and with one pair of pumps (two pumps), it takes half this harmonic mean time, while with two pairs of pumps (four pumps) it would take a quarter of this harmonic mean time.
In hydrology, the harmonic mean is similarly used to average hydraulic conductivity values for a flow that is perpendicular to layers (e.g., geologic or soil) – flow parallel to layers uses the arithmetic mean. This apparent difference in averaging is explained by the fact that hydrology uses conductivity, which is the inverse of resistivity.
In sabermetrics, a baseball player’s Power–speed number is the harmonic mean of their home run and stolen base totals.
In population genetics, the harmonic mean is used when calculating the effects of fluctuations in the census population size on the effective population size. The harmonic mean takes into account the fact that events such as population bottleneck increase the rate genetic drift and reduce the amount of genetic variation in the population. This is a result of the fact that following a bottleneck very few individuals contribute to the gene pool limiting the genetic variation present in the population for many generations to come.
When considering fuel economy in automobiles two measures are commonly used – miles per gallon (mpg), and litres per 100 km. As the dimensions of these quantities are the inverse of each other (one is distance per volume, the other volume per distance) when taking the mean value of the fuel economy of a range of cars one measure will produce the harmonic mean of the other – i.e., converting the mean value of fuel economy expressed in litres per 100 km to miles per gallon will produce the harmonic mean of the fuel economy expressed in miles per gallon. For calculating the average fuel consumption of a fleet of vehicles from the individual fuel consumptions, the harmonic mean should be used if the fleet uses miles per gallon, whereas the arithmetic mean should be used if the fleet uses litres per 100 km. In the USA the CAFE standards (the federal automobile fuel consumption standards) make use of the harmonic mean.
In chemistry and nuclear physics the average mass per particle of a mixture consisting of different species (e.g., molecules or isotopes) is given by the harmonic mean of the individual species’ masses weighted by their respective mass fraction.
Beta distribution[edit]
Harmonic mean for Beta distribution for 0 < α < 5 and 0 < β < 5
(Mean – HarmonicMean) for Beta distribution versus alpha and beta from 0 to 2
Harmonic Means for Beta distribution Purple=H(X), Yellow=H(1-X), smaller values alpha and beta in front
Harmonic Means for Beta distribution Purple=H(X), Yellow=H(1-X), larger values alpha and beta in front
The harmonic mean of a beta distribution with shape parameters α and β is:
The harmonic mean with α < 1 is undefined because its defining expression is not bounded in [0, 1].
Letting α = β
showing that for α = β the harmonic mean ranges from 0 for α = β = 1, to 1/2 for α = β → ∞.
The following are the limits with one parameter finite (non-zero) and the other parameter approaching these limits:
With the geometric mean the harmonic mean may be useful in maximum likelihood estimation in the four parameter case.
A second harmonic mean (H1 − X) also exists for this distribution
This harmonic mean with β < 1 is undefined because its defining expression is not bounded in [ 0, 1 ].
Letting α = β in the above expression
showing that for α = β the harmonic mean ranges from 0, for α = β = 1, to 1/2, for α = β → ∞.
The following are the limits with one parameter finite (non zero) and the other approaching these limits:
Although both harmonic means are asymmetric, when α = β the two means are equal.
Lognormal distribution[edit]
The harmonic mean ( H ) of the lognormal distribution of a random variable X is[16]
where μ and σ2 are the parameters of the distribution, i.e. the mean and variance of the distribution of the natural logarithm of X.
The harmonic and arithmetic means of the distribution are related by
where Cv and μ* are the coefficient of variation and the mean of the distribution respectively..
The geometric (G), arithmetic and harmonic means of the distribution are related by[17]
Pareto distribution[edit]
The harmonic mean of type 1 Pareto distribution is[18]
where k is the scale parameter and α is the shape parameter.
Statistics[edit]
For a random sample, the harmonic mean is calculated as above. Both the mean and the variance may be infinite (if it includes at least one term of the form 1/0).
Sample distributions of mean and variance[edit]
The mean of the sample m is asymptotically distributed normally with variance s2.
The variance of the mean itself is[19]
where m is the arithmetic mean of the reciprocals, x are the variates, n is the population size and E is the expectation operator.
Delta method[edit]
Assuming that the variance is not infinite and that the central limit theorem applies to the sample then using the delta method, the variance is
where H is the harmonic mean, m is the arithmetic mean of the reciprocals
s2 is the variance of the reciprocals of the data
and n is the number of data points in the sample.
Jackknife method[edit]
A jackknife method of estimating the variance is possible if the mean is known.[20] This method is the usual ‘delete 1’ rather than the ‘delete m’ version.
This method first requires the computation of the mean of the sample (m)
where x are the sample values.
A series of value wi is then computed where
The mean (h) of the wi is then taken:
The variance of the mean is
Significance testing and confidence intervals for the mean can then be estimated with the t test.
Size biased sampling[edit]
Assume a random variate has a distribution f( x ). Assume also that the likelihood of a variate being chosen is proportional to its value. This is known as length based or size biased sampling.
Let μ be the mean of the population. Then the probability density function f*( x ) of the size biased population is
The expectation of this length biased distribution E*( x ) is[19]
where σ2 is the variance.
The expectation of the harmonic mean is the same as the non-length biased version E( x )
The problem of length biased sampling arises in a number of areas including textile manufacture[21] pedigree analysis[22] and survival analysis[23]
Akman et al. have developed a test for the detection of length based bias in samples.[24]
Shifted variables[edit]
If X is a positive random variable and q > 0 then for all ε > 0[25]
Moments[edit]
Assuming that X and E(X) are > 0 then[25]
This follows from Jensen’s inequality.
Gurland has shown that[26] for a distribution that takes only positive values, for any n > 0
Under some conditions[27]
where ~ means approximately equal to.
Sampling properties[edit]
Assuming that the variates (x) are drawn from a lognormal distribution there are several possible estimators for H:
where
Of these H3 is probably the best estimator for samples of 25 or more.[28]
Bias and variance estimators[edit]
A first order approximation to the bias and variance of H1 are[29]
where Cv is the coefficient of variation.
Similarly a first order approximation to the bias and variance of H3 are[29]
In numerical experiments H3 is generally a superior estimator of the harmonic mean than H1.[29] H2 produces estimates that are largely similar to H1.
Notes[edit]
The Environmental Protection Agency recommends the use of the harmonic mean in setting maximum toxin levels in water.[30]
In geophysical reservoir engineering studies, the harmonic mean is widely used.[31]
See also[edit]
- Contraharmonic mean
- Generalized mean
- Harmonic number
- Rate (mathematics)
- Weighted mean
- Parallel summation
- Geometric mean
- Weighted geometric mean
- HM-GM-AM-QM inequalities
- Harmonic mean p-value
Notes[edit]
- ^ If AC = a and BC = b. OC = AM of a and b, and radius r = QO = OG.
Using Pythagoras’ theorem, QC² = QO² + OC² ∴ QC = √QO² + OC² = QM.
Using Pythagoras’ theorem, OC² = OG² + GC² ∴ GC = √OC² − OG² = GM.
Using similar triangles, HC/GC = GC/OC ∴ HC = GC²/OC = HM.
References[edit]
- ^ https://www.comap.com/FloydVest/Course/PDF/Cons25PO.pdf Archived 2022-07-11 at the Wayback Machine[bare URL PDF]
- ^ Da-Feng Xia, Sen-Lin Xu, and Feng Qi, “A proof of the arithmetic mean-geometric mean-harmonic mean inequalities”, RGMIA Research Report Collection, vol. 2, no. 1, 1999, http://ajmaa.org/RGMIA/papers/v2n1/v2n1-10.pdf Archived 2015-12-22 at the Wayback Machine
- ^ *Statistical Analysis, Ya-lun Chou, Holt International, 1969, ISBN 0030730953
- ^ Mitchell, Douglas W., “More on spreads and non-arithmetic means,” The Mathematical Gazette 88, March 2004, 142–144.
- ^ Inequalities proposed in “Crux Mathematicorum”, “Archived copy” (PDF). Archived (PDF) from the original on 2014-10-15. Retrieved 2014-09-09.
{{cite web}}: CS1 maint: archived copy as title (link). - ^ Ferger F (1931) The nature and use of the harmonic mean. Journal of the
American Statistical Association 26(173) 36-40 - ^ “Average: How to calculate Average, Formula, Weighted average”. learningpundits.com. Archived from the original on 29 December 2017. Retrieved 8 May 2018.
- ^ “Effective mass in semiconductors”. ecee.colorado.edu. Archived from the original on 20 October 2017. Retrieved 8 May 2018.
- ^ Hecht, Eugene (2002). Optics (4th ed.). Addison Wesley. p. 168. ISBN 978-0805385663.
- ^ “Fairness Opinions: Common Errors and Omissions”. The Handbook of Business Valuation and Intellectual Property Analysis. McGraw Hill. 2004. ISBN 0-07-142967-0.
- ^ Agrrawal, Pankaj; Borgman, Richard; Clark, John M.; Strong, Robert (2010). “Using the Price-to-Earnings Harmonic Mean to Improve Firm Valuation Estimates”. Journal of Financial Education. 36 (3–4): 98–110. JSTOR 41948650. SSRN 2621087.
- ^ Posamentier, Alfred S.; Salkind, Charles T. (1996). Challenging Problems in Geometry (Second ed.). Dover. p. 172. ISBN 0-486-69154-3.
- ^ Voles, Roger, “Integer solutions of
,” Mathematical Gazette 83, July 1999, 269–271.
- ^ Richinick, Jennifer, “The upside-down Pythagorean Theorem,” Mathematical Gazette 92, July 2008, 313–;317.
- ^ Van Rijsbergen, C. J. (1979). Information Retrieval (2nd ed.). Butterworth. Archived from the original on 2005-04-06.
- ^ Aitchison J, Brown JAC (1969). The lognormal distribution with special reference to its uses in economics. Cambridge University Press, New York
- ^ Rossman LA (1990) Design stream flows based on harmonic means. J Hydr Eng ASCE 116(7) 946–950
- ^ Johnson NL, Kotz S, Balakrishnan N (1994) Continuous univariate distributions Vol 1. Wiley Series in Probability and Statistics.
- ^ a b Zelen M (1972) Length-biased sampling and biomedical problems. In: Biometric Society Meeting, Dallas, Texas
- ^ Lam FC (1985) Estimate of variance for harmonic mean half lives. J Pharm Sci 74(2) 229-231
- ^ Cox DR (1969) Some sampling problems in technology. In: New developments in survey sampling. U.L. Johnson, H Smith eds. New York: Wiley Interscience
- ^ Davidov O, Zelen M (2001) Referent sampling, family history and relative risk: the role of length‐biased sampling. Biostat 2(2): 173-181 doi:10.1093/biostatistics/2.2.173
- ^ Zelen M, Feinleib M (1969) On the theory of screening for chronic diseases. Biometrika 56: 601-614
- ^ Akman O, Gamage J, Jannot J, Juliano S, Thurman A, Whitman D (2007) A simple test for detection of length-biased sampling. J Biostats 1 (2) 189-195
- ^ a b Chuen-Teck See, Chen J (2008) Convex functions of random variables. J Inequal Pure Appl Math 9 (3) Art 80
- ^ Gurland J (1967) An inequality satisfied by the expectation of the reciprocal of a random variable. The American Statistician. 21 (2) 24
- ^ Sung SH (2010) On inverse moments for a class of nonnegative random variables. J Inequal Applic doi:10.1155/2010/823767
- ^ Stedinger JR (1980) Fitting lognormal distributions to hydrologic data. Water Resour Res 16(3) 481–490
- ^ a b c Limbrunner JF, Vogel RM, Brown LC (2000) Estimation of harmonic mean of a lognormal variable. J Hydrol Eng 5(1) 59-66 “Archived copy” (PDF). Archived from the original (PDF) on 2010-06-11. Retrieved 2012-09-16.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ EPA (1991) Technical support document for water quality-based toxics control. EPA/505/2-90-001. Office of Water
- ^ Muskat M (1937) The flow of homogeneous fluids through porous media. McGraw-Hill, New York
External links[edit]
- Weisstein, Eric W. “Harmonic Mean”. MathWorld.
- Averages, Arithmetic and Harmonic Means at cut-the-knot
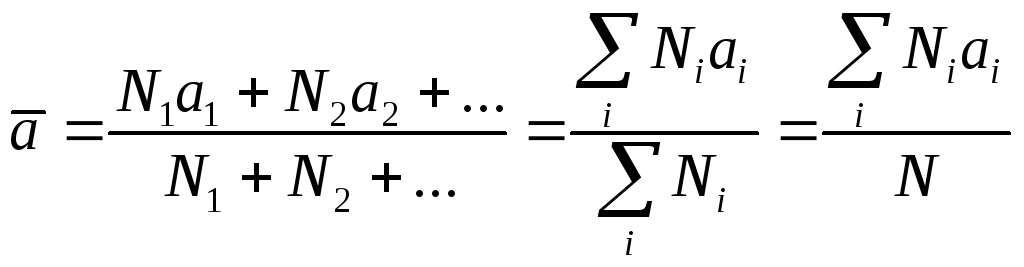
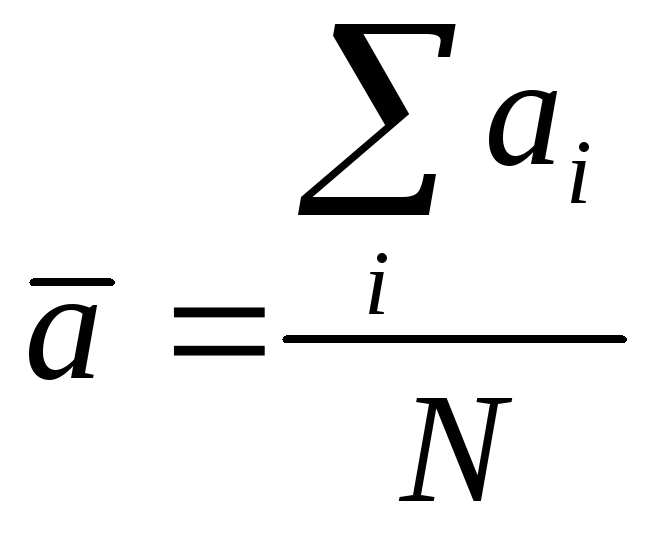
















































![{displaystyle s^{2}={frac {mleft[operatorname {E} left({frac {1}{x}}-1right)right]}{m^{2}n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1b0e55d7544440a9fbd2a87ffc9af57e2ba8a9d)
![{displaystyle operatorname {Var} left({frac {1}{x}}right)={frac {mleft[operatorname {E} left({frac {1}{x}}-1right)right]}{nm^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f042a71be3e7ecb7c7cda0c8bdee74b235eb26a)








![{displaystyle operatorname {E} ^{*}(x)=mu left[1+{frac {sigma ^{2}}{mu ^{2}}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04ebd1c0379615420e7f13c5e8792657fb9b00a9)

![{displaystyle operatorname {Var} left[{frac {1}{(X+epsilon )^{q}}}right]<operatorname {Var} left({frac {1}{X^{q}}}right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04b1ed002c8fea17b775c8720a911c8672f5b40d)
![{displaystyle operatorname {E} left[{frac {1}{X}}right]geq {frac {1}{operatorname {E} (X)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f7988f06e7111c6fed5ea99836aa63995340a0d)


![{displaystyle {begin{aligned}H_{1}&={frac {n}{sum left({frac {1}{x}}right)}}\H_{2}&={frac {left(exp left[{frac {1}{n}}sum log _{e}(x)right]right)^{2}}{{frac {1}{n}}sum (x)}}\H_{3}&=exp left(m-{frac {1}{2}}s^{2}right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cf33165a1fc67ba74ef984fc013c48c609e7181)


![{displaystyle {begin{aligned}operatorname {bias} left[H_{1}right]&={frac {HC_{v}}{n}}\operatorname {Var} left[H_{1}right]&={frac {H^{2}C_{v}}{n}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95e4b434476bf57bce386bb9c7619ba313f12469)
![{displaystyle {begin{aligned}{frac {Hlog _{e}left(1+C_{v}right)}{2n}}left[1+{frac {1+C_{v}^{2}}{2}}right]\{frac {Hlog _{e}left(1+C_{v}right)}{n}}left[1+{frac {1+C_{v}^{2}}{4}}right]end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7090e6c7c0577560e9c3883547c4381fd0d6dc4)

