Содержание:
- Определение и формула давления
- Среднее давление
- Давление идеального газа
- Гидростатическое давление
- Единицы измерения давления
- Примеры решения задач
Определение и формула давления
Определение
Давление – это физическая величина,характеризующая состояние сплошной среды. Оно равно пределу отношения нормальной составляющей силы,
которая действует на участок поверхности тела площади
$Delta S$ к размеру данной площади при
$Delta S rightarrow 0$ . Обозначается давление буквой p. Тогда математической
записью определения давления станет формула:
$$p=lim _{Delta S rightarrow 0} frac{Delta F_{n}}{Delta S}=frac{d F_{n}}{d S}$$
Выражение (1) определяет давление в точке.
Среднее давление
Средним давлением на поверхность называют величину:
$$langle prangle=frac{F_{n}}{S}(2)$$
где Fn – нормальная составляющая силы, которая действует на рассматриваемую поверхность, S – площадь этой поверхности.
Давление идеального газа
Давление идеального газа вычисляют, используя основное уравнение молекулярно – кинетической теории:
$$p=n k T(3)$$
где $n=frac{N}{V}$– концентрация молекул газа
(N – число частиц), k=1,38•10-23 Дж/К – постоянная Больцмана, T – абсолютная температура газа.
Гидростатическое давление
Гидростатическое давление – давление внутри столба жидкости или газа, находится по формуле:
$$p=p_{0}+rho g h(4)$$
где $rho$ – плотность вещества, g=9,8 м/с2 –
ускорение свободного падения, h- высота столба вещества. p0 – внешнее давление на газ или жидкость.
Искривление поверхностного слоя жидкости ведет к возникновению дополнительного давления на жидкость, тогда давление под искривленной
жидкостью определяется как:
$$p=p_{0}^{*}+2 sigma H(5)$$
где $mathrm{P}_{0}^{*}$ –поверхностное натяжение жидкости,p0* – давление под не искривлённым слоем жидкости,
H – средняя кривизна поверхности жидкости, вычисляемая по закону Лапласа:
$$H=frac{1}{2}left(frac{1}{R_{1}}+frac{1}{R_{2}}right)$$
R1, R2 – главные радиусы кривизны.
Единицы измерения давления
Основной единицей измерения давления в системе СИ является: [p]=Па (паскаль)
Внесистемные единицы давления: [p]=мм рт.ст.(миллиметр ртутного столба),мм в.ст (мм водяного столба),атмосфера,бар.
Па= Н/м2 и 1 бар=105 Па.
Техническая атмосфера ~1 бар. Физическая атмосфера 1,01 бар=760 мм рт.ст.. 1 мм рт.ст.=133 Па.
Примеры решения задач
Пример
Задание. Каково давление в море на глубине h=8,5 м, если атмосферное давление равно
p0=105 Па, плотность морской воды равна
$rho$=1,03•103 кг/м3
Решение. Основой для решения задачи служит выражение:
$$p=p_{0}+rho g h(1.1)$$
Все данные в задаче указаны в системе СИ, поэтому можно провести вычисления:
$p=10^{5}+1,03 cdot 10^{3} cdot 9,8 cdot 8,5=1,88 cdot 10^{5}$ (Па).
Ответ. $p=1,88 cdot 10^{5}$ (Па)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Каково давление струи на неподвижную плоскость, если струя воды ударяет ее под углом
$alpha$ к нормали
плоскости, и упруго отскакивает от нее без изменения скорости? Скорость струи v.
Решение. Сделаем рисунок.
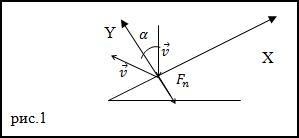
За время $Delta t$ о стенку ударяется масса воды равная:
$$m=l S rho=v Delta t S rho$$
где S – поперечное сечение струи, $rho$ – плотность воды. В соответствии с законом сохранения импульса имеем:
$$F Delta t=m Delta v rightarrow F=frac{m Delta v}{Delta t}(2.2)$$
где F – сила, с которой вода действует на стенку.
Примем за положительное направление нормали внешней к опоре и учитывая, что струя отскакивает от стены без потери скорости, получаем:
$$Delta v=v_{2} cos alpha-left(-v_{1} cos alpharight)=v_{2} cos alpha+v_{1} cos alpha=2 v cos alpha(2.3)$$
Подставим $Delta v$ из (2.3) в выражение (2.2), учтем выражение (2.1) имеем:
$$F=frac{m 2 v cos alpha}{Delta t}=frac{v Delta t S rho 2 v cos alpha}{Delta t}=2 operatorname{Sov}^{2} cos alpha(2.4)$$
В таком случае искомое давление струи на стенку будет равно:
$$p=frac{F_{n}}{S}=2 rho v^{2}$$
Ответ. $p=2 rho v^{2}$
Читать дальше: Формула закона Ома.
Формула для среднего давления газа на стенку сосуда
Это уравнение устанавливает связь между давлением p идеального газа, массой молекулы m0, концентрацией молекул n, средним значением квадрата скорости и средней кинетической энергией поступательного движения молекул. Его называют основным уравнением молекулярно-кинетической теории газов.
Таким образом, давление газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.
В основное уравнение молекулярно-кинетической теории газов входит произведение концентрации молекул n на среднюю кинетическую энергию поступательного движения. Если предположить, что газ находится в сосуде неизменного объема V, то (N – число молекул в сосуде) . В этом случае изменение давления Δp пропорционально изменению средней кинетической энергии. 
Как найти среднюю силу давления воды на боковую стенку сосуда?
Физика 7 класс
Анонимный вопрос
4 мая 2019 · 5,6 K
ОтветитьУточнить
Алена Щитова346
Безусловно, моя стихия – это семья, дети и кулинария. Однако образование и личный опыт… · 4 мая 2019
Расчитать давление жидкости на стенку сосуда, можно по формуле:
pгидр=ρ0gh2,
где ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота вертикальной стенки сосуда (столба жидкости).
5,0 K
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
Асламазов Л. Гидростатика // Квант. – 1995. – № 1. – С. 51-55.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Давление и силы давления
Жидкость оказывает давление на стенки сосуда, в котором она находится, или на любую другую поверхность, соприкасающуюся с ней. Давление – величина скалярная. Оно измеряется абсолютной величиной нормальной (перпендикулярной поверхности) силы, действующей со стороны жидкости на единицу площади поверхности:
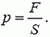
Давление в различных точках поверхности может быть разным. Поэтому площадь S мы должны брать достаточно маленькой.
По закону Паскаля давление жидкости не зависит от ориентации поверхности. Как бы ни была расположена поверхность в данном месте жидкости, давление на нее будет одним и тем же.
Сила давления всегда перпендикулярна поверхности. В обычных условиях она направлена так, как если бы жидкость стремилась расшириться.
Задача 1. В сосуд, имеющий форму куба с ребром a, налита доверху жидкость плотностью ρ. Определите силы давления жидкости на дно и стенки сосуда.
Давление жидкости на дно сосуда равно весу столба жидкости высотой a с площадью основания, равной единице: 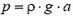 , где g – ускореннее свободного падения. (Для простоты здесь и в других задачах, где это специально не оговорено, предполагается, что атмосферное давление отсутствует). Сила давления на дно сосуда (рис. 1, а)
, где g – ускореннее свободного падения. (Для простоты здесь и в других задачах, где это специально не оговорено, предполагается, что атмосферное давление отсутствует). Сила давления на дно сосуда (рис. 1, а)
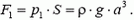
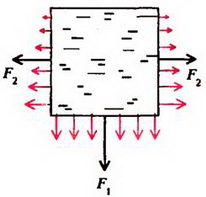
а

б
Рис. 1
Давление на боковую грань куба будет зависеть от расстояния до поверхности жидкости. На глубине h давление 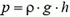 . Так как давление изменяется с глубиной по линейному закону (рис. 1. б), для определения силы давления мы должны среднее давление
. Так как давление изменяется с глубиной по линейному закону (рис. 1. б), для определения силы давления мы должны среднее давление
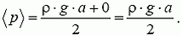
умножить на площадь боковой грани
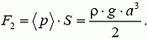
Задача 2. В цилиндрический сосуд диаметром D = 0,7 м вставлен поршень с длинной вертикальной трубкой диаметром d = 0,05 м (рис. 2). Максимальная сила трения между поршнем и стенками сосуда Fтp = 100 Н. Через трубку в сосуд наливают воду. При каком уровне воды в трубке H поршень начнет двигаться? Чему будет равна при этом сила давления воды на дно сосуда? Поршень расположен на высоте h = 0,2 м от дна сосуда. Плотность воды ρ = 103 кг/м3. Массой поршня с трубкой пренебречь.
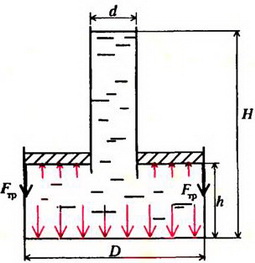
Рис. 2
Давление в жидкости на уровне поверхности поршня определяется расстоянием от этого уровня до свободной поверхности жидкости:
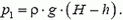
Поршень начнет двигаться, когда сила давления на него со стороны жидкости станет равной максимальной силе трения:
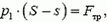
где 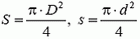 – плошали поперечных сечений сосуда и трубки соответственно. Подставляя сюда выражение для p1, находим
– плошали поперечных сечений сосуда и трубки соответственно. Подставляя сюда выражение для p1, находим
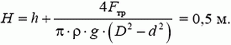
Давление на дно сосуда 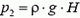 .
.
Сила давления 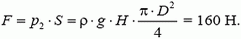
Задача 3. Длинная вертикальная труба с поршнем опущена одним концом в сосуд с водой. Вначале поршень находится у поверхности воды, затем его медленно поднимают. Как зависит сила, прикладываемая к поршню, от высоты h ее поднятия? Площадь поперечного сечения трубы S, атмосферное давление p0. Изменением уровня воды в сосуде, массой поршня и ею трением о стенки трубы пренебречь.
При поднятии поршня вода под действием атмосферного давления будет вначале заполнять трубу (рис 3, а). Давление в трубе на уровне жидкости в сосуде равно атмосферному давлению p0. Давление воды на поршень меньше атмосферного на величину веса столба жидкости высотой h и площадью основания, равной единице:
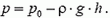
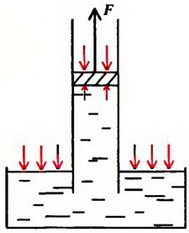
а
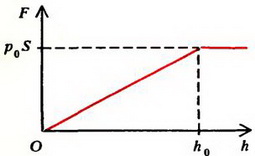
б
Рис. 3
Сверху на поршень по-прежнему действует атмосферное давление. Поэтому для удержания поршня на высоте h к нему надо приложить силу, равную
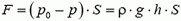
и направленную вверх.
С увеличением h давление воды на поршень будет уменьшаться. На высоте
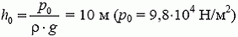
давление обратится в ноль. При дальнейшем поднятии поршня уровень воды в трубе изменяться не будет, тан как сила атмосферного давления, действующая на столб жидкости в трубе снизу, уравновесится силой тяжести. Для удержания поршня на высоте h > h0 к нему надо приложить силу 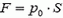 .
.
Зависимость прикладываемой к поршню силы F от высоты его поднятия h изображена графически на рисунке 3, б.
Высота столба воды в трубе 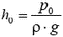 , очевидно, может служить для измерения атмосферного давлении p0. Однако обычно в барометрах используют ртуть, и нормальному атмосферному давлению тогда соответствует значительно меньшая высота столба ртути
, очевидно, может служить для измерения атмосферного давлении p0. Однако обычно в барометрах используют ртуть, и нормальному атмосферному давлению тогда соответствует значительно меньшая высота столба ртути 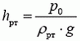 = 0,76 м (плотность ртути ρрт = 1,36×104 кг/м3).
= 0,76 м (плотность ртути ρрт = 1,36×104 кг/м3).
Примером другого гидростатического устройства, широко используемого в практике, являются сообщающиеся сосуды. Известен закон сообщающихся сосудов: если давление над жидкостью в сосудах одинаково, то уровни жидкости в них равны. Нетрудно доказать этот закон для случая цилиндрических сосудов (рис. 4). Так как жидкость в соединительной трубке находится в равновесии, то давления на нее с обеих сторон должны быть одинаковы. Поэтому равны и уровни жидкости в сосудах.
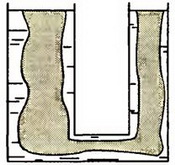
Рис. 4
В общем случае для доказательства закона сообщающихся сосудов можно воспользоваться принципом отвердевания, который часто используют в гидростатике. Суть этого принципа заключается в следующем: всегда можно представить себе, что часть жидкости отвердела – равновесие оставшейся части жидкости от этого не нарушится. Так, в цилиндрических сообщающихся сосудах мы можем мысленно выделить часть жидкости, которая заполняла бы сообщающиеся сосуды любой извилистой формы (см. рис. 4), и представить себе, что остальная часть жидкости отвердевает. Тогда равновесие выделенной нами части жидкости не нарушится, и, следовательно, уровни жидкости в извилистых сообщающихся сосудах будут такими же, какими были в цилиндрических сосудах, т.е. одинаковыми.
Закон сообщающихся сосудов справедлив только для однородной жидкости. Если в сосуды налиты жидкости разных плотностей, то уровни в сосудах могут быть разными.
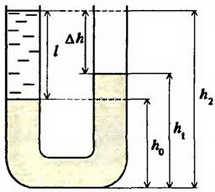
Задача 4. В U – образную трубку налита ртуть. Поверх ртути в одно из колен трубки налили воду (рис. 5, a). Высота столбика воды l = 0,1 м. Определите разность уровней жидкостей в коленах трубки. Нарисуйте график зависимости давления в обоих коленах трубки от высоты. Плотность ртути ρрт = 1,36×104 кг/м3, плотность воды ρрт = 103 кг/м3. Атмосферное давление не учитывайте.
а
б
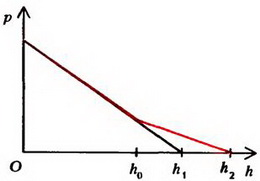
Рис. 5
Давления на ртуть на уровне ho соприкосновения воды и ртути в обоих коленах должны быть одинаковы (закон сообщающихся сосудов для однородной жидкости). Поэтому
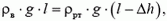
где разность уровней h2 – h1 обозначена через Δh. Отсюда
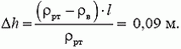
Давление в колене, содержащем только ртуть, меняется с высотой h по закону
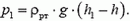
Эта формула справедлива и в изогнутой части трубки. (Представите себе, что изогнутое колено сообщается с прямым цилиндрическим сосудом, в котором тоже находится ртуть. Тогда давления на одинаковой высоте в обоих сосудах должны быть равны). В другом колене в области 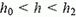 , где находится только вода, давление
, где находится только вода, давление
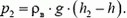
Ниже уровня h0 зависимость давления от высоты дается той же формулой, что и в первом колене:
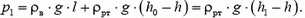
Зависимость давления в коленах трубки от высоты изображена графически на рисунке 5, б. Как видно, выше уровня h0 давления на одинаковой высоте разные.
Выталкивающая сила
На тело, погруженное в жидкость, как известно, действует выталкивающая сила. Эта сила является равнодействующей сил давления жидкости на тело. Найдем, например, выталкивающую силу, действующую на кубик с ребром a целиком погруженный в жидкость плотностью ρ. Сила давления со стороны жидкости на верхнюю грань кубика равна
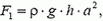
где h – расстояние от этой грани до поверхности жидкости (для простоты мы считаем, что плоскость верхней грани кубика параллельна поверхности жидкости). На нижнюю грань кубика действует сила
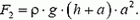
Силы давления на боковые грани кубика уравновешивают друг друга. Равнодействующая сил давлении, т.е. выталкивающая сила, равна
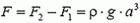
и направлена вертикально вверх. Мы получили закон Архимеда: выталкивающая сила равна силе тяжести, действующей на вытесненную телом жидкость.
В общем случае закон Архимеда можно доказать с помощью принципа отвердевания. Мысленно заменим погруженное тело жидкостью. Очевидно, что эта жидкость будет находиться в равновесии. Следовательно, сила тяжести, действующая на нее, уравновешена силами давления со стороны окружающей жидкости. Если теперь представить себе, что выделенная нами часть отвердела, то равновесие оставшейся части не нарушится, и поэтому не изменятся силы давления на отвердевшую жидкость. Равнодействующая этих сил будет по-прежнему равна силе тяжести.
При доказательстве мы считали, что тело целиком погружено в жидкость. Однако аналогичные рассуждения легко провести и в случае, когда только часть тела находится в жидкости (проделайте это сами). И мы опять получим, что выталкивающая сила равна силе тяжести, действующей на вытесненную телом жидкость:
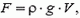
где ρ – плотность жидкости, V – объем погруженной в жидкость части тела, g –ускорение свободного падения.
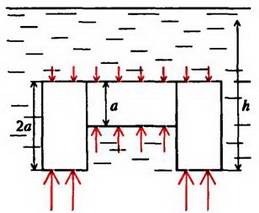
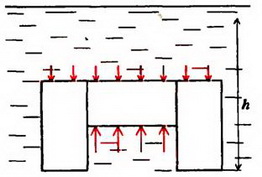
Задача 5. На дне водоема установлена П – образная конструкция из трех одинаковых балок, соединенных между собой (рис. 6). Как зависит сила давления этой конструкции на дно от уровня воды в водоеме? Рассмотрите два случая: 1) вода подтекает под опоры; 2) опоры плотно соприкасаются с дном. Балки имеют квадратное сечение со стороной a, длина балки l = 2a. Плотность материала балок ρ0. плотность воды ρ.
а
б
в
Рис. 6
Сила давления Fд на дно определяется разностью силы тяжести конструкции 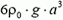 и выталкивающей силы F. В первом случае, когда вода подтекает под опоры (например, если дно водоема покрыто галькой – рисунок 6, а), справедлив закон Архимеда. Зависимость выталкивающей силы от высоты уровня воды h дается формулами:
и выталкивающей силы F. В первом случае, когда вода подтекает под опоры (например, если дно водоема покрыто галькой – рисунок 6, а), справедлив закон Архимеда. Зависимость выталкивающей силы от высоты уровня воды h дается формулами:
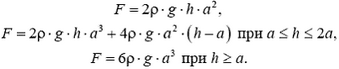
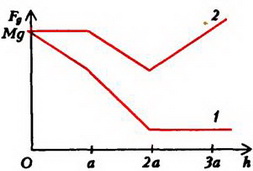
Соответствующий график для силы Fд изображен на рисунке 6, в – он обозначен цифрой 1.
Во втором случае отсутствует давление воды на опоры снизу (рис.6, б), и пользоваться законом Архимеда уже нельзя. Для определения силы F необходимо найти равнодействующую сил давления:
F = 0 при h ≤ a,
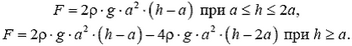
Последнее выражение обращается в нуль при 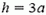 и при больших h становится отрицательным. Это означает, что при
и при больших h становится отрицательным. Это означает, что при 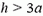 силы давления не выталкивают конструкцию из воды, а наоборот, прижимают ее ко дну. Зависимость силы давления на дно от высоты уровня воды показана на втором графике рисунка 6, в.
силы давления не выталкивают конструкцию из воды, а наоборот, прижимают ее ко дну. Зависимость силы давления на дно от высоты уровня воды показана на втором графике рисунка 6, в.
Задача 6. Пробковый кубик с ребром a = 0,1 м погрузили в воду на глубину h = 0,2 м с помощью тонкостенной трубки диаметром d = 0,05 м (рис. 7). Определите, какой груз надо положить в трубку, чтобы кубик от нее оторвался. Плотность пробки ρ0 = 200 кг/м3, плотность воды ρ = 103 кг/м3.
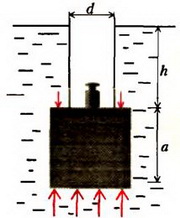
Рис. 7
Вес груза равен разности выталкивающей силы F действующей на кубик, и силы тяжести кубика 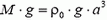 . Если бы кубик был окружен со всех сторон водой, то на него по закону Архимеда действовала бы выталкивающая сила
. Если бы кубик был окружен со всех сторон водой, то на него по закону Архимеда действовала бы выталкивающая сила 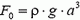 . В нашем случае выталкивающая сила будет большей, так как на часть поверхности верхней грани кубика, «заключенную» в трубку, не действует давление воды:
. В нашем случае выталкивающая сила будет большей, так как на часть поверхности верхней грани кубика, «заключенную» в трубку, не действует давление воды:
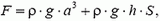
где 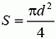 – площадь сечения трубки. Таким образом, сила тяжести грузика
– площадь сечения трубки. Таким образом, сила тяжести грузика
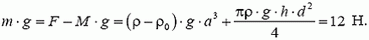
Масса грузика т = 1,2 кг.
Выталкивающую силу, действующую на кубик, можно найти и другим способом. Рассмотрим кубик с трубкой как единое тело, вытесняющее объем воды
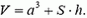
Тогда по закону Архимеда на кубик с трубкой действует выталкивающая сила
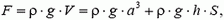
которая равна выталкивающей силе, действующей на кубик, так как равнодействующая сил давления воды на трубку равна нулю.
Жидкость в движущемся сосуде
Изучим теперь равновесие жидкости в сосуде, движущемся с ускорением. По второму закону Ньютона в этом случае векторная сумма всех сил, действующих на любой выделенный элемент жидкости, должна равняться 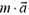 , где m – масса выделенной жидкости,
, где m – масса выделенной жидкости, 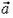 – ускорение сосуда. Но на выделенный элемент жидкости действуют сила тяжести и силы давления со стороны окружающей жидкости. Их равнодействующая и должна быть равна
– ускорение сосуда. Но на выделенный элемент жидкости действуют сила тяжести и силы давления со стороны окружающей жидкости. Их равнодействующая и должна быть равна 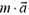 .
.
Задача 7. Сосуд с жидкостью плотностью ρ падает с ускорением a. Определите давление жидкости на глубине h и силу давления на дно сосуда. Высота уровня воды в сосуде H, площадь дна сосуда s.
Выделим столбик жидкости высотой h с площадью основания s. На него действуют сила тяжести 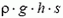 и сила давления
и сила давления 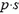 , направленная вверх. Равнодействующая этик сил создает ускорение столбика:
, направленная вверх. Равнодействующая этик сил создает ускорение столбика:
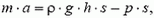
где 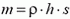 – масса столбика. Для давления p на глубине h отсюда находим
– масса столбика. Для давления p на глубине h отсюда находим
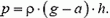
Сила давления на дно сосуда
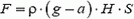
будет тем меньше, чем больше ускорение сосуда a. При 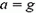 (свободное падение) сила давления жидкости обращается в ноль – наступает состояние невесомости. При
(свободное падение) сила давления жидкости обращается в ноль – наступает состояние невесомости. При 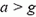 жидкость будет свободно падать с ускорением g, а сосуд – с большим ускорением, и вода вытечет из сосуда.
жидкость будет свободно падать с ускорением g, а сосуд – с большим ускорением, и вода вытечет из сосуда.
Задача 8. На дне сосуда с жидкостью лежит тело. Может ли тело всплыть, если сосуд начнет двигаться вверх с ускорением? Определите силу давления тела на дно сосуда, если ускорение сосуда a, плотность жидкости ρ0, плотность тела ρ, его объем V.
На тело, лежащее на дне сосуда, действуют сила тяжести mg сила реакции дна N и выталкивающая сила F (рис. 8). Если сосуд покоится, то сумма этих сил равняется нулю. При движении сосуда с ускорением a вверх по второму закону Ньютона имеем
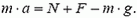
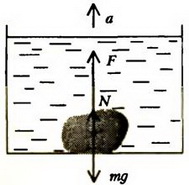
Рис. 8
Определим выталкивающую силу F. Аналогично решению предыдущей задачи, легко получить, что при ускоренном движении сосуда, вверх давление на глубине h дается формулой
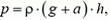
т.е. давление в 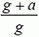 раз больше, чем в неподвижном сосуде. Соответственно будет большей и выталкивающая сила:
раз больше, чем в неподвижном сосуде. Соответственно будет большей и выталкивающая сила:
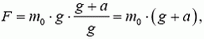
где 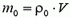 – масса вытесненной телом воды.
– масса вытесненной телом воды.
Подставляя это выражение в формулу второго закона Ньютона, для силы реакции дна получаем
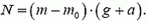
Легко видеть, что в сосуде, движущемся с ускорением вверх, сила реакции дна всегда больше, чем в неподвижном. Поэтому тело не только не всплывает, а наоборот, сильнее прижимается ко дну.
Задача 9. Сосуд с жидкостью движется горизонтально с ускорением a. Определите форму поверхности жидкости в сосуде.
Выделим горизонтальный столбик жидкости длиной l и площадью поперечного сечения S (рис. 9). По второму закону Ньютона
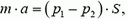
где 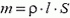 – масса столбика, p1 и p2 – давления на него слева и справа.
– масса столбика, p1 и p2 – давления на него слева и справа.
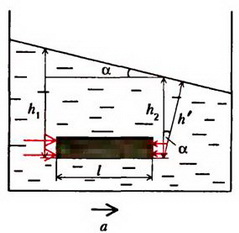
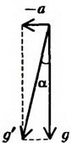
Рис. 9
Давление на глубине h определяется по обычной формуле 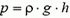 (по вертикали ускорения нет). Подставляя выражения для m и p в уравнение второго закона Ньютона, получаем
(по вертикали ускорения нет). Подставляя выражения для m и p в уравнение второго закона Ньютона, получаем
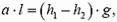
или
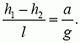
Но  – это разность высот точек поверхности жидкости. Мы получаем, что поверхность жидкости – плоскость, наклоненная к горизонту под углом α, причем
– это разность высот точек поверхности жидкости. Мы получаем, что поверхность жидкости – плоскость, наклоненная к горизонту под углом α, причем 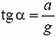 .
.
Заметим, что давление жидкости на данной высоте здесь не одно и то же. Линии равного давления параллельны поверхности жидкости. Если ввести расстояние h´ от точки до поверхности жидкости, то давление в этой точке
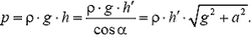
Поэтому можно сказать, что ускоренное движение сосуда эквивалентно замене ускорения свободного падения 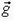 на величину
на величину 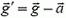 . Это утверждение в равной степени относится и к предыдущим двум задачам.
. Это утверждение в равной степени относится и к предыдущим двум задачам.
Упражнения
1. Три сосуда, имеющие формы цилиндра, усеченного конуса и перевернутого усеченного конус с одинаковыми площадями оснований и рапными объемами, доверху наполнены водой. Как соотносятся между собой силы давлении воды на дно сосудов?
2. Трубка ртутного барометра подвешена нити. Определите натяжение нити, если высота уровня ртути и трубке Н = 0,76 м, внешний диаметр трубки D = 0,02 м, внутренний d = 0,017 м. нижний конец трубки погружен в ртуть на глубину h = 0,1 м, масса трубки m = 0,3 кг, плотность ртути ρ = 1,36×104 кг/м4. Считайте, что торцы трубки плоские.
3. Длинная вертикальная трубка погружена одним концом в сосуд с ртутью. В трубку наливают m = 0,71 кг воды, которая не вытекает из трубки. Определите изменение уровня ртути и сосуде. Диаметр сосуда D = 0,06 м, плотность ртути ρ = 1,36×104 кг/м4. Толщиной стоим трубки пренебречь.
4. В сосуде с водой плавает кусок льда. Изменится ли уровень воды в сосуде, если лед растает? Что будет, если в лед вморожен а) кусочек свинца: б) кусочек пробки?
5. В цилиндрические сообщающиеся сосуды диаметрами D = 0,06 м и d = 0,02 м налита вода. Как изменятся уровни воды в сосудах, если в один из сосудов поместить тело массой т = 0,02 кг, которое будет плавать в воде? Плотность воды ρ = 103 кг/м3.
6. Сосуд с водой скользит без трения по наклонной плоскости с углом наклона α. Определите, как расположится поверхность воды и сосуде.
Ответы
1. Сила давления на дно наибольшая у сосуда, имеющего форму усеченного конуса, наименьшая – у перевернутого конуса.
2. 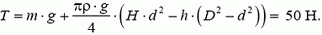
3. 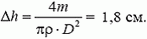
4. Если лед чистый или в него вморожен кусочек пробки, то уровень воды не изменится. Если же в лед вморожен кусочек свинца, уровень воды понизится.
5. 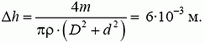
6. Поверхность параллельна наклонной плоскости.
Гидростатическое давление: формула и свойства.

Гидростатическое давление – это давление, производимое на жидкость силой тяжести.
Гидростатикой называется раздел гидравлики, в котором изучаются законы равновесия жидкостей и рассматривается практическое приложение этих законов.
Для того, чтобы понять гидростатику необходимо определиться в некоторых понятиях и определениях.
В этой статье мы подготовили для Вас, всю необходимую информацию о гидростатическом давлении, начиная от закона Паскаля и определения формулы гидростатического давления и до свойств давления и применения законов гидростатики в повседневной жизни.
Содержание
- Закон Паскаля для гидростатики.
- Определение и формула гидростатического давления
- Сила гидростатического давления
- Измерение гидростатического давления
- Свойства гидростатического давления
Закон Паскаля для гидростатики.
В 1653 году французским ученым Б. Паскалем был открыт закон, который принято называть основным законом гидростатики.
Звучит он так:
Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.
Закон Паскаля легко понимается если взглянуть на молекулярное строение вещества. В жидкостях и газах молекулы обладают относительной свободой, они способны перемещаться друг относительно друга, в отличии от твердых тел. В твердых телах молекулы собраны в кристаллические решетки.
Относительная свобода, которой обладают молекулы жидкостей и газов, позволяет передавать давление производимое на жидкость или газ не только в направлении действия силы, но и во всех других направлениях.
Закон Паскаля для гидростатики нашел широкое распространение в промышленности. На этом законе основана работа гидроавтоматики, управляющей станками с ЧПУ, автомобилями и самолетами и многих других гидравлических машин.
Определение и формула гидростатического давления
Из описанного выше закона Паскаля вытекает, что:
Величина гидростатического давления не зависит от формы сосуда, в котором находится жидкость и определяется произведением
P = ρ& #215; g × h , где
ρ – плотность жидкости
g – ускорение свободного падения
h – глубина, на которой определяется давление.

Для иллюстрации этой формулы посмотрим на 3 сосуда разной формы.
Во всех трёх случаях давление жидкости на дно сосуда одинаково.
Полное давление жидкости в сосуде равно
P = P0 + ρ × g × h , где
P0 – давление на поверхности жидкости. В большинстве случаев принимается равным атмосферному.
Сила гидростатического давления
Выделим в жидкости, находящейся в равновесии, некоторый объем, затем рассечем его произвольной плоскостью АВ на две части и мысленно отбросим одну из этих частей, например верхнюю. При этом мы должны приложить к плоскости АВ силы, действие которых будет эквивалентно действию отброшенной верхней части объема на оставшуюся нижнюю его часть.

Рассмотрим в плоскости сечения АВ замкнутый контур площадью ΔF, включающий в себя некоторую произвольную точку a. Пусть на эту площадь воздействует сила ΔP.
Тогда гидростатическое давление формула которого выглядит как
Рср = ΔP / ΔF
представляет собой силу, действующую на единицу площади, будет называться средним гидростатическим давлением или средним напряжением гидростатического давления по площади ΔF.
Истинное давление в разных точках этой площади может быть разным: в одних точках оно может быть больше, в других – меньше среднего гидростатического давления. Очевидно, что в общем случае среднее давление Рср будет тем меньше отличаться от истинного давления в точке а, чем меньше будет площадь ΔF, и в пределе среднее давление совпадет с истинным давлением в точке а.
Для жидкостей, находящихся в равновесии, гидростатическое давление жидкости аналогично напряжению сжатия в твердых телах.
Единицей измерения давления в системе СИ является ньютон на квадратный метр (Н/м2) – её называют паскалем (Па). Поскольку величина паскаля очень мала, часто применяют укрупненные единицы:
килоньютон на квадратный метр – 1кН/м2 = 1×103 Н/м2
меганьютон на квадратный метр – 1МН/м2 = 1×106 Н/м2
Давление равное 1×105 Н/м2 называется баром (бар).
В физической системе единицей намерения давления является дина на квадратный сантиметр (дина/м2), в технической системе – килограмм-сила на квадратный метр (кгс/м2). Практически давление жидкости обычно измеряют в кгс/см2, а давление равное 1 кгс/см2 называется технической атмосферой (ат).
Между всеми этими единицами существует следующее соотношение:
1ат = 1 кгс/см2 = 0,98 бар = 0,98 × 105 Па = 0,98 × 106дин = 104 кгс/м2
Следует помнить что между технической атмосферой (ат) и атмосферой физической (Ат) существует разница. 1 Ат = 1,033 кгс/см2 и представляет собой нормальное давление на уровне моря. Атмосферное давление зависит от высоты расположения места над уровнем моря.
Измерение гидростатического давления

На практике применяют различные способы учета величины гидростатического давления. Если при определении гидростатического давления принимается во внимание и атмосферное давление, действующее на свободную поверхность жидкости, его называют полным или абсолютным. В этом случае величина давления обычно измеряется в технических атмосферах, называемых абсолютными (ата).
Часто при учете давления атмосферное давление на свободной поверхности не принимают во внимание, определяя так называемое избыточное гидростатическое давление, или манометрическое давление, т.е. давление сверх атмосферного.
Манометрическое давление определяют как разность между абсолютным давлением в жидкости и давлением атмосферным.
Рман = Рабс – Ратм
и измеряют также в технических атмосферах, называемых в этом случае избыточными.
Случается, что гидростатическое давление в жидкости оказывается меньше атмосферного. В этом случае говорят, что в жидкости имеется вакуум. Величина вакуума равняется разнице между атмосферным и и абсолютным давлением в жидкости
Рвак = Ратм – Рабс
и измеряется в пределах от нуля до атмосферы.
Свойства гидростатического давления

Гидростатическое давление воды обладает двумя основными свойствами:
 Оно направлено по внутренней нормали к площади, на которую действует;
Оно направлено по внутренней нормали к площади, на которую действует; Величина давления в данной точке не зависит от направления (т.е. от ориентированности в пространстве площадки, на которой находится точка).
Величина давления в данной точке не зависит от направления (т.е. от ориентированности в пространстве площадки, на которой находится точка).
Первое свойство является простым следствием того положения, что в покоящейся жидкости отсутствуют касательные и растягивающие усилия.
Предположим, что гидростатическое давление направлено не по нормали, т.е. не перпендикулярно, а под некоторым углом к площадке. Тогда его можно разложить на две составляющие – нормальную и касательную. Наличие касательной составляющей из-за отсутствия в покоящейся жидкости сил сопротивления сдвигающим усилиям неизбежно привело бы к движению жидкости вдоль площадки, т.е. нарушило бы её равновесие.
Поэтому единственным возможным направлением гидростатического давления является его направление по нормали к площадке.
Если предположить что гидростатическое давление направлено не по внутренней, а по внешней нормали, т.е. не внутрь рассматриваемого объекта а наружу от него, то вследствие того, что жидкость не оказывает сопротивления растягивающим усилиям – частицы жидкости пришли бы в движение и её равновесие было бы нарушено.
Следовательно, гидростатическое давление воды всегда направлено по внутренней нормали и представляет собой сжимающее давление.
Из этого же правило следует, что если измениться давление в какой-то точке, то на такую же величину измениться давление в любой другой точке этой жидкости. В этом заключается закон Паскаля, который формулируется следующим образом: Давление производимое на жидкость, передается внутри жидкости во все стороны с одинаковой силой.
На применение этого закона основываются действие машин, работающих под гидростатическим давлением.

![]()
Ещё одним фактором влияющим на величину давления является вязкость жидкости, которой до недавнего времени приято было пренебрегать. С появлением агрегатов работающих на высоком давлении вязкость пришлось так же учитывать. Оказалось, что при изменении давления, вязкость некоторых жидкостей, таких как масла, может изменяться в несколько раз. А это уже определяет возможность использовать такие жидкости в качестве рабочей среды.
Вместе со статьей “Гидростатическое давление: определение, формула и свойства.” смотрят:

Закон Паскаля для газов и жидкостей в гидростатике

Уравнение Бернулли для потока и струйки жидкости

Гидростатический парадокс и сила давления на стенку
