Как найти среднее гармоническое четырех чисел - Сайт, где вы сможете решить свои вопросы

Среднее гармоническое

Среднее гармоническое — один из способов определения среднего значения числового ряда (наряду с медианой и средним арифметическим). Мы сделали калькулятор, который может рассчитать среднее гармоническое двух, трех — да любого количества чисел.

Рассчитывается среднее гармоническое по простой формуле и является обратной величиной к среднему от обратных к числам.

Среднее гармоническое удобно применять для решения задач, которые начинаются словами «первую половину пути автомобиль проехал со скоростью…». Например, первую половину пути автомобиль проехал со скоростью 60 км/ч вторую 90 км/ч. Найдите среднюю скорость. Просто введите в калькулятор два числа — 60 и 90 и получите ответ — 72 км/ч.

Калькулятор среднего гармонического

Как найти среднее гармоническое чисел

Лучше показать это на примере. Найдем среднее гармоническое двух чисел 1 и 2. Подставив значения в формулу получим такое выражение:

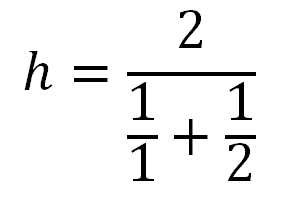
Здесь в числителе количество чисел (2), а в знаменателе сами числа. В результате расчета получаем, что среднее геометрическое чисел 1 и 2 равно 1,6666… или 1,(6).

Ваша оценка

[Оценок: 162 Средняя: 3.1]

Среднее гармоническое Автор admin средний рейтинг 3.1/5 – 162 рейтинги пользователей

Источник

Онлайн калькулятор для расчета среднего гармонического двух, трех, четырех и более чисел. Средняя гармоническая величина ( или Среднее гармоническое ) получается от деления числа данных величин на сумму величин обратных данным.

Формулы для нахождения среднего гармонического: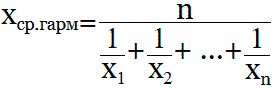

Формула средней гармонической взвешенной:

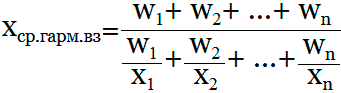
Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также

Источник

Среднее гармоническое

Главная
/
Математика
/
Арифметика
/
Среднее гармоническое

Чтобы найти среднее гармоническое нескольких чисел воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Среднее гармоническое:

Округление ответа:

Просто введите положительные числа и получите среднее гармоническое этих чисел. Для того чтобы добавить в ряд более двух чисел воспользуйтесь зелёной кнопкой “+”.

Теория

Средним гармоническим H_{(X₁,…,X_n)} двух и более чисел является обратная величина к среднему арифметическому их обратных.

Формула

H_{(x₁,…,x_n)}	=	n
¹⁄_x₁ + ¹⁄_x₂ + … + ¹⁄_{x_n}

Примеры

Для чего служит средняя гармоническая чисел? К примеру, для определения средней скорости:

Среднее гармоническое двух чисел

Представим, что автомобиль проехал некий путь, при этом первые полпути он ехал со скоростью 80 км/ч, а вторые полпути – со скоростью 20 км/ч. И нам надо определить его среднюю скорость. Для этого нам понадобится найти среднее гармоническое для двух чисел: 80 и 20.

H_{(80, 20)}	=	2	=	2	= 32
¹⁄₈₀ + ¹⁄₂₀	0.0125 + 0.05

Таким образом, средняя скорость автомобиля равна 32 км/ч.

Среднее гармоническое трех чисел

Если же наш автомобиль треть пути ехал со скоростью 80 км/ч, треть – со скоростью 20 км/ч и треть со скоростью 8 км/ч, то его среднюю скорость определяем так:

H_{(80, 20, 8)}	=	3	=	3	= 16 км/ч
¹⁄₈₀ + ¹⁄₂₀ + ¹⁄₈	0.0125 + 0.05 + 0.125

См. также

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 ноября 2022 года; проверки требуют 2 правки.

Сре́днее гармони́ческое — один из способов, которым можно понимать «среднюю» величину некоторого набора чисел. Его можно определить следующим образом: пусть даны положительные числа $x_{1},ldots ,x_{n}$ , тогда их средним гармоническим будет такое число , что

${displaystyle {frac {n}{H}}={frac {1}{x_{1}}}+ldots +{frac {1}{x_{n}}}}$

Можно получить явную формулу для среднего гармонического:

${displaystyle H(x_{1},ldots ,x_{n})={frac {n}{{frac {1}{x_{1}}}+{frac {1}{x_{2}}}+cdots +{frac {1}{x_{n}}}}}={frac {n}{sum limits _{i=1}^{n}{frac {1}{x_{i}}}}}}$

т. е. среднее гармоническое есть обратная величина к среднему от обратных к числам $x_{1},ldots ,x_{n}$ .

Свойства[править | править код]

Среднее гармоническое действительно является «средним», в том смысле что ${displaystyle min(x_{1},ldots ,x_{n})leqslant H(x_{1},ldots ,x_{n})leqslant max(x_{1},ldots ,x_{n})}$ .
Вообще, среднее гармоническое является средним степени -1.
Среднее гармоническое двойственно среднему арифметическому в следующем смысле:

${displaystyle H(x_{1},ldots ,x_{n})=A^{-1}(x_{1}^{-1},ldots ,x_{n}^{-1})}$

${displaystyle A(x_{1},ldots ,x_{n})=H^{-1}(x_{1}^{-1},ldots ,x_{n}^{-1})}$

(когда последнее определено).

Неравенство о средних утверждает, что среднее гармоническое чисел не превосходит среднее геометрическое, среднее арифметическое и среднее квадратическое, причём все средние равны только в случае равенства всех чисел ${displaystyle x_{1}=ldots =x_{n},}$ то есть:

{displaystyle Hleqslant Gleqslant Aleqslant S,}

где

— среднее гармоническое;

— среднее геометрическое;

— среднее арифметическое;

— среднее квадратическое.

Среднее гармоническое взвешенное[править | править код]

Пусть есть набор неотрицательных чисел $x_{1},ldots ,x_{n}$ и набор чисел $w_{1},ldots ,w_{n}$ , где $w_{i}$ называется весом величины $x_{i}$ . Тогда их взвешенным средним гармоническим называется число

${displaystyle H=sum _{i=1}^{n}w_{i}{bigg /}sum _{i=1}^{n}{frac {w_{i}}{x_{i}}}={dfrac {w_{1}+w_{2}+ldots +w_{n}}{w_{1}/x_{1}+w_{2}/x_{2}+ldots +w_{n}/x_{n}}}.}$

Из формулы следует, что при ${displaystyle w_{1}=ldots =w_{n}neq 0}$ (когда все величины «равноправны») получается обычное среднее гармоническое.

У трапеции длина отрезка, проходящего через точку пересечения диагоналей параллельно основаниям, равна среднему гармоническому длин оснований^[1]

Диаметры заполненных аквамариновым цветом кругов, называемых кругами-близнецами^[en], одинаковые и равны среднему гармоническому радиусов полуокружностей, построенных на отрезках AB и BC как на диаметрах.

Приложения и примеры[править | править код]

В статистике среднее гармоническое применяется в случае, когда наблюдения, для которых требуется получить среднее арифметическое, заданы обратными значениями.

В формуле тонкой линзы удвоенное фокусное расстояние равно среднему гармоническому расстояния от линзы до предмета и расстояния от линзы до изображения. Подобным образом среднее гармоническое входит и в аналогичную формулу для сферического зеркала.

Средняя скорость на пути, разделенном на равные участки, скорость на которых постоянна, равна среднему гармоническому скоростей на этих участках пути. Более обще, если путь разбит на участки, скорость на каждом из которых постоянна, то средняя скорость будет равна взвешенному среднему гармоническому скоростей (каждая скорость идет с весом, равным длине соответствующего ей отрезка).

Средняя плотность сплава равна взвешенному среднему гармоническому плотностей сплавляемых веществ (веса — массы частей соответствующих веществ).

Сопротивление, получающееся при параллельном подключении нескольких резисторов, равно среднему гармоническому их сопротивлений, деленному на их количество. Аналогичное утверждение верно для емкостей последовательно соединенных конденсаторов.

Примечания[править | править код]

↑ Роу С. Геометрические упражнения с куском бумаги. — 2-е изд. — Одесса: Матезис, 1923. — С. 65. Архивная копия от 24 мая 2012 на Wayback Machine

См. также[править | править код]

Гармоническая пропорция
Гармонический ряд

Ссылки[править | править код]

Weisstein, Eric W. Harmonic Mean / MathWorld–A Wolfram Web Resource

Источник

Download Article

The harmonic mean is a way to calculate the mean, or average, of a set of numbers. Using the harmonic mean is most appropriate when the set of numbers contains outliers that might skew the result. Most people are familiar with calculating the arithmetic mean, in which the sum of values is divided by the number of values. Calculating the harmonic mean is a little more complicated. If working with a small set of numbers you may be able to solve by hand using the formula. Otherwise, you can easily use Microsoft Excel to find the harmonic mean.

1

Set up the formula for the harmonic mean. The formula is ${frac {n}{{frac {1}{a_{{1}}}}+{frac {1}{a_{{2}}}}+{frac {1}{a_{{3}}}}+...+{frac {1}{a_{{n}}}}}}$ , where is the number of values in the set of numbers, and $a_{{1}}$ , $a_{{2}}$ , $a_{{3}}...$ are the values in the set.^[1]
2
Determine the values you need to find the harmonic mean for. This can be any set of numbers.^[2]
- For example, you may need to find the harmonic mean for the numbers 10, 12, 16, and 8.
Advertisement
3
Plug the value of into the formula. This will equal the number of values in your set.
- For example, if you are finding the harmonic mean of the numbers 10, 12, 16, and 8, you are working with 4 values, the numerator of your formula will be 4:
  ${frac {4}{{frac {1}{a_{{1}}}}+{frac {1}{a_{{2}}}}+{frac {1}{a_{{3}}}}+...+{frac {1}{a_{{n}}}}}}$
4

Plug the values your are averaging into your formula. You will take the reciprocal of each number and add them in the denominator of the formula. Remember, when you take the reciprocal of a whole number, you turn the number into a fraction by placing a 1 in the numerator and the whole number in the denominator.^[3]

1
Add the fractions in the denominator. You can use a calculator, or add them up by hand. If you are not using a calculator, remember to find a common denominator first. To learn more about adding fractions, read Add Fractions.
- For example:
  ${frac {4}{{frac {1}{10}}+{frac {1}{12}}+{frac {1}{16}}+{frac {1}{8}}}}={frac {4}{{frac {89}{240}}}}$
2

Divide the numerator by the denominator. Remember that dividing by a fraction is the same as multiplying by its reciprocal.^[4]
3

Convert to a decimal to find the harmonic mean of your set of numbers. To convert a fraction to a decimal, divide the numerator by the denominator.^[5]

1
Enter the values into your spreadsheet. Make sure to only place one value in each cell.
- For example, if you need to find the harmonic mean of 10, 12, 16, and 8, you might type each of these values into a separate cell in the spreadsheet, cells A1-A4.
2
Enter the function for the harmonic mean. The function is HARMEAN(number 1, [number 2]…).^[6] To select the function, begin typing “=HARMEAN” into a blank cell of the spreadsheet, then double-click on the function when it pops up.
- For example, type “=HARMEAN” into cell A5 of your spreadsheet and double-click on the function.
3
Highlight the cells containing the values you are averaging. Hit the enter key. Excel will calculate the harmonic mean for you and display it in the spreadsheet.
- For example, highlight cells A1-A4 of your spreadsheet and hit enter. Excel will calculate 10.78652 as the harmonic mean.

Add New Question

Question

What are the harmonic means of 5, 6 and 7?

3/(1/5+1/6+1/7) = 3/(42/210 + 35/210 + 30/210 ) = 3/( 107/210) = 3 x 210/107= 630/107 = 5.89
Question

What is the harmonic mean of x1,x2,x3.xn?

This is just asking for the formula: n/(1/x1 + 1/x2 + 1/x3 +…+1/xn)
Question

Can you tell me the harmonic mean of 0 2 4 6?

There’s no harmonic mean when zero is one of the values in the set. That’s because the formula would have 1/0 as one of the terms in the denominator, and 1/0 is infinity and not usable.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

To calculate the harmonic meaning, start by determining the number of values in your set of numbers. For example, if you’re working with 10, 12, 16, and 8, you have 4 numbers, so the value is 4. Then, rewrite the numbers you’re working with as denominators over the number 1. For example, if you’re working with 10, 12, 16, and 8, write them as 1/10, 1/12, 1/16, and 1/8. Then, divide 4 by the sum of the fractions to find the harmonic mean. To calculate the harmonic meaning using a calculator, keep reading!

Did this summary help you?

Thanks to all authors for creating a page that has been read 147,288 times.

Reader Success Stories

Monahil Monahil

Jul 17, 2017

“Very useful and helpful. You must read this article. It is a very simple way of solving problems.”

Did this article help you?

Источник

Калькулятор среднего гармонического

Как найти среднее гармоническое чисел

Смотрите также

Среднее гармоническое

Онлайн калькулятор

Теория

Формула

Примеры

Среднее гармоническое двух чисел

Среднее гармоническое трех чисел

См. также

Свойства[править | править код]

Среднее гармоническое взвешенное[править | править код]

Приложения и примеры[править | править код]

Примечания[править | править код]

См. также[править | править код]

Ссылки[править | править код]

Video

References

About This Article

Reader Success Stories

Did this article help you?

Вам также может понравиться

Как по двум проекциям найти третью

Как найти человека в ростове ярославском

Как найти клиентов в турагентство

Добавить комментарий Отменить ответ