Как найти среднее гармоническое в трапеции – Сайт, где вы сможете решить свои вопросы

Утверждение 1

Отрезок, проходящий через точку пересечения диагоналей трапеции параллельно основаниям, делится этой точкой пополам.

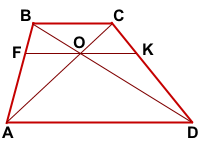otrezok-cherez-tochku-peresecheniya-diagonalej-trapecii Дано: ABCD — трапеция, AD||BC,

AC∩BD=O, F∈AB, K∈CD,

FK||AD, O∈FK

Доказать: O — середина FK.

Доказательство:

1-й способ доказательства

Рассмотрим треугольники AOD и COB.

∠AOD=∠COB (как вертикальные),

∠DAO=∠BCO (как внутренние накрест лежащие при AD||BC и секущей AC).

Значит, треугольники AOD и COB подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

$[ frac{{AD}}{{BC}} = frac{{AO}}{{OC}} = frac{{DO}}{{BO}}. ]$

Обозначим AD=a, BC=b, тогда

$[ frac{a}{b} = frac{{AO}}{{OC}} = frac{{DO}}{{BO}}. ]$

Рассмотрим треугольники ABC и FBO.

∠B — общий,

∠BAD=∠BFO (как внутренние накрест лежащие при AD||FK и секущей AB).

Значит, треугольники ABC и FBO подобны (по двум углам).

Следовательно,

$[ frac{{AD}}{{FO}} = frac{{BD}}{{BO}}. ]$

$[ frac{{AD}}{{FO}} = frac{{BD}}{{BO}} = frac{{DO + BO}}{{BO}} = frac{{DO}}{{BO}} + frac{{BO}}{{BO}} = frac{{DO}}{{BO}} + 1, ]$

$[ frac{a}{{FO}} = frac{a}{b} + 1, Rightarrow frac{a}{{FO}} = frac{{a + b}}{b}, ]$

откуда

$[ FO = frac{{ab}}{{a + b}}. ]$

Аналогично, треугольники ACD и ОСК подобны и

$[ frac{{AD}}{{OK}} = frac{{AC}}{{OC}}. ]$

Отсюда

$[ frac{{AD}}{{OK}} = frac{{AO + OC}}{{OC}} = frac{{AO}}{{OC}} + frac{{OC}}{{OC}} = frac{{AO}}{{OC}} + 1, ]$

$[ frac{a}{{OK}} = frac{a}{b} + 1, Rightarrow frac{a}{{OK}} = frac{{a + b}}{b}, ]$

$[ OK = frac{{ab}}{{a + b}}. ]$

Следовательно, FO=OK, то есть точка O — середина отрезка FK.

Что и требовалось доказать.

В ходе доказательства выразили длины FO и OK через длины оснований. Отсюда можно получить формулу для нахождения длины FK.

Утверждение 2

Длина отрезка, проходящего через точку пересечения диагоналей трапеции параллельно её основаниям, равна частному от деления удвоенного произведения длин оснований на сумму оснований:

$[ FK = frac{{2 cdot AD cdot BC}}{{AD + BC}}, ]$

или

$[ FK = frac{{2ab}}{{a + b}}. ]$

Определение.

Средним гармоническим нескольких положительных чисел называют число, обратное среднему арифметическому чисел, обратных данным.

Для чисел x₁, x₂,…, x_n среднее гармоническое

$[ h = frac{1}{{(frac{1}{{x_1 }} + frac{1}{{x_2 }} + ... + frac{1}{{x_n }}):n}} = frac{n}{{frac{1}{{x_1 }} + frac{1}{{x_2 }} + ... + frac{1}{{x_n }}}}. ]$

Так как

$[ frac{1}{{(frac{1}{a} + frac{1}{b}):2}} = frac{1}{{frac{{b + a}}{{ab}}:2}} = frac{{2ab}}{{a + b}}, ]$

Длина отрезка, проходящего через точку пересечения диагоналей трапеции параллельно её основаниям, равна среднему гармоническому длин оснований.

2-й способ доказательства

Доказать, что что медиана, проведённая к стороне треугольника, делит пополам любой отрезок, параллельный этой стороне, с концами на двух других сторонах треугольника.
Доказать замечательное свойство трапеции: точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции и середины оснований трапеции лежат на одной прямой.

Тогда в треугольнике, две вершины которого — концы большего основания трапеции, а третья — точка пересечения продолжения боковых сторон трапеции, отрезок, соединяющий точку пересечения продолжения боковых сторон трапеции с серединой большего основания — медиана. А значит, она пополам делит отрезок, проходящий через точку пересечения диагоналей трапеции параллельно её основаниям.

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 ноября 2022 года; проверки требуют 2 правки.

Сре́днее гармони́ческое — один из способов, которым можно понимать «среднюю» величину некоторого набора чисел. Его можно определить следующим образом: пусть даны положительные числа $x_{1},ldots ,x_{n}$ , тогда их средним гармоническим будет такое число $H$ , что

${displaystyle {frac {n}{H}}={frac {1}{x_{1}}}+ldots +{frac {1}{x_{n}}}}$ .

Можно получить явную формулу для среднего гармонического:

${displaystyle H(x_{1},ldots ,x_{n})={frac {n}{{frac {1}{x_{1}}}+{frac {1}{x_{2}}}+cdots +{frac {1}{x_{n}}}}}={frac {n}{sum limits _{i=1}^{n}{frac {1}{x_{i}}}}}}$ ,

т. е. среднее гармоническое есть обратная величина к среднему от обратных к числам $x_{1},ldots ,x_{n}$ .

Свойства[править | править код]

Среднее гармоническое действительно является «средним», в том смысле что ${displaystyle min(x_{1},ldots ,x_{n})leqslant H(x_{1},ldots ,x_{n})leqslant max(x_{1},ldots ,x_{n})}$ .
Вообще, среднее гармоническое является средним степени -1.
Среднее гармоническое двойственно среднему арифметическому в следующем смысле:

${displaystyle H(x_{1},ldots ,x_{n})=A^{-1}(x_{1}^{-1},ldots ,x_{n}^{-1})}$ и

${displaystyle A(x_{1},ldots ,x_{n})=H^{-1}(x_{1}^{-1},ldots ,x_{n}^{-1})}$ (когда последнее определено).

Неравенство о средних утверждает, что среднее гармоническое чисел не превосходит среднее геометрическое, среднее арифметическое и среднее квадратическое, причём все средние равны только в случае равенства всех чисел ${displaystyle x_{1}=ldots =x_{n},}$ то есть:

${displaystyle Hleqslant Gleqslant Aleqslant S,}$

где $H$ — среднее гармоническое;

$G$ — среднее геометрическое;

$A$ — среднее арифметическое;

$S$ — среднее квадратическое.

Среднее гармоническое взвешенное[править | править код]

Пусть есть набор неотрицательных чисел $x_{1},ldots ,x_{n}$ и набор чисел $w_{1},ldots ,w_{n}$ , где $w_{i}$ называется весом величины $x_{i}$ . Тогда их взвешенным средним гармоническим называется число

${displaystyle H=sum _{i=1}^{n}w_{i}{bigg /}sum _{i=1}^{n}{frac {w_{i}}{x_{i}}}={dfrac {w_{1}+w_{2}+ldots +w_{n}}{w_{1}/x_{1}+w_{2}/x_{2}+ldots +w_{n}/x_{n}}}.}$

Из формулы следует, что при ${displaystyle w_{1}=ldots =w_{n}neq 0}$ (когда все величины «равноправны») получается обычное среднее гармоническое.

У трапеции длина отрезка, проходящего через точку пересечения диагоналей параллельно основаниям, равна среднему гармоническому длин оснований^[1]

Диаметры заполненных аквамариновым цветом кругов, называемых кругами-близнецами^[en], одинаковые и равны среднему гармоническому радиусов полуокружностей, построенных на отрезках AB и BC как на диаметрах.

Приложения и примеры[править | править код]

В статистике среднее гармоническое применяется в случае, когда наблюдения, для которых требуется получить среднее арифметическое, заданы обратными значениями.

В формуле тонкой линзы удвоенное фокусное расстояние равно среднему гармоническому расстояния от линзы до предмета и расстояния от линзы до изображения. Подобным образом среднее гармоническое входит и в аналогичную формулу для сферического зеркала.

Средняя скорость на пути, разделенном на равные участки, скорость на которых постоянна, равна среднему гармоническому скоростей на этих участках пути. Более обще, если путь разбит на участки, скорость на каждом из которых постоянна, то средняя скорость будет равна взвешенному среднему гармоническому скоростей (каждая скорость идет с весом, равным длине соответствующего ей отрезка).

Средняя плотность сплава равна взвешенному среднему гармоническому плотностей сплавляемых веществ (веса — массы частей соответствующих веществ).

Сопротивление, получающееся при параллельном подключении нескольких резисторов, равно среднему гармоническому их сопротивлений, деленному на их количество. Аналогичное утверждение верно для емкостей последовательно соединенных конденсаторов.

Примечания[править | править код]

↑ Роу С. Геометрические упражнения с куском бумаги. — 2-е изд. — Одесса: Матезис, 1923. — С. 65. Архивная копия от 24 мая 2012 на Wayback Machine

См. также[править | править код]

Гармоническая пропорция
Гармонический ряд

Ссылки[править | править код]

Weisstein, Eric W. Harmonic Mean / MathWorld–A Wolfram Web Resource

Источник

В материалах различных контрольных работ и экзаменов очень часто встречаются задачи на трапецию, решение которых требует знания ее свойств.

Выясним, какими же интересными и полезными для решения задач свойствами обладает трапеция.

После изучения свойства средней линии трапеции можно сформулировать и доказать свойство отрезка, соединяющего середины диагоналей трапеции. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.

MO – средняя линия треугольника ABC и равна 1/2ВС (рис. 1).

MQ – средняя линия треугольника ABD и равна 1/2АD.

Тогда OQ = MQ – MO, следовательно, OQ = 1/2AD – 1/2BC = 1/2(AD – BC).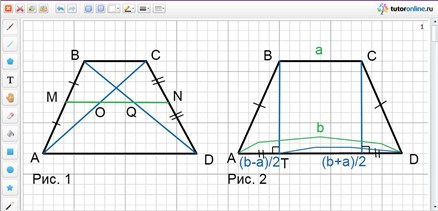 Полезные свойства трапеции

При решении многих задач на трапецию одним из основных приемов является проведение в ней двух высот.

Рассмотрим следующую задачу.

Пусть BT – высота равнобедренной трапеции ABCD с основаниями BC и AD, причем BC = a, AD = b. Найти длины отрезков AT и TD.

Решение.

Решение задачи не вызывает затруднения (рис. 2), но оно позволяет получить свойство высоты равнобедренной трапеции, проведенной из вершины тупого угла: высота равнобедренной трапеции, проведенная из вершины тупого угла, делит большее основание на два отрезка, меньший из которых равен полуразности оснований, а больший – полусумме оснований.

При изучении свойств трапеции нужно обратить внимание на такое свойство, как подобие. Так, например, диагонали трапеции разбивают ее на четыре треугольника, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики. Это утверждение можно назвать свойством треугольников, на которые разбивается трапеция ее диагоналями. Причем первая часть утверждения доказывается очень легко через признак подобия треугольников по двум углам. Докажем вторую часть утверждения.

Треугольники BOC и COD имеют общую высоту (рис. 3), если принять за их основания отрезки BO и OD. Тогда S_BOC/S_COD = BO/OD = k. Следовательно, S_COD = 1/k · S_BOC.

Аналогично, треугольники BOC и АОВ имеют общую высоту, если принять за их основания отрезки CO и OA. Тогда S_BOC/S_AOB = CO/OA = k и S_А_O_В = 1/k · S_BOC.

Из этих двух предложений следует, что S_COD = S_А_O_В.

Не будем останавливаться на сформулированном утверждении, а найдем связь между площадями треугольников, на которые разбивается трапеция ее диагоналями. Для этого решим следующую задачу.

Пусть точка O – точка пересечения диагоналей трапеции АBCD с основаниями BC и AD. Известно, что площади треугольников BOC и AOD равны соответственно S₁ и S₂. Найти площадь трапеции.

Так как S_COD = S_А_O_В, то S_АВС_D = S₁+ S₂ + 2S_COD.

Из подобия треугольников BОC и AOD следует, что ВО/OD = √(S₁/S₂).

Следовательно, S₁/S_COD= BO/OD = √(S₁/S₂), а значит S_COD= √(S₁ · S₂).

Тогда S_АВС_D = S₁ + S₂ + 2√(S₁ · S₂) = (√S₁ + √S₂)².

С использованием подобия доказывается и свойство отрезка, проходящего через точку пересечения диагоналей трапеции параллельно основаниям.

Рассмотрим задачу:

Пусть точка O – точка пересечения диагоналей трапеции ABCD с основаниями BC и AD. BC = a, AD = b. Найти длину отрезка PK, проходящего через точку пересечения диагоналей трапеции параллельно основаниям. На какие отрезки делится PK точкой О (рис. 4)?

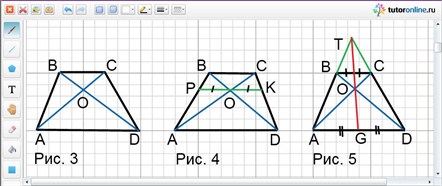
Полезные свойства трапеции

Из подобия треугольников AOD и BOC следует, что АO/OС = AD/BC = b/a.

Из подобия треугольников AOР и ACB следует, что АO/AС = PO/BC = b/(a + b).

Отсюда PO = BC · b / (a + b) = ab/(a + b).

Аналогично, из подобия треугольников DOK и DBC, следует, что OK = ab/(a + b).

Отсюда PO = OK и PK = 2ab/(a + b).

Итак, доказанное свойство можно сформулировать так: отрезок, параллельный основаниям трапеции, проходящий через точку пересечения диагоналей и соединяющий две точки на боковых сторонах, делится точкой пересечения диагоналей пополам. Его длина есть среднее гармоническое оснований трапеции.

Следующее свойство четырех точек: в трапеции точка пересечения диагоналей, точка пересечения продолжения боковых сторон, середины оснований трапеции лежат на одной линии.

Треугольники BSC и ASD подобны (рис. 5) и в каждом из них медианы ST и SG делят угол при вершине S на одинаковые части. Следовательно, точки S, T и G лежат на одной прямой.

Точно так же на одной прямой расположены точки T, O и G. Это следует из подобия треугольников BOC и AOD.

Значит, все четыре точки S, T, O и G лежат на одной прямой.

Так же можно найти длину отрезка разбивающего трапецию на две подобных.

Если трапеции ALFD и LBCF подобны (рис. 6), то a/LF = LF/b.

Отсюда LF = √(ab).

Таким образом, отрезок разбивающий трапецию на две подобные трапеции, имеет длину равную среднему геометрическому длин оснований.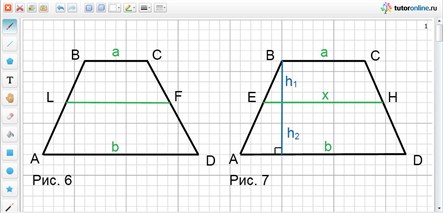 Полезные свойства трапеции

Докажем свойство отрезка, делящего трапецию на две равновеликие.

Пусть площадь трапеции равна S (рис. 7). h₁ и h₂ – части высоты, а х – длина искомого отрезка.

Тогда S/2 = h₁ · (a + x)/2 = h₂ · (b + x)/2 и

S = (h₁ + h₂) · (a + b)/2.

Составим систему

{h₁ · (a + x) = h₂ · (b + x)
{h₁· (a + x) = (h₁ + h₂) · (a + b)/2.

Решая данную систему, получим х = √(1/2(а² + b²)).

Таким образом, длина отрезка, делящего трапецию на две равновеликие, равна√((а² + b²)/2) (среднему квадратичному длин оснований).

Итак, для трапеции ABCD с основаниями AD и BC (BC = a, AD = b) доказали, что отрезок:

1) MN, соединяющий середины боковых сторон трапеции, параллелен основаниям и равен их полусумме (среднему арифметическому чисел a и b);

2) PK, проходящий через точку пересечения диагоналей трапеции параллельно основаниям, равен
2ab/(a + b) (среднему гармоническому чисел a и b);

3) LF, разбивающий трапецию на две подобные трапеции, имеет длину равную среднему геометрическому чисел a и b, √(ab);

4) EH, делящий трапецию на две равновеликие, имеет длину √((а² + b²)/2) (среднее квадратичное чисел a и b).

Признак и свойство вписанной и описанной трапеции.

Свойство вписанной трапеции: трапеция может быть вписана в окружность в том и только в том случае, когда она равнобедренная.

Свойства описанной трапеции. Около окружности можно описать трапецию тогда и только тогда, когда сумма длин оснований равна сумме длин боковых сторон.

Полезные следствия того, что в трапецию вписана окружность:

1. Высота описанной трапеции равна двум радиусам вписанной окружности.

2. Боковая сторона описанной трапеции видна из центра вписанной окружности под прямым углом.

Первое очевидно. Для доказательства второго следствия необходимо установить, что угол COD прямой, что так же не составляет большого труда. Зато знание этого следствия позволяет при решении задач использовать прямоугольный треугольник.

Конкретизируем следствия для равнобедренной описанной трапеции:

Высота равнобедренной описанной трапеции есть среднее геометрическое оснований трапеции
h = 2r = √(ab).

Рассмотренные свойства позволят более глубоко познать трапецию и обеспечат успешность в решении задач на применение ее свойств.

Остались вопросы? Не знаете, как решать задачи на трапецию?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

Источник

XI
региональная научно-практическая конференция

«Физика
и математика в условиях научно-технического прогресса»

Трапеция
и числовые средние величины

Выполнил
Ерофеев Алексей Олегович,

ученик
9 класса,

воспитанник
кружка «Юный математик»

МКОУ
ДО ДДТ МО Ейский район

Краснодарского
края

Руководитель
Ерофеева Татьяна Сергеевна,

руководитель
кружка «Юный математик»

МКОУ
ДО ДДТ МО Ейский район

Ейск

2019

Содержание

1. Введение

2. Числовые
средние величины

2.1.
Определение числовых средних величин

2.2.
Анализ и обзор информации по исследуемому
вопросу

2.3.
Числовые средние величины в трапеции

2.3.1.Среднее арифметическое

2.3.2. Среднее
геометрическое

2.3.3. Среднее
квадратичное

2.3.4. Среднее
гармоническое

2.3.5. Доказательство
неравенств о числовых средних величинах с помощью трапеции

3.
Заключение

4.
Список литературы

ЕРОФЕЕВ Алексей
Олегович

Краснодарский край,
Ейский район, поселок Советский,

МКОУ ДО дом
детского творчества МО Ейский район, кружок «Юный математик»,

9 класс

ТРАПЕЦИЯ И ЧИСЛОВЫЕ
СРЕДНИЕ ВЕЛИЧИНЫ

Научный руководитель
Ерофеева Татьяна Сергеевна,

руководитель кружка
«Юный математик» МКОУ ДО ДДТ МО Ейский район

1.
Введение

В
школьном курсе геометрии изучаются определение трапеции, определение и свойства
средней линии трапеции, свойство углов, прилежащих к боковой стороне, свойства
диагоналей и углов равнобедренной трапеции. Изучив эти свойства, я
заинтересовался «внепрограммными» свойствами трапеции. И особо интересным мне
показался материал, связывающий трапецию со средними числовыми величинами.

Гипотеза: трапеция
обладает свойствами, полезными для решения задач повышенной сложности.

Цель работы: исследовать
свойства, дополнительные построения в трапеции, применить полученные знания для
сравнения числовых средних величин с помощью трапеции.

Объект исследования:
трапеция.

Предмет исследования:
геометрическая интерпретация числовых средних величин с помощью трапеции.

2.
Числовые средние величины

2.1.
Определение числовых средних величин

•
Средним арифметическим нескольких чисел
называют частное от деления суммы этих чисел на число слагаемых

•
Средним геометрическим чисел называется
такое число, которым можно заменить каждое из данных чисел так, чтобы их
произведение не изменилось.

Средним
геометрическим двух положительных чисел а и в называется число, равное
квадратному корню из произведения чисел а и в.

• Средним
гармоническим нескольких положительных чисел называется число, обратное
среднему арифметическому их обратных.

•

2.2.
Анализ и обзор информации по исследуемому
вопросу

В «Энциклопедическом словаре юного
математика»[7] достаточно много места уделено теме «Средние величины»:

«Классическими
средними значениями для двух положительных чисел а и b принято считать:

1) среднее
арифметическое ,

2) среднее
геометрическое ,

3) среднее
гармоническое ,

4) среднее
квадратичное .

В
одном из древнегреческих текстов, который приписывают древнегреческому
математику Архиту (примерно 428 – 365 гг. до нашей эры), среднее арифметическое
m,
среднее геометрическое g и среднее
гармоническое h определялись как равные
члены арифметической, геометрической и «гармонической» пропорций
соответственно:

1)
a
– m = m – b;

2)
a
:
g
= g : b;

3)
(a – h)
: a
= (h – b) : b

Среднее
квадратичное чисел a и b
было введено несколько позже и также стало классическим» [7:с.280].
В данном источнике рассматриваются неравенства , решаемые с помощью
прямоугольного треугольника, вписанного в полуокружность.
[7:с.281]. Авторы делают вывод: «Неравенства для средних и сами средние широко применяются
не только в алгебре, геометрии, математическом анализе, но и в статистике, в
теории вероятностей (откуда пришло среднее квадратичное), при обработке
результатов измерений». [7:с.282].

В
книге Блинкова А.Д. «Классические средние в арифметике и геометрии» в задаче
5.2 предлагается рассмотреть трапецию с основаниями a
и b,
найти отрезки, параллельные основаниям трапеции и равные четырем классическим
средним чисел a и b,
и, используя расположение найденных отрезков, автор доказывает неравенства о средних.
[2: с.44-46]

Наибольший
интерес у меня вызвала статья «Числовые средние и геометрия», опубликованная в
журнале «Квант»[5: с.62-65]. Авторы статьи А.Гольдман и Л.Звавич не дают
готовых решений при доказательстве неравенств о средних величинах, а дают лишь
указания, которыми я и воспользовался при выполнении данной работы.

2.3.
Числовые средние величины в трапеции

2.3.1. Среднее
арифметическое

Средней
линией трапеции называют отрезок, соединяющий середины её боковых сторон.
[6: с.44]

Докажем,
что средняя линия трапеции параллельна основаниям и равна их полусумме (рисунок
1)

Дана трапеция ABCD со средней
линией KL. Для доказательства проведём прямую через точки B и L до
пересечения с прямой AD.

Рассмотрим полученные
треугольники LBC и LQD:

1. По
определению средней линии точка L является серединой
отрезка CD. Отсюда следует, что отрезки CL и LD равны.

2. ∠
BLC = ∠
QLD как вертикальные.

3. ∠
BCL = ∠
LDQ как накрест лежащие при параллельных прямых AD и BC и
секущей CD.

Из этих 3 равенств следует, что
треугольники LBC и LQD равны по стороне и двум прилежащим
к ней углам. Следовательно, ∠
LBC = ∠
LQD, BC=DQ и BL=LQ => KL,
являющаяся средней линией трапеции ABCD, также является и средней линией
треугольника ABQ. Согласно свойству средней линии
треугольника получаем:

1. KL
= 1/2AQ = 1/2 (AD+DQ) = 1/2 (AD+BC)

2. KL
|| AD по свойству средней линии треугольника. А так
как AD || BC по определению трапеции, то KL || BC.

Если
обозначить основания трапеции a
и b,
то получим среднее арифметическое: . Итак, среднее
арифметическое – это длина средней линии трапеции.

2.3.2. Среднее
геометрическое

Отрезок, разбивающий
трапецию на две подобные трапеции, имеет длину, равную среднему геометрическому
длин оснований.

Докажем
это (рисунок 2). Отрезок MN делит
трапецию ABCD на
две подобные трапеции AMND
и MBCN.
Значит, отношения соответствующих сторон в этих трапециях равны.

; ; . Обозначим длину
отрезка MN буквой
g.

2.3.3. Среднее
квадратичное

Докажем, что
длина отрезка, делящего трапецию на две равновеликие трапеции, равна среднему
квадратичному длин оснований.

Доказательство:
Отрезок TG, проведенный
параллельно основаниям (рисунок 3), делит трапецию ABCD на
две равновеликие трапеции. P
– точка пересечения боковых сторон трапеции. Площади трапеций ATGD
и TBCG
обозначим S, так как они равны.
Площадь треугольника BPC обозначим . Т.к.
треугольники BPC,
TPG и
APD подобны,
то можно применить свойство: отношение площадей подобных фигур равно квадрату
коэффициента подобия. Длину отрезка TG обозначим
через x.

1)
Рассмотрим подобные треугольники BPC
и TPG.
Коэффициент   k = . Получим

2)
Рассмотрим подобные треугольники APD
и TPG.
Коэффициент k = .

3)
Складываем оба равенства, получаем:

+ = ; = ;

; ;

2.3.4. Среднее
гармоническое

Задача
1. Пусть EF
– отрезок длиной х с концами соответственно на боковых сторонах AB
и CD
трапеции ABCD, параллельный её
основаниям a и b.
Найдите х, если известно, что = .[5:с.63]

Для решения выполним
дополнительное построение. Проведём через точку F PH AB.
Треугольники FCP и FDH
подобны по первому признаку, так как CFP
= DFH
как вертикальные, а FCP
= FDH
как накрест лежащие при параллельных прямых BP
и AD
и секущей CD.

CP
= x–a;
HD
= b–x.

Из подобия треугольников и из условия задачи
следует, что =

x-a = (b-x);

x – a = x;

x + x = + a;

x = (*)

Задача 2.
Найдём х, если отрезок EF проходит через
точку О – точку пересечения диагоналей трапеции.

Решение: = = .

В данной задаче = .

Подставим это значение в (*), получим EF=(a
+ b)
/ (1 + ) =

= (2a)/(1 + )
= .

2.3.5. Доказательство
неравенств о числовых средних величинах с помощью трапеции.

Итак, в трапеции ABCD
появились все упомянутые средние чисел a
и b.

Докажем
неравенство

Доказательство:

Пусть EF
– отрезок, длина которого равна среднему гармоническому чисел a
и b;
длина отрезка MN равна
среднему геометрическому чисел a
и b,
KL
– отрезок с длиной, равной среднему арифметическому чисел a
и b,
TG
– отрезок, длина которого равна среднему квадратичному чисел a
и b.

Тогда = .

Найдем отношение .

Так
как трапеции AMND
и MBCN
подобны, значит, отношения соответствующих сторон в этих трапециях равны. = = =

Так
как KL
средняя линия трапеции, то отношение = 1.

Но
< < 1, значит, .

Теперь
докажем последнее неравенство: .

Для
доказательства воспользуемся формулой для нахождения площади трапеции. Пусть высота трапеции TBCG,
а – высота трапеции ATGD.
Так как площади этих трапеций равны, то

(a
+ ): 2 = (b
+ ):2;

/ = (b
+ )/ (a
+ ). Так как ab,
то / 1. Значит, .

3.
Заключение

Данная работа была выполнена с
целью исследования свойств трапеции с помощью дополнительных построений, применения
полученных знаний для сравнения числовых средних величин с помощью трапеции.

В ходе исследования
выявлено, что для трапеции ABCD
с основаниями AD и BC
(BC
= a,
AD
=b,
a<b)
справедливы следующие утверждения:

1)
Отрезок KL,
соединяющий середины боковых сторон трапеции, параллелен основаниям и равен их
полусумме (среднее арифметическое чисел a
и b).

2)
Отрезок МN,
разбивающий трапецию на две подобные трапеции, имеет длину, равную среднему
геометрическому чисел a и b,
).

3)
Отрезок EF,
проходящий через точку пересечения диагоналей трапеции параллельно основаниям,
равен (среднее гармоническое
чисел a
и b).

4)
Отрезок TG,
делящий трапецию на две равновеликие трапеции, имеет длину, равную (среднее квадратичное
чисел a
и b).

Чтобы увидеть связь между этими
отрезками, построили их для данной трапеции на одном чертеже. Положение
отрезков указывает на связь между числовыми средними величинами. Трапеция
позволяет наглядно сравнить средние величины и убедиться в выполнении этих неравенств.

Итак, мы доказали неравенства и
убедились в том, что при a<b
все неравенства – строгие. Нетрудно видеть, что если какие-либо два из
отрезков, длины которых мы сравнивали, равны, то ABCD
– параллелограмм и, следовательно, все неравенства превращаются в равенства.[5:
с.63-64]

Доказаны
зависимости между основаниями трапеции и отрезками, параллельными основаниям.
Появился новый блок знаний, с помощью которых можно продвинуться в решении
задач повышенной сложности. Эти знания понадобятся и на занятиях
математического кружка, и при подготовке к олимпиадам. Но числовые средние
величины можно рассматривать и с помощью прямоугольного треугольника и с
помощью правильного пятиугольника. Это будет тема моей следующей работы.

4.
Список использованной литературы

Атанасян Л.С. и др. Геометрия. Учебник для 7-9
классов средней школы. – М.: Просвещение, 2007
Блинков А.Д. Классические средние в арифметике и
геометрии. – М.: МЦНМО, 2012
Ваховский Е.Б., Рывкин А.А. Задачи по
элементарной математике. – М.: Наука, 1971
Виленкин Н.Я. и др. Математика. 5 класс. Учебник
для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2012
Гольдман А., Звавич Л. Числовые средние и
геометрия. – Квант №9, 1990
Мерзляк А.Г. и др. Геометрия. 8 класс. Учебник
для учащихся общеобразовательных учреждений. – М.: Вентана – Граф, 2016
Энциклопедический словарь юного математика. Сост.
Савин А.П. – М.: Педагогика, 1989

Источник

Instruction: Join the legs of the trapezoid with a segment that is parallel to the bases and whose length is equal to the harmonic mean of their length.

Goal: 3L 5E

Available tools:

Move
Point
Line
Circle
Perpendicular Bisector
Perpendicular
Angle Bisector
Parallel
Non-collapsing Compass
Intersect

Pack: Iota

Previous level: 9.2

Next level: 9.4

3L solution[]

Consider the trapezoid ABCD with AB || CD.

Construct line AC.
Construct line BD, intersecting line AC at E.
Construct line parallel to AB through E.

5E solution[]

Construct line AC.
Construct line BD, intersecting line AC at E.
Construct circle B with radius BE, intersecting BD at F.
Construct circle A with radius AF, intersecting circle B at G.
Construct line EG.

Explanation[]

EG intersects BC,AD at H,I. By Thalès theorem we have ${displaystyle {frac {EH}{a}}={frac {CE}{CA}}={frac {BE}{BD}}={frac {EI}{a}}}$ , so ${displaystyle EH=EI={frac {c}{2}}}$ , where ${displaystyle HI=c}$ .

But ${displaystyle {frac {c}{2a}}+{frac {c}{2b}}={frac {EH}{a}}+{frac {EH}{b}}={frac {BG}{BC}}+{frac {CG}{CB}}=1}$ , we must have ${displaystyle c={frac {2ab}{a+b}}}$ .

Источник

Свойства[править | править код]

Среднее гармоническое взвешенное[править | править код]

Приложения и примеры[править | править код]

Примечания[править | править код]

См. также[править | править код]

Ссылки[править | править код]

3L solution[]

5E solution[]

Explanation[]

Вам также может понравиться

Как найти уровень боковых лепестков

Как найти ортогональную проекцию точки на плоскость

Увидеть во сне как нашла ребенка

Добавить комментарий Отменить ответ