Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции СРГАРМ в Microsoft Excel.
Описание
Возвращает среднее гармоническое множества данных. Среднее гармоническое — это величина, обратная среднему арифметическому обратных величин.
Синтаксис
СРГАРМ(число1;[число2];…)
Аргументы функции СРГАРМ описаны ниже.
-
Число1, число2,… — от 1 до 255 аргументов, для которых вычисляется среднее геометрическое. “Число1” обязательно, последующие числа — нет. Вместо аргументов, разделенных точками с запятой, можно использовать один массив или ссылку на массив.
Замечания
-
Среднее гармоническое всегда меньше среднего геометрического, которое, в свою очередь, всегда меньше среднего арифметического.
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
-
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения пропускаются; однако ячейки, которые содержат нулевые значения, учитываются.
-
Аргументы, содержащие значения ошибок или текст, который нельзя преобразовать в числа, приводят к возникновению ошибки.
-
Если любая точка данных ≤ 0, то СЛМЕСЯ возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Уравнение для среднего гармонического имеет следующий вид:
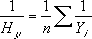
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|
4 |
||
|
5 |
||
|
8 |
||
|
7 |
||
|
11 |
||
|
4 |
||
|
3 |
||
|
Формула |
Описание |
Результат |
|
=СРГАРМ(A2:A8) |
Среднее гармоническое данных ячеек A2:A8. |
5,028376 |
Нужна дополнительная помощь?
Нужны дополнительные параметры?
Изучите преимущества подписки, просмотрите учебные курсы, узнайте, как защитить свое устройство и т. д.
В сообществах можно задавать вопросы и отвечать на них, отправлять отзывы и консультироваться с экспертами разных профилей.
Функция СРГАРМ возвращает среднее гармоническое множества данных.
Описание функции СРГАРМ
Возвращает среднее гармоническое множества данных. Среднее гармоническое — это величина, обратная среднему арифметическому обратных величин.
Синтаксис
=СРГАРМ(число1; [число2],…)Аргументы
число1, число2…
от 1 до 255 аргументов, для которых вычисляется среднее гармоническое. «Число1» обязательно, последующие числа — необязательные. Вместо аргументов, разделенных точками с запятой, можно использовать один массив или ссылку на массив.
Замечания
- Среднее гармоническое всегда меньше среднего геометрического, которое, в свою очередь, всегда меньше среднего арифметического.
- Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
- Функция учитывает введенные непосредственно в списке аргументов логические значения и числа в текстовом виде.
- Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения пропускаются; ячейки, содержащие нулевые значения, учитываются.
- Аргументы, содержащие значения ошибок или текст, который нельзя преобразовать в числа, приводят к возникновению ошибки.
- Если какая-либо из точек данных меньше или равна нулю, функция СРГАРМ возвращает значение ошибки #ЧИСЛО!.
- Уравнение для среднего гармонического имеет следующий вид:

Пример
Download Article
Download Article
The harmonic mean is a way to calculate the mean, or average, of a set of numbers. Using the harmonic mean is most appropriate when the set of numbers contains outliers that might skew the result. Most people are familiar with calculating the arithmetic mean, in which the sum of values is divided by the number of values. Calculating the harmonic mean is a little more complicated. If working with a small set of numbers you may be able to solve by hand using the formula. Otherwise, you can easily use Microsoft Excel to find the harmonic mean.
-

1
Set up the formula for the harmonic mean. The formula is
, where
is the number of values in the set of numbers, and
,
,
are the values in the set.[1]
-

2
Determine the values you need to find the harmonic mean for. This can be any set of numbers.[2]
- For example, you may need to find the harmonic mean for the numbers 10, 12, 16, and 8.
Advertisement
-

3
Plug the value of
into the formula. This will equal the number of values in your set.
- For example, if you are finding the harmonic mean of the numbers 10, 12, 16, and 8, you are working with 4 values, the numerator of your formula will be 4:
- For example, if you are finding the harmonic mean of the numbers 10, 12, 16, and 8, you are working with 4 values, the numerator of your formula will be 4:
-

4
Plug the values your are averaging into your formula. You will take the reciprocal of each number and add them in the denominator of the formula. Remember, when you take the reciprocal of a whole number, you turn the number into a fraction by placing a 1 in the numerator and the whole number in the denominator.[3]
Advertisement
-

1
Add the fractions in the denominator. You can use a calculator, or add them up by hand. If you are not using a calculator, remember to find a common denominator first. To learn more about adding fractions, read Add Fractions.
- For example:
- For example:
-

2
Divide the numerator by the denominator. Remember that dividing by a fraction is the same as multiplying by its reciprocal.[4]
-

3
Convert to a decimal to find the harmonic mean of your set of numbers. To convert a fraction to a decimal, divide the numerator by the denominator.[5]
Advertisement
-

1
Enter the values into your spreadsheet. Make sure to only place one value in each cell.
- For example, if you need to find the harmonic mean of 10, 12, 16, and 8, you might type each of these values into a separate cell in the spreadsheet, cells A1-A4.
-

2
Enter the function for the harmonic mean. The function is HARMEAN(number 1, [number 2]…).[6]
To select the function, begin typing “=HARMEAN” into a blank cell of the spreadsheet, then double-click on the function when it pops up.- For example, type “=HARMEAN” into cell A5 of your spreadsheet and double-click on the function.
-

3
Highlight the cells containing the values you are averaging. Hit the enter key. Excel will calculate the harmonic mean for you and display it in the spreadsheet.
- For example, highlight cells A1-A4 of your spreadsheet and hit enter. Excel will calculate 10.78652 as the harmonic mean.
Advertisement
Add New Question
-
Question
What are the harmonic means of 5, 6 and 7?

3/(1/5+1/6+1/7) = 3/(42/210 + 35/210 + 30/210 ) = 3/( 107/210) = 3 x 210/107= 630/107 = 5.89
-
Question
What is the harmonic mean of x1,x2,x3.xn?

This is just asking for the formula: n/(1/x1 + 1/x2 + 1/x3 +…+1/xn)
-
Question
Can you tell me the harmonic mean of 0 2 4 6?

There’s no harmonic mean when zero is one of the values in the set. That’s because the formula would have 1/0 as one of the terms in the denominator, and 1/0 is infinity and not usable.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
References
About This Article
Article SummaryX
To calculate the harmonic meaning, start by determining the number of values in your set of numbers. For example, if you’re working with 10, 12, 16, and 8, you have 4 numbers, so the value is 4. Then, rewrite the numbers you’re working with as denominators over the number 1. For example, if you’re working with 10, 12, 16, and 8, write them as 1/10, 1/12, 1/16, and 1/8. Then, divide 4 by the sum of the fractions to find the harmonic mean. To calculate the harmonic meaning using a calculator, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 147,375 times.
Reader Success Stories
-

Monahil Monahil
Jul 17, 2017
“Very useful and helpful. You must read this article. It is a very simple way of solving problems.”
Did this article help you?
Функция HARMEAN возвращает среднее гармоническое предоставленного набора значений. Среднее гармоническое является обратной величиной среднего арифметического обратных величин.

Синтаксис
=HARMEAN(number1, [number2], …)
аргументы
- номер1 (обязательно): Первое положительное число или диапазон положительных чисел, для которых вычисляется среднее гармоническое.
- [номер2], … (необязательно): Второе и до 253 положительных чисел или диапазонов положительных чисел, для которых вычисляется среднее гармоническое.
Возвращаемое значение
Функция HARMEAN возвращает положительное числовое значение.
Примечания к функциям
- Аргументы могут быть числами, массивами или ссылками, содержащими числа.
- HARMEAN игнорирует пустые ячейки.
- Если на текстовое значение ссылается функция HARMEAN, HARMEAN проигнорирует его; Если текстовое значение передается непосредственно в HARMEAN (например, =HARMEAN(“kutools”)), функция вернет значение #СТОИМОСТЬ! ошибка.
- Если функция HARMEAN ссылается на логическое значение, HARMEAN проигнорирует его; Если логическое значение передается непосредственно в HARMEAN, функция будет рассматривать его как число (ИСТИНА=1, ЛОЖЬ=0).
- Если какие-либо предоставленные значения не являются положительными (≤ 0), HARMEAN вернет #NUM! значение ошибки.
- Если в любом из аргументов есть какие-либо значения ошибки, HARMEAN вернет первое значение ошибки.
- Уравнение для среднего гармонического:

- √ Примечание. Дополнительные сведения о среднем гармоническом значении см. Средняя гармоническая страница Википедии.
Пример
Предположим, у вас есть таблица с числами, как показано ниже, чтобы получить среднее гармоническое чисел, скопируйте или введите одну из приведенных ниже формул в пустую ячейку и нажмите Enter чтобы получить результат:
=ХАРМААН(5,2,1,11,11,8,50,50,1.5,5,6.5,9,4)
=ХАРМААН({5,2,1;11,11,8;50,50;1.5,5;6.5,9,4})
Или используйте ссылки на ячейки, чтобы сделать формулы динамическими:
=ХАРМААН(B3: D7)
=ХАРМААН(B3: B7,C3: C7,D3: D7)

Связанные функции
Функция Excel ГЕОМЕАН
Функция GEOMEAN возвращает среднее геометрическое массива или диапазона положительных чисел. Среднее геометрическое может использоваться для набора чисел, значения которых предназначены для перемножения друг с другом или имеют экспоненциальный характер, например набор цифр роста.
Функция Excel ОБРЕЗНОЕСРЕДНЕЕ
Функция Excel ТРИММЕАН вычисляет среднее (среднее), исключая выбросы. Количество исключаемых точек данных указывается в процентах.
Лучшие инструменты для работы в офисе
Kutools for Excel – Помогает вам выделиться из толпы
Хотите быстро и качественно выполнять свою повседневную работу? Kutools for Excel предлагает 300 мощных расширенных функций (объединение книг, суммирование по цвету, разделение содержимого ячеек, преобразование даты и т. д.) и экономит для вас 80 % времени.
- Разработан для 1500 рабочих сценариев, помогает решить 80% проблем с Excel.
- Уменьшите количество нажатий на клавиатуру и мышь каждый день, избавьтесь от усталости глаз и рук.
- Станьте экспертом по Excel за 3 минуты. Больше не нужно запоминать какие-либо болезненные формулы и коды VBA.
- 30-дневная неограниченная бесплатная пробная версия. 60-дневная гарантия возврата денег. Бесплатное обновление и поддержка 2 года.

Вкладка Office – включение чтения и редактирования с вкладками в Microsoft Office (включая Excel)
- Одна секунда для переключения между десятками открытых документов!
- Уменьшите количество щелчков мышью на сотни каждый день, попрощайтесь с рукой мыши.
- Повышает вашу продуктивность на 50% при просмотре и редактировании нескольких документов.
- Добавляет эффективные вкладки в Office (включая Excel), точно так же, как Chrome, Firefox и новый Internet Explorer.

Комментарии (0)
Оценок пока нет. Оцените первым!

- Гармоническая средняя формула

Формула гармонического среднего (Содержание)
- Гармоническая средняя формула
- Примеры формулы среднего гармонического (с шаблоном Excel)
- Калькулятор формулы гармонического среднего
Гармоническая средняя формула
Гармоническое среднее – это, в основном, тип усреднения, который используется в статистике, который является обратной величиной от среднего арифметического обратных величин. Среднее гармоническое всегда меньше, чем среднее арифметическое одного и того же набора данных. Среднее гармоническое обычно не используется в качестве арифметического или геометрического среднего и используется в определенных ситуациях или при работе со средними значениями единиц, такими как средняя скорость перемещения и другие соотношения. Это также используется в области финансов для расчета кратных цен, таких как отношение цены к прибыли, отношение цены к продажам и т. Д. Причина этого заключается в том, что если мы используем взвешенное арифметическое среднее значение для вычисления этих значений, точки с высокими данными получат более высокий вес и более низкие значения данных приведут к меньшему весу, что создаст проблему и не даст нам правильное значение.
Предположим, что у нас есть набор данных с n точками данных и определяется как X: (X1, X2, X3 …… ..Xn).
Формула для гармонического среднего
Harmonic Mean = n / (1/X1 + 1/X2 + 1/X3 ………… 1/Xn)
Где:
- X1, X2, … Xn – Точки данных
- n – общее количество точек данных
Шаги для вычисления среднего гармонического:
- Возьмите обратную величину всех точек данных в наборе данных.
- После этого найдите среднее / среднее из этих значений.
- Следующим и последним шагом является взятие обратной величины из этого значения, чтобы получить гармоническое среднее.
Примеры формулы среднего гармонического (с шаблоном Excel)
Давайте рассмотрим пример, чтобы лучше понять вычисление гармонического среднего.
Вы можете скачать этот шаблон гармонического среднего здесь – шаблон гармонического среднего
Формула гармонического среднего – пример № 1
Допустим, у вас есть набор данных с 10 точками данных, и мы хотим рассчитать среднее гармоническое для этого.
Набор данных: (4, 6, 8, 9, 22, 83, 98, 45, 87, 10)
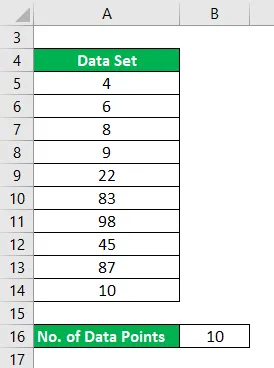
Взаимное будет рассчитываться как:
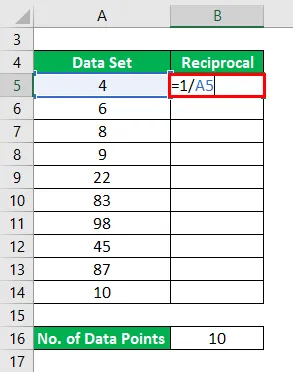
Результат будет таким, как указано ниже.
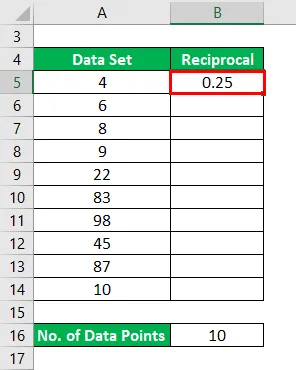
Точно так же, мы должны рассчитать Взаимное для всех точек данных.
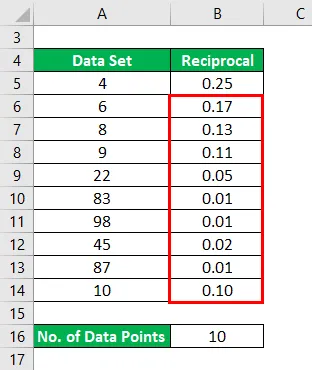
Теперь среднее значение взаимного рассчитывается как
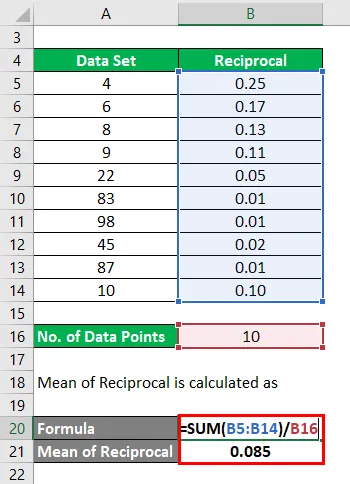
- Среднее взаимного = (0, 25 + 0, 17 + 0, 13 + 0, 11 + 0, 05 + 0, 01 + 0, 01 + 0, 02 + 0, 01 + 0, 10) / 10
- Среднее Взаимное = 0, 85 / 10
- Среднее взаимного = 0, 085
Среднее гармоническое рассчитывается по формуле, приведенной ниже
Среднее гармоническое = n / (1 / X1 + 1 / X2 + 1 / X3 ………… 1 / Xn)
Среднее гармоническое = 1 / среднее взаимного
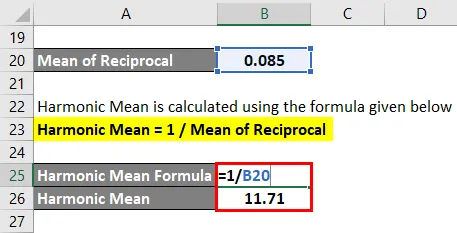
- Среднее гармоническое = 1 / 0, 085
- Среднее гармоническое = 11, 71
Формула среднего гармонического – пример № 2
Теперь давайте посмотрим на некоторые другие примеры из практической жизни, чтобы понять значение более четко и увидеть разницу между арифметическим и гармоническим средним.
Допустим, вы едете на машине и едете в другой город. Общее время в пути составляет 4 часа, из которых вы едете со скоростью 60 км / час в течение 1- го часа, 50 км / час в течение 2- го часа, 100 км / час в течение 3- го часа и 40 км / час в течение 4- й час
Таким образом, ваша средняя скорость может быть рассчитана простым способом:
- Средняя скорость = (60 + 50 + 100 + 40) / 4
- Средняя скорость = 250/4
- Средняя скорость = 62, 5 км / час
Но, скажем, приведенная информация такова, что в течение первой половины времени вы двигались со скоростью 55, 5 км / час, а в следующей половине – со скоростью 70 км / час. В этом случае нам нужно использовать среднее гармоническое, чтобы найти среднюю скорость.
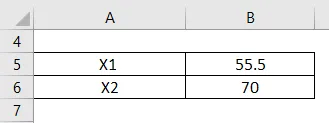
Среднее гармоническое рассчитывается по формуле, приведенной ниже
Среднее гармоническое = n / (1 / X1 + 1 / X2 + 1 / X3 ………… 1 / Xn)
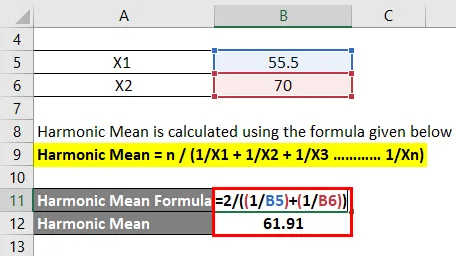
- Среднее гармоническое = 2 / ((1 / 55, 5) + (1/70))
- Среднее гармоническое = 61, 91 км / час
Если вы видите здесь, значение гармонического среднего меньше простого среднего.
объяснение
Хотя среднее гармоническое значение в основном используется для нахождения среднего значения набора данных, подобно простому среднему арифметическому, оно не рассчитывается как просто среднее арифметическое. Если у нас большой набор данных, вычисление среднего значения гармоник станет сложным и трудоемким. Со сложностью приходит путаница и вероятность ошибки. Поэтому нужно быть очень осторожным при расчете среднего гармонического значения для большого набора данных. Так как мы берем взаимное значение при расчете среднего гармонического, наибольший вес задается наименьшему значению и наоборот. Иногда это не требуется.
Другой недостаток состоит в том, что если любая из точек данных в наборе данных равна 0, среднее гармоническое не может быть рассчитано, поскольку х / 0 не определено. Таким образом, в некотором смысле гармоническое среднее имеет очень ограниченную область действия в отличие от среднего арифметического. Кроме того, это чрезвычайно чувствительно к выбросам и экстремальным значениям.
Актуальность и использование формулы среднего гармонического
Мы видели множество ограничений среднего гармонического, и это причина того, что он не имеет большого практического применения. Но есть и положительные стороны. Среднее значение гармоники жестко определено и поэтому подходит для дальнейших математических операций. Кроме того, в отличие от среднего геометрического, оно не зависит от колебаний выборки. Поскольку он дает больший вес небольшим наборам данных, что иногда желательно, чтобы данные не были смещены в сторону больших значений. Ситуации, которые вовлекают время и нормы, среднее гармоническое дает лучшие и точные результаты, чем простое среднее.
Все сказанное и выполненное, среднее гармоническое имеет мало преимуществ, но, поскольку оно имеет ограниченную область применения и больше недостатков, оно используется не очень часто и имеет ограниченное присутствие.
Калькулятор формулы гармонического среднего
Вы можете использовать следующий Harmonic Mean Calculator
| N | |
| X1 | |
| X2 | |
| X3 | |
| Гармоническая средняя формула | |
| Формула гармонического среднего = |
|
|
Рекомендуемые статьи
Это было руководство к Гармонической Средней Формуле. Здесь мы обсуждаем, как вычислить Гармоническое Среднее вместе с практическими примерами. Мы также предоставляем калькулятор Harmonic Mean с загружаемым шаблоном Excel. Вы также можете посмотреть следующие статьи, чтобы узнать больше –
- Руководство по формуле диапазона
- Лучшие примеры формулы удвоения времени
- Калькулятор формулы погашения фонда
- Как рассчитать DPMO?


