В данной публикации мы рассмотрим, с помощью какой формулы можно найти среднее геометрическое чисел, а также разберем примеры задач для ее демонстрации на практике.
- Расчет среднего геометрического
- Пример задачи
Расчет среднего геометрического
Чтобы вычислить среднее геометрическое двух или более чисел, требуется их перемножить, а затем из полученного результата извлечь корень, степень которого равняется их количеству.
Допустим, у нас есть числа a1, a2, … , an. Среднее геометрическое находится по формуле:
![]()
Частные случаи формулы:
Пример задачи
Задание 1
Найдем среднее геометрическое чисел 3, 6 и 12.
Решение:
Воспользуемся соответствующей формулой для трех чисел:
![]()
Задание 2
Среднее геометрическое четырех чисел равняется 4, а также известны три из них – 2, 2 и 4. Найдем четвертое.
Решение:
Обозначим число, которое требуется найти буквой x. Формула выглядит следующим образом:
![]()
Помещаем число 4 под знак корня, сохранив равенство (для этого возводим его в четвертую степень, т.е. 44 = 256):
![]()
Следовательно, x = 256 : 16 = 16.
Загрузить PDF
Загрузить PDF
Среднее геометрическое — математическая величина, которую легко спутать с более часто применяемым средним арифметическим. Для вычисления среднего геометрического следуйте методам, приведенным ниже.
-

1
Возьмите два числа, среднее геометрическое которых необходимо найти.
- Например, 2 и 32.
-

2
-

3
Реклама
-

1
Подставьте числа в приведенное уравнение. Если это, скажем, 10 и 15, то подставьте их так, как показано на рисунке.
-

2
Найдите «х». Начните с перемножения крест-накрест, что означает перемножение пар чисел по диагонали и расстановку результатов умножения по разные стороны знака =. Так как х*х = х2, то уравнение приводится к виду к виду: х2 = (результат умножения ваших чисел). Для вычисления «х» извлеките квадратный корень из результата перемножения используемых чисел. Если в результате вычисления корня получится целое число — отлично. Если нет, дайте ответ в виде десятичной дроби или запишите его со знаком корня (в зависимости от того, что требует преподаватель). Ответ, приведенный выше на рисунке, записан в виде упрощенного квадратного корня.
Реклама
-

1
Подставьте числа в приведенное уравнение.Среднее геометрическое = (a1 × a2 . . . an)1/n[3]
- a1 — первое число, a2 — второе число и так далее
- n — общее количество чисел
-

2
Перемножьте числа (a1, a2 и так далее).
-

3
Извлеките корень n степени из полученного числа. Это и будет среднее геометрическое.[4]
Реклама
-

1
Найдите логарифм каждого числа и сложите полученные значения. Найдите клавишу LOG на своем калькуляторе. Затем введите: (первое число) LOG + (второе число) LOG + (третье число) LOG [+ столько чисел, сколько дано] =. Не забудьте нажать «=», или показанный вам результат будет логарифмом последнего введенного числа, а не суммой логарифмов всех чисел.
- Например, log 7 + log 9 + log 12 = 2,878521796
-

2
Разделите результат сложения на общее количество изначально данных чисел. Если вы сложили логарифмы трех чисел, делите полученный результат на три.
- Например, 2,878521796 / 3 = 0,959507265
-

3
Вычислите антилогарифм полученного результата. На калькуляторе нажмите кнопку переключения регистра (активирует функции верхнего регистра — над клавишами), а затем нажмите LOG, чтобы получить значение антилогарифма. Этот результат и будет средним геометрическим.[5]
- Например, antilog 0,959507265 = 9,109766916. Поэтому среднее геометрическое 7, 9, и 12 равно 9,11.
Реклама
Советы
- Различия между средним арифметическим и средним геометрическим:
- Для вычисления среднего арифметического, например, чисел 3, 4 и 18, необходимо их сложить 3 + 4 + 18, а затем разделить на 3 (потому что изначально даны три числа). Ответ равен 25/3 или примерно 8,333; это означает, что если сложить 8,3333 три раза подряд, то ответ будет таким же, как при сложении чисел 3, 4, и 18. Среднее арифметическое отвечает на вопрос: «Если все величины имеют одинаковое значение, то каким это значение должно быть, чтобы при суммировании получился один результат?»
- Напротив, среднее геометрическое отвечает на вопрос: «Если все величины имеют одинаковое значение, то каким это значение должно быть, чтобы при перемножении получился один результат?» Поэтому, чтобы найти среднее геометрическое чисел 3, 4 и 18, мы перемножаем эти числа: 3 x 4 x 18. Получаем 216. Затем мы берем кубический корень из полученного результата перемножения (кубический корень, так как в вычислении участвуют три числа). Ответ будет 6. Другими словами, так как 6 x 6 x 6 = 3 x 4 x 18, то 6 является средним геометрическим чисел 3, 4 и 18.
- Среднее геометрическое всегда меньше или равно среднему арифметическому. Более подробно читайте тут.
- Среднее геометрическое рассчитывается только для положительных чисел. Схема решения различных прикладных задач с использованием среднего геометрического не будет работать в случае наличия отрицательных чисел.
Реклама
Об этой статье
Эту страницу просматривали 131 740 раз.
Была ли эта статья полезной?
Дано
Ряд чисел
1, 2, 4, 2
Задача
Найти среднее геометрическое
Решение
Находить среднее геометрическое будем по формуле
(large a_{ср.геом.} = sqrt[n]{a_1 times a_2 times a_3 times … times a_n} )
(large a_{ср.геом.} = sqrt[4]{1 times 2 times 4 times 2} = )(large sqrt[4]{16} = 2)
Среднее геометрическое чисел 1, 2, 4, 2 равно 2
Правила ввода
Ноль вводить нельзя.
Вводить можно только положительные целые(1, 2, 3, 7), десятичные(0.25, 1.15), дробные(1/8, 32/9). Если необходимо ввести смешанное число, то нужно перед вводом перевести его в неправильную обыкновенную дробь. Т.е. 1 целая 1/2 вводить нужно будет как 3/2.
При вводе десятичных дробей использовать точку. Запятая зарезервирована под разделитель.
В качестве разделителя можно использовать любой символ кроме цифр(0-9), слэша(/), точки(.), знака минус(-). Остальные символы и перенос строки будут программой заменены на разделители.
Ссылка на результат
https://calc-best.ru/matematicheskie/statistika/srednee-geometricheskoe-chisel?str=1_2_4_2
Похожие калькуляторы
Данный калькулятор предназначен для расчета среднего геометрического чисел онлайн.
Среднее геометрическое чисел – это математическая величина, которая вычисляется путем извлечения корня из произведения данных чисел, при этом показатель корня равен количеству чисел.
Формула среднего геометрического следующая:
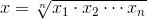
Чтобы подсчитать среднее геометрическое двух, трех и более чисел, необходимо выбрать количество чисел и ввести их значения в соответствующие ячейки.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также
Среднее геометрическое
- Главная
- /
- Математика
- /
- Арифметика
- /
- Среднее геометрическое
Чтобы найти среднее геометрическое нескольких чисел воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Среднее геометрическое:
0
Округление ответа:
Просто введите положительные вещественные числа и получите среднее геометрическое этих чисел. Для того чтобы добавить в ряд более двух чисел воспользуйтесь зелёной кнопкой “+”.
Теория
Среднее геометрическое нескольких положительных вещественных чисел – это такое число, которым можно заменить каждое из этих чисел так, чтобы их произведение не изменилось.
Формула
x̅геом = n√x1 ⋅ x2 ⋅ … ⋅ xn
Пример
К примеру, рассмотрим три числа 3, 8 и 9. Среднее геометрическое этих трёх чисел:
x̅геом = 3√3 ⋅ 8 ⋅ 9 = 3√216 = 6
Таким образом:
3 ⋅ 8 ⋅ 9 = 216 = 6 ⋅ 6 ⋅ 6
