Как найти среднее геометрическое чисел калькулятор

Как найти среднее геометрическое чисел калькулятор

Данный калькулятор предназначен для расчета среднего геометрического чисел онлайн.
Среднее геометрическое чисел – это математическая величина, которая вычисляется путем извлечения корня из произведения данных чисел, при этом показатель корня равен количеству чисел.

Формула среднего геометрического следующая:
онлайн Среднее геометрическое вычисляется по следующей формуле

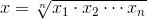
Чтобы подсчитать среднее геометрическое двух, трех и более чисел, необходимо выбрать количество чисел и ввести их значения в соответствующие ячейки.

×

Пожалуйста напишите с чем связна такая низкая оценка:

×

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также

Источник

Среднее геометрическое

  1. Главная
  2. /
  3. Математика
  4. /
  5. Арифметика
  6. /
  7. Среднее геометрическое

Чтобы найти среднее геометрическое нескольких чисел воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Среднее геометрическое:

0

Округление ответа:

Просто введите положительные вещественные числа и получите среднее геометрическое этих чисел. Для того чтобы добавить в ряд более двух чисел воспользуйтесь зелёной кнопкой “+”.

Теория

Среднее геометрическое нескольких положительных вещественных чисел – это такое число, которым можно заменить каждое из этих чисел так, чтобы их произведение не изменилось.

Формула

x̅геом = n√x1 ⋅ x2 ⋅ … ⋅ xn

Пример

К примеру, рассмотрим три числа 3, 8 и 9. Среднее геометрическое этих трёх чисел:

x̅геом = 3√3 ⋅ 8 ⋅ 9 = 3√216 = 6

Таким образом:

3 ⋅ 8 ⋅ 9 = 216 = 6 ⋅ 6 ⋅ 6

См. также

Источник

Правила ввода

Ноль вводить нельзя.

Вводить можно только положительные целые(1, 2, 3, 7), десятичные(0.25, 1.15), дробные(1/8, 32/9). Если необходимо ввести смешанное число, то нужно перед вводом перевести его в неправильную обыкновенную дробь. Т.е. 1 целая 1/2 вводить нужно будет как 3/2.

При вводе десятичных дробей использовать точку. Запятая зарезервирована под разделитель.

В качестве разделителя можно использовать любой символ кроме цифр(0-9), слэша(/), точки(.), знака минус(-). Остальные символы и перенос строки будут программой заменены на разделители.

Определение среднего геометрического

Среднее геометрическое чисел это корень из произведения этих чисел, показатель степени которого равен количеству этих чисел.

Формула среднего геометрического

(Large a_{ср.геом.} = sqrt[n]{a_1 times a_2 times a_3 times … times a_n})

Пример нахождения среднего геометрического

Дан ряд чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 необходимо найти среднее геометрическое этих чисел.

(large a_{ср.геом.} = sqrt[10]{1 times 2 times 3 times 4 times 5 times 6 times 7 times 8 times 9 times 10} =)(large sqrt[10]{3628800} = 4.5287286881168)

Пример нахождения среднего геометрического дробей

Даны дроби 1/2, 1/3, 1/4 необходимо найти среднее геометрическое этих чисел.

(large a_{ср.геом.} = sqrt[3]{1/2 times 1/3 times 1/4} =)(large sqrt[3]{1/24} = 0.34668064642013)

Пример нахождения среднего геометрического десятичных дробей

Даны десятичные дроби 0.2, 0.3, 0.4 необходимо найти среднее геометрическое этих дробей.

(large a_{ср.геом.} = sqrt[3]{0.2 times 0.3 times 0.4} =)(large sqrt[3]{3/125} = 0.28844991406148)

Источник


Инструкции:

Используйте этот Калькулятор среднего геометрического, чтобы ввести пример данных ниже, и решатель обеспечит пошаговый расчет среднего геометрического.

Подробнее об этом калькуляторе среднего геометрического

Во-первых, среднее геометрическое — это мера центральной тенденции, но это разновидность менее часто используемой меры центральной тенденции, гораздо менее распространенной, чем среднее геометрическое.

среднее выборочное значение

или

медиана

.

Калькулятор Среднего Геометрического

Как вычислить среднее геометрическое?

Среднее геометрическое, также известное как

среднее геометрическое

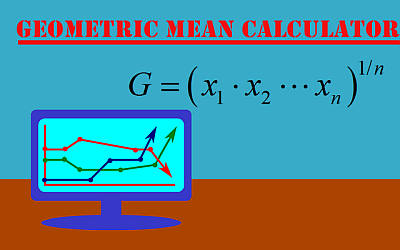
вычислить несколько сложнее, чем вычислить среднее арифметическое. Математически, с точки зрения его расчета и формулы, используемой для его расчета, он рассчитывается с использованием следующей формулы среднего геометрического

[G = left( x_1 cdot x_2 cdot cdot cdot x_n right)^{1/n}]

В целом для выборки ({x_1, x_2, …, x_n}) среднее арифметическое больше среднего геометрического.

Итак, как найти

среднее геометрическое

? Просто вы умножаете n членов в образце и применяете n-й корень к этому произведению. Простой.

Приложения среднего геометрического

Существуют различные типы приложений, в которых среднее геометрическое является подходящей мерой центра, или некоторые другие случаи, когда

гармоническое среднее

является подходящей мерой центра.

Тем не менее, безусловно, в большинстве приложений в качестве меры центра используется среднее арифметическое, хотя и нередко встречаются особые ситуации.

Но все же, несмотря на популярность среднего арифметического, будут ситуации, когда вам потребуется найти среднее геометрическое или другую подходящую меру центральной тенденции, отвечающую конкретным характеристикам данных, с которыми вы работаете.

Вам нужно вычислить среднее значение в любом случае?

Да, вам удобно использовать это

Калькулятор среднего

чтобы получить среднее значение выборки, а также

медиана

и

режим

, вместе с

гармоническое среднее

, чтобы иметь полное представление обо всех доступных мерах центральной тенденции.

Источник
bold{mathrm{Basic}} bold{alphabetagamma} bold{mathrm{ABGamma}} bold{sincos} bold{gedivrightarrow} bold{overline{x}spacemathbb{C}forall} bold{sumspaceintspaceproduct} bold{begin{pmatrix}square&square\square&squareend{pmatrix}} bold{H_{2}O}
square^{2} x^{square} sqrt{square} nthroot[msquare]{square} frac{msquare}{msquare} log_{msquare} pi theta infty int frac{d}{dx}
ge le cdot div x^{circ} (square) |square| (f:circ:g) f(x) ln e^{square}
left(squareright)^{‘} frac{partial}{partial x} int_{msquare}^{msquare} lim sum sin cos tan cot csc sec
alpha beta gamma delta zeta eta theta iota kappa lambda mu
nu xi pi rho sigma tau upsilon phi chi psi omega
A B Gamma Delta E Z H Theta K Lambda M
N Xi Pi P Sigma T Upsilon Phi X Psi Omega
sin cos tan cot sec csc sinh cosh tanh coth sech
arcsin arccos arctan arccot arcsec arccsc arcsinh arccosh arctanh arccoth arcsech
begin{cases}square\squareend{cases} begin{cases}square\square\squareend{cases} = ne div cdot times < > le ge
(square) [square] ▭:longdivision{▭} times twostack{▭}{▭} + twostack{▭}{▭} – twostack{▭}{▭} square! x^{circ} rightarrow lfloorsquarerfloor lceilsquarerceil
overline{square} vec{square} in forall notin exist mathbb{R} mathbb{C} mathbb{N} mathbb{Z} emptyset
vee wedge neg oplus cap cup square^{c} subset subsete superset supersete
int intint intintint int_{square}^{square} int_{square}^{square}int_{square}^{square} int_{square}^{square}int_{square}^{square}int_{square}^{square} sum prod
lim lim _{xto infty } lim _{xto 0+} lim _{xto 0-} frac{d}{dx} frac{d^2}{dx^2} left(squareright)^{‘} left(squareright)^{”} frac{partial}{partial x}
(2times2) (2times3) (3times3) (3times2) (4times2) (4times3) (4times4) (3times4) (2times4) (5times5)
(1times2) (1times3) (1times4) (1times5) (1times6) (2times1) (3times1) (4times1) (5times1) (6times1) (7times1)
mathrm{Радианы} mathrm{Степени} square! ( ) % mathrm{очистить}
arcsin sin sqrt{square} 7 8 9 div
arccos cos ln 4 5 6 times
arctan tan log 1 2 3 –
pi e x^{square} 0 . bold{=} +

Подпишитесь, чтобы подтвердить свой ответ

Подписаться

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

  • среднее:геометрическое:1,:2,:3,:4,:5,:6

  • среднее:геометрическое:left{0.42,:0.52,:0.58,:0.62right}

  • среднее:геометрическое:4,:5,:6,:9,:1

  • среднее:геометрическое:left{9,:9,:5,:6,:7,:8,:8,:7,:7,:6,:6,:8,:8right}

  • среднее:геометрическое:frac{31}{100},:frac{23}{105},:frac{31}{205},:frac{54}{205}

  • среднее:геометрическое::left{1,:7,:12,:4,:9right}

  • Показать больше

Описание

Шаг за шагом найти среднее геометрическое набора данных

geometric-mean-calculator

ru

Блог-сообщения, имеющие отношение к Symbolab

  • Lies, Damned Lies, and Statistics

    Statistics is about analyzing data, for instance the mean is commonly used to measure the “central tendency” of…

    Read More

    • Введите Задачу

    Сохранить в блокнот!

    Войти

    Источник

    Добавить комментарий