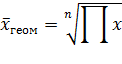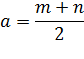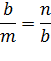Как найти среднее геометрическое значение элементов - Сайт, где вы сможете решить свои вопросы

Средним геометрическим нескольких положительных вещественных чисел называется такое число, которым можно заменить каждое из этих чисел так, чтобы их произведение не изменилось. Более формально:

$G(x_{1},x_{2},ldots ,x_{n})={sqrt[ {n}]{x_{1}x_{2}cdots x_{n}}}=left(prod _{{i=1}}^{n}x_{i}right)^{{1/n}}$

Среднее геометрическое двух чисел также называется их средним пропорциональным^[1], поскольку среднее геометрическое двух чисел $a_{1}$ и $a_{2}$ обладает следующим свойством: ${displaystyle {frac {a_{1}}{g}}={frac {g}{a_{2}}}}$ , то есть среднее геометрическое относится к первому числу так же, как второе число к среднему геометрическому.

Свойства[править | править код]

Так же, как и любое другое среднее значение, среднее геометрическое лежит между минимумом и максимумом из всех чисел:

${displaystyle operatorname {min} (x_{1},x_{2},ldots ,x_{n})leqslant G(x_{1},x_{2},ldots ,x_{n})leqslant operatorname {max} (x_{1},x_{2},ldots ,x_{n}).}$

Среднее геометрическое двух чисел $a=A_{0},b=G_{0}$ является средним арифметическим-гармоническим этих чисел, то есть равно пределу двух последовательностей:

${displaystyle A_{i}={frac {A_{i-1}+G_{i-1}}{2}},quad G_{i}={sqrt {A_{i-1}G_{i-1}}}.}$

Среднее геометрическое двух чисел равно среднему геометрическому их среднего арифметического и среднего гармонического^[2].

Среднее геометрическое взвешенное[править | править код]

Среднее геометрическое взвешенное набора вещественных чисел $x_{1},ldots ,x_{n}$ с вещественными весами $w_{1},ldots ,w_{n}$ определяется как

${displaystyle {bar {x}}=left(prod _{i=1}^{n}x_{i}^{w_{i}}right)^{1/sum _{i=1}^{n}w_{i}}=quad exp left({frac {1}{sum _{i=1}^{n}w_{i}}};sum _{i=1}^{n}w_{i}ln x_{i}right).}$

В том случае, если все веса равны между собой, среднее геометрическое взвешенное равно среднему геометрическому.

В геометрии[править | править код]

Среднее геометрическое отрезков:

Высота прямоугольного треугольника, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу, а каждый катет есть среднее пропорциональное между гипотенузой и его проекцией на гипотенузу.

Это даёт геометрический способ построения среднего геометрического двух (длин) отрезков: нужно построить окружность на сумме этих двух отрезков как на диаметре, и тогда высота, восстановленная из точки их соединения до пересечения с окружностью, даст искомую величину.

Расстояние до горизонта сферы есть среднее геометрическое между расстоянием до самой ближней точки сферы и расстоянием до самой дальней точки сферы.

Обобщения[править | править код]

Примечания[править | править код]

↑ «Среднее пропорциональное». — статья из Большой советской энциклопедии.
↑ Роу С. Геометрические упражнения с куском бумаги. — 2-е изд. — Одесса: Матезис, 1923. Архивная копия от 13 августа 2020 на Wayback Machine

См. также[править | править код]

Геометрическая пропорция
Геометрическая прогрессия
Неравенство Швейцера

Источник

В данной публикации мы рассмотрим, с помощью какой формулы можно найти среднее геометрическое чисел, а также разберем примеры задач для ее демонстрации на практике.

Расчет среднего геометрического
Пример задачи

Расчет среднего геометрического

Чтобы вычислить среднее геометрическое двух или более чисел, требуется их перемножить, а затем из полученного результата извлечь корень, степень которого равняется их количеству.

Допустим, у нас есть числа a₁, a₂, … , a_n. Среднее геометрическое находится по формуле:

Частные случаи формулы:

Пример задачи

Задание 1
Найдем среднее геометрическое чисел 3, 6 и 12.

Решение:
Воспользуемся соответствующей формулой для трех чисел:

Задание 2
Среднее геометрическое четырех чисел равняется 4, а также известны три из них – 2, 2 и 4. Найдем четвертое.

Решение:
Обозначим число, которое требуется найти буквой x. Формула выглядит следующим образом:

Помещаем число 4 под знак корня, сохранив равенство (для этого возводим его в четвертую степень, т.е. 4⁴ = 256):

Следовательно, x = 256 : 16 = 16.

Источник

Средние величины в статистике дают обобщающую характеристику анализируемого явления. Самая распространенная из них – среднее арифметическое. Она применяется, когда агрегатный показатель образуется с помощью суммы элементов. Например, масса нескольких яблок, суммарная выручка за каждый день продаж и т.д. Но так бывает не всегда. Иногда агрегатный показатель образуется не в результате суммирования, а в результате умножения.

Такой пример. Месячная инфляция – это изменение уровня цен одного месяца по сравнению с предыдущим. Если известны показатели инфляции за каждый месяц, то как получить годовое значение? С точки зрения статистики – это цепной индекс, поэтому правильный ответ: с помощью перемножения месячных показателей инфляции. То есть общий показатель инфляции – это не сумма, а произведение. А как теперь узнать среднюю инфляцию за месяц, если имеется годовое значение? Нет, не разделить на 12, а извлечь корень 12-й степени (степень зависит от количества множителей). В общем случае среднее геометрическое рассчитывается по формуле:

То есть корень из произведения исходных данных, где степень определяется количеством множителей. Например, среднее геометрическое двух чисел – это квадратный корень из их произведения

Среднее геометрическое трех чисел – кубический корень из произведения

и т.д.

Если каждое исходное число заменить на их среднее геометрическое, то произведение даст тот же результат.

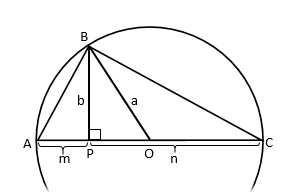
Чтобы лучше разобраться, чем отличаются среднее арифметическое и среднее геометрическое, рассмотрим следующий рисунок. Имеется прямоугольный треугольник, вписанный в круг.

Из прямого угла опущена медиана a (на середину гипотенузы). Также из прямого угла опущена высота b, которая в точке P делит гипотенузу на две части m и n. Т.к. гипотенуза – это диаметр описанного круга, а медиана – радиус, то очевидно, что длина медианы a – это среднее арифметическое из m и n.

Рассчитаем, чему равна высота b. В силу подобия треугольников АВP и BCP справедливо равенство

Откуда

Значит, высота прямоугольного треугольника – это среднее геометрическое из отрезков, на которые она разбивает гипотенузу. Такое наглядное отличие.

В MS Excel среднюю геометрическую можно найти с помощью функции СРГЕОМ.

Все очень просто: вызвали функцию, указали диапазон и готово.

На практике этот показатель используют не так часто, как среднее арифметическое, но все же встречается. Например, есть такой индекс развития человеческого потенциала, с помощью которого сравнивают уровень жизни в разных странах. Он рассчитывается, как среднее геометрическое из нескольких индексов.

Ниже видео, как найти среднее геометрическое чисел в Excel.

Поделиться в социальных сетях:

Источник

Download Article

The geometric mean is another way to find the average value of a number set, but instead of adding the values and dividing like you would to find the arithmetic mean, you multiply them together before taking the root. The geometric mean can be used to calculate average rates of return in finances or show how much something has grown over a specific period of time. In order to find the geometric mean, multiply all of the values together before taking the nth root, where n equals the total number of values in the set. You can also use the logarithmic functions on your calculator to solve the geometric mean if you want.

Geometric Mean Help

1
Multiply the values you want to find the geometric mean for. You can either use a calculator or do the math by hand when you find the product. Multiply all of the numbers in the set you’re calculating so you can find the product. Write down the product so you don’t forget it.^[1]
- For example, if the value set is 3, 5, and 12, then you would write: (3 x 5 x 12) = 180.
- For another example, if you want to find the geometric mean for the set 2 and 18, then write: (2 x 18) = 36.
2
Find the nth root of the product where n is the number of values. Count how many values are in the set you’re calculating the geometric mean for the value n. Use the n value to determine which root you need to take of the product. For example, take the square root if you have 2 values, cube root if you have 3 values, and so on. Use your calculator to solve the equation and write down your answer.^[2]
- For example, for the set of 3, 5, and 12, write: ∛(180) ≈ 5.65.
- In the second example with a set of 2 and 18, write: √(36) = 6.
Variation: You can also write the value as an exponent 1/n if it’s easier to type in your calculator. For example, for the set 3, 5, and 12, you can write (180)^1/3 instead of ∛(180).

Advertisement
3
Convert percentages to their decimal multiplier equivalents. If the number set is written out as increases or decreases in percentages, avoid using the percent value in the geometric mean since it will skew your results. If the percent is an increase, move the decimal point 2 spaces to the left and add 1 to it. If there’s a percent decrease, then move the decimal point 2 places to the left and subtract it from 1.^[3]
- For example, say you want to find the geometric mean of the value of an object that increases by 10%, and then falls by 3%.
- Convert 10% to a decimal and add 1 to it to get 1.10.
- Then convert 3% to a decimal and subtract it from 1 to get 0.97.
- Use the 2 decimal values to find the geometric mean: √(1.10 x 0.97) ≈ 1.03.
- Convert the number back to a percent by moving the decimal point 2 places to the right and subtracting 1 from it to find a total of a 3% increase in value.

1
Add the logarithmic values for each number in the set. The LOG function takes a value out of base-10 and determines how many times you need to multiply 10 together to equal that value. Locate the LOG function on your calculator, which usually is on the left side of the keypad. Click the LOG button and enter the first value in the set. Type in a “+” before putting in LOG for your second value. Continue separating the LOG functions for each value with a plus sign before finding the sum.^[4]
- For example, with a set of 7, 9, and 12, you would type in log(7) + log(9) + log(12) before hitting “=” on your calculator. When you solve the functions, your sum will be about 2.878521796.
- You may also calculate each of the logarithms separately before adding the answers together.
2
Divide the sum of the logarithmic values by the number of values in the set. Count the number of values in your set and then divide the sum you just found by that number. The answer you get will be the logarithmic value of the geometric mean.^[5]
- In this example, there’s a set of 3 numbers, so type in: 2.878521796 / 3 ≈ 0.959507265.
3
Take the antilog of the quotient to determine the geometric mean. The antilog function is the inverse of the LOG function on your calculator and it converts the value back to base-10. Look for the symbol “10^x” on your calculator, which is usually a secondary function of the LOG button. Press the “2nd” button in the top left corner of the calculator followed by the LOG button to activate the antilog. Type in the quotient you found in the last step before solving the equation.^[6]
- For this example, your calculator will read: 10^{(0.959507265)} ≈ 9.11.

Add New Question

Question

How do I identify average numbers geometric mean, arithmetic mean and harmonic mean?

See wikiHow’s articles on each of those subjects.
Question

What is the geometric mean of 2, 4, 16, and 32?

To make this trivially easy, use logarithms Base 2. Then the logarithms are 1, 2, 4, and 5. The simple average of those logarithms is 3, so the geometric mean of 2, 4, 16, and 32 is 2^3 = 8.
Question

How do I find the geometric mean of 3 and 7?

3 x 7 = 21. √21 = 4.58.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

You cannot find the geometric mean of negative numbers.^[7]
Any set that has 0 in it will have a geometric mean of 0.

Thanks for submitting a tip for review!

Things You’ll Need

Calculator

References

About This Article

Article SummaryX

To calculate the geometric mean of 2 numbers, multiply those 2 numbers together, then calculate the square root of the resulting product. If you have 3 or more numbers, multiply all of the numbers together, then raise them to the power of 1 divided by n, where n is the total number of entries in the data set. To learn how to calculate the geometric mean of a data set using logarithms, read on!

Did this summary help you?

Thanks to all authors for creating a page that has been read 858,076 times.

Did this article help you?

Источник

Загрузить PDF

Среднее геометрическое — математическая величина, которую легко спутать с более часто применяемым средним арифметическим. Для вычисления среднего геометрического следуйте методам, приведенным ниже.

1
Возьмите два числа, среднее геометрическое которых необходимо найти.
- Например, 2 и 32.
2
3

Реклама

1

Подставьте числа в приведенное уравнение. Если это, скажем, 10 и 15, то подставьте их так, как показано на рисунке.
2

Найдите «х». Начните с перемножения крест-накрест, что означает перемножение пар чисел по диагонали и расстановку результатов умножения по разные стороны знака =. Так как х*х = х², то уравнение приводится к виду к виду: х² = (результат умножения ваших чисел). Для вычисления «х» извлеките квадратный корень из результата перемножения используемых чисел. Если в результате вычисления корня получится целое число — отлично. Если нет, дайте ответ в виде десятичной дроби или запишите его со знаком корня (в зависимости от того, что требует преподаватель). Ответ, приведенный выше на рисунке, записан в виде упрощенного квадратного корня.

Реклама

1
Подставьте числа в приведенное уравнение.Среднее геометрическое = (a₁ × a₂ . . . a_n)^1/n^[3]
- a₁ — первое число, a₂ — второе число и так далее
- n — общее количество чисел
2

Перемножьте числа (a₁, a₂ и так далее).
3

Извлеките корень n степени из полученного числа. Это и будет среднее геометрическое.^[4]

Реклама

1
Найдите логарифм каждого числа и сложите полученные значения. Найдите клавишу LOG на своем калькуляторе. Затем введите: (первое число) LOG + (второе число) LOG + (третье число) LOG [+ столько чисел, сколько дано] =. Не забудьте нажать «=», или показанный вам результат будет логарифмом последнего введенного числа, а не суммой логарифмов всех чисел.
- Например, log 7 + log 9 + log 12 = 2,878521796
2
Разделите результат сложения на общее количество изначально данных чисел. Если вы сложили логарифмы трех чисел, делите полученный результат на три.
- Например, 2,878521796 / 3 = 0,959507265
3
Вычислите антилогарифм полученного результата. На калькуляторе нажмите кнопку переключения регистра (активирует функции верхнего регистра — над клавишами), а затем нажмите LOG, чтобы получить значение антилогарифма. Этот результат и будет средним геометрическим.^[5]
- Например, antilog 0,959507265 = 9,109766916. Поэтому среднее геометрическое 7, 9, и 12 равно 9,11.
Реклама

Советы

Различия между средним арифметическим и средним геометрическим:
- Для вычисления среднего арифметического, например, чисел 3, 4 и 18, необходимо их сложить 3 + 4 + 18, а затем разделить на 3 (потому что изначально даны три числа). Ответ равен 25/3 или примерно 8,333; это означает, что если сложить 8,3333 три раза подряд, то ответ будет таким же, как при сложении чисел 3, 4, и 18. Среднее арифметическое отвечает на вопрос: «Если все величины имеют одинаковое значение, то каким это значение должно быть, чтобы при суммировании получился один результат?»
- Напротив, среднее геометрическое отвечает на вопрос: «Если все величины имеют одинаковое значение, то каким это значение должно быть, чтобы при перемножении получился один результат?» Поэтому, чтобы найти среднее геометрическое чисел 3, 4 и 18, мы перемножаем эти числа: 3 x 4 x 18. Получаем 216. Затем мы берем кубический корень из полученного результата перемножения (кубический корень, так как в вычислении участвуют три числа). Ответ будет 6. Другими словами, так как 6 x 6 x 6 = 3 x 4 x 18, то 6 является средним геометрическим чисел 3, 4 и 18.
Среднее геометрическое всегда меньше или равно среднему арифметическому. Более подробно читайте тут.
Среднее геометрическое рассчитывается только для положительных чисел. Схема решения различных прикладных задач с использованием среднего геометрического не будет работать в случае наличия отрицательных чисел.

Об этой статье

Эту страницу просматривали 131 683 раза.

Была ли эта статья полезной?

Источник

Свойства[править | править код]

Среднее геометрическое взвешенное[править | править код]

В геометрии[править | править код]

Обобщения[править | править код]

Примечания[править | править код]

См. также[править | править код]

Расчет среднего геометрического

Пример задачи

Geometric Mean Help

Things You’ll Need

References

About This Article

Did this article help you?

Советы

Об этой статье

Была ли эта статья полезной?

Вам также может понравиться

Как найти кнопку далее в игре доп

Как найти страховой полис по номеру авто

Как исправить кривой кий

Добавить комментарий Отменить ответ